Analyse numérique du changement de phase solide-liquide autour d'un tube horizontal soumis à une sollicitation thermique périodique

Analyse numérique du changement de phase

solide-liquide autour d’un tube horizontal soumis à une

sollicitation thermique périodique

Mémoire

Christian Chabot

Maîtrise en génie mécanique

Maître ès sciences (M. Sc.)

Québec, Canada

© Christian Chabot, 2016

Analyse numérique du changement de phase

solide-liquide autour d’un tube horizontal soumis à une

sollicitation thermique périodique

Mémoire

Christian Chabot

Sous la direction de :

iii

Résumé

Ce mémoire présente un modèle mathématique et numérique pour analyser le comportement d’une unité de stockage thermique à changement de phase solide-liquide représentée par un tube autour duquel se trouve le matériau à changement de phase. Le système est soumis à une charge oscillant entre le chauffage et le refroidissement. Une analyse d’ordre de grandeur permet de prédire le comportement du système en fonction des principaux nombres adimensionnels. Un paramètre adimensionnel est proposé pour délimiter les concepts dans lesquels la conduction domine par rapport à ceux où la convection naturelle domine. L’étude dévoile l’impact des paramètres de conception de l’unité de stockage thermique sur son fonctionnement et approfondit les connaissances dans le domaine du changement de phase avec convection naturelle. Différents indicateurs ont été développés pour analyser la performance du système, tels que les dimensions de la zone affectée thermiquement, le volume fondu ou solidifié et une analyse fréquentielle. Des corrélations sont proposées pour déterminer facilement le comportement du système.

iv

Abstract

This master thesis presents a mathematical and numerical model to analyze the behavior of a latent solid-liquid heat storage unit represented by a tube surrounded by phase change material. The system is undergoing an oscillating load of heating and cooling. A scale analysis predicts the behavior of the system with regard to the main governing dimensionless numbers. A normalized parameter is proposed to delineate designs in which conduction dominates compared to those in which natural convection dominates. The study reveals the impact of major thermal storage unit design parameters on its operation and deepens our knowledge in the field of phase change with natural convection. Various indicators, such as the size of the thermally affected zone around the tube, the molten or solidified volume and a frequency analysis, have been developed to analyze the system performance. Correlations are proposed to easily determine the system behavior.

v

Table des matières

Résumé ... iii

Abstract ... iv

Table des matières ... v

Liste des tableaux ... vii

Liste des figures ... viii

Nomenclature... ix Remerciements ... xi Avant-propos ... xii Chapitre 1 : Introduction ... 1 1.1 Problématique ... 1 1.2 Objectifs ... 4 1.2.1 Objectif principal ... 4 1.2.2 Objectifs secondaires ... 4

1.3 Méthode et présentation du document ... 4

1.3.1 Chapitre 2 – Présentation du modèle mathématique, du modèle numérique et adimensionnalisation ... 5

1.3.2 Chapitre 3 – Analyse numérique du changement de phase solide-liquide autour d’un tube avec condition frontière transitoire ... 5

Chapitre 2 : Présentation du modèle mathématique, du modèle numérique et adimensionnalisation ... 7

2.1 Présentation du modèle mathématique ... 7

2.2 Analyse dimensionnelle et équations sans dimension ... 14

2.3 Résolution numérique par volumes finis ... 18

Chapitre 3 : Solid-liquid phase change around a tube with periodic heating and cooling: scale analysis, numerical simulations and correlations (article)... 25

Résumé ... 26

Abstract ... 26

3.1 Introduction ... 27

3.2 Mathematical Modeling ... 29

3.3 Numerical modeling and validation ... 33

3.4 Scale analysis ... 35

vi

3.4.2 Convection dominated scenarios – heating ... 36

3.4.3 Cooling ... 38

3.4.4 Verification of the scale analysis ... 38

3.5 Results for reference case ... 41

3.5.1 Temperature and velocity profiles... 41

3.5.2 Frequency analysis ... 43

3.5.3 Spatial extension of the solid/liquid around the tube ... 45

3.6 Effect of Rayleigh number ... 45

3.7 Effect of Stefan number ... 48

3.8 Effect of cycling period ... 50

3.9 Effect of far-field temperature ... 51

3.10 Fittings from a design perspective ... 52

3.11 Conclusions ... 54

Chapitre 4 : Conclusion ... 55

Bibliographie ... 59

Annexe 1 : Configurations de FLUENT ... 62

Annexe 2 : Exemple de fonction personnalisée pour le flux de chaleur ... 64

Annexe 3 : Résultats de l’analyse par FFT sur la température de surface du tube pour le cas de référence et ses variations ... 65

vii

Liste des tableaux

Table 2.1 Propriétés physiques de la paraffine et du système ... 13 Table 2.2 Synthèse des équations sans dimension ... 17 Table 2.3 Gamme de paramètres étudiés sans dimension ... 22 Table 2.4 Propriétés physiques variables pour obtenir respectivement les paramètres

sans dimension du tableau 2.3 ... 23 Table 2.5 Propriétés physiques fixes du matériau et du système ... 23 Table 3.1 Values of dimensionless parameters investigated in the present study ... 33

viii

Liste des figures

Figure 1.1 Charge journalière d’un système de climatisation jumelé à une unité de

stockage thermique [7] ... 2

Figure 1.2 Exemple d’échangeur de chaleur de type tube-calandre [9] ... 3

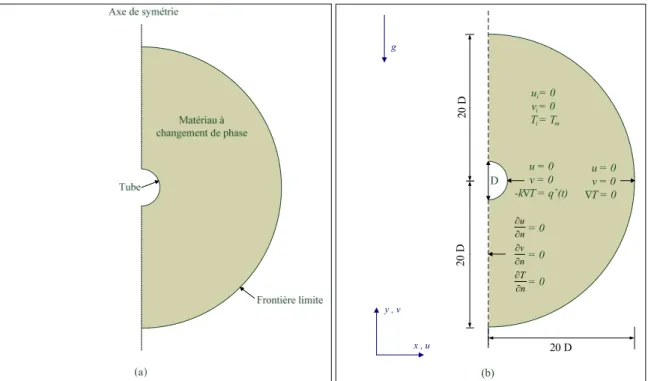
Figure 2.1 Modèle 3D (a) et 2D (b) représentant un tube transportant un fluide caloriporteur dans un matériau à changement de phase ... 8

Figure 2.2 Représentation du domaine étudié (a) et dimensionnement du domaine (b) avec les conditions initiales et conditions aux frontières ... 14

Figure 2.3 Prise d’écran de la géométrie et du maillage dans GAMBIT ... 20

Figure 2.4 Prise d’écran du maillage raffiné par FLUENT ... 20

Figure 3.1 Tube surrounded by an infinite PCM domain ... 30

Figure 3.2 Comparison of the instantaneous heat transfer rate and thermal energy stored as a function of time between experimental and numerical results from Ref. [16], and the results achieved with our model ... 35

Figure 3.3 Representation of the molten area affected around a tube of diameter D and the triggering of natural convection ... 36

Figure 3.4 Ratio between the minimal and maximal tube surface temperatures as a function of _{Pr τRa Ste}



_ 1 5



_{... 40}

Figure 3.5 (a) Maximal thickness of solid around the tube, and (b) minimal tube surface temperature during cooling for different combinations of cycle periods, Stefan numbers and Prandtl numbers ... 40

Figure 3.6 Relationship between maximal temperature reached at the tube surface and Ra ... 40

Figure 3.7 Liquid fraction and stream function around the tube at different times: (a) beginning of heating, (b) heating peak, (c) beginning of cooling, and (d) cooling peak, for the reference case ... 42

Figure 3.8 Average temperature at the surface of the pipe as a function of time for: (a) the reference case, and (b) Fourier transform of that function ... 42

Figure 3.9 Definition of the maximal extension of the liquid and solid zones during the cycle (S , _u S , _s S are shown) ... 44 _d Figure 3.10 Effect of Rayleigh number on: (a) The extent of the phase change domain, and (b) The maximum solid and liquid areas during the heating/cooling cycle 46 Figure 3.11 Effect of Stefan number on: (a) The extent of the phase change domain, and (b) The maximum solid and liquid areas during the heating/cooling cycle 49 Figure 3.12 Effect of the period on: (a) The extent of the phase change domain, and (b) The maximum solid and liquid areas during the heating/cooling cycle ... 51

ix

Nomenclature

Lettres latines

a amplitude de transformée de Fourier

A constante de zone pâteuse, matrice de coefficients b vecteur de terme source

cp chaleur spécifique, J kg-1 K-1 D diamètre du tube, m2 e énergie interne, J kg-1 f fraction liquide F force, N g accélération gravitationnelle, m s-2 k conductivité thermique, W m-1 _K-1 L longueur, m p,P pression, Pa Pr nombre de Prandtl q flux de chaleur, W m-2 r rayon, m Ra nombre de Rayleigh s terme source

S distance du front de changement de phase Ste nombre de Stefan

t temps, s T température, K

u,v composantes de la vitesse en x,y, m s-1

V vitesse, m s-1

x,y,z coordonnées cartésiennes

Lettres grecques

 diffusivité thermique, m2 _s–1

β coefficient d’expansion thermique, K-1

δ épaisseur de couche limite, m ε petit nombre

θ différence de température

λ enthalpie de changement de phase, J kg-1

μ viscosité dynamique, kg s–1 _m–1 ν viscosité cinématique, m2 _s-1 π 3.14159 ρ densité, kg m–3 σ contrainte visqueuse, Pa τ période d’oscillation, s

x

Indices

0,1,2…Harmoniques de transformée de Fourier b poussée d’Archimède (buoyancy) c refroidissement (cooling) d vers le bas (downward)

h chauffage (heating) ∞ valeur de référence i initial

l liquidus

m changement de phase (melting) mush zone pâteuse (mushy zone) ref valeur de référence

s solidus, vers le côté (sideward) S surface

T thermique u vers le haut (upward) ~ sans dimension

Acronymes

CVAC Climatisation, Ventilation et Air Climatisé

PCM matériau à changement de phase (phase change material)

SHTES stockage de chaleur sensible (sensible heat thermal energy storage) LHTES stockage de chaleur latente (latent heat thermal energy storage) CFD mécanique des fluides numérique (computational fluid dynamics) FFT Transformée de Fourier rapide (Fast Fourier Transform)

xi

Remerciements

La rédaction de ce mémoire a d’abord été rendu possible grâce au soutien financier de plusieurs organismes publics et privés. J’aimerais remercier le Conseil de recherches en sciences naturelles et en génie (CRSNG), le Fonds québécois de recherche sur la nature et les technologies (FQRNT) et l’entreprise MDA qui m’ont octroyé des bourses pour la poursuite de mes études à la maîtrise.

J’aimerais ensuite remercier les gens sans qui l’accomplissement de ce projet n’aurait pas été possible. Je tiens tout d’abord à remercier Louis Gosselin de m’avoir accepté dans son équipe et de m’avoir supporté depuis mon stage au premier cycle jusqu’à la fin de ma maîtrise. De par ses connaissances et de son expérience scientifique, il a su me guider à chaque fois qu’un obstacle se présentait. C’est un chercheur et un professeur exceptionnel et son support a été indispensable à la réussite de mes études supérieures. Parmi cette équipe figure entre autre Jonathan Dallaire, François Mathieu-Potvin, Maxime Tye-Gingras, Félix Robert, Mai-Thi Do et Jean-Michel Dussault. Leurs conseils m’ont grandement aidé à compléter ce travail. J’aimerais aussi remercier Hugo Marcoux et Olivier Lachance qui ont tous deux fait le baccalauréat en génie physique avec moi et qui ont poursuivi à la maîtrise. Leur support et conseils ont été indispensables. Je considère que c’est un privilège d’avoir travaillé avec vous tous.

Finalement j’aimerais remercier ma famille sans qui je n’aurais pas pu me rendre où je suis. Je remercie mes frères Alexandre et Vincent pour leur encouragement. Un énorme merci à mes parents Michelin Chabot et Lucie Deschênes pour leur soutien financier inconditionnel, pour m’avoir fourni logis tout au long de mes études. Ils ont cru en moi et m’ont toujours supporté.

xii

Avant-propos

L’article formant le corps de ce mémoire a été coécrit par l’auteur du mémoire, Christian Chabot, et son directeur de recherche, Louis Gosselin. La programmation, les simulations numériques, le traitement des résultats, les recherches, l’écriture de ce mémoire et l’essentiel de l’article ont été effectués par Christian Chabot. La collaboration de Louis Gosselin a été indispensable quant à la supervision des travaux de recherche, à l’analyse des résultats, à l’aide à la rédaction et à la correction de l’article. L’article est présentement soumis pour publication. Par rapport à la version originale, des modifications de formes ont été apportées à l’article afin d’en faciliter la lecture et pour être conforme aux exigences de la Faculté des études supérieures et postdoctorales. La pagination, les numéros de tableaux et de figures, l’inclusion des figures dans le texte et la numérotation des références bibliographiques ont été adaptées suivant le corps du mémoire.

1

Chapitre 1 : Introduction

1.1 Problématique

L’utilisation des énergies renouvelables ne cesse de croitre, elle a atteint une contribution de 19% de la consommation énergétique totale mondiale en 2012 [1]. On définit comme énergie renouvelable toutes les énergies provenant de sources qui se régénèrent sur une échelle de vie humaine. Parmi les énergies renouvelables, on inclut la biomasse (ex. : bois, éthanol), l’hydroélectricité, la géothermie, le solaire et l’éolien [2]. En général, ces sources d’énergies ont l’avantage d’être inépuisables, d’avoir un impact minimum sur l’environnement et d’avoir une bonne rentabilité à long terme, mais ont comme désavantages d’avoir une petite densité d’énergie, d’être souvent éloignées du lieu de consommation, de nécessiter un plus grand capital initial et d’être intermittentes [3]. Il faut donc de grands espaces, souvent loin des villes plutôt qu’à l’endroit où nous en avons besoin, pour obtenir une quantité raisonnable d’énergie. Il faut aussi capter l’énergie quand elle est disponible plutôt que lorsque nous en avons besoin. Il s’agit d’une lacune inhérente aux énergies renouvelables qui limite leur expansion dans le marché [4].

Le stockage d’énergie remédie en partie à ces problèmes inhérents. Parmi les manières de stocker l’énergie, il y a l’eau derrière les barrages, les piles électriques, le stockage d’air comprimé, les volants d’inertie et le stockage thermique [5], ce dernier étant le sujet de ce mémoire. Un des intérêts du stockage thermique est d’emmagasiner l’énergie quand elle est disponible pour la relâcher quand elle est demandée. Les chauffe-eau solaires sont basés sur ce principe et connaissent une très grande expansion dans le monde [6]. On estime que ces systèmes fournissent la majorité de l’eau chaude pour 70 millions de ménage dans le monde [6]. Le stockage thermique permet aussi de sous-dimensionner un système CVAC (Climatisation, Ventilation et Air Climatisé) en aplanissant les pics de consommation et en utilisant les appareils plus souvent dans leur plage d’opération nominale [7]. Là où l’électricité a un prix différent selon l’heure de la journée, les unités de stockage thermique permettent aussi de consommer l’énergie quand elle est moins chère (la nuit) pour la stocker et la décharger lorsqu’elle est plus chère (heure de pointe). La figure 1.1 montre un exemple fictif de charge de climatisation journalière pour un système CVAC. En gris, le système

2

stocke du froid lorsque la demande est nulle, la nuit par exemple. En bleu pâle, le système CVAC fournit une puissance nominale de climatisation en se servant de froid stocké durant la nuit pour compenser la charge réelle demandée en bleu foncé. Cette figure met en évidence le fait qu’il est possible de sous-dimensionner les équipements de chauffage et de climatisation lorsqu’ils sont couplés avec du stockage thermique. Étant donné que les appareils fonctionnant à leur puissance nominale sont plus efficaces, l’inclusion d’unité de stockage thermique a pour effet d’augmenter l’efficacité énergétique des systèmes. Malgré un coût initial potentiellement plus élevé, elle permet de réaliser des économies d’argent à long terme.

Figure 1.1 - Charge journalière d’un système de climatisation jumelé à une unité de stockage thermique [7].

Il y a deux catégories de stockage thermique, soit le stockage de chaleur sensible et le stockage de chaleur latente. La chaleur sensible est échangée sans qu’il n’y ait de changement de phase, elle s’accompagne d’un changement de température (ex. chauffe-eau). Le stockage de chaleur sensible est peu coûteux mais requiert un grand volume. La chaleur latente est échangée sous forme de changement de phase, alors que la température reste presque constante (ex. glace). Les matériaux à changement de phase tels les sels fondus et les paraffines sont typiquement plus coûteux que l’eau [8]. Les matériaux à changement de phase ont cependant l’avantage de conserver une température constante lors du changement de phase et de stocker beaucoup d’énergie dans un petit volume. Ils occupent donc des niches particulières d’application où l’espace est restreint comme au centre-ville et où la température

3

d’un procédé doit rester constante comme dans une industrie. Un exemple d’échangeur de chaleur de type tube-calandre est présenté à la figure 1.2.

Figure 1.2 - Exemple d’échangeur de chaleur de type tube-calandre [9].

Parmi les matériaux à changement de phase, les paraffines ont l’avantage d’avoir une excellente stabilité thermique aux cycles de fonte et solidification et ne se dégradent pas au contact de métal [10]. Elles sont donc des candidates idéales pour les applications en bâtiments. Cette étude sera donc basée sur les unités de stockage thermique à changement de phase de type tube-calandre utilisant la paraffine dans une optique d’application pour les bâtiments.

Plusieurs études ont déjà été faites au sujet des unités de stockage thermique à chaleur latente [11-15]. Nous avons jugé qu’il y avait des lacunes dans la littérature quant à la compréhension du phénomène de fonte et solidification successive en régime périodique dans un milieu où la convection naturelle est prise en compte. L’étude présentée ici se consacre donc à approfondir les connaissances dans le domaine du changement de phase transitoire avec convection naturelle. C’est la physique qui décrit le mieux le comportement des unités de stockage thermique à chaleur latente. En comprenant mieux les phénomènes qui se produisent à l’intérieur de ces unités, il sera possible d’optimiser le choix des variables de conceptions et les conditions d’opérations pour avoir une performance optimale.

4 1.2 Objectifs

1.2.1 Objectif principal

La présente étude a pour but d’approfondir notre compréhension de l’alternance entre la fonte et la solidification d’un matériau à changement de phase dans une unité de stockage thermique de type tube-calandre où la convection naturelle est prise en compte. La compréhension du phénomène physique permet de mieux concevoir les unités de stockage thermique pour augmenter l’efficacité énergétique et ainsi diminuer le temps de retour sur l’investissement des systèmes dans lesquels elles sont intégrées.

1.2.2 Objectifs secondaires

i. Proposer des modèles mathématique et numérique représentant le comportement périodique du changement de phase dans un fluide en prenant compte de la convection naturelle. Des modèles mathématique et numérique juste permettent de simuler et de prédire avec précision des phénomènes qui seraient difficiles à analyser de manière empirique.

ii. Analyser l’impact des principales variables de conception et de fonctionnement sur la performance d’une unité de stockage thermique à chaleur latente lors d’une utilisation reflétant le plus possible la réalité. Ceci permet de savoir au préalable sous quelles conditions d’opération une unité de stockage thermique est performante.

1.3 Méthode et présentation du document

L’analyse du phénomène de changement de phase avec convection naturelle nécessite l’utilisation d’un modèle mathématique. Ce modèle mathématique doit être capable de modéliser le transfert de chaleur, le changement de phase, la convection naturelle et le mouvement de fluide de manière transitoire, c’est-à-dire en respectant l’évolution dans le temps. Ce modèle est développé en premier lieu, en se basant sur les équations de Navier-Stokes. La résolution des équations qui décrivent le modèle mathématique nécessite l’utilisation d’un modèle numérique de résolution. Ce modèle numérique doit être capable de résoudre les équations avec une assez grande précision et une assez bonne vitesse, car plusieurs simulations numériques différentes doivent être réalisées. Pour réduire le nombre

5

de simulations à effectuer et faire ressortir les paramètres d’importance, il a été nécessaire d’adimensionner les équations du modèle mathématique. En deuxième lieu, l’impact de chaque paramètre d’importance sur le fonctionnement de l’unité de stockage thermique est analysé. Cette analyse a permis de tirer des conclusions quant au spectre de paramètres qui optimise l’utilisation et la performance d’une unité de stockage thermique à changement de phase sous condition de charge-décharge fréquente. Il est à noter que la méthode a été uniquement effectuée dans un cadre de simulation numérique; aucun test expérimental n’a été effectué.

Ce mémoire est présenté sous forme d’un chapitre explicatif traitant de l’objectif secondaire 1.2.2.i et d’un chapitre présentant l’article scientifique soumis auprès du journal scientifique « International Journal of Thermal Sciences » traitant de l’objectif secondaire 1.2.2.ii. L’article scientifique est présenté dans sa version intégrale au chapitre 3.

1.3.1 Chapitre 2 – Présentation du modèle mathématique, du modèle numérique et adimensionnalisation

Le chapitre 2 présente d’abord le développement du modèle mathématique à partir des équations de Navier-Stokes en mettant en évidence les hypothèses qui ont été faites pour les simplifier. Une fois que les équations sont obtenues, elles sont adimensionnées pour réduire le nombre de paramètres et faire ressortir les paramètres adimensionnels d’importance. Ensuite, le modèle numérique est présenté. Le mailleur ANSYS GAMBIT et le solveur ANSYS FLUENT sont introduits. La méthode effectuée dans le cadre de ce mémoire est décrite de manière à ce que n’importe qui puisse reproduire les résultats obtenus. Finalement, une brève explication de la méthode de résolution des équations de conservation par volumes finis, utilisée par FLUENT, est présentée.

1.3.2 Chapitre 3 – Analyse numérique du changement de phase solide-liquide autour d’un tube avec condition frontière transitoire

Le chapitre 3 est le cœur de ce mémoire, il présente l’article « Numerical Analysis of Solid-Liquid Phase Change Around a Tube with Transient Boundary Conditions » qui a été soumis au journal « International Journal of Thermal Sciences » le 18 avril 2016. Ce chapitre s’attarde principalement sur la présentation et l’analyse des résultats obtenus par simulation

6

numérique. L’étude met en lumière l’effet individuel des nombres de Rayleigh, de Stefan, de la période du cycle de change/décharge et de la température initiale et l’effet de groupe qu’ils peuvent avoir ensemble sur la manière dont l’énergie est distribuée dans le matériau à changement de phase.

Les sections 3.2 et 3.3 décrivent les modèles mathématique et numérique ainsi que la validation du modèle numérique. La section 3.4 présente une analyse d’ordre de grandeur qui estime la quantité de MCP fondu et solidifié autour du tube selon le flux de chaleur imposé. Cette analyse permet d’identifier des groupes de paramètres adimensionnels d’intérêt ainsi que certaines valeurs critiques. Ces résultats sont ensuite validés à l’aide de plusieurs simulations numériques. La section 3.5 présente le cas de référence, c’est-à-dire le cas qui représente le plus fidèlement le problème de fonte de paraffine autour d’un tube similaire à la référence [16]. L’évolution du front liquide-solide ainsi que le volume totale de MCP fondu et solide sont suivis pendant plusieurs cycles de fonte/solidification pour atteindre un régime périodique. Les phénomènes physiques menant à ces observations sont expliquées. Suite à l’analyse du cas de base, l’effet d’une variation d’un seul paramètre sur l’évolution du front liquide-solide a été analysé. De cette manière, la section 3.6, 3.7, 3.8 et 3.9 présentent respectivement l’effet de la variation du nombre de Rayleigh, du nombre de Stefan, de la période du cycle fonte/solidification et de la température initiale. Ensuite, des propositions sont faites quant à la manière dont devrait être conçue les unités de stockages thermiques à changement de phase.

7

Chapitre 2 : Présentation du modèle mathématique, du modèle numérique

et adimensionnalisation

Ce chapitre présente le modèle mathématique utilisé pour représenter l’unité de stockage thermique, allant des équations de conservation aux propriétés du système et du matériau. Une analyse dimensionnelle est ensuite faite dans le but de transformer les équations de conservation en équation sans dimension et en faire ressortir les nombres adimensionnels caractéristiques. Finalement, la méthode de résolution numérique est présentée. Les logiciels utilisés, soit ANSYS GAMBIT et ANSYS FLUENT, sont introduits et un aperçu de la méthode de résolution par volumes finis est présenté.

2.1 Présentation du modèle mathématique

Cette section présente le modèle mathématique adopté pour résoudre la physique dans l’unité de stockage thermique. Le changement de phase dans une unité de stockage thermique latent de type tube calandre est à la fois un problème de transfert thermique, de changement de phase et de mécanique des fluides. Tout d’abord, les équations théoriques de base couvrant cette physique seront présentées. Ensuite, les hypothèses faites pour simplifier ces équations pour en arriver à celles qui sont résous dans ce travail seront présentées. Finalement, les informations requises pour pouvoir résoudre ce problème mathématiquement seront présentées. Le modèle utilisé pour représenter les phénomènes physiques en jeu est celui d’un tube transportant un fluide caloriporteur, comme par exemple de l’eau chaude, dans un milieu infini rempli de matériau à changement de phase, comme de la paraffine, tel qu’illustré à la figure 2.1.

Heureusement, il existe un système d’équation permettant de résoudre chacun de ces aspects du problème, soit les équations de Navier-Stokes auquel on adjoint le bilan de masse pour l’incompressibilité et le bilan d’énergie. Les équations de Navier-Stokes modifiées sont un système de trois équations aux dérivées partielles qui assurent respectivement la conservation de la masse (éq. 2.1), la conservation de la quantité de mouvement (éq. 2.2) et la conservation de l’énergie (éq. 2.3) dans l’espace (x,y,z) et dans le temps (t). Lorsqu’elles

8

sont combinées, elles permettent de décrire mathématiquement la dynamique des fluides et le transfert thermique.

Figure 2.1 - Modèle 3D (a) et 2D (b) représentant un tube transportant un fluide caloriporteur dans un matériau à changement de phase.

Dans ces équations,  représente la densité [kg m-3_{], u} _{représente vectoriellement la}

vitesse d’une particule de fluide dans les directions x,y,z [m s-1_{], preprésente le champ de}

pression [Pa],  représente le tenseur de contraintes visqueuses [Pa], g représente les forces volumétriques qui s’exercent sur chaque particule de fluide [N kg-1_{], e représente l’énergie}

interne d’une particule [J kg-1_{], q} _{représente le flux de chaleur par conduction thermique [W}

m-2_].

9

 

u 0 t  _        (2.1)

On peut interpréter cette équation comme ceci : le changement de masse dans un certain volume est égal au flux de masse entrant ou sortant de ce volume. Cette équation permet d’assurer qu’il n’y a pas création ni destruction de masse dans le domaine étudié.

Quant à la conservation de la quantité de mouvement, on peut l’écrire ainsi : Du p g Dt           (2.2)

Cette équation peut être interprétée comme la deuxième loi du mouvement de Newton « ma F ». L’accélération d’une particule dépend du gradient de pression autour de cette particule, des contraintes qu’exercent les particules voisines sur celle-ci et de force volumétrique qui s’applique sur chaque particule telle la gravité. Cette équation assure que la quantité de mouvement dans le domaine est conservée.

Finalement, la conservation de l’énergie est exprimée par l’équation :





2 D u u e g u u q Dt  _   _                 (2.3)

Cette équation dit que le changement d’énergie totale (énergie interne, sensible et latente, et énergie cinétique) d’une particule de fluide dépend du travail des forces de volume, du travail des tensions de surface et de la chaleur transférée à la particule par conduction. Cette équation assure que l’énergie dans le domaine étudié est conservée.

Cependant, ce système d’équations non linéaires couplées est à ce jour irrésolvable de manière analytique dans la plupart des cas. Plusieurs hypothèses doivent être faites pour simplifier ces équations. À la base, l’approximation de milieu continu a été faite; elle dit que le domaine n’est pas constitué d’atome ni de vide, mais d’une substance homogène qui remplit tout l’espace. L’hypothèse de fluide newtonien qui implique que la relation contrainte-vitesse de déformation est linéaire a été utilisée. L’approximation de Boussinesq qui suppose que la densité est considérée constante partout dans le domaine sauf dans le terme de gravité de l’équation 2.2 a été utilisée. Le but est de simuler la convection naturelle

10

qui est due à une différence de température qui induit une différence de densité dans le fluide. L’hypothèse que les autres propriétés du fluide (chaleur spécifique cp [J kg-1 K-1],

conductivité thermique k [W m-1 _K-1_{], viscosité dynamique μ [kg m}-1 _s-1_{], coefficient}

d’expansion thermique β [K-1_{], enthalpie de changement de phase λ [J kg}-1_{]) sont}

indépendantes de la position et de la température est faite. L’énergie cinétique et potentielle du fluide ainsi que la contribution énergétique des tensions de surface sont négligées. Finalement, l’hypothèse que le problème d’un tube dans un milieu « infini » peut être analysé en deux dimensions est faite. La solution obtenue dans le plan perpendiculaire à la section du tube est la même peu importe la profondeur tel qu’illustré à la figure 2.1, négligeant les effets de bout et la chute de température du fluide caloporteur.

L’approximation de Boussinesq suppose une relation linéaire entre la densité et la température :

 

T 1



T T



      (2.4)

où _ est la densité de référence et T_est la température de référence (ici, la température de changement de phase T ). Les particules ayant une température plus élevée auront une _m densité plus faible et auront tendance à flotter sur celles qui sont plus froides et plus denses. Tel que mentionné précédemment, le terme 

 

T se trouve uniquement devant le terme de la gravité de l’équation 2.2 alors que _ se trouve partout ailleurs.

La variation d’énergie interne est définie comme étant la combinaison de la variation d’énergie sensible et de l’énergie latente tel que

p

e c T  f

     (2.5)

où f est la fraction liquide et  est l’enthalpie de changement de phase. La fraction liquide est la variable qui représente l’état d’une particule de fluide, allant de 0 si la particule est solide à 1 si la particule est liquide. La fraction liquide f d’une particule dépend de sa température. Il est pratique de définir l’état d’un fluide selon sa température. On définit comme température solidus T la température la plus élevée à laquelle 100% des particules _s de fluides sont solides. On définit pareillement comme température liquidus T la _l

11

température la plus basse à laquelle 100% des particules de fluides sont liquides. On appelle zone pâteuse toute zone où la température se trouve entre T et _s T . Suivant ces définitions, _l on peut décrire la relation entre la fraction liquide et la température ainsi :

 

0 1 s s s l l s l T T T T f T T T T T T T T      _{ }     _  (2.6)

Pour pouvoir représenter à la fois le domaine liquide et le domaine solide en utilisant les mêmes équations, il faut introduire un artifice de calcul. Il faut introduire un terme dans l’équation 2.2, qui modélise le mouvement, pour fixer la position des particules solides tout en laissant les particules liquides libres de se déplacer. On ajoute donc le terme source suivant à l’équation 2.2 [16]









2 3 1 mush mush f S A u f      (2.7)

où A_mush est la constante de zone pâteuse et



est un petit nombre pour éviter les divisions par 0. Lorsqu’une particule est liquide, f 1 et le terme source S_mush tend vers 0. Il devient effectivement négligeable. On constate cependant que lorsqu’une particule est solide,f 0

et le facteur multipliant la vitesse tend vers l’infini. Étant donné que l’équation 2.2 est un bilan de quantité de mouvement, si un terme comme celui-ci devient énorme, il doit nécessairement être compensé par un autre terme de l’équation. Étant donné qu’aucun autre terme de l’équation ne peut lui arriver à la hauteur, le système d’équation va plutôt arriver à un équilibre en faisant tendre u vers 0 pour multiplier le terme qui tend vers l’infini. Ultimement, la vitesse des particules solides va tendre vers 0 alors que les particules liquides ne seront pas affectées, ce qui est l’objectif souhaité par l’introduction de ce terme source.

Pour obtenir la forme finale des équations de Navier-Stokes qui sont résolues dans ce mémoire, toutes ces définitions et ces hypothèses sont appliquées aux équations 2.1 à 2.3. Le bilan de conservation de la masse devient

0 u v x y  _ _

12

Le bilan de conservation de la quantité de mouvement s’exprime comme :









2 2 2 2 2 3 1 mush f u u v P u u u u A u t x y x x y f            _  _  _{ } _  _  _        (2.9)

pour la direction « x » en utilisant la notion de pression augmentée : P p _gy et comme :













2 2 2 2 2 3 1 mush m f v u v P v v v v A v g T T t x y y x y f               _  _  _{ } _  _  _{  }        (2.10) pour la direction « y ».

Finalement, après simplifications, le bilan de conservation de l’énergie s’écrit comme :

2 2 2 2 p T T T f f f T T c u v u v k t x y t x y x y _ _     _ _{ }     _ _  _               (2.11)

en utilisant la loi de Fourier: q  k T .

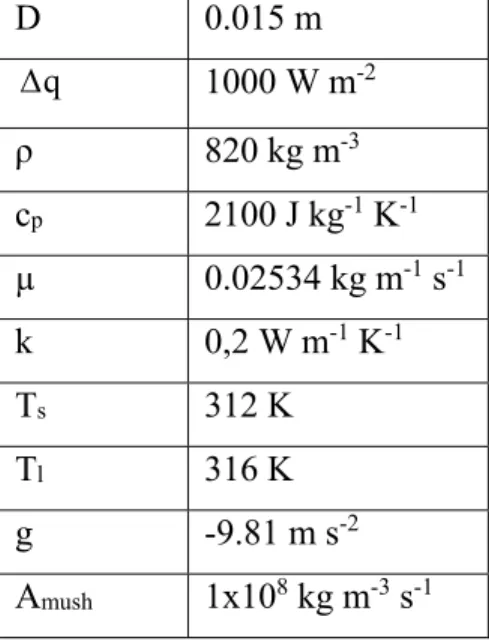
Il est à noter que le système d’équations formé des équations 2.8 à 2.11 est un système à 4 équations et 4 inconnues (u,v,P,T ). L’écoulement du fluide caloriporteur n’est pas modélisé, l’énergie contenue dans le fluide est conduite directement dans le matériau à changement de phase par la paroi du tube. De ce fait, le domaine étudié se limite uniquement à l’enceinte contenant le matériau à changement de phase. Le matériau utilisé à titre de référence dans ce travail est la paraffine de grade industriel RT42 [17]. Ses propriétés physiques et le diamètre typique du tube sont donnés dans le tableau 2.1.

Pour que le problème soit bien posé, il est nécessaire de spécifier la condition initiale ainsi que les conditions aux limites (soit de Dirichlet en imposant la valeur des inconnus, soit de Neumann en imposant la dérivée normale des inconnus à la frontière). Initialement, les vitesses sont nulles partout dans le domaine et la température est la température de changement de phase T , à moins d’indication contraire. À la surface du tube, on impose le _m non-glissement (vitesse nulle) ainsi que le flux de chaleur.

13

Tableau 2.1. Propriétés physiques de la paraffine et du système.

D 0.015 m ρ 820 kg m-3 cp 2100 J kg-1 K-1 k 0,2 W m-1 _K-1 μ 0,02534 kg m-1 _s-1 β 0.001 K-1 λ 141600 J kg-1 Ts 312 K Tl 316 K g -9.81 m s-2 Amush 1x108 kg m-3 s-1

Le flux de chaleur imposé [W/m2_{] est}

 

sin 2 q t q  t       _{ }   (2.12)

où q représente l’amplitude d’oscillation du flux de chaleur tant en chauffage qu’en refroidissement et τ représente la période d’un cycle complet de stockage/déstockage imposé au système. Étant donné qu’il n’y a rien qui différencie le côté droit du tube du côté gauche du tube, il est pratique de mettre un axe de symétrie vertical entre les deux. En terme mathématique, les conditions aux limites d’un axe de symétrie sont un flux de chaleur nul et un taux de cisaillement nul (gradient de vitesse nul) à l’interface. Il est facile de s’en convaincre parce que la température et la vitesse sont supposés être les mêmes d’un côté à l’autre. La dimension du domaine doit tout de même être limitée. Le but est de modéliser le transfert de chaleur dans un matériau à changement de phase qui s’étend à l’infini pour éviter l’impact que pourrait avoir un mur sur la solution obtenue. Les tests de validation ont démontré qu’il est adéquat de limiter le domaine à 20 fois le diamètre du tube, tel qu’illustré dans la figure 2.2, pour trouver un juste compromis entre la justesse de l’approximation et le temps de calcul. Sur cette paroi, on impose un flux de chaleur nul et une vitesse nulle.

14 g x , u y , v (b) D 20 D 20 D 20 D u = 0 v = 0 -k T = qˈ(t)   ∆ = 0 = 0 = 0 u = 0 v = 0 T = 0 ∆   u = 0 v = 0 T = T i i i m ˈ u n   v n   T n  

Figure 2.2 - Représentation du domaine étudié (a) et dimensionnement du domaine (b) avec les conditions initiales et conditions aux frontières.

La résolution de ce problème est possible avec un code de CFD. Pour les travaux réalisés dans ce mémoire, ANSYS FLUENT a été retenu. Dans la section 2.3, on va brièvement montrer la procédure à suivre pour résoudre un problème à l’aide de FLUENT ainsi qu’un aperçu de la méthode de résolution numérique par volumes finis.

2.2 Analyse dimensionnelle et équations sans dimension

Dans cette section, une analyse dimensionnelle des équations (2.8) à (2.11) est faite afin de les transformer en un système d’équations sans dimension. Le but de l’exercice est de réduire le nombre de paramètres pouvant avoir un impact sur l’ensemble de solutions obtenus tout en décrivant le plus généralement possible la physique du système. L’analyse va mener à un changement de variables et à la création de nombres adimensionnels [18].

La première étape consiste à identifier les dimensions du système d’équations. Il y a la position, la vitesse, la pression, le temps et la température. La deuxième étape est de définir

15

des dimensions de référence, soit respectivement L_ref ,V_ref ,P_ref,t_ref, . La troisième étape _ref consiste à définir des nouvelles variables normalisées comme :

, , ref x y x y L    , , ref u v u v V    ref P p P   , , ref t t t      m ref T T     (2.13)

où le tilde signifie « sans dimension ». La quatrième étape est de réécrire les équations ainsi que les conditions initiales et conditions aux limites en termes des variables normalisées. Les cinquième et sixième étapes consistent à réarranger les équations avec variables normalisées afin qu’elles deviennent des équations non dimensionnelles et d’identifier les groupes de paramètres adimensionnels influençant la solution du problème. Le choix ultérieur des quantités de référence doit respecter quatre conditions; (1) elles doivent être pertinentes au problème, (2) si possible, elle doivent mener à des variables normalisées d’ordre 1, (3) les éléments caractéristiques du problème (ex. : diamètre du tube, flux de chaleur imposé) doivent être représentés, (4) elles doivent minimiser le nombre de paramètres adimensionnels résultant de l’étape 6.

Pour ces raisons, on définit la longueur de référence comme étant le diamètre du tube :

ref

L D (2.14)

Le flux de chaleur imposé doit être représenté dans la température de référence; avec la loi de Fourier, la relation à la paroi du tube est :

 

sin 2 ref

paroi ref paroi

k T q t q t k r L r             _{ }        (2.15)

où r est la coordonnée radiale normale à la surface du tube. La condition à la limite sans dimension se réécrit comme :

 

sin 2 ref paroi k q t t qD r           _{ }          (2.16)

Pour minimiser le nombre de paramètres adimensionnels, la température de référence peut être définie de manière à ce que ce paramètre disparaisse; il faut donc que

1 ref ref k qD qD k        (2.17)

Le soin est laissé au lecteur de réécrire les équations en termes des variables normalisées et de les réarranger pour mettre en évidence les paramètres adimensionnels. Les

16

équations adimensionnelles résultantes de ce processus pour la conservation de la masse, de la quantité de mouvement et de l’énergie sont respectivement:

0 u v x y           (2.18)









2 2 2 2 2 2 3 1

ref ref mush ref

ref ref ref ref ref ref

L u u v P p u u A L f u u u V t t x y V x V L x y V f         _  _  _{ }  _  _ _       _  _                 (2.19)









2 2 2 2 2 2 3 2 1

ref ref mush ref ref ref

ref ref ref ref ref ref ref

L v u v P p v v A L f g L v v v V t t x y V y V L x y V f V     _ _      _  _  _{ }  _  _ _{ }       _  _                 (2.20) 2 2 2 2 p ref f f f u v u v t x y c t x y x y                            _  _ _{  }  _{  }  _{ }                  (2.21)

où la viscosité cinématique est     et la diffusivité thermique est  k cp .

Pour minimiser le nombre de paramètres adimensionnels apparaissant dans les équations (2.18) à (2.21), les quantités de références peuvent être choisies judicieusement tel que :

1 _ref

ref ref ref

V V L L D  _{  }  _ (2.22) 2 2 2 1 2 ref ref ref ref P P V V D            (2.23) 2 1 ref ref ref

ref ref ref

L L D D t V t V D  _      (2.24)

De plus, on peut réécrire la nouvelle constante de zone pâteuse comme :

mush ref mush ref A L A V _   _(2.25)

Les dimensions de référence du problème sont maintenant toutes définies. Il reste cependant certains paramètres adimensionnels qu’on ne peut plus faire disparaitre, ils sont en fait les paramètres sans dimensions influençant la solution. Il est pratique de regrouper ces paramètres sans dimension et de leur donner un nom. Le nombre de Prandtl se définit comme

17 Pr 



 . Le nombre de Stefan se définit comme _Ste cp ref



 . Finalement, le dernier

paramètre adimensionnel restant se développe comme :

3

2 2

ref ref ref

ref g L g D Ra V Pr          (2.26)

où on définit le nombre de Rayleigh comme

3 4 ref g D g qD Ra k        . Le tableau 2.2

résume les changements apportés aux équations de conservation pour les rendre sans dimension.

Tableau 2.2. Synthèse des équations sans dimension. Changement de variable x y, x y, D    u v, u v, D     ₂ 2 P p D  _   t, t,₂ D       T Tm qD k  _ (2.27) Équations sans dimension

















2 2 2 2 2 3 2 2 2 2 2 3 0 1 1 1 mush mush u v x y f u u v p u u u u A u t x y x x y f f v u v p v v Ra v v A v t x y y x y f Pr f f u v u t x y Ste t x               _  _  _{ } _ _ _                               _  _  _  _  _{  }  _{ }             _                _                  2 2 2 2 1 f v y Pr x y      _  _  _    _  _{ }        (2.28)

Nombres sans dimension

4 g qD Ra k     _Ste c qDp k   Pr    (2.29)

Chaque nombre adimensionnel a un sens physique. Le nombre de Rayleigh peut être vu comme le ratio entre la poussée d’Archimède générée par la différence de température et les forces visqueuses. Lorsque ce nombre est petit (105_{), les forces visqueuses dominent la}

18

de transfert de chaleur est la conduction. À l’inverse, lorsqu’il est grand (107_{), la poussée}

d’Archimède domine les forces visqueuses et des cellules convectives prennent forme, le mode principal de transfert de chaleur est la convection naturelle. Le nombre de Stefan peut être vu comme le ratio entre la chaleur sensible et la chaleur latente. Lorsque ce nombre est petit (0.1), l’énergie nécessaire pour opérer le changement de phase est nettement supérieure à l’énergie nécessaire pour changer la température du fluide, le fluide va stocker l’énergie en changeant de phase plutôt qu’en modifiant sa température. À l’inverse, lorsqu’il est grand (10), l’énergie nécessaire pour opérer le changement de phase est nettement inférieure à l’énergie nécessaire pour changer de température. Le nombre de Prandtl peut être vu comme le ratio entre la diffusivité de la quantité de mouvement et la diffusivité de la chaleur. Lorsque ce nombre est grand, le profil de température est très affecté par le profil de vitesse. L’énergie est plus transportée par convection que par conduction. À l’inverse, lorsque ce nombre est petit, le profil de température n’est pas affecté par le profil de vitesse, la conduction est plus importante.

Il est à noter que les trois nombres sans dimension des équations (2.28) (Ra, Ste, Pr) regroupent d’une manière unique et indépendante neuf paramètres (g, β, ∆q, D, k, ν, α, cp, λ)

qui étaient dissimulés dans les équations avec dimensions (2.8) à (2.11). Ces nombres sans dimension sont les seuls paramètres qui font varier la solution obtenue. Normalement, pour avoir une idée de ce qu’est la solution des équations avec dimensions, il faudrait 9 dimensions pour représenter l’impact de chacun des neuf paramètres. En réalité, il existe plusieurs similitudes qui ont comme conséquences que plusieurs solutions sont similaires. Par exemple, on peut s’attendre à une solution similaire entre une unité de stockage thermique qui a un cp de 1000 [J kg-1 K-1] et un λ de 100 000 [J kg-1] et une unité de stockage thermique

qui a un cp de 2000 [J kg-1 K-1] et un λ de 200 000 [J kg-1] si elles sont soumises à la même

différence de température (même nombre de Stefan).

2.3 Résolution numérique par volumes finis

Dans cette section, on va montrer la procédure à suivre pour résoudre le problème décrit dans les sections précédentes à l’aide de FLUENT 14.5, qui a été utilisé comme logiciel de simulation numérique. Lorsque les bonnes options sont sélectionnées, ce code commercial

19

solutionne les équations (2.8) à (2.11) ou (2.28). La méthode de résolution utilisée par ce logiciel sera ensuite brièvement vulgarisée, soit la méthode des volumes finis.

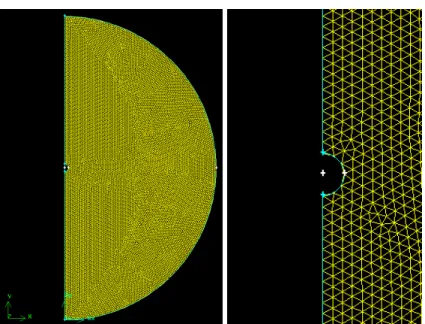
Avant même de démarrer FLUENT (solveur), il est nécessaire de générer la géométrie et le maillage du domaine dans un autre logiciel, un mailleur. Le mailleur utilisé dans le cas présent est ANSYS GAMBIT. Il permet de générer n’importe quelle géométrie, que ce soit en 1D, 2D ou 3D, à l’aide d’opération de base tel que positionner des points, relier des points avec des lignes droites ou courbes, combiner une série de lignes fermées pour créer une surface, combiner une série de surfaces fermées pour créer un volume. Une fois la géométrie complétée, le mailleur va discrétiser le domaine en une série de sous-élément 2D. La dimension des mailles est critique car c’est ce qui détermine à la fois le niveau de raffinement des résultats obtenus et le temps de calcul. Ces deux aspects sont en conflit et il faut trouver un compromis. Typiquement, on effectue une analyse d’indépendance de maillage pour s’assurer qu’il est assez fin. Une analyse d’indépendance de maillage consiste à commencer les simulations avec un maillage grossier puis à le raffiner graduellement jusqu’à ce que les résultats obtenus ne changent plus dans une certaine marge d’erreur acceptable, par exemple 1% de différence en doublant le nombre de maille. Cette analyse d’indépendance de maillage a mené au maillage présenté à la figure 2.3. Il est à noter que FLUENT est capable de raffiner le maillage dans les zones critiques, ce qui a été fait autour du tube car c’est la zone d’intérêt. Le maillage raffiné est présenté à la figure 2.4.

Une fois que le maillage est fait, il faut l’ouvrir dans FLUENT et suivre les étapes qui sont présentées dans le menu de gauche. Les options utilisées sont inspirées des travaux de Guillaume Vidalain [19] et de Sabar Tehar [20] qui ont eux aussi analyser les phénomènes convectifs lors du changement de phase solide-liquide. Des justifications concernant la raison de leur utilisation y sont aussi présentées. Un rapport détaillé des options utilisées dans les simulations de ce travail est présenté dans l’annexe 1.

20

Figure 2.3 - Prise d’écran de la géométrie et du maillage dans GAMBIT.

Figure 2.4 - Prise d’écran du maillage raffiné par FLUENT.

Pour imposer une condition frontière qui varie dans le temps, il faut fournir à FLUENT une UDF (User Defined Function) qui définit le profil du flux de chaleur sur chaque face de cellule touchant au tube. Cette UDF est écrite en langage de programmation C++ à l’aide de Microsoft Visual Basic. Pour qu’elle soit utilisée dans FLUENT, il faut aller dans Define > User Defined > Functions > Interpreted, sélectionner le fichier de code source (extension .c) et l’interpréter. Une fois que l’UDF est interprétée, il est possible d’imposer la

21

condition frontière transitoire à la frontière désirée. Un exemple de code source représentant un flux de chaleur de 1000 W oscillant sur une période de 7283 secondes tel que :

 

1000sin 2 7283 q t  _  t_

  (2.30)

est présenté dans l’annexe 2.

Le problème adimensionnel a été analysé en faisant des simulations dimensionnelles sur FLUENT. FLUENT n’a pas été programmé pour pouvoir résoudre les équations de Navier-Stokes de manière adimensionnelle. Entre autre, il ne permet pas d’avoir des températures négatives (en kelvin), qui seraient perçues comme une transgression du zéro absolu, alors que la plage de température adimensionnelle devrait osciller approximativement entre -1 et 1. Il est tout de même possible de fixer les paramètres des équations pour que FLUENT résolvent « inconsciemment » les équations adimensionnelles, ce qui a été fait. Il faut simplement mettre les équations adimensionnelles que l’on veut résoudre à côté des équations dimensionnelles qui sont résolues par le logiciel et imposer la valeur de chaque paramètre pour qu’elles correspondent. Par exemple, si on veut résoudre









2 2 2 2 2 3 1 mush f v u v p v v Ra v v A v t x y y x y f  Pr   _  _  _{ } _ _ _{ }              _          (2.31)

alors que FLUENT résout













2 2 2 2 2 3 1 mush m f v u v P v v v v A v g T T t x y y x y f                                    (2.32)

il faut imposer _  , 1  1, g 1 et  Ra Pr. On peut ensuite transformer les résultats adimensionnels obtenus pour les champs de vitesse, de pression et de température avec le changement de variable effectué initialement pour avoir des résultats dimensionnels.

Une autre approche a été testée et retenue pour ce travail. Les groupes de paramètres sans dimension (Ra, Ste, Pr) à analyser ont été identifiés et des groupes de paramètres avec dimensions qui correspondent exactement à ceux-ci ont été sélectionnés. Le problème dans FLUENT a été résolu avec dimensions et les résultats obtenus ont ensuite été adimensionné

22

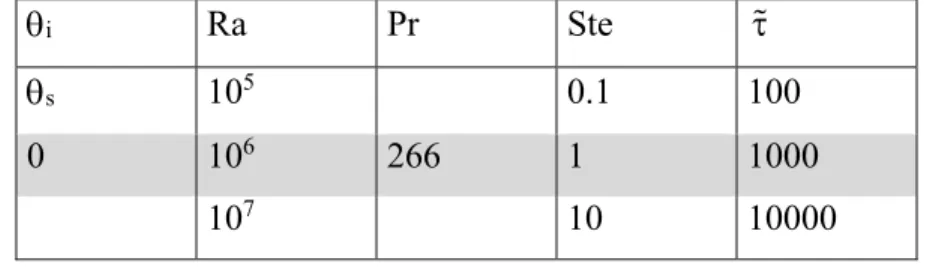
à l’aide du changement de variables. Le tableau 2.3 représente l’ensemble des paramètres étudiés sans dimension. Le groupe de paramètres sans dimension représentant le plus fidèlement les paramètres de la paraffine RT42 énumérés dans le tableau 2.1 sont _Ra106_,

266

Pr , Ste , 1   1000 et une température initiale _i  (0 T_i T_m). Ce cas sera appelé le cas de base et ses nombres sans dimension sont ombrés dans le tableau 2.3. Chaque situation analysée est une variation d’un seul paramètre par rapport au cas de base, dans le but de vérifier l’impact d’un paramètre à la fois. L’impact du nombre de Rayleigh est analysé en comparant les résultats du cas de base avec les résultats pour un cas où le nombre de Rayleigh est 10 fois plus faible et un autre cas où il est 10 fois plus grand. L’impact du nombre de Stefan et de la période d’oscillation sera pareillement analysé. L’impact du nombre de Prandtl n’a pas été analysé car celui-ci ne fait référence qu’aux propriétés intrinsèques du matériau; c’est une quantité invariable pour une unité de stockage thermique dont le matériau est connu. Il pourrait cependant être intéressant d’analyser le même problème avec un nombre de Prandtl de 7 pour remplacer la paraffine par de l’eau. Finalement, l’effet de la température initiale est analysé en comparant l’évolution du profile de température lorsque le domaine est initialement au milieu de la plage de température de changement de phase et lorsque le domaine est complètement solide.

Tableau 2.3. Gamme de paramètres étudiés sans dimension.

i Ra Pr Ste 

s 105 0.1 100

0 106 _{266 1 1000}

107 _{10 10000}

Pour que les simulations avec dimensions soient effectuées avec les paramètres souhaités sans dimension, il faut fixer quelques paramètres avec dimensions et en faire varier d’autres. Par exemple, pour représenter la variation du nombre de Rayleigh, on peut varier le coefficient d’expansion thermique β. Parmi les paramètres sans dimension, le coefficient d’expansion thermique n’a d’impact que sur le nombre de Rayleigh et n’affecte aucun autre aspect du problème. De même, la variation du nombre de Stefan se fait à l’aide de l’enthalpie de changement de phase. Le tableau 2.4 représente la variation des propriétés physiques pour

23

obtenir les nombres sans dimension du tableau 2.3. Les propriétés physiques fixes sont présentées dans le tableau 2.5. Par exemple, pour obtenir _Ra106 _{et Ste , il faut 1}

4 4 6 9.81 1000 0.015 -1 10 0.001445 K 0.02534 0.2 0.2 820 820 2100 g qD Ra k   _      _{ }      _{ }    (2.33)





2100 1000 0.015 1 157500 J kg 0.2 p c qD Ste k            (2.34)

Tableau 2.4. Propriétés physiques variables pour obtenir respectivement les paramètres sans dimension du tableau 2.3. Ti [K]  [K-1]  [kg m-1 s-1] [J kg-1] [s] 312 _{1.445 10} 4 _{1.575 10} 6 _{7.283 10} 2 314 _{1.445 10} 3 _{2.534 10} 2 _{1.575 10} 5 _{7.283 10} 3 2 1.445 10_  _{1.575 10} 4 _{7.283 10} 4

Tableau 2.5. Propriétés physiques fixes du matériau et du système.

D 0.015 m q  1000 W m-2 ρ 820 kg m-3 cp 2100 J kg-1 K-1 µ 0.02534 kg m-1 _s-1 k 0,2 W m-1 _K-1 Ts 312 K Tl 316 K g -9.81 m s-2 Amush 1x108 kg m-3 s-1

En ce qui concerne les paramètres numériques, le pas de temps choisi est de 2 secondes. Le nombre maximum d’itérations par pas de temps est de 4000. Le nombre de pas de temps typique d’une simulation est 27 000, soit environ 7 cycles de stockage/déstockage.

24

Toutes les informations nécessaires pour reproduire avec exactitude les simulations dans FLUENT ont été fournies à l’annexe 1. Pour analyser les résultats des simulations, un fichier de sauvegarde et un fichier d’exportation de données étaient enregistrés à chaque 25 pas de temps. Le fichier d’exportation contient une liste décrivant la position, la température, l’enthalpie et la surface de chaque cellule. Un autre fichier d’exportation contient la température moyenne à la surface du tube à chaque pas de temps. Ces informations sont nécessaires pour vérifier la conservation de l’énergie, pour suivre l’évolution temporelle du front solide-liquide et pour analyser la relation entre le flux de chaleur imposé à la surface du tube et sa température. Le traitement de donnée est fait avec MATLAB. Une procédure est programmée pour importer automatiquement les données des fichiers d’exportation et pour détecter la position des particules solides et liquides, leur température, leur enthalpie ainsi que la surface des cellules correspondantes. Les graphiques et les images ont été réalisés avec MATLAB.

Finalement, pour résoudre les équations de conservation, FLUENT utilise la méthode des volumes finis. Cette méthode consiste à discrétiser le domaine en multitude de volume de contrôle, soit le maillage, puis à satisfaire localement les équations de conservation pour chaque volume par rapport aux volumes voisins. Ce qui en résulte est un système de n équations algébriques formant un système matriciel, où n est le nombre de maille, qui est résout de manière itérative. Par exemple, l’équation pour trouver la température à chaque maille peut s’écrire

    

A T  b  (2.35) 0

où A est la matrice des coefficients qui lie chaque maille avec leurs mailles voisines, b est un vecteur de terme source et T est un vecteur représentant la température de chaque volume de contrôle. Le principal atout de cette méthode est qu’elle est conservative, c’est-à-dire qu’elle est basée sur le principe que ce qui entre dans une cellule doit nécessairement venir des cellules voisines. Les méthodes conservatives sont parfaitement adaptées pour résoudre des équations de conservation.

25

Chapitre 3 : Solid-liquid phase change around a tube with periodic heating

and cooling: scale analysis, numerical simulations and correlations (article)

Titre :

SOLID-LIQUID PHASE CHANGE AROUND A TUBE WITH PERIODIC HEATING AND COOLING: SCALE ANALYSIS, NUMERICAL SIMULATIONS

AND CORRELATIONS

Co-auteurs :

Christian Chabot, Louis Gosselin

Journal :

26 Résumé

Ce travail analyse le changement de phase solide-liquide autour d’un tube horizontal dans une unité de stockage thermique latent soumis à des cycles de chargement et de déchargement (i.e. alternance entre le chauffage et le refroidissement), tout en prenant en compte la convection naturelle. Une analyse d’ordre de grandeur permet de prédire la température à la surface du tube et de l’extension de la zone fondue et solide autour du tube en fonction des paramètres sans dimensions principaux (nombre de Stefan, nombre de Rayleigh et la période d’oscillation imposée du taux de transfert de chaleur). Un modèle numérique est ensuite développé pour simuler le phénomène en régime permanent et pour vérifier l’analyse d’ordre de grandeur. La température, la fraction liquide et la fonction de courant sont présentées en fonction des paramètres principaux sans dimensions. Une analyse fréquentielle est proposée afin d’améliorer la compréhension du comportement du système. Il est démontré que le groupe sans dimension _{Pr τRa Ste}



_ 1 5



_{permet de déterminer l’importance de la convection}

naturelle dans le système. Les résultats montrent que les dimensions de la zone affectée par l’alternance entre le chauffage et le refroidissement augmentent quand la période d’oscillation et le nombre de Stefan augmentent, mais est moins sensible au nombre de Rayleigh. Des corrélations sont proposées afin de déterminer les dimensions maximales atteintes par le matériau fondu et par le matériau solide autour du tube.

Abstract

This work studies solid-liquid phase change around a tube in a latent energy storage unit with cyclic thermal loading and unloading (i.e. alternate heating and cooling), while taking into account natural convection. A scale analysis is used to predict the tube surface temperature and the extent of the molten and solidified zones around the tube as a function of the main governing dimensionless parameters (Stefan number, Rayleigh number and period of the imposed sinusoidal heat transfer rate). A numerical model is then developed to simulate the process under a periodic regime and verify the scale analysis. Temperature, liquid fraction and flow fields are reported as a function of the main governing parameters. A frequency analysis is also proposed to develop a better understanding of how the system behaves. It is