Cyclic branched covers, foliations, orderability, L-spaces and strongly quasipositive links

ORDONNABLES, L-ESPACES ET ENTRELACS FORTEMENT QU ASIPOSITIFS

THÈSE PRÉSENTÉE

COMME EXIGENCE PARTIELLE DU DOCTORAT EN MATHÉMATIQUES

PAR IDRISSA BA

UNIVERSITÉ DU QUÉBEC À MONTRÉAL Service des bibliothèques

Avertissement

La diffusion de cette thèse se fait dans le respect des droits de son auteur, qui a signé le formulaire Autorisation de reproduire et de diffuser un travail de recherche de cycles supérieurs (SDU-522 – Rév.10-2015). Cette autorisation stipule que «conformément à l’article 11 du Règlement no 8 des études de cycles supérieurs, [l’auteur] concède à l’Université du Québec à Montréal une licence non exclusive d’utilisation et de publication de la totalité ou d’une partie importante de [son] travail de recherche pour des fins pédagogiques et non commerciales. Plus précisément, [l’auteur] autorise l’Université du Québec à Montréal à reproduire, diffuser, prêter, distribuer ou vendre des copies de [son] travail de recherche à des fins non commerciales sur quelque support que ce soit, y compris l’Internet. Cette licence et cette autorisation n’entraînent pas une renonciation de [la] part [de l’auteur] à [ses] droits moraux ni à [ses] droits de propriété intellectuelle. Sauf entente contraire, [l’auteur] conserve la liberté de diffuser et de commercialiser ou non ce travail dont [il] possède un exemplaire.»

A D STRONGLY QUASIPOSITIVE LINKS THESIS PRESENTED AS PARTIAL REQUIREMENT TO THE PH.D IN MATHEMATICS BY IDRISSA BA

JULY 2019

ACKNOWLEDGMENTS

Firstly, I would like to thank my advisor, Steve Boyer for his consistent encour-agement and support throughout this PhD program, and introducing me to the fascinating world of low dimensional topology.

In addition, I also would like to thank Olivier Collin for very useful advice in th begining of my thesis and encouragement, and Cameron Gordon for encourage-ment and very useful discussions.

I want to thank Kenneth Baker, Frédéric Rochon, Adam Clay, Baptiste Chantraine, Liam Watson, Huygens C. Ravelomanana and all the CIRGET's members in the UQAM mathematics department. I would like to extend my gratitude to the UQAM Department of Mathematics and the ISM for their support.

Finaly, I also want to thank my family, particularly to my mother Souadou Ba, for their support all the way during this process.

INTRODUCTION

0.1 Cyclic branched covers 0.2 Foliations . .

0.3 Organization

CHAPTER I ORDERABILITY 1.1 Characterization of LO groups . 1.2 Convex subgroups ... . .. .

1.3 T he dynamic realization of a left-order 1.4 Left-orderable 3-manifold groups . ..

CHAPTER II HEEGAARD FLOER HOMOLOGY 2.1 Heegaard splittings and diagrams, Morse fonctions

1 3 6 8 10 16 21 22 23 28 28 2.2 Symmetric products, Whitney and holomorphie disks, spinc structures 31

---2.3 Holomorphie disks and HF 34

2 .4 L-spaces . . . 36

CHAPTER III STRONGLY QUASIPOSITIVE QUASI-ALTERNATING

LINKS AND MONTESINOS LINKS 38

3.1 Introduction . . . 38 3.2 Strongly quasipositive quasi-alternating links . 40 3.3 Strongly quasipositive Montesinos links . . . . 55

IV CHAPTER IV TWO-BRIDGE KNOTS AND THE L-SPACE CONJEC-TURE . . . 61

4.1 Background notions, terminology, and notation 62

4.2 Left-orderability and genus 1 two-bridge knots 64

4.3 L-spaces and genus 2 two-bridge knots 77

4.3.1 ThelinkA(t; *,*,*) .. 4.3.2 Proof of Theorem 4.3.1 .

79

88

4.4 Left-orderability and genus 2 two-bridge knots 100

CHAPTER V LEFT-ORDERABILITY AND DOUBLE BRANCHED COV-ERS OF LINKS . . . 116

5.1 Background notions, terminology, and notation 116

5.2 Universal range of tangles . . . 122

5.3 Non-left-orderable double branched covers 126

CONCLUSION . . 130

4.3 The determinants of the link A for t

>

1 and its resolutions. 84 4.4 The determinants of the link B for and its resolutions. 93 4.5 The determinants of the link L for l

>

l and its resolutions. 95

LIST OF FIGURES

Figure

1.1 Rolfsen move. . . . 1.2 The link L12 and the Whitehead link respectively. 1.3 The link L1

1.4 The link L2

1.5 Link obtained after Rolfsen moves 1. 1.6 Link obtained after Rolfsen moves 2. 1. 7 Link obtained after Rolfsen moves 3. 1.8 Link obtained after Rolfsen moves 4. 2.1 The resolutions L00 and Lo respectively.

3.1 A negative crossing and a positive crossing respectively. 3.2 The links L_, L+, L00 and L0 respectively.

3.3 We call L_, L+ and Lo Conway moves . ..

3.4 Links obtained by applying half-twist to all the diagrams of Figure Page 24 25 25 25 26 26 26 27 37 41 42 43 3.3. . . 43 3.5 Surfaces Sand S'. 45 3.6 Surfaces

So

and

S_. .

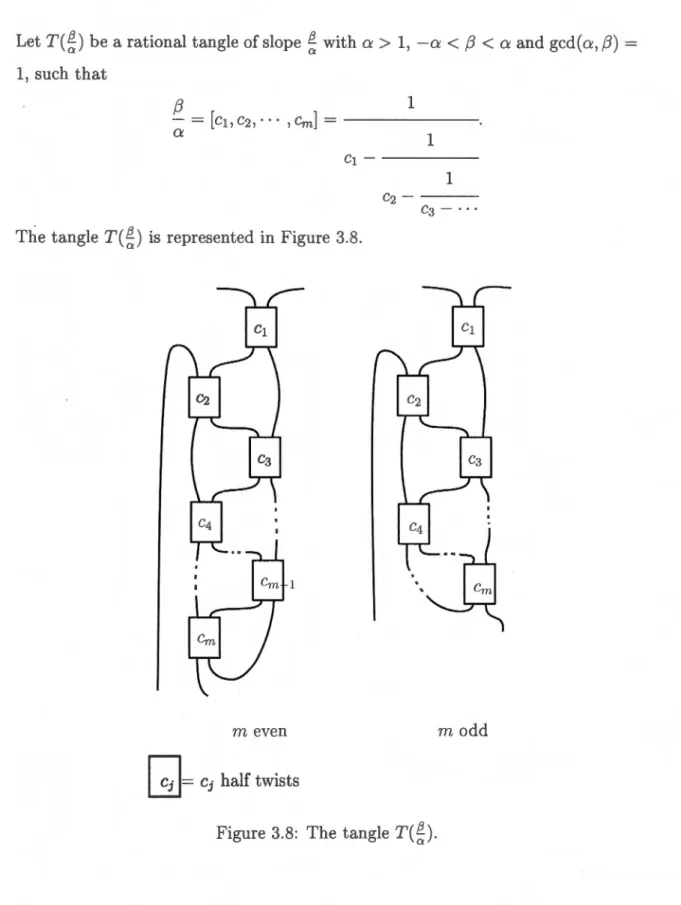
47 3. 7 A Montesinos link. 55 3.8 The tangle

T(¾)-

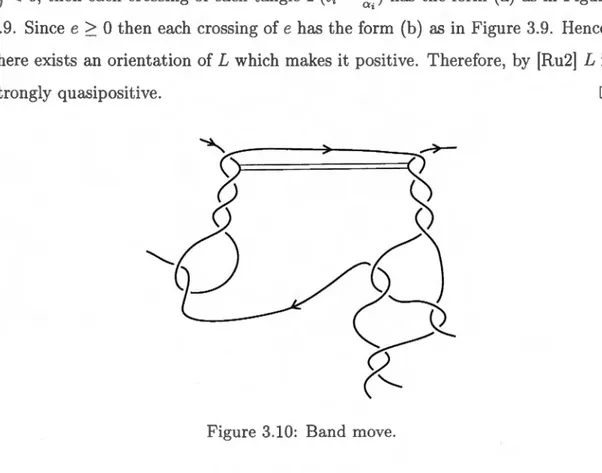
56 3.9 Type of crossings. 3.10 Band move. . . . 57 58

4.5 The link A(t; oo, *, * ) .. 4.6 The link A(t; 0,

*, * ). .

4.7 The link A(t; oo, oo, *). 4.8 The link A(t; oo, 0, * ) ..

4.9 The links A(t;0,0,*) , A(t;oo,0,0) and A(t;0,oo,0) .. 4.10 The link A(t;0,oo,*) . . .

4.11 The link A(t;oo, oo,oo).

79 80 80 80 81 81 81 4.12 Up to ambient isotopy, this diagram represents the links A(t; oo, oo, 0), ·

A(t;0,oo,oo) and A(t;oo,0,oo). 82

4.13 The link L. . . . 88

4.14 The link L for l

=

1. 88

4.15 The link L(l;0,*,*). 89

4.16 The link L(l; oo, *, * ). . 89

4.17 The links L(l; 0, 0, * ), L(l; oo, 0, 0) and L(l; 0, oo, 0) . 89

4.18 The link L(l;oo, oo,*). 90

4.19 The link L(l;0,oo,*).. 90

4.20 The link L(l;oo,0,*).. 90

4.21 Up to ambient isotopy, this diagram represents the links L(l; 0, oo, oo),

L(l;oo,oo,0) and L(l;oo,0,oo). 91

4.22 The link L(l;oo, oo,oo). . . 91 4.23 The link B(* , *, *)

=

L(l

=

1, *, *, *). 93

5.1 A tangle ... . . . 5.2 Operations for tangles.

Vlll

117 118 5.3 The sign convention + 1 and -1 respectively. 119 5.4 The universal polyhedron P(i , j). Each circle represents a rational

or algebraic tangle (including the tangles O or oo). The circle will be called vertices and the line connecting them edges. The vertices are arranged into i rows of j vertices each. 122

5.5 Convention for elementary tangles. . 122

5.6 The link Ln for n

=

6 and its graph. 5. 7 The link Ln and its graph. . . .

125 126

K [-2q,2s, - 2t,2t] , est un L-espace et on groupe fondamental n'est pas ordonnable à gauche. Ceci montre que le revêtement ramifié à 3 feuillets des noeuds de pont de genre 2 vérifie la conjecture sur les L-espaces. ous avons aussi montré que le groupe fondamental du revêtement ramifié à 5 feuillets des noeuds de pont de genre 1, K [2k,-2t], n'est pas ordonnable à gauche, ce qui complète la preuve du fait que le revêtement ramifié à 5 feuillets des noeuds de pont de genre 1, K[2k, - 21J, vérifie la conjecture sur les L-espaces. Nous avons donné une caractérisation de familles d' ntr lac fort ment quasipositifs quasi-alternés (incluant les entrelacs alternés) et aussi construit de nouvelles classes d'entrelacs de Montesinos qui sont soit fortement quasipositifs ou non-fortement quasipositifs. On a aussi étudié la conjecture sur les L-espaces pour le revêtement ramifié à 2 feuillets de certaines familles d'entrelacs, en particulier certaines familles d'entrelacs quasi-alternés.

Mots-clés: Revêtements ramifiés, feuilletages tendus, groupe ordonnable à gauche,

ABSTRACT

This thesis studies strongly quasipositive links and the L-space conjecture which is a relationship between three different domains of pure mathematics: analysis (L-spaces), algebra (left-orderability) and tcipology ( taut foliations). In this di-rection, we show that the 3-fold cyclic branched cover of any genus 2 two-bridge knot K[-2q,2s, -2t,2t] is an L-space and its fond amental group is not left-orderable.

Therefore the family of 3-fold cyclic branched covers of genus 2 two-bridge lrnots

K[-2q,2s,-2t,2t] verifies the L-space conjecture. We also show that the fondamental group of the 5-fold cyclic branched cover of any genus 1 two-bridge knot K [2k,-21J is not left-orderable, which will complete the proof that the 5-fold cyclic branched cover of any genus one two-bridge knot verifies the L-space conjecture. We give a characterization of families of strongly quasipositive quasi-alternating links (in-cluding alternating links) and detect new classes of strongly quasipositive Mon-tesinos links and non-strongly quasipositive MonMon-tesinos links. We also study the L-space conjecture for the double branched covers of some families of links, m particular some families of quasi-alternating links.

Keywords: Cyclic branched covers, taut foliations, left-orderable group, L-spaces, strongly quasipositive links and quasi-alternating links.

Recently strong relations have been discovered in three distinct areas, that is, analysis, topology and algebra, in mathematics, particularly in low dimensional topology. Thenceforth, people have devoted a lot of attention to such relation-ships. Let M be a closed oriented, connected 3-manifold, we denote by,

a) CTF: M admits a cooriented taut foliation, which is a topological condition. This means that M can be foliated by surfaces and each surface has a closed loop transverse to the foliation which intersects it .. Therefore, if M is CTF, then the fondamental group of Mis infinite because each of those closed loop will represent an element of infinite order in the fondamental group of M. It is also known that if M is CTF, then it is irreducible. Therefore, the fondamental group of a closed oriented 3-manifolds M which is CTF, is torsion free (see [CC], [Nol).

b) LO: the fondamental group of Mis left-orderable, which is an algebraic con-dition. This means that 1r₁

(NI)

is non-trivial and has a strict total order which is invariant under left-multiplication.

c) LS: M is not an L-space, which is an analytic condition. L-space manifolds have very simple Heegaard Floer homology (see [OSz05bl).

In 2013 and 2014, Boyer-Gordon-Watson and, independently, Juhasz, made the following conjeture, called the L-space conjecture:

2

Conjecture 0.0.1. Let M be a closed, connected, oriented ahd irreducible three-manifold.

1. (Boyer-Gordon-Watson 2013) 1r_{1 (} NI) is LO if and only if M is NLS. 2. (Juhasz 2014) M is CTF if and only if Mis NLS.

In this thesis the equivalence (1) is also called the L-space conjecture.

Let M, N be two oriented 3-manifolds. By the connected sum of M and N we mean

NI#N

=

(NI - int(Bf))

LJ(N -

int(BJ))

h

identifying the boundaries by some orientation reversing homeomorphism h

a

BJ

---+

a

Br.

Definition 0.0.2. We say that a three-manifold

NI

is prime if M §3 and, if

M

=

M1 #M2, then Mi

~

§3 for some i.

Theorem 0.0.3. (Prime Decomposition Theorem, Kneser-Milnor) If a 3-manifold M is compact, oriented and

NI

§3, then

where each Mi is prime. Futher, the Mi are uniquely determined up to order and orientation preserving homeomorphism.

A 3-manifold

M

is called irreducible if each locally-flat 2-sphere in

NI

bounds a 3-ball in M . If M is not irreducible then it is called reducible. The only prime, compact, orientable 3-manifold that is not irreducible is §2 x §1 .

Let M be a compact reducible, orientable three-manifold. Then its fondamental group has also the following properties:

M is orientable then the union of a product neighborhood S x I of S with a tubular neighborhood of an arc C joing S x O and S x 1 in the complement of S x I is a manifold diffeomorphic to §2 x §1 minus a

ball. Thus M has §2 x §1 as a connected summand. Since M is prime then NI '.::::::'. §2 x §1.

(b) If M is not prime then, by the Prime Decomposition Theorem, we can write M

=

1V[1

#M

2 · · · #Nin, where Mi §3 and each Mi is prime for any 1 :::; i :::; n. Therefore, by the Van Kampen Theorem, n1(M)

=

1r1(M1)

*

1r1(M2)

* · · · *

n1(Mn)- Since, by the proof of the

Poincaré Conjecture, the only simply connected closed 3-manifold is §3 and since a nontrivial free product of nontrivial groups is infinite, then the fondamental group of M is infinite.

2. If M has boundary, then the fondamental group of M can be finite. Indeed, take a compact 3-manifold M with finite fondamental group and make a connected summand with the 3-ball. We will get a reducible manifold with same fondamental group as M.

0.1 Cyclic branched covers

In this section we give a very brief survey on some results about cyclic branched covers. Our references are [R], [Li] and [BuZ] .

A lmot K in the three-sphere §3 is the image of a smooth embedding of §1. A

4 A knot K is prime if, whenever we write K

=

K1#K2 , one of the two knots K1 , K2 is the trivial knot.

The exterior of a knot K

c

§3, denoted by MK, is the complement of the interior of a tubular neighborhood N(K) of K i.e NJI<

=

§3 \ int(N(K)).

Let K be an oriented knot in §3, a meridian µ is a simple closed curve in a MI< that bounds a disk in N(K) and a longitude À is a simple closed curve in aMI<

that is null-homologous in MJ< . A Seifert surface for K is a connected, compact, orientable surface that has Kas boundary. This always exists using what is called Seifert 's algorithm ( see [R]).

General definitions

Definit ion 0.1.1. Given M and N two compact n-manifolds with proper sub-manifolds V C M and W C N of codimension

2,

a continuous map

f :

M --+ N is called branched covering with branched sets V and W if it satis.fies the following two conditions:

1. components of preimage of the open sets of N are a basis for the topology of M·

_'

2. f(V) = W, f (M \ V) = N \ W and g = flM\V M \ V --+ N \ W is a covering map.

The map g is called the associated unbranched covering. Since M is compact, g is

finite sheeted, and each branched point x E V has a branched index some n

<

oo . This means that

f

is

n

ta one near

x,

and this number is constant on components of V.

degree n. Therefore

f

is an n-fold branched covering. Cyclic branched cover over a knot

Let K be an oriented lmot in §3 . Let J\([K be the exterior of K and S be a Seifert

surface for K . Isotope S so that SnéJMK is a longit ude of K and let F

=

Snl\lIK.

Let C be a tubular neighborhood of F in MK. Then C is homeomorphic to

F x

[- 1, l] .

Let Y := MK \ int(C). The boundary of Y has two copies p

-F x

{-1}

and p + F x

{1}

of F. We have a triple (Y, F+, p - ). Consider n copies of this, denoted by (Y;;, F/,

Fi- ),

i

=

0, · · · , n- l , and glue them together by identifying Fa+ C Ya with F1- C Y1 , F/ C Y1 with F2- C Y2 , · · · , F;t_2 C Yn- 2 with F;:_1 C Yn- l and F;t_1 C Yn- l with Fa- C Ya. Cali the resulting space Yn. There is a regular covering map g : Yn -+ Mg and its group of deck transformations is isomorphic to Zn . The manifold Yn is called the n-fold cyclic cover of Mg and its fondamental group isomorphic to K er(n1(MK) -+ Zn )- To construct the n-fold

cyclic branched cover En(K ), we have to glue a solid toms V D2 _{x §}1 _{to Yn by} identifying the meridian é) D2 x { 1} of V with the preimage of the meridian µ of

aMg under g: Yn -+ Mg . The manifold En(K) is a closed oriented 3-manifold .

Theorem 0.1.3. ([BuZ]) Th e n-fold cyclic branched caver En(K) of a knot K is a rational homology sphere if and only if no root of its Alexander polynomial i::i.g(t) is an nth _{root of unity ti, i}

=

_{0, • • • , n - l , and in this case}

n- l

IH1(En(K)) I

=

1

II

f::i.g(ti) I i=a

6

Theorem. 0.1.4 . ([MSY],[MB]) Let K c §3 be a knot. The manifold Bn(K) is

prime if and only if K is prime. 0.2 Foliations

Let M be an n-manifold. In this section we give some definitions and examples arising from the notion of a foliation on M. Good references are

[CCI

and [No]. Definition 0.2.1. Let Y be a compact codimension one submanifold of M . We say that Y is 2-sided in M if there is an embedding

h: Y x [- 1, 1] ---+ M

with h(x, 0) = x for each x E Y and h(Y x [- 1, 1])

n

8M = h(BY x [- 1, 1]). This

implies that the normal bundle of Y is trivial.

D efinition 0 .2.2. A k-dimensional distribution D on M is a map which assigns to every point x E M a k-dimensional vector subspace Dx of TxM the tangent space of M at x. A distribution D is called smooth if for every x E M there exists a neighborhood U of x in M and smooth vectors .field Vi , · · · , Vi on U such that for every y EU, Vi(y) , · · · , Vi(y) forma basis for

Dx-An immersed submanifold Y of M is an integral manifold for D if for each y E Y

diy(TyY)

=

Dy , where iy is the inclusion map. The distribution D is integrable if through each point of M there is an integral manifold.

D efinition 0.2.3. A k-codimensional foliation denoted by F of M is a collection of charts {(Ui , <Pi )}iEI i.e {UdiEI is an open covering of !VI and

</Ji : ui ---+ IRn-k X IRk

zs a di.ffeomorphism for each i E

I,

such that on each nonempty Ui

n

Uj the coordinate change takes the f orm

F which has a closed transversal circle.

2) Let Y be a closed transversal to a foliation F on M. Bec a use Y and F are of complementary dimensions, transversality means simply that TyY

n

TyF

=

{O} , for each y E Y. Closed transversals are only common in codimension 1 foliations, and in this case, a closed transversal circle is a smoothly embedded circle Y and the transversality condition means that Y is nowhere tangent to F.

3) If the determinant of the Jacobian matrix of

cJ>-;1ocJ>i

is positive i.e IJq,-:-10</Ji l

>

0,

J

then NI is orientable.

4) If the determinant of the Jacobian matrix off is positive i.e IJ1I

>

0, then this gives each leaf of F an orientation, and we say that F is orientable, where

f

is defined as in Definition 0.2.3.

5) If

l

1₉1

>

0, this gives an orientation to the transversals, and we say that F is

co-oriented or transversely oriented, where

f

is defined as in Definition 0.2.3.

D efinition 0 .2.6 . A rectangular neighborhood in ffi.P is an open subset of the form

r

=

11

x · · ·

Ip, where each Ji is a (possibly unbounded) relatively open interval in the ith coordinate axis. If 11 is of the form ( a,

ü],

we say that

r

has boundary

ar = {(o,

x2, ... , xp)

E r}.

A foliated chart on NI of codimension k is a pair (U, c/>), where U Ç NI is open and

8 rectangular neighborhood in JRk.

Examples 0.2.7. Let

f:M-+Y

be a submersion, where Y is a k-dimensional manifold and both M and Y are closed and connected. By the submersion theorem, for each point x E M, there is a coordinate neighborhood (U, Xi, ··· , Xn) of x in M and a coordinate neighbor-hood (V, Yi,··· , Yk) of f(x) in Y, relative to which the formula for fu becomes f(xi, · · · , xn)

=

(xi,· ·· , xk)- It follows that the level sets 1- i(y) are properly imbedded submanifolds of M of dimension n - k and that, locally, these subman-ifolds fit together exactly like parallel copies of IR.n- k in ]Rn. Thus, the connected components of the nonempty level sets of

f

are the leaves of a foliation F of codimension k

=

dimY.

0.3 Organization

This thesis is organized as follows.

Chapters 1, 2. In chapter 1, we give a very brief survey on some results about orderable groups and, at the end, we construct examples of 3-manifolds with left-orderable fondamental groups. The aim of Chapter 2 is to understand the

---meaning of the Heegaard Floer homology HF and L-spaces.

Chapter 3. In this chapter we give a characterization of families of strongly quasipositive quasi-alternating links (including alternating links) and detect new classes of strongly quasipositive Montesinos links and non-strongly quasipositive Montesinos links.

Chapter 4. In this chapter we show that the 3-fold cyclic branched cover of any genus 2 two-bridge knot K[- 2q,2s, - 2t,2t] is an L-space and its fondamental group is

conjecture.

Chapter 5. In this chapter we also study the L-space conjecture for the double branched covers of some families of links, in particular some families of quasi-alternating links.

CHAPTER I

ORDERABILITY

In this chapter we first give a very brief survey on some results about orderable groups and, at the end, we construct examples of 3-manifolds with left-orderable fondamental groups. Our references are [CR], [Sik], [R], [BH], [Con] and [Gla]. An action of a group G on IR by order preserving homeomorphisms is the same as a representation in Homeo+(IR), where Homeo+(IR) is the group of orienta-tion preserving homeomorphisms of IR. We also call H omeo+ (§1 ) the group of orientation preserving homeomorphisms of §1 .

A total order :::; on a set S is a binary relation satisfying the following conditions: 1. If a :S band b :S a then a= b (antisymmetry);

2. If a :S band b :S c then a :S c (transitivity);

3. Given any two elements a, b in S, either a :Sb or b :Sa (totality).

A binary relation

<

on a set S is asymmetric if a

<

b then b

1-

a for any a, b in S. A strict total order

<

on a set S is an asymmetric, transitive binary relation satisfying that, given any two elements a, b in S, exactly one of the three relations a

<

b, a

=

b and b

<

a is true. Based on a total order :::;, a strict total order

<

• G -/- 1;

• there exists a strict total order

<

on G such that, for any g, h, and k in G such that g

<

h, then kg

<

kh.

This means that

<

is left-invariant.

Definition 1.0.2. A group G is right-orderable (RO) if

• G-/-

1;

• there exists a total order

<

on G such that for any g, h, and k in G such that g

<

h then gk

<

hk.

This means that

<

is right-invariant.

Definition 1.0.3. 1. A group G is bi-orderable (BO) if it is left-invariant and right-invariant for the same order.

2. A subgroup C of a lejt-orderable group ( G,

<)

is called convex if for any

c, d E C and g E G such that c

<

g

<

d then g E C.

3. A group G is locally indicable (LI) if for any nontrivial finitely generated subgroup H of G, there is an epimorphism <p: H --+ Z.

Let G be a group. We denote by

12

2. RO ( G)

= {

right orders on G}; 3. 0( G)

=

{bi - orders on G}.

We have the following well-known properties of LO(G). Properties 1.0.1. 1. There is a bijection

LO(G) ----+ RO(G) I

< f-+ <

2. There is a bijection LO(G)----+ LO(G) where g

<

0 P h <=> h

<

g.

3. An element g E G is positive if g

>

l, and negative if g

<

l. If g is positive its inverse is negative.

Proposition 1.0.4. Lejt-orderable groups are torsion-free.

Proof. Let G be a left-orderable group with a left-order

<.

Suppose that G has a nontrivial torsion element denoted by g, i.e. gn

=

1 for some positive integer n. Without loss of generality, we can assume that g

>

l. Since the order is invariant under left multiplication, we have a chain of inequalities

1

<

g

<

g2

< · · · <

gn

=

l, which leads to a contradiction.

Proof. 1. Let

<

be defined as

. { rp(g) <H rp(g') , if g-1 g' t/:. K or

g

<

g' <*

1 <1< g- 1g' , if g- 1g E K , where rp : G ---+ H.

2. The order

<

is a LO . Indeed, One can see that

<

is a total order, so we need to verify that it is left-invariant. Let x, y and z E G with x

<

y. If x- 1y t/:. K , t hen rp(x ) <H rp(y) which implies since H is LO 'P(zx)

=

rp(z)rp(a) <H rp(z)rp(y)

=

rp(zy). Hence zx

<

zy. If x-1y E K, then 1 <1< x- 1y

=

(zx)- 1(zy) which implies zx

<

zy.

Examples 1.0.6. 1. The usual order used to compare two real numbers makes the group of all real numbers (ffi., +) a left-orderable group. Since the group (ffi.,

+)

is abelian, it is also a bi-order on (ffi.,

+ ).

2. H omeo+ (ffi.) is left otderable. Indeed , we equip ffi. with a fixed left-order. Recall that H omeo+(ffi.) is the group of order-preserving homeomorphisms from ffi. to itself. We show that H omeo+(ffi.) is a left-orderable group. First, one lists the set of rational numbers

Q

= {

x1, x2 , · · · , xi, · · · } . Since

ra-tional numbers Q are dense in ffi., given any two distinct fonctions

f ,

g E

Homeo+(ffi.) , there exists at least one Xi in Q such that f(xi)

::J

g(xi) - We set

f

<

g if

f

(xk) is less than g(xk) as two real numbers, where xk is the

14

first number in the sequence

Q

= {

x1 , x2 , · · · , Xn, · · · } that has distinguished images un der homeomorphisms

f

and g.

Claim: This order defines a left-invariant order of Homeo+(IR). Indeed, let f, g E H omeo+(IR) be such that f

<

g. Let t E H omeo+(IR), we have, f

<

g f(xk)

<

g(xk) where xk is defined as before. Hence t(f(xk))

<

t(g(xk)) because t is monotone increasing, so tf

<

tg because tf and tg are in H omeo+(IR).

Remark 1.0. 7. 1) If (E, <) is a totally ordered set and G is a nontrivial group which acts faithfully on the left of E by order preserving automorphisms, then G is LO.

2) Let G be a topological group which is connected, locally path connected, and admits a universal covering

p:

G

---r G.

Let e be the trivial element of G and fixed

e

E p -1 ( e) . We have the commutative

diagrams ~ ~ 3µ, ~

( c

x

c, ( e,

e)) ---'---+ (

c,

e)

1r(p,p)l

lp

(G

x

G,

(e, e))

(G,

e)

~ 31 ~

( c,

e) --=---+ (

c,

e)

pl

lp

(G, e) (G, e)

where

I(g)

=

g-1 , µ is the multiplication map. Then (

G,

µ,

i,

e) is a topological group and µ(g,i(g))

=

e,

for any g E

G.

Let X be a connected, locally path con-nected space which admits a universal covering q :

(X,

ii) ---,

(X, a). Assume G

ei0 M rotation by ei0

Therefore H~+(§1 ) , the universal cover of Homeo+(§1), acts faithfully on IR by order preserving homeomorphisms. Thus H ~+ (§1 ) is LO .

Definition 1.0.9.

Let (G,

<) be an LO group. The positive cane of G is the

subset

P

=

P( <)

=

{g E G

I

g

>

1}

We have the following well-known properties, good references are [Sik] and [CR] . Properties 1.0.2. 1. P · P C P

2. G

=

P LJ {1} LJ p - l where p - l

=

{g- 1 1 g E P}

3. Endow Gand 2

=

{O,

1} with the discrete topologies and 2G P(G) with the product topology. T hen the map

LO ( G)

--+

2c < MP(< )

identifies L (G) with subset of 2c. Endow LO(G) with the subspace topology. Note that 2° is compact by Tychenoff's theorem.

Let U₉

=

{A Ç G

I

g E A} and

ui

=

{A Ç G

I

g f/:; A} for any g E G. Then the set D

=

{U_{9 ,} UJ

I

g E G} is a subbasis for the product topology on 2c ([Sik]) .

16

1.1 Characterization of LO groups

Definition 1.1.1. a) Let G be a nontrivial group and

{Bd

be a sequence of increasing subsets of G i.e {1}

ç

B1

ç

B2

ç . .. ç

u k2:l Bk= G. We say that

this sequence is balanced if Bk

=

B-;

1 .

b) A proper k-partition (pkp) with respect to Bk is a subset Q of Bk such that

2. Q

n

Q-1

=

0;

Theorem 1.1.2. (Clay-Rolfsen, 2015) The group G is LO if and only if there exists a proper k-partition of Bk for any k.

Proof. =})

If<

is a LO on G then Q

=

P(

<)

n

Bk is a pkp for any k.

{=)

Suppose that for any k, Bk admits a pkp. Set Pk

= {

A Ç G I A

n

Bk is a pkp of Bk}. Then Pk

=/-

0

for any k and

0

C P1 C Pk C · · · C Pk C · · · 2°. Claim, 1.1.3. The set Pk is closed in 2°.

Proof. We have that

Pk

=

{ A Ç G

I

Q

=An

Bk is a pkp of Bk}

=

{A ç G

I

Q

=An

Bk,

Q · Q

n

Bk

ç Q, Q

n

Q-1

₌

₀

_and Bk= Q LJ {1} LJ Q-1 } .

(1.1) Let

show that L, M and N are closed. We have that

u

is open in 2c , hence L is closed.

Mc =

LJ

(U9

n

U9-1)

gEB1c

is open in 2c , hence

!VI

is closed.

Ne =

LJ

(U;

n

u;-1)

gEB1c \ {l}

is open in 2c, hence N is clos d.

We have that n k2::1

pk =

Pi

=1-

0.

The conclusion cornes from the fact that

The following theorem offers alternative criteria for left-orderability, a good ref-erence is [CR].

Theorem 1.1.4. Let G be a nontrivial group. Then G is LO if and only if each finit ely generated subgroup H of G is LO.

Prooj. ==>) Take the LO induced by the one on G.

{=)

Let

F

be a fini te nonempty subset of

G

such that 1 t/:. F. Define

Q(F)

= {

Q

Ç

G

I

Q

n

(F) is a positive cone for LO on (F)}

18

Q(F) is not empty by hypothesis and it is closed in 2G (similar proof as Pk is closed). Therefore { Q(F) 1

0

=/

F finite

c

G \ {1}} is a family of closed nonempty subsets of G. Hence, if

Fi,··· ,

Fn are fini te nonempty subsets of G\ {1} then

0

=/

Q(Fi

U · · · U Fn) Ç Q(F1)

n • • • n

Q(Fn)- Since 2c is compact, then LO(G)

=

nF

Q(F)

=/

0

([CR]) .

Theorem 1.1.5. An abelian group G is LO if and only if it is torsion free. Proof. =}) Proposition 1.0.4

{=)

Let 1

=/

H

:S:

G be a finitely generated subgroup of G. Since G is abelian and torsion free, then H

zn

for some positive n. Therefore H is LO, and hence G is LO.

Let G be a nontrivial group and X a subset of G. Define

S(X)

=

{g1 · · · 9n

I

n

2'.

1 and 91 , · · · , 9n EX}

Theorem 1.1.6. (Conrad, 1959) A group Gis LO if and only if for all x1 , · · · , Xk E

G\ {1} there exists E1, · · • ,Ek E {±1} such that l (/. S(x~1, • • • ,x~k ).

Proof. be an LO on Gand x1, · · · ,xk E G\ {l}. Then for each i there exists a unique Ei E {±1} such that x1i

>

l. Therefore S(x~1, • • • , x?) CP which does not contain 1.

{=)

Without loss of generality assume that G is finitely generated ( cf. Theorem 1.1.4) .

Fix a finite balanced generating set for G. Let Bk be the (k

+

1)-ball in the associated length metric such that { 1} Ç B1 Ç B2 Ç · · · Ç u k2'.1 Bk. Set Bk \

{1}

=

{x1, • · · , Xn} - By assumption, there is E1, · · · , En E {±1} such that 1 (/. S(x~1

2) Let g E Q. If g- i E Q, then 1

=

gg- i E S(x11_{, • • • ,} x~n ), which is impossible.

Thus Q

n

Q-1

₌

0.

3) For each i

=

1, --- , n , we have xfi E S(x~1

, • - • , x~n )

n

Bk

=

Q. Then Xi , xii E

Q LJ Q- i and {xi, --- , xn } Ç Q LJ Q- i, which implies Bk C Q LJ

{1}

LJ Q- i_ This

proves the daim and therefore the theorem.

Theorem 1.1. 7. (Burns and Hale, 1972) Let G be a nontrivial group. Then G

is LO if and only if for any finitely generated subgroup 1 =/= H

:s;

G, there exists a nontrivial homomorphism <p : H

--r

L, where L is an LO group.

Proof.

=})

Take the inclusion map.

<==)

Let {xi,· ·· ,xn} Ç

G-{l} .

We show that there exists ci, ··· ,En E {±1}

such that 1

tj.

S(x~1_{, • • • ,} x;~) and then apply the previous theorem. We show this

by induction on n.

Case 1: Assume that n

=

1. Let H

=

(xi) =/= 1. By assumption there is an epimorphism <p : H

--r

L , where L is LO. The subgroup H being cyclic, L is

also cyclic and therefore isomorphic to Z. Since L is LO then it is torsion free. Without loss of generality assume cp(xi)

=

1, hence

cp(xn

k which implies S(xi)

=

{xi,

Xî , · · · ,

xÎ, · · ·

h :::1-

Therefore 1

tj.

S (xi

20

r

<

n. Fix {x1 , · · ·

,xn}

Ç G \ {1}. By hypothesis, there is an epimorphism (() : (x1 , · · · , Xn) ---+ L. Let

<

be an LO on L. Up to reindexing x1, · · · , Xn, we

can assume there exists 1 :::; r :::; n such that,

{

-le

1, if 1 :::; i :::; r

VJ(Xi)

=

1 if r

+

l :::; i :::; n

Choose c1 , ···,cr so that VJ(xfi)

>

1 for all 1 :::;

i:::;

r.

By induction, there exists ér+l , · · · , En such that 1 t/:. S(.-.r::+₁1, • • • , x;:' ). Suppose that there is a nontrivial product w of

.-r1

1_{, • · · ,}

x;:'

such that _w

=

_l i.e 1 _E

S(x11, · · · ,x~n ). Then VJ(w) is a product of (l)(xf;) for all 1 :::; i :::; r which is equals 1. But (l)(xf;) E P( <) for all 1 :::; i :::; r. Hence VJ(w) is an empty product of VJ(xf;) for all 1 :::; i :::; r. Then w is a product of x:,'./₁

1, · · · ,

x~n, and we have 1

=

w E S(x::V, · · · , x~n) . This is a contradiction.

Corollary 1.1.8. Any free group F is LO.

Proof. Let H be a nontrivial finitely generated subgroup of F. Since each non-trivial subgroup of a free group is a free group, H is free and admits a nontrivial epimorphism onto Z . Hence by the Burns-Hale Theorem Fis LO.

Theorem 1.1.9. (Vinogradov, 1949) Let { Gi}iEI be a family of nontrivial groups and G

=

*iEIGi· Then G is LO if and only if each Gi is LO.

Proof.

==>)

if Gis LO then it induces an LO on each of the Gi.

ç=)

Every finitely generated nontrivial subgroup H of G is contained in some Gi1

*

Gi2

* · · · *

Gin. It suffi.ces to show that Gi1

*

Gi2

* · · · *

Gin is LO.

Let

K

=

ker(G ZJ

*

G-i2

* · · • *

G -Zn ---+ G Z1 x G Z2 x · · · x G ) Zn

and Gi1 x Gi2 x · · · x Gin is LO by taking the lexicographie order. Then K is a

1.2 Convex subgroups

Definition 1.2.1. Let ( G, <) be a LO group. A subgroup C of G is convex if, for any a, b E C and g E G, we have that a

<

g

<

b implies g E C.

Example 1.2.2. Let K = (x, y

I

x-1yx = y-1), C = (y), and fix an LO

<

on

K.

Then,

1) We have that x-1

<

_yn

<

_{x, for all n if x}

_>

_{1. Indeed, If there exists} an n E Z such t hat x

<

yn then 1

<

x-1_yn

=

_{y- nx - 1, which implies that}

yn

<

x-1

_<

_x

_<

_{yn, which is a contradiction.}

2) Similarly we have that x

<

yn

<

x-1 , for all n if x

<

1.

In fact we have that, if ya

<

xmyn

<

yb for some a, b, n, m , then m

=

O. Hence C 1s convex.

Lemma 1.2.3. (Glass, 1999) Let (G , <) be an LO group. Then the set C

= {

C

I

C is a convex subgroup of G}

is totally ordered by inclusion.

Proof. Let C , D E C such that D

</:

C . Let d E D \ C be a positive element (such

an element

d

exists because

D

is a subgroup of

G).

If c E

C,

then c

<

d-1

<

1

implies d-1 _{E C which is a contradiction, and d}

_<

_{c implies that d E C, which is} also a contradiction. Thus d-1

_<

_c

_<

_{d and c E D , which implies CC D .}

22

Lemma 1.2.4. (Glass, 1999) Let (G, < ) be an LO group and Ca convex subgroup of G. Then

<

indu ces a totally order

<

E on E

=

G / c.

1.3 The dynamic realization of a left-order

D efinition 1.3.1. Let (G, < ) be a countable LO group. For g, h E G, the intervals (g , h), [g , h), (g,h], (-oo, h) , (g,oo) (-oo,h], [g,oo) are determined by < in the usual way.

Theorem 1.3.2. (Linnell, 1999) Let (G, <) be a countable LO group. Then G is LO if and only if it is isomorphic to a subgroup of H omeo+ (]R) .

Proof. {=) Since Homeo+(IR) is LO , then Gis LO .

::::} ) Fix an enumeration {g0

=

1, g1, g2 , · · · } of G. Inductively define an order-preserving embedding

t :

G ---+ IR as follows. Begin by setting t(g0 )

=

O. If

t(g0 ) , • • • , t(gn) have already been defined and 9n+l is either larger or smaller than

all previously embedded elements, then set:

{

max{t(go), · · · , t(gn)}

+

1 if 9n+1 > max{go, · · · , 9n} t(gn+1)=

min{t(go), · · · , t(gn)} - 1 if 9n+i

<

min{go , · · · , g,.,,}

Otherwise there exists a unique pair j , k E {O, · · · , n} such that .9J

<

9n+1

<

9k

and there is no l E {O, · · · , 1} such that 9J

< 9t

<

9k· Set

We have that

t(

G) is unbounded above and below and a

This is a homeomorphism of t(G).

2)

This action of G on

t(

G) extends by a Cauchy sequence argument to an action of G on t(G) by homeomorphisms.

3) lR \

t(

G) is a countable disjoint union of open intervals. The action of G ont( G) extends affinely on the complementary intervals. This gives an action of G on JR, by orientation preserving homeomorphism. Therefore we have a homomorphism

'P: G - t H omeo+(IR)

and 'P is one to one and this action does not have global fixed point.

1.4 Left-orderable 3-manifold groups

The notion of orderability has played a key role in low dimensional topology in the past ten years, with respect to the L-space conjecture. Therefore, following this direction, in this section we will gives some results about this.

A closed, oriented connected 3-manifold is excellent if it admits a co-oriented taut foliation and its fondamental group is left-orderable.

Let L

=

K1 U · · · U K m be a link in the three-sphere. Let NI be the three-manifold obtained by doing (El , · ·· , E!!l )-surgery along L. The symmetric matrix A = (liJ·),

QI Qm

{

Ei if i

=

j

i , j

=

l , · · · , m with th entries lij

=

q;~' . . . lk(Ki, K j) 1f i

i-

J,

24 is called the linking matrix of L. The matrix F

=

(qili₁₎ is called the framed matrix of L and is a presentation matrix for H1 ( M). Therefore, M is an integer homology sphere if and only if det F

=

±1

or, equivalently det A=

±-

_{q1 ·· •q,n} 1 -. Let L

=

K1 U · · · U Km be a link in the three-sphere. To perform a Rolfsen move (see Figure 1.1), we need an unknotted component K in our surgery diagram (see Figure 1.1). If K has initially coefficient E _g E QU {oo}, then the resulting

coefficient is _+P _{q np} (see Figure 1.1, see also Rolfsen book). For each component Ki, the surgery coefficient changes from ri to ri

+

n(lk(Ki, K) )2 .

RM

K n

q

QJJ)_E_

1 1 1 q+np

a-1

c-1

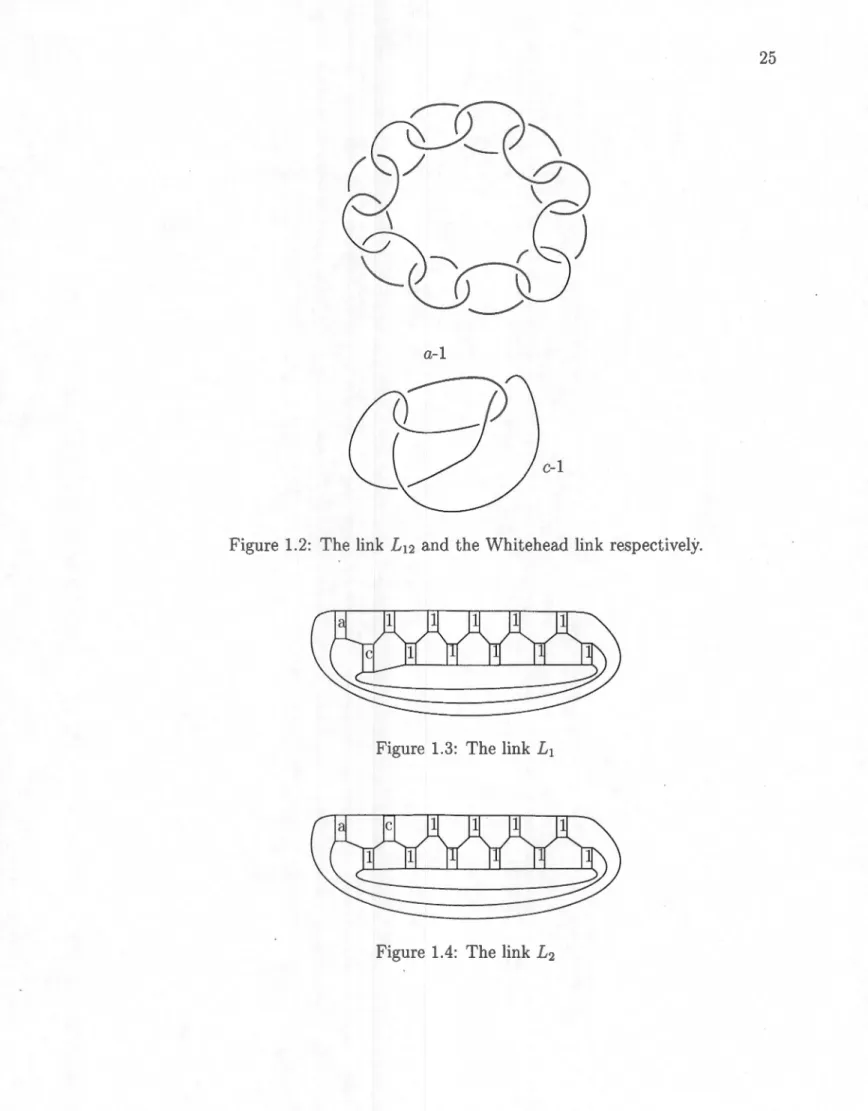
Figure 1.2: Th link L12 and the Whitehead link respectively.

Figure 1.3: The link L1

26

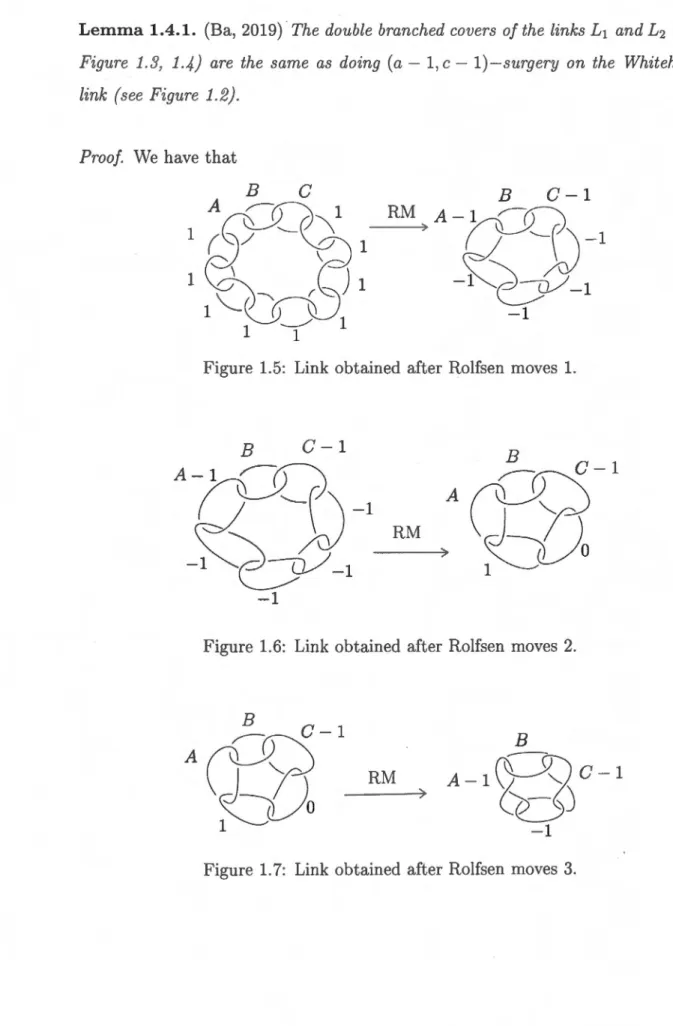
Lemma 1.4.1. (Ba, 2019) · The double branched covers of the links L1 and L2 (s ee Figure 1.3, 1.4) are the same as doing (a - 1, c - 1)-surgery on the Whitehead link (see Figure 1.2).

Proof. We have that

RM

Figure 1.5: Link obtained after Rolfsen moves 1.

Figure 1.6: Link obtained after Rolfsen moves 2.

RM

Figure 1.8: Link obtained after Rolfsen moves 4.

By taking B = l , A = a and C = c or C = 1, A = a and B = c and ap-plying again a Rolfsen move, we have that doing (a, c, 1, · · · , 1)-surgery and (a, 1, c, 1, · · · , 1)-surgery on the link L12 is the same as doing (a-1 , c-1)-surgery on the Whitehead link. Mulazzani and Vesnin [MV] have shown that the double branched covers of the links L1 and L2 are the same as the manifolds obtained by doing (a, c, 1, · · · , 1) -surgery and (a, 1, c, 1, · · · , 1)-surgery, respectively, on the link L12 .

Theorem 1.4.2. (Ba, 2019) Let a= and c

=

E (Q). If (p- q)(r - s)

=

0, then the double branched covers of the links L1 and L2 are excellent.

Proof. Assume that (p - q)(r - s)

=

O. Without loss of generality assume that r

=

s, and hence c

=

1. By Lemma 1.4.1, the double branched covers of the links L1 and L2 are the same as doing (a - l, c - 1)-surgery on the Whitehead link. Since c

=

1 and th linking number of the Whitehead link is zero, then H1(°I:,2(L1 )) and H1(°I:,2(L2 )) are infinite. Thus the manifolds °I:,2(Li) and 'I:,2(L1 ) are excellent.

CHAPTER II

HEEGAARDFLOERHOMOLOGY

----The aim of this chapter is to briefly present Heegaard Floer homology HF and L-spaces. At first we will state some tools which will be usefol for that. Our references are (Peter Ozsvath and Zoltan Szab6, 2004, 2005, 2006) , (John Milnor, 1963) and (James Singer, 1933).

2.1 Heegaard splittings and diagrams, Morse fonctions

Let M be a closed, oriented, connected 3-manifold. Let

f :

M lR be a fonction. The fonction fis called Morse fonction if all its critical points are non-degenerate. Assume

f

is Morse foction then it is called self-indexing if for each critical point x we have f(x)

=

index(x), where the index is the number of negative entries in the diagonalazed matrix of the Hessian matrix.

Proposition 2.1.1. (Milnor, 1963) Let M be a closed, oriented, connected 3-manifold. Then M admits a self-indexing Morse function with a unique inde.X 0 and index 3 critical points.

Definition 2.1.2. A Heegaard splitting for Mis a decomposition M

=

Uo UJ U1

Proof. Choose

f :

NI

----+

[ü,

3] a self-indexing Morse fonction with a unique index O and index 3 critical points. Then the level set E

=

1-

1 ( ~ ) is an oriented, connected clos d surfac with genus g equal to the number of index 1 critical points. Therefore, the decomposition

defines a Heegaard splitting of NI of genus g, with Heegaard surface E

=

1-

1(~)

-We can describe a handlebody U by ( a1 , · · · , a_{9 )} a g-tuple of disjoint simple closed curves embedded in âU bounding disks in U with [a1], • • • , [a_{9 ]} linearly independent in H1 ( aU) Co,! Z29 .

So, a Heegaard splitting

can be described by a Heegaard diagram (E, a,

/3 ),

where

• a= (a1 , · · · , a_{9 ) ,} g-tuple of simple closed curves embedded disjointly in E .

• /3

=

(/31 , · · ·

/3

_{9 ) ,} g-tuple of simple closed curves embedded disjointly in E.

• Each a i bounds a disk in U0 .

30 But a particular Heegaard splitting can be represented by many diagrams, consider the inclusion

t :

---+ Ui, where i

=

0, 1. Then there is a diagram for each choice of basis for ker(t*),

Different tuples _I are related up to isotopy by handleslides i.e

[ïi]

f---+

[ïi]

±

[ïj] =

[,:] with i =/= j (Singer, 1933). So we can write

{Heegaard splittings}

=

{Heegaard diagrams} / isotopy, handleslide

We compute H*(M) using.Heegaard diagrams:

Since Mis closed and connected, by Poincaré duality we have,

It remains to compute H1 (

M),

and this is done by using the Mayer-Vietoris se-quence, which yields

We can also adjoint Heegaard diagrams

(~, a, ,B), (~', a',

,B')

by

(~U~',

a LJ a', ,B LJ ,B').

2.2 Symmetric products, Whitney and holomorphie disks, spinc structures Let N be a smooth manifold. The symmetric product of N is the quotient

where the Sp-action permutes the factors of the product. Sym0_{(N) = {point}}

and Sym1_{(N) = N . In general this action is not free, therefore this may not be a}

manifold. But for closed surfac , we have the following theorem.

Lemma 2.2.1. (Ozsvâth and Szab6, 2004) Let I: be a Riemann surface. Then SymP(I:) is a smooth manifold of dimension 2p.

We consider the particular case where N = E is a closed surface and p =gis the genus of I:.

Let

Define := ~ /s₉, the action of S₉ on E9 - is free.

Let (I:, a,

,B)

be a He gaard diagram of !VI of genus g. Define

1fo = a1 X · · · X a₉ and 1f 13 = ,81 x · · · x ,8₉

32

Consider (E, a, (3, z ) a pointed Heegaard diagram of M of genus g. Then z induces a subspace

Vz

:= {z} x Sym9- 1

(E),

which is a codimension 2 submanifold of

Sym9

(E).

_{Futhermore, since z is in the complement of a and (3,}

Vz

_{is disjoint}

from 1I' °' and 1I' f3 .

One can show that H1(Sym9(E)) H1(E). Since we have shown that

we have the following isomorphism:

Definition 2.2.2. Let Il)) be the unit disk in C, c1 and c2 respectively the subarcs R e(z ) 2:: 0 and R e(z ) :::; 0 in oll)). Let x, y E 'II'°'

n

1I'f3. A Whitney disk joining x

and y is a continuous map u: Il))---+ Sym9_{(E) with the properties that} u(-i)

=

x,

u(i)

=

y,

u(ci)

C 'II'a,

u(c2)

C 1I'f3 ,

Set n2 ( x, y) :

=

{homotopy classes of Whitney disks from x to y}. Let 0 E n2 ( x, y). Define

We would like to study 0 E n2(x, y) by studying domains in E. Let R1 , · · · ,

Rri

be the clos ures of the corn ponen ts of E \ (

a

U (3 ), and choose

zi

E int

(Ri)

for each i

=

1, · · · ,n.

Definition 2.2.3. Let u be a Whitney disk from x to y. The domain of u is the

linear combination _n

D(u)

=

L

nzi (u)Ri i=l

Remark 2.2.4.

D(u)

depends only on the class of

u

in n2(x, y). When

u

is holomorphie, nz;( u) 2:: 0 for all i.

x to y: a :

[0,

1]

--+

'II'a, b:

[0,

1]

--+

11',a. Let v(x, y) be the image in H1(M) of b - a under the map t. Assume xi E ai

n

/3i and Yi E ai

n

fJ<r(i) where ΠE S_{9 .}

Definition 2.2.5. 1. A domain connecting x and y is a f ormal linear combi-nation A

=

L~i

aiR where ai E Z such that

• 8A1ai is a l-chain with boundary Yi - Xi • 8A1,ai is a l -chain with boundary xi - Y<r(i)

We denote the set of domains connecting x and y as D (x , y). 2. Given any 0 E 1r₂(x, y) , the domain of0 is

n

D(0) :=

L

nz;(0)Ri

i= l

3. A periodic domain is a 2-chain P

=

L~=l aiR such that 8P is a union of a and /3 circles (i.e fJfJP

=

0) and nz(P)

=

O.

Proposition 2.2 .6. (Ozsvath and Szabô, 2004) The map D: 1r2(x, y)

--+

D(x, y) is a

• bijection if g

>

2 • surjection if g

=

2

• injection if g

=

l.

34

1. v (x, y)

f-

0 implies that 1r2(x, y)

=

0

2. v(x,

y)=

0 implies that 'D(x,

y)

=/ 0

Since M is closed orientable 3-manifold, then it has a trivial Euler characteristic. Two nowhere vanishing vector fields X and Y are said to be homologous if there is a ball B in M such that XIM- B is homotopie to YIM- B· This gives an equivalence relation. Call

S(M)

the set of all equivalent classes. The elements of

S(NI)

are called Spinc-structure on M.

Fixing a base point z one can now define a map

as follows. Given

f

a Morse fonction on M compatible with the attaching circles

a1 , · · · , a_{9 ,} (31 , · • • , (3_{9 ,} for each x E 1l'cl<

n

11',9 we have a g-tuple of trajectories for

Vf

connecting the index 1 critical points to index 2 critical points. In a same way z gives a trajectory connecting the index O critical point with the index 3 critical point. Deleting tubular neighborhoods of these g

+

l trajectories, we obtain the

complement of disjoint union of balls in ]\If where the gradient vector field V

f

does not vanish. Since each trajectory connects critical points of different parties, the gradient vector field has index O on all the boundary spheres, so it can be extended as a nowhere vanishing vector field on M . Therefore a homology class of this vector field gives a Spinc-structure. This element will be denoted by

Sz(x) .

2.3 Holomorphie disks and HF

Given I; a complex structure this will induce a complex structure on Sym9(I;) ,

and fixed 0 E 1r_{2 (} x, y) . Define the set

For more details on the Maslov index see (Robbin and Salamon, 1993).

Since a composition of an element of M (0) with an automorphim of the unit disk gives another holomorphie disk and, as we want to count holomorphie disks, let define

.M(0)

to be the quoti nt by this action.

Definition 2.3.2. Assume

M

is a rational homology sphere i.e b1

(NI)

=

O. Let

(E, a,

/3,

z ) be a pointed Heegaard diagram of genus g for M and s E S(M). Pick

a complex structure on E and a suitable perturbation of the induced complex struc-ture on Sym9(E). Let CF(M, a,

/3,

s) be the free abelian group generated by the

points x E 'Il'c~

n

11',a such that Sz(x)

=

s . De.fine the map

â: CF(NI,a ,/3,s)-+ CF(M,a,/3,s)

by

âx

=

IM(0)1 ·

y

{yE1ron1f,B, 0E1r2(x,y) 1 S , (y) =s, µ(0) = 1, n,(0)=O}

Remark 2.3.3. T he fact that b1 (NI)

=

0 ensures the existency of a 0 E 1r₂(x, y) such that nz(0)

=

0 for any x, y E 11'0

n

11',a. The summation is finite.

Theorem 2.3.4. (Ozsvath and Szab6, 2004) The map â is a difj'erential, that is 82

=

_O.

Therefore (CF(lilf, a,

/3,

s) , â) is a complex chain and we denoted its homology group by HF(M, a, /3, s).

36

Theorem 2.3.5. (Ozsvath and Szab6, 2004) The homology HF(M, a,

/3,

s) does not depends to the chaise of a particular pointed Heegaard diagram.

(Ozsvath and Szab6, 2004) Therefore we can reduce the notation of HF(M, a,

/3,

s) to

HF(

M, s). Define the Heegaard Floer homology of M by

HF(M):=

L

HF(M,s)

sES(M)

Definition 2.3.6. Let x, y E ]'°' n ]'/J with v(x, y)= 0 and 0 E n2(x, y) . Define

gr(x, y)

=

µ(0) - 2nz(0)

Since

b

1

(M)

= 0, gr(x, y) does not depend on the choice of 0 E n2(x, y) . Since the

sum in fJ counts only holomorphie disks with µ(0) = 1 and nz(0) = 0, then fJ lowers the relative grading by 1. Therefore we can compute the Euler characteristic of HF(M).

Proposition 2.3.7. (Ozsvâth and Szab6, 2004) We have that rankHF(M)

2:

IH1(M) I

Example 2.3.8. The Heegaard Floer homology of

§

3 _is

_HF(§

_{3 ) c::,; Z.} 2.4 L-spaces

Definition 2.4.1. Let M be a closed, oriented, connected 3-manifold. Then M is called an L-space if it is a rational homology sphere with

rankHF(M) = IH1(M)

I-Definition 2.4.2. The set Q of quasi-alternating links is the smallest set of links which satisfies the following properties:

• det(L)

=

det(L0) + det(L00 ) ;

then L is in Q.

Such a crossing c is called a quasi-alternating crossing.

---

,...----._

Lo

Figure 2.1 : The resolutions L00 and L0 respectively.

Theorem 2.4.3. (Ozsvath and Szab6, 2005) The double branched caver of a quasi-alternating link, E2 ( L) is an L-space, i.e

CHAPTER III

STRONGLY QUASIPOSITIVE QUASI-ALTERNATING LINKS AND MONTESINOS LINKS

3.1 Introduction

In this chapter we assume, unless otherwise stated, that links are oriented and con-tained in §3 . A Seifert surface S is quasipositive if it is isotopie to a braided Seifert surface

S[b]

forsome positive bandword b (see Rudolph [Ru5]). A link Lis strongly quasipositive if it has a quasipositive Seifert surface. Let L be a link. Let x(L) (x4 (L)) be the maximal Euler characteristic number of an oriented 2-manifold

without closed components smoothly embedded in §3 (in D4 respectively) with boundary L . Let g(L), g4(L), and g!0P(L) be the 3-sphere genus, smooth 4-ball

genus, and topologically (locally fiat) 4-ball genus of L, respectively. Let O" be the

signature of L.

Let L be a link. We say that Lis definite if g(L)

=

½( lü(L)I - (m - 1)), where m is the number of components of L.

For an oriented quasi-alternating link L with a quasi-alternating crossing

c,

the link L0 is given as in Figure 3.2.

Theorem 3.1.1. ([Ba2]) Let L be an oriented alternating link with a quasi-alternating crossing c such that L0 is alternating. Then L is definite if and only

1. fibred, or more generally

2. has a unique minimal genus Seifert surface.

Then L is definit e if and only if it is strongly quasipositive (up to mirroring). Based in Theorem 3.1.1 and Theorem 3.1.2 we made the following conjecture: Conjecture 3.1.3. Let L be an oriented quasi-alternating link. Then L is definite if and only if it is trongly quasipositive ( up to mirroring).

Proposition 3.1.4. ([Ba2]) If L is an oriented quasi-alternating link which is definite then L0 is also definite.

Let M(e; t1 , · · · , tr) be a Montesinos knot or link, where ti

=

!:

= [ci, ··· , c~iJ

We make the following assumptions below: ai

>

1 and -ai

<

f3i

<

ai, with gcd(ai,

/3i )

=

1. We follow the convention that

1 1

1

Proposition 3.1.5. ([Ba2]) Let L

=

M(e;t1 , · · · , tr) be a Montesinos link with e

1. If e 0 and ti

=

[2qi, 2si, 2qi , 2st · · · , 2q~i , 2s~J where q;

<

0, s_;

<

0 for any i

=

l , · · · , r1 j

=

l , · · · , ni, then L is strongly quasipositive.