Parametrized automata simulation and application to service composition

Any correspondence concerning this service should be sent

to the repository administrator:

tech-oatao@listes-diff.inp-toulouse.fr

This is a publisher’s version published in:

http://oatao.univ-toulouse.fr/22622

To cite this version:

Belkhir, Walid and Chevalier, Yannick and

Rusinowitch, Michaël Parametrized automata simulation and application to

service composition. (2015) Journal of Symbolic Computation, 69. 40-60.

ISSN 0747-7171

Official URL

DOI :

https://doi.org/10.1016/j.jsc.2014.09.029

Open Archive Toulouse Archive Ouverte

OATAO is an open access repository that collects the work of Toulouse

researchers and makes it freely available over the web where possible

Parametrized

automata

simulation

and

application

to

service

composition

✩

Walid Belkhir

a

,

Yannick Chevalier

b

,

Michael Rusinowitch

a a_{INRIANancy–GrandEst&LORIA,54600Villers-lès-Nancy,France}

b_{UniversitéPaulSabatier&IRITToulouse,France}

a

b

s

t

r

a

c

t

Keywords: Parametrizedautomata Service Simulation preorder Compositionsynthesis Infinite alphabet

The service composition problemasks whether, givenaclient and a community of available services, there exists an agent (called the mediator) thatsuitablydelegatesthe actionsrequested bythe client to the available community of services. We address this problem in a general setting where the agents communication actions are parametrized by data from an infinite domain and possibly subjectto constraints.Forthispurpose, wedefine param-etrized automata (PAs), where transitionsare guarded by conjunc-tion ofequalities and disequalities.We solve the service composi-tion problem by showing that the simulation preorder of PAs is decidable and devising a procedure to synthesize a mediator out of a simulation preorder. We also show that the Nonemptiness problemofPAs isPSPACE-complete.

1. Introduction

Service Oriented Architectures (SOA) consider services as self-contained components that can be published, invokedover anetwork and combined withother services throughstandardized protocols in order to dynamically build complex applications (Alonso et al., 2004; Reisig, 2008). Service com-position is required when none of the existing services can fulfil some client needs but a suitable coordination of them would satisfy the client requests. How to find the right combination and how toorchestratethiscombination are amongthe keyissues for servicearchitecture development.

✩ ThisresearchispartlysupportedbyFP7NESSoSproject (Grantno.256980),andextendssubstantiallyresultspresentedat SYNASC2013.

E-mailaddresses: walid.belkhir@inria.fr (W. Belkhir),ychevali@irit.fr (Y. Chevalier),rusi@loria.fr (M. Rusinowitch). http://dx.doi.org/10.1016/j.jsc.2014.09.029

Servicecompositionhas beenstudied in manyworkse.g.Hull and Su (2005), Martín et al. (2012),

Berardi et al. (2008). The related problem of system synthesisfrom libraries of reusablecomponents has been thoroughly investigatedtoo Lustigand Vardi (2009).

In this paper we address the composition synthesis problem for web services in which the agents are parametrized, i.e. the client and the available services exchange data ranging over an infinite domain and they are possibly subject to some dataconstraints. More precisely, the compo-sition synthesis problem we consider can be stated as follows: (e.g. Nourine and Toumani, 2012; Cheikh, 2009): given a client and a community of available services, compute a mediator which will enable communication between the client and the available services in such a way that each client request isforwardedto anappropriateservice.

This problemwasreduced to show that thereexists asimulation relation betweenthe target ser-vice (specifyinganexpectedservicebehaviourforsatisfying theclientrequests)and theasynchronous product ofthe availableservices.Ifsuchasimulationrelationexiststhenit canbe easilyusedto gen-erate a mediator, that is a function that selects at each step an available service for executing an action requested by theclient.

One of the most successfulapproachesto compositionamounts toabstract services as finite-state automata (FA) and applyavailable tools from automata theory tosynthesize a new service satisfying the given client requests from anexisting communityof services. However it is notobvious whether the automata-based approachtoservicecompositioncan stillbe appliedwithinfinite alphabetssince simulation often gets undecidable in extended models like Colombo (Akroun et al., 2013). Starting from theapproach initiatedin Belkhiret al. (2013)our objectiveisto defineexpressiveclassesof au-tomata on infinite alphabetswhich are well-adapted to the specification and composition of services and enjoynice closure properties and decidable simulationpreorder. Compared toour previouswork (Belkhiretal.,2013) weintroduceastrictly moreexpressiveservicespecificationformalismthanks to the use of guardedtransitions.

1.1. Contributions

Inthispaper werely on automata-based techniquestotackle the problemof composition synthe-sis of parametrized services. We introduce anextension of automata called parametrizedautomata or

PAs, that allows a natural specification and decidable synthesis of parametrized services. In PAs, the transitions are labelled by letters or variablesranging overan infinitealphabets and guarded by con-junction of equalities and disequalities. Besides, some variables canbe refreshed in some states,that is, these variables canbe released so that new letters canbe bound to them. Refreshing mechanism is useful when computationsstart new sessions.

We introduceasimulation preorder forPAs and show its decidability.The proofrelies on a game-theoretic characterizationof simulation.We show howthisresult canbeapplied tothesynthesisofa mediator for web services.Althoughnot detailedhere, the simulationdecisionprocedure canhelpto solve language containment problems which are important ones in formal verification. The potential applicability of our model in verification also follows from the fact that PAs are closed under inter-section, union, concatenation and Kleene operator. An advantage of PAs with respect to alternative automatamodelsis thesuccinctservice representationtheypermit, thankstothe useof variable and guards (e.g. with negative conditions). This benefit will be formally supported in the paper. Finally we have shown that for PAs the Nonemptiness problem is PSPACE-complete, and the membership problemis NP-complete.

1.2. Relatedwork

Logic-based techniques for the synthesis problem (e.g. Feuillade and Pinchinat, 2007; Pathak et al., 2007)havebeen consideredinthe literature.Narayananand McIlraith (2002)relyon thesituation calculusandGologlogic programminglanguageforautomaticconstructionofWebservices.Waldinger (2001)employsSnark theorem-provertogetsoftwareagentsdistributedoverthenettocooperateand answer aqueryorperformatask.Manyworkshavealsoaddressed servicecompositionbyelaborating planning techniquesfromartificialintelligence(e.g. Pistoreet al.,2005; Hoffmann,2008; Hoffmannet

al., 2007). Service compositionproblem, in the case of finitesets of actions, is reduced in Balbiani et al. (2010) toadecidable controlproblemfor nondeterministic communicatingautomata.

In the Roman model web services behaviours are specified with activity-based finite state au-tomata. The corresponding services composition problem was reduced to PDL satisfiability (e.g.

Berardi et al., 2003; Cheikh, 2009). Thanks to the relation between PDL and Description Logic (DL), several DL reasoning tools can be applied in the latter case. The composition problem can also be reduced to computing a simulation preorder as in Berardi et al. (2008). This approach cannot be ex-tendedtothedata-centric

Colombo

modelof Berardietal. (2005)for servicessinceaswementioned above simulation is undecidable in this case. Known decidable cases of the composition synthesis problemin Colomboframework need restrictionssuch as determinismor finitedomain for values.

The

Colombo

k,b model is a restrictionof the

Columbo

model in which suitablehypotheses en-sure that only a finite number of domain values (and thus a finite number of different records) are considered. In Berardi et al. (2005) the composition problem for this model was proven decidable when the clients are represented as deterministic guarded automata. Besides, their proof relies on (a priori) bounding two parameters of the synthesized mediator. More precisely, they assume that the mediator is

(

p

,

q

)

-bounded, where p is the number of states, and q is the number of variables representing records in its global store. Theyconjecture thattheir decidability resultcan be obtained without mentioningthese bounds.We havebeenable toprove thatthere wasno need foraboundq

on variablesin the synthetised servicenor on its number p ofstates.

In De Giacomo et al. (2013), the authors address a related problem of synthesizing a controller generator from which one can compute new controller when the environment or the available ser-viceschange.The controllerimplementsafully controllabletarget behaviourby suitablycoordinating available partially controllable behaviours that are to execute within a shared, fully observable, but non-deterministic environment. The behaviours and the environment are represented as finite state transitionsystems. Theyconstructatableofstates relatedin asimulation, andare abletoupdate this table on the fly when the available services change. For efficiency reasons they also consider safety games for generatinganew controller fromthistable.

Thoughour resultsonlyaddressthesynthesisofonecontrollerinanunmutablesetting,our under-lying model is more general than finite transition systems as it allows the exchange of datafrom an infinite domain. Though our simulation game also uses a bounded number of constants, it is worth mentionning that an unbounded execution of the synthesized controller can handle an unbounded number of differentconstants.

In Hassen et al. (2008) the authors also obtain an interesting positive result for the case where services are described by finite state machines but the number of instances of existing services that canbe used in agivencomposition isnotbounded apriori.

Several automata models have been designed recently for infinite alphabets. However they have not been applied to service composition.

Usages

nominal calculus (Degano et al., 2012) is a com-putational model based on infinite alphabets and dynamic creation of resources. PAs are incompa-rable with

Usages

. We give a procedure to decide the simulation preorder for PAs. Simulation has never been investigated for related classes of automata over infinite alphabets (Neven et al., 2004; Kaminski and Zeitlin, 2010; Degano et al., 2012), with the exception of the strictly less expressive class of fresh-variable automata in Belkhir et al. (2013). Compared to Belkhir et al. (2013) the proof technique has been improved and allows us to extract easily a mediator from a simulation game. Moreover we have shown that the complexity of Nonemptiness for PAs is higher than for the class defined in Belkhiret al. (2013).

Webservices behaviourshavebeen describedby contractsin severalworks(Castagnaet al.,2007). A theory of contracts that formalises the compatibility of a client to a service has been devised in

Castagna et al. (2009). Contracts ensures that every possible interaction between compatible clients andservices canbecompletedsuccessfully.ThefinitecontractsstudiedinCastagnaetal. (2009)seem tobe less expressive thanPAs for specifyingbehaviours.

Aservicebehaviourcanbe expressed byaPetri nettoo (seeHamadiand Benatallah, 2003),where actions are modelled by transitions and the state is modelled by places. However it seems hard to extendour synthesisresult toPetri nets servicespecification because of the negativeresult of Jancar

(1995). Howeversimulationbetweenfinitestatemachinesandwell-structuredtransitionsystems(and so Petrinets) is decidableas shown in Finkel andSchnoebelen (2001).

1.3. Paperorganization

Section 2 recalls standard notions. Section 3 introduces the new class of parametrized automata. Section 4 studies closure properties and the complexity of Nonemptiness for PAs. Section 5 uses the parametrized automata to solve the composition synthesis problem, more precisely, Section 5.1

introduces thesimulation preorderof PAs, Section5.2showsits decidability,Section5.3appliesthese resultstoservicecompositionby devising aprocedurefor mediator synthesis,and Section5.4applies thisprocedure to anexample. Future workdirectionsare given inSection 6.

2. Preliminaries

Let

X

be a finite set of variables,

Σ

an infinite alphabet of letters. A substitution

σ

is an idem-potentmapping

{

x₁

7→

α

1

,

. . . ,

xn

7→

α

n

}

∪

S

a∈Σ

{

a

7→

a

}

withvariablesx1

,

. . . ,

xn in

X

and

α

1

,

. . . ,

αn

in

X ∪ Σ

. We call

{

x1

, . . . ,

xn

}

its properdomain, and denote it by dom

(

σ

)

. We denote by Dom

(

σ

)

the set dom

(

σ

)

∪ Σ

. We denote by codom

(

σ

)

the set

{

a

∈ Σ | ∃

x

∈

dom

(

σ

)

s.t.

σ

(

x

) =

a

}

. If all the

αi

,

i

=

1

. . .

n are letters then we say that

σ

is ground. The empty substitution (i.e., with an empty proper domain) is denoted by

∅

. The set of substitutions from

X ∪ Σ

to a set A is denoted by

ζ

X ,A, or by

ζ

X, or simply by

ζ

if there is no ambiguity. If

σ

1 and

σ

2 are substitutions that co-incide on the domain dom

(

σ

1

)

∩

dom

(

σ

2

)

, then

σ

1

∪

σ

2 denotes their union in the usual sense. If

dom

(

σ

1

)

∩

dom

(

σ

2

)

= ∅

then we denote by

σ

1

⊎

σ

2 their disjoint union. We define the function

V : Σ ∪ X −→ P(X )

by

V(

α

)

= {

α

}

if

α

∈ X

, and

V(

α

)

= ∅

, otherwise. For a function F

:

A

→

B,

and A′

⊆

A, the restrictionof F on A′ is denotedby F|A′.

Definition1.A two-players game is atuple

h

PosE

,

PosA

,

M

,

p⋆

i

, where PosE

,

PosA are disjointsets of

positions:

Eloise

’s positions and

Abelard

’s positions. M

⊆ (

PosE

∪

PosA

)

× (

PosE

∪

PosA

)

is a set

of moves, and p⋆ _{is the starting position. A strategy for the player}

_Eloise

_{is afunction}

ρ

_:

_Pos

E

→

PosE

∪

PosA, such that

(℘,

ρ

(℘))

∈

M for all

℘ ∈

PosE. A (possibly infinite) play

π

= h℘

1

,

℘

2

,

. . .i

follows a strategy

ρ

for player

Eloise

iff

℘

i+1

=

ρ

(℘

i

)

for all i

∈ N

such that

℘

i

∈

PosE. Let

W

be a (possibly infinite) set of plays. A strategy

ρ

is winning for

Eloise

from a set S

⊆

PosE

∪

PosA

according to

W

iff everyplaystartingfrom apositionin S andfollowing

ρ

belongs to

W

.

3. Parametrizedautomata

In this section we define formally the class of PAs. Firstly, we illustrate the practical use of PAs througha servicecompositionproblem.

3.1. Amotivatingexample

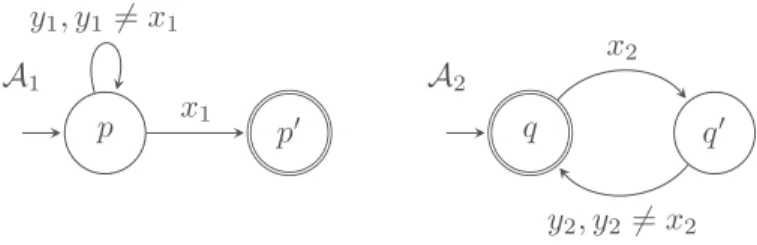
In Fig. 1 we have an e-commerce Web site allowing clients to open files, search for items in a largedomainthatcanbe abstractedasinfiniteand save themtoanappropriatefile dependingon the type of theitems(whether theyare in promotionor not).Thethree agents: CLIENT,FILEand SEARCH communicate with messages ranging over a possibly infinite set of terms. The problem is to check whetherFILEand SEARCHcanbe composedinorder tosatisfytheCLIENT requests.FollowingBerardi et al. (2008)the problemreducestofindasimulationbetweenCLIENT and theasynchronous product of FILE and SEARCH. We emphasize that the variables x and y are refreshed (i.e. freed to get a new value) when passing through the state p0. In the same way variables z and w are refreshed at p2. Thevariablesm andn are refreshedatq0;thevariables i and j arerefreshed atr0.Forsavingspace, a transition labelled by aterm, say

write(m, n)

, abbreviates successive transitionslabelled by the root symbol andits arguments, here

write

,

m

and

n

, respectively.We notice thatthisexamplecannot be handled within the subclass of fresh-variable automata (Belkhir et al., 2013) since they do not have

Fig. 1. PROM example.

guards. InSubsections 5.3and 5.4 wewill show how our resultspermit to synthesizea mediator for suitablyscheduling the availableservices and providethe target servicetothe client.

Before introducing formally the class of PAs, let us first explain the main ideas behind them. The transitions of a PA are labelled with letters or variables ranging over an infinite set of letters. These transitions can also be labelled with guards consisting of equalities and disequalities. Its guard must be true for the transition to be fired. We emphasize that while reading a guarded transition some variables of the guard might be free and we need to guess their value. Finally, some variables are refreshed in some states, that is, variables can be freed in these states so that new letters can be assigned tothem. Firstly,we introducethe syntax andsemantics of guards.

Definition2. Theset

G

of guards over

Σ ∪ X

isinductivelydefined as follows:

G

:= true |

α

= β |

α

6= β |

G

∧

G

,

where

α

,

β ∈ Σ ∪ X

. We write

σ

|H

g ifasubstitution

σ

satisfies aguard g.

We notice thatadding the disjunction operator to the guards would not increase the expressivity of our model.Aguard isatomiciff it iseither

true

, anequality, or aninequality.Let g_i, i

=

1

,

. . . ,

n,

be atomic guards. Then we define the free variables of a guard by extending the function

V

to a mapping

Σ ∪ X ∪ G

→ P(X )

as follows:

V(

V

_i=1,ngi

)

=

S

i=1,n

V(

gi

)

and

V(

α

∼ β)

= V(

α

)

∪ V(β)

,

where

∼

belongs to

{=, 6=}

and

α

,

β ∈ Σ ∪ X

. The finite set of letters of a guard g can be defined similarly and it willbe denotedby

Σ

g. The application of a substitution

γ

to a guard g, denoted by

γ

(

g

)

, isdefined in theusual way.We shallwrite

σ

⊢

g if thereexistsasubstitution

γ

s.t.

σ

⊎

γ

|H

g.

The formaldefinitionof PAsfollows.

Definition3. APA is atuple

A

= hΣ,

X ,

Q

,

Q0

,

δ,

F

,

κ

i

where

• Σ

is aninfinite setof letters,

• X

is afiniteset ofvariables,

Fig. 2. Two PAs A1 and A2 where thevariable y1 isrefreshed inthestate p,and thevariables x2,y2 are refreshed inthe

state q.

•

Q0

⊆

Q is asetof initial states,

• δ :

Q

× (Σ

A

∪ X ∪ {

ε

})

× G

→

2Q is atransition function where

Σ

A is afinitesubset of

Σ

,

•

F

⊆

Q is asetof accepting states,and

•

κ

: X →

2Q iscalled the refreshing function.

The run of a PA is defined over configurations. A configuration is a pair

(

γ

,

q

)

where

γ

is a sub-stitution such that for all variables x in dom

(

γ

)

,

γ

(

x

)

is the current value of x, and q is a state of the PA. Intuitively, when a PA

A

is in state q, and

(

γ

,

q

)

is the current configuration, and there is a transition qα

→

,gq′ in

A

then:

i) if

α

is a free variable (i.e.

α

∈ X \

dom

(

γ

)

) then

α

stores the input letter and some values for all the other free variables of

γ

(

g

)

are guessed such that

γ

(

g

)

holds, and

A

enters the state

q′

∈ δ(

q

,

α

,

g

)

,

ii) if

α

is a boundvariable or a letter(i.e.

α

∈

Dom

(

γ

)

) and

γ

(

α

)

is equal tothe input letter l then

some valuesfor all the freevariables of

γ

(

g

)

are guessed suchthat

γ

(

g

)

holds,and

A

entersthe stateq′

_{∈ δ(}

_q

_,

α

_,

_g

₎

_.

Inboth caseswhen

A

entersstateq′ _{all thevariableswhichare refreshedin q}′ _{arefreed.Thusthe} purpose of guards istocompare letters and toguess newletters that mightbe readafterward.

Fora PA

A

, we shall denote by

Σ

A the finiteset of letters thatappear in the transition function of

A

. We shall denote by

κ

−1

:

Q

→

2X the function that associates to each state of the PA the set of variables beingrefreshed in thisstate. That is,

κ

−1

₍

_q

₎

_{= {}

_x

_{∈ X |}

_q

_∈

_κ

₍

_x

_)}

_.

Theformal definitionsof run and recognizedlanguagefollow.

Definition4. Let

A

= hΣ,

X ,

Q

,

Q₀

,

δ,

F

,

κ

i

be a PA. We define atransition relation overthe config-urations as follows:

(

γ

1

,

q1

)

⇒ (

a

γ

2

,

q2

)

, where a

∈ Σ ∪ {

ε

}

, iff there existsa substitution

σ

such that

dom

(

σ

)

∩

dom

(

γ

1

)

= ∅

and either:

i) a

∈ Σ

and in this case thereexists alabel

α

∈ Σ ∪ X

such thatq₂

∈ δ(

q₁

,

α

,

g

)

,

(

γ

1

⊎

σ

)(

α

)

=

a,

(

γ

1

⊎

σ

)

|H

g and

γ

2

= (

γ

1

⊎

σ

)

|D, with D

=

Dom

(

γ

1

⊎

σ

)

\

κ

−1

(

q2

)

. Or,

ii) a

=

ε

and in thiscase

(

γ

1

⊎

σ

)

|H

g and

γ

2

= (

γ

1

⊎

σ

)

|D, with D

=

Dom

(

γ

1

⊎

σ

)

\

κ

−1

(

q2

)

. We denote by

⇒

⋆ the reflexive and transitive closure of

⇒

. For two configurations c

,

c′ and a letter

a

∈ Σ

, we write c

→

a c′ iff there exists two configurations c₁ and c₂ such that c

⇒

ε ⋆c₁

⇒

a c₂

⇒

ε ⋆c′.

A finite word, or a trace, w

=

a1a2

. . .

an

∈ Σ

∗ is recognized by

A

iff there exists a run

(

γ

0

,

q0

)

a1

→

(

γ

1

,

q1

)

a2

→ . . .

→ (

an

γ

n

,

qn

)

, such thatq0

∈

Q0 andqn

∈

F . Theset of wordsrecognizedby

A

is denoted

by L

(A)

.

Example 1. Let

A

₁ and

A

₂ be the PAs depicted above in Fig. 2 where the variable y₁ is re-freshed in the state p, and the variables x2

,

y2 are refreshed in the state q. That is,

A

1

=

½

δ1(

p

,

y1, (y1

6=

x1)) = {p

}

and

δ1(

p

,

x1, true) = {p′

},

and

κ

1

(

y1

) = {

p

}

And

A

₂

= hΣ,

{

x2

,

y2

},

{

q

,

q′

},

{

q

},

δ

2

,

{

q′

},

κ

2

i

with

½

δ

2

(

q

,

x2

, true) = {

q′

}

and

δ(

q′

,

y2

, (

y2

6=

x2

)) = {

q

},

and

κ

2(x2) =

κ

2(y2) = {q

}.

We notice that while making the first loop over the state p of

A

₁, the variable x1 of the guard

(

y₁

6=

x₁

)

isfree and its valueis guessed.Then thevariable y₁ is refreshedin p,and at eachloop the input lettershould be different than thevalue of the variable x1 already guessed.More precisely, the behaviourof

A

₁ on aninput wordisas follows. Beingin the initialstate p,either:

•

Makesthetransition p

→

p′ by readingthe inputsymbolandboundingthe variable x1 toit, then entersthe state p′_{. Or,}

•

Makesthe transition p

→

p by:

(1) Reading theinput symboland bounding the variable y1 toit.

(2) Guessing a symbol in

Σ

that is different than the input symbol (i.e. the value of x1) and boundsthe variable y₁ tothe guessedsymbol, then entersthe state p.

(3) From the state p, refresh the variable x1, that is, it is no longer bound to the input symbol. Then,start again.

We illustratethe runof

A

₁ on the word w

=

abbc, startingfromthe initialconfiguration

(∅,

p

)

as follows:

(∅,

p

)

→

a

¡

{

x1

7→

c

},

p

¢

b

→

¡

{

x1

7→

c

},

p

¢

b

→

¡

{

x1

7→

c

},

p

¢

c

→

¡

{

x1

7→

c

},

p′

¢

Hence, thelanguage L

(A

1

)

consistsofall thewords in

Σ

⋆ in whichthelast letterisdifferentthan all the other letters. By following similar reasoning, we get L

(A

2

)

= {

w1w′₁

· · ·

wnwn′

|

wi

,

w′_i

∈ Σ,

n

≥

1

,

and w_i

6=

w′

i

,

∀

i

∈ [

n

]}

.

4. Propertiesofparametrizedautomata

Closure properties are important for the modular development of services. PAs enjoy the same closurepropertiesas finiteautomataexceptforcomplementation(seeTheorem 5).Moreoverchecking whethera servicesatisfies a policy canoften be reduced toshow that the intersection of the service PA with a PA specifying the forbidden executions is empty. We give an example in Subsection 4.1. Since the class of PAs is closed under intersection, (Theorem 5), and Nonemptiness is decidable as shownin Subsection4.1,we canperformthisverification.Onthe otherhandifthe policyisexpressed as a language of authorized traces and if this language is recognized by a PA, say

Q

, then checking whetheraservice

M

respects the policy amountstocheckthe containment L

(M)

⊆

L

(Q)

. However, the containment for PAs is undecidable, as stated in Theorem 6 below. In practical cases it is often sufficient (in order toget this inclusion)to show the existence of asimulation preorder between

M

and

Q

: thisproblemis decidable,as we prove itin the following (Theorem 26).

Therefore we study the closure properties of PAs and the decidability and complexity of classical decision problems: Nonemptiness (given

A

, is L

(A)

6= ∅

?), Membership (given a word w and

A

, is

w

∈

L

(A)

?), Universality (given

A

, is L

(A)

= Σ

∗?), and Containment (given

A

₁ and

A

₂, is L

(A

1

)

⊆

L

(A

2

)

?).

We have that:

Theorem5.PAsareclosedunderunion,concatenation,Kleeneoperatorandintersection.Theyarenotclosed undercomplementation.

Proof. Let

A

₁

= hΣ

1

,

X

1

,

Q1

,

q1₀

,

δ

1

,

F1

,

κ

1

i

and

A

2

= hΣ

2

,

X

2

,

Q2

,

q2₀

,

δ

2

,

F2

,

κ

2

i

be two PAs. Up to variable renaming it issufficient to considerthe closure under the above operations for two PAsthat do notsharevariables.

The closure under Kleene operation and concatenation holds since PAs have

ε

-transitions. More precisely, theKleene closure

A

⋆₁ amounts toaddingan (unguarded)

ε

-transition between the accept-ing states and initial states of

A

₁. Andthe concatenation

A

₁

· A

2 amounts toaddingan (unguarded)

ε

-transition between theaccepting states of

A

₁ and the initialstates of

A

₂.

The closure under intersection follows from the fact that the intersection of two PAs

A

₁ and

A

₂

denoted by

A

₁

∩ A

2 canbe defined as follows:

A

1

∩

A

2

=

­

Σ1

∪ Σ2,

X

1

∪

X

2,Q1

×

Q2,q1₀

×

q2₀

, δ,

F1

×

F2,

κ

®

,

where

δ

and

κ

are defined by:







(

q′₁

,

q′₂

) ∈ δ((

q1

,

q2

), (

α

1

, (

α

1

=

α

2

) ∧

g1

∧

g2

))

iff q′₁

∈ δ1

(

q1

,

α

1

,

g1

)

and q′₂

∈ δ2(

q2,

α

2,g2).

(

q1

,

q2

) ∈

κ

(

x

)

iff q1

∈

κ

1

(

x

)

or q2

∈

κ

2

(

x

).

The proof that L

(A

1

)

∩

L

(A

2

)

=

L

(A

1

∩ A

2

)

is straightforward.

✷

Forthe maindecisionprocedure we havethat:

Theorem6.ForPAs,MembershipisNP-complete,UniversalityandContainmentareundecidable.

Proof. Let

A

be a PAand w

=

w1

· · ·

wn awordin

Σ

⋆.

Fortheupper boundofthe membership,anon deterministicpolynomialalgorithm guessesapath in

A

of length

|

w

|

such that the final state is accepting; and a series of substitutions

σ

1

,

. . . ,

σ

|w|, where

σi

: X → {

w_j

,

1

≤

j

≤ |

w

|}

, then checkswhether the corresponding run on w is possible. The lowerbound,i.e.theNP-hardness,followsfromthefactthatthemembershipproblemforPAswithout guards, i.e. fresh-variable automata, isNP-complete (Belkhir etal., 2013,Theorem3).

TheundecidabilityofContainmentandUniversalityisaconsequenceoftheundecidabilityof these problems for subclassesof PAs(Nevenet al., 2004).

✷

Itis worth mentionningthat regularlanguagescanbe complementedwithin the class of PAs:

Proposition7.ThecomplementofaregularlanguageisPA-recognizable.Thatis,givenaFA F thereexistsa PA

A

suchthatL

(A)

= Σ

⋆

\

L

(

F

)

.

Proof. The construction of

A

is similar tothe one forFAs (over afinite alphabet).We assume that F

is deterministic. Firstly, we make the completion of F , i.e. we construct anequivalent PA so that for each stateq of F and for each letterl

∈ Σ

there is aunique transition outgoing from q that readsl.

Secondly, we swapthe accepting and non-acceptingstates.

Formally, assume F

= hΣ,

Q

,

p0

,

δ,

F

i

, with Q

= {

q1

, . . . ,

qn

}

, and define

A

= hΣ,

X ,

Q′

,

p0

,

δ

′

,

F′

,

κ

i

by































X

= {

x1

, . . . ,

xn

}

Q′

=

Q

∪ {

qi1

,

qi2

,

i

=

1, . . . ,n

}

F′

_{= (}

_Q

_\

_F

_{) ∪ {}

_q i1

,

qi2

,

i

=

1, . . . ,n

}

δ

′

= δ ∪ {

qi xi,Vj(xi6=aj)

−→

qi1

|

for all aj s.t. qi a_j

→

qi′

∈ δ} ∪ {

q_i2 x_i

→

qi2

}

κ

(

xi

) = {

qi2

}

Notice that F rejects aword w iff

A

accepts w.

✷

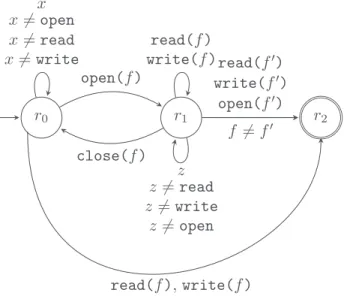
Fig. 3. A usage policy for opening and reading files.

4.1. NonemptinessisinPSPACE

We motivate the study of PA Nonemptiness problem through an example of a service policy for reading and writing files, which is a variant of the example in Degano et al. (2012) and Reger et al. (2013). The PA of Fig. 3 defines a usage policy for opening and reading files by specifying (i.e. accepting)the forbiddenexecutions. Itstates that(i) afile named f mustbe openbefore beingused, where f is a variable,and (ii) the number of files which are open at the same time is at most one. Moreprecisely onceafile f is openthe PA entersstater1 allowingthe file f to be readand written. Besides, any attempt to read or write in a file whose name is different than f leads the PA to the offending state r₂. On the other hand, starting from r₀ any attempt to read or write in a file that is not open leads the PA to the offending state r2. We recall that a transition labelled by a term, say

open(f)

, abbreviates two successive transitions labelled by the root symbol and its arguments, here

open

and f , respectively. In this PA, the variables x and f are refreshed at r₀, the variable z

is refreshed at r1, and the variables f′ is not refreshed in any state. As mentioned above, checking whether a service specified by PA M (with all states accepting, to be simple) respects the policy amountstocheck the emptinessof M

∩

P .

We recall that Nonemptiness is NL-complete for the subclass of fresh-variable automata (Belkhir et al., 2013) and it is NP-complete for the subclass of registerautomata (Sakamoto and Ikeda, 2000). Firstly we show that Nonemptiness is in PSPACE. Given a PA

A

, we shall show that

A

recognizes a non-empty language over

Σ

iff

A

recognizes a non-empty language over a finite set of letters. For thispurpose,and in order torelatethe two runsof

A

(the oneover aninfinitealphabet and the one overa finitealphabet)we introduceacoherence relation betweensubstitutions.

Definition8. Let C bea finite subset of

Σ

. The coherence relation

✶

_C

⊆ ζ × ζ

betweensubstitutions is defined by

σ

¯

✶

C

σ

iff the threefollowing conditionshold:

(1) dom

( ¯

σ

)

=

dom

(

σ

)

,

(2) If

σ

¯

(

x

)

∈

C or

σ

(

x

)

∈

C then

σ

¯

(

x

)

=

σ

(

x

)

, for any variable x

∈

dom

(

σ

)

, and (3) forany variables x

,

y

∈

dom

(

σ

)

,

σ

¯

(

x

)

= ¯

σ

(

y

)

iff

σ

(

x

)

=

σ

(

y

)

.

The claimsin the following lemma are nothard toprove.

Lemma9.LetC

⊆ Σ

beafinitesetofletters,

σ

¯

and

σ

twosubstitutions,x,anda aletterinC .Thefollowing hold.

(1) If

σ

¯

✶

_C

σ

then

|

codom

( ¯

σ

)|

= |

codom

(

σ

)|

.

(2) If

σ

¯

✶

_C

σ

andD

⊆

Dom

(

σ

)

then

σ

¯

|D

✶

C

σ

|D.

(3) If

( ¯

σ

1

⊎ ¯

σ

2

)

✶

(

σ

1

⊎

σ

2

)

withdom

( ¯

σ

i

)

=

dom

(

σ

i

)

,then

σ

¯

i

✶

σ

i,fori

=

1

,

2.

(4) If

σ

¯

✶

_C

σ

and

γ

isasubstitutionwithdom

(

γ

)

∩

dom

(

σ

)

= ∅

andcodom

(

γ

)

⊆

C ,then

σ

¯

⊎

γ

✶

_C

σ

⊎

γ

.

(5) If

σ

¯

✶

_C

σ

with

σ

¯

(

y

)

= ¯

a and

σ

(

y

)

=

a forsome variable y, and x

∈

/

dom

(

σ

)

then

σ

¯

⊎ {

x

7→ ¯

a

}

✶

_C

σ

⊎ {

x

7→

a

}

.

(6) If

σ

¯

✶

_C

σ

anda

¯

∈

/

C

∪

codom

( ¯

σ

)

anda

∈

/

C

∪

codom

(

σ

)

and x

∈

/

dom

(

σ

)

then

σ

¯

⊎ {

x

7→ ¯

a

}

✶

_C

σ

⊎

{

x

7→

a

}

.

(7) Letg beaguardsuchthat

Σ

g

⊆

C .If

σ

✶

C

σ

¯

,then

σ

|H

g iff

σ

¯

|H

g.

(8) Assumethat

σ

✶

_C

σ

¯

,andletg beaguardsuchthat

Σ

g

⊆

C .Then,

σ

⊢

g iff

σ

¯

⊢

g.

In order to prove that only a finite number of constants is needed to cover all possible moves in the simulation game, we have to prove that if two substitutions are equivalent wrt the winning condition—i.e., if

σ

₁

✶

_C

σ

2 where C will be the setof letters occurring in thetransitions of the simu-lation game—then for each substitution

γ

1, there existsa substitution

γ

2 such thatfor any transition with a guard g such that

σ

₁

⊎

γ

1

|H

g onealso has

σ

2

⊎

γ

2

|H

g. This substitution

γ

2 canactually be computed explicitely from

σ

1

,

σ

2

,

γ

1.

Inwhatfollowswelet S1

⊆ Σ,

S2

⊆ Σ

betwo (possiblyinfinite)setsofletters with

|

S1

\

S2

|

> |X |

and

|

S₂

\

S₁

|

> |X |

and S₁

∩

S₂

=

C

6= ∅

.

Definition10. We definethe functions

Θ

_CS1,S2

, Θ

_CS1,S2

: ξ

X,S₁

× ξ

X,S₁

× ξ

X,S₂

→ ξ

X,S₂

as follows.Let

σ

1

,

γ

1

∈ ξ

X ,S1,

σ

2

∈ ξ

X ,S2. Then,

Θ

S1,S2

C

(

σ

1

,

γ

1

,

σ

2

)

isdefined onlywhen

|

dom

(

γ

1

)|

=

1

and dom

(

γ

1

)

∩

dom

(

σ

1

)

= ∅

and

σ

1

✶

C

σ

2 by:

Θ

S1,S2 C

(

σ

1

,

γ

1

,

σ

2

) =











γ

1 if

γ

1

(

x

) ∈

C

{

x

7→

σ

2(y

)}

if

γ

1(x

) ∈

codom

(

σ

1) \C and

σ

1

(

y

) =

γ

1

(

x

),

y

∈

X

{

x

7→

get

(

S2

\

codom

(

σ

2

))}

if

γ

1

(

x

) ∈

S1

\ (

C

∪

codom

(

σ

1

))

where dom

(

γ

1

)

= {

x

}

. And

Θ

_CS1,S2

(

σ

1

,

γ

1

,

σ

2

)

is defined onlywhen dom

(

γ

1

)

∩

dom

(

σ

1

)

= ∅

by:

Θ

S1,S2 C

(

σ

1,

γ

1,

σ

2) =























Θ

S1,S2 C

(

σ

1

,

γ

1

,

σ

2

)

if

|

γ

1| =1

γ

₂′

⊎ Θ

S1,S2 C

(

σ

1

⊎

γ

1′

,

γ

1′′

,

σ

2

⊎

γ

2′

)

if

|

γ

1| ≥2,

γ

1

=

γ

1′

⊎

γ

1′′ and

|

γ

′ 1

| =

1, where

γ

′ 2

= Θ

S1,S2 C

(

σ

1,

γ

1′

,

σ

2) Thefunction

Θ

will be used in the proof of Lemma 12 and in the proof of the decidabilityof the simulation preorder in Section5.2. Letus nowprove that thisconstructioniscorrect.

Lemma11.Let

σ

,

γ

1

∈ ξ

X ,S1 and

σ

′

_{∈ ξ}

X ,S2 besubstitutionswithdom

(

σ

)

∩

dom

(

γ

1

)

= ∅

and

σ

✶

C

σ

′_.We

havethat

(

σ

⊎

γ

1

) ✶

C

¡

σ

′

⊎ Θ

_CS1,S2

¡

σ

,

γ

1

,

σ

′

¢¢

(1)

Proof. By induction on

|

dom

(

γ

1

)|

.

Base Case. If

|

dom

(

γ

1

)|

=

1 then assumedom

(

γ

1

)

= {

x

}

and let

γ

2

= Θ

_CS1,S2

(

σ

,

γ

1

,

σ

′

)

. We distinguish threecases depending on

γ

1

(

x

)

.

•

If

γ

1

(

x

)

∈

C then it follows from the definition of

Θ

_CS1,S2 that

γ

2

=

γ

1. From Item (4) of

•

If

γ

₁

(

x

)

∈

codom

(

σ

)

\

C then in this case we recall that

γ

₂

= {

x

7→

σ

′

₍

_y

_)}

_where

σ

₍

_y

₎

₌

γ

1

(

x

)

forsome variable y

∈ X

. Thefactthat

(

σ

⊎ {

x

7→

γ

1

(

x

)})

✶

C

σ

′

⊎ {

x

7→

σ

′

(

y

)}

follows

from Item (5) ofLemma 9.

•

Otherwise, i.e.if

γ

1

(

x

)

∈

S1

\ (

C

∪

codom

(

σ

))

then thefact that

(

σ

⊎ {

x

7→

γ

1

(

x

)})

✶

C

(

σ

′

⊎

{

x

7→

get

(

S2

\

codom

(

σ

′

))})

follows fromItem (6) of Lemma 9.

Induction Case. Assume

γ

₁

=

γ

′

1

⊎

γ

1′′ with

|

γ

1′

|

=

1. Let











γ

₂′

= Θ

_CS1,S2

(

σ

,

γ

₁′

,

σ

′

),

and

γ

₂′′

= Θ

S1,S2 C

(

σ

⊎

γ

1′

,

γ

1′′

,

σ

′

⊎

γ

2′

)

and

γ

2

= Θ

_CS1,S2

(

σ

,

γ

1

,

σ

′

) =

γ

₂′

⊎

γ

₂′′ Fromthe induction hypothesis it followsthat

½

σ

⊎

γ

₁′

✶

_C

σ

′

_⊎

_γ

′ 2

(

σ

⊎

γ

₁′

) ⊎

γ

₁′′

✶

_C

(

σ

′

⊎

γ

₂′

) ⊎

γ

₂′′ Therefore

σ

⊎

γ

1

✶

C

σ

′

⊎

γ

2

✷

Lemma12.Let

A

beaPAover

Σ

withk variablesandm letters

Σ

A

= {

c1

, . . . ,

cm

}

.Let

Σ

= {

a1

,

. . . ,

ak

,

c1

,

. . . ,

cm

}

.Then,

A

recognizesanon-emptylanguageover

Σ

⋆if,andonlyif,itrecognizesanon-emptylanguage

over

Σ

⋆.

Proof. Let C

= {

c1

, . . . ,

cn

}

. We show that there is a run

(

σ

0

,

q0

)

→ . . . → (

σn

,

qn

)

over

Σ

⋆ in

A

iff

thereisarun

(

σ

′

0

,

q0

)

→ . . . → (

σ

n′

,

qn

)

over

Σ

⋆ in

A

such that

σi

✶

C

σ

_i′ forall i

=

0

,

. . . ,

n. Theproof

is by induction onn in both directions. Thebasecase n

=

0 holds triviallysince

σ

0

=

σ

₀′

= ∅

. Assume thatthe claim holds upton andletus prove itfor n

+

1.

⇒

) Assumethereisatransition qn

αn,gn

→

qn+1 in

A

where

αn

∈ Σ ∪ X

and gn isaguard.Fromthe

in-duction hypothesiswe havethat

σ

n

✶

C

σ

n′. Itfollows fromItem (7)of Lemma 9that

σ

n

(

gn

)

holds

iff

σ

′

n

(

gn

)

holds. Thus, the transition in

A

over

Σ

is possible. We describe next this transition.

From Definition 4 of the run of PAs, there exists a substitution

γn

: V(

σn

(

αn

))

∪ V(

σn

(

gn

))

→ Σ

such that

(

γ

n

⊎

σ

n

)(

gn

)

holds.Hence,wemustfindasubstitution

γ

n′

: V(

σ

n′

(

α

n

))

∪ V(

σ

n′

(

gn

))

→ Σ

such that

(

γ

_n′

⊎

σ

_n′

)(

gn

)

holds.We define

γ

n′ by

γ

n′

= Θ

Σ,ΣC

(

σn

,

γn

,

σ

n′

)

. From Lemma 11 we have

that

(

σ

n

⊎

γ

n

)

✶

C

(

σ

n′

⊎

γ

n′

)

. Hencefrom Item (7) of Lemma 9it follows that

(

γ

n′

⊎

σ

n′

)(

gn

)

holds.

It remains to show that

σn

+1

✶

C

σ

_n′₊₁. But

σn

+1

= (

σn

⊎

γn

)

|D and

σ

_n′₊₁

= (

σ

n′

⊎

γ

n′

)

|D, for some

set D

⊆ X

. FromItem (2) of Lemma 9 it follows that

σn

+1

✶

C

σ

n′+1.

⇐

) Sameproof butwe callthe function

Θ

Σ ,Σ

C

(

σ

n′

,

γ

n′

,

σn

)

instead of

Θ

Σ,Σ

C

(

σ

n

,

γn

,

σ

n′

)

.

✷

Definition13.(Restrictedconfiguration)Arestrictedconfiguration ofaPA

A

withk variables x₁

,

. . . ,

x_k

and m constantsc1

,

. . . ,

cm isa tuple

(

q

,

α

1

,

. . . ,

αk

)

where

α

1

,

. . . ,

αk

∈ {

a1

,

. . . ,

ak

,

c1

,

. . . ,

cm

}

.

Note that the number of different restricted configurations is exponentially bounded in the size of

A

. From Lemma 12it followsthat:

Lemma14.Assume

A

isaPAthatrecognizes anon-emptylanguage.Thenthereisan acceptingrunq₁

→

. . . →

q_l suchthati

6=

j impliesq_i

6=

q_j,andeachq_i isarestrictedconfiguration.

As acorollary, we obtain thatif a PA recognizes a non-empty language L it has an accepting run consistingof restrictedconfigurationsthateach appearatmostonce.Henceits lengthislessthan the number of configurations, which can be encoded in binary in space linear in the size of

A

. We thus obtain:

Theorem15.TheNonemptiness problemforPAsisinPSPACE.

4.2. NonemptinessisPSPACE-hard

To show that Nonemptiness of PAs is PSPACE-hard, we reduce the reachability problem for bounded one-counter automata (known to be PSPACE-hard) to the Nonemptiness problem of PAs. Inthe restof thissubsection, we first introducebounded one-counterautomata, and thenproceed to PAs.

Definition 16 (Boundedone-counter automata). (See Fearnley and Jurdzinski, 2013.) A bounded one-counterautomaton (

Boca

) is atuple

(

Q

,

b

,

1,

q0

)

where Q is afinite set of states,b

∈ N

is a global counterbound, q₀ is the initialstate, and

1

⊂

Q

× [−

b

,

b

]

×

Q isthe transition relation.

A

Boca

configuration is atuple

(

q

,

p

)

withq

∈

Q and 0

≤

p

≤

b.Given

τ

= (

q

,

p

,

q′

)

∈ 1

and two configurations c₁

= (

q₁

,

p₁

)

and c₂

= (

q₂

,

p₂

)

wedenote c₁

→

τ c₂ if q₁

=

q, q₂

=

q′_{, p}

2

=

p1

+

p. Note thatmandating thatc₂ isa configuration implies two implicitinequalitytesting 0

≤

p₁

+

p

≤

b.

The reachability problem for

Boca

consists in determining whether there exists asequence of tran-sitions starting from the configuration

(

q₀

,

0

)

and ending in a configuration

(

q

,

p

)

. This problem has been showntobe PSPACE-completein FearnleyandJurdzinski (2013). WereduceittoPA’s Nonempti-ness as follows:

•

Assuming 2k−1

_≤

_b

_≤

₂k_{, we build aPA withk}

₊

_{1 variables x}

1

,

. . . ,

xk

,

r, where each xi contains

the ith bitin thebinary representationofthe counter p,andr standsfor aregisterthatwillhold the current carryof abit-per-bit binaryaddition;

•

Addition of a positive constant to the counter is encoded by a sequence of k

+

1 half-adders. Each half-adder reads xi, and depending on the value of r and the ith bit of the number to

add, refreshes x_i and r, and sets (using a guard) the correct new value for these two variables. A constant number of states is necessary at each half-addition step, and thus the encoding is linear in k

= ⌈

log₂b

⌉

, and thusin the size ofthe input

Boca

. Notethatthe result isgreaterthan 2⌈log2b⌉ _{if,and onlyif, theregister r contains1 in theend;}

•

Bitwise 2-complement of a register is similarly performed bit-per-bit, using a number of states linear in k;

•

Substraction of a positiveinteger is encoded by two bitwise 2-complement computations on the counterarounda positiveinteger addition. Ifthe final counteris negativethe intermediate addi-tion step willyielda numbergreaterthan 2k;

•

Finally, we test after each addition of a positiveinteger that the counteris smaller or equal to b

by adding2k

−

b toit, and then substracting thissamenumber;

•

The final configuration

(

q_f

,

p_f

)

is encoded by a transition from states of the PA encoding q_f to its unique final state havingas guard the equality test of the variables x1

,

. . . ,

xk withthe bits in

the binaryencoding of p_f.

The details are in the companion report tothis paper.The PSPACE-hardnessof the reachability prob-lem for

Boca

and Theorem 15 imply:

Theorem17.TheNonemptiness problemforPAsisPSPACE-complete.

Notethatwe needonlytwo letters in

Σ

A (i.e.

Σ

A

= {

0

,

1

}

) in theencoding we haveemployed to prove the hardness result.

5. Servicesynthesiswithparametrizedautomata

We defineand studythe simulation preorder for PAs, anextension of the simulation preorder for FAs. Then we show how to synthesis a mediator (i.e. a PA) allowing the communication between a

client and the community of available services. To simplify the presentation, we shall only consider in thissectionPAswithout

ε

-transitionsand in whichthere isaunique initialstateand all the states areaccepting.Theproof ofthe decidabilityofsimulationfor PAswith

ε

-transitionsis discussedat the endof Subsection 5.2.

5.1. SimulationpreorderforPAs,andsymbolicgames

Simulation for PAs is arelation defined overpairs of configurations instead of pairs of states as it is thecase for FAs.

Definition18 (Simulation preorder). Let

A

₁

= hΣ,

X

₁

,

Q₁

,

q1₀

,

δ

1

,

F1

,

κ

1

i

and

A

2

= hΣ,

X

2

,

Q2

,

q2₀

,

δ

2

,

F2

,

κ

2

i

be two PAswhere

X

1

∩ X

2

= ∅

. Asimulationof

A

1 by

A

2 is arelation

✂

⊆ (ζ

X₁,Σ

×

Q1

) × (ζ

X₂,Σ

×

Q2

)

such that: 1.

(∅,

q1₀

)

✂

(∅,

q2₀

)

, and 2. if

(

σ

1

,

q1

)

✂

(

σ

2

,

q2

)

and if

(

σ

1

,

q1

)

a

→ (

σ

′

1

,

q′1

)

for a

∈ Σ

then there exists a state q′2

∈

Q2 and a substitution

σ

₂′ such that

(

σ

2

,

q2

)

→ (

a

σ

₂′

,

q′₂

)

and

(

σ

₁′

,

q′₁

)

✂

(

σ

₂′

,

q′₂

)

.

In order to show the decidability of simulation for PAs we shall provide agame-theoretic formu-lation of simulation in termsof symbolicsimulationgames. Roughly speaking, the arena of a symbolic gameis aPA in whicheachstateis controlledbyone ofthe twoplayers,

Eloise

or

Abelard

. From a state under his control, the player chooses an outgoing transition and instantiates the (possible) free variable that labels this transition and all the free variables in the constraint of this transition. Firstly, we introducesymbolic games in Definition 19 and their concretisationin Definition 20. Then, we show in Definition 21how toformulatethe simulation preorder for PAsas asymbolic game.

Definition19 (Symbolicgames). A symbolic game is apair

(A,

λ)

where

A

= hΣ,

X ,

Q

,

q0

,

δ,

F

,

κ

i

is a PA and

λ

:

Q

→ {E, A}

is the labelling function. The states labelled by

E

(resp.

A

) correspond to

Eloise

(resp.

Abelard

) states.

Theconcretisationofasymbolicgameamountstoinstantiateits variablesfroma(possiblyinfinite) set of letters. The resulting game is a two-players game in the sense of Definition 1. The formal definitionfollows.

Definition 20 (Concretisation of symbolic games). Let

(A,

λ)

be a symbolic game where

A

=

hΣ,

X ,

Q

,

q0

,

δ,

F

,

κ

i

. Let S

⊆ Σ

be a set of letters. The concretisation of the symbolic game

(A,

λ)

withletters in S,denotedby

G(A,

λ,

S

)

,is thetwo playersgame

h

PosE

,

PosA

,

M

,

p⋆

i

where theinitial positionis p⋆

= (∅,

q0

)

and thesetof positionsPos

=

PosA

∪

PosE isthesetof positionscontaining p⋆ and reachablefrom themoves M:

M

=

©

(

σ

,

q

) →

¡

σ

′

,

q′

¢

where

(

σ

,

q

)

→

a

¡

σ

′

,

q′

¢

for all a

∈ Σ

ª

Finally,

½

PosE

= {(

σ

,

q

) ∈

Pos where

σ

∈ ζ

X,Sand

λ(

q

) = E}

PosA

= {(

σ

,

q

) ∈

Pos where

σ

∈ ζ

X,Sand

λ(

q

) = A}

Definition21(Symbolicgamesforsimulation).Let

A

₁

= hΣ,

X

₁

,

Q₁

,

q1₀

,

δ

1

,

F1

,

κ

1

i

and

A

2

= hΣ,

X

2

,

Q2

,

q2₀

,

δ

2

,

F2

,

κ

2

i

be two PAsand let S

⊆ Σ

be asetof letters.Thesymbolicsimulationgame of

A

1 by

A

2 is thesymbolic game

(M,

λ)

where

M

= hΣ,

X ,

Q

,

q0

,

δ,

F

,

κ

i

is defined by:

Q

⊆

Q1

×

Q2

∪

Q1

×

Q2

× (Σ

A₁

∪

X

1) q0

=

q10

×

q20

δ = 1

0

∪ 11

,

where







1

0

= {(

q1

,

q2

)

α1,g1

−→ (

q′₁

,

q2

,

α

1

),

for all q1 α1,g1

−→

q′₁

∈ δ1}

1

1

= {(

q1

,

q2

,

α

1

)

α2,g2∧(α1=α2)

−→

(

q1

,

q′₂

),

for all q2 α2,g2

−→

q′₂

∈ δ2}

κ

=

κ

1

×

κ

2

and the labelling function

λ

is defined by

λ((

q1

,

q2

))

= A

and

λ(

q1

,

q2

,

α

)

= E

, for every

(

q1

,

q2

),

(

q1

,

q2

,

α

)

∈

Q .

Thesimulation gameof

A

₁ by

A

₂ overletters in S, denotedby

G

_S

(A

1

,

A

2

)

, is the concrete game

G(M,

λ,

S

)

.

Finally,anyinfiniteplayin

G(M,

λ,

S

)

iswinning for

Eloise

,and anyfiniteplayis losingforthe player who cannot move.

The simulation problem for PAs is the following: given two PAs

A

₁ and

A

₂, is

A

₁

✂ A

2? This amountstoaskingwhetherplayer

Eloise

hasawinning strategyinthe concretegame

G

_Σ

(A

1

,

A

2

)

.

Thefollowing lemma states animmediateproperty of the symbolic games.

Lemma22.Let

(M,

λ)

beasymbolicgameandS

⊂ Σ

.IfS isfinitethentheconcretegame

G

_S

(M,

λ)

isfinite too.

5.2. Decidabilityofthesimulationproblem

We show that the simulation problem is decidable by showing that solving symbolic games is decidable. The idea is that the problem of solving a symbolic game can be reduced to solving the same game in which the two players instantiate the variables from a finite setof letters, see Propo-sition 25. In order to relate these two games we need to adapt the notion of coherence between substitutions given in Definition 8 to the coherence between game positions. The definition of the coherence betweengame positions,stilldenoted by

✶

_C, follows.

Definition23.Let

M

be aPAand q be astateof

M

. Let S₁

,

S₂ besubsets of

Σ

where C

=

S₁

∩

S₂

6=

∅

. Let

(

q

,

σ

)

P (resp.

(

q

,

γ

)

P) be a position of player

P

∈ {E, A}

in the two-players game

G

S1

(M,

λ)

(resp.

G

_S2

(M,

λ)

). Define

(

q

,

σ

)

P

✶

C

(

q

,

γ

)

P iff

σ

✶

C

γ

.

Let

(M,

λ)

be a symbolic game where

M

= hΣ,

X ,

Q

,

q0

,

δ,

F

,

κ

i

is aPA. Let k

= |X |

. We define

C0 to be thefinite setof letters:

C0

= Σ

A

⊎ {

c1, . . . ,ck

}

(2)

Let us take the abbreviations

G

_Σ

= G

Σ

(M,

λ)

and

G

C0

= G

C0

(M,

λ)

. Now we are ready to show

that the games

G

_Σ and

G

_C0 are equivalent. For the direction “

⇒

” we show that out of a winning strategy of

Eloise

in

G

_Σ

(M,

λ)

weconstruct awinning strategyfor her in

G

_C0

(M,

λ)

.

For this purpose, we show that each move of

Abelard

in

G

_C0

(M,

λ)

can be mapped to an

Abelard

move in

G

_Σ

(M,

λ)

, and that

Eloise

response in

G

_Σ

(M,

λ)

can be actually mapped to an

Eloise

move in

G

_C0

(M,

λ)

. Formally,weneed to defineafunction f

f

:

Pos

¡

G

_Σ

(

M

, λ)

¢

→

Pos

¡

G

_C0

(

M

, λ)

¢

in order to make possible thismapping as shown in the Diagram below. It follows that this is suffi-cient to argue that if there is aninfinite play in

G

_Σ

(M,

λ)

then we can constructan infinite play in