Thermal conduction properties of microcracked media: Accounting for the unilateral effect

OATAO is an open access repository that collects the work of Toulouse

researchers and makes it freely available over the web where possible

Any correspondence concerning this service should be sent

to the repository administrator:

tech-oatao@listes-diff.inp-toulouse.fr

This is an author’s version published in: http://oatao.univ-toulouse.fr/25239

To cite this version:

Rangasamy Mahendren, Sharan Raj

and Welemane, Hélène

and Dalverny, Olivier

and Tongne, Amèvi

Thermal conduction

properties of microcracked media: Accounting for the unilateral

effect. (2019) Comptes Rendus de Mécanique, 347. 944-952. ISSN

1631-0721

Contents lists available atScienceDirect

Comptes

Rendus

Mecanique

www.sciencedirect.com

Thermal

conduction

properties

of

microcracked

media:

Accounting

for

the

unilateral

effect

Propriétés

de

conduction

thermique

des

milieux

microfissurés :

prise

en

compte

de

l’effet

unilatéral

Sharan

Raj Rangasamy Mahendren,

Hélène Welemane

∗

,

Olivier Dalverny,

Amèvi Tongne

UniversitédeToulouse,INP/ENIT,LGP,47,avenued’Azereix,65016Tarbes,France

a

r

t

i

c

l

e

i

n

f

o

a

b

s

t

r

a

c

t

Articlehistory:

Received10April2019 Accepted7October2019 Availableonline22October2019

Keywords: Microcracking Heatconduction Thermalproperties Homogenization Unilateraleffect Mots-clés : Microfissuration Conductionthermique Propriétésthermiques Homogénéisation Effetunilatéral

Studies dedicated to the homogenization approach of microcracked media are largely focused on the determination of effective elastic properties. Some works investigate other properties, but most of them consider only open cracks. This paper intends to provide effective thermal properties related to the conduction problem taking into accountthe unilateraleffect(opening/closureofcracks). Suchanalysisconsiders steady-state heat transfer within an initially isotropic media weakenedby randomly oriented cracks. Accordingto the boundary conditions,estimatesand bounds basedon Eshelby-like formalism are developed to derive closed-form expressions for effective thermal conductivityandresistivityinafixedmicrocrackingstate.

2019Académiedessciences.PublishedbyElsevierMassonSAS.Thisisanopenaccess articleundertheCCBY-NC-NDlicense (http://creativecommons.org/licenses/by-nc-nd/4.0/).

r

é

s

u

m

é

Les techniques d’homogénéisation des milieux microfissurés sont principalement em-ployéespourl’étudedescomportementsmécaniquesélastiques.D’autresapplicationssont égalementpossibles,maisellesdemeurentleplussouventlimitéesàlaconsidérationde défautsouverts.Cetravailviseàdéterminerlespropriétéseffectivesthermiquesdemilieux microfissurés dans le cadre d’une conduction stationnaire. Les matériaux étudiés sont initialementisotropesetprésententdesmicrofissuresd’orientationarbitrairepouvantêtre ouvertesoubienfermées(effetunilatéral).S’appuyantsurunedémarchedetypeEshelby, les expressions des conductivités et résistivités effectives issues de différents schémas d’homogénéisationetbornesd’encadrementsonticiprésentéesetdiscutées.

2019Académiedessciences.PublishedbyElsevierMassonSAS.Thisisanopenaccess articleundertheCCBY-NC-NDlicense (http://creativecommons.org/licenses/by-nc-nd/4.0/).

*

Correspondingauthor.

E-mailaddress:helene.welemane@enit.fr(H. Welemane).

https://doi.org/10.1016/j.crme.2019.10.004

1631-0721/_{2019Académiedessciences.PublishedbyElsevierMassonSAS.ThisisanopenaccessarticleundertheCCBY-NC-NDlicense}

Homogenization is a usefultool for the modellingand analysis of the behaviour of heterogeneous materials. One of its mainobjectives istoestimate their overall propertiesfromtheirmicrostructuralfeatures (phaseproperties,inclusions distribution andgeometry, etc.). This topic is even more interesting when there is a lack ofexperimental data. Several studies have been dedicated to the micromechanical analysis of microcracked media, especially to address their elastic behaviour(forinstance[1–3] forinitiallyisotropicmaterials).Still,manypracticalapplicationsrequirepropermodellingof otherpropertiessuchasthermal,transportandpiezoelectricproperties,whicharenotinvestigatedmuch[4–8].

Taking into account the unilateral effect (opening and closure of cracks) makes the estimation of the said effective propertieschallenging,andthisevenmoreasmicrocracksare orienteddefects.Someauthorshaveinvestigatedtheelastic problemtakingintoaccountboththeinducedanisotropyandrecoveryphenomenonduetocrackclosure,throughaveraging up-scaling methods [1,9–11]. Such modelling strategy has never been applied before for a steady-state heat conduction problem. So,inthiswork, we intendtoaddress thisissuethroughan Eshelby-like approachandderive effectivethermal propertiesofmicrocrackedmedia,focusingmainlyontheunilateraleffect.

2. Theoreticalframework

Assuminglengthscaleseparation,thisstudydealswithcontinuummicromechanics.Ahomogenizationprocessproviding microstructure–propertiesrelationshipsisconductedthroughmean-fieldtheory.Presentdevelopmentsforeffectivethermal propertiesareinspiredbythemathematicalanalogybetweenelasticityandsteady-stateheatconductionproblems[12,13]:

stress

σ

⇐⇒

heat flux q

strain

ε

⇐⇒

temperature gradient g stiffness

C ⇐⇒

thermal conductivity

λ

compliance

S ⇐⇒

thermal resistivity

ρ

Hooke’s law

⇐⇒

Fourier’s law

Similarly to the macroscopic stress and strain under equilibrium conditions, the macroscopic temperature gradient G (respectively macroscopic heat flux Q ) corresponds to the average values of its microscopic quantity g (resp. q) under stationarythermalconditions[14]:

G

=

1

Ä

Z

Ä

g d

Ä = h

g

i

and Q

= h

q

i

(1)

with

Ä

beingthevolumeoftheRepresentativeVolumeElement(RVE).

Moreover,thelinearthermalbehaviourisgivenbyFourier’sheatconductionlaw:

q

= −λ ·

g and g

= −

ρ

·

q (2)

where

λ

(resp.

ρ

)isthesymmetricsecond-orderthermalconductivity(resp.resistivity)tensor.

Letus considera 3D RVEof amicrocracked media. Such materialexhibits a matrix-inclusiontypology inwhich each phase(matrix,cracks)aresupposedtoexhibitahomogeneousbehaviour.Twodifferentboundaryconditionscanbeimposed attheouter boundary

δÄ

oftheRVE,i.e.eitheruniformmacroscopictemperaturegradient

(G

imposed at

δÄ)

oruniform macroscopicheatflux

(Q imposed at

δÄ).

Assuminganinitialnaturalstate,themicroscopicandmacroscopicquantitiescan belinkedlinearlyas[15]:

g

(

x

) =

A

(

x

) ·

G and q

(

x

) =

B

(

x

) ·

Q

∀

x

∈

Ä

(3)

where A (resp. B)isthesecond-ordergradientlocalization(resp.fluxconcentration)tensorsuchthat

h

A

i

= h

B

i

=

I (I being the second-order identity tensor). The average temperature gradient G and heat flux Q of the heterogeneous media as obtainedby(1) canthusberelatedbyeffectivethermaltensors:

Q

= −λ

_hom

·

G and G

= −

ρ

hom

·

Q (4)

where

λ

hom(resp.

ρ

hom)istheoverallthermalconductivity(resp.resistivity)ofthemicrocrackedmedia.Letdenote

λ

mand

ρ

m

= λ

−m1 thematrixconductivityandresistivity,

λ

c,i and

ρ

c,i

= λ

−c,1i theconductivityandresistivityoftheith (i

=

1...N) familyofparallelcracksand fc,itheirvolumefraction.Simplifyingassumptionsregardingphasedistributionallow

approxi-matinglocalfieldswithinconstituentsbytheirphaseaverages,sothattheoverallthermalpropertiesforthemicrocracked mediacanbegivenas:

Fig. 1. (a) RVE with arbitrarily oriented microcracks, (b) penny-shaped crack geometry.

λ

hom

= λ

m

+

N

X

i=1 fc,i

(λ

c,i

− λ

m

) · h

A

i

c,i (5)

ρ

hom

=

ρ

m

+

N

X

i=1 fc,i

(

ρ

c,i

−

ρ

m

) · h

B

i

c,i (6)

where

h·i

r=_Ä1_r

R

_Är

·

dÄdenotestheaveragevalueoverthevolumeofthephaser forr

= {m,

ci

}.

Atthispoint,effective ten-sors

λ

hom(directly derivedfromuniformgradient-basedboundaryconditions)and

ρ

hom(naturallyobtainedfromuniform

flux-basedboundaryconditions)strictlydescribethesameequivalenthomogeneousmedia,sothatthesetensorsareinverse ofeachother,i.e.

λ

hom

=

ρ

−hom1 .

Followingthismodellingstrategy,closed-formapproximationsofeffectivethermaltensorscanbederivedwhenever lo-calizationandconcentrationtensors(denoted as

h

A

i

est_c,i and

h

B

i

est_c,i resp.)areestimated.Worksonthesingle-inhomogeneity problem, initiated by Eshelby [16] in elasticityand extendedto thermoelasticity [13,17], provide some solutions to such issueiftheinclusionsareellipsoidal.Indeed,thetemperaturegradientandheatfluxlocalfieldsinthecrackcanbe approx-imatedbytheuniformrespectivelocalfieldsobtainedinanellipsoidembeddedinan infinitematrixsubjectedtouniform boundaryconditionsdenotedasG∞andQ∞.Assumingperfectinterfaces,severalrepresentationscanbedeveloped

accord-ingtotheremoteconditions,matrixproperties,phasevolumefractions,geometryandpropertiesoftheinhomogeneity. Forthe presentcase, theRVE iscomposed ofan initially isotropic homogeneous media,considered asthe matrix.Its thermalconductivity and resistivity tensors are given by

λ

m

= λ

mI and

ρ

m

=

ρ

mI (

λ

m and

ρ

m are the scalar thermal

conductivity andresistivity, with

λ

m

=

ρ

m−1) respectively. This matrix is weakened by randomly distributed microcracks

witharbitraryorientations(Fig. 1a).A convenientwayto representsuchkindofdefectisundertheformofa flatoblate ellipsoid(meansemi-axesa andc,Fig.1b).Fortheith familyofparallelmicrocracks, nidenotestheirunitvector,

ω

i

=

ci

/

ai

theirmeanaspectratio,anddi

= N

ia3i their scalarcrackdensityparameter(

N

i isthenumberofcracksintheith family perunit volume,[18]).Thecrackvolume fractionisthus fc,i

=

43

π

di

ω

i.Undertheseassumptions,estimatedsolutionsfor localizationandconcentration tensors

h

A

i

est_c,i and

h

B

i

est_c,i depend on the followingdepolarization tensor SE_i (similarto the Eshelbytensorofelasticproblems)[19]:

SE_i

=

³

1

−

π

2

ω

i

´

ni

⊗

ni

+

π

4

ω

i

(

I

−

ni

⊗

ni

)

(7)

Thelast importantpointsfortheconsidered problemdeal withthe geometryandpropertiesofthecracks.Regarding the former,theconfigurationofpenny-shaped crackscorresponds tothe limitcase

ω

i

→

0,whichmustbe introducedatthe veryendofthemathematicaldevelopments.Moreover,thefactthatmicrocrackscanbeeitheropenorclosedaccordingto compressiveloadsisintroducedthroughthelatterpoint.Inbothcases,cracksareassumedtobeisotropic(λc,i

= λ

c,iI and

ρ

c,i

=

ρ

c,iI),buttheybehavedifferentlydependingonthestateofthemicrocrack:

•

fortheopencase,

λ

c,i

=

0 and

ρ

c,i

→ ∞,

whichcorrespondstoadiabaticconditionsonthecrackslips,

•

followingthe works ofDeudé etal.[10], closedcracks are represented by a fictitious isotropic materialwith scalar conductivity

λ

c,i

= λ

∗ and resistivity

ρ

c,i

=

ρ

∗, which accounts for some heat transfer continuity at the closure of cracks (frictionless contact).Taking

λ

∗

= λ

m and

ρ

∗

=

ρ

m may seem natural, butwe willnevertheless continue the

developmentforageneralcasewhere

λ

∗ _and

ρ

∗ _{arescalarswiththeconditions}

_λ

∗

₆₌

_{0 and}

ρ

∗

_{6→ ∞.}

3. Gradient-basedformulation

Bygradient-basedformulation,wemeantoimposeauniformmacroscopictemperaturegradientG attheouterboundary

δÄ

ofthe RVE.Such asituationcorresponds to theclassical strain-based condition ofEshelby’sproblem. Letusconsider threedifferentapproachestoderivetheeffectiveproperties.

Fig. 2. Phase properties and boundary conditions at infinity: (a) imposed temperature gradient G∞, (b) imposed heat flux Q∞.

3.1. Dilutescheme

In a first approach,we are going to estimate the homogenized propertiesassuming a dilute densityof cracks, which amounts to considerno interactionbetween defects.Remoteconditions onthe Eshelby problemleadin that casetothe macroscopicgradient(G∞

=

G,seeFig.2a).Hence,thegradientlocalizationtensorisgivenby:

h

A

i

dil_c,i

=

h

I

+

PE_i

·

¡ λ

c,i

− λ

m

¢

i

−1

(8)

wherePE_i

=

SE_i

·

ρ

m isthesymmetricsecond-orderinteractiontensor(equivalenttothefirstHilltensorinelasticity).Eq. (8)

canbesimplifiedas:

h

A

i

dil_c,i

=

h

I

−

SE_i

¡

1

− ξ

i

¢

i

−1 with

ξ

i

=

λ

c,i

λ

m (9)

Eq. (5) thusleadsto:

λ

dil_hom

= λ

m

"

I

−

4 3

π

N

X

i=1 di

ω

i

¡

1

− ξ

i

¢ h

A

i

dilc,i

#

(10)

Wecanseethatthe

λ

dil_homdependsontheaspectratio

ω

i inourcase.However,weshowthatthequantity

ω

i

¡

1

− ξ

i

¢ h

A

i

dilc,i tendstoalimit Ti when

ω

i

→

0,so:

λ

dil_hom

= λ

m

·

"

I

−

4 3

π

N

X

i=1 diTi

#

with Ti

=

lim ωi→0

ω

i

¡

1

− ξ

i

¢

h

I

−

SE,i

¡

1

− ξ

i

¢

i

−1 (11)

Suchexpansionincludesbothcrackconfigurations,i.e.,foropencracks

λ

c,i =0,so

ξ

i

=

0,whileforclosedcracks

λ

c,i

= λ

∗

6=

0,so

ξ

i

6=

0.Takingthisintoaccount,tensorTi fortheith familyofcracksisgivenby:

Ti

=







2

π

ni

⊗

ni

,

if cracks are open

0

,

if cracks are closed

(12)

Accordingly,Eq. (11) canbesimplifiedas:

λ

dil_hom

= λ

m

·

"

I

−

8 3

X

i/open dini

⊗

ni

#

(13)

inwhichonlyopencrackscontribute inan additivemanner.Asanexample,theeffectivethermalconductivityofamedia weakenedbyasinglefamilyofparallelmicrocrackswithunitnormal n anddensityd takestheform:

λ

dil_hom

=







λ

m

−

8

3d

λ

mn

⊗

n

,

if cracks are open

λ

m

,

if cracks are closed

3.2.Mori–Tanakascheme

In linewith the Eshelby-like approach, the Mori–Tanaka(MT) scheme [20] considerscracks embedded in an infinite media(with matrixproperties)that issubjectedto theaveragetemperaturegradient overthematrix phase(G∞

= hgi

m,

see Fig. 2a). Introducing inhomogeneities inside a thermally-stressed matrix in this way amounts to account for some interactionsbetweencracks.Averagingrule(1) leadstothefollowinglocalizationtensor:

h

A

i

MT_c,i

= h

A

i

dil_c,i

·

"

fmI

+

N

X

j=1 fc,j

h

A

i

dilc,j

#

−1 (15)

NowEq. (5) canbewrittenas:

λ

MT_hom

= λ

m

·

"

I

+

4 3

π

N

X

i=1 diTi

#

−1

= λ

m

·

"

I

+

8 3

X

i/open dini

⊗

ni

#

−1 (16) since lim ωi→0

ω

i

h

I

−

SE,i

¡

1

− ξ

i

¢

i

−1

=

Ti also.Accordingly,thespecificconductionbehaviourforthesimplecaseofasingle familyofparallelmicrocracksaccordingtotheirstatusdescribedisasfollows:

λ

MT_hom

=











λ

m

−

8 3d

λ

m 1

1

+

8d₃ n

⊗

n

,

if cracks are open

λ

m

,

if cracks are closed

(17)

3.3.PonteCastañeda–Willisupperbound

Based on theHashin–Shtrikman bounds [21], Ponte Castañeda andWillis (PCW) derived explicit strain-based bounds forthe effectivestiffness of composite materials withellipsoidalinclusions [3]. Theirestimate corresponds to a rigorous upper bound for the class of cracked media in which the matrix is the stiffest phase. The PCW formulation separately accountsfortheinclusionshapeandspatialdistribution,respectively,throughfourth-orderinteraction

P

E

i andspatialcrack distribution

P

d

c tensors.Usingasimilar approachforthethermalproblemwithasecond-orderspatial distributiontensor Pd_c,theeffectiveconductivitycanbegivenby:

λ

PCW_hom

= λ

m

+

Ã

I

−

N

X

i=1 fc,i

h

¡λ

c,i

− λ

m

¢

−1

+

PE_i

i

−1

·

Pd_c

!

−1

·

Ã

_N

X

i=1 fc,i

h

¡λ

c,i

− λ

m

¢

−1

+

PE_i

i

−1

!

(18)

Itisalsoconvenienttoobservethat:

λ

PCW_hom

= λ

m

·

Ã

I

+

N

X

i=1 fc,iMc,i

· λ

m

·

Pdc

· λ

m

!

−1

·

Ã

I

−

N

X

i=1 fc,iMc,i

·

Qdc

!

(19) where Mc,i

=

h

¡

ρ

c,i

−

ρ

m

¢

−1

+

QE_i

i

−1

,QE_i

= λ

m

·

¡

I

−

PEi

· λ

m

¢

(equivalenttothesecondHilltensorinelasticity)andQdc

=

λ

m

·

¡

I

−

Pdc

· λ

m

¢

.Forsimplicity,asphericalspatialdistributionisadoptedinthisstudy,forwhichPdc reads:

Pdc

=

1

3

ρ

m (20)

Eventhough,thePCWformulationisderived fromtheenergyapproach,Eq. (18) canbeinterpretedintheformofEq. (5) throughthefollowinglocalizationtensor:

h

A

i

PCW_c,i

= h

A

i

dil_c,i

·

Ã

fmI

+

N

X

j=1 fc,j

h

I

+

¡

PE_j

−

Pd_c

¢ · ¡ λ

c,j

− λ

m

¢

i

· h

A

i

dil_c,j

!

−1 (21)

AsalreadyemphasizedbyPonteCastañedaandWillis,itcanbeobservedthat,whenPdc

=

PEi,thePCWschemecorresponds totheMori–Tanakaestimate(Eq. (21) comestoEq. (15))whilethecasePd_c

=

0 leadstothediluteapproximation(Eq. (21) reducestoEq. (8)).

TakingintoaccountEqs. (18)–(19),orequivalentlyEqs. (21) and(5),thecorrespondingeffectiveconductivityreads:

λ

PCW_hom

= λ

m

·

"

I

−

Ã

4 3

π

N

X

i=1 diTi

!

·

Ã

I

+

4 9

π

N

X

i=1 diTi

!

−1

#

(22)

λ

PCW_hom

= λ

m

·

I

−

8 3

X

i/open dini

⊗

ni

·

I

+

8 9

X

i/open dini

⊗

ni (23)

whichreducesto:

λ

PCW_hom

=











λ

m

−

8 3d

λ

m 1

1

+

8d₉ n

⊗

n

,

if cracks are open

λ

m

,

if cracks are closed

(24)

forasingle familyofparallelmicrocracks.NotethatMT(Eq. (17))andPCW (Eq. (24))tendtodilute prediction(Eq. (14)) whend

→

0.

4. Flux-basedformulation

Thissection considersauniformmacroscopicheatflux Q at

δÄ.

Estimatesandboundare basedonthelocalfieldsof cracks embeddedinsideamatrixsubjectedtoa uniformheatflux atinfinity( Q∞). Accordingly,thetemperaturegradient

g(x) tends to

ρ

_m

·

Q∞ when

|x|

→ ∞.

This,therefore, amounts tothe gradient boundary conditionsof theEshelby-like

problem that provide the averagetemperature gradient

hgi

c over the cracks volume. From theaverage heat flux in this

phase

hqi

c =

λ

c

· hgi

c,estimatesoftensor B canbederived.

4.1. Dilutescheme

Forthedilutescheme,theconditionsatinfinitycorrespondtothemacroscopicheatflux( Q∞

=

Q ,seeFig.2b),sothat

h

B

i

dil_c,i

= λ

c,i

· h

A

i

dilc,i

·

ρ

m

=

h

I

+

QE_i

·

¡

ρ

c,i

−

ρ

m

¢

i

−1

(25)

SubstitutingEq. (25) intoEq. (6),weget:

ρ

dil_hom

=

ρ

m

·

"

I

+

4 3

π

N

X

i=1 diTi

#

(26)

Aspreviouslymentioned,Eq. (26) accountsforthecracksstate.Foropencracks,

ρ

c,i

→ ∞,

soagain

ξ

i

=

0,whileforclosed cracks

ρ

c,i

=

ρ

∗

6→ ∞,

so

ξ

i

6=

0 withtherelatedexpressionoftheTi tensorsprovidedinEq. (12).Now,

ρ

dil_hom

=

ρ

_m

·

"

I

+

8 3

X

i/open dini

⊗

ni

#

(27)

Takingthisintoaccount,theexpressionoftheeffectiveresistivitytensorforasinglefamilyofcracksbecomes:

ρ

dil_hom

=







ρ

m

+

8

3d

ρ

mn

⊗

n

,

if cracks are open

ρ

m

,

if cracks are closed

(28)

Itshouldbenotedthat,accordingtotheboundarycondition,thediluteapproximationleadstoadifferentrepresentationof thethermalbehaviourintheopenstateofthecracks,

λ

dil_hom

6= (

ρ

dil

hom

)

−1.Asimilarresultisobtainedinelasticityaswell.Yet,

theeffectiveconductivityandresistivityareobviouslyinverseofeachotherfortheclosedstateofcracks,

λ

dil_hom

= (

ρ

dil_hom

)

−1, whileinthiscasestrain-basedorstress-basedformulationsofelasticitystillremaindifferent[11,22].

4.2. Mori–Tanakascheme

Inthiscase,theremoteconditionscorrespondtotheaverageheatfluxoverthematrixphase( Q∞

= hqi

m,Fig.2-b)and

again,usingtheaveragerule,thefluxconcentrationtensorisgivenby:

h

B

i

MT_c,i

= h

B

i

dil_c,i

·

"

fmI

+

N

X

j=1 fc,j

h

B

i

dilc,j

#

−1 (29)

IntroducingEq. (29) intoEq. (6) finallygives:

From Eqs. (16), (27) and (30), itis clearthat theMori–Tanakaapproach leads tothe samepredictions undergradientor fluxconditions,bothforopenandclosedmicrocracks,i.e.

λ

MT_hom

= (

ρ

MT_hom

)

−1_{.Thesameconclusionhasbeendrawnforelastic}

propertiestoo[11,22].

4.3.PonteCastañeda–Willislowerbound

Asinspiredby[3],DormieuxandKondo[11] derivedavariationalstress-basedlowerboundfortheeffectivecompliance usinganenergyapproach.Similarlytothiswork,thethermalresistivitycanthusbegivenas:

ρ

PCW_hom

=

Ã

I

−

N

X

i=1 fc,iMc,i

·

Qdc

!

−1

·

Ã

I

+

N

X

i=1 fc,iMc,i

· λ

m

·

Pdc

· λ

m

!

·

ρ

m (31)

FromEqs. (19) and(31),wecanobservetheequivalencebetweentheupperandlowerPCWbounds,since

λ

PCW_hom

= (

ρ

PCW_hom

)

−1. Asforthegradient-basedbound,theaboveestimatecanbeinterpretedthroughthefollowingconcentrationtensor:

h

B

i

PCW_c,i

= h

B

i

dil_c,i

·

Ã

fmI

+

N

X

j=1 fc,j

h

I

+

¡

QE_j

−

Q_cd

¢ · ¡

ρ

c,j

−

ρ

m

¢

i

· h

B

i

dil_c,j

!

−1 (32)

Takingintoaccount thespatial distributionadoptedinEq. (20),theflux-basedPCW boundleadstothefollowingeffective thermalresistivity:

ρ

PCW_hom

=

"

I

+

Ã

4 3

π

N

X

i=1 diTi

!

·

Ã

I

−

8 9

π

N

X

i=1 diTi

!

−1

#

·

ρ

m (33)

AfterintroducingEq. (12),weget:

ρ

PCW_hom

=

"

I

+

Ã

8 3

X

i/open dini

⊗

ni

!

·

Ã

I

−

16 9

X

i/open dini

⊗

ni

!

−1

#

·

ρ

m (34)

Forasinglefamilyexampleconsideredthroughoutthestudy,theaboveequationcomesto:

ρ

PCW_hom

=











ρ

m

+

8 3d

ρ

m 1

1

−

16d₉ n

⊗

n

,

if cracks are open

ρ

m

,

if cracks are closed

(35)

whichagaintendstothedilutecase(Eq. (28))ford

→

0.

5. Discussion

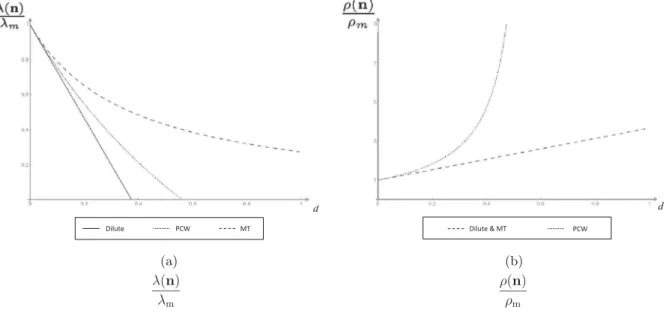
We propose to highlight the consequences of microcracks on thermal properties through the case of a matrix with a single familyofparallel cracks, forwhichclosed-form expressions of diluteandMori–Tanaka estimatesandvariational boundshavebeenprovidedinthetext.

Forthe open cracks, we note that the material exhibits a damage-induced anisotropy, irrespective of the scheme or boundaryconditions.Tobeprecise,theeffectivethermalpropertiesaretransverselyisotropicaroundaxisn ofcracks(see Eqs. (14),(17),(24) and(28),(30),(35)).Especially,conductivity(respectivelyresistivity)ismostlydegraded(resp.enhanced) alongthedirectionorthogonaltothesurfaceofthecracks,whichisconsistentwiththeadiabaticconditionsonthelipsof thecracks. Asan illustration, Fig. 3presentsthe rosediagramsofthe generalizedscalarconductivity

λ(

v

)

andresistivity

ρ

(

v

)

inthedirectionoftheunitvectorv definedby:

λ(

v

) =

v

· λ

hom

·

v and

ρ

(

v

) =

v

·

ρ

hom

·

v (36)

Onthecontrary,wenotethatclosedcracksdonotcontributetothedegradationorenhancementofthermalconduction properties.This resultis true regardlessof the scheme,boundary conditions,fictitious properties(λ∗_,

ρ

∗_{) or considered}

directionv.Indeed,inallcases,effectiveconductivityandresistivityinanydirectionrecovertheirinitialvalue(ofthevirgin material)attheclosureofmicrocracks,i.e.:

λ(

v

) = λ

m and

ρ

(

v

) =

ρ

m

,

∀

v, if cracks are closed (37)

Thismeansthatthe continuityofheat transferisfullyensuredwhenmicrocracksare closed,witha conductionresponse equaltothatinsidethehomogeneousisotropic(virgin)matrix.Suchaconclusionclearlydiffersfromtheresults microme-chanicallyestablishedforelasticproperties.Indeed,underfrictionlessconditions,crackclosureleads topartialrecoveryof

Fig. 3. Generalizedthermalconductivityλ(v)andresistivityρ(v)normalizedbytheirinitialvaluesforamaterialweakenedbyasinglefamilyofparallel microcracksofunitnormaln (cracksdensityd=0.1).

Fig. 4. Predictionsofhomogenizationestimatesandboundsforthegeneralizedthermalconductivityλ(n)andresistivityρ(n)foramaterialweakenedby

asinglefamilyofopenparallelmicrocracksofunitnormaln.

mechanicalproperties.Considering,forinstance,theYoungmodulusE

(

v

)

= [

v

⊗

v

: S :

v

⊗

v

]

−1(resp.theelongation modu-lusL(v

)

= [

v

⊗

v

: C :

v

⊗

v

])

with

S

thecompliancetensor(resp.

C

thestiffnesstensor)forastress-basedformulation(resp. forastrain-basedformulation),ithasbeendemonstratedthatclosedcracksdonotinfluencetheYoungmodulusE

(

n

)

(resp. theelongation modulus L(n

))

inthedirection n normaltothecracks,butstill remainactiveforothersdirections[23,24]. Thecompletedamagedeactivationforheat-conductionpropertiescanbeattributedtothelessercomplexityoftheproblem itselfandalsotothesimpledefinitionofthedepolarizationtensor.Comparedtoelasticcase,theEshelby-liketensorSE for

conductionbehaviour(Eq. (7))contains onlybasicinformation,asitis ofthesecondorder, symmetric,anddependsonly ontheaspectratio

ω

andtheorientation n ofthecrack(no dependencyonthematrixproperties,liketheEshelbytensor doesintheelasticcaseforinstance).

Atlast,itseemsrelevanttocomparethehomogenizationestimatesaccordingtothemicrocrackdensityparameter. Con-clusionsfortheclosedstateofmicrocracksareobvioussinceinallcasesthermalpropertiesarenotaffectedbythedefects. Ontheotherhand,theopenstateshowssomesignificantdifferencesbetweendiluteandMori–TanakaestimatesandPCW variationalboundsofconductivity,especiallyascrackdensityincreases(Fig.4(a)).Yet,similarlytocomplianceinelasticity, theMori–Tanakaformulationcoincideswiththedilutecaseforresistivity(Eq. (30)).Thisisduetothecombinationofboth thespatialcrackdistributionconsideredby MT(correspondingtoEshelby distribution)andthespecificthermalresistivity oftheopencrack(

ρ

c

→ ∞).

Suchpointisconfirmedbytheevolutionofthelowerboundestablishedin[11],whichclearly

differsfrombothpreviousschemes.Fig.4(b)illustratesthesignificantroleofinteractionsinresistivityprediction.

6. Conclusion

Thisnoteprovides homogenization-basedestimatesandboundsofsteady-stateheatconductionpropertiesfor microc-racked media. Especially,the influenceof unilateraleffects (accordingto the open orclosedstatus ofthe cracks)on the effectivethermalbehaviour istakenintoaccount.Results showthatcrackclosureleads toatotalrecoveryofthethermal conductivityandresistivityofthematerial,irrespectiveofthehomogenizationmethods(takingintoaccountornot interac-tionsbetweenmicrocracks)orboundaryconditions.Thisthusprovidesrelevantinformationforfurtherworksthatwillbe dedicatedtothethermo-mechanicalmodellingofmaterialswithevolvingdamage.

References

[1]M.Kachanov,Elasticsolidswithmanycracksandrelatedproblems,Adv.Appl.Mech.30(1993)259–445.

[2]S.Nemat-Nasser,M.Hori,Micromechanics:OverallPropertiesofHeterogeneousMaterials,North-HollandSeriesinAppliedMathematicsandMechanics, vol. 37,ElsevierScience,Amsterdam,1993.

[3]P.PonteCastañeda,J.Willis,Theeffectofspatialdistributionontheeffectivebehaviorofcompositematerialsandcrackedmedia,J.Mech.Phys.Solids 43(1995)1919–1951.

[4]L.Dormieux,D.Kondo,F.-J.Ulm,Microporomechanics,Wiley&Sons,Chichester,UK,2006.

[5]I.Sevostianov,M.Kachanov,Ontheeffectivepropertiesofpolycrystalswithintergranularcracks,Int.J.SolidsStruct.156–157(2019)243–250.

[6]D.Su,M.H.Santare,G.A.Gazonas,Aneffectivemediummodelforelasticwavesinmicrocrackdamagedmedia,Eng.Fract.Mech.75(2008)4104–4116.

[7]X.D. Wang,L.Y. Jiang,The effective electroelastic property ofpiezoelectric media with parallel dielectriccracks, Int.J. Solids Struct. 40(2003) 5287–5303.

[8]A.Giraud,C.Gruescu,D.P.Do,F.Homand,D.Kondo,Effectivethermalconductivityoftransverselyisotropicmediawitharbitraryorientedellipsoidal inhomogeneities,Int.J.SolidsStruct.44(2007)2627–2647.

[9]S.Andrieux,Y.Bamberger,J.Marigo,Unmodèledematériaumicrofissurépourlesbétonsetlesroches,J.Méc.Théor.Appl.5(1986)471–513.

[10]V.Deudé,L.Dormieux,D.Kondo,etal.,Propriétésélastiquesnonlinéairesd’unmilieumésofissuré,C.R.Mecanique330(2002)587–592.

[11]L.Dormieux,D.Kondo,Stress-basedestimatesandboundsofeffectiveelasticproperties:thecaseofcrackedmediawithunilateraleffects,Comput. Mater.Sci.46(2009)173–179.

[12]Z.Hashin,Analysisofcompositematerial–asurvey,J.Appl.Mech.50(1983)481–505.

[13]S.Torquato,RandomHeterogeneousMaterials.MicrostructureandMacroscopicProperties,SpringerScience+BusinessMedia,NewYork,2002.

[14]B.Valès,V.Munoz,H.Welemane,etal.,Heatsourceestimationinanisotropicmaterials,Compos.Struct.136(2016)287–296.

[15]R.Hill,Elasticpropertiesofreinforcedsolids:sometheoreticalprinciples,Int.J.Mech.Phys.Solids11(1963)357–372.

[16]J.D.Eshelby,Thedeterminationoftheelasticfieldofanellipsoidalinclusion,andrelatedproblems,Proc.R.Soc.A421(1957)379–396.

[17]J.G.Berryman,GeneralizationofEshelby’sformulaforasingleellipsoidalelasticinclusiontoporoelasticityandthermoelasticity,Phys.Rev.Lett.79 (1997)1142–1145.

[18]B.Budiansky,R.J.O’Connell,Elasticmoduliofacrackedsolid,Int.J.SolidsStruct.12(1976)81–97.

[19]H.Hatta,M.Taya,Equivalentinclusionmethodforsteadystateheatconductionincomposites,Int.J.Eng.Sci.24(1986)1159–1172.

[20]T.Mori,K.Tanaka,Averagestressinmatrixandaverageelasticenergyofmaterialswithmisfittinginclusions,ActaMetall.21(1973)571–574.

[21]Z.Hashin,S.Shtrikman,Avariationalapproachtothetheoryofelasticbehaviorofmultiphasematerials,J.Mech.Phys.Solids11(1963)127–140.

[22]Q.Z.Zhu,Applicationsdesapprochesd’homogénéisationàlamodélisationtridimensionnelledel’endommagementdesmatériauxquasifragiles : for-mulations,validationsetimplémentationsnumériques,PhDthesis,Lille,France,2006.

[23]H.Welemane,F.Cormery,Someremarksonthedamageunilateraleffectmodellingformicrocrackedmaterials,Int.J.DamageMech.11(2002)65–86.