Pépite | Outils géométriques dans l'étude des grandes déformations, de l'endommagement et de la mécanique non régulière
Texte intégral
(2) HDR de Marius Buliga, Lille 1, 2007. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(3) HDR de Marius Buliga, Lille 1, 2007. Pour Claudia, Matei, Ioan. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(4) HDR de Marius Buliga, Lille 1, 2007. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(5) HDR de Marius Buliga, Lille 1, 2007. Remerciements Je voudrais commencer par rendre hommage a` mes professeurs roumains qui, par leurs exemples personnels et par leurs cours de math´ematiques et de m´ecanique, m’ont donn´e envie de faire ce m´etier, notamment a` Eugen S´oos et Alexandru Popescu-Zorica. Je dois sans doute l’entr´ee dans le monde de la recherche actuelle a` la co¨ıncidence de l’acc`es a` la biblioth`eque de l’Ecole Polytechnique de Palaiseau et du d´ebut de la grande aventure de l’Internet. Je remercie ensuite Tudor Rat¸iu pour l’opportunit´e qu’il m’a donn´e de passer une p´eriode de travail longue et intense au D´epartement de Math´ematiques de l’Ecole Polytechnique F´ed´erale de Lausanne. Beaucoup des r´esultats pr´esent´es dans ce m´emoire ont germ´e au bord du Leman. Ce m´emoire a ´et´e ´ecrit suite a` l’insistance de G´ery de Saxc´e. Je le remercie pour son soutien et j’esp`ere que notre collaboration continuera longtemps. Je tiens ´egalement a` remercier Claude Vall´ee pour les nombreuses discussions fertiles et aussi pour l’occasion qu’il m’a accord´ee de participer a` plusieurs ´editions du Colloque International de Th´eories Variationnelles qui sont ch`eres a` ma m´emoire. Je suis tr`es honor´e que Pierre Alart, Ioan Ionescu et Tudor Rat¸iu aient accept´e de rapporter mon travail. Je remercie ´egalement Olivier Allix, Djimedo Kondo, Claude Vall´ee et G´ery de Saxc´e pour avoir accept´e de faire partie de mon jury. Ma plus grande reconnaissance va a` ma famille – Claudia, Matei et Ioan – pour les nombreuses fa¸cons par lesquelles ils ont chang´e ma vie pour toujours.. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(6) HDR de Marius Buliga, Lille 1, 2007. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(7) HDR de Marius Buliga, Lille 1, 2007. 1 Introduction. 9. 2 Curriculum vitae ´ 2.1 Etat civil . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.2 Fonction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.3 Diplˆomes, qualifications, titres ´etrangers . . . . . . . . . . . . . . 2.4 Vie professionnelle . . . . . . . . . . . . . . . . . . . . . . . . . . 2.5 Activit´es de recherche . . . . . . . . . . . . . . . . . . . . . . . . 2.6 Activit´es p´edagogiques . . . . . . . . . . . . . . . . . . . . . . . . 2.7 Travaux. Articles. R´ealisations . . . . . . . . . . . . . . . . . . . 2.8 Communications a` des congr`es et colloques . . . . . . . . . . . . 2.9 Rapports de contrats . . . . . . . . . . . . . . . . . . . . . . . . . 2.10 Participation a` des comit´es scientifiques des congr`es et colloques . 2.11 Activit´es administratives et autres responsabilit´es collectives . . . 2.12 Citations par les auteurs d’autres publications . . . . . . . . . . .. . . . . . . . . . . . .. . . . . . . . . . . . .. . . . . . . . . . . . .. 11 11 11 11 12 12 14 16 19 21 21 21 21. 3 R´ esum´ e des activit´ es. 23. 4 M´ ecanique de la rupture fragile et la fonctionnelle Mumford-Shah 4.1 Description du sujet . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.2 Contributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.3 R´esum´es des articles . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.3.1 Energy minimizing brittle crack propagation . . . . . . . . . . . 4.3.2 Equilibrium and absolute minimal solutions of brittle fracture models based on energy-minimization methods . . . . . . . . . . 4.3.3 Microfractured media with a scale and Mumford-Shah energies .. 27 27 28 28 28. 5 Bipotentiels 5.1 Description du sujet . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.2 Contributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.3 R´esum´es des articles . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.3.1 Existence and construction of bipotentials for graphs of multivalued laws . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.3.2 Construction of bipotentials and a minimax theorem of Fan . .. 33 33 34 34. 6 Calcul des variations, quasiconvexit´ e, ´ elasticit´ e 6.1 Description du sujet . . . . . . . . . . . . . . . . . . . . . . 6.2 Contributions . . . . . . . . . . . . . . . . . . . . . . . . . . 6.3 R´esum´es des articles . . . . . . . . . . . . . . . . . . . . . . 6.3.1 Lower semi-continuity of integrals with G-quasiconvex. 37 37 37 38 38. . . . . . . . . . . . . . . . . . . potential. 30 31. 34 35. 7. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(8) HDR de Marius Buliga, Lille 1, 2007. 6.3.2. Four applications of majorization to convexity in the calculus of variations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 7 G´ eom´ etrie sub-riemannienne et structures de dilatations 7.1 Description du sujet . . . . . . . . . . . . . . . . . . . . . . . . 7.2 Contributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.3 R´esum´es des articles . . . . . . . . . . . . . . . . . . . . . . . . 7.3.1 Dilatation structures I. Fundamentals . . . . . . . . . . . 7.3.2 Contractible groups and linear dilatation structures . . . 7.3.3 Linear dilatation structures and inverse semigroups . . . 7.3.4 Dilatation structures with the Radon-Nikodym property 7.3.5 Dilatation structures in sub-riemannian geometry . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. 38 41 41 43 44 44 46 47 48 48. 8. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
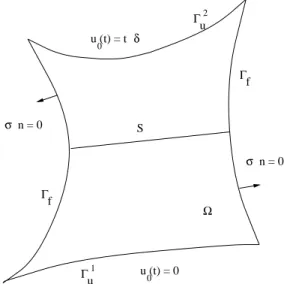
(9) HDR de Marius Buliga, Lille 1, 2007. 1. Introduction. La synth`ese des travaux de recherche qui suit est bas´ee sur une s´election d’articles group´es en quatre th`emes de recherche: 1. M´ecanique de la rupture fragile (3 articles) 2. Bipotentiels (2 articles) 3. Calcul des variations, ´elasticit´e, quasiconvexit´e (2 articles) 4. G´eom´etrie sub-riemannienne et structures de dilatation (5 articles) Des douze articles pr´esent´es ici,`a cet instant 4 sont publi´es, 1 accept´e pour publication et 7 sont soumis a` publication. Parmi les articles soumis a` publication se trouve un qui a ´et´e cit´e plusieurs fois. J’ai choisi ces articles a` partir d’une liste de 32 articles: 11 publi´es, 8 soumis a` publication, 14 e-prints arXiv non publi´es. Cette distribution inhabituelle vient de mon choix de mettre mon travail sur les arXiv, la plus grande collection des article en ligne, qui repr´esente un futur probable pour la communication des recherches en math´ematiques. 3 des articles publies, et tous les articles soumis a` publications sont des e-prints arXiv. Parmi les 23 e-prints il y a 4 qui sont cit´es plusieurs fois. Toutefois, a` partir de 2006 j’ai d´ecide de retourner a` la fa¸con habituelle de publier, motiv´e principalement par des raisons pratiques. L’ann´ee derni`ere, j’ai soumis 9 articles pour publication (de ces 9 j’ai soumis 8 aux arXiv, donc il s’agit des articles nouveaux); 3 ont ´et´e accept´es pour publication et pour les 6 autres j’attends le r´esultat final. J’envisage dans le futur proche de soumettre les autres articles qui se trouvent dans les arXiv, sous la forme pr´esente ou sous une forme nouvelle, en accord avec mes points de vue actuels. Chaque des quatre th`emes de recherche commence par un article publi´e et continue par des article nouveaux. La liste des articles publi´es qui ne seront pas pr´esent´es ici est la suivante: [19] M. Buliga, Topological Substratum of the Derivative, Stud. Cerc. Mat. (Mathematical Reports), 45, 6, 453-465, (1993) [9] P. Ballard, M. Buliga, A. Constantinescu, Reconstruction d’un champ de contraintes r´esiduelles a` partir des contraintes mesur´ees sur des surfaces successives. Existence et unicit´e. C. R. Acad. Sci., Paris, S´er. II 319, No.10, 1117-1122 (1994) [20] M. Buliga, On Special Relativistic Approach to Large Deformations in Continuous Media, Rev. Roum. de Math. Pures et Appl., t. XLI, 1-2, 5-15, (1996). 9. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(10) HDR de Marius Buliga, Lille 1, 2007. [22] M. Buliga, Geometric evolution problem and action-measures, in: Proceedings of PAMM Conference PC 122, Constanta 1998, Tech. Univ. Budapest, (1998) [23] M. Buliga, Brittle crack propagation based on an optimal energy balance, Rev. Roum. des Math. Pures et Appl., 45, no. 2, 201–209 (2001) [97] G. de Saxc´e, M Buliga, C. Vall´ee, C. Lerintiu, Construction of a bipotential for a multivalued constitutive law, PAMM, 6 , 1 (December 2006), Special Issue: GAMM Annual Meeting 2006 - Berlin [28] M. Buliga, Vr˘anceanu’ nonholonomic spaces from the viewpoint of distance geometry, (in romanian, original title: Spat¸iile neolonome ale lui Vr˘anceanu din punctul de vedere al geometriei distant¸ei), to appear in Revista Fundat¸iei Acad. Prof. Gh. Vr˘ anceanu, (2007). 10. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(11) HDR de Marius Buliga, Lille 1, 2007. 2. Curriculum vitae ´ Etat civil. 2.1. Nom patronymique: Buliga Prenoms: Marius, Luchian. Date et lieu de naissance: 22 novembre 1967, Bucarest, Roumanie. Nationalit´ e: Roumaine. Situation de famille: mari´e, deux enfants. Adresse personnelle: Str. Antiaeriana 115, bl. A1, sc. 11, ap. 139, sector 5, Bucarest, Roumanie Num´ ero de t´ el´ ephone: +40 (0) 21 420 11 08.. 2.2. Fonction Charg´e de Recherche, D´epartement de M´ecanique de Milieux Continus, Institut de Math´ematiques de l’Acad´emie Roumaine, Bucarest (Roumanie) ´ Etablissement actuel: Institut de Math´ematiques de l’Acad´emie Roumaine, Adresse PO-BOX 1-764, 014700, Bucarest, Roumanie m´ el: Marius.Buliga@imar.ro Page web: (vivement conseill´e pour une image d´etaill´e de mes travaux) http://www.imar.ro/~mbuliga/. 2.3. Diplˆ omes, qualifications, titres ´ etrangers 1997 – Th`ese de Doctorat en Math´ematiques de l’Institut de Math´ematiques, Acad´emie Roumaine, intitul´ee: ”Formulations variationnelles en m´ecanique de la fissuration fragile”, Directeur de th`ese Eugen S´oos. ´ 1995 – Diplˆome de master (DEA) (m´ecanique non lin´eaire) de l’ Ecole Polytechnique, Paris, dissertation intitul´ee: ”Mod´elisation de la d´ecoh´esion d’interface fibres-matrice dans les mat´eriaux composites”. ´ 1994 – Diplˆome d’auditeur, majeure Science de l’Ing´enieur, Ecole Polytechnique, Paris. Titre de la dissertation: ”Reconstruction d’un champ de contraintes r´esiduelles a` partir des contraintes mesur´ees sur des surfaces successives”. 11. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(12) HDR de Marius Buliga, Lille 1, 2007. 1992 – Diplˆome de math´ematicien , Facult´e de Math´ematiques, Universit´e de Bucarest. Titre de la dissertation: ”Le contenu topologique de la diff´erentiabilit´e”.. 2.4. Vie professionnelle 2000 – Charg´e de Recherche, D´epartement de M´ecanique de Milieux Continus, Institut de Math´ematiques de l’Acad´emie Roumaine, Bucarest (Roumanie) 2001 – 2006 Chercheur invit´e, post-doctorant, Chaire d’Analyse G´eom´etrique, ´ Institut de Math´ematiques B, Ecole Polytechnique F´ed´erale de Lausanne (Suisse). 1998 – Chercheur, Institut de Math´ematiques, D´epartement de M´ecanique des Milieux Continus, Acad´emie Roumaine 1997-2000 – Professeur Associ´e, Facult´e de Math´ematiques, Universit´e Hyperion, Bucarest 1995 – Assistant de Recherche, Institut de Math´ematiques, D´epartement de M´ecanique des Milieux Continus, Acad´emie Roumaine 1993 – Assistant de Recherche, Facult´e de Math´ematiques, Universit´e de Bucarest, et l’Institut de G´enie Civil 1992-1993 – Professeur d’Informatique, Lyc´ee Petru Poni , Bucarest (Sept. 1992 - Feb. 1993). Chercheur invit´ e ´ 2000 D´epartement de Math´ematiques, Ecole Polytechnique F´ed´erale de Lausanne, pour 3 mois ´ 2004 Institut des Hautes Etudes Scientifiques, Nov. 2004 2005 Laboratoire de M´ecanique de Lille - UMR CNRS 8107, pour un mois. 2.5. Activit´ es de recherche. 3 contrats de recherche sur fonds nationaux et internationaux Grandes orientations: Mes recherches sont consacr´ees a` la M´ecanique des Solides dans ses aspects th´eoriques et num´eriques, et a` l’Analyse G´eom´etrique des espaces m´etriques. Les th`emes abord´es concernent:. 12. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(13) HDR de Marius Buliga, Lille 1, 2007. La M´ ecanique de la rupture fragile: une formulation rigoureuse de la rupture fragile bas´ee sur la fonctionnelle de Mumford-Shah et sur des techniques d’analyse g´eom´etrique. Des fissures avec des formes complexes peuvent apparaˆıtre et se propager sans prescription sur leur g´eom´etries. J’ai montr´e que une th´eorie bas´ee seulement sur la fonctionnelle Mumford-Shah conduit a` des r´esultats non raisonnables du point de vue m´ecanique. En cons´equence j’ai propos´e des crit`eres de propagation fragile des fissures qui g´en´eralisent les crit`eres bien connues de Griffith et Irwin. Le travail est illustr´e par des r´esultats num´eriques. ´ Elasticit´ e non lin´ eaire, Convexit´ e et Calcul de Variations: des ´etudes sur les propri´et´es de quasiconvexit´e d’un potentiel ´elastique non lin´eaire. Par un r´esultat classique de Morrey, les propri´et´es de continuit´e de certaines fonctionnelles sur des espaces de Sobolev sont en relation avec la quasiconvexit´e de la fonction potentiel w. Le cas des espaces de Sobolev des fonctions u : Ω ⊂ R n → Rn est tr`es int´eressant pour la m´ecanique des milieux continus. En ´elasticit´e le potentiel w n’est pas en g´en´eral d´efini sur un espace vectoriel de matrices n × n (l’alg`ebre de Lie gl(n, R)) mais sur l’ensemble des matrices n × n avec d´eterminant positif (le groupe de Lie GL(n, R)). Parfois la fonction w est d´efinie sur un sous-groupe, comme c’est le cas de l’´elasticit´e incompressible, ou il faut consid´erer le groupe des matrices de d´eterminant 1, i.e. le groupe SL(n, R). Pour n pair , un autre groupe qui attire l’attention est Sp(n, R), le groupe des matrices symplectiques. Il est donc int´eressant de trouver des conditions n´ecessaires et/ou suffisantes pour l’inf´erieure semi-continuit´e de la fonctionnelle et de notions (qui restent a` trouver) de convexit´e du w : G → R, avec G un groupe de matrices. Tr`es peu est connu sur la continuit´e des int´egrales associ´ees aux potentiels diffquasiconvex. Il est cependant facile a` prouver que la diff-quasiconvexit´e, introduite par Giaquinta, Modica, Soucek est une condition n´ecessaire. J’ai introduit la notion de quasiconvexit´e multiplicative qui est mieux adapt´ee au cas de grandes d´eformations, quand il est important de prendre en compte le fait que les d´eformations sont invertibles. J’ai ´egalement ´etudi´e l’importance de la convexit´e de Schur pour le comportement des mat´eriaux ´elastiques isotropes, notamment les ´elastom`eres nematiques. Bipotentiels: Les lois constitutives des materiaux standard sont en g´en´eral multivalu´ees et ´egalement associ´ees. Le graphe d’une telle loi constitutive est inclus dans le graphe de la sous-differentiale d’un super-potentiel φ (qui est aussi inf´erieur semi-continu). La loi constitutive prend alors la forme d’une inclusion diff´erentielle, y ∈ ∂φ(x). Cependant, certaines des lois constitutives sont non-associ´ees. Elles ne peuvent pas ˆetre trait´es dans le cadre des mat´eriaux standard. Pour contourner ce probl`eme, une 13. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(14) HDR de Marius Buliga, Lille 1, 2007. r´eponse possible, propos´ee d’abord par Gery de Saxc´e, consiste en construisant une fonction b (le bipotential) avec deux variables, bi-convexe, qui satisfait une in´egalit´e g´en´eralisant celle de Fenchel. Physiquement, le bipotential repr´esente la dissipation. En collaboration avec G. de Saxc´e et C. Vall´ee, nous sommes en train de donner une base rigureuse du point de vue math´ematique a` la th´eorie du bipotentiel. Nous utilisons pour cela des outils de l’analyse convexe et de g´eom´etrie symplectique. G´ eom´ etrie sub-riemannienne: La g´eom´etrie sub-riemannienne, ou de CarnotCarath´eodory, ou encore g´eom´etrie non-holonome, est un sujet de recherche en contact avec plusieurs domaines, notamment: l’analyse des op´erateurs hypoelliptiques, th´eorie du contrˆole, l’analyse dans les espaces m´etriques mesur´es. Parmi les principaux contributeurs a` ce sujet on compte H¨ormander, Gromov, Cheeger , Folland, Stein, Margulis, Mostow. La g´eom´etrie intrins`eque des liaisons non holonomes n’est pas riemannienne, ce qui engendre le besoin d’adapter les outils d’analyse non lin´eaire. Cela est possible grˆace a` des r´esultats nouveaux d’analyse g´eom´etrique dans espaces m´etriques plus g´en´erales que les espaces riemanniens. Mon interet pour le sujet de recherche de la g´eom´etrie sub-riemannienne a commenc´e pendant le temps pass´e au d´epartement de math´ematiques de l’EPFL. J’ai propos´e et ´etudi´e la notion de structure de dilatations, les propriet´es de courbure d’une variet´e sub-riemannienne et quelques applications dans la m´ecanique hamiltonienne. Il semble maintenant que les structures de dilatation sont int´eressantes par ellesmˆemes, avec un champ d’applications possibles contenant strictement la g´eom´etrie sub-riemannienne, mais aussi les espaces ultram´etriques ou les groupes contractibles. Autres: un probl`eme de reconstruction de contraintes r´esiduelles dans un solide ´elastique, mesur´ees par diffraction des rayons X, apr`es un enl`evement de mati`ere qui induit la redistribution des contraintes, et donc le tenseur mesur´e est diff´erent du tenseur original. Un ´etude de la m´ethode de Roug´ee pour la description des propri´et´es locales d’un milieu continu, appliqu´ee pour un milieu continu en relativit´e restreinte.. 2.6. Activit´ es p´ edagogiques. 6 enseignements de cours et/ou travaux dirig´es 2 fascicules de cours polycopi´es r´edig´es 1 support de cours en forme ´electronique (page web). 14. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(15) HDR de Marius Buliga, Lille 1, 2007. Description de charges 1993-1994- cours de Th´eorie de la Relativit´e , 4eme semestre, cours, 28 h/semestre, pendant deux ans, suite a` l’initiative de Prof. L. Beju qui a propos´e d’exp´erimenter l’enseignement de ce cours en deuxi`eme ann´ee d’´etudes, Facult´e de Math´ematiques, Universit´e de Bucarest. 1993-1994- travaux dirig´es de l’Introduction a` l’Informatique 1er semestre, t.d. 56 h/semestre, l’Institut de G´enie Civil, Bucarest 1995-1999- cours et t.d. de M´ecanique des Milieux Continus pour math´ematiciens, 7eme semestre, cours 28 h/semestre, t.d. 140 h/semestre (2h de t.d./semaine pour 5 groupes), a` la Facult´e de Math´ematiques, Universit´e de Bucarest. 1997-1999- cours et t.d. de G´eom´etrie lin´eaire, deux premiers semestrs, cours 84 h/an, t.d. 168 h/an, a` la Facult´e de Math´ematiques, Universit´e Hyperion, Bucarest 1997-1999- cours et t.d. de G´eom´etrie Diff´erentielle, les 2 semestres suivants, cours 84 h/an, t.d. 168 h/an, a` la Facult´e de Math´ematiques, Universit´e Hyperion, Bucarest. 2001-2006 t.d. Analyse I et II, t.d. 108 h/an, pour le cours de T. Ratiu a` l’EPFL 2001-2006 Collabore occasionnellement a` l’enseignement du cours d’ Analyse I et II a` l’EPFL. Cr´ eations d’enseignement 1998- Cours avanc´e ”Probl`emes a` discontinuit´e libre”, Institut de Math´ematiques de l’Acad´emie Roumaine 1999- Cours avanc´e ”M´ethodes ´energ´etiques en m´ecanique de la fissure fragile”, Institut de Math´ematiques de l’Acad´emie Roumaine 2001-2002- avec T. Ratiu, s´eminaire de travail ”Sub-Riemannian geometry and Lie groups”, EPFL 2003- un des organisateurs du S´eminaire Borel 2003, dans le cadre du 3`eme Cycle Romand de Math´ematiques, intitul´e ”Tangent spaces of metric spaces”, Universit´e de Berne (Suisse), ( 2 expos´es en 12 semaines) Cours polycopi´ es et support de cours - R´edaction de notes du cours ”Th´eorie de la Relativit´e restreinte” (1993). - R´edaction de notes du cours et t.d. de ”G´eom´etrie lin´eaire” (1998). - R´edaction de notes du cours et t.d. de ”G´eom´etrie Diff´erentielle” (1998). - support informatique pour les t.d. de Analyse I, II, EPFL (2003-2006) 15. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(16) HDR de Marius Buliga, Lille 1, 2007. 2.7. Travaux. Articles. R´ ealisations. Publications dans des revues avec comit´e de lecture 1. M. Buliga, Topological Substratum of the Derivative, Stud. Cerc. Mat. (Mathematical Reports), 45, 6, 453-465, (1993) 2. P. Ballard, M. Buliga, A. Constantinescu, Reconstruction d’un champ de contraintes r´esiduelles a` partir des contraintes mesur´ees sur des surfaces successives. Existence et unicit´e. C. R. Acad. Sci., Paris, S´er. II 319, No.10, 1117-1122 (1994) 3. M. Buliga, On Special Relativistic Approach to Large Deformations in Continuous Media, Rev. Roum. de Math. Pures et Appl., t. XLI, 1-2, 5-15, (1996) 9 cit. - 4. M. Buliga, Energy Minimizing Brittle Crack Propagation, J. of Elasticity, 52, 3, 201-238, (1999) 3 cit. - 5. M. Buliga, Brittle crack propagation based on an optimal energy balance, Rev. Roum. des Math. Pures et Appl., 45, no. 2, 201–209 (2001) 1 cit. - 6. M. Buliga, Lower semi-continuity of integrals with G-quasiconvex potential, Z. Angew. Math. Phys.,bf 53, 6, 949-961, (2002) 7. M. Buliga, G. de Saxc´e, C. Vall´ee, Existence and construction of bipotentials for graphs of multivalued laws, J. of Convex Analysis, 15, 1, (2008) 8. M. Buliga, Dilatation structures I. Fundamentals, J. Gen. Lie Theory Appl., Vol 1 (2007), No. 2, 65-95 Publications accept´ees dans une revue a` comit´e de lecture 9. M. Buliga, Equilibrium and absolute minimal solutions of brittle fracture models based on energy-minimization methods, Int. Journal of Fracture, (2007) 10. M. Buliga, Vr˘anceanu’ nonholonomic spaces from the viewpoint of distance geometry, (en roumain, titre original: Spat¸iile neolonome ale lui Vr˘anceanu din punctul de vedere al geometriei distant¸ei), Revista Fundat¸iei Acad. Prof. Gh. Vr˘ anceanu, (2007) Communication a` des congr`es et colloques avec actes publi´es 11. G. de Saxc´e, M Buliga, C. Vall´ee, C. Lerintiu, Construction of a bipotential for a multivalued constitutive law, Proc. Appl. Math. Mech., vol. 6 , no. 1 (2006), 153-154. 16. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(17) HDR de Marius Buliga, Lille 1, 2007. 12. M. Buliga, Geometric evolution problems and action-measures, PAMM Appl. Math. Bull., vol. LXXXVI (1998), T. U. Budapest, 53-58 Articles soumises au publication 13. M. Buliga, G. de Saxc´e, C. Vall´ee, Construction of bipotentials and a minimax theorem of Fan, (submitted), http://arxiv.org/abs/math.FA/0610136, (2006) 14. M. Buliga, Contractible groups and linear dilatation structures, (submitted) http://xxx.arxiv.org/abs/0705.1440, (2007) 15. M. Buliga, Linear dilatation structures and inverse semigroups, (submitted) http://xxx.arxiv.org/abs/0705.4009, (2007) 16. M. Buliga, Microfractured media with a scale and Mumford-Shah energies, (submitted) http://xxx.arxiv.org/abs/0704.3791, (2007) 17. M. Buliga, Four applications of majorization to convexity in the calculus of variations, (submitted) (2007) 18. M. Buliga, Dilatation structures in sub-riemannian geometry, (submitted) http://arxiv.org/abs/0708.4298, (2007) 19. M. Buliga, Self-similar dilatation structures and automata, (submitted), (2007), 20. M. Buliga, Dilatation structures with the Radon-Nikodym property, (submitted) http://arxiv.org/abs/0706.3644, (2007) Publications ´electroniques 2 cit. - 21. M. Buliga, Majorisation with applications to the calculus of variations, http://arxiv.org/abs/math.FA/0105044, (2001), see also the updated version ”Four applications of majorization to convexity in the calculus of variations” 1 cit. - 22. M. Buliga, Sub-Riemannian geometry and Lie groups. Part I, http://arxiv.org/abs/math.MG/0210189, (2002) 1 cit. - 23. M. Buliga, Symplectic, Hofer and sub-Riemannian geometry, http://arxiv.org/abs/math.SG/0201107, (2002) 24. M. Buliga, Volume preserving bi-Lipschitz homeomorphisms on the Heisenberg group, http://arxiv.org/abs/math.SG/0205039, (2002) 25. M. Buliga, Tangent bundles to sub-Riemannian groups, http://arxiv.org/abs/math.MG/0307342, (2003) 17. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(18) HDR de Marius Buliga, Lille 1, 2007. 26. M. Buliga, Curvature of sub-Riemannian spaces, http://arxiv.org/abs/math.MG/0311482, (2003) 27. M. Buliga, Sub-Riemannian geometry and Lie groups. Part II. Curvature of metric spaces, coadjoint orbits and associated representations, http://arxiv.org/abs/math.MG/0407099, (2004) 28. M. Buliga, Energy concentration and brittle crack propagation, http://arxiv.org/abs/math.AP/0510225, (2005) 29. M. Buliga, Quasiconvexity versus group invariance, http://arxiv.org/abs/math.AP/0511235, (2005) 30. M. Buliga, Perturbed area functionals and brittle damage mechanics, http://arxiv.org/abs/math.AP/0511240, (2005) 31. M. Buliga, Energy minimizing brittle crack propagation II, http://arxiv.org/abs/math.AP/0511301, (2005) 32. M. Buliga, The variational complex of a diffeomorphisms group, http://arxiv.org/abs/math.AP/0511302, (2005) 33. M. Buliga, Dilatation structures II. Linearity, self-similarity and the Cantor set, (2006), http://xxx.arxiv.org/abs/math.MG/0612509 34. M. Buliga, On the Kirchheim-Magnani counterexample to metric differentiability, http://arxiv.org/abs/0710.1350, (2007) Preprints, m´emoires, dissertations, notes 1. Lower semicontinuity of variational integrals defined on groups of diffeomorphisms, IMAR preprint 17/1998 2. Variational Formulations in brittle fracture mechanics (in Romanian), PhD Thesis, Institute of Mathematics of the Romanian Academy, 1997 3. Mod´elisation de la d´ecohesion d’interface fibres-matrice dans les mat´eriaux com´ posites, m´emoire de D.E.A., Ecole Polytechnique, 1995 4. Energetic criteria in fracture mechanics, scientific report, grant MCT-ANSTI 627/1998-1999. 18. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(19) HDR de Marius Buliga, Lille 1, 2007. 2.8. Communications ` a des congr` es et colloques. 1992- Lie-Lobacevski Symposium, Universit´e de Bucharest, 1996- Conf´erences Nationales de M´ecanique des Solides (Roumanie), Constanta 1996, Iasi 1997 1996- Differential Equations and Calculus of Variations, summer school and workshop, Pisa, 1996 1999- M. Buliga, Energetic criterions in brittle fracture mechanics, The Fourth International Congress on Industrial and Applied Mathematics (ICIAM 99), 1999 1999- Applied Analysis and Mechanics Seminars, Hilary Term 1999, Mathematical Institute, Oxford, ”Quasiconvexity versus group invariance”, invited by J.M. Ball 1999- Scuola Internazionale Superiore di Studi Avanzati, Trieste, ”The variational complex of a diffeomophisms group”, invited by A. Braides ´ 2000- D´epartement de Math´ematiques, Ecole Polytechnique F´ed´erale de Lausanne, ”Variational rigidity”, invited by T. Ratiu 2002- Mathematical Institute, University of Bern, ”Towards rectifiability in Carnot groups: a theory of irreducible representations of volume preserving bi-Lipschitz homeomorphisms”, invited by M. Reimann ´ 2004- Centre Bernoulli, Ecole Polytechnique F´ed´erale de Lausanne, ”A claim about Hamiltonian mechanics”, invited by T. Ratiu 2004- Mathematical Institute, University of Bern, ”Metric profiles and Mitchell theorem 1”, invited by M. Reimann 2004- IMA - EPFL , ”Majorisation and multiplicative quasiconvexity”, invited by B. Dacorogna 2004- Journ´ees d’automne de la Soci´et´e Math´ematique Suisse, ”Curvature of metric profiles” 2004- Universit¨at Stuttgart, Fakult¨at Mathematik und Physik, ”Convexity notions, groups and nonlinear elasticity” invited by A. Mielke. 2005- Mathematical Institute, University of Bern, ”Differential structures for sub-Riemannian spaces”, invited by M. Reimann. 2005- Centre de Math´ematiques et d’Informatique, Universit´e de Provence, S´eminaire de G´eom´etrie et Singularit´es, ”Flots hamiltoniens d’isom´etries” invited by B. Kolev. 19. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(20) HDR de Marius Buliga, Lille 1, 2007. 2005- Laboratoire de M´ecanique de Lille, ”Un test pour les crit`eres ´en´ergetiques de rupture”, invited by G. De Saxc´e. 2006- GAMM 2006, Berlin, Germany, G. De Saxc´e, M. Buliga, C. Vall´ee, C. Lerint¸iu, Construction of a bipotential for a multivalued constitutive law 2006- 8-`eme Colloque Franco-Roumain de Math´ematiques Appliqu´ees, Chamb´ery, ”Convexit´e de Schur et ´elastom`eres n´ematiques” 2006- Geometric and Asymptotic Group Theory with Applications, Manresa,Spain, ”Dilatation Structures” 2006- December Monthly Conference of the Institute of Mathemathics of the Romanian Academy, Bucharest, ”Travelling salesman through fractals” 2007- Geometric linearization of graphs and groups, January 22-26, 2007, Centre Interfacultaire Bernoulli, EPFL, Lausanne, Switzerland, ”Dilatation structures and linearization of self-similar actions” 2007- International Symposium on Defect and Material Mechanics, March 25-29, 2007 - Aussois, France, ”Fracture fattening and energy release rates” 2007- 6-th Congress of Romanian Mathematicians, June 28 - July 4, 2007 - Bucharest, Romania, Section: Theoretical Computer Science, Operations Research and Mathematical Programming, ”Self-similar dilatation structures and automata” 2007- Viertes Deutsch-Rum¨anisches Seminar u ¨ ber Geometrie Dortmund, 15-18 July 2007, ”Linear dilatation structures and conical groups” 2007- The eight international workshop on differential geometry and its applications, August 19-25, 2007, ”Babe¸s-Bolyai” University, Cluj-Napoca, Romania, ”nonholonomic spaces and geometric group theory”. 20. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(21) HDR de Marius Buliga, Lille 1, 2007. 2.9. Rapports de contrats. - M. Buliga, Energetic criteria in fracture mechanics, rapport scientifique, contrat de recherche du Minist`ere de la Recherche et des Technologies (Roumanie), MCTANSTI 627/1998-1999. 2.10. Participation ` a des comit´ es scientifiques des congr` es et colloques. - j’ai fait partie des organisateurs du S´eminaire Borel 2003, 3`eme Cycle Romand de Math´ematiques, intitul´e ”Tangent spaces of metric spaces”, Universit´e de Berne (Suisse).. 2.11. Activit´ es administratives et autres responsabilit´ es collectives. - grant owner MCT-ANSTI 627/1998-1999 ”Energetic Criteria in Fracture Mechanics” - grant member CEEX06-11-12/2006 - repr´esentant de la partie roumaine, dans le programme SCOPES, financ´e par le Fond National Suisse de Recherche, ”Lausanne-Bucharest common project on topology, geometry and mechanics”, (2001-2005).. 2.12. Citations par les auteurs d’autres publications. - B. Dacorogna, Some geometric and algebraic properties of various types of convex hulls, dans ”Nonsmooth mechanics and Analysis: Theoretical and Numerical advances” in honour of J. J. Moreau; edited by P. Alart, O. Maisonneuve and R. T. Rockafellar, in Advances in Mechanics and Mathematics, Springer (2006), 25-34, (1 citation) - A. Mielke, Necessary and sufficient conditions for polyconvexity of isotropic functions. J. Convex Analysis, 12, (2005), 291-314, (2 citations) - A. Mielke. Evolution in rate-independent systems (ch. 6). In C. Dafermos and E. Feireisl, editors, Handbook of Differential Equations, Evolutionary Equations, volume 2, pages 461-559. Elsevier B.V., 2005, (2 citations) - M. Negri, A finite element approximation of the Griffith’s model in fracture mechanics. Numer. Math., 95 (2003), no. 4, 653–687, (1 citation). 21. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(22) HDR de Marius Buliga, Lille 1, 2007. - A. Braides, A. .Defranceschi, E. Vitali, Relaxation of elastic energies with free discontinuities and constraint on the strain. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5), 1 (2002), no. 2, 275–317, (1 citation) - G. Oleaga, On the Path of a Quasi-static Crack in Mode III. J. of Elasticity, 76, (2004), 163-189, (2 citations) - G. Oleaga, The Classical Theory of Univalent Functions and Quasistatic Crack Propagation. a` parraitre, (2 citations) - A. Kaplan, F. Levstein, L. Saal, A. Tiraboschi, Horizontal submanifolds of groups of Heisenberg type, arXiv:math/0509601, (2005), (1 citation) - L. Ambrosio, N. Fusco, L. Pallara. Functions of bounded variation and free discontinuity problems, Oxford:Clarendon Press,2000, (1 citation) - R. Alicandro, M. Focardi, MS Gelli. Finite-difference approximation of energies in fracture mechanics. Ann. Scuola Norm. Sup. Pisa Cl. Sci. bf (4) 29 (2000), no. 3, 671–709, (1 citation) - P. Birtea, J.P. Ortega, T. Ratiu, Metric convexity in the symplectic category, http://arxiv.org/abs/math.SG/0609491 (1 citation). 22. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(23) HDR de Marius Buliga, Lille 1, 2007. 3. R´ esum´ e des activit´ es. Mes recherches sont consacr´ees a` la M´ecanique des Solides dans ses aspects th´eoriques et num´eriques, et a` l’Analyse G´eom´etrique des espaces m´etriques. J’ai donc une double sp´ecialisation, comme m´ecanicien et math´ematicien, qui s’explique par mon parcours et par l’organisation des ´etudes universitaires en Roumanie pendant les ann´ees ’80 et ’90. ´ a. Etudes en Roumanie (1987-1994) En Roumanie j’ai suivi des ´etudes de la section de M´ecanique des Solides de la Facult´e de Math´ematiques, Universit´e de Bucarest. Apr`es 2 ann´ees d’ ´etudes g´en´erales de math´ematique, les membres de la section de M´ecanique ont suivi pendant 3 ans des cours approfondis en e.d.p, calcul de variations, analyse fonctionnelle, mais aussi des cours d’´elasticit´e, plasticit´e, rh´eologie, fluides, ... La p´eriode totale des ´etudes ´etait de 5 ans (compar´ee a` 4 ans pour les autres sections de la Facult´e de Math´ematique) et les ´etudiants de cette section ´etaient pr´epar´es pour faire ensuite de la recherche. J’ai suivi ce double enseignement, math´ematique et m´ecanique, par passion de la math´ematique mais aussi parce que j’ai ´et´e toujours fascin´e par la physique. J’ai eu la chance de faire partie d’un petit groupe des ´etudiants s´electionn´es par le professeur Eugen S´oos depuis le commencement des ´etudes. En plus de cet enseignement non standard, nous avons b´en´efici´e des cours suppl´ementaires, donn´es par les meilleurs rechercheurs roumains, ex-membres de l’Institut de Math´ematiques de l’Acad´emie Roumaine, d´etruit par les autorit´es communistes. Pour nous, la distinction entre la m´ecanique et les math´ematiques est artificielle. Apr`es la r´evolution roumaine, toutes les institutions ont subi des grandes transformations. La deuxi`eme partie de mes ´etudes en Roumanie est faite dans des conditions meilleures (l’Institut a ´et´e refait), mais dans une atmosph`ere de transition et de confusion du point de vue de l’organisation. Suite a` 5 ann´ees d’´etudes j’ai re¸cu une diplˆome de math´ematicien. En pr´esent, pour les mˆemes ´etudes l’Universit´e de Bucarest offre une diplˆome de master. Je sais maintenant qu’`a cette ´epoque, les connaissances des ´etudiants roumains sur le syst`eme d’enseignement dans l’Union Europ´eenne ´etaient tr`es minces. D’ailleurs, il me semble que la situation ´etait sym´etrique de l’autre cˆot´e du rideau de fer. Apr`es la fin des ´etudes universitaires, j’ai travaill´e une premi`ere p´eriode comme professeur d’informatique dans un lyc´ee de Bucarest. Peu apr`es j’ai eu la chance d’enseigner le cours de relativit´e restreinte a` la Facult´e de Math´ematique, suite a` la proposition du professeur Iulian Beju. Mes domaines de recherche du d´ebut ´etaient les milieux continus en relativit´e restreinte et la topologie g´en´erale. ` la fin ce cette p´eriode, tous les membres du groupe selection´e par S´oos ont continu´e A ´ les ´etudes ailleurs, notamment en France et les Etats Unis. 23. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(24) HDR de Marius Buliga, Lille 1, 2007. b. P´ eriode parisienne (1994-1995) ´ Mon arriv´ee a` l’Ecole Polytechnique, comme ´el`eve auditeur (et apr`es comme ´etudiant en D.E.A. de M´ecanique non lin´eaire) m’a permis d’´elargir mes horizons, en particulier a` cause de l’acc`es a` une grande biblioth`eque de sp´ecialit´e. En collaboration avec Patrick Ballard et Andrei Constantinescu, nous avons r´esolu un probl`eme inverse d’´elasticit´e (d´etermination des contraintes r´esiduelles par mesure de contraintes sur de surfaces successives). Pendant le stage de D.E.A. fait au LPMTM, Universit´e Paris 13, j’ai eu l’occasion de m’initier au domaine naissant des formulations ´energ´etiques en la m´ecanique de la rupture fragile. Le sujet de stage ´etait de contribuer a` la formulation d’un mod`ele de rupture fragile qui utilise la fonctionnelle Mumford-Shah. J’ai vite prouv´e que un mod`ele bas´e exclusivement sur cette fonctionnelle (et sur une simple discr´etisation temporelle) ne donne pas de bons r´esultats dans le cas d’apparition d’une fissure. J’ai propos´e donc un mod`ele modifi´e, en utilisant des id´ees des probl`emes inverses ´ d’´elasticit´e (que j’avais appris auparavant, pendant les ´etudes a l’Ecole Polytechnique ), notamment la fonction de Dirichlet-Neumann. c. Deuxi` eme p´ eriode roumaine (1995-1999) Pour des raisons personnelles, je retourne en Roumanie. Je m’inscrit en th`ese, sur le sujet ”Formulations variationnelles en m´ecanique de la rupture fragile”, Directeur de th`ese: Eugen S´oos. D´ecid´e d’apprendre plus sur le sujet de la fonctionnelle MumfordShah, je contacte par m´el. le principal sp´ecialiste, Luigi Ambrosio (ENS Pisa), qui a la gentillesse de m’envoyer ses articles et avec qui je noue pour une p´eriode une ` ma d´eception je ne trouve pas la mˆeme ouverture aupr`es de l’´equipe collaboration. A fran¸caise qui poursuit le mˆeme but: un mod`ele rigoureux de rupture fragile bas´e sur la fonctionnelle Mumford-Shah. N´eanmoins, au but d’un an et demi, j’arrive a` formuler un tel mod`ele, en tenant compte aussi des faiblesses que j’ai d´ecouvert auparavant. Trois publications et cinq publications ´electroniques sont ensuite d´edi´ees a` ce sujet, dont le premier est mentionn´e dans la monographie de r´ef´erence de L. Ambrosio, N. Fusco, L. Pallara. J’ai obtenu un contrat de recherche de la part du Minist`ere de la Recherche et des Technologies Roumain sur le sujet des crit`eres ´energ´etiques en m´ecanique de la rupture fragile. Plus tard je commence a` ´etudier avec E. S´oos et M. Craciun le crit`ere de fissuration de Sih. Apr`es la th`ese de doctorat ( en math´ematiques!), je deviens int´eress´e par l’´elasticit´e non lin´eaire. Le raison est simple: trouver une extension du mod`ele de fissuration fragile pour des mat´eriaux ´elastiques non lin´eaires. Je d´ecouvre vite que l’´elasticit´e est un domaine int´eressant en soi et j’essaye de trouver des conditions n´ecessaires et/ou suffisantes pour la semi-continuit´e inf´erieure de la fonctionnelle ´energie ´elastique et des notions de convexit´e du potentiel ´elastique d´efini sur un groupe de matrices, au lieu d’un espace vectoriel. En deux articles j’ai introduit la bonne notion de quasiconvexit´e 24. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(25) HDR de Marius Buliga, Lille 1, 2007. dans le sens variationnel, associ´ee a` un groupe d’hom´eomorphismes bi-Lipschitziens. Suite a` une invitation de la part de J.M. Ball j’ai eu l’occasion de pr´esenter la notion de quasiconvexit´e multiplicative dans un expos´e a` l’Oxford Mathematical Institute. Au mˆeme temps je fais une s´erie de visites a` l’ENS (Pise) et SISSA (Trieste), ou j’ai l’occasion d’´echanger des id´ees avec L. Ambrosio et A. Braides, sur le sujet de formulations ´energ´etiques de la rupture fragile. Par l’interm´ediaire de E. S´oos je commence une collaboration avec C. Vall´ee (Poitiers) qui continue jusqu’`a pr´esent. c. P´ eriode suisse (2000-2006) Suite a` une visite de T. Ratiu en Roumanie, j’ai l’occasion de discuter avec lui de l’analyse sur de groupes de diff´eomorphismes, domaine dans lequel Ratiu a d´emontr´e des r´esultats fondamentaux. Il est int´eress´e par les utilisations que j’ai donn´e en m´ecanique de la rupture et l’´elasticit´e et il m’invite pour 3 mois dans sa chaire a` l’EPFL. Apr`es cette visite il m’offre la possibilit´e de passer quelques ann´ees a` l’EPFL. D’une position d’invit´e, je suis devenu ensuite premier assistant. ` l’EPFL j’ai d´ecouvert les relations entre la convexit´e de Schur et les notions de A convexit´e en ´elasticit´e, suite a` une co¨ıncidence : j’ai eu l’occasion d’apprendre plus, en mˆeme temps, sur la convexit´e de Schur (de la part de Ratiu) et sur sur la convexit´e de rang un, de la part de Dacorogna. Ensuite, pendant 4 ans, je travaille sur le sujet de la g´eom´etrie sub-riemannienne, qui reste parmi mes principales th`emes de recherche. J’ai collabor´e dans ce sujet avec l’´equipe de M. Reimann (Berne), avec S. Vodop’yanov (Novosibirsk) et j’ai fait une visite a` l’IHES pour discuter ce sujet. J’ai organise avec Tudor Ratiu le s´eminaire de travail ”Sub-Riemannian geometry and Lie groups”, en 2001-2002, a` l’EPFL. J’ai ´et´e parmi les organisateurs du s´eminaire Borel 2003, ”Tangent spaces of metric spaces”, ou j’ai pr´esent´e des constructions de fibr´es tangents d’un group sub-riemannien. La p´eriode de travail a` l’EPFL signifie pour moi la libert´e totale de recherche, sans soucis mat´eriels. J’en ai profit´e pleinement. Depuis 2004 j’ai recommence a` ´etudier des sujets de m´ecanique de la rupture et d’´elasticit´e, suite a` la collaboration avec C. Vall´ee. La fa¸con de mod´eliser l’´evolution quasistatique d’une fissure a attir´e l’attention de A. Mielke (WIAS), et j’ai eu l’occasion de collaborer avec lui a` l’EPFL et en Allemagne. Enfin, une collaboration a ´et´e ´etablie avec G. Oleaga (Madrid) sur le sujet de la m´ecanique de la rupture. Plus tard j’ai rencontr´e G. De Saxc´e (Lille-1), avec lequel nous avons travaill´e sur une m´ethode de construction des bipotentiels. d. Le pr´ esent (2006-2007) Je suis retourn´e en Roumanie a` partir de juillet 2006 et j’ai repris mon poste de charg´e de recherche a` l’Institut de Math´ematiques de l’Acad´emie Roumaine. D`es mon arriv´ee, je commenc´e une p´eriode de travail intense, en essayant de mettre sur le papier 25. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(26) HDR de Marius Buliga, Lille 1, 2007. toute une suite d’id´ees plus ou moins d´evelopp´ees pendant le stage en Suisse. Depuis mon rencontre avec G. De Saxc´e, le sujet des bipotentiels est parmi mes pr´eoccupations. Trois articles ont ´et´e ´ecrits en collaboration avec G. De Saxc´e et C. Vall´ee. Deux sont publi´es et le troisi`eme attends le verdict final. Deux autre articles soumis a` publication portent sur la fissuration fragile. J’ai la satisfaction de voir que mes premiers essais en la mati`ere semblent pointer dans une bonne direction. Dans le premier de ces deux articles, je propose une analyse rigoureuse des mod`eles de fissuration fragile bas´es sur la fonctionnelle Mumford-Shah. L’analyse porte sur des diff`erent fa¸cons de d´efinir l’´evolution quasistatique d’un corps ´elastique fissur´e et sur les implications physiques des hypoth`eses math´ematiques assez techniques. Dans le deuxi`eme article je traite sur une m´ethode d’homogeneization non standard de la fonctionnelle Mumford-Shah, qui semble pr´edire correctement la concentration d’endommagement dans un milieu ´elastique p´eriodique microfissur´e. Les deux articles sont soumis a` publication. Enfin, j’ai commenc´e a` jeter les bases de la g´eom´etrie sub-riemannienne a` partir de la notion de structure de dilatation. Cette notion ´etait deja esquiss´ee dans des preprints arXiv de la p´eriode suisse. Maintenant je commence un ´etude pouss´e dans cette direction, et je produis 6 articles (un publi´e et 5 soumises a` publication) sur le sujet. Je consid`ere ce sujet de travail comme le plus important dans ma carri`ere jusqu’`a cette date. L’´etendue de la notion de structure de dilatation est plus g´en´erale que la g´eom´etrie sub-riemannienne. J’ai ´etabli aussi des connections avec l’analyse dans les corps ultram´etriques et avec la th´eorie des automates. Dans le dernier an j’ai pr´esent´e ce travail lors de cinq expos´es, en Espagne (dans le cadre d’une conf´erence satellite de l’ICM2006), en Suisse, en Allemagne et deux fois en Roumanie.. 26. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(27) HDR de Marius Buliga, Lille 1, 2007. 4. M´ ecanique de la rupture fragile et la fonctionnelle Mumford-Shah. 4.1. Description du sujet. Une grande partie de la difficult´e des probl`emes de fissuration fragile consiste en la nature g´eom´etrique de la fissure. Les premiers contributions en ce domaine concernent surtout le comportement d’un materiau fragile. Parmi les r´ef´erences fondamentales se trouvent: Eshelby [54], Griffith [68], Irwin [60], Gurtin [72] [73], Rice [94]. Dans presque toutes les ´etudes, la g´eom´etrie de la fissures est a priori fix´ee. Parmi les peu nombreuses exceptions, on trouve les articles de Stumpf, Le [110], ou Ohtsuka [89] [90] [91] [92]. La g´eom´etrie de la fissure peut ˆetre prescrite de mani`ere forte, comme dans le cas des fissures rectangulaires ou elliptiques, qui pr´eservent leur forme le long de l’´evolution. Une prescription faible de la g´eom´etrie de la fissure apparaˆıt, par exemple, dans le cas d’une fissure unidimensionnelle qui ´evolue dans une configuration de r´ef´erence bidimensionnelle, a` la condition que la fissure soit a` tout instant une courbe simple. Dans ce cas, l’´evolution de la fissure est r´eduite au mouvement d’un point. Dans tous ces cas, la nature g´eom´etrique de la principale inconnue du probl`eme – la fissure – n’est pas prise en compte. Une nouvelle direction de recherche dans ce domaine commence avec l’article de Mumford et Shah [88], sur un probl`eme de traitement d’image. Ce probl`eme de segmentation de l’image, c.a.d. trouver l’ensemble des contours d’une image et construire une version plus simple de l’image en tenant compte de l’ensemble des contours, est similaire du point de vue math´ematique au probl`eme d’´evolution quasistatique des fissures fragiles. Dans l’article [88] Mumford et Shah proposent l’approche variationnel suivant pour le probl`eme de segmentation d’image: soit g : Ω ⊂ R2 → [0, 1] l’image initiale, comprise comme une distribution des niveaux de gris (1 c’est blanc et 0 c’est noir) sur le support Ω de l’image. Soit g : Ω ⊂ R2 → R l’image cherch´ee et K ⊂ Ω l’ensemble des contours. K est (contenu dans) l’ensemble des points ou la fonction u n’est pas continue, c.a.d. u ∈ C 1 (Ω \ K, R). On cherche une paire (u, K) qui minimise la fonctionnelle Z Z 2 I(u, K) = α | ∇u | dx + β | u − g |2 dx + γH1 (K) . (4.1.1) Ω. Ω. Le param`etre α contrˆole la r´egularit´e de la fonction u, le param`etre β contrˆole la distance L2 entre l’image u et l’image initiale g et le param`etre γ contrˆole la longueur (mesure de Hausdorff 1D) de l’ensemble K des contours. Les auteurs remarquent que pour β = 0 la fonctionnelle I peut ˆetre utilis´ee pour un traitement ´energ´etique du probl`eme de fissuration fragile.. 27. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(28) HDR de Marius Buliga, Lille 1, 2007. 4.2. Contributions. Mes contributions dans ce sujet, [21] M. Buliga, Energy Minimizing Brittle Crack Propagation, J. of Elasticity, 52, 3, 201-238, (1999) [22] M. Buliga, Geometric evolution problems and action-measures, PAMM Appl. Math. Bull., vol. LXXXVI (1998), T. U. Budapest, 53-58 [23] M. Buliga, Brittle crack propagation based on an optimal energy balance, Rev. Roum. des Math. Pures et Appl., 45, no. 2, 201–209 (2001) [29] M. Buliga, Equilibrium and absolute minimal solutions of brittle fracture models based on energy-minimization methods, (submitted), 2007 [33] M. Buliga, Microfractured media with a scale and Mumford-Shah energies, (submitted), http://xxx.arxiv.org/abs/0704.3791, (2007) [41] M. Buliga, Energy concentration and brittle crack propagation, http://arxiv.org/abs/math.AP/0510225, (2005) [43] M. Buliga, Perturbed area functionals and brittle damage mechanics, http://arxiv.org/abs/math.AP/0511240, (2005) [44] M. Buliga, Energy minimizing brittle crack propagation II, http://arxiv.org/abs/math.AP/0511301, (2005) sont li´ees a` la propagation des fissures fragiles dans un milieu ´elastique. Ma dissertation de D.E.A., ”Mod´elisation de la d´ecoh´esion d’interface fibre-matrice dans les mat´eriaux composites”, a ´et´e faite apr`es un stage a` LPMTM, Universit´e Paris ` la fin du D.E.A., j’ai d´ecid´e de retourner en Roumaine, ou plus tard 13, 1995. A j’ai soutenu un doctorat en math´ematiques (1997), a` l’Institut de Math´ematiques de l’Academie Roumaine, avec le titre ”Thermo-m´ecanique de la rupture. Formulations variationnelles en m´ecanique de la rupture fragile”.. 4.3 4.3.1. R´ esum´ es des articles Energy minimizing brittle crack propagation. Cet article porte sur la mod´elisation de la fissuration quasistatique d’un solide ´elastique fragile. Les hypoth`eses du travail sont les suivantes : le corps ´elastique lin´eaire, avec ou sans fissures initiales, ´evolue d’une mani`ere quasistatique suite a` l’action des d´eplacements impos´es sur la fronti`ere. Au cours de son ´evolution, des fissures de g´eom´etrie arbitraire peuvent apparaˆıtre et/ou se propager.. 28. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(29) HDR de Marius Buliga, Lille 1, 2007. Dans ce qui suit, je pr´esente un mod`ele d’apparition d’une fissure fragile suite au d´eplacement impos´e sur la fronti`ere d’un corps ´elastique. L’´etat d’un corps fragile avec la configuration de r´ef´erence Ω est d´ecrit par une paire d´eplacement-fissure. (u, K) est une telle paire si: (1) K est une fissure dans le corps, vue comme une surface quelconque, (2) u est un d´eplacement du corps fissur´e avec la fissure K ⊂ Ω, compatible avec le d´eplacement impos´e sur la fronti`ere u0 , c.a.d. u ∈ C 1 (Ω \ K) et u = u0 sur ∂Ω. L’´energie totale du corps dans l’´etat (u, K) a la forme d’une fonctionnelle MumfordShah: Z E(u, K; u0 ) = w(∇u) dx + F (u0 , K) . Ω. Le premier terme de la fonctionnelle E repr´esente l’´energie ´elastique du corps soumis au d´eplacement u. Le terme suivant repr´esente l’´energie utilis´ee pour produire la fissure K dans le corps, avec le d´eplacement impos´e u0 comme param`etre. Dans ce mod`ele l’apparition de la fissure est vue comme un probl`eme d’´equilibre. Quand le d´eplacement u0 est impos´e sur la fronti`ere (ext´erieure) ∂Ω, l’´etat (v, S) du corps fragile minimise l’´energie totale E(·, ·; u0 ). La fissure qui apparaˆıt est S. Remarquez que S peut ˆetre aussi l’ensemble vide; dans ce cas le mod`ele nous dit que le corps soumis au d´eplacement u0 ne se fissure pas. L’apparition des fissures fragiles et la segmentation de l’image sont deux probl`emes a` discontinuit´e libre. Les inconnus, la fissure ou la collection des contours, sont des surfaces (lignes) de discontinuit´e pour le d´eplacement ou pour l’image finale; leur position ou g´eom´etrie sont compl`etement libres. Nous allons utiliser un approche ´energ´etique du probl`eme de l’´evolution de la fissuration fragile, quasistatique. Nous allons discr´etiser le temps et transformer le probl`eme en une suite des probl`emes de minimisation d’´energie. Francfort et Marigo [59] proc`edent de la mˆeme mani`ere dans le cas de l’endommagement fragile brutal. Pour bien formuler ce passage du discret au continu (par rapport au temps), nous allons utiliser le cadre des mouvements minimisants g´en´eralis´es, introduit par De Giorgi [64]. Pour cela nous introduisons dans la Section 2 la notion de mouvement minimisant de l’´energie, comme un cas particulier d’un mouvement minimisant g´en´eralis´e. Dans la Section 3, apr`es les pr´eliminaires concernant la statique d’un corps fragile, nous pr´esentons une variante du crit`ere de Griffith pour la propagation d’une fissure fragile en Sous-section 3.3, comme un crit`ere de s´election parmi les possibles ´evolutions de la fissure. A la fin de cette section nous formulons le probl`eme d’´evolution quasistatique d’une fissure fragile sous la forme (14). Dans Subsection 4.1 est donn´ee une formulation de ce probl`eme, en termes de mouvements minimisants d’´energie, en utilisant une fonctionnelle Mumford-Shah (D´efinition 4.1). Dans ce mod`ele, il y a une seule constante de materiau reli´ee a` la fissuration: la constante G de Griffith. Quelques propri´et´es du mod`ele sont explor´es dans la Soussection 4.2, dans les cas antiplan et unidimensionnel. Nous prouvons que dans ce mod`ele 29. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(30) HDR de Marius Buliga, Lille 1, 2007. l’apparition des fissures peut se produire. Dans la relation (23) se trouve l’expression du σc , la tension critique qui conduit a` la rupture, d’apr`es le mod`ele, dans le cas d’un exp´erience de traction unidimensionnelle. On d´eduit d’ici que σc et G ne peuvent pas ˆetre tous les deux des constantes de materiau dans ce mod`ele. Dans la Section 5 est contenue la formulation faible du mod`ele introduit dans la D´efinition 4.1, discr´etis´e par rapport au temps. La Sous-section 5.1 traite des fonctions sp´eciales a` variation ou d´eformation born´ee. L’existence des solutions du mod`ele discr´etis´e (D´efinition 5.1, Th´eor`eme 5.3) est une cons´equence des r´esultats dus aux De Giorgi et Ambrosio [65], Ambrosio [1] [2], Ambrosio, Coscia et Dal Maso [4]. Le cas antiplan est discut´e en Sous-section 5.3. Nous comparons les solutions faibles (D´efinition 5.1) et fortes (D´efinition 4.1) dans la Sous-section 5.4. Dans la Section 6 nous comparons notre mod`ele avec le mod`ele de Ambrosio et Braides [3], qui est aussi bas´e sur des mouvements minimisants g´en´eralis´es. Dans cet mod`ele sont introduites des forces de viscosit´e et la propagation des fissures pendant un d´eplacement impos´e constant en temps est permise; par contre, l’apparition des fissures ne peut pas se produire d’une mani`ere physiquement acceptable. Dans la Section 7 nous prouvons un r´esultat partiel d’existence des solutions du mod`ele en variable temporelle continue, sous l’hypoth`ese d’une borne sup´erieure uniforme (par rapport au temps) de la puissance communiqu´ee par le reste de l’univers au corps fissur´e. La Section 8 est d´edi´ee a` l’approche num´erique du mod`ele. Nous utilisons des r´esultats de convergence variationnelle de Ambrosio-Tortorelli [5] et la m´ethode num´erique de Richardson-Mitter [95]. 4.3.2. Equilibrium and absolute minimal solutions of brittle fracture models based on energy-minimization methods. Nous pouvons distinguer quatre directions de recherche li´ees aux mod`eles de fissuration fragile, vus comme des probl`emes a` discontinuit´e libre, et bas´es sur la minimisation d’une fonctionnelle ´energie de Mumford-Shah. Ces directions sont : (i) l’´etude qualitative du mod`ele, a` supposer que les solutions du mod`ele existent, (ii) la comparaison avec l’exp´erience et les autres mod`eles classiques, (iii) la formulation faible du mod`ele, l’´etude de la r´egularit´e des solutions faibles, (iv) la recherche des r´esultats d’approximation qui peuvent mener aux algorithmes num´eriques. Pour un chercheur int´eress´e a` la m´ecanique, les directions (i), (ii) et (iv) sont plus int´eressant que (iii). Pour le chercheur orient´e plus vers la math´ematique les points d’int´erˆet sont compl´ementaires. Dans cet article, nous sommes int´eress´es par les deux premi`eres directions mentionn´ees auparavant. Nous formulons un mod`ele g´en´eral de fissuration fragile quasistatique, puis nous d´efinissons des ´etats d’´equilibre et des ´etats minimaux absolus et nous explorons leurs propri´et´es fondamentales. Dans le cas de la rupture fragile 3D nous prouvons une relation entre une g´en´eralisation de l’int´egrale de Rice et la concentration 30. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(31) HDR de Marius Buliga, Lille 1, 2007. d’´energie ´elastique, toutes les deux vues dans le sens de la th´eorie de la mesure. 4.3.3. Microfractured media with a scale and Mumford-Shah energies. Nous voulons comprendre la concentration d’endommagement observ´ee dans les milieux ´elastiques micro-fissur´es. En raison du comportement diff´erent par rapport au changement d’´echelle de l’aire et du volume (ou de longueur et de l’aire en 2D) la m´ethode traditionnelle d’homog´en´eisation qui emploie des tableaux p´eriodiques des cellules semble ´echou´er, une fois appliqu´e a` la fonctionnelle Mumford-Shah et aux domaines p´eriodiquement micro-fissur´es. Dans cet article nous nous ´ecartons de l’homog´en´eisation traditionnelle. Le principal r´esultat concerne l’utilisation des ´energies de Mumford-Shah et m`ene a` une explication de la concentration observ´ee de l’endommagement dans les corps ´elastiques micro-fissur´es. Le premier r´esultat d’homog´en´eisation, au sujet de la fonctionnelle Mumford-Shah semble ˆetre dˆ u a` Braides, Defranceschi, Vitali [18]. L’article de Focardi , Gelli [58] (voir aussi les r´ef´erences l`a-dedans) fait partie d’une autre piste de recherche qui pourrait ˆetre pertinente pour cet article: homog´en´eisation des domaines perfor´es. Le r´esultat principal de cet article concerne l’utilisation de l’´energie Mumford-Shah pour donner une explication de la concentration d’endommagement observ´ee dans les corps ´elastiques micro-fissur´es. Au lieu d’effectuer une homog´en´eisation de l’´energie du corps micro-fissur´e et d’´etudier alors les minima de l’´energie homog´en´eis´ee, nous proc´edons d’une mani`ere diff´erente. Nous ´etudions une suite des probl`emes sur des corps ´elastiques contenant une distribution p´eriodique des fissures, avec la configuration de r´ef´erence Ωε , indic´ee par un param`etre d’´echelle ε. Pour chaque ε la configuration Ωε est compos´ee d’un nombre M (ε) ≈ ε−3 des cellules fissur´ees de dimension ε. Pour chaque ε on a un probl`eme de minimisation d’une fonctionnelle Mumford-Shah pour lequel on peut prouver l’existence d’une solution. Notons avec N (ε) le nombre de cellules endommag´ees de la configuration Ωε . Nous prouvons une estimation de la grandeur de N (ε) qui montre que N (ε) ≈ ε−2 . Cela veut dire que l’endommagement a tendance a` se concentrer en bandes de petit volume, ce qui est conforme aux resultats exp´erimentaux.. 31. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(32) HDR de Marius Buliga, Lille 1, 2007. 32. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(33) HDR de Marius Buliga, Lille 1, 2007. 5. Bipotentiels. 5.1. Description du sujet. Les outils de base de la m´ecanique de milieux continus sont les ´equation de compatibilit´e cin´ematique et d’´equilibre. De l’information additionnelle doit ˆetre fournie par les lois constitutives traduisant le comportement mat´eriel. Sous sa forme la plus simple, une loi de comportement est donn´ee par un graphe rassemblant des couples des variables duales; souvent ce graphe r´esulte de l’essai exp´erimental. Pour beaucoup de situations physiquement pertinentes, les lois de comportement sont multivoques et ´egalement associ´ees. Le graphe d’une telle loi constitutive est inclu dans le graphe du sous-differentiel d’un surpotentiel φ (qui est aussi semi-continu inf´erieurement ). La loi de comportement prend la forme d’une inclusion diff´erentielle, y ∈ ∂φ(x). Tout surpotentiel φ a une fonction polaire φ∗ qui satisfait une relation fondamentale, l’in´egalit´e de Fenchel, ∀x, y φ(x) + φ∗ (y) ≥ hx, yi. La loi de comportement peut ˆetre ´egalement ´ecrite comme x ∈ ∂φ∗ (y). Dans la litt´erature, ce genre de mat´eriaux s’appellent souvent des mat´eriaux standard ou des mat´eriaux standard g´en´eralis´es [74]. Du point de vue des applications, il est important de savoir si un surpotentiel existe pour un graphe donn´e, et de le construire. La r´eponse a` ce probl`eme est fournie par un th´eor`eme c´el`ebre dˆ u a` Rockafellar [96] qui assure qu’un graphe admet un surpotentiel si et seulement si le graphe est cycliquement monotone maximal. Cependant, certaines lois de comportement sont non-associ´ees. Elles ne peuvent pas ˆetre trait´es dans le cadre des mat´eriaux standard. Pour contourner ce probl`eme, une r´eponse possible, propos´ee d’abord dans [98], consiste a` construire une fonction b a` deux variables, bi-convexe, qui satisfait une in´egalit´e g´en´eralisant celle de Fenchel, c.a.d. ∀x, y b(x, y) ≥ hx, yi. G. de Saxc´e appelle une telle fonction bipotentiel. Physiquement, le bipotentiel repr´esente la dissipation. Dans le cas des lois de comportement associ´ees, le bipotentiel est s´epar´e : b(x, y) = φ(x) + φ∗ (y). Quant aux lois de comportement non associ´ees qui peuvent ˆetre exprim´ees avec l’aide des bipotentiels, elles ont la forme d’une relation implicite entre les variables duales, y ∈ ∂b(·, y)(x). En m´ecanique, nous dirons que ces lois sont des lois de normalit´e implicites ou faibles. Les applications des bipotentiels a` la m´ecanique des solides sont diverses: la loi du frottement du Coulomb [99], le mod`ele non-associ´e de Dr¨ uckerPrager [100] et le mod`ele Cam-Clay [101] en m´ecanique des sols, la plasticit´e cyclique ([99], [13]) et la viscoplasticit´e [77] des m´etaux avec une loi cin´ematique non lin´eaire d’´ecrouissage, la loi d’endommagement de Lemaitre [12], les lois coaxiales ([53], [113]). De tels mat´eriaux s’appellent des mat´eriaux standard implicites. Un synth`ese concernant ces lois exprim´ees en termes de bipotentiels peut ˆetre trouv´e dans [53] et [113]. L’utilisation des bipotentiels dans les applications est particuli`erement attrayante dans des simulations num´eriques par la m´ethode des ´el´ements finis, mais l’int´erˆet n’est pas limit´e a` ces aspects. Par exemple, les th´eor`emes de borne de l’analyse limite ([103], 33. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
(34) HDR de Marius Buliga, Lille 1, 2007. [16]) et de la th´eorie de l’adaptation plastique ([105], [53], [17], [14]) peuvent ˆetre reformul´es dans le cadre plus large des lois faibles de normalit´e. D’un point de vue num´erique appliqu´e, la m´ethode du bipotentiel sugg`ere de nouveaux algorithmes, rapides mais robustes, comme les estimateurs variationnels d’erreurs ´evaluant la pr´ecision du maillage en ´el´ements finis ([75], [76], [102], [104], [15], [78], [79]). Les applications a` la m´ecanique de contact [55], a` la dynamique des mat´eriaux granulaires (([56], [57], [62][106]), a` la plasticit´e cyclique des m´etaux [102] et a` la plasticit´e de sols ([11], [78]) illustrent la pertinence de cette approche.. 5.2. Contributions. Mes contributions a` ce sujet sont due a` une collaboration avec G. de Saxc´e (qui a introduit les bipotentiels) et C. Vall´ee: [97] G. de Saxc´e, M Buliga, C. Vall´ee, C. Lerintiu, Construction of a bipotential for a multivalued constitutive law, PAMM, 6 , 1 (December 2006), Special Issue: GAMM Annual Meeting 2006 - Berlin [25] M. Buliga, G. de Saxc´e, C. Vall´ee, Existence and construction of bipotentials for graphs of multivalued laws, J. of Convex Analysis, 15, 1, (2008) [26] M. Buliga, G. de Saxc´e, C. Vall´ee, Construction of bipotentials and a minimax theorem of Fan, (submitted), http://arxiv.org/abs/math.FA/0610136, (2006). 5.3 5.3.1. R´ esum´ es des articles Existence and construction of bipotentials for graphs of multivalued laws. Dans tous les articles d´ej`a mentionn´es au sujet des applications m´ecaniques, des bipotentiels ont ´et´e construits pour certaines lois de comportement multivoques. N´eanmoins, afin de comprendre mieux l’approche du bipotentiel, on doit r´esoudre les probl`emes suivants : 1) (existence) quels sont les conditions a` satisfaire par une loi multivoque telle qu’elle peut ˆetre exprim´ee avec l’aide d’un bipotentiel ? 2) y a-t-il un proc´ed´e pour construire une classe des bipotentiels pour une loi multivoque ? On s’attend a` ce que g´en´eriquement la loi ne d´etermine pas uniquement le bipotentiel. Nous donnons un premier traitement math´ematique de ces probl`emes et nous prouvons des r´esultats d’existence (th´eor`eme 3.2) et de construction (th´eor`eme 6.7) des bipotentiels pour une classe des lois multivoques. 34. © 2008 Tous droits réservés.. http://www.univ-lille1.fr/bustl.
Figure

Documents relatifs
the generating functional of a continuous convolution semigroup of probability measures on a Hilbert-Lie group.. The proof is inspired by the one given in the
It should be noted that : 1° Kirillov, in his original paper [3], proved that the map from the orbit space to dual is continuous and that the bijection is a homeomorphism on an
L’accès aux archives de la revue « Cahiers de topologie et géométrie différentielle catégoriques » implique l’accord avec les conditions générales d’utilisation
We deduce that for G an infinite definably compact group definable in an o-minimal expansion of a field, G 00 is bi- interpretable with the disjoint union of a (possibly trivial)
According to the idea of a paper [20], one can construct irreducible nonlocal representations of the group of measurable G-valued func- tions on X, G being a Lie
is its group of components ; subgroup will always mean closed subgroup ; and cyclic group will mean a compact Lie group containing an element, called the generator, whose powers
This Lie algebra is therefore free, and its quotient is A/(a). This proves the theorem.. Under the hypothesis of Theorem 2, we show that d 2 = 0 and that the spectral
The bouquet bch(E , A ) will be called the bouquet of Chern characters of the bundle E with connection A (in fact, we will have to modify the notion of G-equivariant vector bundle
