Ondes baroclines longues forcées par un échauffement local

" " . ' <

1

,'" • 1 f'

..

, ,

ONDES BAROCLINES LONGUÈS jORCEES PAR tJN EDHAUFFEMENT LOCAL

par ~

.

, ,~

.

-'"

l

@

Pierre Gauthier

,

~ ----~~-~'--~--~:

Ce mémoire est présenté à la Facult~ de recherche et des études gr~uées

CGlmme exigep.ce ~ielle de la maîtrise ès sciences.

DéP,à-rtement de météorolo~ie Université Mc Gill Montréal, Canada

\

A

•

Septembre 1982

,

, e

,

& ~ 1 i J

;

\

1

, ",

_,

r

,f

'E

t

\

(

,

,

..

Résumé.

Utilisant un

~odèle

barocline quasi :'géostroFlhe dans lequel une stra-' tification continue et une dissipation par pompage d'Ekman o~t été incluses,

"

on montre que les ondes longues quasi-stationnaires forcées par une topo-graphie et un échauffement diahatique sont décrites par une équation de

,

Korteweg-de Vries non-hornogè~~. L' 8pproche de Warn et Brasnett (1982) pour des ondes,forcées par une topographie est reprisé ici pour étudier les effets

1" ~

d'un forçage par échauffement diabatique. Après avoir examiné les solu-tians du pro bJ ème linédri sé, on se demande comment la présence d'un échauf-fement affectera l'évolution d'un système atmosphérique modélis~ ici par une onde soli taire dont l'amplitude a et la phase

ç/,

varient dans le temps. Un système autonome décrivant l'évolution de a et ~ est dérivé. Les solu-tians stationnaires stables sont identifiées aux situations de blocage atmo-sphérique régional. On montre ensuite que des perturbations peuvent être

1

capturées par la zone d'échauffement; celles-ci sont alors caractérisées

~taprès leur amplitude initiale et leur vitesse de déplacement.

'. -" , ,

,

l t

,.

" _", Abstract • .

Using a q~asi-geostrophic baroclinic model with ~ontinuous strati-fication and dissipation by Ekman pumping, i t is shown that long,

quasi-~tatiônary

waves forced by

topogr~phy

and

dia~atic

heating are described

byan inhornogeneous Korteweg-de Vries equation, The approach of Warn and Brasnett (1982) for waves forced by topügraphy ls then used to study, the effects of diabatic forcing. Af'ter a look at the solutions of the

.li~-1

rized prob1ern, we examine how hea:Li ng can affect the evolution of an

atmo-~ spheric system associ a ted here wi th a soli tary wave of which the amplitude a and phase ~ now vary in time.

".-An autonomous system is deri ved for the evolution of a and ~. The stable stationary solutions of this system are identified wi th situations oC rogional atmospheric blocking. I t 18 found that disturbances can be captured by the heating zonej these are then

charac-('

terized by their mi tial amplitude and Bpeed.

/

1 w,

/

1

/

-,

(

Remerciemept,p

'-.,

Je voudrais reme;rcier sincèrement mon directeur de recherche

j

le pz:ofesseur T. Warn, qui m' a dét~rminé le sujet de ce mémoire. J"e le

remercie pour ses conseils et ses nombreuses suggestions qui sont plu"

.

' _{que largement reflétés dans ce mémoire.}

,

Je remercie également le département de météorologie de

l'Univer-si té Mc Gill pour son soutien financi er de même que le CNRSG qui ID' a

ac-cordé une bourse d'études pour l'année académique 79-80.

ï f 1 "

..

,(

J •

;, \

.

i

., t t CI l, ;~ ~7

.

1 -\. l, :. ~ " -, '. /~ ~

.

_{~ '~}

~

't ... ;-c~ \ • !

TABLE

; DES MATIERES

...

u u ~~

Abstract

; ... "

... ..

Remerciements l ' ... t . . . " .. 't! ... Il . . . " " " . . . ..

Table des matières

! • • • • • • • • " • • • • • • • • ., • • • • • • • • • • • • • • • • • • • • • & • • • • • • • •

Liste des figures . . . .. . . 1. . . . ..

Liste des symboles • • • • • • • • p • • • • • ", •• " • • • • • • • • • • • • • • • • • • • • ., • • • • • • • • • •

_4" ,

CHAPITRE' l Introduction. . . . lit . . . ..

Réduction du problème à l'équation ds;,

Korteweg-de Vries .... oJ '" . . . 0 . . . CI . . . .. 2.1". Position du problème ...

Réduction à ] 'équation de Korte~ ..

eg-.'

de Vries .,

... .

2.). Discussion des limiteR inhérenteG à

11 111 Iv v /\, vii lx l

5

9 cet te approche ... D • • .. • • • • • • • • • • • • • ..

15

CHAPITRE III CHAPITRE IV

Approche faiblement non-linéaire •••...••.••••••• 17

_..

).1. Cas faiblement non-linéaire et sans

dissipation .•....•...•...••.••.•••••• 17 J.2. Création d' ondes stationnaires dans le

cas où nY > 0 ... , .. .. • .. . . . .. • .. ..

23

J.).

Etud~

d'{!nL''''passage dJun flot 'au-dessus d,'une

'zone d'échauffement de longueur finie • • . • • • • •

27

Etude de l'évolution d'une onde solitaire forcée

I!§l!" un échauffement local ... III • • " . . . . )0

4.1. Equation de Korteweg-de Vries faiblement

forcée ... ., ... , ... , ... 0 • •

JI

4.2.

La méthode de diffusion inversée . . . , . . . . Il •

4.3.

,Calcul do l'équation d'évolution de l'ampli-/ tude par la méthode des échelles multiples

2Analyse

de quelques cas SinlPle~~ ••••••• '" ••••

)2

)5

38

.',

,

•

"

"

1

._~-.. - - ... !_::,~ ..

~-•

(

~ CHAPITRE V CHAPITRE VJ; Bi bl.iographia , , i }

1

r.

L

f, ,,'

(

, "

}

Solutions stationnaires de l' équation de Ko,rteweg- " de Vries et bloc,age atmosphérique ••.••.•.••••••••

Solutions associées aux ondes de grande

a.rnplitude ... t'" • • • • • • • • • _, • • • • • • • " , • • • • • • • •

Etude de la stabilité g,es états

station-naires

...

"

...

,

.. .

Etude de cas

...

,

..

Conclusio"n

...

,

... .

'-P

.

...

• • • • • • • J • • • • • • • • , • • • • • • Il • • • • • • • • • • • • • • • • • • •

. .

.

. . .

)

.

.

) ... '

vi

45

" \ ,

51

61

70

t't

73

i

1

.1

...

USl'E DES FIGURES 1

Figure

).1 Déformation du contour d'intégration pour les inté-gra.les de

l'éq.().5).

~

.

).2 Conto& d'intégration lorsque x

>

0 et x - at

>

O.

3.3

Contour d

~

ntégrati on lorSrtllp. x-'l( 0 et x - at < O.

3.4

Graphe de

]~

solution A(O)(x,t) du prolüèm8 faible-ment non-li néai n"c, ] orsflue a > 0, y < O.

).5

Déformation de cont.our lor::>CjuIJ uy >0.

3.6

}.7

3.8

4.1

5·4

5·5

5.6

5.7

5.8

Graphe ùe A(O)(x,t) lonqne u < 0, y < O.

GraphF; de A(O)(x,L) lorsque uy < 0, ex> 0 et at

>

1 pour un échauffenrent cow,tanL eur l'intervalle

[0,1J.

-Graphe ùe A(O)(x,t) lorsque exy> 0, ex < 0 et -

~t

>

1 pour -'un échauffement constant sur l'intervalle

[L,OJ.

Graphe forcée

de la solution de l'équation de KdV faiblement Graphe

lorsque R(u) := - ru.

1

de la fonction de potentiel V(~) lorsque eex

>

0:

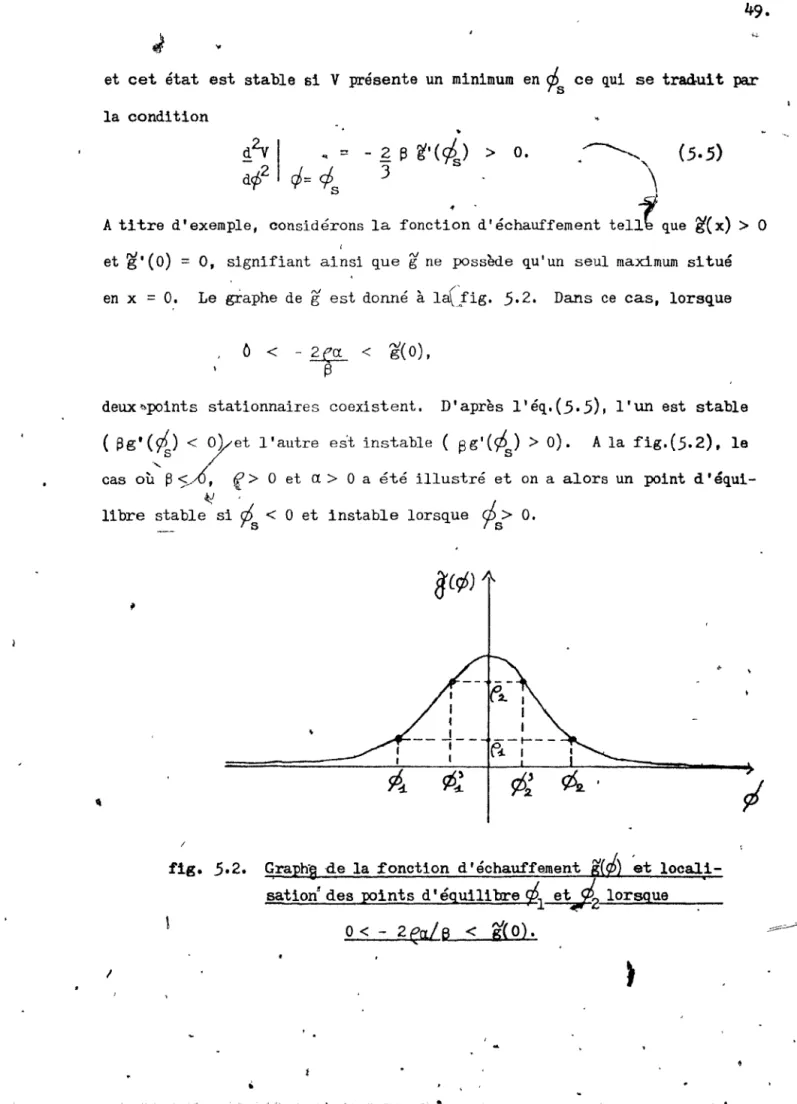
Graphe de la fonction d'échauffement t(~) et localisa-tion des poin Lü d' équili bre CPl et

sz5

2 Idrsque

0<- 2ea

/f3

< g(O).

Configuration d'un champ de vecteurs près d'un point d'équilibre a) stable,

b)

instable.

Configurations ~ossibles d'un champ de vectours défini

par une équation de la forme dX' ::: DX(O,O) X'. dt

Configurations possibles du flot extérieur en fonction

sign~ des pararnè~es a et _,

13.

ReprésentaLion des états stationnaires et

r;b.

-en fonction de Flot dans le plan "de phase lorsque

_f3

< 0, c >

°

_{et ((, >}

1

)

Flot dans le plan de phase lorsque _S > 0, c < 0, cr >\0 et 0 < f<

_fc'

du

E:

o.

"

~

19

20

'21

22 _".

24

26

28

29

"

34

48

49

53

55

60

62

63

6)

Î \

(

1

5.10

5.11

5·12

\

Flot dans le plan de phase lorsque cr > 0, 13 < 0 et c < O. Flot dans le plan de phase c<f1prenan~- un cycle-limite.

(--Graphe de l ' éq.

(5.11).

Flot dans le plan de phase lorsque

cr

> 0,

13

< 0, cl > 0 et c 2 >

o.

J

-" (

1

"

..

/

•

•

r

viii

65

66

68

68

(

LIS'I'li~ DES SYHBOLRS

~

: foqction dE: courant."

t· ::

A( x,

"d

.rfCy

f !!.): f oncti. on de courant de perturbation.

t. :

paramèYf' '.k ppr'turluUon. E v nom br" cl' l';i;:man. ti · nomr,rt"} dp Ji ).,sby. •

11

(x,y,z) : taux d'échauffement dû à l'advection et aux pources internes

dt' ché'Lleur.

S(z) :

\\(y,

z)

d ensi t,s de liai r pour une a trnosphère standard. paramèLre de st r;ülfication.

'J. ...

-t. factr~'Jl [le Lourhi llon planétaire.

H(x,y) "- .- O(x,yJ : prc.fil dA la topographie.

\

fkU'arnèLy~ de di."é,tP<1 tinJ1.

l'

a.

S.

y, r Pé.ramèLre;-; do l ' é<]uaticlE de KorV'lWog-de Vries.

k nombr", d 'on.-:1e.

f( x) f' . f'Ç'él{';r'? ~~ H l t éc;u dion j p KdV j CJ a la t 0 pOfÇY''l pl d (> •

eex)

1'- c,,;age ,0 p _{l '}

IILulti on (lf.l _KriV , _{l' ':l'..:hauff}D0IenL -'-- -' -' <J

cv • 'f"(l')

} e( L),

) <.

'.

r " u(

'7.

t) :ë:nluLi _(1 de ] • 0Q. (h. l). b( t )"

c;: (

L a( t ), () ( L ,

J" C·C U Ol! ;' "'p()horÜlf;]" cacac!(--ü,anl la dyn"mlque :lc8 éq,(4.9)

C'~ t LO ; ~ f' • DX(as ' ts) À1' 1..₂

,

À, S = sech T

.

:;:; _tanh ,h,UIlP , t (h. À rJ z

, ' vr'LL-'dr'. f.n:' lf~ pl",: dl) il},,', ~.e dr1~;1i p:-tI ]f!G éq.,'h'.9)

\ J) •

/

4

,

l

_.'

i

d l, r î t lJ~ ! " (1' '1 t_

t

t

, .;: t ~

ft

~, ~~ ~ - k

f'

,

' H

1

:r, "

J

1,

,~

~

_..

' "-:i.

f:

~ .. " f

~

"

v

i:

'F;

t

': )'

;.;'

,

_1, !l

t

~. If.'

l

f. ~ ~

,..

'7

,

,

•

~ - 1-t: ~

"

~ \~ r " " t~

_

:"'?'l'"). , " ~ .;'r-~. •

(:

t

CHAPITRE l

INT RonycT ION

"

;

Depuis quelques années, plusieurs chercheurs se sont intéressés à

l'étude des ondes atmosphériques quâsi-stationnaires principalement à cau-se du lien existant entre celles-ci et les anomalies persistentes du flot zonal si souvent observées en météorologie. Le blocage atmosphérique est l'une de ces anomalies.

--Charney et Devore (1979) ont tout d'abord abordé le problème en con- 1 sidérant un modèle barotrope forcé par une topographie. Utilisant une repré-sentation spectrale lOrtement tronquée, ils

~ntrèrent

que le caractère

non~

\

,-.

~.

li~éaire des équations à résoudre conduit à l'existence d'états d'équilibre

..

multiples. L'étude de la stabilité de ces états établit qu'au moins deux d'entre eux sont stables: l'un est associé à une situation où le flot est zonal, l'autre à une situation de blocage. Cette stabilité de la configu-ration de blocage si~nifie que de légères perturbations du flot se résorbe-ront graduellement et la configuration de blocage se maintiendra.

\ Utilisant une approche analytique ou numérique, plusieurs-auteurs ont examiné différents aspects de ce prOblème tant pour un modèle barotrope que· barocline ( éharney et Strauss (1980), Egger (1978, 1981). Hart

(1979),

Mitchell et Dutton (1981), Ped10sky (1981), P1umb (1979, 1981), Trevisan et

Tou-,

-.

, ,

,.

(

2.

tefois, dans tous les cas, le système était forcé par une topographie ou un échauffement périodique selon x, la coordonnée du plan

S

associée à la lon-gitude. Los résultats obtenus s'appliquent donc essentiellemen~ aux ondes planétaires.

Dans

l'étude de Charney, Shukia et Mo

(1981),

'on compare les observations météorologiques aux résultats obtenus à partir d'un modèle

ba-rotrope pour conclure que cette approche réussit à expliquer assez bien les situations de blocage associées aux nombre d "onde 2 et

J.

Par contre, plu-sieurs situations à caractère régIonal échappent à l'analyse.

Le blocage atmo:3phérique régional a été étudié par Malguzzi et Spe-ranza

(1981)

dont l'approche demeure toutefois analogue aux précédentes puis-qu'on y considère une topographie de la fone

h == B(Ex) cos kx,

,

l'amplitude variant selon une échelle spatiale allongée. Patoiné et Warn

(1982)

abordèrent le problème différemment. Se situant dans le contexte des

ondes quasi-stationnaires baroclines~longues et forcées topographie, la fonction de courant s'exprime alors

+

(

x, y, z, 'l')

= -

J

Y u( y' , z) dy'

où E

«

l, u(y, z) étant le vent de base et t" une échelle de temps ralentie.

La fonction

Sb

est obtenue en résolvant le problème au premier ordre tandis que A(x,~) est déterminée par une condition de solvabilité du problème

à

l'ordre suivant. Ils montrèrent alors que A(x.~) doit satisfaire l'équation

A + uA + ~AA + yA = f'(x),

~ x x xxx

(1.1)

où f(x) est déterminée par la topographie. Les autres paramètres dépendent essenf:iellement de

l

et de u(y, z). Lorsque fex) =: 0, l'éq. (1.1) est l'une des formes de l'équation de Korteweg-de Vries (KdV) à laquelle les 0~e6

so-,

,

, 1 , '

'1

(

" ~~ :-f " ~ ,t 1 _ç ' ....

1

1

.'

Îr fT {

..

• r,'

"'"

z.-t

-l' t :t " (---= ;

"

Il

;

lA

~

~

t,

~

~

_li. ~ f-t

(

+

!'

1·

,

l,

'-I1taires (ou soll~Oris) sont des solutions. Patoine et W~n étudièrent alors

-comment la topographie pouvait affecter l'évolution du soliton qui est asso-cié ici à une perturbation atmosphérique.

Nous nous proposons dans ce mémoire d'étudier l'évolution des ondes solitaires lorsque le système est f~é par un échauffement local au lieu d'une topographie. Tout comme Warn et Brasnett

(1982),

une dissipation pax

,

pompage d'Ekman est ajoutée. L'équa-tion d'évolution de A(x,'C:') fait l'objet du deuxième chapître dans lequel on trouvera essentiellement une version dé-taillée de la dérivation de Patoine et Warn en incluant en plus les mécanis-mes d'échauffement et de dissipation. Il y est montré que A(x,~) obéit

à

l'équation

SAA + y A :::

x xxx - rA + f'(x) +.g(x), (1.2)

où

r provient de la dissipation, g(x) de ~'échauffement et f'(x) de la

topo-\

~

graphie. Une analyse d'échelle révèle que cette étude est particulière~ent appropriée pour des phénomènes se produisant à l'échelle synoptique •

Au troisième chapitre, nous supposons le problème faiblement non-li-néaire' et considérons ~

«1.

Le problème est alors résolu au premier ordre à l'aide de la transformée de Fourier. Après avoir exposé les techniques 'd'évaluation asymptotique d'intégrales reliées à ce problème, on obtient les

solutions du problème à l'ordre un (problème linéarisé) qui montrent que

l'ef-"'-

fet de l'échauffement se résume à une al tératlon du vent zonal en aval. Lors-_, que ~y

>

0, il y a en plus un train d'ondes stationnaires qui s'établit en amont du flot.

Lorsque le membre de droite de l'éq.(1.2) est nul, l'équation de KdV 1

possède des solutions exactes comme par exemple, les ondes solitaires. l Au

, ,

-~-(

•

•

4 .

quatrième chapitre, nous tirons parti de ceci en supposant que le lProblème

CI

faibfement forcé admet égalemfnt comme solution les ondes solitaires mais dont les paramètres (amplitude et phase) évoluent lentement dans le temps. Se référant à Karpman (1979), la méthode de" diffusion inversée appliquée à l'équation de KdV faiblement forcée permet d'obtenir des équations d'évolu-tion pour ces paramètres. Une dérivad'évolu-tion de l'équad'évolu-tion d'évolud'évolu-tion de l'am-plitude basée sur une technique de perturbation simple est donnée et est montr~e correspondre à celle obtenue par diffusio~ inversée. On termine ce chapitre en résolvant ces équations dans quelques cas particuliers pour lesquels on ne considère que des solitons se déplaçant rapidement, réduisant ainsi l'interaction de la perturbation atmosphérique avec la zone d'échauffe-ment.

_Au chapitre V, nous abordons l'étude des ondes stationnaires et de leur stabilité. Dans le cas des ondes de grande amplitude, l'évolution des solitons peut être décrite par une fonction "potentiel". On montre alors que les points critiques de cette fonctlon correspondent aux s~tions sta-tionnaires, celles qui sont stables étant

asso~+~es

à un minimJb de la fonc-tion potentiel.

Pour le cas plus général, les équations d'évolution formant un systè-me autonosystè-me de premier ordre, nous les linéarisons au voisinage des points d'équilibre (a ,ri ) correspondant à l'amplitude et la phase d'une onde

sta-s 'f'sta-s ,

tionnaire, ayant au préalable établit les critères d'existence de solutions stationnaires. Nous déterminons Ensuite les caractéristiques des ondes so-litaires susceptibles d'être capturées par la zone d'échauffement. Ceci nous amène à penser que le blocage atmosphérique régional pourrait être engendré'

par la capture d'une perturbation atmosphérique par une zone d'échauffement

ou par une topographie ( Warn et Brasnett

(1982».

i

; r i,

r-l

,

, '.

'\

(

(

,

,'-~ ~ t.'

.

,," ~ CHAPITRE II

• REDUCTION DU PROBLEME AL' EQUATION DE KORTEWEI;-DE VRIES FORCEE

Dans ce chapitre, il sera montré qu'en présence d'une topographie

1

et/ou d'un échauffement local, l'évolution des ondes atmosph?riques quasi-stationnaires de faible amplitude et de grande longueur d'onde peut être décrite par une équation de Korteweg-de Vries forcée. Le terme de forçage apparaissant dans cette équation comprend, en plus de l'échauffement, un terme dissipatif associé à un pompage d'Ekman.

La démonstration présentée ici est une version légèrement modifiée de celle de Patoine et Warn (1982) à laquelle ont été ajoutés t'effet dissi- 1

patif (Warn et Brasnett (1982)) et l'échauffement local. Comme-eux: nous considérons une atmosphère non-visqueuse continûment stratifiée et obéis-sant à l'é~~ation du tourbillon pqtenttel quasi-géostrophe sur un plan ~,

l'

2.1. Position du problème

Se référant à Pedloskyo(1979), l'équation du tourbillon potentiel quasi-géostrophe pour un fluide stratifié prend la furme

+

~<f! ~

-

~O/ ~

)

(

~

xx +

t

yy +

BY

+

l

(~s-Jkz-)z)

l 2.

(-/dj{) ,

(

_~

=

ot OX oy oy àx

_(s

_{S (SOZ}

(2.1)

r

est la

Il

le ,

fonction de courant, taux d'échauffement dû à l'advection ou

i

1

"'

J l j

.' ,

.

",

. 1

(

et aux sources internes de chaleur (e.g. condensatipn),

fs(z)

la densité 'de l'air pour une atmosphère standard, S(Z) un paramètre de stratification

'"

et ~ le facteur de tourbillon planétaire.

Pour une définition plus détaillée de ces paramètres, le lecteur se réfèrera à Pedlosky en notant que l'éq.(2.1) co~espond à l'éq.(6.5.lB)

6.

de cette référence. L'équation (2.1) est ici écrite dans sa forme non-dimen-sionnelle. D'ailleurs, il sera implicitement admis dans ce mé~oire que les équatio~s sont toujours dans leur forme non-dimensionnelle, _, à moins qu'il n'en soit spécifié autrümL~t.

Considérant la fonction de courant sous la forme

.

f

(x,y,z:t)::: - JYu(y',z) dy' + Ef'(x,y,z,t)

où u{y,zJ représente le vent zonal et ~. est l~ perturbation pax rapport

à cet état de base, l'éq.(2.l) devient

où

~(a

+ li 0 ) q + ê

r'

Q at ôx x y - u yy 2 + €. 'J(

t'

,q)

et J(f,g)

=

f g -f g est l'opérateur jacobien. x y y x

(2 •.

2)

Nous supposons maintenant que l'écoulement se produlttdans un canal étroit selon y. Ainsi si L et L sont les échelles spatiales en x et y

x y

respectivement, alors L/Lx :::

f

et

.!

~l,l. Donc, en considérant que

L rv

~l),

nous pouvons redimensionaliser l'échelle selon x en introduisant

y

Ir

.

"

;

r'

,

.

,

."

.

.

'.

le changement de variable x'~

xl; .

L'éq.(2.2)

devient alors

(.!~.+uo)q

l'

ct

ox

(2.)

où

2,J/

dl'

q =

f

fxx

-1:-

r

yy

et on a noté x' par x pour alléger la notation.

Pour résoudre cette équation, des conditions·aux frontières doivent être imposées. Ainsi, nous demandons que

Ylx := 0, en y:= 0 et y:= l,

(2.4)

ce qui signifie que l'écoulement est entièrement contenu à l'intérieur du

~

canal.

Ensuite, lorsque Z-7oo , nous avons

~

0 ->0,

~----?>O

et

"-'-~ lS , l i -)0, cette

convergence vers zéro s'effectuant suffisamment rapidement. Comme nous le verrons par la suite, cette convergence devra être suffisamment rapide , pour que les diverses intégrales apparaissant dans cette étude soient

con-\ vergentes.

Finalement, la condition en z

=

°

est obtenue en considérant une topographie z

=

êh(x,y), une fonction d'échauffement I!(x,y,z) et une dissipation due à un pompage d'Ekman. Se référant à la section

6.6

du livre de Pedlosky, la condition en z

=

0 se ramène à

en z := E h( x,

y) ,

~

;

~ i

.

-t;

(

'. r

(-8.

où Ra est le nombre de Rossby et Ev le nombre d 'Ekman ...

En défini ssant

f{(x,y,z) ::: 1I*(y,z)

+

I!'(x,y,z) ""

(2.5)

telle que "

/!*(y,z)

= 1

-

~JQJ.

§ill

u (y,a) 2R

-PnTz)

y o

,-8

le terme

fY*(y,z)

agit en source d'énergie permettant de

compense~

pour

celle dissipée par le vent zonal. La cond~tio~ frontière en

z

=

-f

h(x,y) se réduit alors à

( !

~

+ u

~

)

"tll'

+

ê

J ( f};' ,

dl'

+

t

~t

dX

r

z , '(

r

z +

SE~_

(/2,1"

+

ri,' )

=

~!

'(xx '( yy Sh) - u

d;,

zfx

+ Suh x

(2.6)

où ?V'a été noté par

~

dans cette

der~ière

équation. On peut également considérer que

ft{

correspond à

~'

dans l'éq.(2.3) puisque si l'éq.(2.5)

int~oduite'dans

l'éq.(2.J), seul le terme

n"(x,y,z)

demeuce car

~

( f}s(z)I/*(y,z)

1

S(z)

:::

Q.

àz \.:

Ainsi,

~ans

tout

ce

qui

sui~a.

nous supposerons que

~(xIY'z)

correspond

au

~'

de l'éq.(2.5), comme pour les

éq.(2.3)

et (2.6);

est

Les éq. (2.3), (2.4)' ,~t (2.6) constituent le :point de départ de cette

étude. ~

-.

, ' ..

1

1

,

~ >, 1

1

t

" ,

.

2.2. Réduction à l'équation dé Korteweg-de Vries

Pour être en mesure d'obtenir un problème intéressant, il nous

î

faudra choisir les échelles des différentes quantités apparaissant dans nos équations de base de telle sorte que la dissipation, l'échauffement

et la topographie agissent au même ordre. De plus, puisque nous désirons } considérer des processus quasi-stationnaires, une échelle de temp~

ralen-, ,

1

t.

~

.

i

_,

tie devra également être uLilisée. Sans

présum~r

quoi que ce soit de ces

,

échelles, posons simplement que

~ _N ,-

_,

re=

_{fl(E) t,}

1/=

f

2

(E)Jf.

, ,. , J~ ~ t ~ , " 'V

où

t

est une échelle de t€llpps ralentie et

Il.

S2(x,y) et À sont d'ordre

un

«(9(1».

Une analyse d'échelle déterminera

ultérie~ement

les fonctions

"

,

"

..

de

E

apparaissant plus haut.

1 .( .,l;, li ~ L'éq.(2.J) devient alors • , ~ 1), j,

.'

~ _,

...

, i~ t, ,~

t'

t

. (.4:_l

hl

2.

+ u

2. )

~,ô~

ôx 1 tandis que l'éq.(2.6) q +

r:

Qy + E J (

fi

,q) = se réécrit

i

t

_,:

t

f ,

f

_~

1

~ l ~

_(-'j

rV

f~

1,( ,

en z

~

E

f

_4(E)JL(x,y).

(2.8)

y

,: 1

,

Sup~sant què fl(E)~

<.<

l

et

fz(E)/r

t..<..

l, l'éq.(Z.7) se

réduit,

au

premier ordre,-à où = ,1,(0)

1

YY +

1:.

(j)

dJCO»'

fs

,Sfz-

z

~

Supposant en plus que

f5(E)/~

«

l, l'éq.(Z.8), au Premier ordre, se réduit à

-?

U

z Ê.

_ox

tl/CO)

_l

=

0, en z

=

0

Ecrivons

~(O)(X,Y,Z,~)

sou: la forme

~(O)(x,y,z,~) = A(x,~) )D(y,z).

L'éq.(2.9) se réécrit alors

~A Lg; :::: 0

èlx

où L est"un'opérateur linéaire défini par

+

1:.

~ (-es- ~ )

+

~

lu

fs ôz S ôz

0 , • .

(2.10)

",

Utilisant les éq.(z.4) et (2.19), les conditions aux frontières se tradui-sent par 1 l "

§=

0, en y :: _{0 €;lt Y}

=

_l,

( a)

)

uffz

~ ~

=

0, en

z

=

O.

(b)

(2.12) dt!" _Z

"'"

r-Le prOblème au premier ordre se résume donc à résoudre l'éq.(2.11)

1

en satisfaisant les conditions (2.12). La fonction A(x,~) sera obtenue à 10.

..

<.

à

l'aide d'une condition de solvabilité du problème à l'ordre suivant. , C'est, donc à ce stade-ci que les échelles fleE), ••• , f

5

(E) sont choisies

pour que la topographie, l'échauffement et la dissipation interviennent au même ordre. Le choix suivant s'impose pour que ces trois effets

apparais-lji(~.. l ' h(x,y) ::: Ei2(x,y),

L'éq.(2.7)

devient alors ( E Cl + u Cl ) q +

li,

~

Q + E

J(

'/1'

,q)

a'e

ox

r

-y

r

où

et

l'éq.(2.8)

se résumelà (E

~

+

u.9..

)1//

+ E

J{tl/,t!/'

+ E

sil)

e~

ex

T

z

'f

r

z . iJ, E ÀS ( E

JI'

_r

+

1/1'

)

xx '( yy 2 .

en z::: EU(x,y)." Le prOblème à l'ordre E est

donc-où

+

E

sun

x

(1)::: M

rI!.l)

+ d)(O)

/J

q,

T

T

xx / et +

Jo

.9.. CPs-.9.. ) :::

L - Q

lu .

es

dZ

's'

oz y

(2.1)

"

(2.14)

(2.15)

11.

-

_i ,

(

(

..

Les

conditions aux frontières sont, à cet ordre,

en z

=

0, et U

z

_0 dl(l)

J

=

-

' f

;r:

z

A

t' -

-

AA x. Y:! Y:! (z;r yz - ':I! ;r: Y ' f

;;r;)

z

ox

tlKl)

=

0 ,

'(x,

t'V - SuD. -

~

S

1i.

A +

fi

(x, y, 0) ,

x

yy

12.

(2.16)

en y

=

0 et y

=

1. Pour ~btenir l'éq.(2.16), nous avons utilisé le ré-sultat

J(

~

(0),

~~

0»

=

AAx

(If

!i

yZ

f}y~

).

~

L'obtention d'une condition de solvabilité à cet ordre est reliée au lemme

J'

suivant.

Lemme 'Z.I. (Soit l(x,y,z) at g(x,y,z) deux fonctions"ontlnûment dif-:férentlàbles. Alors

\

f

fs(

f Lg - g Lf) =

o(

fsC

f g

_{y - g:fy) )y}

+

(-fs-

_{(fgz - fzg) )z}

( Eg,. (Z.18)

où ~ et S ne dépendent que de z et L est l'opérateur défini à l'éq.(Z.ll).

Démonstration. Développant le membre de gauche de

l'éq.(z.18),

on obtient que

) ,

e, (

f Lg - g Lf)

En ajoutant et soustr&yant la quantité f (-eg ). on obtient le

résùl-, z

SS

z

/

tat désiré

à

l'aide des propriétés ul!melles de la dérivation de fonctions.

o

...

1

(

Pui.sque

on montre, à partir de l'éq.(2.15) que

• 0

omAr:. -

fi

A +

l {

tJ

il)

~

xxx U t ) .

-t-sS

z U r \s - AA (

mff)

0 x~ u

- L(#.\) .

u u (2.19)

En utilisant les éq.(2.11) et

2.19),

le lemme 2.1 pour f

~

ff

et g:: fxl)

conduit à

(-€~yl

At -

es

~2

AXXJ( u2 .\'. " +

_--c:-s--

/J

ffJ(

Q

lu)

AA y y x u :::

[é's\Pf~)

-

~~l)_~y

+

[_~(q;#;)

-

~~l)~.)

J-e

Eg • (

2.201)

L'étape finale consjste à éliminer la dépendance en y et z en inté-grant par rapport à ces deux varid.bles sur tout le domaine. En utilisant les conditiono aux frontières données par les éq.(2.12), (2.16) et (2.17),

,

on constate qUE' le problème à l ' o:rdJ:e E ne peut être résolu que si

AC

x

te)

satisfait l'équation

A-e +

S

AAx -+ Yf1Axxx ::: - rA + f'(x) -t g(x),

(2.21)

où

, -1 JI (pel n~2

. y

= -

Ô 0 dy Jo

esY-;

dz,

'. 14.

J

f(x) "::" ₆ -1

_{(;;(0) J;g)(y,O}O(x,y)}

dy, g(x) , - ·1

r1

j'''

}~,"

(

u

CP:.

u,ii> )

dz Ô '0' dy 0

6,;:;-

'"

f' c ùu

Nous y T"vi cndronG au char! t.re IV. I~

(

y

1

'2.J. Discussion des limites inhére~tes à cette approche

La démonstration de la section précédente a pour point de départ l'équation du tourbilïon potentiel quasi-géostrophe. Conséquemment, res résultats obtenus demeurent significatifs en autant que nous soyons dans les limites de cette approximation. Entre autres conditions, on demande que le nombre de Rossby soit petit. Autrement di t, nous nous si tuons dans la limite d' ondes longues puisque l' échelle spatiale correspond alors à

l ' échelle synoptique ( R ru 0.1) ou mieux à celle des olres de Rossby o

( :R NO. 01).

o

I l faut également signa1er quri1 a été supposé qu 1 en l' absence de

topographie, de dissipation et d' pChauffement, la solution au pr<?blème. ,_

~.

linéair.,SL étai t parfaitement stationnaire impliquant ainsi que la vi-tesse de phase linéaire c(k) est nulle lorsque k~O. Pour plus de génsrâlité, nous supposerons que c(k)->fa lorsque k---;>O c'est-à-dire que le problème linéaire est alors quasi-stationnaire.

Il est possible de ramener ce prOblème au précédent

à

l'aide du changement de coordonnées

- IV

X

=

X -

ae','

En effectuant 1 "anallse de la section précédente, on obtient

= rA + f'

(X'

+ a'!:') + g(5{ +

Ctt»,

ce qui devient, lorsqu'on l' exprime en terme de x,

At + aA + SAA + "lA ::: -rA + f' (x) +

g(

x),

x x xxx

(2.22)

Où

dorénavant, ~ sera plutôt noté par

t.

j

1 i

l

-

,..

/

~ t

16.

01

On notera qu'un forçage pourrait être associé _, aux interactions entre les ondes longues et courtes causées par les termes non-linéaires négligés

.

dans la dérivation de l'équation du tourbillon potentiel. Le rôle d'un tel processus serait assez semblable à celui joué par la fonction

d'échauf-fement.

\.

Nous terminons par une analyse d'échelle qui permet de donner un ordre de grandeur aux paramètres que nous venons de définir. Posant que

J

-1

L N 10 km, D rJ 10

!un,

u rv 10 ms et la topographie H rV l km, le

y

paramètre E est donc tel que

f ru

(g)

~

==

o.

J.

Conséquemment, le paramètre de dissipation est tel que

= 0.2

Or on sait également que E

~/2R

I\J 0-(1) pour l'échelle des ondes

planétai-v 0

res (R

o

~

0.01) et E "Î/2R rv Q(lO-l) ,pour l'échelle synoptique (R v 0 0

=:

0.1).

Ainsi pour que les ordres de grandeur concordent, il est préférable de se ~ situer sur l'éche11e synoptique. D'ailleurs, pour E

=

O.) ,

l'échelle de temps correspondante est alors de 2 à

6

jours ce qui convient bien aux phé-nomènes synoptiques.

(:\

_,

1

1

•

,

l

(

.

_'.

CHAPITRE III

Il

APPROCHE FAIBLEMENT NON-LINEAIRE

Pour résoudre l'éq.(2.22),nous supposons, en

p~mière

approxima-tion, que

13«1,

c'est-à-dire que le problème est alors faiblement non-linéaire. La théorie des perturbations est alors utilisée pour résoudre,

La méthode utE"i sRe "i ci est idenhque à celle empleyée par Patoi-ne et Warn (1982). Leur étude concerne un forçage relié à une topographie locale tandis qu'ici une fonction d'échauffement sera considérée. Ceci nous permettra de dégager certaines différences existant entre le

força-ge par topographie et celui par échauffement.

)

\

J.1.

Cas faiblement non-linéaire et sans dissipation

) Lorsque le processus ne comprend ni dissipation, ni topographie

(i.e.

r =

0

et f(x)

=

0),

l'éq.(2.22) se réduit à

At + uA + SAA + yA

=

g(x).

x x xxx

Pour linéariser cette équation, on considère ~« l et on développe A en une série asymptotique de la forme

Au premier ordre, le problème linéaire suivant doit être résolu:

+

aA(O)

+

x

\

g(x) .

(J.2)

(

( -, ~ 1 "

(:

Ceci peut être résolu par la méthode de. la transformée de Fourier. Posant ~ que

...

et g(x)

où

et introduisant ceci dans l'éq.(J.2), on obtient

\,

1\1

Ainsi, A doit satisfaire l'équation

'ar.

+

ik(a. - yk

2

)X

=

g(k).

at

"

Cette dernière est aisément résolue en supposant que A(x,O):=. 0,

c'est-à-

'-dire que la topographie n'est introduite qu'à t=O et 'qu'auparavant, nous

N

avions la solution triviale. Ceci implique que A(k,O)::: O. Cette hypo-thèse correspond à ce que l'on appelle un problème avec "switched-on topo-graphy". Introduisant la solution de ce problème dans l ' éq.

(3.3),

on ob-tient q

18.

=J+OO

-00 'S(k) ( l _ e

-ikta.- yk

2)t) eikxdk ik(a. - yk2)

().4)

Pour évaluer cette intégrale, nous supposerons k complexe. Le contour d'intégration correspond alors à ~a droite réelle dans ce plan complexe. Or, lorsque g(k) est holomorphe au voisinage de l'axe réel,

l'intégrand l'est également. Conséquemment, en vertu du théorème de Cauchy, ce cORtour pourra être déformé de façon à contourner les points k

=

°

et, lorsque

uy

>

0, les points k±

=

±

Vaiy

1. La technique d

'inté~ation

L

(

...

que nous utiliserons nécessite de telles déformations. Notant par C le

contour déformé, l'éq.(J.4) est alors réécrite sous la forme

2 où c(k) =.

a. -

yk • =

J

g(k)

eikx~k

C ik(a.- yk2) =. 1 1

J .

g(k)

e ikex- C(k)t)dk C 2 ik(a- yk ) Lorsque ay < 0, Il et 1

2 ne possèdent qu'un pôle en k = O. Le contour d'intégration est alors déformé tel qu'indiqué à la figure 3.1.

\.

fig. 3.1. Déformation du contour d'intégration P2ur les Inté-flEales de l'éq.(J.5).

t

\

Nous ne chercherons pas à. évaluer exactement ces deux intégrales

19 .

mais tenterons plutôt d' en donner des formes asymptotiques lorsque

[xl»

1

(3

et

lx -

atl»l.

Pour ce faire, le lemme de RiemaniJ.-Lebesgue permet de sim-plifier le :problème.

Lemme J.1 (Riemann-Lebesgue).

_{Soit F(k) une fonction}

"'"

intégrable c'est-à-dire que

J'~

/F(k)1. dk ' . existe. Alors

lim

{J~

F(k) eikx dk}

=

O.

x~oo

Une dém6nstration de ce lemme pourra être trouvée dans

le}ivre de

Royden (1968).

Se référant à Bender et Orszag

(1978)

pour les techniques de déve-loppement asy~ptotique d'intégrales, le lemme de Riemann-Lebesgue permet de montrer qu'en fait, lorsque

Ixl»

l et

\x-

a.~~~, les contributions des parties Cl et C

J

du contour d'intégration sont d' ordre

(9(1/

x)

pour Il et

d'ordre (Q(l/(X- at)) pour 1

2, Ces résultats sont obtenus en effectu~nt

une intégration par parties et en appliquant ensuite le lemme J.l.

Pour intégrer Il sur C

2 lorsque x

>

0, on complète le contour par un demi-cercle tel qu'indiqué à la figure J.2 pour obtenir une courbe fer-mée.

....fig.

3.2.

Contour d'intégration lOlsque x

>

0 et x - crot

>

O.

Appliquant le théorème des résidus, on a alors que

,

,

..

r

l

..

Je

~Ck)

eikxdk

=

2rri Rés[k=O]

.3

ik(a:- "ik2 )

. Or, on montre sans peine que, lorsque x

>

0 et x «l,

Je

g(k) eikxdk

«

1. 4 ik(a- yk2)

Ainsi, lorsque x > 0,

2rr ~(O)

a:

Quand x

<

0, on choisira plutôt le contour. de la figure

3 .

.3

pour montrer que dans ce cas, Il

=

O. Combinant ces deux résultats, on conclut que

Il

~.

2TI

'SC

0)

H(

x) ,

a:

où H(x) -est la fonction de Heaviside •

\.

fig.

3.3.

Contour d'inté&!ation lorsque x

<

0 et

x-

gt

<

O.

- Réé cri vant I 2sous la forme n~",,~ _ _ « _ _ ...,.,.... ... - -- - . 21.

i

\

1

_~I~_-i 1

,'1

(

r ~'

,

_& \ ~, _.,. " \

et utilisant la même technique que ceUe employée pour Il en choisissant le contour de la figure J.2 lorsque x-a:t

>

0 et celui de la figure J.J,

1 lorsque x- at

<

0, on obtient

1

2 :; 21r

g(

0) H( x- at). a:

La solution A(O)(x,t) se comporte alors comme

22.

2'lT

~(o)

(H(x) - H(x-

at) ) +

(Jl(l/x)

+

(Qcl/(x-a:t».

a:

.

En général, lorsque g(x) est localisée au voisinage de x s' écri t plutôt

A(O)(X,t) - 2TT }t(0) (H(x - xo) - H(x - Xo - at»

a

(Eg.

C3.6»

= x A(O)(x

t)

0' ,

~(l/(X-

x -

at». o

(J.?)

1

+ (9(l/(x- xo» +

Le graphe de A(O)(x,t) est illustré à la figure J.4. On constate ainsi que dans la limite où t-xn , l'effet de l'échauffement se résum@ à unt modifica-tian du vent zonal en aval de l'écoulement. Celui -ci prend alors III forme

~(y,z)

=

u(y,z) -ê 2'lT g(O)

~y(y,z)

a: dans la région où x

>

x •

a

""

fig.

).4.

Graphe de la solution A(O)(x,t) du problème faible-. ment'non-linéaire lorsque a

>

0, y < O.

(~!

----l

.

,

< ,.

(

•

•

2).

Remarque. Les termes d'ordre

G<l/(x~-

x _o

»

et (9{l/(x - x - <xt»

0

..

ont pour effet de lis~er les discontinuités de la fonction de Heaviside en x = x pour ,H{x - x ) et en x :::: X + at pour

H(x. -

x -

at).

Ainsi, i l sera

0 " 0 0 0

implicite qkns ce chapitre que les graphes

d~

A(O)(x,t) sont toujours tra-cés en incluant ce lissage aux points de discontinuités.

En

remarquant que

-too

:::: l

J _

00

g(

x) dx :::: E

êrr 2rr

g(

0) peut être compri s comme une mesure de l'apport net d'énergie au sys-tème par échauffement. Ainsi, en se référant à la fig.

).4,

on constate

~u'il y a augmentation de la fonction de courant de perturbation après le

passage du fluide au-dessus de la zone d'échauffement. Le gain est de

E/a.

ce qui rêflète le fait que, pour une vitesse d'écoulement petite, le fluide

,

a plus de temps pour interagir avec la zone d'échauffement dont l ' Intensi-té est donnée par E.

Finalement, on remarquera que si une topographie locale. aval tété

e

considérée,

{t(

0) aurait été remplacé

~

r, (

0) et dans ce cas, on a E ::::

o.

Il n' y a donc pas de gain net d' énergi e mai 5 seulement un processus de

transfert d'énergie cinétique en énergie potentielle et son inverse qui s'é-quili brent dam, le processu~s de montée-descente inhérent au passage ÇI. 'un écoulement au-dessus d'une montagne. _,

3.2.

C~éation d'ondes stationnaires dans le cas où

<1.y

>

0

"

Encore ici, nous supposons que

g(k)

est holomorphe partout sur la droi te réelle. 'Ce cas se distingue du précédent en ce que les intégrales

i-Il et 1

.

, '1

)

(

, 1

..

(

Leurs contribltions devront être rajoutées au résultat de l'éq.(J.7). Le contour d'intégration esltléformé tel qu' indiqué à la fig.

J. 5.

~~-+~~~~~~~~-r~~~~~---~

Rit

k

-c;1.

!

_,

C:.

c"-~

fig.

J.5.

Déformation de contour lorsque ay

>

O.

Pour évaluer les intégrales sur ~+ et C _, nous utilisons le lemme'-suivant.

,

Lemme 4.2. Soit f(k) une fonction holomorphe

_.

sur l'intervalle

.-( k - E, k

+

E) de même que la fonction

" 0 0

W(k)

== ~

~a

(k _ k

)n.

n == 0 n 0 (k - k ) o Alors De plus, si

rx -

a_o

tf

»

l, alors

où H(x) est la fonction de Heaviside.

...

24 •

,

25. ,

Démonstration. mn contournant 'le pôle d 'orore un situé 'en k tel o

qu'lndfqué à la fig.

).5

pour k+ et k_, ce lemme est démontré en effectuant un développement en série de Taylor autour de k et en se servant

ensui-o

te du lemme de Riemann-Lebesgue pour négliger certaines intégrales appa-ralssafrt dans le développement.

o

En appliquant ce lemme aux int~gra1es Il et 1

2 de l'éq.().5) au voisinage de k+ tout en iqentifiant f(k) et GO(k) à

f(k) :::

.L&..tl

-1c

(k - kJ

et W(k)

=.

0 pour Il et

W(k)

=

k

c(k) pour 1 2, on obtient que

J

k++ E

k - E

où

g(k) (l - e-ikc(k)t) eikxdk

= -

~~(k+)

eik+x(H(x) - H(x-

Cgt»,

ik(a- yk2) Cl

C :::

~W{k)

f

=

!!

kC(k)1

"" - 2a.

g dk k:::k dk k=k

+ +

é5t la vitesse de groupe évaluée en k

=

k+. La contribution du voisinage

..

de k_ est obtenue de la mêmG façon. On constate alors que celle-ci .corres- 1

pond au conjugué complexe (noté

c.e.)

du résultat que nous venons

d'obte-nir. Ainsi, en rassemblant tous nos résultats lorsque 0: 'Cf

>

0, A(O)(x,t) peut être approximé par

A(O)(;,t) 2: 21r g(O} (H(x - xo) - H(x - x

o-

a

t )

0:

- 1Tg(k ) eik+x(H(x 1- x ) - H(x - xO+ 2rat» + C.C.

1

cr

\

0

Le graphe de la solution est illustré/à. la figure

).6

~orsque

a <

0 et

x :::

O.

o

\

II<"

1

..

_'\

26.

fj,g.

).6.

Graphe de

A(O~(x,t)

lorsgue cr

<

0,

y

<

O.

j

~/

Comme la défini tion-de y d'après l' éq. (2.21) nous indique que celle-ci est toujours négative, on peut donc associer le cas ay

<

°

à

J'

la propagation d'ondes d'ouest en est et dans la direction opposée lorsq.e rty

>

O. Ainsi la figure

3.6

montre gue si une onde approche la zlDne d' é-chauffement par le côté est, il y' a apparition d'un train d'ondes station-naires en amont de l'écoulement alors qu'il n'en est rien lorsque lorsque l'approche se fait de l'ouest. Cette anisotropie n'est pas sans rappeler celle

ass~ciée

à un écoulement au-dessus d'une

mon~agne où

la

topogFap~ie

,

peut exercer une influence en amont, uniq,uement lorsque le flot,.provtent de l'est,

Le calcul de la correction non-linéaire n'apporte sensiblement rien

.

de neuf sinon que l'on constate" qu 1 il Y a, pour le cas cry

>

0, une onde

stationnaire en aval du courant. T9utefois, l'amplitude de cette onde est

1

l '

d'un ordre de grandeur inférieure à celle qui se propage en amont. Il n'ap-paraît pas utile J'd' explici ter ces calculs ici. Une discussion dans un cadre plus approprié des conséquences de la non-linéàrité sera donnée au chapîtr~

.'

-,

,1

" ,"

1

" ~ ~ , J

1

j

!

\

" , ,

" li

-f

s

J'

_:..

.r t;

•

1

_~. f' " l' " t~ ~ _il. ;1 f; ~

,

' \t

r

, ,

..

~I' '-t.

(

'"

, ,

suivant.

On

trouvera d'ailleurs dans l'article de Patoine et Warn

(1982)

les ré-sultats de cette correction non-linéaire pour le cas forcé par une tc;>pographie.

J.J.

Etude du passage d'un flot au-dessus d' une zone d'échauffement de longueur finie.

Pour illustrer ce qui a été dit aux deux sections précédentes, la fonction d'échauffement

Le

R(x) - H(x - L»

est co~sidérée. Au premier ordre, on doit alors résoudre l'équation

uA (0)

+ yA

(0) :::

X xxx ( H(x) - H(x -

L)).

Ce

problème est résolu en considérant indépendamment les problèmes

IA(O)

l ::: ~R(x),

tA~O)

Puisque, pour g(x) ::: .6R(X)\ on a l ' éq.

(J.4)

conduit à _ 1::,

ftoo

- -00 2rr (1 _ ~kC(k)t2eikxdk. k2(a.- yk2)

Puisque g(k) n'est pas analytique en k

=

0, le contour d'intégration ne

2:1.

"

peut être déformé de façon arbitraire. Nous choisissons alors de 'contourner l,e pôle d 'ordre 2 en k

Hex)

=

0 en passant sous l'axe réel pour nous assurer que

JI

2di

J

_c

ikx e k dk,

où C est le contour illustré, à la figure J.l •

.... ,

,

l l • 1

!

t

,

1·

'~ •

<1

"

('\

ù

/

28.

'Lorsque

a:y

< 0, on obtient

~

O)(x, t) '" {' [x(!!(x) - H(x - ut» +

~t

H(x -

"t~.

En effectuant le changement de coordonnées

X'

=

x - L, on résQud de la même,

façon pour

A~O)(x,t).

Le résultat final est que

A

( 0

lex,

t) '"

.6.

[x(

H(x) - H(x-L) )

+

L(H(x:L) - H(x-o:t»

•

cr

_

(t-L-<I

t)

(H( X-<It) -

H(

x-L-«.

t» ]

Le graphe de cette fonction est donné à. la figure

3.7

lorsque nt

>

L.

• ~ J,\ 1

... 1, .. 1

ù '

fig.

J.7.

Graphe de A (0) (x,

t)

lorsque

rio

<

D, ct

>,

0 et q,t

>

L pour

un échauffement constant sur l'intervalle [O,IJ.

'~l,.

Lorsque cr {f

>

0

(i.

e. cr

<...

0), on contourne les pôles en k

=

0, k-t et k tel qu'indiqué à ,la fig.

).5.

Pour la fonction d' échauffement

g(x) :::

6(

H(x + L) -:

H(x) ),

le ré sul tat obtenu est

•

"

..

'L'l / .<J i , b. ~ I:J~' ", ~ -"" ; .~ " l _,

1

\,~

.

" J.l " ~' 1

l

r

1

}, ~ ,

$

l

.' f " f 1 i'" l ï •

1

(

, a

+4

a

0

(

'\, ".

{X(H(X) - H(x+L)

t

t(H(x-at) - H(xtL»

,

+

(X+L~t)(H(X+1-at)

- H(X-at)]

dont le graphe est donné à la figure J.8.

, t

fig. J.8. Graphe de A(O)(x,t) lorsque

o.y>

0,

a

<

0 et jXt

>

L pour un échauffement constant sur l'intervalle

(-L,g.

Tout comme dans le cas où

g(k)

est une fonction régulière, on

29·

constate que lorsque cry > 0, la zone d'échauffement génère un train d' ondes stationnaires en amont de l'écoulement. De plus,on remarquera qu'ici

J+OO

g(x) dx :::

6L.

-00

On établit <Hors facilement la correspondance avec les résultats précédem-ment obtenus.

•

,

•

-l

CHAPITRE IV

EI'UDE DE 1'EVOLillION D'UNE ONDE SOLITAIRE

,

FORCEE PAR UN ECHAUFFEMENr LOCAL

Lorsque le membre de droite de l'éq,(2,22) est nul, nous sommes en présence de l'équation de

Korteweg-d~

Vries

(KdV)

dont on connart des solutions exactes, parmi lesquelles se trouvent les ondes solitaires, Se référant à Lamb

(1980)

et surtout à Karpman

(1979),

la méthode de dif-fusion inver;::,ée (traduction libre de "inverse-scattering method") combi-née à une technique de perturbation permet de déterminer comment un fal-ble terme de forçage affectera l'évolution d'un soli ton.

Réduisant l'éq,(2.22) à la forme canonique

où R(u,~,t) sera définie plus tard, on en considère des solutions de la forme

,

L'évolution de l'amplitude b(t) et de la phase ~(t) est décrite'à l'ordre

1

-Ci(E), par une paire d'équations drfférentiellés non-linéaires du premier ordre. Une dérivation simfle de l'équation d'évolution de l' ampU;tude se-ra donnée tandi s que l'on se réfèrese-ra à Karpman pour l' ~volu ti oh de la phase. Une discussion des limites d 'appU.cablli té de ces résultats suivra.

..

.:

•

•

(

r

Finalement, on terminera ce chapitre en examinant des solutions

à

ce problème pour quelques cas simples. Bien qu'un échauffement soit consl-déré ici, l'approche suivie ici est analogue à celle de Warn et Brasnett

(1982) pour une topographie.

4.1.

~-Equation de Korteweg-de Vries faiblement forcée

.! ,"

En considérant les changements de variables x - at

173

y u

::: -

_f-~

6Vl/3

:r

l'éq.(2.22) se réécrit sous la forme

où

u - 6uu +

t 'l

(4.1)

+

at)

L'éq.(4.1) est la forme canonique de l'équation d~ Korteweg-de Vries. Lorsque E

RC\J~l),

une solution à cette équation ne peut être obtenue actuellement que par une intégration numérique (cf. Patoine (1981)).

-Toutefois, lorsque l'on considère que R

rV(9(l)

et ( « l , une technique de perturbation peut être appliquée en linéarisant le problème à l

'o~

«J(El

autour des solutions exactes de l'équation homogène non-linéaire qui, elles, sont connues.

Le

problème étudié ici consistera à considérer 'une solution de la forme

uer,

t) ::: -

2b2(

t)

sech2b(

t)(

Y2 -

p,(

t»).

Lorsque R

-=-

0, on montre que b ::: cte et

~:::

4b2

t.

Les propriétés prlnclpa.-les du soliton sont que la vitesse de propagation est proportionnelle

à

l'ampli tude et qu

',p

n' y a pas de dispersion de l'onde, sa forme demeurant

• 1

• ',' < ,

r

~

•

32.

inchangée dans le temps. Cette dernière prtpriété s'expli~ue par un équili-bre existant dans cette équation entre la dispersion et la

non-linéari-..

t~. On trouvera dans Whitham (1974) une discussion assez large de l'équa-tion de KdV non-forcée. En particulier, on y discute de l'interaction en-tre deux solitons pour monen-trer qu'après interaction, les deux solitons ne sont modifiés que par un d~phasage dans leurs posi tions par rapport à celles où ils seraient situés s'il n'y avait pas eu d'interactlon, sans modifi-cation de leurs amplitudes ni de leurs vitessRs. POQT notre part, nous

nous restreignons à l'étude de l'évolution d'un seul soliton.

Pour résoudre le problème perturbé, deux approches peuvent être uti-lisées: la méthode de diffusion inversée et la méthode des échelles multi-pIes. Celles-cl font l'objet des deux prochaines sections.

4~2.

La

méthode de diffusion inversée

Cette méthode est basée sur le lien existant entre l'équation de

SchrBd.lnger et l'équation de.. KdV j + ( À - 6u(~,

t»

y Ut - 6uuVZ + uVZ~~

=

O.

=

0, _(4.2)

(4.))

Pour une valeur de t fixée, l'éq.(4.2) possède un spectre comprenant une partie continue en plus d'une partie discrète. Lorsque l'on laisse varier

t,

~il est normal de s'attendre

à

ce que ce spectre varie également.

Toute-foia,

si u(~,t) satisfait l'éq.(4.)), ce spectre demeure inv~iant.

,

33 .

•

Un problème de diffusion par la fonction de potentiel u(~,t) consiste à déterminer, connaissant u(~,t), le spectre de même que les coefficients de '1réflexion" et de "transmission". L' ensemble formé du spectre et de ces coeffic'ients, pour une valeur de t donnée, est appelé ensemble des données de diffusion (noté set)).

Un problème de diffusion inversée consistera à retrouver la fonc-tian de potentiel lor;;que les données de diffusion sont connues. Ainsi, pour résoudre l' ~q.(IL»), on procèder8 comme suit. Connaissant U(l(,O),on trouve

SeO).

Sachant que les valeurs propres fiont invariantes dans le temps, les données de diffw-lio" S( t) à un temps ultérieur peuvent être calculées. Finalement, à partir de ~;( t) et en utili sant les relations dites de Gelfand-Levi tan, on trouve la fonction u( 1(,

t)

au temps t.

Il est intéressant de noter qu'à tout élément du spectre discret correspond une onde solit₀ire tandis que le spectre continu engendre les solutions di tes "radiatives". Ainsi, si initialement on a un soli ton à

•

t

=

O,le spectre étant invariant, un seul soliton sera présent au temps

t.

Par contre," lorsque l'équation de KdV est forcée, cette invariance n'est plus respectée. Se référant à Karpman

(1979),

il est alors montré que si, initialement, on a un soliton, alors la solution au temps test

asymptoti-1

quement égale à

"*"

ou

OÙ lôul« l et b(t), ~(t) sont obtenus 'à partir des équations suiva.11tess

db

dt

-tao

2

=-E

J

R(us,'{,t) sech z dz ,

4b

-00

(4.4-a)

,

t

"

, [

(

" o

34.

-roc.

2 2

E

f

R(u ,~,t) (z sech z + tanh Z T tanh z)dz, (4.4-b)

-00 s (

4b

J

•

et z ~ b( ~ - ~). La partie OU de la solution provient de l'excitation du spectre continu. Dans le cas où B(u)

=

-"ru (cas purement dissipatif).

ÔU correspond à un plateau qui se crée derrière le soliton (cf. fig. 4.1). Ce cas particulier est traité dans Kodarna et Ablowitz (1981), Kaup et Newell

(1978)

ainsi que dans l'article de Karpman

(1979).

fig. 4..1. Graphe de la solution de l'équation de KdV faiblement forcée lorsque R(u)

=

-ru.

Nous n'irons pas plus avant sur ce sujet. La référence principale

..

.

utilisée ici fut Karprnan

(1979)

tandis que Lamb

(1980)

et Whitham

(1974)

ont fourni une introduction au sujet .

•

Po~ notre part, nous négligerons la partie ou de la solution pour

1 ..

...

nous attarder plutôt à l'évolution d'un soliton lorsque celui-ci interagit avec la zone d'échauffement. Les éq.(4.4) formeront la base de l'étude qui se~a présentée au ~rochain chapitre. Il convient donc de mentionner que ces résultats ne sont valides qu'en autant que l'amplitude du soliton

,

1 i

1

(

1

soit beaucoup plus grandé que la composante ôu. Donc, lorsque

4/b/«

1, les équations (4.4) sont invalidées, les termes d'ordre

E

devenant alors d!ordre un. Par exemple, pour le cas avec dissipation seulement

(R(u) ::: -ru), iJ est montré que jb(t)l---;.o. I l s'ensuit que la solution obtenue ne peut être uniformément valide dans le temps que si on introduit la composante 6u engendrée par exci taUon du spectre continu. Une telle

étude est donnée dans les articles cités plus haut.

4.3. Calcul de l'équation d'évolution de l'amplitude

par

la méthode des échelles multiples

~,

(--- On sait que l'équation de KdV (éq. (4.'1)) \ _{u(?,t ::: - 2b sech} ) 2 2 _{b( Y( -} 'l:) _~

non-forcée a pour solution

où

ç

=

_ _ 4b2t +

e

0' b et

e

_a étant d's constantes lorsque R(u)

=

O. En effectuant le changement de variable 9 :::

tz -

4b2t, l'éCluatipn de KeiV se

" _of

.

réécrit 4b

2

!u

- 6u au + a3u ::: ₀

(4.5)

~e

ae

_èle3 et U ::: - 2b2 sech2

b(e

~

e ).

6 0

Dans ce système de référence, u apparait comme étant stationnaire. KOdama et Ablowitz (1981) supposèrent alors que l'addttion d'un terme de forçage ER n'aurait comme effet que de rendre le processus quasi-stationnaire. Ainsi, en faisant évoluer b et

e

_a selon une échelle de temps ralentie

~ = Et. la solution est toujours représentée par une onde solitaire mais dont les paramètres évoluent lentement dans le temps. Le cas traité dans leur article ne concerne que la fonction R(u) =-ru. Nous fournissons ici

35.

,

,