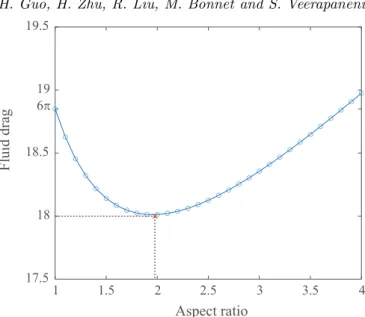
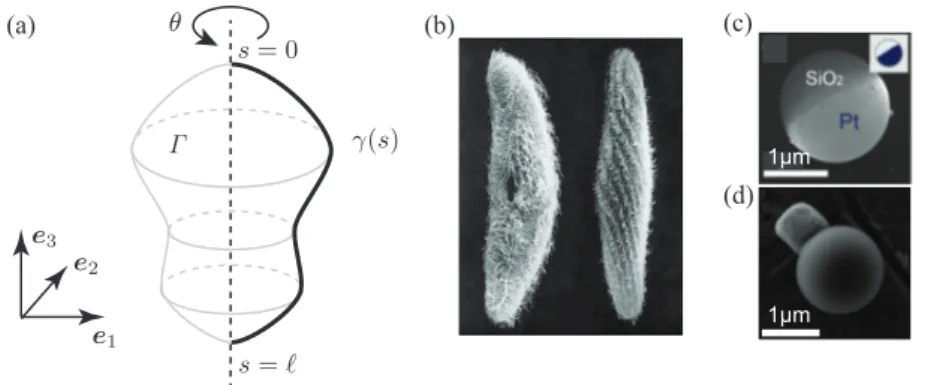
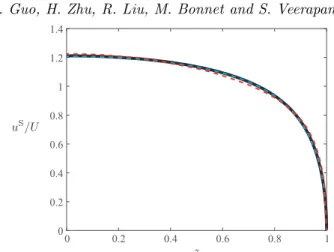
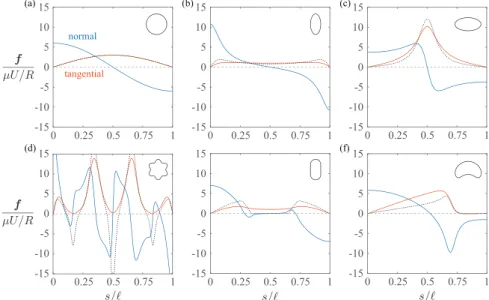
Optimal slip velocities of micro-swimmers with arbitrary axisymmetric shapes

Moreover, we show misdating patterns to correlate not only with the recency of the wage change, but also with respondents’ wage satisfaction, so that people who are more satisfied

If d = 2, in order to have the regularity of the whole boundary, we have to show that Theorem 6.6 and Corollary 6.7 in [1] (which are for solutions and not weak-solutions) are

However, for shape optimization of the type considered here, the situation is slightly better and, as proved in [5],[4], positivity does imply existence of a strict local minimum

Our goal is, on one hand, to write down explicit first and second order optimality conditions for general 2-dimensional shape optimization problems with convexity constraint and, on

Dual parametrization: Since our results are stated for the analytic functionals (4), we may apply them to the dual parametrization of convex sets instead of the parametrization with

Motivated by a long-standing conjecture of P´ olya and Szeg¨ o about the Newtonian capacity of convex bodies, we discuss the role of concavity inequalities in shape optimization, and

In this paper, we prove regularity properties of the boundary of the optimal shapes Ω ∗ in any case and in any dimension.. Full regularity is obtained in

The distinction between types (classes or universals) and instances (individuals or particulars) paralleled, to a certain degree, the distinction between geometric