Étude de la chaîne de spins frustrés par le groupe de renormalisation sur réseau

Etude de la chaîne de spins frustrés par le groupe

renormalisation sur réseau

par

Elmoez Goubaa

au département de physique

en vue de l'obtention du grade de. maître ès sciences (M.Se.)

FACULTÉ DES SCIENCES UNIVERSITÉ DE SHERBROOKE

Library and Archives Canada Published Héritage Branch Bibliothèque et Archives Canada Direction du Patrimoine de l'édition 395 Wellington Street Ottawa ON K1A 0N4 Canada 395, rue Wellington Ottawa ON K1A 0N4 Canada

Yourfile Votre référence ISBN: 978-0-494-83664-4 Ourfile Notre référence ISBN: 978-0-494-83664-4 NOTICE:

The author has granted a

non-exclusive license allowing Library and Archives Canada to reproduce, publish, archive, preserve, conserve, communicate to the public by

télécommunication or on the Internet, loan, distrbute and sell theses

worldwide, for commercial or non-commercial purposes, in microform, paper, electronic and/or any other formats.

AVIS:

L'auteur a accordé une licence non exclusive permettant à la Bibliothèque et Archives Canada de reproduire, publier, archiver, sauvegarder, conserver, transmettre au public par télécommunication ou par l'Internet, prêter, distribuer et vendre des thèses partout dans le monde, à des fins commerciales ou autres, sur support microforme, papier, électronique et/ou autres formats.

The author retains copyright ownership and moral rights in this thesis. Neither the thesis nor substantial extracts from it may be printed or otherwise reproduced without the author's permission.

L'auteur conserve la propriété du droit d'auteur et des droits moraux qui protégé cette thèse. Ni la thèse ni des extraits substantiels de celle-ci ne doivent être imprimés ou autrement

reproduits sans son autorisation.

In compliance with the Canadian Privacy Act some supporting forms may have been removed from this thesis.

While these forms may be included in the document page count, their removal does not represent any loss of content from the thesis.

Conformément à la loi canadienne sur la protection de la vie privée, quelques formulaires secondaires ont été enlevés de cette thèse.

Bien que ces formulaires aient inclus dans la pagination, il n'y aura aucun contenu manquant.

Le 27 mai 2011

le jury a accepté le mémoire de Monsieur Moez Goubaa dans sa version finale.

Membres du jury

Professeur Claude Bourbonnais Directeur de recherche Département de physique

Professeur Patrick Fournier Membre

Département de physique

Professeur David Sénéchal Président rapporteur Département de physique

Table des matières

Table des matières Table des figures Sommaire

Introduction

1 Hamiltonien de la chaîne de spins frustrés

1.1 Introduction

1.2 Représentation fermioniquç

1.3 Antisymétrisation et décomposition de g-olgie 1.3.1 Antisymétrisation :

1.3.2 L'interaction : approche de g-ologie

2 Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés

2.1 Fonction de partition

2.2 Transformation du groupe de renormalisation 2.3 Équation d'écoulement de la vitesse

2.4 Les équations d'écoulement des couplages

2.5 Résultats

2.5.1 Vitesse

2.5.2 Couplages : cas J' = 0

2.5.3 Couplages : cas J' ^ 0

3 Fonctions de réponse

3.1 Fonction de réponse au vecteur d'onde 2kp

3.1.1 Résultats et discussion 3.2 Susceptibilité magnétique uniforme

2 4 i 1 4 4 4 8 8 9 14 14 16 22 24 29 29 30 32 35 35 41 44 2

Table des matières 3

Conclusion 52

A 54

A.l Vitesse 54

A.2 Calculs des intensités des boucles des différents canaux 56

A.3 Calcul de la susceptibilité de Pauli 59

Table des figures

1 Susceptibilité magnétique mesurée par Hase et al. [7] pour le composé

CuGeOa et la comparaison avec la prédiction théorique de Bonner-Fisher[8]

pour une chaîne de spins (Heisenberg) avec J = 88K 2

1.1 Spectre liaison forte pour les quasi-fermions 7

1.2 Amplitude de la rétrodiffusion de g 1 : les flèches correspondent aux dé­ placements des fermions dans l'espace réciproque au voinage du niveau de

Fermi à ±kp 9

1.3 Amplitudes de diffusion vers l'avant de <?2 : les flèches correspondent aux déplacements des fermions dans l'espace réciproque au voinage du niveau

de Fermi à ±kp 10

1.4 Amplitude de diffusion de g$ : la courbe en pointillé correspond au vecteur

du réseau réciproque G impliqué dans le transfert de vecteur d'onde pour

93 10

1.5 Amplitude de diffusion de 10

2.1 Variation de la vitesse en fonction température pour = 0.532J fixée et

différentes amplitudes de frustration 29

2.2 Variation de la vitesse en fonction température pour J* = 0.532J fixée et

différentes amplitudes de frustration 31

2.3 Comportement de g2,i en fonction de l pour différentes températures à

et J' — 0 (sans frustration) ainsi que le comportement critique (T = 0) en

pointillé 31

2.4 Variation de <72,1 en fonction de 1 pour une température nulle et différentes valeurs du couplage de frustration J' à Jz critique fixé ( la courbe pointillé

est pour J'=0.175J et J£=0.532J) 33

2.5 Variation de <731 en fonction de 1 pour une température nulle différentes valeurs du couplage de frustration J' à Jz critique fixé ( la courbe pointillé

pour J' = 0.175J et Jcz = 0.532J) 33

2.6 Variation du gap en fonction de J' 34

3.1 Représentation de l'onde densité de site (ODS en trait continu) et onde

densité de Lien (ODL en trait pointillé) 36

Table des figures 5 3.2 Variation de susceptibilité de ODS ( en trait pointillé) et ODL (en trait

continue) (en échelle semi -logarithmique) en fonction de la température

pourJ' = 0 et Jz = 0.532 41

3.3 Variation de susceptibilité de ODS ( en trait pointillé) et ODL (en trait continue) (en échelle semi -logarithmique) en fonction de la température

pour J' = 0 et Jz = 0.52 42

3.4 Comportement de susceptibilité de ODS (en trait continu) et ODL (en trait pointillé) (en échelle semi -logarithmique) en fonction de la température

pour J' = 0 et Jz = 0.532 43

3.5 Variation LOg-Log de susceptibilité de ODL ( en trait pointillé) et ODS (en trait continue) en fonction de la température en dessous de la valeur

critique de frustration pour J' = 0.15 43

3.6 Variation de 33,2 en fonction de 1 pour une température nulle pour la valeur critique du couplage de frustration J' à Jz critique ( J' = 0.175J et

Jcz = 0.532J) 44

3.7 Diagramme de phase pour le modèle J — J' 45

3.8 Variation en température de la susceptibilité magnétique uniforme pour le

cas J' = 0 et à Jz 49

3.9 Variation en température de la susceptibilité magnétique uniforme pour le

cas J' — 0.18 et à Jz 50

3.10 Susceptibilité magnétique mesurée par Hase et al. [7] pour le composé CuGeOa et la comparaison avec la prédiction théorique de Bonner-Fisher[8]

Sommaire

Dans ce travail, nous examinerons les corrélations magnétiques à grande distance du modèle de la chaîne de spins frustrés avec interactions antiferromagnétiques aux premiers (J) et seconds («/') voisins, soit le modèle J — J'. Pour ce faire, nous appliquerons la méthode du groupe de renormalisation à la représentation fermionique Wigner-Jordan de l'hamiltonien. Les effets du réseau discret sont tenus en compte exactement à l'ordre d'une boucle et leur impact sur les fonctions de réponse comme la susceptibilité magnétique uniforme est discuté et comparé à l'expérience.

Remerciement s

Je tiens à remercier chaleureusement mon directeur de recherche, Claude bourbonnais pour son enthousiasme, sa disponibilité quotidienne et sa patience. J'adresse en même temps mes remerciements aux autres membres de jury Patrick Fournier et David Sénéchal. Je dédie ce mémoire aux martyrs tunisiens qui ont participé à la révolution de la dignité, toute ma famille et mes amis, Hanène pour sa bonne entente ainsi que Saber pour son soutien moral.

Introduction

L'intérêt porté aux systèmes de basse dimensionnalité vient du fait que les fluctuations classiques et même quantiques sont très importantes dans de telles situations. En effet, on sait grâce au théorème de Mermin-Wagner [1] que les fluctuations empêchent la formai tion d'un ordre à longue distance en une dimension à température finie. Il en résulte des compétitions entre divers ordres et des diagrammes de phase variés qui rendent la phy­ sique de ces systèmes très intéressante et donnent lieu à une grande diversité de phases : la supraconductivité, les ondes de densité de spin ou de charge, l'état spin-Peierls. Un cas fréquemment étudié est aussi celui de la transition de Peierls, où la première étude théo­ rique a été faite par Rudholf Peierls [2]. Elle fait intervenir le couplage entre les électrons et les vibrations élastiques du réseau, lesquelles en dessous d'une certaine température amènent le système vers un état dimérisé. Ce phénomène a été observé pour la première fois dans les années 70, se retrouvant dans des composés quasi-unidimensionels, comme le KCP et le TTF-TCNQ [3] [4]. Par la suite, l'étude des composés (TTF)MBDT [5], où M désigne un atome tel que Cu, Au ou Pt, a montré un autre type d'instabilité struc­ turale ayant pour origine l'interaction entre les spins, c'est la transition spin-Peierls. On rencontre cette transition dans les matériaux magnétiques surtout organiques.

La découverte en 1993 par Hase et al [7], du composé CuGe03, constitue le premier

matériau inorganique présentant une transition de spin-Peierls. Il présente des différences notables avec les matériaux spin-Peierls organiques. En effet, dans le CuGeOa, ce sont les électrons localisés de la couche d de Cu2+, porteurs du spin-|, qui sont responsables

du magnétisme, alors que dans les composés organiques, le spin est porté par les élec­ trons non appariés des orbitales 7r d'ions complexes planaires comme la molécule de TTF. Ce matériau inorganique cristallise dans la structure orthorhombique. Parmi les carac­ téristiques intéressantes de ce matériau, mentionnons la présence d'une chaîne de spins unidimensionnelle où le couplage antiferromagnétique Jc selon la direction Jc = 135K

est très important par rapport aux couplages Jb et Ja selon les directions a et b. Grâce

Introduction 2 single-crystal CuGe03 Bonner and Fisher J = 88 K H = 1 T 100 200 300 Temperature (K)

FIGURE 1 - Susceptibilité magnétique mesurée par Hase et al. [7] pour le composé CuGe03 et la comparaison avec la prédiction théorique de Bonner-Fisher[8] pour une

chaîne de spins (Heisenberg) avec J = 88K.

aux mesures de susceptibilité magnétique, une transition vers un état non magnétique de spin-Peierls est observée à Ts p = 14.2K. Dans la phase paramagnétique au-dessus de Ts p,

à savoir là où le système est dominé par ses propriétés essentiellement magnétiques, il y a un désaccord avec la courbe théorique obtenue par Bonner-Fisher pour la susceptibilité magnétique uniforme ( figure 1). Cela indique qu'un modèle purement unidimensionnel de type Heisenberg avec interaction J spin-spin aux premiers voisins n'est pas suffisant. Ainsi, pour mieux expliquer la dépendance en température de la susceptibilité, Castilla

et al. ont suggéré la présense d'un couplage antiferromagnétique aux seconds voisins J'

frustrant l'ordre antiferromagnétique venant de J entre spins

Des calculs numériques de diagonalisation exacte sur une chaîne de spins frustrés, décrite par un modèle de spins d'interaction J — J' ont montré que le comportement en température de la susceptibilité pouvait être expliqué par l'influence du terme de frustration J'.

Les objectifs de ce mémoire sont d'étudier les corrélations magnétiques à grande distance des chaînes de spins frustrés avec interactions antiferromagnétiques aux premiers (J) et seconds (J') voisins, soit le modèle J J'. Pour ce faire, nous appliquerons la méthode du groupe de renormalisation à la représentation fermionique de l'hamiltonien. Les effets du réseau discret sont tenus en compte exactement à l'ordre d'une boucle et leur impact sur les fonctions de réponse comme la susceptibilité magnétique uniforme est

Introduction 3

discuté et comparé à l'expérience.

La reformulation Wigner-Jordan des spins en termes de pseudofermions a l'avantage de nous faire travailler avec des particules ayant la statistique de Fermi et de mettre en évidence le spectre de type liaison forte, ainsi que des interactions dépendantes de la quantité de mouvement dans l'espace réciproque. Grâce à l'antisymétrisation des cou­ plages, nous pourrons expliciter la structure de l'interaction en mettant en évidence une décomposition de type g-ologie pour les amplitudes de diffusion normale et anormale (Umklapp) en fonction de J et J'. Alors, nous traiterons la chaîne de spin sur réseau avec l'influence complète du réseau discret et leur impact sur les fonctions de réponse à énergie finie comme la susceptibilité magnétique uniforme en fonction de la tempérar ture [9] [10] [11].

La technique du groupe de renormalisation Kadanoff-Wilson peut être adaptée à ce type de problème en incluant les effets discrets du réseau pour surpasser les limitations l'approche du continuum habituelle où les effets du réseau sont négligés à la fois dans le spectre et les interactions.

Chapitre 1

Hamiltonien de la chaîne de spins

frustrés

1.1 Introduction

Dans cette section, nous traiterons de la transformation de l'hamiltonien de la chaîne de spins frustrés en hamiltonien de fermions sans spin tel qu'obtenu par la méthode de Jordan-Wigner. Cette représentation est le préalable de l'approche du groupe de renor­ malisation Kadanoff-Wilson (K-W) présentée au chapitre deux. Cette théorie permettra d'établir les propriétés des fonctions de corrélation de la chaîne de spins.

1.2 Représentation fermionique

L'hamiltonien de la chaîne de spins frustrés est donné par :

HJ J, = Hx x z + H' (1.1)

N

= £ A S f S f ^ + S>S?+ l + A S - S f+ 1) + J'Si.Sl+2 (1.2)

i = l

où J et J' sont respectivement les intégrales d'échange entre sites plus proches voisins et deuxièmes plus proches voisins. La première partie Hxxz de l'hamiltonien contient le terme d'échange J selon x et y et le terme Jz — J A selon z. On remarque que si

Chapitre 1. Hamiltonien de la chaîne de spins frustrés 5

le paramètre d'anisotropie d'échange selon z, A = 1, alors Jx = Jy = Jz = J, et dans

ce cas, nous parlons de l'hamiltonien isotrope de Heiseinberg. Si A = 0, Jz — 0 et

Hxxz HXY devient l'hamiltonien XY. La deuxième partie H' de l'hamiltonien est

une terme de frustration d'amplitude J' > 0. On supposera donc que J et J'sont positifs et donc antiferromagnétiques. On peut réécrire HJJ> sous la forme :

N 1 H J J , = ^ J W S ^ + S F S & L J + A S Î S F , . , ) ,.1 2 N + £j'(5(^Sf+2 + SrS+2) + SfS^ (1.3) i = l k2

où Sf = Sf ± iSf. Pour une chaîne de spins frustrés, nous allons exprimer HJ J > à l'aide

des opérateurs de fermions de la seconde quantification issus de la transformation Jordan-Wigner [12]. Celle-ci consiste à remplacer les opérateurs de spin par des opérateurs de pseudo-fermion grâce aux relations suivantes :

s ; = c,+ C i-i (1.4)

s< = (1 5)

j<i

Ici (^représente l'opérateur de création (annihilation) de fermion sans spin sur le site i.

Grâce aux relations d'anticommutation pour les fermions :

{cj>ci}=kj . {ci,ci} = 0 (1.6)

ces pseudo-fermions préservent les relations de commutation des opérateurs de spin :

[sr, Sf] = , [s?, Sf] = 0 (1.7)

où £apy est le tenseur de Levi-Civita. Les fermions sans spin commutent entre différents

sites et les relations de commutation de spin sur chaque site sont vérifiées. La présence d'un fermion correspond à un état de spin Sz = | et l'absencé de fermion à un état de

Chapitre 1. Hamiltonien de la chaîne de spins frustrés 6

(1.3), on obtient :

* 1 11

HJ,J, = ^E-î(c+ci+1+c+1c() + A(c+ci--)(c+lci+1--) (1.8)

i = 1

N

i-1

c,+ (! - 2cî+ici+i)ci+2 + h.c + (etCi - -)«2ci+2 - -)

Dans cette représentation, la partie XY de Hxxz donne un terme de saut d'amplitude

— La partie Jz donne une interaction fermion fermion d'amplitude J A. Il est commode

d'utiliser une forme plus compacte de l'hamiltonien où tous les termes quadratiques en opérateurs de fermions pour Jz et J' sont omis. On peut vérifier que ces derniers

sont exactement compensés par les corrections de type Hartree au potentiel chimique en théorie de perturbation. Ainsi, il sera utile de prendre la forme suivante de HJJI :

N J

HJ,J> = J2-~(cfci + l +ct¥ 1ci) (1.9)

i=1

N N

+ S

JAC

'

t

+ 5Z

1 = 1 i = l

N

+ J' Ctcî+lci+lci+2 + h-c) i=1

Dans l'approche perturbative du groupe de renormalisation appliqué à cet hamiltonien (chapitre 2), il s'agira d'omettre toutes les corrections de type Hartree du groupe de renormalisation.

Afin d'exprimer H dans l'espace des quantités de mouvement, nous appliquons la

transformation de Fourier à l'hamiltonien. Nous considérons ainsi les transformations suivantes :

c4 —> c(x)y/â (110)

E

/f

(»•»)

Chapitre 1. Hamiltonien de la chaîne de spins frustrés

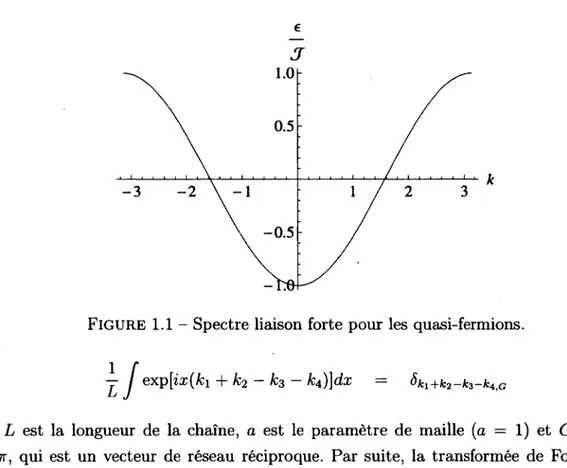
FIGURE 1.1 - Spectre liaison forte pour les quasi-fermions.

-j- J exp[ix(A:1 + k2 - k3 - k4)]dx = ôkl+k2-k3-k4,G (113)

où L est la longueur de la chaîne, a est le paramètre de maille (a = 1) et G = 0 ou +27T, qui est un vecteur de réseau réciproque. Par suite, la transformée de Fourier des opérateurs de création (annihilation) devient :

c<+>(x) = -^=Çc<+,e<->ifa (1.14)

où L est la longueur de la chaîne et k est un vecteur d'onde appartenant à la première zone de Brillouin. Ainsi, le terme cinétique devient dans l'espace de Fourier :

ffo = X>(*)c£cfc (1.15)

k OÙ

e(k) = —Jcosk (1-16)

est le spectre de type liaison forte (voir figure 1.1). Nous remarquons que même en présence du terme d'échange J', nous avons préservé le fait que la bande soit demi-remplie avec un niveau de Fermi maintenu à kp = ±|,ce qui assure que (S.f) = 0. La vitesse de Fermi est égale à v = J. Pour le terme d'interaction Hj, nous avons la forme suivante dans l'espace de Fourier :

Chapitre 1. Hamiltonien de la chaîne de spins frustrés 8

Les sommations sur k portent sur tous les vecteurs d'onde de la première zone de Brillouin

dans l'intervalle [—7r, ir\.

1.3 Antisymétrisation et décomposition de g-olgie

1.3.1 Antisymétrisation :

Il est utile de considérer chaque terme d'interaction sous leur forme antisymétrisée. Ainsi, on s'assure que pour chacun d'eux, la création (anihilation) de deux particules avec la même quantité de mouvement est strictement nulle (principe de Pauli) [15]. L'antisymétrisation d'un facteur de la forme e,a(fcl±fc3) avec a = ±1 et ±2, appartenant

aux fonctions trigonométriques de (1.17-1.19) peut s'écrire :

Alors nous obtenons une forme antisymetrisée pour Hj :

* Cf e 3 Ck < L Ck ï Ck \ à k l + k 2 ~ k 3 - k i x ;

+ y J' sin(&i — fa) sin(fc3 — fc4)

Lj r ^

Chapitre 1. Hamiltonien de la chaîne de spins frustrés 9

FIGURE 1.2 - Amplitude de la rétrodiffusion de gl : les flèches correspondent aux dépla­

cements des fermions dans l'espace réciproque au voinage du niveau de Fermi à ±fcj?.

* c* 3Ck \Ck 2Ck \ ^ k l I k ' 2 — k 3 — ki tG

l r * , w /k\ + k2 — k3 — £4. . fk\ — k2^ . ,£3 —fc4. h

-~2^4J cos( - )sm(—-—)sm(—-—) (1.21)

X COs(fcx ~f~ k2)Cji3Cje^CiC2CiCl^ki+k2—k3—k^G

où nous avons cos(fc'ffc2~fc3~/c4) = ±1, car ki + k2 — k3 — fc4 = G. Grâce à cette anti­

symétrisation, nous vérifions que le principe de Pauli est satisfait pour les interactions. En effet, deux fermions créés (ou annihilés) avec le même vecteur d'onde produiront un terme nul.

1.3.2 L'interaction : approche de g-ologie

Suite à la transformation de Fourier et l'antisymétrisation, nous décomposons le spectre en deux branches d'indice p = ±1, selon que k > 0 ou k < 0, respectivement. Ainsi, chaque sommation sur les opérateurs de destruction (création ) d'un fermion de Wigner-Jordan deviendra :

(

)

k p,k

Cette décomposition permet de réécrire le terme d'interaction par l'approche dite de g-olgie [13]. Cette séparation par branche permet de considérer quatre processus de diffusion notés <ft=i,...4(voir figures 1.2-1.4) :

gi : représente la rétrodiffusion de deux fermions de branches opposées qui vont s'échanger une quantité de mouvement près de 2kp.

<72 : décrit une diffusion vers l'avant. Au cours de celle-ci, chaque fermion reste sur la même branche. Le transfert d'impulsion individuel est dans ce cas faible.

<73 : c'est un processus umklapp pour lequel deux fermions d'un même côté du niveau de Fermi sont retrodiffusés. Ce processus ne conserve pas la quantité de mouvement et

Chapitre 1. Hamiltonien de la chaîne de spins frustrés 10

, - 0

,

kp o kp

FIGURE 1.3 - Amplitudes de diffusion vers l'avant de g2 : les flèches correspondent aux

déplacements des fermions dans l'espace réciproque au voinage du niveau de Fermi à

àzkp.

G

-<

FIGURE 1.4 - Amplitude de diffusion de <73 : la courbe en pointillé correspond au vecteur

du réseau réciproque G impliqué dans le transfert de vecteur d'onde pour g3.

<74 : il s'agit de la diffusion de deux particules sur une même branche qui échangent une petite quantité de mouvement.

On note cependant que pour les fermions sans spin, le couplage gi est par échange indiscernable du couplage g2. Il peut être replié par échange sur un couplage de type g2 qui

rassemblera les deux contributions. Les parties HQ (1.15) et Hi (1.22) sont transformées

et écrites sous la forme :

H = + (1.23)

p,fc { k i }

v— , , —

- k p o k p

Chapitre 1. Hamiltonien de la chaîne de spins frustrés 11

4E^(W)c+(Mcî(fc»)c-(fe)c+(fci) (1-24)

{M +j^M{k})cX(kz)cl(kA)C_(k2)C+(k1) (1.25) { k i } + i2>3,.(«)<£(*3)<(*4)C-1,(fclK,,(fc2) (1-26) {**} +^5l;j93.2{{fc»c+(fc3)c+(A:4)c_„(fcl)c_I,(fc2) (1.27) { k i } +j52023mK(h)c;(kt)c_p(h)c_r(k2) (i.28) { k i } + T^p4A{k})4(k3)cî(k4)cp(k2)cp(kl)

(

)

À l'aide de changement de variable k —> k + pkp, le spectre liaison forte s'écrit :

ep(k) = vpsink (1-32)

où k est maintenant la déviation de vecteur d'onde par rapport à kp- Les interactions peuvent être rassembleés en deux groupes, le premier groupe consiste en quatres termes :

#2,l(W) = 52,l^fcl+fc2-fc3-fc4,0 (1.33)

02,2({&}) = 92,2 cos(fcl 2 fc2)cos(fc3 2 k4)Skl+k^k3-k4,o

(1 - 6kl,-fc2)(l - Ska _fc4) (1.34)

M { k } ) = g3,isin(fcl 2 fc2)sin(fc3 g k 4)Sk l + k 2.k 3-k i G (1-35)

AuCM) = g4,i sin(^1 2 fc2)sin(fc3 g k4)Skl+k^k3-ki0 (1-36)

Pour lequel la diffusion vers l'avant est séparée en deux termes 02,i et @2,2, soit une partie locale @2,i,u n e partie dépendante de k, 02,2• Les amplitudes initiales dépendantes de J

Chapitre 1. Hamiltonien de la chaîne de spins frustrés 12

et J' sont données par :

32.1 = 4JA-8J' (1.37)

52.2 = 4JA-8J' (1.38)

33,I = JA-2J' (1.39)

<74,1 = JA-2J' (1.40)

Le deuxième groupe d'interaction est donné par :

o / f i n • 2 rki + (k i ~ k2. , k z — k4.

M { k } ) = 32,3 sin^—-—)cos(—-—)cos(—-—)

^fci+fca-fca-fc^oC1 _ ~ ^k3,-k4) (1-41)

^3,2({fc}) = g3,2sin(A:i - A:2)sin(A:3 -/c4)41+fc2_fc3_jfc4 G (1.42)

Q / f ; 1 \ *2 / k2 \ • / k\ k2 v . / k3 k4. _ /1 >i o\

M{k}) = 93,3 sin(—-—) sin(—-—)sm(—-—)41+fc2_fc3_fe40 (1.43)

R> / ri i \ - 2 / k2 \ . / k\ k2 v . / k3 k4. _ /-T A A\

Mik}) = 94,2Sin2(—-—) sin(—-—)sm(—-—)6kl+k^k3-kt,0 (1-44)

/ ^ ( { f c } ) = 94, 3 s m ( k i - k2) s i n ( k3- k4) Sk,+ k 2_k 3_ k4, o (1.45)

qui sont toutes dépendantes de k avec des amplitudes en fonction uniquement de J' :

92,3 = 16J' (1.46)

93,2 = -J' (1-47)

<fe,3 = -4/ (1.48)

94,2 = J' (1-49)

Dans ce premier chapitre, nous avons donc transformé l'hamiltonien de la chaîne de spins frustrés en celui composé de pseudo-fermions à l'aide de la transformation Jordan-Wigner.Cette reformulation a l'avantage de nous faire travailler avec des particules ayant la statistique de Fermi et de mettre en évidence le spectre de liason forte, ainsi qu'une partie d'interaction dépendante de la quantité de mouvement dans l'espace réciproque. Grâce à l'antisymétrisation du couplage, nous avons explicité la structure de l'interaction en mettant en évidence une décomposition de type g-ologie pour les amplitudes de diffu­

Chapitre 1. Hamiltonien de la chaîne de spins frustrés 13

nous présenterons le calcul par groupe de renormalisation des propriétés de la chaîne de spins frustrés en tenant compte des effets du réseau ici considéré comme, c'est-à-dire sans vibrations.

Chapitre 2

Groupe de renormalisation sur réseau

appliqué à la chaîne de spins frustrés

Nous présenterons dans ce chapitre une approche théorique qui nous permettra de comprendre les propriétés physiques des corrélations de la chaîne de spins frustrés. Une étude théorique utilisant une formulation intégrale fonctionnelle combinée à la technique du groupe de renormalisation de type Kadanoff-Wilson permettra de comprendre l'in­ fluence du terme de frustration J' sur les corrélations de spin sans négliger l'existence du réseau discret.

2.1 Fonction de partition

On utilise la fonction de partition Z pour l'étude des propriétés à l'équilibre de notre

modèle. Dans l'ensemble grand canonique, Z s'exprime sous la forme suivante :

Z = Tr exp —0H (2.1)

comme une trace sur les états de nombre d'occupation de l'espace de Fock. Dans le

but d'appliquer le groupe de renormalisation, il est cependant commode d'exprimer Z

sous la forme d'une intégrale fonctionnelle par l'introduction de variables de Grassman anti-commutantes ^'décrivant les degrés de liberté fermioniques. Cette réécriture est

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés\5

standard [16] et permet alors d'exprimer la trace sous la forme :

Z = J F D T I W S W R T (2.2)

où la mesure d'intégration est donnée par :

DrDi>= drp(k,un)dMk,0Jn) (2.3)

p, k.UJn

où sont les variables de fermions appelées variables de Grassman, satisfisant les

relations d'anticommutation { ^p* \ k , u )n) , i p ^ \ k ' , c u 'n) } = 0 pour tout p , p ' , k , k', et u jn, u j 'n.

Ici ujn est la fréquence fermionique de Matsubara, uin = irT(2n 4-1), où n 6 Z. L'action S [ip*,ip] s'exprime sous la forme suivante :

s [ r m = sq{ r m + si\ r m • (2.4)

qui consiste en une partie libre Sq :

So w m = £ [^(fc)]"1 ppwp& ) (2-5)

p, k

où l'on a introduit le propagateur de fermion libre :

G°p(k) = —7TT (2.6)

F U Vn - £ p( k )

avec ep( k) qui est donné par (1.32), et un terme d'interaction S i [ t p * , t p ] qui possède une

structure semblable à Hj donnée en (1.25-1.35) :

s, [</>*, v] = -IÇÂ,i({fc})v;(w_(fc4)V'-(Â2^+(fc1) (2.7) w (2-8) M{k})^p(h)^p(k)^-p(ki)^-p(k2) (2.9) M*} ~ ^2 h,i[\k^)i>l{h)^p{h)%{k2)i>p{ki) (2.10)

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés 16 { k } ~z ^2 03d{k}wp(h)^p(k)^-p(k)rp-p(k2) -j ^2 ^3,3({^})V'p(^3)V'p(fc4)^-p(fcx)V'-p(fc2) p>w - j ^ 2 ^ a { k } ) ^p( h ) ^p( h ) ^p( k 2 ) % ( h ) p>W (2.11) (2.12) (2.13) (2.14) (2.15) p>W -Wn,4 * où on note k i = ( ki yu jn >i ) et = / 3i, j( { k } ) ôU J n l + u l n 2^u l n 3.l À

2.2 Transformation du groupe de renormalisation

L'approche du groupe de renormalisation (GR) est une méthode qui permet d'obtenir une théorie de l'action S effective pour les degrés de liberté de basse énergie situés

près du niveau de Fermi, suite à l'intégration successive des degrés de liberté de haute énergie. Pour y parvenir, nous utiliserons dans ce qui suit la formulation Kadanoff-Wilson

du GR [14] dans l'espace des quantités de mouvement pour la fonction de partition Z

donnée en (2.2). Il y a deux étapes à cette formulation. La première est la transformation

de Kadanoff qui consiste en l'intégration partielle pour Z des degrés de liberté notés

lesquels sont situés pour tout un dans la coque externe (c.e) de l'espace k, définie par :

k G k € ko ? -k0 s U ko » ? ko m s P = + (2.16) i i o -s ll 1, 3 i 1 U -k —k0 O) S P = ~ (2.17)

où k0 = | est la coupure naturelle du réseau pour le spectre liaison forte. Ici s = eM est le facteur d'échelle avec dl « 1. Suite à cette intégration partielle, la zone

de Brillouin se trouve rétrécie et aussi la maille élémentaire augmentée d'autant (a —>

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrésH

k ' = s k , ce qui restaure la coupure à sa valeur initiale, k0 = |, et donc la maille de

réseau initiale précédant l'intégration partielle. La remise à l'échelle des quantités de mouvement induira à son tour une remise à l'échelle de toutes les quantités : énergie,

fréquences, champs,...etc., entrant dans l'action S, qui est elle sans dimension. Ces deux

étapes peuvent être représentées sous la forme :

oc

UL

I L

[ / / . D l j } * D l f > eS^ * + (5 /'2) c . e+ 3 ( (S /-2>2) c . e (2.18)

où Si i est la partie interaction de l'action avec un nombre i = 1...4 de champs ap­ partenant à la coque externe qui est à intégrer. Le passage de la première ligne à la seconde est effectué grâce aux théorèmes des graphes connexes et de Wick sur les valeurs moyennes. Ainsi, les moyennes statistiques sur les notées (•••)ce, sont faites par

rapport à l'action libre de la coque S o [ 4 > * , $ :

Lorsqu'on se limite à l'ordre d'une boucle pour les diagrammes (graphes), on se limite à l'évaluation des deux moyennes statistiques (Sj^)ce et {(S'/,2)2)c e • Ainsi, on arrive après

intégration partielle à une action similaire à l'originale, mais avec des paramètres modifiés ou renormalisés. Suite aux deux étapes du GE, nous obtenons à l'ordre d'une boucle, les relations de récurrence suivantes pour les parties libre et d'interaction :

[•W.Ï'IM = (2.20)

= + . (2-21)

Conséquence de la remise à l'échelle, les champs sont transformés par le facteur Ç3.

On peut déterminer ce facteur à partir d'une analyse dimensionnelle des paramètres de l'action. Ainsi, suite à la transformation de remise à l'échelle de la quantité de mouvement

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrésl8

forme :

e ' ( k ' ) = C (dJ)e(fc) (2.22)

À partir d'un développement de Taylor, on trouve facilement dans la limite d l —> 0

cm = (2.23)

= l + (jfccot k ) d l (2.24)

-» e(fecot m (2.25)

Ainsi, la remise à l'échelle du spectre dépend de la variable k . Proche du bord de zone de

Brillouin k —| > et £ —>• s0. Le spectre est alors sans dimension d'échelle (puissance de s ) .

Par contre, près du niveau de Fermi lorsque k —» 0, C —• s1, le spectre a une dimension un

comme pour le cas d'un spectre linéaire correspondant à la limite du continuum. Comme

les fréquences de Matsubara entrent dans G° de la même manière que e(k), nous aurons

la même relation pour les fréquences :

u/n = C(dl) wn (2.26)

À partir de la définition des fréquences de Matsubara u in = (2n + l ) i r T , on obtient alors

la remise à l'échelle similaire de la température :

T = C ( d l ) T (2.27)

Maintenant comme S o [ i p * , i ( ) ] dans (2.5) est sans dimension sous remise à l'échelle, les

champs doivent alors se transformer :

^ 'P( k ' ) = C hP( k ) (2.28)

qui est la transformation du champ introduite en (2.20-2.21). Par conséquent, les cou­ plages de Sj vont acquérir une remise à l'échelle qui dépendra de C- Dans un premier

temps, selon (2.22-2.28), la partie Si se transforme suivant :

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés 19

! t '

= s Ç { d l )1 (2-30)

lr

p.{fc}

La transformation des est fonction de leur dépendance en vecteur d'onde. Suivant la

forme de Âj(|fc|) donnée en (1.35—1.38) et (1.43—1.47), on distingue alors trois groupes de transformations : pour le premier groupe, fotdk}), /^({fc}), #3,i({^})i /^4,2({&}) et /?4,i({k})) on a la même transformation :

&,2 ( { k ' } ) = C2( d l ) / 33,2( { k } ) (2.31)

/M{£'}) = C2W2>2({fc}) (2.32)

^3,i({^'}) = C2(dl)M{k}) (2.33)

M { k ' } ) = C2( d l ) M { k } ) (2-34)

= C2( d l ) P A , i ( { k } ) (2-35)

Pour le deuxième groupe, /^({^^/^({^^/^({A;}), nous avons

= C \ d l ) / 33 t 3{ k } ) (2.36)

M{h} ) = C \ d l ) l 32 t 3( { k } ) (2.37)

^,3( { f c ' } ) = C4( d l ) f 34 t 3( { k } ) (2.38)

Finalement, pour le troisième groupe, 0 2, i ( { k } ) indépendant de k, nous avons

/ M { * ~ ' } ) = s- 1C { d l ) h A { k } ) (2.39)

En combinant les transformations (2.30) et (2.31-2.39), on obtient alors la transformation les constantes de couplage j après les deux étapes de renormalisation à l + d l :

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés20 9 2 , 2 ( 1 + d l ) = s - ' C i d l ) -1 [ 9 2 , 2( 1 )+ 0( g2) ] 92,3( l + d l ) = s - W l ) -3 [ g 2 ,3( l ) + 0( g2) ] g ^ ( l + d l ) = s - ' a d l ) '1 [ g3A l ) + 0 ( g2) } 9 3,2( 1 + d l ) = s -lC ( d l ) -3 [<73,2

(0

En raison des facteurs d'échelle fonction de s et on distingue les trois types de variation

de constantes de couplage dans un groupe de renormalisation. Ainsi, si gitj décroît en

fonction de l, on dit que c'est un couplage non pertinent. Par contre, si gtj ne change pas, on dit que c'est un terme marginal. Finalement, si le couplage gtj croît alors, il est

pertinent. Cependant les corrections de Kadanoff 0(g2) provenant de la première étape

et qui apparaissent dans les expressions entre crochets peuvent changer la pertinence ou la non pertinence du couplage. Par exemple, on verra que pour g3ti, on peut passer

d'un couplage qui est non pertinent vers un couplage qui est pertinent si l'amplitude g2,1

dépasse un certain seuil critique.

Il est aussi intéressant de regarder la limite du continum où le spectre est considéré approximativement comme linéaire près du niveau de Fermi. Dans cette limite, le réseau discret disparaît et seuls les couplages 5*2,1 > 53,1 et g4t 1 demeurent. Ainsi, à partir des

expressions de liaison forte, on prend / —> 00 pour faire le passage à la limite de continuum,

pour lequel Ç(l,dl) —¥ s. Par suite, les couplages s'écriront sous la forme suivante après

les deux étapes de renormalisation :

9 2 , i ( l + d l ) = [ g 2 , i ( 0 + 0 ( g2) \ t o , i ( l + d l ) = s '2 [ g3 t l( l ) + 0 ( g2) ] g4, i ( l + d l ) = s '2 [ 5 4 , 1 ( 0 + 0 ( g2) ] (2.49) (2.50) (2.51) Dans ce cas, nous avons un couplage <72,1 marginal ; par contre les autres termes sont non

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés21

dans le cadre de la théorie de la bosonisation [17].

Attardons-nous maintenant à la transformation de Kadanoff qui permettent d'expli­ citer les corrections dans les expressions entre crochets. L'expression (2.20) permet de déterminer la correction de la vitesse alors que la relation (2.21) corrige les termes de

couplage. Nous pouvons distinguer deux contributions au terme d'interaction Sj 2 avec

deux champs dans la coque, soit une contribution normale des termes g2,i et et une

autre anormale provenant des termes Umklapp. Schématiquement, nous avons :

Pour les couplages normaux g2 t i et <?4,i,le S^2 se scinde de la manière suivante :

On note que les deux champs à intégrer dans la coque peuvent appartenir à quatre canaux. Les deux premiers canaux correspondent à mettre deux particules ou deux trous dans la coque (canaux de Cooper (C) et Cooper parallèle (C') ; le troisième canal correspondant à une particule et un trou de branches opposées (canal de Peierls (P)) et finalement, le canal de Landau (L) correspondant à une particule et un trou de la même branche.

De la même manière, on sépare le terme Umklapp :

S i , 2 = S ?< 2 + S Ï< 2 = > + . . . . ) - i - + . . . . ) (2.52) (2.53) _ qN,C , qN,C , qN,P , QN,L ~ ^1,2 ^1,2 •" ^12 T U/ 2 O- (tpliplip-ip+ + c.c + '0p^p'0pV,p + perm) + ((•0^* + C.C)

+('0*1/'* ^-"0+ + perm + ip*ï}*ï>pi(jp + perm)

(2.54) (2.55) — Dj 2 "t" <3/,2 ('0* V'+'0-V'- + perm + c.c) + ip+ilf+iï-ï)- + c.c) (2.56) (2.57)

qui consiste en une décomposition de type Peierls, suivie d'une de type Cooper parallèle. Cette séparation de Sj<2 mènera à des relations de récurence en fonction de l sous

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés22

ordre y introduit comme nous le verrons, une renormalisation du terme quadra­

tique de l'action (potentiel chimique et vitesse de Fermi). Les couplages g2,i, «foi, 54,i vont

renormaliser à l'aide des termes \ ((<S/,2)2)ce

i (<S«)2>„ = 5 (<S,T)2 + (Sîf)2 + 2 (S,y S,Y) + (2.58)

On note que les termes impliquant les canaux de Landau sont négligés parce qu'ils sont négligeables face à ceux de nature logarithmique provenant des canaux de Peierls et Cooper.

<*»

2.3 Equation d'écoulement de la vitesse

La méthode du groupe de renormalisation sur réseau permet de corriger la vitesse des

fermions sans spin, correction qui provient du canal de Landau et des couplages 52,2 etg2,3

ainsi que de <74,1,54,2 et 54 3. L'expression de la valeur moyenne(5/ 2)c e prend la forme :

(s?S) =

-77 y ] pi,2({£'}) (ipp$$pipp + C.c + perm) (2.63)

p,W)

-JJ ^2 &.3({FC'}) + CC + PERM) (2-64)

C h a p i t r e 2 . G r o u p e d e r e n o r m a l i s a t i o n s u r r é s e a u a p p l i q u é à l a c h a î n e d e s p i n s f r u s t r é s 2 3

La moyenne statistique donne

(s?iL) = ~ • pyk ' E c . e , k arpt 3

-17 T,

où k est élément de la coque externe. Avec les méthodes d'intégration dans le plan com­

plexe, ainsi que la considération de deuxième étape de remise à l'échelle, nous obtenons la valeur moyenne statistique Sfy1 en fonction des termes d'échange J et J' tel que on

ignore les contributions Hartree et les corrections aux seconds voisins (Voir annexe A) : (2.65)

(2.66)

($m) = -g*°C) tanh(E° (2T)]} s i n h°{l)dt (2'67)

x ^(8JA — 16J')psinkip*(k)ipp(k) (2.68)

p.W où

e0 (MO) = v(l) sin (MO) (2.69)

et

MO = ^ exp(-Z) (2.70)

En ajoutant cette contribution comme correction à la partie libre de l'action de fermions, ce terme est de la forme psink et corrige alors la vitesse. La relation de récurrence de la vitesse devient :

-v(l + dl) = —1»(0 - (92,2 + 4g4,i) sin MO ^MO tanh(£° ^ ) (2.71)

ce qui implique dans la limite dl -ï 0 :

= -?-M0 tanh(^%^)(8JA - 16J') sin MO (2-72)

(Il 47T ZI

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés24

2.4 Les équations d'écoulement des couplages

Les termes issus de | ((<SJ)2)2)oc contiennent quatre champs de fermion " i p " en dehors

de la coque et vont corriger les giti à la suite de l'intégration partielle dans la coque.

La décomposition au paragraphe précédent de S/2 permet d'expliciter les contributions

suivant le type de processus de diffusion, Umklapp ou normal et suivant le type de canal de diffusion Peirels ou Cooper.

Canal de Cooper :

La contribution de Cooper s'écrit sous la forme :

ï((s"C)2)« = 51? £ x + c-c)(ï>*+ï>-ip-ip+ + c.c)) (2.73) = 2L v i l ) ^ 9 2^9 2'l^5M 2 - h - kif i {*},{*} xlc(qc,dl

)r

)r

Seul le couplage g2,i contribue au canal de Cooper car les vecteurs d'onde pour les termes

de couplage sont pris au niveau de Fermi. Dans ces conditions, les autres couplages qui

dépendent de k donnent des contributions nulles.

Canal de Peierls :

La contribution de Peierls donne les valeurs moyennes statistiques | ^(•S/^)2^ ,

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés25 ^((s,T)2) = ê E iJ,W x + c . c ) ( ' i p *+i p * _ î > ^+ + c.c)) (2.76)

- ^Efe,^<o

+

i&(o

+

^(0+^,(^(0

La contribution provenant des termes Umklapp est égale à :

5 (< s«) 2L = ^ E & , < ( « ) & „ ( { * ' »

P, W U k }

x {(ï>*p^*pî>-p^-p + -)(%i>$-p'*l>-p + -))0.c (2-78)

= I^i) E M',^)41+fe-*J-/..,o(29l,I(0+49322(i)

n p , { k ' } , { k }

+2^3,3(0 + 293'1^93'3^ + 53,2(053,3(0 + 253,2(053,1 (0)

x^+(k3)r-(k4)Mki)Mk2) (2.79)

Nous avons introduit l'intensité (boucle) Peierls :

Ip = v ( l ) j Y , G ° _ { k - 2kF, un) G °+( k , c on) (2.80) k € c . e

un

Les corrections des termes couplage Umklapp 53,1,53,2 et 53,3 proviennent de l'expression (Sïf.sïf) qui est égale à :

\ ' ' / o , c (sïf-sïf) = Ç E h>m)fhA&)) p,{fc'},{fe} X ((^V-V'-^+ + c-cmpippijj-pip-p + perm)) T = or n\ y>53,1(053,i(Q + 252,2(053,i(0 + 52,3(053,1(0)

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés26 x I p ( J , d l ) s i n ( — — — ) si n ( — - g — — ) *rp(k3)^(fc4)^-p(fci)^-p

(fc

)^

fe

-fc

;(fe

-

(fc

/P(i, dl) sin (—^—) sin(—2—^Sm^—2—?

(2-83) À partir de toutes les contributions de Kadanoff, nous obtenons les relations de récurrence pour les couplages :

9 v( i + di) = + 52e//,3(0, 93,2 ,n T 85I3 92,l(l)92,2(l) r "1Mô~/p " MÔ(/)/p " MÔ(z)/p " MO /p 92,1(1)92,3(1) T 92,2(1)92,3(1) T 2v(l) P 4v(l) P A 93,1(1)93,3(1) r 0 53,1 (053,2 (0 r n93,3(1)93,2(1) J , ^0 / l N -4 2v(() ~2 4v(i) / p "2 2v(() , p | ( 2'8 4 ) 9 3 , 1 ( 1 + d l ) = »-'C('fl)-'b»,i(l)-48!t'^'(')/f

053

53,I

,3

53,

(052,

(0

53

,3

q

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés27 O03,3(0^2,2(0 r 93,3{l)92,3(l) T 1 /I Q-7\ "2 2 v ( l ) h ~ 2 v ( l ) I p ] ( 2"8 7 ) g2,2(l + dl) = s-'adiy'g^l) (2.88) 92,3(1+ dl) = s~l<;(dl)-3g2t3(l) (2.89) 94, i ( l + d l ) = s - \ ( d l ) -lgi t l( l) (2.90) 94,2(1+ dl) = s-\(dl)~l g i,2(l) (2.91) 94,3(1+ dl) = s-\(diy3g4 < 3(l) (2.92)

L'évaluation des intensités (boucle) de Peirels et Cooper est donnée par ( voir annexe A ) : l e = 2 v ( l ) j Y G ° - ( ~ k , - u >n) G °+( k , u ;n) (2.93) L, fe€c.e UJN (2.94) v 2 T ' 2

Finalement, dans la limite dl —¥ 0, nous transformons les relations en système d'équations

différentielles ou équations d'écoulement pour les constantes de couplage :

= 02,I(O(MO cotk0(l) - 1) - ^-92,1 + <?3,I(0 TANH(£°^Y^)

£2,2(0 ,,£0 (MO \ . 02,3(0 ,/£() (MO %

tanh( o rr ) + ôô tanh(-^ )

8 v 2T ' 32 v 2 T

+^-(5!») + 4sï,3(i) tanh (f°M>)

+Sa.i(')«w(')j tanh(^y')) + g21(/)g23(()I t a nh(?^M!l)

+§2,2(002,3(0ggtanM °^(') + 53,3(093,2(0tanh( 0)

+293., Wsm(0 tanh(^M)) + 93,i(093,2(0; tanh(^û) (2.95)

= -9 3 , i ( 0 ( 1 + *(i(')«>'*.«(()) ~ +293,i(092,i(/)tanh( ° ' )

C h a p i t r e 2 . G r o u p e d e r e n o r m a l i s a t i o n s u r r é s e a u a p p l i q u é à l a c h a î n e d e s p i n s f r u s t r é s 2 8

= "53,2(0(1 + MO

MO)

3,2 + 253,

(0£2,I(0tanh(^>)

+53,2(/)52,2(/) tanh(^Ml) + ±g3,2(l)g2,3(l) tanh(^M^) (2.97)

= -93,3(0(1 + 3 M 0 cot k0(l)) - ^ 9 3 , 3 ( 0 + 293,3(0P2,i(0 t a n h (g o^ ^ )

+93,3(092,2(0 tanh(£°^y^) + ^93,3(092,3(0 tanh(g Q^ y ^ )

= - 9 2 ,2( l ) - r r v ( l ) ( l

+ MO cot MO)

^^92,2(0

MO)

= - 54,2(0^(0(1 + M0 cot MO) - -77T94,2(0

(2.101)

M O ) -

Ici nous avons normalisé tous les couplages (5 = ^yj) P31" largeur de bande effective

2t>(0 à l'étape l. On note que cette normalisation de part et d'autre des équations de

récurrence mène à une correction de remise à l'échelle proportionnelle à ce qui change

le coefficient du terme linéaire en gtj qui est en fait la dimension effective du couplage.

Pour les couplages, la fonction thermique, tanh("°^^), agit comme une limitation dans l'évolution de la renormalisation. Ce terme nous indique que pour des températures faibles par rapport à l'énergie de fermi, la renormalisation des couplages s'arrête (du moins pour les canaux considérés ici). Ceci donne la limite de la contribution logarithmique de la renormalisation. Bien souvent ce terme est évalué à 1 mais la renormalisation, de sorte que la renormalisation conserve une dépendance en température. Nous avons choisi ici de conserver la dépendance explicite en température dans l'équation d'écoulement et ainsi effectuer la renormalisation jusqu'à Z —» 00. De cette façon notre résolution numérique suit strictement la théorie du groupe de renormalisation.

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés29

> I*. 1.20

J'=0.1J

t _ 2 J

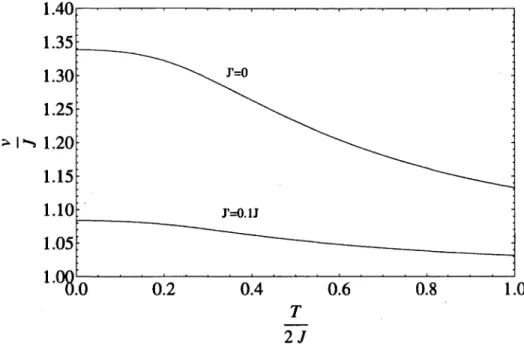
FIGURE 2.1 - Variation de la vitesse en fonction température pour = 0.532J fixée et différentes amplitudes de frustration.

2.5

Résultats

2.5.1 Vitesse

Nous nous intéressons dans un premier temps à la variation de la vitesse de Fermi

en fonction de la température telle qu'obtenue par l'équation (2.72) à température T .

Plaçons-nous en premier lieu dans le cas sans frustration, à J' = 0. Selon le figure 2.1 ,

nous observons qu'à T —¥ oo, la vitesse tend vers J car les fluctuations thermiques ré­

duisent les corrélations entre fermions qui deviennent essentiellement indépendants dans cette limite. Par contre, en baissant la température, la vitesse est supérieure à la valeur initiale car les corrélations entre fermions deviennent importantes. La vitesse à tempéra­ ture nulle obtenue par le groupe de renormalisation est selon (2.72) :

v , 2A

— = 1 -I

j 7T (2.103)

Ce résultat coïncide avec celui trouvé dans l'approximation de Hartree-Fock à tempéra­ ture nulle :

,H.F _{= J +} 2 Jz

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés30

Maintenant, si J ' ^ 0, nous obtenons un comportement similaire au cas J ' — 0, mais dont

l'amplitude est inférieure. En effet, à haute température, la vitesse retrouve sa valeur J .

Cependant à basse température la vitesse, bien que supérieure à la valeur initiale, est inférieure au cas sans frustration. La valeur de vitesse à température nulle est donnée par :

On constate alors que la frustration diminue la vitesse et donc la rigidité antiferroma­ gnétique.

2.5.2 Couplages : cas

= 0

Nous regardons maintenant le comportement des couplages en fonction de l (voir figures 2.2 et 2.3) pour J' = 0. Nous observons que si l'anisotropie selon z de J, A < 0.532,

le couplage marginal <72,1 tend vers une valeur non universelle si l -» 00. Par contre, tous

les autres termes <73,1 , <74,1 et <72,2 sont non pertinents et tendent vers zéro sil —ï 00. Si

maintenant A > 0.532, nous avons une divergence des couplages <?2,iet <73,1 à l = lc finie

à température nulle. Un couplage tendant vers l'infini est synonyme d'ouverture d'un gap d'excitations. Comme il s'agit du modèle Hxxz> ce gap marque le passage vers un

état de spin de type Ising antiferromgnétique (voir plus bas). On note que la solution

exacte par Ansatz de Bethe donne A = 1 comme valeur critique de Jz au-dessus de

laquelle, le système tombe dans la limite Ising Antiferromagnétique avec gap [18]. On

peut comprendre l'origine de la valeur critique = 0.532J . On peut réecrire l'équation

d'écoulement de <73,1 sous la forme suivante :

^- = hi(l)de (2.106)

avec :

de = 2</2,I(0 tanh(£° - (1 + fco(OcotMO) ~ ~7^

ZI v\ l )

+92,2(0 tanh(^S) + 92,3(05 tanh(^ï^)

(2.107)

de représentant la dimension effective du couplage <73,1. Ainsi si de < 0, <73,1 est non

pertinent et il n' y a pas de gap. Pour de > 0, <73,1 est pertinent et est synonyme de

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrésSl #2,1 2 v ( / )

1.2

1.0

0.9

0.8

FIGURE 2.2 - Variation de la vitesse en fonction température pour j% = 0.532j fixée et différentes amplitudes de frustration.

é>3,l 2 v ( / ) 0.4 0.3 7Z = 0.5327 0.2 ^-10- 15-- — 20 jz = 0.53 7 7Z = 0.52 0.0

FIGURE 2.3 - Comportement de <72,1 en fonction de l pour différentes températures à et j' = 0 (sans frustration) ainsi que le comportement critique (t = 0) en pointillé.

C h a p i t r e 2 . G r o u p e d e r e n o r m a l i s a t i o n s u r r é s e a u a p p l i q u é à l a c h a î n e d e s p i n s f r u s t r é s 3 2

sans correction de vitesse, on a alors :

de = 2g2 A - 2 (2.108)

ou retrouve alors le résultat connu où si g2 ,1 < 1, de < 0 correspond à la situation sans

gap. Dans le cas contraire, où g2,i > 1 et g3ti diverge, ce qui donnera la valeur critique Jcz = 0.5J au dessus de laquelle il y a un gap. Par contre, si nous regardons l'équation

(2.103) dans laquelle il y a les termes liés à l'effet de réseau, où les corrections liées aux termes de couplages supplémentaires et au réseau et à la vitesse modifient la dimension effective et pousse la valeur critique vers le haut et donc un peu plus près de la valeur exacte.

2.5.3 Couplages : cas

0

Maintenant si on augmente J ' (voir figures 2.4 et 2.5) tout en restant à Jz = 0.532J,

nous retombons dans un état sans gap. La frustration J' qui a tendance à nuire à l'éta­

blissement de corrélations antiferromagnétiques, éloigne le système de la limite Ising . Ce­ pendant cet état sans divergence g3tx ne persiste pas pour tout J'. Pour J' > J'c = 0.175J,

il y a de nouveau une divergence de g3ti avec selon (2.107) de > 0. Il est intéresant de

noter que sans les effets des termes non pertinents 2.107 dus au réseau, la valeur critique obtenue est de J' = 0.01 J et est donc très faible.

On verra que physiquement la nature du régime couplage fort à J ' > J 'c est différent

de celui prédit à A > Ac et J' = 0 pour le modèle Hxxz qui était de type Ising. Le

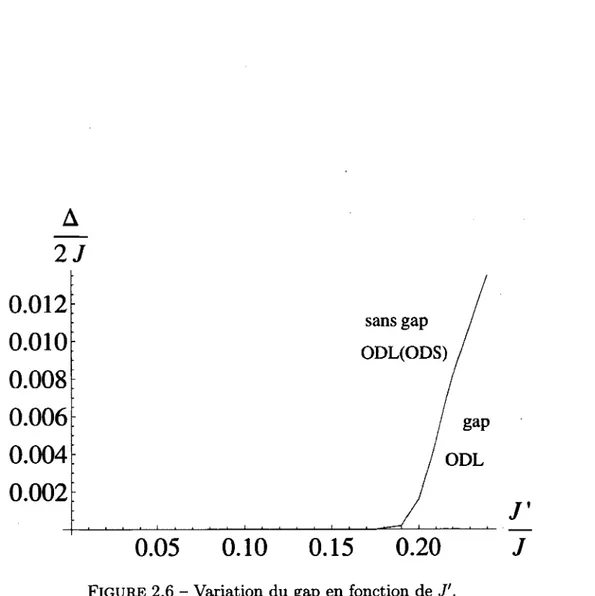
gap ( voir figure 2.6) est lié à une mise en ordre de lien, mais qui est aussi caractérisée par un gap de spin. On note aussi que la valeur de J'c déduite par les calculs numériques

comme la diagonalisation exacte est J'c = 0.241 «/, donc au-dessus de celle déduite par GR

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés33 g 2,1 2 v ( / ) 1.6 1.4 1.0 0.8 0.6 30

FIGURE 2.4 - Variation de <72,1 en fonction de 1 pour une température nulle et différentes valeurs du couplage de frustration J' à Jz critique fixé ( la courbe pointillé est pour

J'=0.175J et J2C=0.532J). 8 3 , 1

2 v ( / )

0.30

0.25

0.20

= 0.057

0.15

0.10

0.05

FIGURE 2.5 - Variation de <734 en fonction de 1 pour une température nulle différentes valeurs du couplage de frustration J' à Jz critique fixé ( la courbe pointillé pour J ' =

Chapitre 2. Groupe de renormalisation sur réseau appliqué à la chaîne de spins frustrés34

2 J

0.012

0.010

0.008

0.006

0.004

0.002

0.05

0.10

0.15

0.20

J

Chapitre 3

Fonctions de réponse

Dans ce chapitre, nous traiterons de la réponse du système à un champ source externe. Ce champ source peut être un champ de création de fluctuations d'onde de lien (diméri-sation) et onde de site (antiferromagnétisme) de vecteur d'onde 2kp = 7r, ou encore un

champ de création de fluctuation uniforme pour la susceptibilité magnétique uniforme. À partir de l'analyse de la réaction du système, nous pouvons déterminer le diagramme de phase ainsi que la susceptibilité magnétique en fonction de la température et ainsi comparer à l'expérience.

3.1 Fonction de réponse au vecteur d'onde 2

k p

La réponse du système à la formation des paires particule-trou à 2kp dans le canal de Peirels correspond à la réponse pour la formation d'une onde de densité de vecteur d'onde 2kp. Cette onde de densité peut être centrée sur les sites ou sur les liens. Pour les spins, l'onde de densité de lien correspond à une résonance de lien (RVB ou ODL) et l'onde de densité de site correspond à une onde antiferromagnétique (AF ou ODS) (voir figure 3.1).

Dans le modèle JJ' de liaison forte, nous introduisons des combinaisons de champs particule-trou symétrique et antisymétrique

0 ± ( q ) = \ { o * { - q ) ± o ( q ) ) (3.1)

Chapitre 3. Fonctions de réponse 36

FIGURE 3.1 - Représentation de l'onde densité de site (ODS en trait continu) et onde densité de Lien (ODL en trait pointillé).

° ( q ) =

(

-

)

k

ce qui correspond à un champ 0_ pour l'onde de densité de lien ODL (—) et 0+, pour

l'onde de densité de spin ODS (+). Nous considérons alors un couplage linéaire avec un

champ source externe infinitésimal qui s'ajoute à la partie d'interaction de l'action

Si h*, h] = st [r, i>\+sh (3.3)

tel que :

Sh[r,i>} = YZM)0;(q)+c.c (3.4)

et /x = ± correspond aux cas ODS et ODL. Comme on s'intéresse à la réponse linéaire du

système dans la limite des faibles champs, on peut considérer S h comme une perturbation

au même titre que Si. est un facteur de renormalisation du couplage linéaire qui à

l'étape t = 0, est fixé à Z^(£ = 0) = 1. Le terme perturbatif total pour l'action sera donc la somme de ces deux termes. Tout comme précédemment avec les couplages, on se limitera à l'ordre d'une boucle, ce qui nous limite à quelques termes d'ordre 2. Pour la transformation de Kadanoff (2.20,2.21), on remplacera simplement Sit2 dans (2.58) par

Chapitre 3. Fonctions de réponse 37

sh [ p m = +c c (3-5)

M.?

et ô; est le champ avec le particule et le trou dans la coque externe (2.16). On aura donc à l'ordre d'une boucle :

\ ( ( SH

+ S,

)

>„ =

<(&,,)">„ +

<(3»)

>„ +

(3.6)

où le prémier terme est le même que celui déjà traité au chapitre 2 avec = 0, le deuxième terme permet de déterminer la susceptibilité associée. Le troisième terme est proportionnel à hM et renormalise donc Z^. Si on s'intéresse dans un premier temps

l'expression correspondant à | ((Sh)2)ÔC , on a :

\ «

")

>

,

= E \ ((

MÔ'M+K(-I)Ô

(-I))(K(<I)O:(I) + A;(-«')<5„(-«')))„

(3.7) Il est utile de tenir compte des relations suivantes :

0 *±( q ) = ± 0 ± ( - q ) (3.8)

h *±( g ) = ± h±( - q) (3.9)

Alors l'équation (3.7) pour les cas ODS et ODL est proportionnel à h * h et fait intervenir

(ô*ôM) = IP qui est la boucle de Peierls IP évaluée à l'annexe A :

\ <(&)% =

E

(3.IO)

Ceci correspond à un nouveau terme constant, proportionnel à h * h , qui s'ajoute pour

chaque étape à S. Comme l'action S correspond à la densité d'énergie libre, la dérivée