Construction de la matrice de l'élément fini triangulaire à déformation constante pour l'étude des problèmes à potentiel à partir de critères de consistance

HAL Id: hal-01005992

https://hal.archives-ouvertes.fr/hal-01005992

Submitted on 11 May 2017

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Distributed under a Creative Commons Attribution| 4.0 International License

Construction de la matrice de l’élément fini triangulaire

à déformation constante pour l’étude des problèmes à

potentiel à partir de critères de consistance

Peter Bettess, Bernard Peseux, Omar Laghrouche

To cite this version:

Peter Bettess, Bernard Peseux, Omar Laghrouche. Construction de la matrice de l’élément fini

tri-angulaire à déformation constante pour l’étude des problèmes à potentiel à partir de critères de

consistance. Mécanique Industrielle et Matériaux, Groupement pour l’avancement de la mécanique

industrielle, 1999, 52 (2), pp.66-70. �hal-01005992�

CONSTRUCTION DE LA MATRICE DE L'ÉLÉMENT FINI

TRIANGULAIRE A DÉFORMATION CONSTANTE POUR L'ÉTUDE

DES PROBLÈMES A POTENTIEL A PARTIR DE CRITÈRES

DE CONSISTANCE

DERIVATION OF CONSTANT STRAIN TRIANGULAR FINITE ELEMENT FOR POTENnAL

PROBLEMS FROM CONSISTENCY CRITERIA

P. BETTES$". B. PESEUX'". O. LAGHROUCHE"

ABSTRACT

/RÉSUMÉ

Ce papier court démontre comment la matrice d'un élément fini triangulaire à trois noeuds peut être construite de façon très simple, pour l'étude des problèmes à potentiels, à partir des conditions de consistance de << mouvement de solide rigide , et de symétrie, sans aucune référence aux fonctions d'Interpolation, aux conditions de compatibilité, ou toute autre méthodologie conventionnelle en

éléments finis. Cette démarche démontre également que la matrlc:e de l'élément triangulaire à trois noeuds

est unique.

This short pitper demonstr.-.tes how the mittrlx for it three node trl.-.ngulitr potentlitl fln/te element Citn be derlved

very slmply from the conslstency conditions of "rlgld body movement" .-.nd symmetry, whlthout itny reference to sh.-.pe functlons, comp.-.tlblllty, .-.nd it/1 the other conventlonitl fln/te element methodology. This .-.Iso demonstr.-.tes thitt conventlonal three node llnear element ls unique.

KEY WORDS/

MOTS CLÉS

Élément fini - Élément triangulaire - Problèmes

à

potentiel - Matrice

<< raideur ,, - Conditions de consistance.

Fln/te element - Trl.-.ngulitr fln/te element - Potentla/ field problems - "Stlffness" matrlx - Conslstency conditions.

1. INTRODUCTION

Depuis quelques années, Bergan et Hanssen ( 1) ont montré qu'il est possible de générer les matrices d'éléments finis par la prise en compte d'un certain nombre de conditions qui n'ont pas de relation avec les fonctions d'interpolation. Leur approche repose sur un critère de convergence concernant un seul élément. contr ai-rement au patch test qui considère l'équilibre d'un groupe d' élé-ments. Ils ont alors introduit le test sur un élément pris indivi-duellement (lndividual Element Test) dont l'extension a conduit au test sur l'élément d'ordre supérieur (High Order Element Test). Le premier test assure que l'élément possède les modes de mou-vement de solide rigide ainsi que ceux relatifs aux déformations constantes. et le deuxième utilise des modèles de déformations d'ordre supérieur. Ces conditions ne sont pas utilisées comme des tests a posteriori sur l'élément, mais inteNiennent directement dans la formulation de l'élément fini. Plus tard. Bergan et Nygard [2) ont introduit une nouvelle formulation dite • libre •. Dans cette dernière. le champ de déplacements doit contenir les modes de déformation fondamentaux qui doivent être linéairement indé-pendants.

Dans le présent papier, en utilisant les conditions de symétrie et de mouvement de solide rigide, on détermine la matrice de l'élément triangulaire à • déformation constante " utilisé pour résoudre les problèmes à potentiels. Afin d'expliciter la démarche, on détermine successivement les matrices d'un triangle rectangle isocèle. puis celle d'un triangle rectangle quelconque, et enfin on généralise la méthode en traitant le cas d'un triangle scalène. Une simple interprétation géométrique des éléments de la matrice de cet élément triangulaire est présentée à la fin du papier.

• School of Engineering. University of Durham. Science Lal>oratories. South Road, Durham. DHI 3LE, Great Britain.

·: l..ll>oratoire de MéC<Inique et Matériaux, Division Mécanique des Structures. Ecole Centrale de Nantes. 1. rue de la Noë, 44321 cedex 03. France.

Notons que le premier élément triangulaire fut utilisé par Courant (3]. Il a développé l'idée de minimiser une fonctionnelle en utilisant une approximation linéaire de la fonction de contrainte à travers des surfaces triangulaires pour résoudre le problème de torsion d'un cadre carré. Selon Gupta et Meek [4]. Courant peut être le premier à utiliser la procédure des éléments finis et en l'occurrence l'élément triangulaire.

Pour les problèmes d'élasticité, la première formulation des élé-ments triangulaires est due à Turner et al. (5] qui ont déterminé la matrice raideur de l'élément dans le cas de l'état de contraintes planes. Les auteurs mentionnent que non seulement l'élément tri

-angulaire est simple, comparé à l'élément rectangulaire, mais sera utilisé comme élément de base dans les problèmes de plaques de formes arbitraires.

Concernant les problèmes à potentiels. le premier élément tri

-angulaire a été formulé dans le papier de Zienkiewicz et Cheung [6]. Les auteurs ont analysé le problème de transfert de chaleur couplé à la torsion d'arbres de section circulaire. Ils ont introduit la notion de topologie du système ainsi que le concept de conti

-nuité de la fonction considérée à travers les frontières communes des éléments.

Dans ce qui suit. avant d'entamer la procédure basée sur les conditions de consistance. on détermine la matrice d'un élément triangulaire quelconque à trois noeuds en suivant la démarche habi

-tuellement utilisée dans la méthode des éléments finis.

2. MÉTHODE CONVENTIONNELLE

Cette méthode est rencontrée dans tous les ouvrages d'él é-ments finis [7] (8]. Soit un triangle quelconque ( 1, 2, 3) à trois nœuds de coordonnées respectives (x_1• y₁₎. (x2 • y2). (x3, y3)

(figure 1 ). La matrice de cet élément est construite pour traiter un problème tel que le champ inconnu <!> à déterminer soit un champ scalaire.

J 1

p,

.

,

Figure 1 : Elément trl.tngu/;tlre quelconque .t trois noeuds. A fln/te trl.tngul.tr '--- - - -- - --' element.

En supposant une variation linéaire du champ cp dans l'élé -ment. celui-ci peut s'exprimer par:

<!>

=

a

+ bx + cy ( 1 )

En écrivant l'équation ( 1) pour chaque nœud. on obtient le sys

-teme:

f

cp

,\

-<1>·

-\

~

~

f

1

x

,

y

,

{

a

\

1 X~Y2 b

f

1

x

,y,

c

(2)

Avec quelques manipulations algébriques simples, on peut

résoudre le système d'équations (2) pour déterminer les constantes a. b etc en termes des coordonnées nodales ainsi que des valeurs nodales ljl₁• $~et

<

h

En remplaçant a. b. etc par leurs expressions

dans l'équation ( 1 ). le potentiel <1> pourra s'écrire sous la forme sui-vante:

.

<t>=

_•

L

₁

N

,

<i>,

{

3

)

Les fonctions de forme N, sont données par :

N

,

(x

.

y

)

=

~

(

A

,+

D

;.x

+ C;

y

)

où:

A,

=

XzY3-X3Y2 Az

=

X3Y1- x,y3

B,=yz-Y3 Az=Y3-y,

C, =x~~-Xz C₂ = x, - x3

t:.

est faire de l'élément exprimée par:

' 1 x, y, _ 1

t.-

2

1 x~ Y! 1 x.,YJ A3

=

x1y2 - xz:;1 83

=

Y1-Yz C3=xz- x, (4) (5) (6)

Le vecteur gradient peut s'écrire sous la forme:

J

_-

à

o

.x

$

\

=_j-

₁

B,

B~

B

.,

_l

_{

q>:

_<i>

₎

\

~cp

f

2.'\ C,

Gz

C, <j>: \dy soit:

d

X

1 <Jl,

f

_d

_<j)

_}

_{( )}

\

~<!>

=I

B

J

:

:

\dy (7) {8)

La matrice • raideur" de l'élément est alors donnée par l'expres-sion:

[

k

]

=

j

)

s

r (

s

]

cts

(9)

où {B]r est la matrice transposée de (B] et dS est un élément de surface de l'élément triangulaire.

L'intégration est immédiate puisque dans (B] tous les coefficients sont constants. Soit finalement l'expression de la matrice " rai-deur•:

s

;

+c

;

B2B,+C1C, B,B, +C,C,

B

,

B!+C, C! B~ +C; B,~+C,C1 B, B~+C, C .• B2 s~ +

c

l

c

.

.

< t

o

)

s

;

+C;

Dans ce qui suit, la matrice • raideur • est reconstruite mais cette fois-ci on ne fait pas inteNenir les fonctions d'interpolation. Seules les conditions de " mouvement de solide rigide • et de symétrie sont utilisées. On commence par traiter le CC\S d'un triangle rec-tangle isocèle, puis celui d'un triC\ngle rectangle quelconque. Afin de pouvoir généraliser la méthode, on s'intéresse au cas d'un triangle scalène.

3.

UTILISATION

DES

CONDITIONS

DE CONSISTANCE

3. 1. TRIANGLE RECTANGLE ISOCELE

On considere le triangle rectangle isocèle ( 1, 2, 3) d'hypothé-nus aJ2. (figure 2}. A partir de considération de symétrie. la matrice raideur [k] peut être écrite sous la forme :

(Il)

av~c les conditions suivC\ntes :

<

X

= 2~

et Y=

o

+

1

3

(12)

En construisant de la même façon la matrice correspondçmt C\U triangle (2. 3, 4). puis en assemblant les deux triangles on obtient :

(X-~-~

0

k 1 _ -

p

21'- 2o -

p

- - P- 2o2'f- 13

0

-

p

-·~

('(

a { 13) figure l : Assembl.tge de deux trl.tngles rect.tngles Isocèles. Assembly of two ,, rlght-.tngled lsocele

'-

o

- - - -

- -

--

- - - -

-

--·

-'

trl.tngles.

L'étape suivC\nte consiste à imposer un potentiel unité aux nœuds 2 et 4, et nul aux nœuds 1 et 3. Soit donc $1

= 0

, 4>₂

=

1, .1\ _{'!'l =} 0 _• .1\ _{t4 =} 1 _.

c

_{es con} d' _1t1. _{ons 1}. _{mp 1que}l' _{nt que "'.}

!l~

_{i" =~}

J

_{a ,et~}

~

_,

_{= .}

0

vX ~~ <1Y

Le flux aux nœuds 1 et 3 est égal à -1/2 et aux nœuds 2 et 4 à l/2. On obtient alors : 2

_~

_-

_~

-P

0

{

o

)

{

-

l/

2

)

- ~ 2y - 2o - ~ 1 \ _ 1 12

-

~

- 2

15

2y - ~ 0

f -

-

1 /2 0 -

p

-

~ 2~ 1 1/2

Ce qui conduit aux VC\Ieurs :

P=

'

f

=~.

o=

O

La matrice [k] du triangle rectangle isocèle s'écrit alors:

J

_

l.=J.

2 2

_l

1

tl

2

2

__ 2J 0 '1

2

(14) ( 15) (16)

matrice que l'on obtient à pC\rtir de la forme générale donnée par l'équC\tion (10) pour x, = 0, y1 = O. x2

=

1, y2 = 1, x3 = 0 et Y3 = 1.

3.1. TRIANGlE RECTANGlE QUELCONQUE

On considère le triangle rectangle ( 1, 2, 3) de cotés a et b

mon-tré sur la figure 3. figure 3 - Assemblage de deux triangles rectangles quelconques. Assembly of two L--~~---~---~----~--~---" rlght-angled triangles.

La matrice raideur de ce triangle peut-ètre écrite directement sous la forme :

e

<X [3

]ki

{X ù) -y ( 17) ~ y 0

e

<X+!} avec ù) _CX+Y ( j 8)

0

!}+y

En assemblant les deux triangles rectangles, celle-ci s'écrit:

e

-(X -~ ()

u. <ü+o- !}

!}

_-

(l) + 0 Ct.

(19)

() !} -Ct. (1

Comme précédemment, si le potentiel est nul aux nœuds l et 3

et à l'unité aux noeuds 2 et 4,

$

1 0, $2 1,

$

3 0,

$

4 1,

cela entraîne et

=o.

Le flux aux nœuds l et 3 est égal

à-b/2a et aux nœuds 2 et 4 à b/2a. On obtient alors :

8 (X !} () ₍₎ -bi 2a (X (l) + 0 -2y -~ 1 b/2a ~ W+O Ct. () b/2a () _~ (Y.

e

1 bi 2a (20)

On obtient ainsi les valeurs :

(21)

Si le potentiel est nul aux nœuds et 2 et égal à l'unité

aux nœuds 3 et 4,

$

1 0,

$

2 0,

$

3 1,

$

4 = 1, cela entraîne

o<jl ()et = 1 Le flux aux nœuds 1 et 2 est égal à-a/2b et aux

ax

b'

nœuds 3 et 4 à a/2b. Ceci conduit aux valeurs :

y=O (22)

Et finalement la matrice [k] du triangle rectangle ( 1, 2, 3) s'écrit:

b

2a

()

0 ₍₂₃₎

matrice que l'on obtient à partir de la forme générale donnée par

l'équation (9) pour x1 0, y1 = 0, x2 a, y2 = 0, x3 0 et y3 =b.

3.3. GÉNÉRALISATION : TRIANGLE QUElCONQUE

Cette construction concerne le cas général qui est naturellement le plus intéressant. La forme générale de la matrice " raideur ,

romr"P tenU deS COnditiOnS de symétrie eSt donnée pOUr le tri-(1, 2, 3) par:

-{X ù) -y

!} -y

8

(24)

Les conditions ( 18) sont toujours applicables.

Considérons maintenant un assemblage de deux triangles ( 1 , 2,

3) et (4. 2, 3) tel que montré par la figure 4:

figure 4 : Assemblage de deux triangles quelconques. Assembly of two

'---~---~---' ordlnary triangles.

La matrice assemblée des deux

e

ft. -!} 0

]k]

-(X (0 +

8

-!}

!} 2y (0 +

0

(X (25)

()

- r)

(X 8

Une étape préliminaire consiste à déterminer les longueurs

des cotés a, b etc ainsi que celles des hauteurs d, e et f.

Les longueurs des cotés du triangle ( 1, 2, 3) sont obtenues en

appliquant le théorème de Pythagore (figure 4) :

a [(Xz-XJ)2+(yz-YYl112

b [(x3 Xz)2 + (y3 Yz)2]112 (26)

c [(x 1 - x3)z + (y 1 Y3)Z]I/Z

Les hauteurs sont trouvées en considérant le vecteur perpen-diculaire au coté considéré puis en projetant un coté adjacent sur ce vecteur. En prenant l'exemple de la hauteur d, le vecteur

per-pendiculaire au vecteur

à

défini par la direction 1-2 est donné par:

li,

y,)

r-

x,)

.i

(27)

où

i'

et désignent les vecteurs unitaires suivant les axes de

coordonnées x et y.

La distance du nœud 3 au coté 1-2 est égale à la projection du

vecteur

b

défini par la direction 2-3 sur

na,

soit :

d (28)

ce qui donne :

d (29)

De façon identique on obtient :

(30)

L'étape suivante, consiste à appliquer une variation linéaire

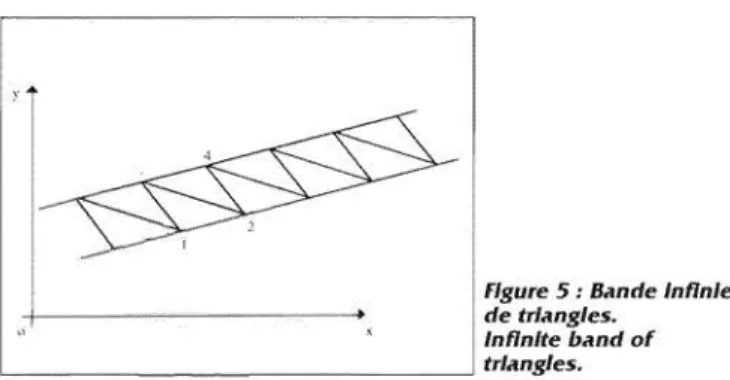
du potentiel dans la direction perpendiculaire au coté 1-2 sur une bande infinie de paires de triangles quelconques ( 1, 2, 3) . (4, 2, 3) tel que montré par la figure 5.

Le fait de travailler sur une bande de triangles infinie, permet de

réduire la matrice de l'assemblage à une matrice de dimension 2

en additionnant les lignes et les colonnes 1 et 2 ainsi que 3 et 4. On obtient alors :

2(~+y) -2 (~+y)

2(~+y)

2

(~+y)

Figure 5 : 8dnde Infinie de trldngles.

Infinite bdnd of ,_ _ _ __ _ _ _ _ _ _ _ _ _ _ _) trldngles.

Maintenant on impose un potentiel unité aux nœuds 3 et 4 et nul aux nœuds 1 et 2, <1>₁ = 0, <!>2 =O. <j>3 = 1, <j)4

=

1. ce qui

cor-respond à :

~$.

=

J

ct

ô<P

= 0, avct.: ti.. qui désigne la direction CjJl,, d

iJt

.

normale au coté 1-2 et t'a la direction tangentielle. Le flux aux nœuds 1 et 2 est égal à -a/d, celui aux nœuds 3 et 4 est égal à

a/cl . A partir de l'équation (31). on obtient alors la condition :

(32)

E.n substituant cette valeur et en comparant avec la valeur théorique obtenue en position (3.3) de la matrice de l'expression

( 1 0). on vérifie que cette valeur est correcte. Les termes diagonaux

de la matrice sont obtenus par permutation circulaire.

,?

(X+y±

.S

- 46 Cl+ r) ₁ :!:

~

bl

- 46 (33)

Considérons à nouveau l'expression (32). E.n remplaçant a.

celle-ci peut être réécrite sous la forme :

P

+y

~ ~

=

4~

1

~

(

)(

?

-

x,

)(

x

;:-

.x,

)

+

{

Y7-Yt

)(

Y

:-

Y

t

}l

=

t

n

j

~h-x,)t(x~

-

,

,,

)

+Ü

':-

YJ}(Y:!-

x~)

l

+

4~

jh

-

:x,

l(

x

3-

x,

)

+

(

y

~

-

y,

)tl

y

r

y,

Jj

(34)

Ce qui est parfaitement en accord avec les résultats des expres

-sions suivantes :

•

(

x

,-

x2

Jf

x

,

.

- x

,)

+

{

Y:!

-

y

,

}

•

(

y

,-

Yz.)

p

-

4!

-r-

- -'-"---"

'

h

-

.

>.

.

,)h-

x

,J

,r

{

y

,

-

yJ{Y.•-

y,

)

y= -4ù (35)

Ceci peut être vérifié aussi pour le terme a en utilisant l'une des égalités de l'expression (33). On obtient ainsi tous les termes de

la matrice de l'élément triangulaire, qui correspondent à ceux obte-nus par la méthode conventionnelle et ceci en utilisant simplement les conditions suivantes :

- symétrie de la matrice ;

- mouvement de solide rigide ;

- un potentiel constant sur l'élément induit un flux nul ; - un gradient linéaire du potentiel induit un flux constant.

Dans ce qui suit, on présente une interprétation simple des élé

-ments de la matrice de l'élément triangulaire à trois nœuds en rela-tion avec sa géométrie.

3.4.

SIMPLE

INTERPRÉTA

liON

GÉOMÉTRIQUE

Considérons le triangle quelconque ( 1. 2. 3) de cotés a. b etc,

et de hauteurs cl. e et f, tel que montré par la figure 6. Les élément de la matrice de ce triangle peuvent être déduits en ne

considé-rant que les distances des nœuds aux cotés opposés ainsi que les

projections orthogonales de chaque coté du triangle sur les deux

autres.

rrenons l'exemple des éléments de la première ligne de la

matrice élémentaire (24). L'élément ( 1,2) caractérise l'influence du

nœud 1 sur le nœud 2. Il est déterminé par le module de la pr

o-jection orthogonale du coté opposé au nœud 2 sur celui opposé

au nœud 1. rapporté à la distance séparant le nœud 1 elu coté opposé: Figure 6 : E.lément trldnguldlre quelconque. Ordln;uy trl<tngulitr (36) ' - - - -- - - ' element.

L'élément ( 1,3) est alors déterminé par le module de la

pro-jection orthogonale du coté 1-2 sur le coté 2-3. rapporté à la hau-teur e :

(37)

L'élément

6

est obtenu en additionnant

ex

et

p

.

De la même

façon. les éléments des deux autres lignes sont déterminés. La

matrice de l'élément triangulaire aura la forme suivante :

b -b,- b:

2

'

ë

2e -2e

l

kl=

-c

,

c -~·l

2

J

2.1

2

7

- <li - il: u '2(1 2-d

1ti

(38)

E.n appliquant de simples relations entre les divers triangles for

-més par les cotés a. b etc ainsi que les hauteurs d, e et

f

de la

figure 6, on peut montrer que la matrice de l'expression (38) est symétrique.

En prenant l'exemple des éléments ( 1.2) et (2, 1 ), on peut

montrer qu'ils sont égaux en exprimant, d'une part. l'aire du tr i-angle ( 1. 2, 3) :

A = e.b

=

f.c (39)

avec

c = c, + c₂ (40)

et en écrivant, d'autre part, les relations déduites du théorème de

pythagore:

c2 _{= b~ + e}2

b2

=

c~ + !2

En remplaçant (41) dans (39}. on aboutit à l'égalité:

c,,- b,

]

-

e

(41)

(42)

et par conséquent. les éléments ( 1,2) et (2,1) de la matrice de

l'expression (38) sont identiques.

De la même façon, on peut vérifier la symétrie de la matrice pour les autres éléments.

De même on peut vérifier de façon relativement simple que les éléments de cette matrice correspondent bien à ceux de la matrice de l'expression ( 10}.

En prenant l'élément (1.2), il peut s'écrire:

- b, - - b,.b

-

-b

.

ç

Te

-

2 e.b

-

45

-

(43)

E.n calculant le produit scalaire des vecteurs!'$ et

2.

on aboutit

à l'expression de l'élément ( 1.2} de la matrice en ( 1 0).

4

.

CONCLUSION

Dans ce papier, la matrice • raideur • de l'élément triangulaire à • déformation constante » est construite en utilisant les cond

i-tions de symétrie et de • mouvement de solide rigide ». Cette méthode est très simple et présente divers avantages devant la

méthode conventionnelle en éléments finis. A partir de cette analyse, on peut tirer les conclusions suivantes:

- La matrice élémentaire peut être construite de façon très simple en calculant juste quelques éléments, les autres en seront déduits.

- En utilisant cette méthode. on est pas confronté à la condition de continuité des éléments et on ne fait aucune référence aux fonctions d'interpolation.

- La matrice de l'élément triangulaire à trois nœuds est unique: il n'y a pas d'autres matrices possibles pour cet élément.

- Les éléments de la matrice ont une signification simple en rapport avec la géométrie de l'élément triangulaire.

- Ces conclusions sont en accord avec le concept de MacNeal [9] concernant les limites de perfection d'un élément.

Notons également que cette méthode peut être utilisée pour construire les matrices d'autres éléments [10]. pour les pro-blèmes à potentiels. sans avoir recours à la procédure conven-tionnelle faisant intervenir les fonctions d'interpolation ainsi que diverses conditions liées à la définition de l'élément.

BIBLIOGRAPHIE

[ 1 1 P.G. BERGAN and L. HANSSEN. 1976 : • A new approach for

deri-ving "good" element stiffness matrices •. in The Mathematics of Fini te

Elements and AppliCéttions 11-MAFELAf' 1975. J. R. Whiteman (Ed.).

Academie Press. 483-497.

[2] P.G. BERGAN and M.K. NYGRAD. 1984 : • Finite elements with increased freedom in choosing shape functions ... lntem,ltion<JI

journal for Numerica/ Methods in Engineering. 20. 643-663.

[3] R. COURANT. 1942: • Variational methods for the solution of pro·

blems of equilibrlum and vibrations "• Trans. Amer. Math. Soc .. l-23. [4) K.K. GUPTA and J.L. MEEK. 1996: • A brief his tory of the biginning

of the fini te element method •. lntemational journal for Numeric.ll

Methods in Engineering. 39.3761-3774.

[5] M.J. TURNER. R.W. CLOUGH. H.C. MARTIN and L.T. TOPP: 1956. • Stiffness and deflection analysis of complex structures •.

f.

Aerotl<lut.

Sei., 25, 805-823.

[6] O.C. ZIENKIEWICZ and Y.K. CHEUNG. 1965: " Fini te elements in the

solution of field problems •. The Engineer. 220. 507-510.

[7] O.C. ZIENKIEWICZ and R.L. TAYLOR. 1989 : The Finite Element

Method. Vol. 1. McGraw Hill. Maidenhead.

(8) G. DHA TI &. G. TOUZOT. 1984 : Une Présentation de /a Métl1ode des Éléments Finis. Collection Université de Compiègne. Maloine S.A. Édi

-tion.

[9] R.H. MACNEAL. 1992 : • On the limits of finite element perfectilbi·

lity •. International joumal for Numerical Methods in Engineering. 8. 1589-1601.

( 10] P. Bf.TIESSand O. LAGHROUCHE. 1998: • Derivation ofrect,,nguiM

finite element for potential problems from consistency criteria -.