La propagation verticale des ondes planetaires /

c

c

C

-•

... 1 o _,

LA PROPAGATION VERTICALE DES

) ONDES PLANETAIRES

par

,

,

@

Daniel

Beau~laamp

•

.

,

...

...

, 1

'rhèse soumise a la "Facuity of Graduate Studies and"

Research" comme partie des exig~nces reqùises pour

A

l'obtent~on de la Maitrise en Sciences

"

Départ.ment de Météorologie ".

,-'

,

..

Universite McGUl

.r

Montréal Ç"

..

•

.1

..

-

...

f • ,.r-l ' Mai 1988

•

o

•

> ;;'.'::"'.)1

RESUME

., Avec un modèle numérique sur un plan b;ta on simule la propnglltion verticale d'une impulsion contenue dans les conditions )titiales d'un modlle

atmosPhériqUe. Différentes méthodes sont essayées

pcS~r

trouver une façon

efficace de suivre la propagation verticale de l'impulsion. Divers profils du vent zonal sont utilisés dans un modèle linéaire.

<>

Une coupe de l'énergie cinétique en altitude et le temps montre un

maximum d'énergie qui se propage du bas au sommet de l'atmosphère

à

la'

vitesse théorique du mode vertical le plus rapide. Une coupe de l' tntens 1 te

y

ondulatoire en altitude et le temps se comporte comme celle de l'énergie totale. Dans le cas où le vent zonal a un profil en forme de Jet, llflC:> bllls~C'"

de la vitesse de propagation verticale du maximUfll d'énergié est ob~E'rv(>f'

Dans le cas où le canal est élargi 1 une hausse de la vi tesse de

~prOP~B,~t

lolt

verticale du maximum

d'~nergie

est observée. \

,

t

(

(

(

ABSIRACT

1:"

'~e

vertical

pr~pagation

of a pulse of energy ls simulated by means of a IDa 'plane numerical atmospheric modeV Different ways are tried to find an efficient way of followlng the vertical propagation of the pulse. Different zonal wind profiles are used with a linear model.

A time-altitude cross section of klnetic energy shows a bottom to top vertical propagatiop of an energy maximum at the fastest vertical mode

.peed. The wave action is found to behave similarly to the total energy. When a jet zonal wind ls used, a decrease in the vertical component of the propagation speed ls observed. In the case where the channel width ls

Increased, an increase ln the bottom to top speed is observed.

-

.

1

,

.

,

•

•

•

R~ERÇIEMENTS

J' aimerais remercier grandement mon direc teur de mémoire. Q Dr. J aeque.

Dero~e. pour l'aide scientifique tout au long de l'accompli~8e~nt de cette

étude. J'aimerais, le remercier également de sa patience et de 80n

i •

encouragement. Les explications mathematiques de Sylvie Gravel ainsi que les

,

.

explications de Pierre Dionne et du Dr. Hersch Mitchell concernant le modele

numérique ont ete grandement appréciées: Egalement, je remercie Alan

....

Schwartz de m'avoir dépanné dans divers problèmes d'informatique. #

Finalement. je désire remercier le Département de Météorologie de

l'Université McGill pour son aide financière au cours de ma maltrise.

>,

'"

.

..

c

c

c'

aé.umé

Ab.tract Remerciements \

Table des matières Liste des figures

TABLE DES NATIERES

\

Liste des tableaux

CHAPITRE 1

INTRODUCTION

CHAPITRE

2

THEORIE DE

LA

eROPAGATION VERTICALE

2.1

• Introduction

2.2

Notion de vitesse de groupe u

2.3

Vitesse de groupe appliquée à l'atmosphère

2.4

Flux

d'Eliassen-Palm

2.5

Solution pour une at&osphère finie

2.6

Instabilité barocline

CHAPITRE

3

LE

MODELE

NUMERIQUE

3.1

Introduction

3.2

Le modèle

,

CHAPITRE 4

EXPERIENCES NpMERIQUES LINEAIRES

4.1

Introduction

4.2

Caractéristiques du modèle linéaire

4.3

Modèle à haute résolution

4.4~ _{Modèle à basse résolu71on}

iv , '1\ \ ,

\\

Page , > l

,

,

l i Ui iv vi lx 1 10 10 13 16 20 25 31

31

( 39 .f' 39 41 47

0

CHAPITRE 5

5.1

5.2

5.3 ~ 1'" .> CHAPITRE 6 APPENCICE A APPENDICE 8 APPENDICE C REFERENCES

o

o

..

(

CISAILLEMENT DANS LE VENT ZONAL Introduction

Cisaillement vertical:

ü -

f(z)

Cisaillement horizontal: ü - f(y)

SOMMAIRE ET CONCLUSIONS

LISTE DES SYMBOLES UTILISES

f

,

61 61 f 66 76 79

CALCUL DE LA VITESSE DE GROUPE VERTICALE DANS LE 81

CAS D'UN CISAILLEMENT MERIDIONAL DU VENT ZONAL

~,

DEFINITION DES TERMÉS MODE

DE

TRANSMISSION

NUMERO l ET 2

,

,

83 84

1

c

(

c

Liste des figures

Figure

l.la) Erreur moyenne, de la hauteur géopotentielle d'un

ensemble de previsions moyennees selon la formule de

l'écart-type

à

56oN, en fonctidh de la pression et du

temps. Les harmoniques zonales m - 1

à

20 ont été

in-cluses. L'intervalle entre les contours est 5 m. b) La

dérivée par rapp'ort au temps de a) en prenant des

dif-férences finies

à

l2-heures d'intervalle. Les unités

sont m/(12h) et l'intervalle entre les contours est 2

unités. (de Derome, 1981)

1.2

Diagramme montrant la séparation des ondes forcées qui

se propagent et celles qui sont bloquées pour le -. cas d'un forcage stationnaire avec un vent zonal constant

dan! l' espa~e et le t~~s. La courbe est le graphique

de u -

P/(K

+ f02/ 4H N ). (de Derome,

197~)

1.3

Pour l'explication' complète du graphique il faut se

{éférer

à

l~article de Shukla (198!). Le temps t _{i -peut}

etre observe en prenant le temps ou les courbes

"pers-istance error" et "error" se croisent. La figure' du

haut est pour les ondes planétaires et les calculs pour

les ondes synoptiques sont représ~ntés

â

la f,igure du

bas.

1.4 Décomposition en longueur d'onde et fréquence de la

variance des ondes transitoires du champ des hauteurs

géopotentielles ~ 500 mb le long de SaoN pour( 14

hivers. (de Shukla, 1981)

\.

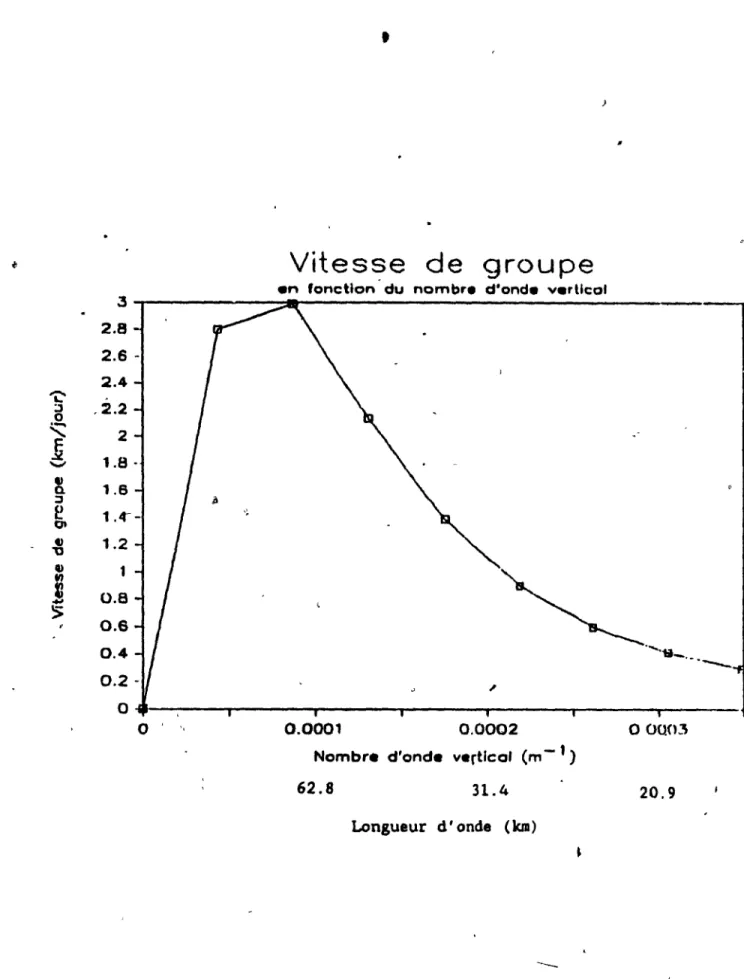
2.1

Vitesse de groupe verticale en km/jour en fonction du

\1 nombre d'onde vertical m (ou de la longueur d'onde)

selon l'équation (2.13) pour l'onde 1 en x et y.

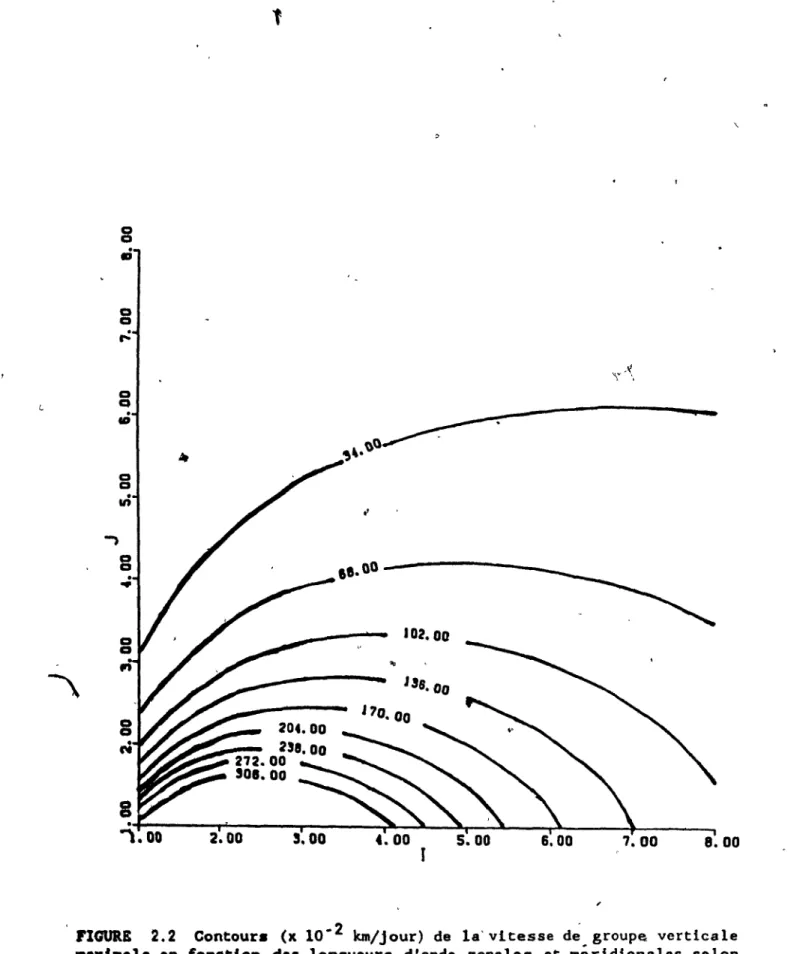
2.2.

Contours (x

10. 2

km/jour) de la vitesse de groupe ver-ticale maximale en fonction des longueurs d'onde zonale et méridionale selon l'équation (2.14). Les entiers i

et j (abscisse et ordonnée) satisfont aux relations k

-2d/L et 1 - lfj/D où L et D sont les dimensions du

"canal. 1 page 6 7 ~'8 9~ 28 29

2.3

•

4.1 , 4.2 4.3 4.5 . 4.6

.,

4.7

4.8

.'0

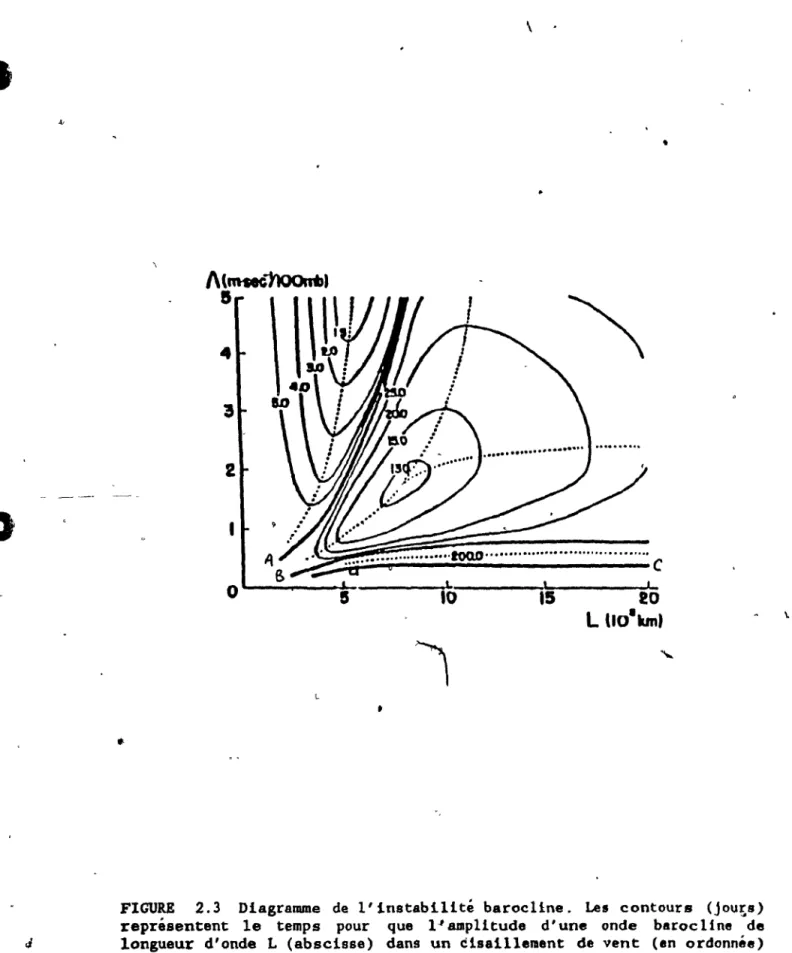
Diagramme de l'instabilité baroc1ine. Les contours

(jours) représentent le temps pour que l'amplitude

'd'une onde barocline de longueur d'onde L (abscisse) dans un cisaillement quelconque (en ordonnée) double. Les contours A,S et C indiquent un temps infini. Les lignes .pointil1ées indiquent les ondes et les cisaille-_{4 •} ments les plus instables. (de Hirota, 1968).

f

Contours (x 1016 joules) de l'énergie cinétique de

per-turbat±on~yennée sur la surface du canal pour le cas

linéaire avec un vent lia de 8 mis. L'amplitude de la 'montagne est HO ~ 500 m.

Qpntours (x 1017 joules) de l'énergie cinétique de per-turbâtion moyennée sur la surface du canal pour le cas linéaire avec un vent lia de 8 mis. L'amplitude de la

mont~gne est ~0~2~0 m. ~'ouvertu:e du canal est de 30.

degres au lieu de 60 degres comme a la Figure

4.1.

Contours (mis) du vent de la perturbation moyenné sur

la surface du canal pour le cas. HO 500m et ua - 8

mis.

Contours (oK) de la température de la perturbation

moyennée sur

la

surface du canal pour le cas HO - 500 m

et

ua -

8 mis.

Contours (x 10 2 mis)

moyennee sur y pour HO

de l'intensité ondulatoire

500 m et liO - 8 mis.

.

.

~

Diagrammes representant une coupe meridionale des flux d'E1iassen-Palm pour les jours 4.5, 9, 13.5 et 18 pour le cas d~ la Figure 4.1. Les valeurs maxima1e~ po~r 1.

composaote en

z

sont O. 73x10· l , 0.39, 0.'39xlO At

O.18xl02 m~/s2 respectivement. L'ordre des jours est de gauche a droite et de haut en bas.

t

Diagrammes representant une coupe méridionale de la

divergence des flux d'Eliassen·Palm pour les jours 4.5,

9, 13.5 et 18 pour le c~s de la Figur~ 4.1. Les vale~fs

des co~tours doivent etre mulfipliefs par O.lxIO

O.lxlO· , 0.lxlO·3 et O.lxlO· mis respectivement.

L'ordre des jours ~st de gauche

à

droite et de haut en bas.

Contours (x 0.1 kg/m2s) de l'intensité ondulatoire

multipliée par la densité moyennée sur ,y pour HO - 500

vU . 30 50 51

..

52 53 54 55 • 56

•

57

(

4.9

4,.10 4.11

5.1

~.2

5.3

(

5.4

5.5

5.6

5.7

c

fi ..

Comme a la Figure

4.1

sauf que

l'~ntervalle 6~

entre 1 •• niveaux verticaux du modèle numérique est de~ km.

-~

.

.

58

59

Comme a la Figure 4:1 S8\if que Az - 8 km.

Comme

à

la Figure 4:1 sauf que Az - 12-km.

Profil ,vertical du vent zonal satisfaisant l'équ~ti~~

(5

1

2) ou

ua -

8 rn/s, ul - 67 rn/s, 01 - 0.65847.5 'x 10

)60

~- 69 m- • et %0 - 60 km. (de Mitchell; 1962) 1

Conto~rs (x

1017

joules) de l'énergie cinétique de per-turbation moyennée sur la surface du canal pou~le cas, linéaire avec un vent

ua

de

15

rn/s. L'amplitu de

la

montagne est HO - 500 m.

\.l

Contours (x 1019 ,Joules)

d~' l'énerg:\.~

cinétique de per-turbation moyennee sur la surface du canal pour le ca~

linéaire avec un vent

ua

de 45 rn/s., L'amplitude de la montagne est HO - 500 m.

Contours

(x 1017

joules)

~e

l'énergie cinétique de per-turbation pour le cas 1ineaire avec un vent comme a la ./ Figure

5.1.

L'amplitude de la montagne est

HO - 500 m .

•

Contours (x

0.1

kg/m2s) de l'intensité ondulatoire

multipliée par la densité moyennée sur y pour HO - 500

m et un vent comme

à

la Figure 5.1. /

Contours (x

1016

joules) de l'énergie cinétique de per-turba~ion moyennée sur la slirface du canal avec un vent u - 12.6 sin(Jry/D). L'interaction entre le vent zonal et les ondes n'est pas permise. Il y a 1 mode en, x et 5 modes en y de permis. L'amplitude de la montagne est "0 - 500 m.

Diagrammes représentant une coupe méridionale des

flux

d'Eliassen-Palm pour les jours 4.5, 9, 13.5 et 18 pour le cas d~ la Figure 5.6. Les valeurs ma~imales pOUf la cOlllposaste en y sont O. 28xlOl, O.lsxlO , 0, 20xlO et 0.76xlO 1112/52 respectivement. Les valeur}

Jj1aximale~

pour La corpo/a~te en z sont 0.14, O.13xlO , 0.12xl0

et 0.38xlO m /s

respectlveme~t. L'ordre des jours est de gauche

à

droite et de haut en bas.

~ 70 71 72 73 74 ,.~

."",

--75

-•

,0

Q

,

o

Tableàu 4.1 ~ , " " ' • c

.

" ListN~lea\m

Vite •• e de

grOU~rtieal.

pour différente. re.01ut10n.

•

..

\

/

lx

..

Page 49

(

c

•

Cbapitre 1 Introduction ~

Dan. une étude parue en 1981, Derome examine les erreurs moyennes d'un en.emble de prévisions de 10 jours faites au Centre européen pour les previ-.ion. météorologiques

à

moyen termé par Hollingsworth et al. (1980) a l'aide d'un modèle- globa1. rl présente l'évolution temporelle des champs d"erreur et en part;.iculier une figure suscite

/) notre attention. Celle-ci

a ete reprodui te

à

la Figure 1.1. Derome mentionne l' intér;t qu'on peut porter a ce genre de diagramme qui peut donner de l'information sur le taux a

laquelle l'erreur d'une préviSion peut se propager verticalement. On voit a

"

la Figure l.lb une crete qui s' etend de p 250 mb

à

t - 13_{/ 4} j ours

à

1000 mb

à

t - 3 jours. suggérant la propagation de l'erreur vers le bas a uI)e vitesse moyenne d'environ 8 km/jour. Simi1airement on distingue une large

1\

erreur dont le maximum apparait au niveau du sommet

à

7 jours; celle-ci .emble ~pager rapidement vers le bas.

L'observation de la Figure l.lb nous amene a conclure que les ~rreurs

peuvent se propager verticalement. ~eux causes possibles d'erreur .Yltématique nous concernent principalement, soit: i) la présence d'un sommet rigide dans un modèle numérique et ii) une erreur de paramétrisation qans les éléments de surface (montagnes, sources de chaleUr).)

Des études (par exemple. Derome. 1979) montrent que la presence d' u~ .olllllet rigide introduit des réflections d'énergie. Une source d'erreur exilt. donc dans les prévisions numériques

à

cause de ces réflections et cellea-ci peuvent se propager comme il a ete observé

à

la Figure l.lb.

,.

L'avantage de conna1tre l'évolution dans le temps de l" erreur est la con-naia . . nce de la fiabilité des préVisions numériques

à

chaque altitude. Par ex.ap1e. l'erreur prendra un c'ertain temps (te) pour se ~ropager du sommet

<

•

/

•

o

•

au sol. On peut calculer ce temps analytiquement pour ulmOdèle lIn.alre sur

un plan (3 avec un vent zonal constant dans le temps et l'espace (voir Chapitre 2 pour la démonstration),

l'étude de Derome (198)), celui-ci

Pour le modè le globa l ment ionne

..

a une altitude d'environ 2'5 km et

dans

t ~

e

7.6 jours. Quand le modèle est non-linéaire te n'est pas calculable analytiquement et des expériences nWl\ériques sont necessai res pour conna i t re ce dernier. y.2,.

Les erreurs décrites par Derome sont 'celles d'un modele global et la vue d'un tel diagramme nous rend curieux d' obse rver la propagation vtJrt ica le

d'une erreur dans un modèle plus simple" Dans un modele de la sorte on pourrait perturber un état initialement

à

l'équilibre et regarder cette per-tUTbation évoluer J

~alement

dans le temps. Cette perturbation pourra i t

A

etre générée soit au salau soit au sommet déJ'llndant du type d'erreur que

.

l'on veut simuler. Clarke (1972) a résolu' numériquement, et assymptot iquemant le problème d'une perLurbation

à

la base d'une atmosphere simulee par un .podèle sur un -pun f3 La perturbation quasi-géostrophique etait declencheE! par une source de mouvement vertical

à

la base. nulle avant t - 0 et une valeur finie constante dans le temps apres t - O. Trois differents profils de vent zonal ont été utilisés dont l'un d'e~tait un vent

ü

indépendant de l'espace et du temps.

Plusieurs auteurs se sont intéressés a la propagation ~ertica1e des ondes planétaires. L'interet

.

. " a ",ymrunence , quand on a tente d'expliquer la circulation stratosphérique hivernale de 1 'hémisphère nord.

Pendant l'hiver, dans la stratosphère, des analyses' (Boville 1961) on-t

c _

montre que des ondes planétaires d'amplitudes significatives sont

A .

persistantes et etaient importantes pour la circulation stratospherique. I:Iirota ~968) a observé que la phase de ces ondes penchait vers l'ouest en

c

'.

'c

t()

c

p

,

altitude. Ceci suggérait qu'il y avait d~ la propagation d'énergie vers le haut (Eliassen and Palm 1961) et impliquait que l'énergie contenue dans ces ondes proviendrait de la troposphire. Egalement en 1968, Deland et Johnson ont trouvé que des ondes de cette échelle se propagen

r

verticalement toute l'année en dessous de 30 km d'altitude. Muench ~ (1968) et'Hirota (1968)

.

ont trouvé que pour l'hiver le

m~me

phénomène exisJt:it pour une altitude de plus de 30 km.

'-Egalement l'étude de Hirota (1968) révélait .. que le vent zonal' principalement de l'ouest oscillait en amplitude avec une période de deux semaines et que parfois le vent zonal devenait de l'est. Une deuxi!ème observation importante corrélée avec l'oscillation du vent zonal était la baisse d'amplitude de ces ondes planétaires quand le vent zonal venait de l'est.

Charney et'brazin (1961) se sont Intéressés au phénomène de propagation verticale et ont démontré avec un modèle theorique simple que des ondes ,~ pouvaient se propager verticalement mais seulemen~ sl le vent zonal était de l'ouest et en dessous d'une valeur critique (Fig 1.2). Cette valeur critique dépend de la long,ueur d'onde et la Figure 1. 2 poùs montre que les ondes les plus longues vont se propager verticalement.

Avec le modèle simple de Charney et Drazin, Hirota et Sato (1969) ont donné une explication a

.

la corrélation entre la baisse soudâine de l'ampli-tude des ondes dans la" stratosphère quand le vent zonal venait de l'eat, De plus, ils présentent une figure montrant la prop~gation verticale de l'onde numéro 1 pOUD des analyses des hivers 1963

à

1967 entre 300 et 10 mb. Une estimation rapide de la vitesse de propagation est de 5 km/j our. Avant Hirota et Sato, l'évidence de la propagation verticale avai t déjà été aoullgnée par Muench (1965) pour l'hiver

~958.

Muench calcula

u~

vitesse de

3

a

•

•

propagation de 6 km/jour. Finalement Clarke (1972) voulut examiner plus en détails comment la propagation verticale était affectée sous différentes conditions de vents zonaux:

Avant de conclure ce' chapitre i l est important de' considérer la

précision à laquelle les modèles numériques opérationnels présents dl\tlS le

monde peuvent prédire un état future de l'atmosphère étant donné lIne

-certaine erreur dans l'état initial.

Si deux états physiques initiaux de l'atmosphère sont tres st'lIlblab lt>s, ceux-ci, dans une simulatiun numérique, vont être très différent:; npres Ulll' certaine période de temps t

i . La caractéristique dE" t l est qu'unp prpvlsloll météorologique quand t > Ci n'est pas meill~re qUl' cellf' obtl'!lue en utilisant la persistance. Si te > _{t i , la connaissa.nce' de la propagallon}

ver-ticale de l'erreur due au sommet rigide n'est pas d'une grande valeur.

Tiré d'un article de Shukla (1981) la Figure 1.3 montre que t

,.

_i varie

selo~ la longueur d'onde en question. Les ondes planétaires donnent un t

l plus grand que celui des ondes synoptiques. Ceci suggere que des modèles

.

numériques faisant des prévisions à moyen\ et a long terme pour des moyennes spatiales et temporelles, qui sont déterminées par les mouvemçnts des ondes planétaires (on peut le voir sur le périodogramme montré il la Figure 1.4), vont ~tre meilleures que la persistance sur une plus longue période que .les ondes synoptiques.

, , '

.1 _\

Dans ce.tt~ mese nous étudierons l'évolution d'une 1mpulsion generee a

, ,.1

la base d'un modèle simple sur un plan {J. Des montagnes serviront de source comme impulsion. Dans un modèle hydrostat1que Bur un plan ~, toute perturba-tion se décompose en série de Fourier dont. les composantes sont les amplitudes des ondes de Rossby. Les ondes planétaires en particulier nous

...

concernent car celles-ci risquent plus de se propager verticalement (Charney 4

-fonction du vent zonal et de la li:>ngueur d'onde. La courbe separe les ondes qui se propagent et celles qui sont bloquées par "ln vent approprié. Si le

modèle est linéaire on connut la théorie reliée

à

la propagation verticale et on la développe au Chapitre 2. Au Chapitre 4. le modèle sera linéaire. On con.ervera seulement l'onde numéro 1 et le vent zonal sera maintenu constant \

dan, l'espace et le temps. Des expériences numériques au Chapitre 5 seront effectuées dans le cas où le vent zonal a un cisaillement dans l'horizontale où la verticale. On tentera de déterminer par ces expériences numeriques l'influence de ces conditions plus réalistes sur la propagation verticale .

•

.

,

)

1

-o

SO~--~~~~~~~~~~~~~r.~.~_ 100 100

:100

(a, ~ lit

:tOO

_..

_lE 100 100 100 , , 1000 0 Z

,

.,

1 t 10 50 100 ( 200 100

-

AI

!400

'''Il00 Cb, lE ~ lit lit 100

'"

lE

..

_fOO 100

a

S 4 5 • 1 t T ... , CDAYIl

FIGURE 1.1 a) Erreur,moyenne de la hauteur géopotel1tiellp d'un .. nsemble

de prévisions moyennees selon la formule de l' éCllrt· type

a

56oN.. en fonction de la pression et du temps. Les harmoniques zonnles m - l

à

20 ont

été

incluses. L'intervalle entre les contours est 5 1ft b) La dérivé.

par rapport au temps de a) en prenant des diff~rences flnl~s

à

12·heur •• d'intervalle. Les unit~. sorlt 1'11/( 12h) et l'intervalle entre les contours

(

(

c

1

'D

l

1

J

o

Prop ••

atina

vava.

•

trapped v.ve. for strona we.terlle •

• nd/or .hort v.veleolth.

Trapp.d vav..

for

.11 vave1.nltil'

in

.a.tarIr vlnd.

,

rlCUllI 1.2

Dt.lr . . . .

IIOntr.nt la ,ép.ration des ondes forcées qui. se

,roPAIent . t c.U.. qui

.ont

bloqué.. pour le cas d'un foreage

sta-tlol\Mlre .vec un vent _zonal c~natan~ da!r. 21' espace et le temps. La

" , .>

l'

-0

, "

....

WAva NUM"" 0-4

•

,ft

..

,.

I.~~~~~~~~~,,~~~~,,~~~~"~~

__

~.~-h~~

.

• n

...

_b

WAVI HU"I!R '-11 tN

..

en

...

"

....

,...

.

...

1

,d~.+·,t-l-1'll'~{'

-~

fi I l

f

..

/

"

.

1 • • 1 • 1 1

,

•

..

l'

,.

I l H I&.I

FlOURE 1.3 l'our l' ."pUeation eOMplète du ,~aph. i l féut •• r.ferer

à

l'.rtlc1~ de Shukla

(1981).

Le

tempe tl

peut Itr. ob.ervé

en

prlnant

le

t . Ç I ou le. courbe. ·per.l.tene. errorl f _{et Iferror}lf _{le crollenc. La}

fllure du- haut I.t pour le~ ~nd~. 'planétaires . t 1.. calcuh pour 1 .. onde • • ynoptique • • ont rlpr ••• nte. a la fllure du b ...

c

c

~WAvau..1I ,,'~,--T·

__

~;·~wr-n~~~·

__

~~t~t~~'~'--.

1

₁ 1 1

---f

1 1 1 1 1 1 1 1 ____ -J \

nouu

1.4

Déco.position en lonaueur d'onde et f}équence de la

varianc. d •• ond •• transitoire. du champ de. hauteurs geopotentlelles a

500

ab

1. lona de SOoN pour 14 hiver.. (de Shukla, 1981)

o

Chapitre 2

Théorie de la propaiation verticale

2.

1 Introduction

Le phénomène qui n~us intéresse dans cette étude est la propagation ver· tieale des ondes de Rossby. Dans les chapt tres 4 et 5 des expériences numériques seront effectuées· pour étudier la propagation verticale dans diverses conditions. Une impulsion d'énergie sera introdui te dans ,le bas

d'une atmosphère initialement sans perturbations avec différents types de

"

vent zonal. Forcement, avec ces conditions initiales on assistera a une propagation de l'énergie vers le haut.

Quand l'énergie des perturbations est petite devant l'énergie du vent zonal, l'atmosphère peut ;tre traitée de façon linéaire et des solutions

~ " A

analytiques peuvent etre derlvees. De meme, la vitesse

à

laquelle l'énergie

"

se propage vers le haut peut etre calculée. "

Sous certaines conditions i l peut etre démontré que l'énergie voyage a

la vitesse de groupe. La prochaine section illustre cette idée. En premier

..

lieu, on définira la vitesse de groupe telle que connue dans la théor ie r ondulatoire. On imagine ensuite un système physique

à

une dimension dont la dynamique est décrite par une équation différentielle linéaire. De la, le

-

.

principe lineaire de superposition est appliqué pour déduire le déplacement de l'énergie

à

la vitesse de groupe.

_,

2.2

Notion de vitesse de

Iroupe

, ~,

(

(

cos(le z - 0 t) _{n n} (2.1)

"

)

,

et On est donne par la relation de dispersion

° -

f(le). Chaque composante se

;-1 t

déplace à la vitesse de phase Pn/kn . La theorle ondulatoire nous dit que si

l'on considère un paquet d'onde qui s'étale de le1 à k2 centré en kO'

ce1ui-ci ae déplace

à

la vitesse de groupe définie par:

,

(2.2)

r

L'étalement de leI et k2 doit satisfaire: k1 - k2

«

ka .

Dans (2.~ kO est

arbitraire et ainsi vg est une fonction dé k, Si vg ne dépend pas de k alors

le aystème est non-dispersif et la vitesse de groupe égale la vitesse de

phase.,

Il s'agit maintenarlt: d'illustrer que l'énergie se déplace a la vitesse

1

de groupe (2.2). Supposons un système physique dont sa dynamique est décrite

par

~ne

équation différentielle linéaire. Le principe de superposition

.' applique , c'est-à-dire,. que si deux harmoniques sont solutions de

l'équa-tion, ,alors toutes combinalso~s lln~~ ~e11es-ci sont aussi sOlutio~S

de l'equation. Si on a une infinite d' harmoniques alors la somme indiquee par (2.1.,) est solution de l'équation et (2.2) s'applique pour notre système phyaique. Trouvons maintenant l'énergie de la somme de deux harmoniques.

Soit deux harmoqiques avec 01' O2 , kl • k2 leurs fréquencelf et nombres

d'onde lati.faisant une relation de dispersion

° -

O(k).

0

.)

o

,.

Si·on addl~ionne les deux harmoniques:

.

"

l

,harmonique (l)+parmonlque (2) _{Auaod(z,t) ,o.(Om}t - 1).%) (2.3)

\

.

ou

_{o -}

_{m (?l} + °2)/2 iT

1<na-

(kl + _k2)/2 r (

,

l"

Aœ~d(z. t) - 2A cos(Omodt ~ ~odz) t,

°mod - (0 ₁ - °2)/2

\

kutod - _{(kl -} .lk_{2 ) /2}

"

"

L" équation (2.3) décrit une onde de fréquence (ùm de nombre

~

avec une

amplitude ~od qui varie dans l'espace et dans le temps. L'énergie d'une

onde est contenue dans son amplitude. L'amplitude modulée ~od se déplace a

la vitesse:

(2.4)

La vi tesse calculée en (2.4) es t la définition de la vi telle de group.. 5 i

nous développons 01' 02 autour de

ka

en .érie de Taylor:

j

.~ 4'

c

O(k 1) - O(km) + (kl~ km)

f:~J~+

~k2) - O(km) + (k2~ km) _{ak ~+}

\

..

En soustrayant 'Ine équation de l'autre et négligeant les termes d'ordre supérieur on obtient:

(2.5)

,..

\;.

(BO/ak) est la définition de la vitesse de groupa. On voit en examinant

-(2.4) et ,(2.5) qUA l'amplitude modulée et l'énergie de la somme de deux harmoniques se déplacent

à

la vitesse de groupe.

)

2.3 Vitesse de iroupe appliquée

à

l'atmosphère

(

Dans cette section la relation de dispersion w - w(k) pour une

atmosphère linéarisée dans un canal plan b~ta'" est dérivée et la vitesse de groupe v~rticale est calculée.

Soit les deux équations quasi- géostrophiques linéarisées du tourbillon

_,

et de la thermodynamique dans un canal plan b~ta:

iL

V2""

-

L

V 2 ."" +

~

, fo

a

_{(pow' )} (2.6) + u _{8y v}

- Po

az

Bt

8x B

(~')

+ 8

(~'J

-- 2

-

_v'

_au

+ ~ 'II' _{- 0 (2} ~7)

Bt

u 8x

az

_fo

Une liste des symboles, leurs significations et leurs valeurs numériques

(.'il Y a lieu) utilisés dans ce chapitre se trouvent

à

l'Appendice ~.

Si)ans (2.6) et (2.7) li est indépendant de y et z et si on élimine w'

c

d. (2.6) et (2.7) on obtient l'équation du tourbillon potentiel avec li 13

•

.

....

o

1

•

constant:

+

~

!Y!' _

0 8x (2.8)

Pour une atmosphère isotherme (N2.constant).

à

partir de cette équation on

peut calculer la vitesse de group~ d'une onde qui se propage dans l'espace

en supposant une solution de la forme:

.p' •

~(z) e z/2H i(kx+ly-6t) e ./ (2.9)

Si on remplace (2.9) dans (2.8) on obtient ~

l~

-

0 (2.10)

st

le facteur entre accolades est positif et inde pendant de z. on peut

trouver une relation de dispersion pour 0 et ainsi la vitesse d. groupe

verticale. Soit, 0 imz e (" (2.11)

."

.'

.

une onde qui se propage en z. En substituant dans (2.10) on trouve:

•

Ok

(2.12)

o - ük

L'équation (2.12) donne la relation de dispersion pour 1.. trois nOflbrel

(

donné.

par

(2.13)

A la Figure 2.1 on trouve un graghique de an/am en fonc tion du nombre d' onde

~ertlca1 m pour l'onde numéro 1 en x et y avec les valeurs des paramètres

à

l'Appendice A. En observant la figure . . trouve une valeur de m te l que la vite.le de groupe verticale est maximale. Cette valeur de m correspond a une

longueur d'onde d'enviro~ 70 km.

Il est important pour les expériences numériques qui suivront dans les

prochains chapitres de calculer le maximum de an/am par rapport

à

m. Alors,

..

\

f 2

1/

0.6495

-lL

2 tJk N2 (k2+12)

f2

3/

--L

2 + 4H2N2 (2.14)

A la ~lgure 2.2 nous presentons un graphique de (80/am)max en fonction des

.

nombrea d'onde k et 1. On observe un maximum pour les longueurs d'onde les

plu. lo~gues. On s'aperçoit qu~ (80/am)max est très sensible

à

la variation

~-de la longueur d'on~-de en

y

pour i.t

<

4 tel que k- 2xi/L et l-nj/D.

Y.leurs nwpériQue,

A

On auppo~e un canal beta d'une largeur de soixante degrés de latitude a

•

o

o

., 1 onde # 1 en'x

(:~)max

3.3

-A

onde # 1 en y jour onde ..# 1 en x (::Jmax -km onde # 2 en y 0.98 jour " _négatif

Le facteur entre acco14deS dans (2.10) peut etre En ces

circonstances, les ondes ne se propagent pas. Pour une valeur donnée de k et

l, en posant Q - 0 (onde stationnaire) le facteur entre accolades en (2.10) devient nu~ pour une certaine valeur de

ü.

Cette valeur Ü_{c qui délimite les}

•

ondes qui se propagent des ondes bloquées a une valeur .de 21.7 mIs pour l'onde numéro 1 en x et

y.

On appellera Ü_{c le vent zonal critique.}

2.4 Fkux d'Eliassen-Palm

Pour pouvoir étudier la propagation verticale des ondes de Rossby i l

faut introduire les variables qui s~ront, n~cessaires pour suivre une

impulsion.

L~

utilisées seront l'énergie

•

Si on multiplie les équations (2.6) et

et "wave activity" .

(2 7) par

_'Po""

et

(f02pO/N2)a~'/az

respectivement, additionne et intègre sur le domaine entre

Zl et

%2

et en tenant compte que v' est nul aux limites nord et ~ud du canal on obtient l'équation d'énergie:

d

I11t-

l f2

(a')

2]

...--

-

Vt/I'P+ -

0

!!l!

p dv

dt 2 2

2

&z 0

V

N

v

J

.;. _(2.15)

où A est la surface du canal. L'énergie totale de la perturbation varie dan. le temps selon une conversion d'énergie potentielle disponible du vent zonal (premier terme du membre de droite de (2.15» plus la convergence du flux

(

(

(

d'énergie dAns le vo lUlDe. Dans l'express ion (2.15) fOw'.,p'

Po

représente le flux vertical d'énergie.

Le deuxième terme du membre de droite de (2.15 ) indique la propagation

.x-verticale d'énergie. Si le premier terme de (2.15) est nul àlors l'énergie variera dans le temps selon la propagation verticale d'énergie et elle nous permettra de suivre la propagation d'une impulsion. Ceci sera le cas quand

8ü/8z - 0, un vent zonal constant par rapport à z.

Pour aü/8z ~ 0, l'énergie totale n'est pas une variable utile pour notre problème de propagation car il y a des sources d'énergie à cause du premier terme de (2.15).

Bien que l'énergie ne soit pas la variable idéale à observer pour la propagation verticale d'onde de Rossby quand aü/8z ~ O. i l Y a une àutre quantité qui pourrait être intéressante pour suivre une impulsion dans les cas linéaires:

Pour introduire cette quantité. intensité ondulatoire (de l'anglais "wave activity") , 11 nous faut d'abord introduire les flux d' Eliassen-Palm. Dans ce qui sui t un résumé décrira ces flux. _,

Le flux d'Ellassen-Palm est une quantité diagnostique très, utile dans

"

les

~des

de propagation verticale et d'interaction vent zonal-perturba-tions. Une théorie en détails avec exemples se trouve dans l'article Edmon et al. (1980). Cet article nous communique que tracer sur graphique les flux d'E1iassen-Palm par des flèches et la divergence des flux par des contours (sections E.P.) fait ressortir les principales ondes transitoires de flux de chaleur, de quantité de mouvement et de tourbillon potentiel sur un diagramme. En outre, les sections E.P montrent la propagation verticale et méridionale des ondes planétaires et leurs effets sur le vent zonal.

EUassen et Palm (1961) ont présenté un théorème pour un ü quelconque.

o

•

Le théorème s'exprime par une quantité vectorielle .,. dont l u composantes sont dans le plan méridional:

ou F - - v'u' (y) f

_o

v'" /

80

-8p

\

} flux nordiques de quantitê de mouvement et de chaleur.

ou en coordonnées logarithmique de pression:

~'~'

8x 8z

Le théorème ci te que la divergence de

F:

ou 8F(y)

V.F -

8y +

+~

_8p 1

a

Po

8z (2.16) (2.18) (2.19) (2.20)

est nulle pour des perturbations inviscldes et adlabatiques et qui

ma~ntiennent leur amplitude constante.

F

peut ~tre vu égalemènt comme une mesure du taux net de transfert d'intensité ondulatoire d'une coordonnée (y,z)

à

une autre. Cette idée est justifiée car

f

a l ' apparence d'un flux dans une relati,\n de conservation pour des cas linéaires, conservatifs avec un vent zona;! constant dans le temps. La "relation de conservation est:

(

(

c

BA :t + V.I'"-O

Bt

où A .'appelle l'intensité ondulatoire. Mathématiquement:

(2.21)

(2.22)

On peut démontrer (2.21) en prenant l'équation linéarisée du tourbillon

•

potentiel avec ü non constant:

aa'

-

Ba'

~

+

u ~ + v'

Bt Bx - 0 .

Multipliant par q' et en prenant la moyenne zonale on t~ouve:

l aq,2

~ Bt + v'q'

!9.

By

- 0

mais comme U est fac"Ue de montrer que

..

V.F

v'q'

(2.23)

(2.24)

on a (2.21). Dans les cas

Où

Bü/ 8z ,. 0, A,

f

et V.F seront des quantités

qui nous informeront sur la propagation verticale de l'onde. Dans le cas où

ü .at une constante la composante verticale de

f

est proportionnelle au flux

vertical d'énergie. Selon (2.15) le flux d'énergie vertical est:

F· _energie - POfO w'

t/J'

z (2.25)

51 on multiplie (2.7) par

t/J',

en utilisant

B/Bt -

-cB/8x et en prenant la

moyenne zonal~ on obtient une expression pour w'~' moyenné zonalement. Pour

19

•

J

•

1

une onde stationnaire (c-O) en remplaçant cette expression dans (2.25) on trouve:

ü

P.i..:

~

8x 8z (2.26)

Pour une.onde stationnaire (c - 0) le facteur entre le flux d'Eliassen-Palm et le flux d'énergie est le vent ~onal Ü.

1

2.5 Solution pour une atmosphère finie

Au Chapitre 4, la première expérience numérique sera linéaire et

effectuée avec un vent zonA constant dans l'espace et dans le temps. Le modèle numérique a un sommet rigide à une certaine hauteur (lit). Il est possible de calculer analytiquement la solution de ce problème et elle sera

très utile afin de comprendre les résultats numériques qui viendront

ultérieurement.

Soit une atmosphère décrite par les équations linéaires (2.6) et (2.7) avec les conditions frontières suivantes:

w (z - Ht ) 0 (2.27)

w (z - 0 )

_Wo

sin kx sin ly (2.28)

où Ht est le sommet de l'atmosphère,et en tout temps:

,-N

2 constanti'

....

Ü constante

Avant t - 0, ~'(x,y,z) - 0 et seulement le vent zonal réside. A t - 0 et en tout temps ultérieur on force le bas de ~atmosphère

_,

selon (2.28).

Si on élimine la variable w' des équations (2. 6) et (2.7) on obtient

l'équation (2.8). En se servant. de l'équation (2.7) les conditions

frontières deviennent:

(

c

-l' ~' _{- 0} à

z -

Ht 3z (2.29)

[1..

_3t + • _u

a~ (~')

_a

_az

N wOsin kx 2 sin ly à

z -

0

La .olution du problème sera de la forme:

1/1' - !/J' libre + 1/1' forcé (2.30) 1/1' libre est la solution homogène du problème décrit par (2.8) et la partie homogène de (2.29), i.e, sans le second de membre de (2.29). ""forcé est la solution de (2.8) et (2.29) avec le second membre (forçage) inclu Le forçage ne dépend pas du temps alors !/J'forcé sera indépendant du temps.

Avant de résoudre (2.8) et (2.29), changeons de variable en fàisant la

transformation:

\

alors, (2.8) devient: (2.31) a Z - H t (2.32)

.

-

-

-.a z - 0 Solut~on de

W'

libre

Soit tlibre - (assin yz + accos yz) sin

Iy

ei(kx-Ot) (2.33)

..

S1 on substitue

(2.33)

dans

(2.31)

on obtient la relation:

1

j

•

o -

Ük - ₂

k

2

+ 1 2

+

:~

[l

+

4~21

frontières nous devons

.atis~r.

Pour les conditions

a~ 1 ~

- 0 z - 0 et H_t

a;-

+ 2H + a ~

(2.34)

En substituant (2.33) dans (2.34) on obtient:

1 ,

z - 0

a s - - 2yH ac a

(2.35)

et ( 4y2 H2 + 1 ) tan yH_t ... 0 :..-<2.36)

ce qui donne comme solution: ' ,

2 _l_ i

_(2.37)

Y

..

_{Y -}

±

2H

4H2

)

ou bien yH_{t -} mn ;m 0,1,2, ...

(2.38)

(

'"

•

Apres quelques manipulations mathématiques la soluti9n correspondant a

".ç. (2.37) est:

- z/2H i

1

i(kx - Dt)

+libre - b e s n

y

e (2.39) avec

et celle correspondant a (2.38) est:

(

(

c

t _{l1bre -} as [ sin

(mg

_H

)

.-

2H mJf cos ( ~

JJ

_{sin. ly} e i(kx - 0 t) m

t _\t H Ht (2.40) 0

-

ük

~k

f2

III [ 2 2 1 ]

k

2+ 1

2

+ 0 _m H1C2 + 4H2

N

2

t avec

et la 8olution l~:_~énéraie est la somme de (2.39) et (2.40):

00

[

m-l

~

_ {b -z/2H i(kx-Ort)+

Ylibre e e am [sin~ mJfZ - 2m~ cos~ H

m'ltz]

e i(kX-Omt.)}

• t t t avec

...

et

o

_r sin Iy

0m donr

é

par (2.40), b, am etant des amplitudes complexes.

Solution forcée

/

La solution forcée sera indépend"nte du temps puisque la· source qui

donne de l'énergie au systeme l'est également. On suppose une solution de la forme:

tr-

(a sin 6z + b cos 6z) cos kx sin ly _(2.41)

En substituant (2.41) dans (2.32) on obtient les valeurs pour a et b. et en remp1acant (2.41) dans (2.31) on trouve que:

(2.42)

•

o

•

e -z/2H 26H [( ) , 2 2 26h tan6H t - l sin 6z f

_o

ük6 tan(6H_t) (46 H + 1) (2.43)

J

+ (tan

6H

t +

26H)COS 6:]

cos kx sin ly

"-La solution générale est la somme,de (2.43), (2.39) et (2.40). A l'aide de

la condition initiale

I/J' -

0 i l est possible de trouver les valeurs des

r

constantes b et am dans (2.39) et (2.40) et la solution générale est:

avec:

et:

t(x,y,z,t) -

~O[(26H

tan

6H

_t -

1)sin 6z

+

(tan 6H

t +

26H)COS 6Z]

.cos kx sin 1y + A GO(z)cos(kx - 0rt) sin 1y +

•

L

m-l

B .

G. (z) cos (kx - 0rnt)

sin

1y

m m

o -

_r

ùk

(2.44)

iJk

0m - ük - k 2 2 1

/

m 1r + -H2 '4H2 t

c

(

c

~O[(268

tan 68t -1) J;t. 1n 6z GO(z) dz + (tan 68t ,268)

f:~os

6ZG_O(Z)dz]

J:t

G

_o

2(Z) dz et le. coefficients Bn sont donnés par

B -

_n

~O[(268

tan 68t -1) J:t.1n 6z Gn(z) dz + (tan 68t +268)

r:~os

6ZGn (Z)dz]

f

itt G 2(z) dz

o

n

A

Il est intéressant de .. connaitre le comportement de la solution quand t -+ O.

Quand t .... 0 :

cos(kct) ~ 1 - 0.5 (kct)2 (2.45)

sin(kct) ~ kct

En gardant les termes d'ordre l et kct, et en se souvenant que. - 0 a t - 0

on obtient que: CIO

\"-BG

(z)

L ....

mm

m-l

sin ly sin kx 0 t m (2.46)

Donc, quand t .st petit, • est proportionn~l in kx et son amplitude

augmente linéairement avec le temps

à

tous les ni eaux.

2.6 Instabilité barocline

La

solution (2.44) contient des ondes libres. qui voyagent aux vitesses

de

phase cr et cm données par 0r/k et 0m/k respectivement. Dans le cas

par-ticulier où le vent zonal est indépendant de z, cr et cm sont réels~ Quand

la baroclinicité est introduite dans le modèle (

au /

8z ~ 0 ). cr et cm

peuvent avoir une partie imaginaire et réelle dépendant du profil du vent ü.

•

...;,

•

On peut écrire eik(x-cmt) comme eCi t eik(x-créel t ) avec c

_m

- c . _ree l + lc _i' 51

-/

ci est positif l'onde voyageant

à

la vitesse de phase créel .'accroltra en

amplitude dans le temps dépendant de la grandeur de ci' nans ce cas, on dit que l'onde barocline est instable.

Une onde barocline peut donc ~tre instable sous certaina profils de vent

et si l'instabilité devient grande. l'effet de propagation verticale des ondes de Rossby peut être masqué. Dans le prochain paragraphe. les résultats

d'une analY,se numérique pour l'instabilité barocline (Hirota, 1968) sera

présentée. t

...

" ~ l'

Soit -les équatiohs (2.6) et (2.7) en coordonnées de pre.sion. Si on prend o-constante et si on suppose une solution de la forme:

~' ~(p) eik(x - ct)

(2.47)

w' _ W(P\ eik(x - ct)

En substituant dans la version de (2.6) et !2.7) en coordonnées de presaicn et en él'minant W(p) de' deux équations on obtient:

d2• [1 d2

û

c-ù+({J/k2) ok2

1

t - 0 (2.48) + -f 2 2 - 2 dp c-u dp c-u ₀

ou en changeant de coordonnée p* - p/po· alors (2.48) devient:

c-ù+~P/k2)

c-u

2 2

Ok~]

. 2 • - 0

fo

(2.49)

En rempla~nt la condition frontière W(p) - 0 •

P. -

0 et l dana l'équation (2.7) en coordonnées p*. on obtient:

c

c·

(

,.

"

_\

(2.50)

Hirota (1968) a solutionné (2.49) et (2.50) numériquement pour du/dp* -conatante

<

0 et a trouvé la partie complexe de c pour identifier

à

que~

A

taux une onde (le, c) va croltre dans le temps. Les résultats sont montrés

à

la Figure 2.3. On remarque qu'il n'y fIL pas de combinaisons

cisaillement-longueur d'onde pour lequel une' onde serait stable. Par contre les lignes pleines indiquent des ondes neutres. Egalement, l'accroissement d'une onde .st beaucoup plus rapide pour ,des valeurs de longueur d'onde en bas de 7xl0 3

laD.

( _,

-)

1 ,}

,.

,-27

,

.•

,

0

o

,

•

Vitesse

de

groupe

en fonction' du nombre d'onde vertical

3

l

2.8 2.6 -2.4 'L:' :J .2.2

,S!.

"

2

~

_1.a·

--

_&

_1.6 :::1 _a

e

1 . ...-- " CIl II) _1.2

"

II)

j

_o.a

>

_0.6 0.4 ... 'Y

-"'--0.2 -

,

0 0 0.0001 0.0002 00U03

Nombre d'onde vertlcol (m-1 )

62.8

31.4

20.9

Longueur d' onde (km)

FIGURE 2.1 Vites.e de groupe verticale en lem/jour en fonc.tion du

1\OIIQre d'onde vertical a (ou de la longueur d' onde) .elon l'equation

-(

o o

,.:

a Q

.

cg a a

.

ln

l

20 •• 00 238,00 ',-. .-",- 272. 00 301.00 2.00 3.00 5 E4 .' 102. Da J!B.OO C.OO

,

5.00 6.00 7.00 8.00 "

FIGURE 2.2 Contours (x

10.

2 km/jour) de la' vitesse de groupe verticale

. . . t.al. en fonction

de.

longueurs d'onde zonales et méridionales selon

l'équation

(2.14).

Les·.ntlers 1 et

J

(abscisse et ordonnée) satisfont

aux relation. k - 2wrl/L et l - 1Ij/D où L et D s . les dimensions du

canal.

-.

o

\

•

0

₅

₁₀

L

₁₅

\

₂₀

1

L

(lo'km,

î

"

•

FIGURE 2.3 Diagramme de l'instabilité barocl1ne. Les contours (jours) représentent le temps pour que Pampl1tude d'une onde barocUne "'de longueur d'onde L (abscisse) dans un ébaillelllent de vent (en ordonnée) double. Les contours A,B et C indiquent un temps infinf. Les ligne. pointillées indiquent les ondes et l u cisaillements les plus ln.tables.

(de Hlrota, 1968).

c

(

c

Chapitre ~ Le modèle numérique 3. 1 lntroduction

Tous les calculs théoriques présentés au chapitre 2 st appliquent pour

de. cas où le modèle est linéaire avec un vent zonal indépendant de y et z. Evidemment, l'atmosphère ne se comporte pas d'une manière aussi simple et de. expériences numériques sont nécessaires pour ajouter plus de réalisme

à

notre modèle atmosphérique.

Pour poursuivre notre étude de la propagation verticale des ondes de Rossby, le modèle numérique de Mitchell (1982) sera utilisé. Mitchell (M82)

décrit en détail son modèle et un résumé sera donné dans les paragraphes qui luivent.

3.2 Le mod;lo

Dans le modèle, on suppose que l',atmosphère est confinée dans un canal "

lur un plan beta avec deux murs rigides aux frontières nord et sud du canal. "

Le modèle est assez simple pour ne pas etre tro.p couteux en temps de calcul. ,.

Le modèle beta est souvent utilisé au-delà des approximations qui le rend

nrictement valide (e.g Garcia and Geisler, 1974; Geisler and Dickinson, 1975; Klrkwood and Derome,1977) parce que malgré sa simplicité les résultats

lont généralement bons qualitativ~ment. Donc, le modèle nous .permettra

d'observer la propagation verticale dans des conditions atmosphériques

,uffisamment réalistes.

Le modèle, résout l'équation quasi-géostrophique du tourbillon "-et celle de

1.

thermodynamique (tiré de K82; . equattons 3.18 et 03.19):

o

. :t

V21/1 + J (1/1, V21/t+f) - fOC) : : (3.1)

:t(~)

+ J

(~,~)

- h

[!!l!' -

_ôq

(~')

_ôq

*]

_, (3.2) /

~ ~

H1n(ps/p)

tl

~

- dp p

J(A,B), -

:~

aB

_ôy

aB

_ÔX ôA _ôy

Les variables utilisées sont: q

z

:la coordonnée logarithmique de pression

0 stabilité

.

fO le parametre d~ Coriolis

..

1/1 la fonction de courant

La lettre "q" est généralement utilisée pour le tourbillon potentiel mais sn signification sera claire selon le contexte.

L'astérisque qu'on voit sur le membre de droite des deux équations

indique une fonction spécifiée extérieurement. Dans (3.1) le m~mbre de

droite repJ::ésente la manière dont le courant zonal est forcé. Ce terme sera

omis dans cette thèse. Le membre de droite en (3 2) est un terme de

refroidissement Newtonien qui fait tendre la perturbation de tempe rature

*

vers la valeur T .

La condition

w -

0 est imposée au ~t du modèle co~e dans la plupart

des modèles numériques, celle-ci donnant lieu a des réflections d'énergie.

L" auteur de H82 ut!1iu la méthode spectrale pour résoudre l.s é q u a t i o n s ) (3.1) et (3.2). Cette methode consiste en la separation des variables

c

(

c

..

série de fonctions de' base Fn<x,y) avec leurs amplitudes spectrales corre.pondantes. Mathématiquement,

•

1/ftx,

y, t) -

L

An

<

t) n-l F (x,y) n (3.3)

Lei fonctions de base sont choisies selon la géométrie et les conditions frontières du problème étudié. Dans notre modèle numérique:

sin(2~)sin(~)

3, ... }

(2

nrnx) . (!!!Y)

, 2 cos --L- Sln D

m , n - l, 2,

ou L, D sont les d!mensions du canal en x et y respectivement. ~

Le modèle divise l'atmosphère en un nombre de niveaux

vertica_u~~,jr

la dépendance en z de (3.1) et....(3.2), i.e, '

)

•

",k(x,y,t) -

L

A~(t)

Fn(x,y)

n-1

i .

L'information de '" est contenue dans-- les amplitudes spectrales (3.4)

Ak (t) n

.

"

.

et

comme

(3.1) et (3.2) determinent l'evolution dans le temps de ~, alors (3.1 et (3.2) d:éterminent l'évolution des Ak (t).

n

Les fonctions Fn(x,y) satisfont ces propriétés:

1

,

••

r

..

o

•

i) (Dy-O,D - - xy . { l si i - j li). Fi Fj _{- 6 ij -} 0 si i ,.. j ( Hi)

où -(--) xy est l'opérateur qui fait une moyenne

horizontale, i.e, ) xy _

L

JD JL ( )

dx dy LD 0 0 2 ,,1" -_i , 2 .

ou ai est

le

carre du nombre d'onde horizontal.

(3.7)

En rempla~nt

l/J

dans (3.1) et (3.2) par (3.4). utilisant les propriétés

....

(3.5)

à

(3.7), on applique une méthode de Galerkin. Pour un modltle

à

3

niveaux, il résulte pour un r arbitraire:

A • F - G ou \ 2

f

~ (1) (2)

o

0 Q - a -_r

0(2)(Aq)2

2 . a -r

o

- a •

2

r "

o

f

_0°

2 (3) (4) _Q 0(4) (âq)2 f₀₀ 2 (4) (5) _a 0(4) (âq) 2

c

(

_OU" "-ü

-,

""-3",(1) _ r _ at 3",(3) F - _r_ _at et G -3",(5) L -at

,

G (3)_ r [ (3) (3) 2 "'1 "'j • a j Crij - (3 i,j f

_o

2 a (3) (4) 0

L

,/. (5) '" (3) ""i j crij a(4) (4q)2 i, j

b

_ri

-G (1) r G (3) r G' (5) r

L '"

₁ (3)b . _rl i f

o

2 IX (3) (2) a o(2)(4q)2 (3.9) +

\"' ,[(3),1.<

1)

L""i

"'j crij i,j

(3.10)

Gr(l)

et

Gr(S)

n'ont

~as

été spécifiés mais peuvent ;tre trouves dans M82., Des deux définitions de bri et Crij et des conditions frontières du

canal b;ta, les relations suivantes de symmétrie peuvent

~tre

démontrées:

b _ . b

ir ri

Soyrcts tt puits d'intraie

)

la friction (pompage d' Eckman,

--~-o

refroidissement Newtonien) n'est pas incluse. alors il devrait

_..

y avoir

"

conservation de l'énergie du système vent zonal-ondes puisque le role de la topographie est seulement de trénsformer l'énergie du vent zonal en energie ondulatoire ou vice-versa.

On remarque que (3.4) est une somme infinie et ceci ne se réalise pas

# ... A ,

numeriquement. Le systeme devra donc etre tronque:

N

k

I/J (x~y, t) -

[

(3.11)

n-l

M;me si le système est tronqué l'énergie totale est conservee a condition

de ne pas inclure les termes de friction. Pour voir ceci. examinons les

différents termes de l'équation (3.10). La troncature risque seulement

•

d'affecter les échanges

é:~ges

d'énergie sont

coeff! ients d'interaction Crij' d'énergie

\

dus aux

entre les différentes

termes non-linéaires

échelles Ces

contenant les

ur comprendre le processus d'échange d'énergie entre échelles

diffe-re et pour plus de simplicité r~tre modele

barotrope. L'~quation (3.9) devient·

G r

L

i,j {J

L

1/J_i

.i

(3. 12)

Pour un modèle barotrope l'énergie du systeme est de type C ijtique

c

.C

c

/

comme: 1

---"2

xy E - , l i

IA",I

-cin L. 1

2

(3.13)

L'énergie de chaque mode est donc a / l/Ir 2 . En multipliant (3.12) par I/J_{r on}

trouve l'évolution de l'énergie de chaque mode r:

'"

d E d

(a

2

r

".2r )

dt

r - dt '1'

(3.14)

Le terme non-linéaire contenant Crij nous informe que deux modes ij vont

interagir ensemble pour modifier le mode r. Dans une interaction, 3 modes

sont impliqués: le trio rij. Plusieurs ~rios rij sont contenus dans (3.14), mais si nous portons attention sur la contribution d'un seul trio:

t

Symmétriquement, des relations similaires peuvent etre écri tes pour les modes i et j:

donc,

o

(3.15)

L'équation (3.15) npus dit que le transfert d'énergie entre chaque trio est l

•

•

conserve. Ceci implique que les systèmes tronqués conservent l'énergie, Ceci se voit en notant que si l'on choisit un trio dont un des membres se trouve

~

en dehors de la série tronquée, alors l'amplitude de celui-ci est nulle.

Puisque les termes dans (3.15) sont proportionnels aux trol~ amplitudes du

trio, ceux-ci vont s'annuler. L'énergie est donc conservée pour ces trios aussi.

Linéarité du modèle

Notre première expérience numérique sera de reproduire ce qui a été

calculé analytiquement dans la dernière partie du chapitre 2 comme référence

,

pour les expériences numériques plus réalistes. Pour ce faire, on tronque le modèle de fayon

à

conserver seulement une onde en x et une onde en y:

v--( 27rx

~ - - uoy + A sin L + B cos L 27rx ) sin

0

1fV (3.16)

En tronquant la sé'rie qui représente ~ ainsi, le modèle devient linéaire. Il est a noter que le premier terme

à

droite de l'équation n'a pas

été

considéré dans la description du modèle mais si on consulte la thèse de Mitchell (1982)

à

l'appendice F, on voit comment incorporer ce terme .

c

c

Chapitre 4

Expériences numérigues linéaires

4.1 Introduction

Le

but des expériences numériques dans ce chapitre est de vérifier si le

modèle n~érique vérifie bien la théorie développée au chapitre 2 Elles

nous serviront ensuite comme référence au Chapitre 5 quand d'autres effets

seront ajoutés au modèle pour observer les cha~gements sur la propagation

De plus, on se familiarisera avec les manières de représenter les quantites (énergie, intensité ondulatoire, flux d'Eliassen et Palm) de facon a pouvoir observer le plus possible la propagation verticale d'une impulsion.

Le chapitre sera divisé en 4 sections. l'introduction, les

caractér-istiques du modèle linéaire, le modèle

à

haute résolution et

à

basse

résolu-tion. Nous avons choisi notre modèle numérique afin qu'il contienne 36

niveaux verticaux

à

intervalles de 2

km.

Ceci constituera le modèle

à

haute

résolution verticale. Dans la section modèle

à

basse résolution, tout en

gardant le sommet du modèle

à

72 km, on diminuera le ffombre de niveaux

ver-ticaux pour voir l'effet de la résolution verticale sur la propagation.

4.2 CaractéristiQues du modèle linéaire

Les caractéristiques du modèle s'accorderont

,

avec les calculs

analytiques au Chapitre 2.

Le canal est centré sur 600N et a 60 degrés de largeur. On rend le

modèle linéaire en tronquant la série (3.4) pour garder l'onde l en x ~t y

de fa con que ~ satisfasse l'égalité (3.16):

• - • üoY

+ + B cos 21rX

•

o

o

1

•

uo est le vent zonal et on choisit la valeur 8 mIs. On gardera le vent zonal constant dans ,le temps et dans l'espace. Par consequent on ne permet

-pas a l'onde d'influencer le vent zonal. Vu que le vent zonal est constant dans le temps et que l'énergie de' l'onde 1 augmente, l'énergie totale du

systeme vent zonal-ondes n'est pas conservée. ~n veut observer la

propaga-,

tion, donc on veut l'isoler le plus possible et on élimine les facteurs qui peuvent la masquer. De plus, comme Üo demeure constant dans le temps les

re-.

lations developpées au Chapitre 2 s'appliquent car elles exigent cette con-dition du vent zonal.

Le modèle est hydrostatique, donc

pg (4.2)

La constance de ua en z implique, par la relation du vent thermique, que la

température de l'état de base ne dépend pas de y. On a choisi que TOb'ase ne

•

varie pas en z de façon

à

satisfaire les calculs faits~ la derniere

partie du Chapitre 2. De cet état de base découle une relation simple entre la stabilité statique et la fréquence de Brunt-Vaissala:

•

o •

1

'\...

(4.3)

Le sommet du modèle est rigide et la condition Ci) - 0 est imposée. PO'.lr

satisfaire la!,relation (2.28) du Chapitre 2, le modèle de Mitchell nou.'1 fournit un terme qui permet d'introduire des montagnes. Les montagnes aurollt la forme:

21rX