Riemannian metrics on 2D-manifolds related to the Euler-Poinsot rigid body motion
Texte intégral
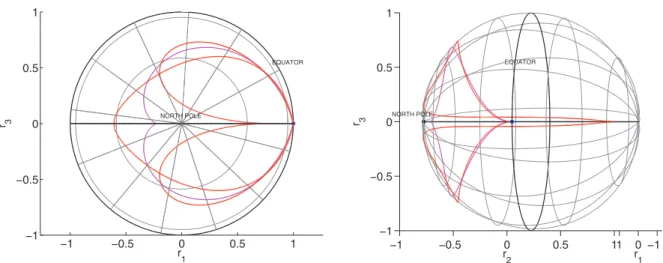
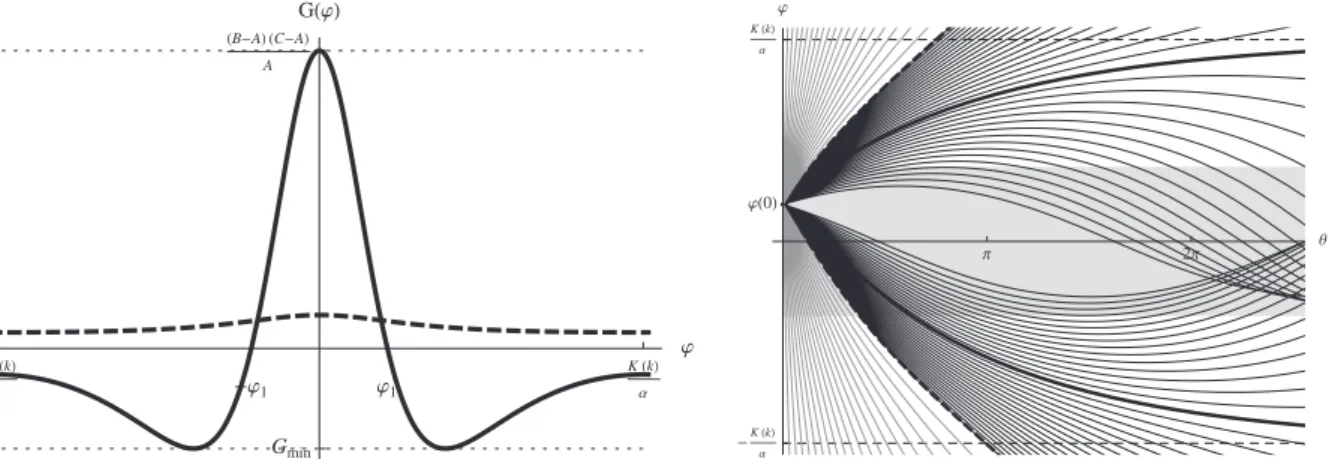
Figure
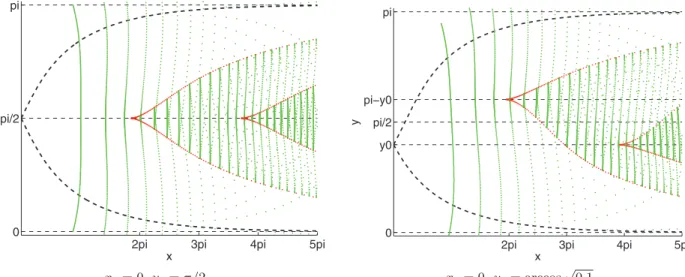
![Figure 5. The deformation of one branch (p ϕ (0) = −2 and p θ (0) ≥ 0) of the conjugate locus with respect to the parameter k ∈ [1, k 3 ]](https://thumb-eu.123doks.com/thumbv2/123doknet/3286769.94287/27.892.159.734.544.997/figure-deformation-branch-ϕ-conjugate-locus-respect-parameter.webp)

Documents relatifs
We can roughly inter- pret this phenomenon by saying that in 3D contact sub-Riemannian spaces there is a one-parameter family of geodesics parametrized by arc length that leave from
To cite this version : Bonnard, Bernard and Cots, Olivier and Shcherbakova, Nataliya Riemannian metrics on 2D manifolds related to the Euler-Poinsot rigid body problemO. Any
Besides the geometric analysis, an important role in our study is played by the Hampath code [12], which allows the explicit numerical computation based on the evaluation of
This analysis is based on the sub-Riemannian Martinet case, where it was shown in the previous Section that the exponential mapping is not proper and that in the generic case the
We study a second-order variational problem on the group of diffeomorphisms of the interval [0,1] endowed with a right-invariant Sobolev metric of order 2, which consists in
The solution of the geodesic equation (Theorem 4.1) gives a precise sense to how geodesics in ( M , g N ) generalize those discovered by Calabi [4,5] for the subspace of Kähler
In the orbit transfer case, the problem we obtain is even Riemannian, in dimension three for coplanar trajectories, five otherwise, for additional control directions associated with
The model is non generic because it is conservative ; moreover the Lie algebra generated by the orthonormal frame is nilpotent.. It is represented on Fig.. We can