Graded cubes of opposition and possibility theory with fuzzy events

(1)

Any correspondence concerning this service should be sent

to the repository administrator:

tech-oatao@listes-diff.inp-toulouse.fr

This is an author’s version published in:

http://oatao.univ-toulouse.fr/19163

To cite this version:

Dubois, Didier and Prade, Henri and Rico,

Agnés Graded cubes of opposition and possibility theory with fuzzy

events. (2017) International Journal of Approximate Reasoning, 84.

168-185. ISSN 0888-613X

Official URL

DOI :

https://doi.org/10.1016/j.ijar.2017.02.006

Open Archive Toulouse Archive Ouverte

OATAO is an open access repository that collects the work of Toulouse

researchers and makes it freely available over the web where possible

(2)

Graded

cubes

of

opposition

and

possibility

theory

with

fuzzy

events

✩

Didier Dubois

a

,

Henri Prade

a

,

Agnès Rico

b,∗ a_IRIT,_UPS-CNRS,₁₁₈_route_de_Narbonne,₃₁₀₆₂_Toulouse_Cedex_09,_France b_ERIC,_Université_Claude_Bernard_Lyon_1,₆₉₁₀₀_{Villeurbanne,}_France

a b s t r a c t

Keywords: Possibilitytheory Fuzzyevent Cubeofopposition

Thepaperdiscussesgradedextensionsofthecubeofopposition,astructurethatnaturally emergesfromthesquareofoppositioninphilosophicallogic.Theseextensionsofthecube ofoppositionagree withpossibilitytheoryandits foursetfunctions.This extendedcube then provides a synthetic and unified view ofpossibility theory. This is an opportunity torevisitbasicnotionsofpossibilitytheory,inparticularregardingthehandlingoffuzzy events.Itturnsoutthatinpossibilitytheory,twoextensionsofthefourbasicsetfunctions to fuzzy events exist, which are needed for serving different purposes. The expressions ofthese extensions involve many-valued conjunction and implication operatorsthat are relatedeitherviasemi-dualityorviaresiduation.

1. Introduction

The square of opposition is a logical structure introduced in Ancient Greek logic, in Aristotle times, in relation with the study ofsyllogisms [31]. It fell into oblivionwith the advent of modern logic at thebeginning ofXXth century. Still studiedinphilosophicallogicinthe1960’s[6],itsinterestwasrediscoveredatthebeginningofthenewcentury [2–5].The cubeofopposition, ofwhichtwofacetsaresquaresofopposition,whiletheotherfacetsexhibitothernoticeablestructures, appearedoncein1952,inathoroughdiscussionofsyllogisms[36],buthasremainedlargelyignoredsincethattime.Ithas however been revived afew yearsago[20]when trying torelate possibility theory[41,14]with thesquareofopposition. Agradedextension thatapplieswhentheitems inoppositionareamatterofdegree,ratherthan beingbinary-valued,has been recentlyproposed andapplied tofuzzy roughsets [8]and more,generally,tothecalculusoffuzzy relations[9]. This paperfocusesontheapplicationofthegradual cubetopossibilitytheory.

Possibilitytheory,aframeworkforuncertaintymodeling,offersarichsettingforexpressinggradedmodalities.Indeedit isbased onabodyoffour setfunctions, whichrespectivelymodel strong(guaranteed)possibility,weakpossibilityviewed as evaluating plain consistency, and their duals that correspond to weak and strong necessity. From the beginning, the (weak) possibility measure has been extended to fuzzy events [41]. By duality, (weak) possibility measures immediately leadto(strong)necessitymeasures[11,43]forfuzzyevents.Thenthe(weak)possibilityofafuzzyeventis0onlyifthereis absolutelyno overlapbetweenthefuzzyevent andthepossibilitydistribution.Conversely,the(strong)necessityofafuzzy event is1only ifthewhole possibilitydistribution (includingallthevalueswith lowbut non-zeropossibility)isincluded

✩ _This_paper_is_part_of_the_virtual_special_issue_on_{tri-partition,}_edited_by_Davide_Ciucci_and_Yiyu_Yao.

*

Correspondingauthor.

E-mailaddresses:dubois@irit.fr(D. Dubois),prade@irit.fr(H. Prade),agnes.rico@univ-lyon1.fr(A. Rico).

(3)

Fig. 1. Square of opposition.

in the core of the fuzzy event (corresponding to the values with maximal membership 1). These two measures of fuzzy events have been at the basis of fuzzy pattern matching [7] for evaluating how much a flexible requirement is fulfilled in presenceof uncertaininformation. They also respectively correspond to optimistic and pessimistic decision criteria in qualitative decisiontheory (thepessimistic criterionis1 onlyif the decisionyields a fullysatisfactory output, even when appliedinasituationhavingalow(non-zero)possibility)[19].

However,ithas beenalsonoticedthat thismeasure of(strong)necessityofafuzzy event,togetherwithasimilar mea-sure of(strong)possibility areno longer suitable for properlyhandling (guaranteed)possibility and necessityqualification of fuzzy events, i.e.,for representing statements ofthe form “it ispossible /certainat level

α

that x is A” (where A is a fuzzy event).This problemhasledtosuggest othermeasuresofstrong possibilityandnecessityforfuzzy events[17],that havebeen usedinfuzzylogicprogramming(forinstanceAlsinetandGodo[1]).

Definitions and results regardingthese extensionsof possibilitytheory tofuzzy events, inthe spiritofZadeh’soriginal intuitions,1_have_remained_sparse_and_lacunary_until_now._The_study_of_the_graded_cubes_of_opposition_offers_an_opportunity to providea complete view of thepossibilistic evaluations offuzzy events. The aim of thispaper is twofold: on the one hand, to unify the different definitions of the four set functions of possibility theory for fuzzy events and to lay bare a minimal algebraic structure that can accommodate them; on the other hand, to show that this algebraic structure is capableofaccountingforthegradedcubeofoppositionanditspossibilitytheoryversion,involvingeightmeasuresoffuzzy events and oftheircomplements. Theseresultsalso systematizepreliminary proposalsin[8,9]regarding conjunctionsand implicationsneededtobuildagradedsquareofopposition.

We start bya reminder on the square and the cube of opposition in Section 2, and then in Section 3, after recalling thetwo-valuedsetting forpossibility theoryand itscubeofopposition, weinvestigate thedifferentextensions ofthefour basic measures of possibility theoryto thecaseof fuzzy events, and laybare a minimalalgebraic structureinvolvingtwo conjunctions and two implications related viasuitable transformations, that supports aqualitative approachto possibility theoryforfuzzyevents.Finally, inSection4weorganizethesefuzzy setfunctionsinagradedsquareofopposition.

2. Thesquareandcubeofopposition:Booleancase

Inthissection,webrieflyrecallwhatasquareofoppositionis,andhowitcanbecharacterized,before alsointroducing thecubeofopposition,arelatedabstractstructurewhichisanextensionofthesquare.

2.1. Thesquareofopposition

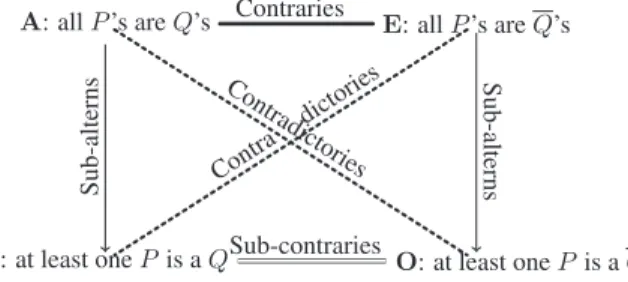
Thetraditionalsquareofopposition[31]isbuiltwithuniversallyandexistentiallyquantifiedstatementsinthefollowing way. Considera statement(A)oftheform “all P ’sare Q ’s”,which isnegated bythestatement(O)“at leastone P is not a Q ”,togetherwiththestatement(E)“no P isa Q ”,whichisclearlyineven strongeroppositiontothefirststatement (A). Thesethreestatements,togetherwiththenegationofthelaststatement,namely(I)“atleastone P isaQ ”canbedisplayed on asquarewhose verticesaretraditionallydenoted bytheletters A, I (affirmativehalf)andE, O (negativehalf)fromthe Latin“AffIrmonEgO”,aspicturedinFig. 1(where Q standsfor“not Q ”).

It is assumed that the set of P ’s is not empty for avoiding existential import problems, otherwise the statement A

(resp. E)maybetruewhileI (resp. O)isfalse[32].Ascanbechecked,noticeable logicalrelationsholdinthesquare.They arethebasisofthefollowingabstractdefinitionofasquareofopposition.

Definition1.Inasquareofopposition AIEO,thefollowingrelationsaresupposedtohold(A, I, E, O areviewed as proposi-tionallogicvariables):

(a) A andO (resp.E and I)arethenegationofeachother,i.e.,A≡ ¬O and E≡ ¬I;

(b) A entailsI,and E entailsO,i.e.,¬A∨I and¬E∨O;

1 _We_do_not_consider_here_definitions_of_the_possibility_and_necessity_of_fuzzy_events_in_the_setting_of_Choquet_integrals,_e.g._Smets_[38]_,_Dubois_and

(4)

Fig. 2. Cube of opposition of set inclusion and non-empty intersection relations.

(c) togetherA and E cannotbetrue,butmaybefalse,i.e.,¬A∨ ¬E;

(d) togetherI and O cannotbefalse,butmaybetrue,i.e.,I∨O.

Thestatements(a),(b),(c)and(d)arenotindependent.Indeedtherearethreeoptionsfordefiningasquareofopposition withindependentconditions[9].Wecantake

• either(a) and(b), • or(a) and(c), • or(a) and(d).

In particular, taking(a) and (c),we can express thecontent ofa square ofopposition in propositional logicusingtwo propositional variables(say A andE)andaknowledgebasecontainingonlytheaxiom¬A∨ ¬E.

Besides,ithasbeenobserved[34]thatsquaresofoppositioncanbecombinedinthefollowingway:

Proposition1.Giventwosquares ofopposition A I E O _and A′I′E′O′_,_then_the_4-tuple₍A_∧A′₎₍I_∨I′₎₍E_∧E′₎₍O_∨O′₎_forms

anothersquareofoppositionsatisfyingthefourcharacteristicconditions.

Proof. It isstraightforward tocheck that (a) and(b) still hold,due to DeMorganlaws andto themonotony propertiesof implication. ✷

2.2. Thecubeofopposition

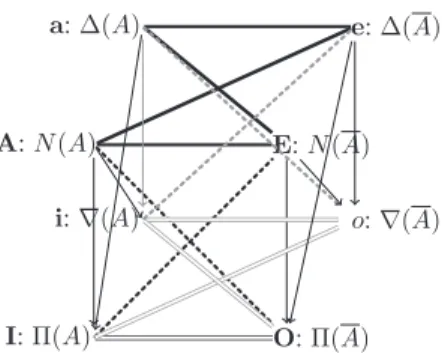
Changing P and Q intotheirnegations, P and Q respectively, leads toanother similarsquareofopposition aeoi, pro-vided that we also assume that the set of “not-P ’s” is non-empty. Then the 8 statements, A, I, E, O, a, i, e, o may be organized inwhat may becalleda cubeofopposition, asin Fig. 2, where, for clarity,the statements arereplaced bytheir counterparts in terms ofrelations betweensets expressing inclusions,or non-emptiness of intersections.In Fig. 2, we re-quire A6= ∅, B6= ∅, A6= ∅, B6= ∅.Theseconditions insuretheconsistencyofthetwo squaresofopposition (otherwise,e.g.,

A⊆B wouldnolonger entail A∩B6= ∅when A= ∅).

This cube,rediscoveredin [20], israrely mentioned; itapparently appearedfor thefirst timeinReichenbach’s modern study ofsyllogisms[36]inthemiddleoflastcentury.Thefrontfacetandthebackfacetofthecubearetraditionalsquares of opposition, wherethethick non-directedsegments relate contraries, thedouble thinnon-directed segmentsrelate sub-contraries,thediagonaldottednon-directedlinescontradictories,andtheverticaluni-directedsegmentspointtosubalterns, and expressentailments.2

Asasummary,acubeofoppositionobeysthefollowingrequirements.

Definition2.Let A,I,E,O,a,i,e,o bepropositionalvariables. Inacubeofopposition AIEOaieo,thefollowingrelationsare supposed tohold:

Frontandbackfacets(twosquaresofopposition): (a) forthediagonals:A≡ ¬O,E≡ ¬I,a≡ ¬o,e≡ ¬i;

(b) fortheverticaledges¬A∨I,¬E∨O,¬a∨i,¬e∨o;

(c) forthetopedges¬A∨ ¬E,¬a∨ ¬e;

2 _This_cube_should_not_be_confused_with_the_so-called_“logical_cube”_introduced_by_Moretti_[29]_and_more_thoroughly_studied_by_Pellissier_[33]_,_where

(5)

(d) forthebottomedgesI∨O,i∨o.

Side facets(entailments): (e) ¬A∨i;

(f) ¬a∨I;

(g) ¬e∨O;

(h) ¬E∨o.

Topandbottomfacets:

(i) a andE cannotbetruetogether,butmaybefalsetogether,i.e.,¬a∨ ¬E;

(j) thesameforA ande,i.e.,¬A∨ ¬e;

(k) i and O cannotbefalsetogether,butmaybetruetogether,i.e.,i∨O;

(l) thesameforI ando,i.e.,I∨o.

Justasinthesquareofoppositionthepropertiesthat defineitarenotindependent,likewisetheconditions thatdefine the cubeare partially redundant. Let us study therelationships between conditions on theside facets,and conditions on thetopandbottomfacetsinthecubeofopposition.

Proposition2.IntheBooleancase,foracubeofopposition,

• thepropertiesonthefrontandbackfacetsassociatedwiththepropertiesonthesidefacetsentailthepropertiesonthetopand bottomfacets;

• thepropertiesonthefrontandbackfacetsassociatedwiththepropertiesonthetop(resp.bottom)facetentailthepropertieson thesidefacetsandofthebottom(resp.top)facet.

Proof.

• Indeed,oneobtains¬a∨ ¬E fromE≡ ¬I and¬a∨I;similarlyI∨o froma≡ ¬o and¬a∨I.

• Thelogicalrelationsofthefront,back,topandbottomfacetsarerespectively:

A

≡ ¬

O

,

E

≡ ¬

I

,

a

≡ ¬

o

,

e

≡ ¬

i

,

¬

A

∨

I

, ¬

E

∨

O

, ¬

a

∨

i

, ¬

e

∨

o

¬

A

∨ ¬

E

, ¬

A

∨ ¬

e

, ¬

a

∨ ¬

E

, ¬

a

∨ ¬

e I

∨

O

,

I

∨

o

,

i

∨

O

,

i

∨

o

.

Applyingthefourequivalenceson thefirstline,thewholesetofformulasabove canbeinferredfromthepropertiesof thetopfacet(line3):¬A∨ ¬E,¬a∨ ¬e,¬A∨ ¬e,¬a∨ ¬E.Thisshowsthat thesefourequivalencestogetherwiththe propertiesofthetopfacetentailthepropertiesofthebottomfacets.Moreover,fromthepropertiesofthetopfacet,we canalsoseethattheentailmentsoftheside facetshold(takingintoaccountthefourequivalences). ✷

Wecanevenreducefurtherthenumberofconditionsthat definethecubeofopposition:

Proposition3.In theBooleancase,thecubeofopposition needsonlythefourvariablesA_,E_,a_,e_,_together_with_the _four_mutual

exclusivenessconstraints(topfacet):¬A_{∨ ¬}E,¬A_{∨ ¬}e,¬a_{∨ ¬}E,¬a_{∨ ¬}e,providedthatwedefineO as¬A,Ias¬E,oas¬a, andias¬e.

Proof. Itisclearthat4variablesareenoughduetoconstraintsonthediagonalsofthefrontandbackfacets.Underthefour mutual exclusivenessconstraintsofthetopfacet,itisclearthat theentailmentrelationsontheside facetstriviallyfollow. For instance,themutual exclusion¬A∨ ¬e also reads A|= ¬e, whichisonearrowon asidefacet.Wecanalsoderive the factthatthebottomverticesonthefrontandtheback,aswellasonthediagonalsarenotmutuallyexclusive.Forinstance, thetruthof¬A∨ ¬E isequivalentwiththetruthofO∨I,etc. ✷

Usingdistributivity,theknowledgebase{¬A∨ ¬E,¬A∨ ¬e,¬a∨ ¬E,¬a∨ ¬e}isclearlyequivalenttothesingleformula (¬A∧ ¬a)∨ (¬E∧ ¬e)whichmeansthatA∨a andE∨e cannotbetruetogether.ThisconditionalsowritesA∨a|= ¬E∧ ¬e,

i.e., A∨a|=I∧i.

Note that theabovecharacterization leavesonly seven possibilitiesintermsof truth-valuesofthevariables (A, E, a, e) (namely threemodels ofA∨a, threemodelsof E∨e, andone interpretation wherebotharefalse). Interestingly, it

(6)

corre-sponds,inagreementwiththelabelingofverticesofFig. 2,tothesevenpossiblerelativepositionsoftwonon-emptyproper subsets A and B of aset,asituation alreadydescribedin[10]3intermsofthefourset-functionsofpossibilitytheory.

Lastly,thecombinationofsquaresofopposition extendstothecube:

Proposition4.GiventwocubesofoppositionassociatedtothevariablesA_,E_,a_,e_andA′_,E′_,a′_,e′_then_the_variablesA_∧A_,E_∧E′_,

a_∧a′,e_∧e′associatedwiththefourmutualexclusivenessconstraints(topfacet)formanothersquareofoppositionsatisfyingallthe characteristicconditions.

Proof. Clearly, thesquare of opposition properties ofthe frontand theback facetsare preserved.It is straightforward to check that theentailment propertiesof theside facetshold. Then byProposition 2,the properties ofthetop and bottom facetshold. ✷

Notethatonemayalsothinkofcombiningthefrontfacetofthefirstcubewiththebottomfacetofthesecondcube.This leadstothecube(A∧a′)(I∨i′)(E∧e′)(O∨o′)(a∧A′)(i∨I′)(e∧E′)(o∨O′),whichalsosatisfiesalltheexpectedproperties. Incasethetwocubes areidentical,withtheinstantiationofFig. 2,thecubereducestoasquarewherethetopverticesare respectively A=B and A=B,andthebottomverticesare A6=B and A6=B respectively.

Cubes ofoppositionshave been appliedto rough set theory[8]where variousupperand lower approximationscanbe attached to verticesofthe cube,and horizontalvertices onthe topfacetrelate orthopairsof disjointsets. Moregenerally, logical modalities asinducedbyrelationscanalsobeorganizedinacubeofopposition [9].Inthispaper,wefocuson the basic setfunctionsofpossibilitytheory.

3. Possibilitytheoryandfuzzyevents

The ideaofpossibility theoryasanon-additive modelingofuncertaintydeparting fromprobability theorywas initially proposed by the English economist G.L.S. Shackle [39]. It was independently rediscovered by L.A.Zadeh [41] in order to account forincompleteinformationexpressedbylinguistic statements,modeledbymeans offuzzysets.

In this section, we provide a reminder on qualitative possibility theory, starting with the particular case of Boolean possibility theory,so astolaybaretherelationwith thecubeofopposition ofFig. 2,asfirstpointedoutin[20].Wethen recall thefour setfunctions ofpossibilitytheoryincaseofclassical (i.e.,crisp)events,along withtheirstandardmax–min extensions tofuzzyevents.Finally,weshowthatthepropercertaintyqualificationoffuzzy statementsintheframeworkof possibility theoryrequiresanalternativeextension ofthefoursetfunctions tofuzzyevents. Wepresentthenotionsinthe minimalalgebraicstructuresneededtodefinethem.

3.1. Booleanpossibilitytheory

We firstintroduce thefourset functions of possibilitytheoryin theBoolean case,and thenwe pointout thefact that thestructureofthecubeofoppositionnaturallycaptures them.

3.1.1. ThefourBooleanindicators

Let E⊂X beanon-empty propersubsetofaset ofsituationsorstates X ,representing theavailableevidence aboutthe valueofanunknownentityx.Inotherwords,allthatisknownisthat x∈E.Let A beanothersubsetrepresentinganevent ( A⊆X ).ThenthefourfollowingBooleanindicatorfunctionscanbedefined:

• potentialpossibility 5(A)= (

1 if A∩E6= ∅; 0 otherwise. Indeed,ifx∈E isknown,thenx ispossiblyin A. • actualpossibility if1(A)=

(

1 if A⊆E; 0 otherwise. Itisenoughthat x∈A tobesurethat x ispossible. • actualnecessity ifN(A)= ( 1 if E⊆A; 0 otherwise. Ifx∈E thenx issurelyin A. • potentialnecessity if∇(A)= ( 1 if A∪E6=X; 0 otherwise. Then,thereisanimpossiblevaluefor x outside A.

(7)

Fig. 3. Cube of opposition of possibility theory.

Undertheassumptionthat A6= ∅;A6=X (theeventisnottrivial)andE6= ∅;E6=X (theevidenceisconsistentandbrings information),itcanbecheckedthatonehas (see,e.g.,[20])

max

(N(A), 1(A)) ≤

min

(5(A

), ∇(A

)).

(1)

Thisjust expresses that A⊆E (or E⊆A)entails A∩E6= ∅and A∩E6= ∅(underthe assumptionthat thetwosubsets and theircomplementsarenotempty).

3.1.2. Booleanpossibilitytheoryandcubeofopposition

AneasypossibilisticcounterpartofthecubeinFig. 2isgiveninFig. 3,whichimmediatelyfollows fromthedefinitionof thefoursetfunctionsofpossibilitytheoryintheBooleancase.

Theinequality(1) suggeststhefollowingresultthatholdsforanyBooleancube.

Proposition5.IntheBooleancontext,considereightBooleanpropositionslabelingacubeAIOEaioe (astheoneinFig. 3).Itisacube ofoppositionifandonlyifthefollowingpropertiesarevalid:

• property(a)namely:AandO,aswellasEandI,aando,andeandiarethenegationofeachother; • theentailmentA_∨a_|=I_∧i_holds.

Proof. Underthe hypothesisA∨a|=I∧i it iseasyto check that theproperties(b),(e) and (f) aresatisfied. Conversely, letussuppose thatAIOEaioe isacubeofoppositionand thatA∨a istrue.If A istruethenI istrue,e isfalseso i istrue. If a istruethenI istrue, e isfalse,i.e.,i istrue.SoA∨a|=I∧i. ✷

Note that in the cube of opposition of possibility theory in Fig. 3, there is an internal negation that is applied when moving fromtherightsidetotheleftside.Thisrelationisaparticularinstanceoftheproperties(c) and(d) ofthecube.

WenowmovefromtheBooleanpossibilitytheorytoitsmany-valuedcounterpart,whenthesubsetE representingwhat is known is replaced by a fuzzy set understood as a gradedpossibility distribution restricting the moreor less possible states of the world [41], with a view to extend the Boolean cube in Fig. 3 to a graded cube for non-Boolean possibility theory.

3.2. Crispevents

Consider apossibility distribution

π

, defined from aset X of possiblestates to atotally ordered scale(L,≤) with top and bottomrespectivelydenotedby1and 0(forinstance, L= [0,1],viewedasanordinalscale).Moreover,weassume L is equipped withanegationfunction,i.e.,adecreasingbijectionfrom L toitselfanorderreversingfunctionthat isinvolutive, denotedby1− ·.Wedenotethisstructureby(L,≤,1− .0,1).Operationsmin,max aredefined asusual,asmin(a,b)=a if and only ifmax(a,b)=b ifand onlyifa≤b.Wedohave min(a,1−a)≤max(b,1−b) sothat itisaKleenealgebra.This istheminimalstructureweneedtodefineanelementaryformofpossibility andnecessityoffuzzyevents.

Thepossibilitydistribution

π

restrictsthemoreorlessplausible statesoftheworldaccordingtotheavailable informa-tion.Onthisbasis,onecanestimatethedegreesof(weak)possibilityand(strong)necessityofanevent A⊆X ,respectively as:

5(A) =

sup

x∈A

π

(x);

N(A) =inf

x∈/A1

−

π

(x).

5(A) evaluatesto whatextent A is consistent with

π

,while N(A) evaluatesto what extent A is certainlyimplied by

π

. Thepossibility-necessitydualityisexpressedby

(8)

where A isthecomplement of A.Generally, 5(X)=N(X)=1 and 5(∅)=N(∅)=0.Possibilitymeasures satisfythebasic “maxitivity”property∀A,B⊆X ,

5(A

∪

B) =max

(5(A), 5(B)).

Necessitymeasures satisfyanaxiomdualtotheoneofpossibilitymeasures,namely N(A

∩

B) =min

(N(

A),N(B)).

On infinitespaces,these axiomsmustholdforunionandintersectionofinfinitefamiliesofsets. Apartfrom 5and N,ameasureofguaranteedpossibilityor(strong)possibilitycanbedefined [18]:

1(A) =

inf

x∈A

π

(x).

It estimatesto whatextentall statesin A areactuallypossible accordingto evidencerepresented by

π

.Incontrast, 5 ap-pears tobeameasure of potential possibility,while 1(A) canbeused asadegree ofevidentialsupportfor A. Byduality, a measure of(weak)necessitycanbedefined:

∇(A) =

1

− 1(

A) =sup

x∈/A

1

−

π

(x);

∇(A)=1 assoonassomestateoutside A isimpossible.Thesetwomeasuresrespectivelysatisfythecharacteristicproperties 1(A∪B)=min(1(A),1(B)and∇(A∩B)=max(∇(A),∇(B)),while1(X)= ∇(X)=0 and1(∅)= ∇(∅)=1.1and∇ are decreasing setfunctions,while5 and N areincreasing.

It can be checked that the inequality (1) still holds provided that the following normalizations from above and from belowhold:∃x,

π

(x)=1;∃x′_,

_π

₍_x′₎₌_0,_to_avoid_again_existential _import_problems;_see_[10]_.

Besides, theonly possibleway to aggregate in anevent-wise mannera set of (weak)possibility measures 51,· · · ,5k

and obtaina(weak)possibilitymeasure againisviaanaggregationfunctionoftheform max

(

f1

(5

1

(A)), · · · ,

fk

(5

k

(A)))

where for each i=1,. . . ,n,fi is a non-decreasing mapping L→L such that fi(0)=0 and fi(1)=1 [16]. By duality,

a similar resultholdsforstrongnecessitymeasures N1,· · · ,Nk aggregatedas

min

(g

1

(N

1

(A)), · · · ,

gk

(N

k

(

A)))

whereforeachi=1,. . . ,n,gi isoftheform gi(a)=1−fi(1−a),i.e.,ithas thesamepropertiesas fi.

Forinstance,wecanuseaweightedmax (resp.weightedmin)combination.Namely, letw1,· · · ,wk asetofnormalized

weightsuchas∀0≤i≤k,wi∈ [0,1],and ∃i,wi=1;then∀A,wecanuse

max

(

min

(5

1

(A),

w1

), · · · ,

min

(5

k

(A),

wk

))

(

resp. min

(

max

(N

1

(A),

1

−

w1

), · · · ,

max

(N

k

(A),

1

−

wk

))).

Thisresultwillfitwiththecombinationofgradedsquaresofoppositiondiscussedinthenextsection. 3.3. Possibilityandnecessityoffuzzyevents

Possibilitymeasures extendtofuzzyevents A. A isnowrepresentedbyamappingfrom X tothetotallyorderedKleene algebra(L,≤,1− .,0,1),andweassumethat A isnormalized(i.e.,∃x,A(x)=1),aswellas A.Zadeh’sdefinition[41]isthe following:

5(A) =

sup

x∈X

min

(A(x),

π

(x))

It can be checked that 5(A)=sup_α_∈[₀_,₁_]min(

α

,5(Aα)), which shows its agreement with the

α

-level cuts view of a

fuzzy set( Aα= {x∈X | A(x)≥

α

}).

Byduality,maintainingN(A)=1− 5(A)(with A(x)=1−A(x)),weget

N(A) = inf

x∈Xmax

(A(x),

1

−

π

(x)).

This extension preservesavery strongview ofthe idea ofinclusion, since N(A)=1 iff {x∈X |

π

(x)>0}⊆A1= {x∈

(9)

Similarly,1and∇ canbeextendedtofuzzyeventsinthesamestyle,namely

1(A) =

inf x∈Xmax

(

1

−

A(x),

π

(x))

∇(A) =

sup x∈X min

(

1

−

A

(x),

1

−

π

(x)) =

1

− 1(A)

Thesedefinitionsstem fromtheproperty1π(A)=N1−π(A),wherethenotation1π makesitclearthat 1iscomputed

from

π

. Thisidentity,validintheBoolean caseiscarriedoverto thegradual case.Moreover, thereisthedualityproperty ∇(A)=1− 1(A).

Theseextensions coincidewiththepreviousdefinitionsincaseofcrisp events,and preservethedecomposability prop-ertiesofthefoursetfunctions incaseoffuzzysets,with A(x)∩B(x)=min(A(x),B(x))and A(x)∪B(x)=max(A(x),B(x)). Several authors have proposed the followingalternative extension of apossibility measure to afuzzy event, usingthe product inplaceofmin when L= [0,1]intheusualsense.The firstonewas Shilkret[40]in1971 (andlaterA.Kaufmann

[27]in1979underthenameof“admissibility”):

5(A) =

sup

x∈X

A(x) ·

π

(x)

Thedecomposabilitypropertyof5withrespecttomax-basedunionisclearlypreserved.

More generally, one could replace min (resp. max) in the expressions of 5,N,1,∇ by any monotonically increasing aggregationfunction∗on L suchthata∗1=1∗a=a (asemi-copulawhen L= [0,1][25])(resp.,theassociatedDeMorgan dual 1− (1−a)∗ (1−b)). In practice, it is natural to require also the commutativity of ∗ (otherwise there would be two distinct notions of possibility of a fuzzy event, as5∗(A)=sup_x_∈_XA(x)∗

π

(x) would differ from sup_x_∈_X

π

(x)∗A(x)) and use forinstance atriangular norm∗ [28]. Define likewise N∗(A)=1− 5∗(A), 1∗(A)=infx∈X(1−A(x)∗ (1−

π

(x))),

∇∗(A)=1− 1∗(A).

We can now establish thefollowing result for such generalizedpossibility and necessityof fuzzy events, that express relationsbetweentopverticestobottomonesinacubeofoppositionextendingtheone ofFig. 3.

Proposition6.Foranymonotonicallyincreasingaggregationfunction∗,suchthat1∗a=a=a∗1, • if∃x,

π

(x)=1 then N∗(A)≤ 5∗(A);

• if∃x,A(x)=1 then1∗(A)≤ 5∗(A); • if∃x,A(x)=0 then N_∗(A)≤ ∇∗(A); • if∃x,

π

(x)=0 then1∗(A)≤ ∇∗(A).

Proof. N∗≤ 5∗:Let x0 suchthat

π

(x0)=1.

N∗

(A) =

inf

x∈X

(

1

− (

1

−

A(x)) ∗

π

(x)) ≤

1

− ((

1

−

A

(x

0

)) ∗

π

(x

0

)) =

A

(x

0

)

=

A(x0

) ∗

π

(x

0

) ≤

sup x∈X

A(x) ∗

π

(x) = 5

∗

(A).

1∗≤ 5∗:Letx′suchthat A(x′)=1.Weproceedlikewise:

1

∗

(A) =

inf x∈X

(

1

−

A(x) ∗ (1

−

π

(x))) =

π

(x

′

)

=

A(x′

) ∗

π

(x

′

) ≤

sup x∈X A(x) ∗

π

(x) = 5

∗

(A).

Thetwootherinequalitiesareprovedlikewise. ✷

Note that weuseallpropertiesofoperation ∗in theproof.Then wegetthegradedextension ofinequality(1), which, asProposition 5shows,isnecessarytogetacubeofopposition.

Corollary 1.For any monotonically increasing aggregation ∗, such that 1∗a= a= a∗1, if ∃x,

π

(x)= 1, ∃x′_,_A₍_x′₎ ₌_1, ∃x′′,A(x′′)=0,∃x′′′,

π

(x′′′)=0,thenmax(1∗(A),N∗(A))≤min(∇∗(A),5∗(A)).

3.4. Representationofcertainty-qualifiedandpossibility-qualifiedstatements

Human knowledge isoften expressed ina declarativeway usingstatements in natural language. It correspondsto ex-pressing (flexible) constraints that theworld issupposed to comply with. Sometimes these fuzzy statement areattached beliefdegrees.Suchaqualificationoffuzzystatements(intermsoftruth,probability,orpossibility)was firstconsideredby Zadeh[42](see also[37]),especially fuzzy statementssuchas“x is A is

α

-possible” (or“

α

-true”, or“

α

-probable”).Inthe following,wefirstdiscussnecessityqualification,andthenguaranteedpossibilityqualification,beforegoingbackto(weak) possibilityqualificationand (weak)necessityqualification.

(10)

Certainty-qualified statements. Certainty-qualified pieces of uncertain information of the form “ A is certain to degree

α

” are modeledbytheconstraint N(A)≥

α

. Incaseofcrisp events, theleast restrictivepossibility distribution reflectingthis informationis[14]:

π

(A,α)

(x) =

½

1 if x

∈

A

1

−

α

otherwise

.

(2)

Morepreciselywehave[14]:

Proposition7.N(A)≥

α

ifandonlyif

π

≤

π

(A,α).

Inthefollowing,westicktothequalitativesetting,usingonlymin andmax on L.When A isafuzzyset,Equation(2)is generalized[35]by

∀x,

π

(A,α)

(x) =

max

(A(x),

1

−

α

),

which still represents the qualified fuzzy statement “x is A is

α

-certain”. This equality can be justified in terms of the level cutsof A [15].Itisaformofdiscountingoftheinformationitem“ A iscertain”,wherebystatesthat wereimpossible according to thisinformation itemnow become allthemore possible asthe level of certainty

α

is smaller. In particular, it can beseen that “x is A is certain” (

α

=1) is equivalent to

π

(A,1)=1A while “x is A is totally uncertain” (

α

=0)is

equivalentto

π

(A,α)=1 (totalignorance).

At thispoint, weneedtofindtheexpressionofadegreeofcertainty of A in theformN (A)=infx∈X

π

(x)→A(x)≥

α

if andonlyif

π

(x)≤max(A(x),1−

α

),usinganimplicationfunction→definedasfollows:

Definition3.Animplication →from L2 _to _{L is}_a _function_that _is_{non-increasing} _in _the_first _place_and _{non-decreasing}_on

thesecondplace,andcoincideswithanimplicationon{0,1}(inparticular,0→a=1 and1→0=0).

Namely, we introduce the residuated implication →G in L, associated to min, such that min(a,b) ≤c ⇔b ≤

a→Gc,∀a,b,c∈L.ThisimplicationisGödelimplication,

a

→

Gc

=

(

c, if a

>

c, 1 otherwise. Thus,weget,aspresentedin[17]:

Proposition8.LetA beafuzzyset.ThenN (A)≥

α

ifandonlyif

π

≤

π

(A,α),providedthatN (A)=infx(1−A(x))→G(1−

π

(x)).

Proof. ∀x,

π

(x)≤max(A(x),1−

α

)⇔ ∀x,1−

π

(x)≥min(1−A(x),

α

)⇔ ∀x,(1−A(x))→G(1−

π

(x))≥

α

,which isofthe

form N (A)≥

α

fora→b= (1−b)→G(1−a),whichisthesymmetriccontrapositiveofGödelimplication. ✷

Somax(A(x),1−

α

)isstilltheleastspecificpossibilitydistributionsuchthatN (A)≥

α

underthischoiceofimplication. It canbecheckedthat N isstill minitive:N (A∩B)=min(N (A),N (B)),and that N (A) and N(A) coincide if A is crisp. Moreover it canbechecked that “x is A is certain”N (A)=1 is stillequivalent to

π

(A,1)=

µ

A, themembership function

of A,while this isnot true if we chooseto interpret ‘x is A is certain” as N(A)=1 using thestandard definitionin the previoussubsection.

Possibility-qualification.Consideruncertainstatementsoftheform“ A is possibletodegree

α

”.Thesestatementsoftenmean that all realizations of A are possible to degree

α

. They are modeled by the inequality1(A)≥

α

. It corresponds to the idea of observed evidence. This type of information is better exploited by assuming an informational principle opposite to the one of minimalspecificity, namely,any situation not yet observed isregarded asimpossible. This issimilar to the closed-worldassumption.Themostspecificdistributionδ(A,α) inagreementwiththisinformationis:

δ

(A,α)

(x) =

½

α

,

if x

∈

A

0 otherwise. (3)

Morepreciselyitisstraightforwardtocheckthat:

Proposition9.1(A)≥

α

ifandonlyif

π

≥ δ(A,α).

Inthefuzzy case[17],theinformationitem“x is A is

α

-guaranteedpossible”isrepresentedbytheconstraintD(A)≥

α

where D(A)=infxA(x)→

π

(x) forasuitableimplication.Asforcertainty-qualificationwewishtopreserveEquation(3)in

theform:

(11)

Fig. 4. Relations between minimum and associated implications and conjunction.

Thenwecanprove[17]:

Proposition10.LetA beafuzzyset.ThenD(A)≥

α

ifandonlyifδ(A,α)≤

π

whereD(A)=infxA(x)→G

π

(x).

Proof. Since min(a,b)≤c⇔b≤a→Gc,wehave,∀x,min(A(x),

α

)≤

π

(x)⇔ ∀x,A(x)→G

π

(x)≥

α

⇔ D(A)≥

α

. ✷

WestillhaveD(A∪B)=min(D(A),D(B)),whileD(A)and1(A)coincideif A iscrisp.NotethatthepropertyD_π₍A)= N₁₋_π₍A)isagainvalid.

Byduality,wecanintroducethefollowingextension ofweakpossibilityP (A)=1− N (A).

Proposition11.P (A)=sup_xA(x)⊗G

π

(x)wherea⊗Gb=b ifa>1−b;a⊗Gb=0 otherwise.

Proof. P (A)=1−infxA(x)→G(1−

π

(x))=supx1− (A(x)→G(1−

π

(x))).Notethat

1

− (A(x) →

G

(

1

−

π

(x))) =

(

0 if A

(x) ≤

1

−

π

(x)

π

(x)

if A

(x) >

1

−

π

(x)

=

A(x) ⊗G

π

(x).

✷

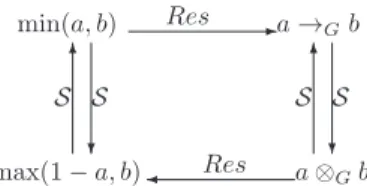
This non-commutative operationrelated to minimum coincides witha conjunctionon {0,1}. Itwas firstintroduced in

[12],noticingthatthediagramonFig. 4 commutes,where Res andS meansresiduationand semi-dualityrespectively:

aRes(min

)b

=

sup

{c

:

min

(a,

c) ≤b} =a

→

Gb and

aS

₍

min

)b

=

1

−

min

(a, (

1

−

b)) =max

(

1

−

a,b).

Note that theexpressionsup_x

π

(x)⊗GA(x), obtained byexchanging theargumentsof ⊗G in P (A) does notreduce to

the standardpossibilitymeasure 5(A) for crisp events A.Likewise, wecannot definenecessitymeasuresfor fuzzy events asinfx

π

(x)→GA(x),asitdoesnotreducetothestandardnecessitymeasure N(A)forcrispevents A.

Wecannowaddresstheproblemofthepossibility-qualificationinthesenseofset-functionP.

Proposition12.P (A)>

α

⇔ ∃x,

π

(x)>max(1−A(x),

α

).

Proof. ∀a,b,c∈L,a⊗Gb≤c⇔b≤max(1−a,c) or equivalently a⊗Gb>c⇔b>max(1−a,c), we can check that:

P (A)>

α

⇔ ∃x,A(x)⊗G

π

(x)>

α

⇔ ∃x,

π

(x)>max(1−A(x),

α

). ✷

This agreeswithintuition.Indeed x is A is consistentlypossible ata level greaterthan

α

, if thereexists anelement x withapossibilitydegreegreaterthan

α

,whichsufficientlybelongsto A (x shouldbelongallthemoreto A asthepossibility ofx is small).

Similarly,wecanintroducebyduality D (A)=1− D(A).

Proposition13. D (A)=sup_x(1−A(x))⊗G(1−

π

(x)).

Proof. D (A)=1−infx(1−A(x))→G

π

(x)=supx1− ((1−A(x))→G

π

(x)). ✷

Thenwealsohavethefollowingequivalence:

Proposition14. D (A)>

α

⇔ ∃x,

π

(x)<min(1−A(x),1−

α

).

Proof. Since (1−a)⊗G(1−b)>c⇔1−b>max(a,c),wehave, D

(A) >

α

⇔ ∃x, (

1

−

A

(x)) ⊗

G

(

1

−

π

(x)) >

α

⇔ ∃x, (

1

−

π

(x)) >

max

(A(x),

α

)

(12)

Fig. 5. Relations between conjunction and associated implications and conjunction.

Itmeansthat thereexists x outside A withalowpossibility,whichagreeswiththeintuitionofthe∇ operator.

We can prove that the same inequalities hold between these set functions as for Zadeh-inspired definitions of the extensions ofpossibilityand necessitytofuzzyeventsshownintheprevioussubsection:

Proposition15.

• If∃x,

π

(x)=1 thenN (A)≤ P(A); • if∃x,A(x)=1 thenD(A)≤ P(A); • if∃x,A(x)=0 thenN (A)≤ D (A); • if∃x,

π

(x)=0 thenD(A)≤ D (A).

Proof. N (A)=infx(1−A(x))→G(1−

π

(x))=0 ifand only if ∃x0 suchthat

π

(x0)=1 and A(x0)6=1.Then N (A)>0 if

and only if ∀x0,whenever

π

(x0)=1 then A(x0)=1; thismeans that N (A)>0 only if core(

π

)⊆core(A).In suchacase

P (A)=sup_xA(x)⊗G

π

(x)=1⊗G1=1.HenceN (A)≤ P(A).

Let x′ _such_that _A₍_x′₎₌_1. _D(_A₎₌_inf

xA(x)→G

π

(x)≤A(x′)→G

π

(x′)=

π

(x′)=A(x′)⊗G

π

(x′)≤supxA(x)⊗G

π

(x)=

P (A).

Takinganx′′ _such_that _A₍_x′′₎₌_0,_{N (}_A₎_≤ D ₍_A₎_can_be_similarly_established.

D

(A)=sup_x(1−A(x))⊗G(1−

π

(x))=1 assoonas∃x′′′suchthat

π

(x′′′)=0 and A(x′′′)6=1;thismeansthat D

(A)<1 onlyif∀x′′′ _such_that

_π

₍_x′′′₎₌_{0 we}_have _A₍_x′′′₎₌_1._Then_D(_A₎₌_inf

xA(x)→G

π

(x)≤A(x′′′)→G

π

(x′′′)=0.HenceD(A)≤ D

(A). ✷

Corollary2.If∃x,

π

(x)=1,∃x′,A(x′)=1,∃x′′,A(x′′)=0,∃x′′′,

π

(x′′′)=0,thenmax(D(A),N (A))≤min( D (A),P (A)).

So, we again get a graded extension of inequality (1), which, as Proposition 5 shows, is necessary to get a cube of opposition.

3.5. Ageneralizedsettingforthepossibilityandthenecessityoffuzzyevents

Intheprevious subsectionswe developedapurelyqualitativeview oftheevaluationsoffuzzy events usingabounded chainequippedwithaninvolutivenegationand aresiduatedimplication.Inthisway,weobtainedtwopairsofimplication andconjunctionconnectivesrelatedviasemi-duality,duetotheinvolutivenegation,eachpairbeingrelatedtotheotherpair viaresiduation.Wehaveshownthateachpairofimplicationandconjunctionconnectivesgeneratesa4-tupleofpossibilistic set functions. One ofthe necessity functions is instrumental in comparing afuzzy set A and a possibility distribution

π

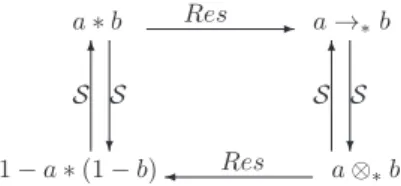
(N(A))andtheothernecessityfunctionproperlyhandlesthepossibilisticmodelingofcertaintyqualifiedfuzzypropositions (N (A)).Thisschemecanbeextendedtomoregeneralconjunctionoperationsthantheminimum.

It has been shown by Fodor [26] that the diagram of Fig. 5 still holds starting from any operation ∗ whenever the residuation operation is well-defined. So it makes sense to study the counterparts of the min-based qualification-based fuzzyset-functionsofthissubsection,replacingtheminimumbyageneralizedconjunction∗alreadymetinSubsection3.3:

Definition4.Aconjunction∗fromL2toL isatwo-placefunctionmonotonicallyincreasinginbothplacesandthatcoincides withconjunctionon{0,1}.

Inthefollowingwealsousethefunctionslinkedtoconjunctionbyresiduation andthesemiduality:

Definition5.The residuation of a operation ∗ is defined byaRes(∗)b=sup{c:a∗c≤b} and itssemi-dual is defined by aS(∗)b=1−a∗ (1−b).

Namely, starting withthepair (∗,S(∗))made of aconjunctionfunction∗and itsassociated semi-dual implication,we can also consider its residuated implication Res(∗)=→∗ and the conjunction S(→∗)= ⊗∗ that is the semi-dual of the latter. Fodor [26] has shown that if Res(∗) exists,4 then, in the finite setting, Res(⊗∗)= S(∗). So we again are in the

(13)

presenceoftwopairsofconjunctionsandimplications.Itiseasytoseethata⊗∗b=0 whenevera≤1−b and 1⊗∗b=b if andonlyif1→∗b=b.

Thepair(∗,S(∗))wasstudiedinSubsection3.3,assumingthat1⊗∗a=a∗1=a.Letusconsiderthepair(⊗∗,→∗).We cangeneralizethedefinitionsofN ,P ,D, D asfollows:

• N∗(A)=infx(1−A(x))→∗(1−

π

(x))=infx1− (1−A(x))⊗∗

π

(x) • D∗(A)=infxA(x)→∗

π

(x)=infx1−A(x)⊗∗(1−

π

(x))=1− N∗(A) • P∗(A)=sup_xA(x)⊗∗

π

(x)

• D ∗(A)=sup_x(1−A(x))⊗∗(1−

π

(x))=1− D∗(A)

Itcanbecheckedthat byconstruction:

Proposition16.Thefollowingequivalenceshold:

• N∗(A)≥

α

ifandonlyif

π

(x)≤1− ((1−A(x))∗

α

) • D∗(A)≥

α

ifandonlyif

π

(x)≥A(x)∗

α

Notethat evenif1∗a=a∗1=a,wemaynothavethat1⊗∗a=a⊗∗1=a aswecanobservefor⊗G.

A generalization of Proposition 6 can then considered for N_∗,P_∗,D_∗, D _∗, replacing ∗ by ⊗∗ in the definition of the possibilitymeasure.ItalsogeneralizesProposition 15tootherconjunctionsthanmin.

Proposition17.Let∗beaconjunctionand→∗=Res(∗):

• If∃x,

π

(x)=1 and(1−a)→∗0≤1− (a→∗0)thenN∗(A)≤ P∗(A); • if∃x,A(x)=1 and1→∗(1−a)≤1− (1→∗a), thenD∗(A)≤ P∗(A); • if∃x,A(x)=0 and1→∗(1−a)≤1− (1→∗a), thenN_∗(A)≤ D ∗(A); • if∃x,

π

(x)=0 and(1−a)→∗0≤1− (a→∗0), thenD_∗(A)≤ D ∗(A).

Proof.

• N∗≤ P∗: we must prove infx(1−A(x))→∗(1−

π

(x))≤supxA(x)⊗∗

π

(x). It is sufficient to find x0,x1 such that

(1−A(x0))→∗(1−

π

(x0))≤A(x1)⊗∗

π

(x1). Pick them suchthat x0=x1=x and

π

(x)=1. Then, it is enough that

(1−A(x))→∗0≤A(x)⊗∗1,whichholdsbyassumption,since A(x)⊗∗1=1− (A(x)→∗0).

• D∗≤ P∗:wemustproveinfxA(x)→∗

π

(x)≤supxA(x)⊗∗

π

(x).Itissufficienttofindx0,x1suchthat A(x0)→∗

π

(x0)≤

A(x1)⊗∗

π

(x1). Pickthem suchthat x0=x1=x and A(x)=1. Then,it isenough that 1→∗

π

(x)≤1⊗∗

π

(x), which

holdsbyassumption,since1⊗∗

π

(x)=1− (1→∗(1−

π

(x))). • N∗≤

D

∗:infx(1−A(x))→∗(1−

π

(x))≤supx(1−A(x))⊗∗(1−

π

(x)).Choosing x with A(x)=0,itisenoughthocheck that1→∗(1−

π

(x))≤1⊗∗(1−

π

(x)),whichholdsbyassumption,since1⊗∗(1−

π

(x))=1− (1→∗

π

(x)).

• D∗≤ D ∗:infxA(x)→∗

π

(x)≤supx(1−A(x))⊗∗(1−

π

(x)).Againpickx with

π

(x)=0.AsufficientconditionisA(x)→∗

0≤ (1−A(x))⊗∗1,whichholdsbyassumption,since(1−A(x))⊗∗1=1− (1−A(x))→∗0). ✷

Theextraconditionsonimplicationfunctions →∗:

(

1

−

a) →∗0

≤

1

− (a

→

∗0

)

and 1

→

∗

(

1

−

a) ≤1

− (

1

→

∗a) (4) seemtobenewanddeservesomecomments.Theformerusestwowaysofexpressingadoublenegation.Itholdswhenever a→∗0=1−a butitisweaker. Thesecondoneistrueif 1→∗a=a, butisweakeraswell.If→∗=max(1−a,b)or→G,

thentheseconditionsaresatisfied.Sotheabovepropositioncoverstheresultsofbothsections3.3and3.4inthecasewhen ∗ isthe minimum. Moreover, forany conjunction∗ suchthat 1⊗∗a=a⊗∗1=a, the two conditions areverified bythe semi-dualimplication1−a∗ (1−b).So,Proposition 6isalsoaparticularcaseofProposition 17.Theconditions(4)arealso verified by residuated implicationsbased on t-norms with continuous generators, especially theproduct and Łukasiewicz t-norms.InthecaseofŁukasiewiczt-norm, itiswell-known thatthediagramonFig. 5collapses,inthesensethat ∗= ⊗∗ and Res(∗)= S(∗),so that(N∗,5∗,1∗,∇∗)= (N∗,P_∗,D_∗, D ∗).

Intermsofconjunctions⊗∗semi-dualto →∗,theinequalities(4)takearemarkableform asfollows: 1

⊗

∗a

≥

1

−

1

⊗

∗

(

1

−

a)and a

⊗

∗1

≥

1

− (

1

−

a) ⊗∗1

.

Undertheconditions (4),byProposition 17,wedopreservetheinequality max

(

D_∗

(A),

N_∗

(A

)) ≤

min

(

D ∗

(A),

P∗

(A)),

(14)

4. Gradedcubesofopposition

In the previous section, we have proposed two versions of possibility theory extended to fuzzy events, motivated by different concerns, and we proved results that suggest an extension of the cube of opposition of Fig. 3 to many-valued propositions that could accommodate these generalized possibilistic set functions. In the followingwe define an abstract many-valued(graded)cubeofoppositionextendingtheoneofFig. 2andprovethatthisisindeedthecase.Gradedsquares and cubesofoppositionwerefirstdefinedin[21],and furtherstudiedin[8]inconnectionwithfuzzy roughsets.

4.1. Definitionofgradedsquareandcube

InSection2,thestatementsassociatedto theverticesofasquareorofacubeofoppositionaresupposedtobetrueor false.Nowwearegoingtoconsiderthatthevalidityofstatementsisamatterofadegreeandismeasuredonanevaluation scaleL,whichisaboundedtotallyorderedscalewithatopelement1 andabottomelement0.Thus,weassociateadegree in L toeachvertex A,E,O,I,denotedby

α

,

ǫ

,o and

ι

respectively.

Letn beaninvolutivenegationfunction,i.e.,adecreasingbijectionfromL toitselfsuchthatn(n(a))=a,n(0)=1,n(1)=0 (possiblydifferentfrom1−).ConsideralsoanimplicationfunctionI,andamany-valuedconjunctionfunctionC .Afunction ⊕fromL2_to _{L defined}_by_De_Morgan_duality_as_D₍_a_,_b₎₌_n₍_C₍_n₍_a_),_n₍_b₎₎₎_is_called_a_disjunction_function._We_introduce_new

notation, nottoconfuse withnegation,implicationandconjunctionfunctions neededfordefiningpossibilityand necessity offuzzyevents.

Therequiredpropertiesneededtoformasquareofopposition shouldbenowwrittenasfollows:

Definition6.Agradedsquareofoppositionisdefined byattaching L-valuedvariables

α

,

ǫ

,o and

ι

toeachvertex A,E,O,I

respectively, insuchawaythat:

(a)

α

ando arethenegationofeachotheraswellas

ǫ

and

ι

:o=n(

α

) and

ι

=n(

ǫ

),foraninvolutivenegationn. (b)

α

entails

ι

and

ǫ

entailso;so,weneedanimplicationI andwrite I(

α

,

ι

)=1,and I(

ǫ

,o)=1.

(c)

α

and

ǫ

cannotbetruetogetherbutmaybefalsetogether;so,weneedaconjunctionC andwrite C(

α

,

ǫ

)=0. (d)

ι

and o cannotbefalsetogetherbutmaybetrue together;so, weneedtouseasymmetricaldisjunction D and write

D(

ι

,o)=1.

Inorderto keeptheotherproperties ofthesquare:(a) (b) imply(c),(a) (b)imply(d), (a) (c)imply(b)and (d), (a) (d) imply(b) and(c);thenegation,theimplication,theconjunctionandthedisjunctionmustbelinked.Moreprecisely,under thecondition:

α

and o arethenegationeachother aswellas

ǫ

and

ι

,thefollowingproperties I(

α

,

ι

)=1 and I(

ǫ

,o)=1, C(

α

,

ǫ

)=0 and D(

ι

,o)=1 mustbeequivalent.Onesolutiontothisproblemisasfollows:

Proposition18.IftheconjunctionC andtheimplicationI aresemi-duals,andthedisjunctionD istheDe-MorgandualofC ,then

αιoǫ

formsagradedsquareofopposition.

Proof. By semi-duality, I(

α

,

ι

)=1 isindeed equivalentto n(C(

α

,n(

ι

)))=1, which is equivalent to C(

α

,

ǫ

)=0, which is equivalentto D(

ι

,o)=1.Likewise, I(

ǫ

,o)=I(n(

ι

),n(

α

))=n(C(n(

ι

),

α

))=n(C(

ǫ

,

α

))=n(0)=1. ✷

Notethatwecanalsoobserveagracefuldegradationofthesquarepropertieswhen I(

α

,

ι

)<1,namely,itcanbechecked that thesmaller I(

α

,

ι

)(i.e.

α

increaseswhile

ι

decreases),thegreaterC(

α

,

ǫ

)=n(I(

α

,n(

ι

)).

Aparticularcaseisproposedin[9]wheretheauthorsuseasymmetricalconjunction(i.e., C(a,b)=C(b,a)).

Example1([21]).For instance, takingthemin for thesymmetric conjunctionand thenegation1− on thescale[0,1] one obtains theKleenesystemleadingtoasquareofopposition:

•

α

=1−o,

ǫ

=1−

ι

• max(1−

α

,

ι

)=1,max(1−

ǫ

,o)=1 (usingKleene–Dienes implication). • min(

α

,

ǫ

)=0

• max(

ι

,o)=1

Other similar examples of graded squares are proposed in [9], especially one based on Łukasiewicz conjunction and implication.

Example2.Letusconsider(L,0,1,≤,n,⊗)wheren isaninvolutivenegation,⊗aleftconjunction,i.e.,aconjunctionsuch that 1⊗x=x,0⊗x=0.

Wedefinetheimplicationbysemi-duality:I(a,b)=n(a⊗n(b)). Wehave I(

α

,

ι

)=1 is equivalentto

α

⊗n(

ι

)=

α

⊗

ǫ

=0.

(15)

Fig. 6. Graded cube of opposition.

However,Proposition 6showsthat wedonotneedthat C besymmetric.For instance,choosingC(a,b)= S(→∗) where →∗ isobtainedfromaconjunction∗byresiduationalsoyields agradedsquare.Thefollowingexampleisnew:

Example 3.For instance, taking the min for ∗ and the negation n=1− (·) on L, →∗=→G, C(a,b)=a⊗Gb, D(a,b)=

a⊕Gb=1− (1−a)⊗G(1−b)one obtainstheGödelsystemleadingtoasquareofopposition:

•

α

=1−o,

ǫ

=1−

ι

•

α

→G

ι

=1,

ǫ

→Go=1 (usingGödelimplication)

•

α

⊗G

ǫ

=0

•

ι

⊕Go=1

Similarlythedefinitionofthecubeofoppositioncanbeextendedtothegradedcaseusinganinvolutivenegationn and animplication I,andmany-valuedconjunctionand disjunctionC andD respectively:

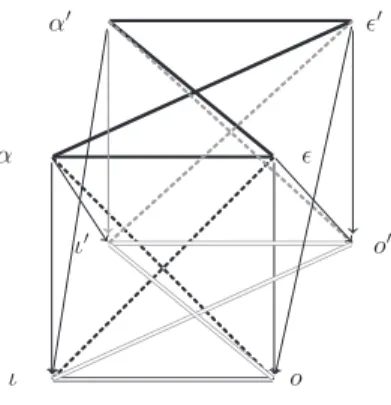
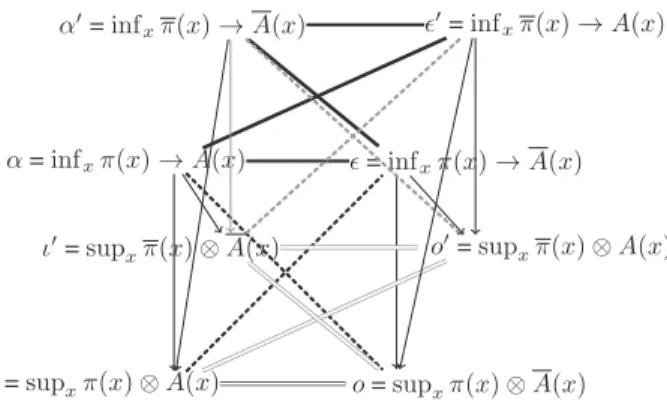
Definition7.Agraded cubeof opposition (Fig. 6) is defined byattaching L-valuedvariables

α

,

ǫ

, o,

ι

,

α

′_,

_ǫ

′_, _o′ _and

_ι

′ _to eachvertex A,E,O,I,a,e, o,i respectively,insuchawaythat:

• Frontand backfacets:

αιǫo and

α

′

ι

′

ǫ

′o′aresquaresofopposition inthesenseofDefinition 6, • Sidefacets(entailments):

(e) I(

α

,

ι

′₎₌_1; (f) I(

α

′

_ι

₎₌_1; (g) I(

ǫ

′_,_o₎₌_1; (h) I(

ǫ

,o′)=1. • Topand bottomfacets:

(i)

α

′ _and

_ǫ

_cannot_be_both_true_but_may_be_false_together,_i.e.,_C₍

_α

′_,

_ǫ

₎₌_0; (j) thesamefor

α

and

ǫ

′_,_i.e., _C₍

_α

_,

_ǫ

′₎₌_0;

(k)

ι

′ _and_{o cannot}_be_false_together_but_may_be_true_together,_i.e., _D₍

_ι

′_,_o₎₌_1; (l) thesamefor

ι

ando′_,_i.e., _D₍

_ι

_,_o′₎₌_1.

Nowweareinapositiontoprovethefollowingresults:

Proposition19.Let

α

,

ι

,o,

ǫ

,

α

′_,

_ι

′_,_o′_,

_ǫ

′_be_eight_L-valued_variables._Let_{n be}_an_involutive_negation,_and_I,_{C ,}_{D be}_many-valued implication,conjunctionanddisjunctionrespectively,suchthat

1. I andC aresemi-dualtoeachother; 2. D(a,b)=n(C(n(a),n(b)).

Then

αιoǫα

′

_ι

′_o′

_ǫ

′_is_a_cube_of_opposition_as_soon_as_we_have

• theproperty(a)namely:

α

=n(o),

ǫ

=n(

ι

),

α

′₌_n₍_o′₎_,

_ǫ

′₌_n₍

_ι

′₎_; • I(max(

α

,

α

′),min(

ι

,

ι

′))=1.

Proof. ThepropertyI(max(

α

,

α

′_),_min(

_ι

_,

_ι

′₎₎₌_{1 implies}_I₍

_α

_,

_ι

₎₌_1,_I₍

_α

_,

_ι

′₎₌_1,_I₍

_α

′_,

_ι

₎₌_{1 and} _I₍

_α

′_,

_ι

′₎₌_1._The_entailment propertiesofthesidefacetsofthecubeentailthemutualexclusivenesspropertiesofthetopfacetbysemi-duality,asforthe proof ofProposition 6.For instance, I(

α

,

ι

′₎₌_{1 implies} _C₍

_α

_,

_ǫ

′₎₌_0._These_properties_on _the_top_fact_imply_the_properties ofthebottomfacet,usingassumption2. ✷

(16)

The setting of Proposition 19 includes the casewhen the implication I is residuatedwith respect to some other con-junction ∗ and C is thesemi-dual ofthe former.For instance,we canchooseagain I=→G,and C(a,b)= ⊗G and extend

Example 3 toacube.Inthiscasewehave that I(a,b)=1 is equivalenttoa≤b.We canalsoextendExample 1 toacube asdonein[8],andwestillhavethat I(a,b)=1 impliesa≤b.

Aparticular systemof implicationand conjunctionthat satisfiesProposition 19 isŁukasiewiczsystem, where C(a,b)= max(a+b−1,0) and I(a,b)=min(1,1−a+b), withof coursen(a)=1−a. See[9]for moredetails.In factwe canuse any t-normanditssemi-dual implication,oranyimplicationresiduatedfromat-norm,and itssemi-dualimplication.

In contrast, to geta gradedsquare of opposition, one cannot usea structure ofthe form (L,≥,I,n,C) where I isthe residuated implication of astrict triangular norm, n(a)=I(a,0), C(a,b)=n(I(a,n(b)). Indeed, it isclear that n(a)=0 as soonasa>0,and C(a,b)=n(I(a,n(b)))=n(I(a,0))=1 assoonasb>0,and0otherwise.Itmeansthat if

α

>0 thenone shouldhave

ǫ

=o=0,whichmeansthathalfofthesquareshouldbeBoolean,even iftheotherhalfisnot.

Besides,theassociativecombinationoftwosquaresortwo cubesofoppositioncanbeextendedforgradedsquaresand cubes.

Proposition 20.Given two graded squares of opposition

α

1

ι

1

ǫ

1o1 and

α

2

ι

2

ǫ

2o2 then the functions min(

α

1,

α

2), max(

ι

1,

ι

2),

min(

ǫ

1,

ǫ

2)andmax(o1,o2)makeanothergradedsquareofopposition.

Proof. Property(a):max(o1,o2)=max(n(

α

1),n(

α

2))=n(min(

α

1,

α

2))andmax(

ι

1,

ι

2)=max(n(

ǫ

1),n(

ǫ

2))=n(min(

ǫ

1,

ǫ

2)).

Sideedges: I(min(

α

1,

α

2),max(

ι

1,

ι

2))≥I(

α

1,

ι

1)=1;

I(min

(

ǫ

1

,

ǫ

2

),

max

(o

1

,

o2

)) ≥

I(

ǫ

1

,

o1

) =

1

.

Topedge:C(min(

α

1,

α

2),min(

ǫ

1,

ǫ

2))≤C(

α

1,

ǫ

1)=1.

Bottomedge: D(max(

ι

1,

ι

2),max(o1,o2))≥D(

ι

1,o1)=0. ✷

Proposition 21.Giventwograded cubesofopposition ofthe form

α

1

ι

1

ǫ

1o1

α

′₁

ι

′₁

ǫ

₁′o′₁ and

α

2

ι

2

ǫ

2o2

α

′₂

ι

′₂

ǫ

₂′o′₂ thenthe functions

min(

α

1,

α

2),max(

ι

1,

ι

2),min(

ǫ

1,

ǫ

2),max(o1,o2)min(

α

′₁,

α

₂′),max(

ι

′₁,

ι

′₂),min(

ǫ

₁′,

ǫ

₂′),max(o′₁,o′₂)makeanothergradedcube

ofopposition.

Proof. From the previous proposition, the functions min(

α

1,

α

2), max(

ι

1,

ι

2), min(

ǫ

1,

ǫ

2) max(o1,o2) and min(

α

₁′,

α

′₂),

max(

ι

′

1,

ι

′2),min(

ǫ

′1,

ǫ

2′)max(o′1,o′2)formfrontandbackfacetsofsquaresofopposition. Moreover,

I(D(min

(

α

1

,

α

2

),

min

(

α

1′

,

α

2′

)),

C(max

(

ι

1

,

ι

2

),

max

(

ι

1′

,

ι

′2

))) ≥

I

(D(

α

1

,

α

1′

),

C

(

ι

1

,

ι

′1

)) =

1

.

So duetoProposition 19,wehavedefinedanewgradedcubeofopposition. ✷

4.2. Cubesofoppositioningradedpossibilitytheory

Nowwe aregoing toconsider thecase whenthestatements associated tothevertices ofacubeof opposition arethe fourset functionsofpossibilitytheory, forcrispevents,aspersubsection3.2,and alsoextendedtofuzzy events,ineachof thetwoformsthatmakesense,asreviewedintheprevioussection.

Inthefollowing,weconsideraset X ,ascaleL,anegation1−on L,apossibilitydistribution

π

:X→L.

Crisp events. Let us extend the cube of opposition for 0–1 possibility theory on Fig. 3 to graded qualitative possibility L-valueddegrees. When weconsider crisp events, the (internal)conjunction definingthe possibility functionisthe mini-mumandthe(internal)implicationassociatedbysemi-dualityisKleene–Dienesimplicationa→K Db=max(1−a,b).Ifthe

distributions

π

and

π

=1−

π

arenormalized(there exists x andx′ _such _that

_π

₍_x₎₌_{1 and}

_π

₍_x′₎₌₀₎_then_we_obtain _a possibilisticcubeofopposition inthesenseofProposition 19,usingthefollowingexternalconnectives:

• n(a)=1−a.

• Theentailmentpropertiesontheside facetsareexpressedbymeans oftheGödelimplication,intheforma→Gb=1

thusexpressinginequalitiesa≤b.

• Theconjunctiondefiningtheconstraints onthetopfacetsisthesemi-dualofGödelimplication,⊗G.

• Thedisjunctiondefiningtheconstraints onthebottomfacetsistheDeMorgandual ⊕G of⊗G.

WecannotapplytheconditionsofProposition 19toFig. 3,usingKleene–Dienesimplicationforexternalimplication,because on thesidefacets,evenifwehavethat max(1−N(A),5(A))=1,wedonothavethat max(1− 1(A),5(A))=1,sincewe only have0< 1(A)≤ 5(A)<1,and likewise0<N(A)≤ ∇(A)<1.

Likewise, for the constraints on the top facet, we do have that min(N(A),N(A))=0, but generally, for instance, min(N(A),1(A))6=0. However we do have that N(A)≤1− 1(A), so that N(A)⊗G1(A)=N(A)⊗GN(A)=0. By

du-ality,wedogetthat5(A)⊕G∇(A)= 5(A)⊕G5(A)=1 forthebottomfacet.