Rabat
Faculté des Sciences, 4 Avenue Ibn Battouta B.P. 1014 RP, Rabat – Maroc Tel +212 (0) 537 77 18 34/35/38, Fax: +212 (0) 537 77 42 61, http://www.fsr.ac.ma
N° d’ordre : 2568
THÈSE DE DOCTORAT Présentée par :
Ali El Akadi
Discipline : Sciences de l’ingénieur Spécialité : Informatique et Télécommunications
Sujet de la thèse :
Publiquement défendue le 31/03/2012 devant le jury composé de :
Président :
Driss ABOUTAJDINE PES, Université Mohammed-V Agdal - Rabat
Examinateurs :
Boujemâa ACHCHAB PES, Université Hassan 1er - Settat
Abderrahim EL QADI PH, Université Moulay Ismaïl - Meknès Raja TOUAHNI PES, Université Ibn Tofail - Kénitra
Mohammed ABBAD PES, Université Mohammed-V Agdal - Rabat Ahmed HAMMOUCH PES, Université Mohammed-V Souissi - Rabat Abdeljalil EL OUARDIGHI PH, Université Hassan 1er - Settat
Le problème de la sélection de variables en classification se pose généralement lorsque le nombre de variables pouvant être utilisé pour expliquer la classe d'un individu, est très élevé. Les besoins ont beaucoup évolué ces dernières années avec la manipulation d'un grand nombre de variables dans des domaines tels que les données génétiques ou le traitement d’image. Néanmoins si l’on doit traiter des données décrites par un grand nombre de variables, les méthodes classiques d’analyse, d’apprentissage ou de fouille de données peuvent se révéler inefficaces ou peuvent conduire à des résultats peu précis. Dans cette thèse, nous proposons des méthodes innovantes pour réduire la taille initiale des données et pour sélectionner des ensembles de variables pertinents pour une classification supervisée.
Notre première contribution concerne la proposition d’une approche hybride pour la sélection de gènes dans le cadre de la classification de différents types de tumeurs (reconnaissance tissu sain/tissu cancéreux ou distinction entre différents types de cancers). Cette approche est basée sur la combinaison de l’algorithme MRMR (redondance minimal-pertinence maximale) et d’une recherche génétique utilisant un classifieur SVM (Support Vector Machine) pour l’évaluation de la pertinence des sous-ensembles candidats. Les performances de notre approche ont été évaluées sur 5 jeux de données publiques du domaine de l’oncologie.
Notre deuxième contribution porte sur une nouvelle approche de sélection des caractéristiques pour la reconnaissance faciale. Au début, la transformée en DCT (Discret Cosine Transform) est appliquée pour convertir l'image en domaine fréquentiel, ensuite une première réduction de la dimensionnalité est opérée par le rejet des composant à haute fréquence. Enfin, un nouveau critère appelé PMI (Ponderated Mutual Information) est utilisé pour sélectionner les coefficients les plus pertinents et moins redondants à partir des coefficients DCT. L’évaluation des performances de l’approche proposée, en particulier le critère PMI, a été effectuée sur une base d’images constituée d’un mélange de deux bases publiques ORL et YALE.
Les différentes expérimentations que nous avons menées montrent de très bonnes performances des approches proposées, surtout pour la sélection des gènes.
Mots-clés : Sélection de variables, Classification supervisée, Puces à ADN, Information mutuelle,
The problem of feature selection for classification is generally arises when the number of features is large. Needs have changed significantly in recent years with the handling of a large number of features in areas such as genetic data or image processing. However if we must treat the data described by many features, the classical methods of analysis, learning or data mining may be ineffective or may lead to imprecise results. In this thesis, we propose innovative methods to reduce the size of initial data and to select relevant sets of features for supervised classification.
Our first contribution concerns the proposal of a hybrid approach for gene selection in classification of different tumor types (recognition of healthy/cancer tissue or distinguish between different types of cancers). This approach is based on the combination of the MRMR algorithm (Minimum Redundancy-Maximum Relevance) and genetic research using SVM (Support Vector Machine) to evaluate the relevance of candidate subsets. The proposed method was tested for tumor classification on five open datasets.
Our second contribution concerns a new feature selection approach for face recognition. At first, the DCT (Discrete Cosine Transform) is applied to convert the image into frequency domain, then a first dimensionality reduction is carried out by the elimination of the high-frequency component. Finally, a new criterion called PMI (Ponderated Mutual Information) is used to select the most relevant and less redundant coefficients from the DCT coefficients. Evaluation of the proposed approach, in particular PMI criterion, was performed on a mixture of two public face databases ORL and YALE.
Experimental results show that the proposed approaches have very good performances.
Keywords: Feature selection, Classification, microarray data, Mutual information, Genetic Algorithms, Face
Les travaux de recherche présentés dans cette thèse ont été effectués au sein du Laboratoire de Recherche en Informatique et Télécommunications (LRIT) à la Faculté des Sciences de Rabat (FSR).
Je tiens à exprimer mes sincères remerciements :
Au Professeur Driss Aboutajdine, mon Directeur de thèse et Directeur du LRIT. Sans l’environnement de recherche qu’il a su créer, je n’aurais pas pu me lancer dans la préparation de cette thèse.
Au Professeur Abdeljalil El Ouardighi mon encadrant de thèse pour son suivi, ses recommandations, sa patience et sa disponibilité tout au long de cette thèse.
Au Professeur Boujemâa Achchab de la Faculté des Sciences Economiques, Juridiques et Sociales de Settat et au Professeur Abderrahim El Qadi de l’Ecole Supérieure de Technologie de Meknès, qui ont accepté de juger ce travail et d’en être les rapporteurs et qui m’ont fait l’honneur d’être parmi les membres du Jury.
Au professeur Raja Touahni de la Faculté des Sciences de Kénitra, au Professeur Mohammed Abbad de la Faculté des Sciences de Rabat et au Professeur Ahmed Hammouch de l’ENSET de Rabat, qui ont bien accepté de faire partie du jury.
Enfin, je voudrais exprimer mes plus profonds remerciements à ma mère, à ma femme, à mes enfants, à ma famille et à ma belle-famille pour leurs sentiments, leurs soutiens et leurs encouragements pendant tout le temps où j’ai effectué cette thèse.
Résumé ... i
Abstract ... ii
Avant-propos ... iii
Tables des matières ... iv
Liste des abréviations ... vi
Liste des figures ... viii
Liste des tableaux ... ix
Introduction générale ... 10
Chapitre 1. Fouille de données et classification ... 15
1.1 Introduction ... 16
1.2 Fouille de données ... 16
1.2.1 Définitions ... 17
1.2.2 Processus d’extraction de connaissances ... 18
1.2.3 Tâches de la fouille de données... 20
1.3 Classification ... 21
1.3.1 Buts et modalités de la classification ... 22
1.3.2 La classification, un domaine multidisciplinaire ... 23
1.4 La classification non supervisée ... 25
1.4.1 Les méthodes hiérarchiques ... 26
1.4.2 Le partitionnement ... 27
1.5 La classification supervisée... 29
1.5.1 Formalisation mathématique ... 29
1.5.2 Le problème de la généralisation... 29
1.5.3 Les techniques de la classification supervisée ... 32
1.6 Conclusion ... 42
Chapitre 2. Sélection de variables pour la classification supervisée ... 43
2.1 Introduction ... 44
2.2 Pertinence et redondance de variables ... 44
2.2.2 Redondance de variables ... 46
2.3 Sélection de variables ... 48
2.3.1 La sélection vue comme un problème d’optimisation ... 49
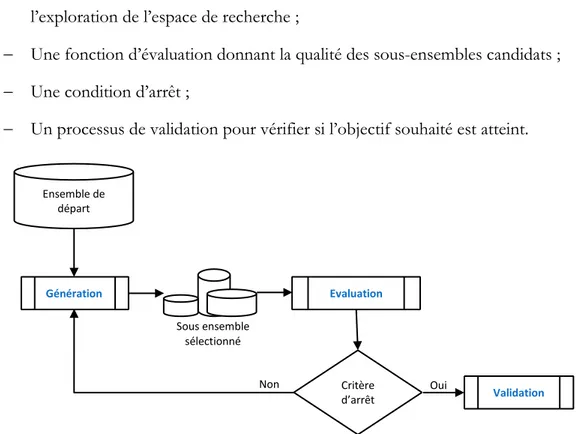
2.3.2 Processus global de la sélection de variables ... 50
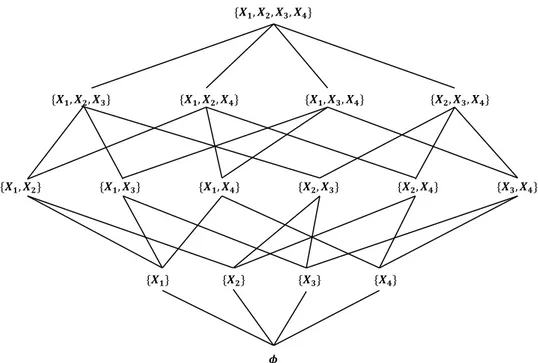
2.3.3 Génération des sous-ensembles de variables ... 51
2.3.4 Evaluation des sous-ensembles ... 54
2.3.5 Critère d’arrêt... 57
2.4 Principaux algorithmes existants ... 58
2.4.1 Les algorithmes d’ordonnancement de variables ... 58
2.4.2 Les algorithmes de construction du plus petit sous-ensemble de variables ... 58
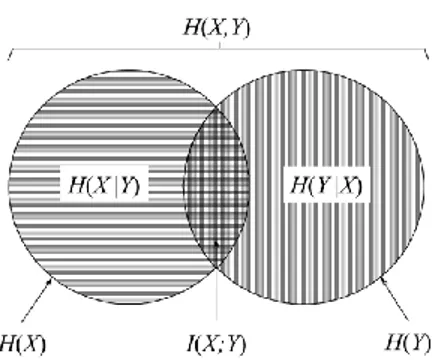
2.4.3 Sélection de variables par information mutuelle ... 60
2.5 Conclusion ... 65
Chapitre 3. Contribution à la sélection de gènes pour les puces à ADN ... 66
3.1 Introduction ... 67
3.2 Technologie des puces à ADN ... 68
3.3 Sélection des gènes pour les puces à ADN ... 69
3.4 L’approche proposée ... 70
3.4.1 Structure générale de l’approche proposée ... 70
3.4.2 Filtrage des gènes par l’algorithme MRMR ... 71
3.4.3 Sélection des sous-ensembles pertinents par Algorithme Génétique ... 73
3.4.4 Expérimentations ... 78
3.5 Conclusion ... 87
Chapitre 4. Contribution à la sélection de variables pour la reconnaissance faciale ... 88
4.1 Introduction ... 89
4.2 La reconnaissance faciale ... 90
4.2.1 Dimensionnalité de l'espace visage ... 90
4.2.2 Principe de fonctionnement d’un système de reconnaissance de visage ... 91
4.2.3 Méthodes de reconnaissance faciale ... 92
4.3 Approche proposée ... 94
4.3.1 Extraction des caractéristiques par DCT ... 95
4.3.2 Sélection des caractéristiques utilisant le critère PMI ... 96
4.3.3 Expérimentations ... 98
4.4 Conclusion ... 103
Conclusion générale et perspectives ... 105
Bibliographie ... 108
ABB Automatic Branch and Band ACP Analyse en Composante Principale ADALINE ADAptive LInear NEuron ADN Acide DésoxyriboNucléique AG Algorithme Génétique
ALL Acute Lymphoblastic Leukemia AML Acute Myeloid Leukemia BE Backward Elimination BN Baysien Naïf
CART Classification And Regression Tree
CHAID CHi-squared Automatic Interaction Detector CMIM Conditional Mutual Information Maximisation DCT Discret Cosine Transform
DNA Deoxyribose Nucleic Acid DTM Decision Tree Method
ECD Extraction de Connaissances à partir des Données FS Forward Selection
GA Genetic Algorithm
KDD Knowledge Discovery in Databases LBP Local Binary Pattern
KNN K-Nearest Neighbor LDA Linear Discriminant Analysis LOOCV Leave-One-Out Cross Validation LVF Las Vegas Filter
LVW Las Vegas Wrapper
MIFS Mutual Information Feature Selector MPM Malignant Pleural Mesothelioma
MRMR Minimum Redundancy Maximum Relevance NCI National Cancer Intitute
NSCLC Non Small Cell Lung Cancer PMI Ponderated Mutual Information PSO Particle Swarm Optimization SIFT Scale Invariant Feature Transform SVM Support Vector Machine
Figure 1-1 : Différentes étapes du processus ECD ... 18
Figure 1-2 : Représentation d’un réseau de neurones multicouches ... 36
Figure 1-3 : Représentation de l’hyperplan séparant linéairement les données dans l’espace des variables... 40
Figure 2-1 : Catégorisation des variables ... 48
Figure 2-2 : Processus de sélection de variables ... 50
Figure 2-3 : Sous-ensembles de variables possibles à partir d’un ensemble de 4 variables ... 53
Figure 2-4 : Digramme de Venn ... 61
Figure 3-1 : Schéma général de l’approche MRMR-GA ... 71
Figure 3-2 : Eléments d’un algorithme génétique ... 75
Figure 3-3 : Croisement à 1 point. ... 77
Figure 3-4 : Exemple de mutation en 3 points... 78
Figure 3-5 : Taux de classification par un classifieur SVM pour les données Lymphoma ... 82
Figure 3-6 : Taux de classification par un classifieur SVM pour les données NCI ... 82
Figure 3-7 : Taux de classification par un classifieur SVM pour les données Lung ... 82
Figure 3-8 : Taux de classification par un classifieur SVM pour les données Leukemia ... 82
Figure 3-9 : Taux de classification par un classifieur SVM pour les données Colon ... 82
Figure 3-10 : Moyenne du taux de classification par un classifieur SVM pour toutes les données ... 82
Figure 3-11 : Taux de classification par un classifieur BN pour les données Lymphoma ... 83
Figure 3-12 : Taux de classification par un classifieur BN pour les données NCI ... 83
Figure 3-13 : Taux de classification par un classifieur BN pour les données Leukemia ... 83
Figure 3-14 : Taux de classification par un classifieur BN pour les données Lung... 83
Figure 3-15 : Taux de classification par un classifieur BN pour les données Colon ... 83
Figure 3-16 : Moyenne du taux de classification par un classifieur BN pour toutes les données ... 83
Figure 4-1 : Schéma général de reconnaissance de visage ... 91
Figure 4-2 : Schéma général de l’approche proposée... 94
Figure 4-3 : Passage du domaine spatial au domaine fréquentiel... 96
Figure 4-3 : Diagramme de Venn pour trois variables ... 97
Figure 4-4 : Exemples de la base des visages (ORL+YALE) ... 99
Figure 4-5 : Comparaison des critères de sélection en utilisant un classifieur SVM ... 102
Tableau 3-1 : Matrice d’expression des gènes ... 68
Tableau 3-2 : Caractéristiques des jeux de données ... 79
Tableau 3-3 : Paramètre de l’algorithme génétique ... 80
Tableau 3-4 : Taux de classification (%) sans sélection de gènes ... 81
Tableau 3-5 : Taux de classification (%) avec 15 premiers gènes sélectionnés pour les 5 jeux de données ... 84
Tableau 3-6 : Moyenne du taux de classification (%) sur l’ensemble de données pour un nombre différent de gènes sélectionnés ... 84
Tableau 3-7 : Comparaison avec d’autres approches ... 86
Tableau 4-1 : Représentation matricielle de la base des images (visages) ... 100
Tableau 4-2 : Taux de classification sans sélection de caractéristiques ... 101
Contexte de travail :
Cette thèse s’inscrit dans le cadre de l’Extraction de Connaissances à partir des Données (ECD), domaine connu sous le nom de Knowledge Discovery in Databases en anglais (KDD). Il s’agit d’une discipline qui se situe à l’intersection de différents domaines tels que l’informatique, l’intelligence artificielle, l’analyse de données, les statistiques et la théorie des probabilités. L’ECD est appelé communément fouille de données ou datamining et a pour objectif l’extraction d’un savoir ou d’une connaissance à partir de grandes quantités de données, par des méthodes automatiques ou semi-automatiques, et l’utilisation industrielle ou opérationnelle de ce savoir. La finalité de l’ECD est de pouvoir traiter des données brutes et volumineuses, et à partir de ces données établir des connaissances directement utilisables par un expert du domaine étudié.
Cependant, le processus d’ECD ne se passe pas sans encombre. De nos jours, l’évolution de l’informatique et des technologies de stockage connait une explosion de volumes des données. Il est maintenant possible d’analyser de grandes quantités de données de dimension élevée grâce aux performances accrues des ordinateurs. Néanmoins si l’on doit traiter des données décrites par un très grand nombre de variables, les méthodes classiques d’analyse, d’apprentissage ou de fouille de données peuvent se révéler inefficaces ou peuvent conduire à des résultats inexacts. De ce fait, il est nécessaire de réduire la dimension des données en sélectionnant les variables les plus intéressantes pour le
problème étudié (John, et al., 1994); (Blum & Langly, 1997); (Dash & Liu, 2006); (Cios, et
al., 2007).
La sélection de variables consiste à choisir parmi l’ensemble global de variables, un sous-ensemble de variables pertinentes pour le problème étudié. Cette problématique peut concerner différentes tâches de fouille de données, mais dans notre cas, nous traitons
uniquement la sélection de variables réalisée en classification supervisée qui consiste à déterminer, sur une base d’un nombre fini d’individus, la relation entre un ensemble de variables explicative et une variable à expliquer qui s’appelle la classe.
Motivations et objectifs :
Au début des années 90, la majorité des travaux sur la sélection de variables portait sur des domaines souvent décrits par quelques dizaines de variables. Ces dernières années, de par l’accroissement des capacités de recueil, de stockage et de manipulation des données, la situation a beaucoup changé. Il n’est plus rare de rencontrer dans certains domaines, en particulier en bio-informatique, en traitement d’image et en fouille de textes, des centaines voire des milliers de variables. Par conséquent, de nouvelles techniques de sélection de variables sont apparues pour tenter d’aborder ce changement d’échelle et de traiter notamment la prise en compte des variables redondantes et des variables non pertinentes. Plusieurs domaines qui intéressent beaucoup la communauté de la fouille de données fournissent des données qui sont décrites par des milliers de variables. C’est le cas par exemple pour le traitement des textes dont les applications issues du web sont très nombreuses. C’est aussi le cas lorsqu’on veut analyser des images de haute résolution. Enfin un domaine plus récent, celui de la bio-informatique fournit également des données de très grande dimension où il n’est pas rare d’avoir à manipuler plusieurs milliers de variables.
Dans cette thèse, les domaines qui ont stimulé notre intérêt pour la problématique de la sélection de variables en vue d’une classification sont la bio-informatique, notamment la génétique, et le traitement d’image, notamment la reconnaissance faciale. Pour les données génétiques, les variables représentent l’expression de gènes à ADN par leur séquence biologique de nucléotides pour un certain nombre de patients. Une classification typique est la séparation des patients sains des patients atteints d’une certaine pathologie basée sur leur « profil génétique ». Dans ce type de jeu assez difficile à construire, on ne possède souvent guère plus de 100 patients pour constituer un jeu d’apprentissage et un jeu de test ; en revanche, le nombre de variables manipulées peut varier de 2000 à 60000. En ce qui concerne la reconnaissance faciale, les individus manipulés sont des images et les variables
sont des caractéristiques extraites de ces images. Dans ce type d’application le nombre de caractéristiques est souvent très élevé et dépend de la technique d’extraction utilisée.
Contribution de la thèse :
Dans les domaines d’analyse des puces à ADN ou de traitement d’images, les données présentent plusieurs variables, ce qui nécessite de proposer des méthodes innovantes pour la sélection des variables les moins redondantes et les plus pertinentes pour accomplir la tâche de classification. Ainsi, nous proposons deux nouvelles méthodes pour réaliser au mieux cette sélection.
Pour la sélection des gènes à ADN nous avons proposé une approche hybride (El Akadi, et
al., 2011) pour la sélection d’un sous ensemble de gènes optimal non redondant et fournissant de bonnes performances en classification. L’approche proposée est basée sur la combinaison de la méthode de filtrage MRMR pour Minimum Redundancy–Maximum
Relevance (Peng, et al., 2005) et d’une méthode de type enveloppe « wrapper » basée sur
une stratégie de recherche utilisant un algorithme génétique (AG) et le classifieur SVM pour l’évaluation des sous-ensembles candidats. Cette approche peut être considérée comme un processus séquentiel en deux étapes qui utilise des techniques complémentaires pour réduire graduellement l’espace de recherche et sélectionner un sous ensemble pertinent de gènes.
Etape 1 : C’est une étape de prétraitement permettant de filtrer les gènes qui ne
sont pas informatifs et d’éliminer les gènes redondants, par exemple des gènes dont les niveaux d’expression sont uniformes quelle que soit la classe. Le résultat de ce prétraitement est un ensemble de gènes classés par ordre de pertinence selon le critère MRMR. Il s’agit d’une étape préliminaire pour la réduction des données de puces à ADN.
Etape 2 : Cette étape se traduit par l’utilisation d’une méthode enveloppe où un
algorithme génétique explore, à partir des gènes retenus par le pré-filtrage précédent, des sous-ensembles candidats et chaque candidat est évalué grâce à un classifieur SVM. Le taux de classification indique si le sous-ensemble candidat permet une bonne discrimination des classes.
Pour la sélection des caractéristiques permettant une meilleure reconnaissance faciale nous avons proposé un nouveau critère de sélection basé sur la théorie d’information appelé
PMI pour Ponderated Mutual Information (El Akadi, et al., 2010). Le critère proposé est
combiné avec la transformée en cosinus discret (DCT) pour sélectionner les caractéristiques permettant d’obtenir les meilleurs taux de classification. Au début, la transformée en DCT est appliquée pour convertir l'image en domaine fréquentiel, ensuite une première réduction de la dimensionnalité est opérée par le rejet des composants à haute fréquence. Enfin, le critère PMI est utilisé pour sélectionner les caractéristiques discriminantes à partir des coefficients DCT.
Organisation du manuscrit :
Ce document est structuré en quatre chapitres. Les deux premiers ont pour objectif d’exposer le contexte et la problématique de la sélection de variables ainsi que les travaux effectués dans cet essor. Les deux derniers chapitres sont dédiés à nos contributions dans ce sujet.
Chapitre 1 : dans ce chapitre nous introduisons et nous exposons les techniques de fouille de données et de la classification. Nous mettons l’accent sur la classification supervisée et particulièrement sur les algorithmes qui seront utilisés dans les chapitres qui suivent. Chapitre 2 : ce chapitre est consacré à la présentation des concepts de base d’un problème de sélection de variables et les notions nécessaires à la construction d’un algorithme de sélection de variables. Nous définissons les différentes procédures de génération que nous trouvons dans la littérature ainsi que les différentes mesures de pertinence rencontrées. Nous illustrons les principaux algorithmes de sélection de variables existants et plus particulièrement les algorithmes utilisant l’information mutuelle, mesure qui a été adoptée dans les approches que nous avons proposées.
Chapitre 3 : dans ce chapitre nous présentons note première contribution relative à la sélection de gènes pour les puces à ADN. Tout d’abord nous introduisons la technologie des puces à ADN et nous montrons l’importance et la nécessité de la sélection de variables dans ce domaine. Ensuite nous présentons notre approche hybride basée sur un filtrage des gènes par l’algorithme MRMR et utilisant un algorithme génétique pour la recherche des sous-ensembles les plus pertinents en définissant tous les points nécessaires à son
implémentation. Nous présentons enfin les performances, de l’approche proposée, obtenues sur des bases de données d’oncologie.
Chapitre 4 : ce chapitre traite le problème d’extraction et de sélection des caractéristiques pour la reconnaissance faciale. Nous présentons un nouveau critère basé sur la théorie d’information permettant de sélectionner les caractéristiques discriminantes à partir des coefficients DCT. Enfin nous présentons les résultats expérimentaux pour l’évaluation de l’approche proposée.
Nous terminons cette thèse par une synthèse de nos différentes contributions, et nous donnons quelques perspectives qui peuvent donner suite à ces travaux.
Chapitre 1. Fouille de données et classification ... 15
1.1 Introduction ... 16
1.2 Fouille de données ... 16
1.2.1 Définitions ... 17
1.2.2 Processus d’extraction de connaissances ... 18
1.2.3 Tâches de la fouille de données ... 20
1.3 Classification ... 21
1.3.1 Buts et modalités de la classification ... 22
1.3.2 La classification, un domaine multidisciplinaire ... 23
1.4 La classification non supervisée ... 25
1.4.1 Les méthodes hiérarchiques ... 26
1.4.2 Le partitionnement ... 27
1.5 La classification supervisée ... 29
1.5.1 Formalisation mathématique ... 29
1.5.2 Le problème de la généralisation ... 29
1.5.3 Les techniques de la classification supervisée ... 32
1.6 Conclusion... 42
1.1 Introduction
La fouille de données (ou datamining) consiste à rechercher et à extraire de l'information, utile et inconnue, à partir de gros volumes de données stockées dans des bases ou des entrepôts de données. Le développement récent de la fouille de données (depuis le début des années 1990) est lié à plusieurs facteurs : une puissance de calcul importante est disponible sur les ordinateurs ; le volume des bases de données augmente énormément ; l'accès aux réseaux de taille mondiale, ces réseaux ayant un débit sans cesse croissant, qui rendent le calcul distribué et la distribution d'information sur échelle mondiale variable. La fouille de données a aujourd'hui une grande importance économique du fait qu'elle permet d'optimiser la gestion des ressources humaines et matérielles.
La classification est la tâche la plus importante de la fouille de données et consiste à examiner des caractéristiques d’un objet afin de l’affecter à une classe d’un ensemble donné.
1.2 Fouille de données
Depuis quelques années, une masse grandissante de données sont générées de toute part par les entreprises, que ce soit des données bancaires, telles que les opérations de carte de crédit, ou bien des données industrielles, telles que des mesures de capteurs sur une chaîne de production, ou toutes autres sortes de données possibles et imaginables. Ce flot continu et croissant d’informations peut être maintenant stocké et préparé à l’étude, grâce aux nouvelles techniques d’entrepôt de données (ou data wharehouse). Les techniques usuelles d’analyse de données, développées pour des tableaux de tailles raisonnables ont largement été mises à mal lors de l’étude de tant de données. En effet, alors que le principal objectif de la statistique est de prouver une hypothèse avancée par un expert du domaine, et donc de confirmer une connaissance déjà connue ou bien présumée, le but de la fouille de données est maintenant de découvrir, au sens propre du terme, des nouvelles connaissances. Et ceci sans faire appel à des hypothèses préconçues. Ce nouveau concept de fouille de données, bien qu’il paraît révolutionnaire pour certains, est en fait une autre vision et une autre utilisation de méthodes existantes, et combinées.
Ainsi, au vue de l’émergence de ces deux champs d’application (fouille et entrepôt de données), une idée nouvelle s’est faite. Pourquoi ne pas associer toutes ces techniques afin de créer des méthodes puissantes de recherche de connaissances, intégrant toutes les étapes, du recueil des données à l’évaluation de la connaissance acquise. C’est ainsi qu’est né le terme d’Extraction des Connaissances à partir des Données (ECD), ou en anglais Knowledge Discovery in Database (KDD).
1.2.1 Définitions
L’extraction de connaissances à partir de données consiste à parcourir d’immenses volumes de données contenus dans une base, à la recherche de connaissances. C’est une discipline qui se situe à l’intersection de différents domaines tels que l’informatique, l’intelligence artificielle, l’analyse de données, les statistiques, la théorie des probabilités, l’optimisation, la reconnaissance de formes, les bases de données et l’interaction Homme-Machine,… Il est ici important de différencier les trois termes suivants :
Donnée : valeur d’une variable pour un objet (comme le montant d’un retrait
d’argent par exemple) ;
Information : résultat d’analyse sur les données (comme la répartition géographique
de tous les retraits d’argent par exemple) ;
Connaissance : information utile pour l’entreprise (comme la découverte du
mauvais emplacement de certains distributeurs).
Ainsi à l’aide de l’ECD, nous pouvons à partir de données sur lesquelles nous ne faisons aucune hypothèse, obtenir des informations pertinentes, et de celles-ci, tirer des connaissances.
Fayyad (Fayyad, et al., 1996) donne une définition de l’ECD, que la communauté
scientifique francophone traduit de la manière suivante : L’ECD est le processus non trivial, interactif et itératif qui permet d’identifier des modèles valides, nouveaux, potentiellement utiles et compréhensibles à partir de bases de données massives.
1.2.2 Processus d’extraction de connaissances
Le terme processus signifie que l’ECD se décompose en plusieurs opérations (voir Figure 1-1).
Figure 1-1 : Différentes étapes du processus ECD
Ces opérations peuvent être regroupées en cinq phases majeures :
Compréhension du domaine étudié : Lors de cette phase, une analyse du problème
et des contraintes qui lui sont attachées doit permettre la collecte de données brutes. Ces données se composent d’individus ou objets et des variables qui leurs sont associées et qui doivent permettre de décrire au mieux le problème traité. L’utilisateur ne sait pas encore si les données qu’il a réunies seront toutes adaptées à son problème ni si ces données seront suffisantes. Nous sommes en présence des données initiales.
Prétraitement : Lors de cette phase, un prétraitement est effectué à la fois sur les
individus et sur les variables. Cette phase de prétraitement consiste à nettoyer les Connaissances Données sélectionnées Modèles Données brutes Données transformées Sélection Préparation Transformation Data Mining Evaluation Données préparées
données, les mettre en forme, traiter les données manquantes, échantillonner les individus, sélectionner et construire des variables. On obtient ainsi un ensemble de données cibles. Cette phase a une place importante au sein du processus d’ECD car c’est elle qui va déterminer la qualité des modèles construits lors de la phase de fouille de données. Elle peut prendre jusqu’à 60% du temps dédié au processus d’ECD.
Fouille de données : Cette phase intègre le choix de la méthode d’apprentissage qui
va être employée et son paramétrage. Ces choix doivent tenir compte des contraintes liées au domaine étudié ainsi que des connaissances que les experts du domaine peuvent nous fournir. L’algorithme sélectionné est alors appliqué aux données cibles dans le but de rechercher les structures sous-jacentes des données et de créer des modèles explicatifs ou prédictifs. Certes la fouille de données n’est qu’une étape du processus de l’ECD, mais elle est sans conteste le cœur et le moteur de tous ce processus.
Post traitement : Cette phase consiste en l’évaluation et la validation des modèles
construits lors de la phase précédente. Ce n’est qu’après cette phase que les données et l’information que l’on en a tirée deviennent des connaissances.
Interprétation et exploitation des résultats : L’interprétation des résultats qui sont
sous forme de modèles ou de règles permet d’obtenir des connaissances. Ce sont ces connaissances qui seront fournies à l’utilisateur.
La finalité de l’ECD est de pouvoir traiter des données brutes et volumineuses, et à partir de ces données, d’établir des connaissances directement utilisables par un expert ou un non expert du domaine étudié.
Les techniques d’ECD deviennent de plus en plus prisées au sein du monde industriel. En effet, les promesses de l’ECD en terme de valorisation de l’information ne peuvent laisser insensibles les acteurs industriels. Tout d’abord parce que l’information apparaît, de nos jours, comme un élément stratégique déterminant. Ensuite parce que les avancées technologiques en informatique permettent d’augmenter les capacités de stockage et de calcul. Ainsi, si l’on considère comme exemple l’ensemble des tickets de caisse d’un supermarché sur une période 10 ans, il est aisé d’imaginer la quantité de données présentes, la diversité des caractéristiques, et donc la difficulté conséquente d’une exploitation de
l’information présente. Pourtant, on dispose là d’une immense source d’information, à savoir une quantité suffisamment importante de données pour établir une classification pertinente de la clientèle ainsi que son comportement typique. Le processus d’ECD résout de manière efficace ces difficultés et fournit les connaissances attendues.
1.2.3 Tâches de la fouille de données
Le choix des techniques de fouille de données à appliquer dépend de la tâche particulière à accomplir et des données disponibles pour l’analyse. La première étape consiste à traduire un objectif en une ou plusieurs tâches.
Les principales tâches de fouille de données sont :
La classification (classification supervisé): consiste à examiner des caractéristiques
d’un objet afin de l’affecter à une classe d’un ensemble prédéfini. Les classes sont discrètes ;
L’estimation : permet d’obtenir une variable continue en combinant les données en
entrée. L’estimation est souvent utilisée pour effectuer une tâche de classification en utilisant un barème ;
La prédiction : ressemble à la classification et à l’estimation, mais les
enregistrements sont classés selon un certain comportement futur prédit ou à une valeur future estimée. s’appuie sur le passé et le présent mais son résultat se situe dans un futur généralement précisé.
Le regroupement par similitudes : consiste à déterminer les objets qui vont
naturellement ensemble ;
La segmentation (classification automatique) : consiste segmenter une population
hétérogène en sous-populations homogènes. Contrairement à la classification, les sous populations ne sont pas préétablis
La description : il s’agit de décrire les données d’une base complexe. Cette tâche
engendre souvent une exploitation supplémentaire en vue de fournir des explications.
Une fois les tâches identifiées, elles sont utilisées pour restreindre la gamme des méthodes prises en compte. En termes généraux, notre but est de sélectionner la technique de fouille de données qui minimise le nombre et la difficulté des transformations de données qui doivent être effectuées pour produire de bons résultats. Les données brutes peuvent demander différentes manières d’être résumées, les valeurs manquantes doivent être traitées, les données redondantes ou non pertinentes doivent être éliminées. Ces transformations sont nécessairement indépendantes de la technique choisie.
1.3 Classification
La classification est l’une des techniques les plus anciennes d’analyse et de traitement de
données. Plusieurs définitions ont été proposées par les spécialistes du domaine :
Pour Mari et Napoli (Mari & Napoli, 1996): "Effectuer une classification, c'est mettre en évidence des relations entre des objets, et entre ces derniers et leurs paramètres".
Un problème de classification selon Henriet (Henriet, 2000): "consiste à affecter
des objets, des candidats, des actions potentielles à des catégories ou des classes prédéfinies".
Michie et al. (Michie, et al., 1994) ont un point de vue axé sur l'apprentissage, ils
définissent la classification par : "La classification est l'action de regrouper en
différentes catégories des objets ayant certains points communs ou faisant partie
d'un même concept,sans avoir connaissance de la forme ni de la nature des classes au préalable, on parle alors de problème d'apprentissage non supervisé ou de classificationautomatique, ou l'action d'affecter des objets à des classes prédéfinies,
onparle dans ce cas d'apprentissage supervisé ou de problème d'affectation" .
Retenons aussi la définition de Bognar (Bognar, 2003): "Le processus de
classification cherche à mettre en évidence les dépendances implicites qui existent
entre les objets, les classes entre elles, les classes et les instances. La classification
recouvre les processus de reconnaissance de la classe d'un objet, et l'insertion
reconnaître un objet en identifiant ses caractéristiques, relativement à la hiérarchie
étudiée. La classification fait intervenir un processus de décision d'appartenance"
Nous présentons dans cette section certaines distinctions relatives à la classification, et
nous précisons des éléments de terminologie à ce champ multidisciplinaire. Nous
détaillons, plus particulièrement, les méthodes de la classification supervisée qui seront utilisées dans les problématiques traitées dans ces travaux de thèse.
1.3.1 Buts et modalités de la classification
La classification repose sur des objets à classer. Les objets sont localisés dans un espace de variables (ont dit aussi attributs, caractéristiques ou critères). Il s’agit de les localiser dans un espace de classes. Ce problème n’a de sens que si on pose l’existence d’une correspondance entre ces deux espaces. Résoudre un problème de classification, c’est trouver une application de l’ensemble des objets à classer, décrits par les variables descriptives choisies, dans l’ensemble des classes. L’algorithme ou la procédure qui réalise cette application est appelé classifieur.
Nous appellerons :
classificateur : une règle établie (estimée) de classification, c’est-à-dire une fonction
sur l’espace des caractéristiques vers l’espace des classes ;
classification : la construction d’un classificateur ;
classement : la mise en œuvre d’un classificateur existant.
Généralement, l’inférence statistique traditionnelle peut couvrir plusieurs problématiques :
exploratoire : déceler des relations hypothétiques ;
prédictive : valider la performance globale d’un système de relations ;
explicative : valider des composantes détaillées d’un système de relations·
comprendre leurs contributions à ce système. On retrouve des distinctions voisines en classification :
On appelle classification automatique, ou non supervisée, un ensemble de
d’identifier, voire de construire, un système de classes sur la base d’observations dans l’espace des caractéristiques.
On appelle classification supervisée un contexte où un ensemble de classes (et une
structure sur cet ensemble) est spécifié à l’avance.
1.3.2 La classification, un domaine multidisciplinaire
La classification a fait l’objet de plusieurs travaux dans différents domaines de recherche. Nous allons en particulier discuter des liens que la classification entretient avec la statistique, la programmation mathématique, l’apprentissage automatique et l’aide multicritère à la décision.
1.3.2.1
Classification et statistique
Les méthodes statistiques sont les techniques les plus anciennes pour la résolution des problèmes de classification supervisée. Elles sont issues de l’analyse des données : Elles supposent l’existence d’un modèle probabiliste décrivant les données. L’objectif de ces méthodes est ainsi de caractériser ce modèle. La littérature nous offre une multitude de
méthodes et d’applications statistiques (Duda, et al., 2001).
L’objectif de ce type de techniques est d’arriver à classer de nouveaux cas, en réduisant le
taux d’erreurs de classification. Selon (Weiss & Kulikowski, 1991), ces méthodes ont fait
leurs preuves pour des données assez simples. Avec le développement de la théorie statistique d’apprentissage, de nouvelles méthodes de classification s’appuyant sur la théorie statistique et se basant sur l’apprentissage sont nées.
1.3.2.2
Classification et programmation mathématique
La programmation mathématique dans un premier temps, a été utilisée en classification
automatique (Hansen & Jaumard, 1997). Le problème de partitionnement est souvent
formulé comme un programme mathématique. Le nombre de classes de la partition est donné à l’avance.
L’objectif à optimiser peut refléter un souci d’homogénéité intra-classe ou de différenciation interclasses. La résolution fait appel à une variété de techniques de programmation mathématique discrètes, exactes ou heuristiques.
En classification supervisée, la programmation mathématique a été utilisée pour optimiser la capacité prédictive du classificateur à construire. Des formes d’approximations très variées ont été proposées, incorporant parfois une mesure d’erreurs empirique, parfois des repères paramétrés, etc. Toutefois, la contribution de la programmation mathématique est beaucoup plus importante en classification automatique qu’en classification supervisée.
1.3.2.3
Classification et apprentissage automatique
Vincent (Vincent, 2003) définit l’apprentissage automatique par «une tentative de
comprendre et de reproduire l’habileté humaine d’apprendre de ses expériences passées et de s’adapter dans les systèmes artificiels». Par apprentissage, on entend la capacité de généraliser et de résoudre de nouveaux cas à partir des connaissances mémorisées et des expériences réussies dans le passé. Appelé souvent la branche connexionniste de l’intelligence artificielle, l’apprentissage automatique puisait initialement ses sources en neurosciences. Au cours des dernières années, il s’est détaché de ses origines pour faire appel à des théories et outils d’autres disciplines : théorie de l’information, traitement du
signal, programmation mathématique, statistique (Vincent, 2003). Des préoccupations
convergentes en analyse de données ont donné naissance à la théorie de l’apprentissage
statistique (Vapnik, 1998).
Il existe trois principales tâches d’apprentissage automatique : apprentissage supervisé, apprentissage non supervisé et apprentissage par renforcement.
Pour un problème de classification, un système d’apprentissage supervisé permet de
construire une fonction de prise de décision (un classificateur) à partir des actions déjà
classées (ensemble d’apprentissage), pour classer des nouvelles actions. Dans le cas de l’apprentissage non-supervisé, on dispose d’un nombre fini de données d’apprentissage sans aucune étiquette. L’apprentissage par renforcement a la particularité que les décisions prises par l’algorithme d’apprentissage influent sur l’environnement et les observations
La classification compte parmi les plus grandes réussites de l’apprentissage automatique. Plusieurs applications illustrent la diversité des domaines d’utilisation : moteur de recherche, reconnaissance de la parole, reconnaissance de formes, reconnaissance de l’écriture manuscrite, aide au diagnostic médical, analyse des marchés financiers, bio-informatique, sécurité des données, etc.
1.3.2.4
Classification et aide multicritère à la décision
Les méthodes de classification multicritère partent en général de classes prédéfinies, elles
relèvent donc de l’apprentissage supervisé (Belacel, 1999) ; (Henriet, 2000) mais avec une
composante contextuelle qui peut être importante. C’est pourquoi elles se distinguent par des modalités particulières d’apprentissage.
La classification en aide multicritère à la décision se situe dans le cadre de la problématique
du tri. Selon Roy et Bouyssou (Roy & Bouyssou, 1993) «Elle consiste à poser le problème
en terme du tri des actions par catégorie». Les actions sont évaluées sur plusieurs critères potentiellement conflictuels et non commensurables. Contrairement aux autres approches de classification, l’aide multicritère à la décision ne cherche pas uniquement à développer des méthodes automatiques pour analyser les données afin de les classer. Dans le cadre de l’affectation multicritère, les préférences du décideur (l’humain) sont aussi prises en
compte. Ainsi, selon (Henriet, 2000) «L’objectif des méthodes de classification multicritère
n’est pas de décrire au mieux les données, mais de respecter un ensemble de préférences qui auront été articulées auparavant».
1.4 La classification non supervisée
Les méthodes de classification non supervisée ou automatique regroupent les objets en un nombre restreint de classes homogènes et séparées. Homogènes signifie que les éléments d’une classe sont les plus proches possible les uns des autres. Séparées veut dire qu’il y a un maximum d’écart entre les classes. La proximité et l’écart ne sont pas nécessairement au sens de distance. L’homogénéité et la séparation entrent dans le cadre des principes de
Les méthodes de classification automatique déterminent leurs classes à l’aide d’algorithmes formalisés. On parle aussi de méthodes exploratoires, qui ne sont pas explicatives. Les méthodes de classification automatique ont apporté une aide précieuse, notamment par leurs applications en biologie, en médecine, en astronomie et en chimie.
Cormack (Cormack, 1971) distingue entre trois familles de méthodes : la classification
hiérarchique, le partitionnement et le groupement. Quant à (Gordon, et al., 2002), il rajoute
trois autres catégories à la taxonomie de Cormack : la classification automatique sous contraintes, la classification automatique floue et les méthodes géométriques.
Hansen et Jaumard (Hansen & Jaumard, 1997) définissent deux autres types d’algorithmes
de classification : les sous-ensembles, et le «Packing».
Pour présenter les méthodes de la classification automatique, nous avons retenu les deux principales catégories : les méthodes de classification hiérarchique et les méthodes de partitionnement. La classification hiérarchique peut être ascendante ou descendante, le nombre de classes n’est pas fixé au préalable. Quant au partitionnement, c’est une classification non hiérarchique en un nombre fixe de classes.
1.4.1 Les méthodes hiérarchiques
La classification hiérarchique, consiste à effectuer une suite de regroupements en classes de
moins en moins fines en agrégeant àchaque étape les objets ou les groupes d’objets les plus
proches. Le nombre d’objets n’est pas fixé a priori mais, sera fixé a posteriori. Elle fournit
ainsi un ensemble de partitions de l’ensemble d’objets (Belacel, 1999). Il existe deux types
de méthodes :
les méthodes ascendantes (algorithmes agglomératifs) ;
les méthodes descendantes (algorithmes divisifs).
1.4.1.1
La classification hiérarchique ascendante
Ces méthodes sont les plus anciennes et les plus utilisées dans la classification automatique. Supposons que nous avons objets à classer. Les algorithmes agglomératifs suivant cette approche, définissent d’abord une partition initiale en classes unitaires. Par la suite, ils fusionnent successivement les classes jusqu’à ce que toutes les entités soient dans la même
classe. Dans chaque étape de fusion des classes, le recalcule des dissimilarités entre les nouvelles classes est nécessaire. Le choix des classes se fait selon le critère qui caractérise la méthode.
Les méthodes de cette catégorie diffèrent selon le critère local choisi et selon la méthode de calcul des dissimilarités interclasses. Nous retrouvons notamment les méthodes issues de la théorie des graphes et les méthodes qui se basent sur la minimisation des carrés des erreurs. Dans les méthodes issues de la théorie des graphes, nous retrouvons la méthode du lien simple, du lien complet et du lien moyen. Quant à la deuxième catégorie, elle regroupe les méthodes de médiane, centroïd, la méthode de Ward et la méthode de la variance.
1.4.1.2
La classification hiérarchique descendante
Dans le paragraphe précédent, nous avons vu que la classification hiérarchique ascendante se base sur un seul critère à la fois. Ceci engendre uniquement une séparation (méthode du lien simple) ou une homogénéité (méthode du lien complet) optimale des classes. Ce qui risque de donner naissance à l’effet de chaînage (deux entités très dissimilaires appartenant aux points extrêmes d’une longue chaîne, peuvent appartenir à la même classe) ou l’effet de dissection (deux entités très similaires peuvent être dans deux classes différentes). Pour faire face à ces deux problèmes, nous retrouvons les algorithmes divisifs de la classification hiérarchique descendante.
Ces algorithmes commencent par former une seule classe qui englobe tous les objets. Par la suite, ils choisissent une classe de la partition en cours selon un premier critère local. Ils procèdent ensuite à une bipartition successive selon un deuxième critère local des classes choisies. Cette bipartition continue jusqu’à ce que toutes les entités soient affectées à
différentes classes (Murtagh, 1983).
1.4.2 Le partitionnement
Les algorithmes divisifs et agglomératifs des méthodes hiérarchiques reflètent le processus naturel de l’évolution qui est le produit de séparation et de regroupement. La classification dans le domaine de la biologie, par exemple, correspond exactement au comportement de ce type d’algorithmes. Or, dans d’autres domaines, supposer qu’il y a uniquement des séparations et des regroupements peut s’avérer restreint. Les méthodes de partitionnement
sont plus générales que les méthodes hiérarchiques. Le principe de cette famille de méthodes, est de trouver une partition des objets qui optimise un critère additif donné. Cette partition est composée d’un nombre de classes fixé au préalable.
Le problème de partitionnement se modélise généralement par un programme mathématique. La fonction objectif représente le critère à optimiser. Quant aux contraintes, elles traduisent les règles de partitionnement à respecter. Les deux règles les plus importantes sont relatives au nombre de classes et à l’appartenance unique d’un élément à une classe donnée.
La programmation mathématique est utilisée avec toutes ses branches en partitionnement : programmation dynamique, théorie des graphes, Branch and Bound, méthodes de coupes
et génération de colonnes (Hansen & Jaumard, 1997).
Les méthodes les plus répandues de partitionnement sont celles qui visent à minimiser la somme des carrées des erreurs. Parmi ces méthodes, nous retenons : la méthode de leader,
la méthode de k-means et la méthode des nuées dynamiques (Belacel, 1999). D’autres
méta-heuristiques ont fait leurs preuves dans le partitionnement : recuit simulé, recherche tabou,
algorithmes génétiques et variable neighborhood search (Hansen & Jaumard, 1997).
Les méthodes de partitionnement permettent de traiter rapidement de grands ensembles d’individus. Grâce à l’évolution de la puissance de calcul des ordinateurs et le développement de nouveaux algorithmes en programmation mathématique, nous arrivons à résoudre le problème mathématique de partitionnement avec de plus en plus de variables. Ces méthodes produisent directement une partition en un nombre de classes fixé au départ. Les classes qui forment la partition finale sont mutuellement exclusives. Toutefois, les techniques de partitionnement présentent un problème au niveau du nombre de classes qui doit être fixé au départ. Si le nombre de classes n’est pas connu ou si ce nombre ne correspond pas à la configuration véritable de l’ensemble d’individus (d’où le risque d’obtenir des partitions de valeurs douteuses), il faut presque toujours tester diverses valeurs, ce qui augmente le temps de calcul. C’est la raison pour laquelle, lorsque le nombre des individus n’est pas trop élevé, on fait appel aux méthodes hiérarchiques.
1.5 La classification supervisée
L’objectif de la classification supervisée est d’apprendre, à l’aide d’un ensemble d’entraînement, une procédure de classification qui permet de prédire l’appartenance d’un nouvel exemple à une classe. En d’autre terme, l’objectif est d’identifier les classes auxquelles appartiennent des objets à partir de leurs variables descriptifs.
1.5.1 Formalisation mathématique
Dans le cadre de la classification supervisée, les classes sont connues et l’on dispose d’exemples (ou individus) de chaque classe.
Un exemple est un couple , où est la description ou la représentation de l’objet et représente la supervision de .
Dans un problème de classification, s’appelle la classe de . Pour la classification binaire
nous utilisons typiquement pour dénoter l’espace d’entrées tel que et
l’espace de sortie tel que .
Soit un ensemble d’exemples de données étiquetées : . Chaque
donnée est caractérisée par variables et par sa classe . On cherche une hypothèse
telle que :
satisfait les échantillons
possède de bonnes propriétés de généralisation.
Le problème de la classification consiste donc, en s’appuyant sur l’ensemble d’exemples à
prédire la classe de toute nouvelle donnée .
1.5.2 Le problème de la généralisation
L’objectif de la classification est de fournir une procédure ayant un bon pouvoir prédictif c’est-à-dire garantissant des prédictions fiables sur les nouveaux exemples qui seront soumis au système. La qualité prédictive d’un modèle peut être évaluée par le risque réel ou
espérance du risque, qui mesure la probabilité de mauvaise classification d’une hypothèse
(Vapnik, 1998).
1.5.2.1
Risque réel
Soit une hypothèse apprise à partir d’un échantillon d’exemplesde .
Le risque réel de est définit par :
∫
(1.1)
où est une fonction de perte ou de coût associé aux mauvaises classifications et où l’intégrale prend en compte la distribution de l’ensemble des exemples sur le produit cartésien de .
La fonction de perte la plus simple utilisée en classification est définie par :
{ (1.2)
La distribution des exemples est inconnue, ce qui rend impossible le calcul du risque réel. Le système d’apprentissage n’a en fait accès qu’à l’erreur apparente (ou empirique) qui est mesurée sur l’échantillon d’apprentissage.
1.5.2.2
Risque empirique
Soit un ensemble d’apprentissage de taille et une
hypothèse . Le risque empirique de calculé sur est défini par :
∑ (1.3)
Avec la fonction de perte présentée ci-dessus, le risque empirique ou apparent est simplement le nombre moyen d’exemples de qui sont mal classés.
On peut montrer que, lorsque la taille de l’échantillon tend vers l’infini, le risque apparent converge en probabilité si les éléments de sont tirés aléatoirement vers le risque réel.
Malheureusement on ne dispose que d’un échantillon limité d’exemples ; le risque empirique est très optimiste et n’est pas un bon indicateur des performances prédictives de l’hypothèse .
1.5.2.3
Évaluation d’une hypothèse de classification
Pour avoir une estimation non optimiste de l’erreur de classification, il faut recourir à une base d’exemples qui n’ont pas servi pour l’apprentissage : il s’agit de la base de test. La base de test contient elle aussi des exemples étiquetés qui permettent de comparer les prédictions d’une hypothèse avec la valeur réelle de la classe. Cette base de test est généralement obtenue en réservant une partie des exemples initiaux et en ne les utilisant pas pour la phase d’apprentissage. Lorsqu’on dispose de peu d’exemples, comme c’est le cas dans le traitement des données d’expression de gènes, il est pénalisant de laisser de côté une partie des exemples pendant la phase d’apprentissage. On peut alors utiliser le processus de validation croisée pour une estimation du risque réel.
L’algorithme de validation croisée à blocs (k-fold cross-validation) consiste à découper l’ensemble initial d’exemples en blocs. On répète alors phases d’apprentissage-évaluation où une hypothèse est obtenue par apprentissage sur blocs de données et testée sur le bloc restant. L’estimateur de l’erreur est obtenu comme la moyenne des erreurs empiriques ainsi obtenues. L’algorithme est alors :
1- Partitionner l’ensemble d’exemples en k sous-ensembles disjoints : 2- Pour tout de à
Appliquer l’algorithme d’apprentissage sur le jeu d’apprentissage pour
obtenir une hypothèse
Calculer l’erreur de sur
3- Retourner ∑ comme estimation de l’erreur
Même s’il n’existe pas pour cela de justifications théoriques claires, l’usage montre que l’évaluation par validation croisée fournit de bons résultats pour . Il faut noter que lorsque le nombre d’échantillons dont on dispose est limité on peut également appliquer le
processus appelé Leave-One-Out Cross Validation (LOOCV) où la validation croisée est appliquée avec le nombre d’échantillons.
1.5.3 Les techniques de la classification supervisée
Pour présenter les techniques de la classification supervisée, nous avons repris la répartition
formulée par Weiss et Kulikowski (Weiss & Kulikowski, 1991) qui sépare ces techniques en
deux catégories :
Les techniques statistiques ;
Les techniques d’apprentissage automatique.
Les techniques statistiques regroupent une panoplie de méthodes. Nous présentons les techniques basées sur l’apprentissage bayésien, l’analyse discriminante et la méthode du k plus proches voisins (KNN). Dans la catégorie apprentissage automatique, nous présentons les réseaux de neurones, les arbres de décision, et les Séparateurs à Vaste Marge SVM (Support Vector Machines).
1.5.3.1
L’apprentissage Bayésien : Classifieur Bayésien Naïf
Comme son nom l’indique, l’apprentissage bayésien est basé sur le théorème de Bayes. Le problème de classification peut se traduire par la minimisation du taux d’erreurs, ce qui peut être formulé mathématiquement en utilisant la règle de Bayes. Dans le cadre de l’apprentissage bayésien, nous retrouvons plusieurs types de classificateurs : classificateur optimal de Bayes, classificateur Baysien Naïf, classificateur de Gibbs et les réseaux
bayésiens (Mitchell, 1997) ; (Wu, et al., 2008).
Dans cette partie nous allons présenter le classificateur Baysien Naïf qui sera utilisé dans nos contributions.
Le classifieur bayésien naïf repose sur l’hypothèse que les solutions recherchées peuvent être trouvées à partir de distributions de probabilité dans les données et dans les hypothèses. Cette méthode permet de déterminer la classification d’un exemple quelconque
d’entrée sont indépendants les uns des autres et tel que pour la classification binaire. La règle de classification de Bayes s’écrit :
(1.4)
On peut remplacer et par des estimations faites sur l’ensemble
d’échantillons (telles que loi de Bernouilli, normale ou bien d’autres). Pour toute classe on estime ̂ par la proportion d’éléments de la classe dans . Étant donné que
l’estimation des n’est pas évidente car le nombre de descriptions possibles
peut être grand, il faudrait un échantillon de taille trop importante pour pouvoir estimer correctement ces quantités. Pour cela on utilise l’hypothèse suivante : les valeurs des variables sont indépendantes connaissant la classe. Cette hypothèse permet d’utiliser l’égalité suivante :
∏ (1.5)
Pour cela il suffit d’estimer, pour tout et toute classe , ̂ par la proportion
d’éléments de classe ayant la valeur pour la i-ème variable. Finalement, le classifieur
bayésien naïf associe à toute description la classe :
∏ (1.6)
Ce classifieur est simple, facile à mettre en œuvre et souvent efficace, mais présente un point négatif qui est la sensibilité à la présence de variables corrélées.
1.5.3.2
L’analyse discriminante
L’analyse discriminante est le fruit des travaux de Fisher depuis 1936. Le but des méthodes de cette approche est de produire des décisions concernant l’appartenance ou non d’un objet à une classe en utilisant des fonctions discriminantes appelées également fonctions de décision.
La discrimination linéaire est la forme la plus simple des méthodes de cette catégorie. Elle présente l’avantage de pouvoir traiter des données de très grande taille. Le mot linéaire fait référence à la combinaison linéaire des évènements, hyperplans, qui va être utilisée afin de séparer entre les classes et de déterminer la classe d’un nouveau cas.
La construction de ces hyperplans de séparation peut être effectuée en utilisant plusieurs techniques, comme c’est le cas avec la méthode des moindres carrées et la méthode du maximum de vraisemblance. Les hyperplans sont construits de manière à minimiser la dispersion des points d’une même catégorie autour du centre de gravité de celle-ci. L’utilisation d’une distance est alors nécessaire pour mesurer cette dispersion.
Intuitivement, nous pouvons qualifier la discrimination linéaire comme une fonction d’agrégation pondérée. Cette technique est considérée comme une méthode de classification très compacte. Le défi dans cette méthode consiste à déterminer les poids de la somme pondérée.
Comme dans l’analyse discriminante linéaire, les modèles logit ont recours à des hyperplans de séparation. Ils se distinguent par le recours à des modèles probabilistes d’erreurs plus robustes (fonctions logistiques par exemple).
La discrimination quadratique est la généralisation de la discrimination linéaire. Au lieu que les classes soient séparées d’hyperplans, elles sont séparées généralement d’ellipsoïdes. On utilise dans ce cas plusieurs métriques (une par classe) pour mesurer la dispersion de
chaque classe par rapport au centre de gravité (Henriet, 2000).
Le choix de la métrique n’est pas toujours évident. En effet, il s’agit de choisir la métrique qui permet d’obtenir des classes où les points d’une même classe pour qu’ils soient les moins dispersés possible autour du centre de gravité de la classe. Ces méthodes sont totalement compensatoires. Dans les deux cas, on constate l’utilisation de fonctions d’agrégation complète. Comme pour les autres méthodes statistiques, cette agrégation ne tient pas compte de l’hétérogénéité des données, ceci renforce le côté arbitraire de la méthode.
1.5.3.3
K plus proches voisins
L’algorithme des k plus proches voisins (noté k-PPV) (Weiss & Kulikowski, 1991) ; (Duda,
(voisinage) entre exemples et sur l’idée de raisonner à partir de cas similaires pour prendre une décision. Le principe de cette méthode est de chercher pour chaque action à classer un ensemble de actions de l’ensemble d’apprentissage parmi les plus proches possibles de l’action. L’action est alors affectée à la classe majoritaire parmi ces k plus proches voisins. La fixation du paramètre est délicate, une valeur très faible va engendrer une forte sensibilité au bruit d’échantillonnage. La méthode va devenir faiblement robuste. Un trop grand va engendrer un phénomène d’uniformisation des décisions. La plupart des actions vont être affectées à la classe la plus représentée. Pour remédier à ce problème, il faut tester plusieurs valeurs de et choisir le optimal qui minimise le taux d’erreurs de classification
(Henriet, 2000).
Le choix de la classe majoritaire entre les classes des voisins peut poser des problèmes dans le cas où l’action à classer se trouve à la frontière de plusieurs classes. Pour remédier à ce problème, on donne des poids aux voisins. Ce poids est généralement proportionnel à l’inverse du carré de la distance du voisin par rapport à l’action à classer.
1.5.3.4
Les réseaux de neurones
Les réseaux de neurones sont nés à partir de plusieurs sources : la fascination des scientifiques par la compréhension, la simulation du cerveau humain et la reproduction de la capacité humaine de compréhension et d’apprentissage. Le fonctionnement d’un réseau de neurones est inspiré de celui du cerveau humain. Il reçoit des impulsions, qui sont traitées, et en sortie d’autres impulsions sont émises. Un réseau de neurones s’exprime sous forme d’un graphe composé de trois éléments : l’architecture, la fonction de transfert et la règle d’apprentissage.
L’architecture concerne le nombre et la disposition des neurones, le nombre de couches d’entrées de sorties et intermédiaires ainsi que les caractéristiques (pondération et direction) des arcs du réseau.
Le nombre de neurones des différentes couches dépend du contexte d’application. Par ailleurs, la détermination du nombre de neurones à y associer demeure dans la plupart du temps arbitraire. En général, les poids initiaux des arcs sont déterminés aléatoirement et les valeurs sont modifiées par le processus d’apprentissage.