Planification de trajectoires et commande d'une classe de systèmes mécaniques plats et liouvilliens

HAL Id: pastel-00838938

https://pastel.archives-ouvertes.fr/pastel-00838938

Submitted on 26 Jun 2013

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Planification de trajectoires et commande d’une classe

de systèmes mécaniques plats et liouvilliens

Balint Kiss

To cite this version:

Balint Kiss. Planification de trajectoires et commande d’une classe de systèmes mécaniques plats et

liouvilliens. Automatique / Robotique. École Nationale Supérieure des Mines de Paris, 2001. Français.

�pastel-00838938�

THESE

L'ECOLE NATIONALE SUPERIEURE DES MINES DE PARIS

par

Balint KISS

pour obtenir Ic' titre de

DOCTEUR DE L'ECOLE DES MINES DE PARIS

Specialite

MATHEMATIQUES ET AUTOMATIQUE

Sujet de la these

PLANIFICATION DE TRAJECTOIRES

ET COMMANDE D'UNE CLASSE DE

SYSTEMES MECANIQUES PLATS ET

LIOUVILLIENS

soutenue le 2:J avril 2U01dcvant lo jury compose de

MM. Michel FLIESS Michel de MATHELIN Rodolphe SEPULCHRE Peter ARATO .lean LEVINE Romeo ORTEGA Rapporteur Rapporteur Examinai.eur Examinatcur Examinateur

Remerciements

Cette these a etc en co-tutello entre rEeole des Mines de Paris et lUniversit e des Sciences Techniques ct de sous les directions de .\'1.\1. Jeanr.evinePI Bela Lantos. Jo me pcrrncts clone de diviser remerciements en deux parties et dexprimer rna gratitude aux personnes concernees clans leurs langues respectives.

.Is t icns rcmcrcier Xi, Jean Levine, mon direct.eur de these 3 I'£:cole des ['vfines de Paris et motivcr mon travail tout an long de la these. Sa riguour et sa mait rise

permis de bcaucoup apprendre.

.Ie suis 6galemcnt reconnaissanr 3 tous les permanents du Centre Automat iquo et Systcmcs pour leur ac:cucil chaleureux au sein du laboratoirc .

.\'les en France ant

etcfinances par nne bourse du Ministerc des Affaircs

~::~:lt j~'prmis[~~e~::::a(\~:~~ltl~~~~~~

S6j~~~::r:~ief<~:nt:~~vail

des administrations

Koszonetnyilvanttas

Koszonct.crnct fejPzem ki Lantos Bol.inak. aki dokt.orit anuhrninvairn alatt temdvczctokl'nt ir.inyitotra 6s kfserle figyeierumcl muukarnat

Halrival Lart ozorn Arat6 Petcrnck, az lr.inyir.astcchnika cs Inlorrnatika Tanszek vezet ojenek birli16 bizott.sagban valo roszvet.eleert.

EgvctemIr;~nyi'tast,ech:nikaesIntormar ika Tanszckenek

Harrnati Ist vrint

es

Vass G,ibort akikkel eK'iiitt a k07.6s munka konferencia- es foly6iratcikket is eredmcnyezett.

Halaval turtozoma labor 6s a t.anszck munkat.arsainak is, akik mcgfelclo korulrncnycket biz-tositottak dokt.ori tanulmanyairnalaites tamogattAk erofeszfteseimet a fokozat mcgszcrzcscrc, tamogatascrt koszonet tel tartozom az OTKA T 020072 cs uz FKFP 0417/1907

Introduction

Cette these porte sur les classes de systemos

Dans le cas des mains de robots. nne littera! me tres riche est disponible dans divers do-maines modclisation [12. 1:3. 21\. ,11\. plauilicat.ion de trajeetoires utilisant des approxi-meltions [11. 6:3]. de trajectoiros pour Ie modele cinemat.ique non-holonomeutilisant entrees oucoust.ant.os par morceaux [:39. 5:3. 24] er stabili-sation delobjcrpar bondage [12. 55].

dct

rnjoc-partie de la lit.teraturc utilise des ucs upprocnes('Ieeommande 67]. Plusicurs

pour dim inner les oscinauons croccs utilisent des tcchniquos(?ner,get.l'f111e~,enexptoitant La con(.riblll.ion de lat hcsoconr-oruc-I" solut.iou

toircs, utilisant la not ion depla.l1,lwieellite.'11,'1,/;'//('(,loWUIHHI"t:lL.Une classillicatiolldes strucr.ures muins-objets est

chaqne Concernant les

fait grue pout ctrr- identifiee un pendnl« si on fixe la longueur du cabl« vertical relie ala

_\lous considerons dubord nne methode de mcdclisation gcncmle unc class« etcndue coinprenanten particulicr lcs inodcles des grue de la

NOliSmontrons que clement deluclusse est dillerent icllcmont

Contents

1 Introduction

2 Robotic manipulation with permanent rolling contacts 2.1 Modelling

2.1.1 Geometry and kinematics

2.1.2 Pivoting and autonomous mot.ions ofthe object 2.1.3 Examples

2.1.4 Dynamics 2. J.5 Inequality constraints 2.1.6 Planar hand-object structures

2.J. 7 Hand-object structures with special morphology 2.2 Holonomy, flatness and Liouvillian properties

2.2.1 Iloionomy and flatness of planar structures 2.2.2 flatness study of the kinematics (examples ] and 2)

10 14 25 26 27 2.2.3 Liouvilliankinematics :39

2.2.4 Liouvilliandynamics of hand-object structures with special morphology 40 2.3 \lotion planning

2.:J.l Motion planning for planar struct ures

42 44 2.3.2 Motionplanning for kinemat ic models (examples of Section 2.1.:3) 4G 2.3.:J Motion planning for hand-object structures wit.h special morphology 49

3 Crane control 53

3.1 Smllll size model of the 1.]S Navy crane 5Ci

3.1.1 Crane in the plane .55

:3.1.2 Crane in three dimension- 63

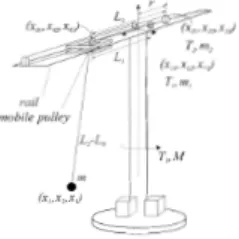
3.2 A gpneral modelling merhod for a class of weight handling equipmcnts 71 :3.2.I Weight handling equipment definition and moddling 72

J.2.2 flatness

3.2.3 Numerical simulation of the dynamics :3.2.4 Examples of weight handling, equipment modelling ~L:j Motion planning

3.4 Global measurement feedback stabilization :\.4.1 Stability definitions and theorems :3.4..2 PD controller for the 2D US Navy crane 3.4.3 PD controller for the JD examples of Section J.2.'1 3.5 Local tracking with measurement feedback

4 Conclusions

Bibliography

A Some notions of analytical mechanics

Contents 77 7K 79 83 87 88 90 96 W7 112 116 122

Chapter 1

Introduction

This work studies the motion planning and control problems related to two classes of mechanical systems: robotic hands and cranes.

objects. Their dext.eritv follows from and the object in contact. hence (he of1hese Illations. Here. we consider the case of contacts without between the surfaces which give rise to kinematic constraints in model. Sinco these constraints arc nor in general. hand-object systems belong to the larger class of nonliolorunruc mechanical systems.

behaviour.

first the choice of a rf'ference hands. the desired objective is to .~ l'~~"'~""""1 ' ' ' ' ' " , ' ' ' ' °and orientation. For cranes. one wishes to thf'

to equilibrium which avoidsthe

Chapter I. Introduction

HErE. WEfirstr-onsirlorIhp 11lo(lPllillP oj aouito][en(;ralclass olweie htUCtlllllUl!','~qurpn re-m.s. including the overhead CTimE and three-dimensional models of cantilever.

We prove that all the models of this class nat and. robotic: hands. we construct reference trajectories load without oscillations at the final point.

the thesis.

Chapter 2

Robotic manipulation with permanent

rolling contacts

The kinematics of the model includes constraints due to the rolling without as-sumpt ions which are linear w.r.t , the time derivatives of the configuration the system and have the form [21. 561:

A(rz)·rj=() (2.1)

whereifis the vector of the configurar ion variables (see also Appendix A).

Motion be applied to a large class of dextrous

problems are using; quasi-static approximations. These

optimization in order to find contact forces. with constant velocity. based on Peshkins minimum power principle [58].

22. 46] and Liouvillian and extended [62] in

Chapter 2. Robotic ma,niplllatiolJ l'\!ith pctuuincnn. tolling contacts

Not.e that. the feedback

design dealt let

for the body case.[:3. 9]with soft fingers and with uncertainties on the and learning control scheme proposed in[55]with unknown inertia paramotcrs of the object

back to motion planning, the flatness property allows an

there can be number

and the additional tunctions ot the output the flatness based approach to motion

differential equations.

We prove that the dynamic model of planar IJOSs arc flat as a consequence of the constraints as the position and orientation attheobjectandcombinations0,1tile contact torces. In the

three-Accorcling to the dimension. the number kinematic) we show that the HOSs can be

(i.e. dynamic or 2,1

hand structure _I of fingers holonomy flatness -no. l.iouvillian

I

20 I >1 ves yes 3D 1 no 3D >I [LO ? yes 3D

+

symmetry >2 no ? ves

Table 2.l: Classification of HOSs

2.1. Modelling

2.1

Modelling

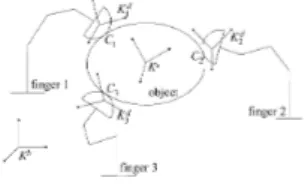
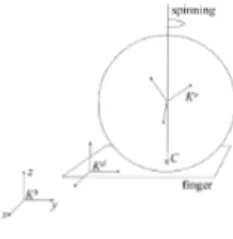
Figure 2.1. Robotic hand with the manipulated object(711=3) where rn is the total number of the fingers of the hand.

Let us start. with an enumeration of (classical) assumptions.

AI. All segments of the hand and the manipulated object are rigid bodies (sec Definition 12 in AppendixA).

A2.Only the last segments of the fingers can be in contact with the manipulated object A3.Surfaces may roll on each other without slipping.

A4.Contacts permanently maintained.

A5.The surface of the manipulated object is strictly convex everywhere. (This implies that the radii of curvature are everywhere finite.)

A6. The surfaces of the fingers arc convex everywhere. Remark 1. The

tadineach other dcjormauons.

body the case

excludes both the penetration contacts. namelynori-oaiuslunq

bodieszn con-surjacc« due to

Remark 2. between the

A5 and A6 allow to clurunaic the case object and the fingers.ilius makuu; the

contact pomis globallyamq·ue. abuse of vocabulary. the manipulated object will be simply referred to as object in the

Cbnpter2, Robotic nuuupulnt.ionwiti] permanell1tollingCOlJfacts

2.1.1

Geometry and kinematics

matico expressing const.ruiutsOJI

Ihe fingers arc needed. Thus. we first exprcss t.he geometric constraun.s and then ones, and finally the relations with

Geometry of the contact

!{" 'vVe denotebyK" the frame fixed to the by the point 0, and by /(;1. the ['ruIllcJ_{fixed to} withI

=

L 2. , m Let us dC110te byp"

expressed in the basis of K" the oricnuu ion ofthr- frameKO (rcsp.

Aforthe' definition and for11short the pair

(2.2)

zivcs th« relative nosit iou (resp. relative orientation) of the object w.r.t transformation matrices lrequent lv llsed in vector

P;

is expressed in the frame/(;1

(see Figure 2,2) Tho contact point byC,.

Figure 2,2: Contact between fingeriand r hr- object

The vectorPc', of the ront act pointC,.expressedillthe

basis ofthe frame (2,2). these vccr ors are connected by the

IThe notationg", would Iw more consequent.

omw"

preferred to avoid double subscripts for readability', sake.

2.1. IVlodellillg equation

p;

+S1(d:{)p~"

-p~,=O. LetCOandc~define the boundaries of tho object and fingeri IfC, is the contact point between the object and fingerI

=0.

(2.:l) A. Definition 12).

(2.4) (2.5) Denote byDc the derivative of a function?C'(i.c. the function R3---7L(]R3,IR)).1t bas the local form

iOC

Dc !!.::.-.,] Dc=

lili dY

a::

coincide at the contart point., or direction. Note that.

referred to as the non-penetration constraint

Kinematics of contact

The velocity state of the object w.r.t . lingeriis given by the pair(v;.[w~x])(sec also AppendixA): [u.!;x]= [ 0 -Wiy

-w;r]

o

This allows to calculate the relative velocity at the contact pointC,(see Equation(A.5)):

2TIJisllotHtion comes from [1]

Cliepter2, Rovuti(: manipulation with peruuuicsn mlling contacts

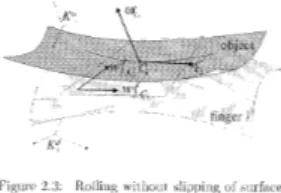
Figure' 2,3: [lolling without slipning of surfaces

Assumption A4, the geometric constraints of in the common plane of the surfaces

rolling without read

(2.8)

Observe thatthcso constraints are' indeed linear w.r.t..the velocities and thus have the same form as (2,1).

Geometry of the fingers

As it has been already mentioned, the robotic hand is a set of m small with kinematic chain:" Figure 2.4), Their modelling follows the standards robotics ar ur« [,10. 48.,521, segments of t.ho fingers are connected via one-degree-of-freedom joints.

Figure 2.4: The open kinematic chain of n finger of tho robotic hand

These joints can be rotational or translational to the possible relative displacement of t he connected segments, Because of t.he openness kinematic chain. the joints of each finger can be enumerated from I to0.,where a, is the number

coordinate of the art iculationj =L .a,)of the fingerI (I= .m) llcnce the vector'11=

I'l,.

c-ontains rhe joint coordinates of lingerI,.

2.1. Modelling

Ifthejth joint of finger i is rotational. therefore the configuration manifold of each andR

E lR/2rrZ.if it is translational. is a Cartesian product of the sets

The direct geometry of fingerIallow to of the frameK,d as functions of the

For. denote byF,the list with elementslR/2rrZandlRsuch that the nth element ofF,is lR(resp.lR/2rrZ)if the nth joint of fingeriis translational (resp. rotational). The notationF, will also be used to denote the Cartesian product of the elements of the list, taken in the order imposed by the list.

Hence the direct geometry function of fingerIis defined by:

d, . F,---+lR3_x50(3).

d,(q,)=(p~. D(</J~)). (2.9) The functiond,sums up the geometry of fingeriand its explicit form can be obtained once the Denavit-Hartenberg parameters of fingeriare known. (Roughly speaking. these Denavit-Hartenberg parameters define the homogenous transformation betweenKb_andK~.)

Borrowing again some notations from the robotics literature. the derivative of the direct geometry functiond; is defined by

J,(.)=Dd,(.)EL(:F" JR3x50(3)). (2.10) and will be referred to as the jacobian of i. Since the orientation of the frame fixed to the fingertip in50(3)is locally described three rotation (see Appendix A). the local expression of the jacobian of the finger a matrix with rows anda,columns. A configurationq, of fingeriis said to be singular if

dimImDd,(q,)<min {dimq"dim(lR3

x50(3))}=min{a,.6}

whereImDd,(q,)stands for the image of the linear mapDd,(q,)underF,. Inventory ofvariables and constraints

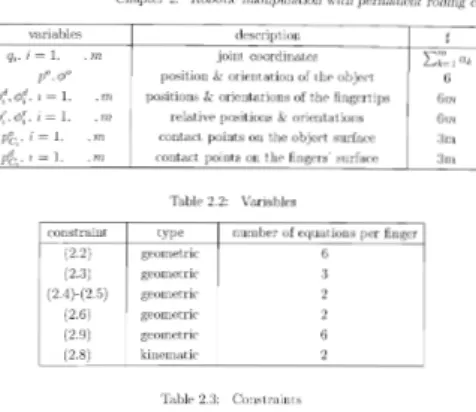
To make an inventory of the variables and cemst:raints introduced tel describe the geornct.ry and the kinematics of a HOS. we summarized them in Tables 2.2 and 2.3. m gives the number anda, gives the number of joints of the fingerIwithI

=

1. .m, All

entries case of three-dimensional (The two-dimensional case is

addressed in Section 2.1.6 where the entries of both are updated accordingly.) By Table 2.2, the configuration manifoldMof the HOS is defined as

x Fmx 5E(3)x5E(3) x x 5E(3)x]R3X X ]R3x]R3X X ]R3, ' - , , - ' ' - , , - ' " ' - v - ' "

2m

where5E=]R3x50(3)is the Euclidean group. In accordance with Table 2.2. the vector of local coordinates in the configuration manifold M reads

10 Chapter 2. Robotic uuuiipulni.ion with periunnont Tolling contacts

variables description D

s..

i=1, .tn jointcoordinates _L~:~lOk

po.¢o position&orientation ofthe object 6 p;/,,!)~/.1.=1, .m positions&orientut ious of the fingertips Gin I =l. .'IIl relative positions&orientations 611! Pc;','I =1. ,m contact. points on the object surface

I

:lm pi." 7=1. .rn contact points on the fingers' surface 3m

Table 2.2: Variables

constraint type I number of equations per finger (2,2) geometric I 6 (2.3) geometric 3 (2,!1)-(2.5) geometric 2 (2.6) geometric 2 (2.9) geometric 6 (2.8) kinematic 2 Table 2.3: Constraints

constraints of Table 2.3 define a sub-manifold of constraints of rolling without by tion of ,\1;\. The' t l l l t " l J C J l l U l 1 l 6 OL'1l'l.Lll,tLl"'1l6U'''L,LIULILLUIL directions of the HOS

2.1.2 Pivoting and autonomous motions of the object The kinematic constraints (2.8) gi,ren in the previous sectionEIreobtained from Assumpt ion and eliminated sliding motions between the object

tions of the object",h;,·},n H w l " ,rlnclPQ;,." hlp These motions arc the

2.1. Modelling

1. the Ve!OC1.ty

0/the

poiniCnaruslu:s the

frame

KII oc=O.

11

to rotations around an tangent plane.

unlli the [{O

t.«

A

2. the tangent plane ofthe olnect at the pouitCremainsuncluuiqal.

These definitions imply that

# ()for any pivoting motions. The following statements can

be easily proven.

Proposition 1.Consider all.objeci.J.'f17'II'f'·/I-ncn-ntr: in1R6_{corrcspoiuiuiq to aprooiuu; moium}

thereisa unique dircctiori pomiC

the unit normal of the object surface at the pointC,expressedin the I. the tangent att he point C to surface has to henceuf must be with I),~" i.e.WO E

n·tA

#

0).By

Cis given by

(2.11)

which must vanish by Definition 1. Using that[ax]b=-[bx]a.and isolating'00 we get

in]RGcorresponding to pivoting around the point C is given by

o

Proposition 2. Consider an oh]eet and two

necessa.n) and suffiC'lenl conditioti forthe pioot.nu; motzon around C1andC2an'

C1and C2 . The correspotuiuuj/.0(J,

12 Chapter 2. Robotic uuiuumuu.ion with permanent rolling rontacts Proof. Since,,;0must

colinear. Hencee<J0₌

satisfy the lol lowing equation obtamcd

() =

[~

[~]

(212)

whereIistho identity matrix of suitable dimensions. This equation has a nonzero solution if and only if

Then we have the relation

giving a umquc directroninJIicorresponding to a pivoting mot ion around bor h points. Observe

which is surface

to the colinearity of the normal vectors with the vector ronnertingI,he

C1andC2 . 0

Corollary 1.C01151.dr:r a siricth] convex object. For a set points {Cl .C2.

Cd.

then no ducciionInlP!.(j corrcspondinqto a piuotiru; mononG~7'01(ndou contact poniis.

tion.

Corollary2.Consider a8truJly {C,:i=1.2. .j}.j>:3,thereISno ProofConsequence of Corollary 1

D

o

Remark 4.Since theotnectiseuerinotiercstrrctliJ'conoextn;,1SS1(mp:twnA5.

the objectsurjor»: Remark 5. In the rase around all su.rfare points face pinnis,

2.1. Modelling

In the literature one calls rolling without surfaces such that pivoting motions me constraints(2.8).

We use Definition2 to obtain the constraint that eliminates the the coordinates of the contact pointC,in

lrame of the outward unit normal vector:

13

relative motion of two rolling without slipping

motions. For. recall inertial reference

p~,=pO+S2((j/))p~"

Definition2asserts r hatj)~'1 =0and =0during pivoting motions for all contact = 1. ,m)on the surface that the second condition is equivalent to =0since the contacts point ar« fixed on tho surface. Calculating these time

Lsing that[WOx]=dSld;")S2((j)°)"' and the anti-symmetry of the cross product we get P~!l IIDcO(PCI)lli)~'1 j)~,,,,

IIDcO(pc,,,,Jlint,

[

ill]

de! cJ° = ' ] (2.13)

defining t he linear map '7· According to Definition2,the

to motions.

the vector for all and orientations the null-space contains8non-null vector for a always a unique non-null component if m=I

Denote 1L!3 (W3EJR.G) the vector spanning the null-space of'I.Then the non-spiuniug constraint

14 Chapter 2. Robotic mnnipuletion with permanent rolling cout nct.s motion has been defined without need to consider the geometry motions around all contact leave both the contact coordiuates of all ringers unchanged. Note in1he case of most robotic controlled variables which implies that pivoting mot ionsCEmneither be generat.ed nor eliminated by the control variables. One rnav ask be

cont~'ollec1

through the joint coordir:ates. Thus we are naturally driven to consider a more general notion of autonomous motions of the HOS defined as follows.

Definition 3 (autonomolls motions). Consider an rectum TAlAcorresponds to an autonomous motion of rollnu; unihout. sltpptru; [Equation (2.8)) and has no 1,8the number ofjoints of jinqeri ), andI=1. . m, (m bezng the

an autonomous motion is such that the joint coordinates of the fingers do not motions of the object around all theIIIcontact points are also autonomous

pointsj=L ,III -1 do not This

multinlo contact points doesn't exclude the of the joints of

Let us turn back our attention to the inventory of the variables (Table2.2) and that of the

constraints INc have and, by adding the non-spinning

kinematic constraint to the 2.:L (19

+

2)m

+

b(l - constraints.

(The functionb is thatb vanishes evervwhere but at(1where it to 1.)

2.1.3

Examples

[ cos -r cos

o

D((6°)= sin ccose' -sinR where 0°=(-r.e,I!').

cospsin0sin u: - sin<pcos'/i' sin<psin

esin

Ii!+cos.pcosu;

cosesinl!J cosOCOSU)

2.1. Modelling

Figure 2.5: Ball rolling on the plane

1.5

The sur lace the coordinates of the contact [JointfJ~'=

(x~",Ye',z('.)and read

(:rc.,)2

+(YC)2+

(Z~,)2 - R2

=

0

4

=

o.

The dorivat iveDcO_ofCOisgiven by

DcO(pc..)=[2xc 2y'(.2z;'.]=2(p'h)/ Similarly,

Since all joints are translational. the direct geometry of the finger (2.9) reads

(2.16)

[

If']

q= 172 =p"

q:]

hence =D(rlifSl(ciJ°) D(ciJ°). SinceIIDcO(pc·)11=2fl,Constraint(2.6) for the tangcnt

t.hp [ - .Os in ep +

~!}('()sep.(,().s(J]

=uJ"= ()cosep+u.'sinepcos(J cP-J'sin() (2.18)

16 Chapter2. Rouot.i: iuuuipulnt.ion with[>01'l11a118111rollin/!, contacts

allowing to calculate

(Jr"

the relative velocity at the contact point:

v;;

=Ji"

+

[uJ'x]~l((b')pc-Jid Tosimplify this expression, note that by (2.3):

[

:r~

..] pi=p~,_ O(rji')pc= )~'

Ilcuco. using (2.17) and replacing in (2.19). one gets

[

- H{)cos .p -RI!}sincpcos

e+

:'4]

- no

sin.p+flli~coscpcose+iJ~,

(2.19)

the vectorsw;lc=(1.0,O)Tand t.he form

(2.20) (2.21) The linear mapIIill Equation (2.1:3) has the matrix

[~

-R

~]

0 '1=

["

2H -2R0

:]

0 0 0

=(0.O.O.O.0.1)1'spans the null-space of'Iandgive~the following

=j; -~'~ill()=0, (2.22)

Lemma 1. The coilist.nlnitionIT1spannedby the one-forms obuuried from (2.20)-(2.21). IW7Jwly

R(cos'{cLe+sill,?co~()dl!') W2=dy1- R(sin cpdH - cos cpcos Bdl!J)

ISfully nnnholonomic. Moreou er. tlie codistrtlmt.tonTI2obtained hyadduu; the non-pvooiuu; constraint (2.22)

w:,=dcp-sill()cZ,ljJ. toWlandCU2 1.Salsofully uonliolouonuc.

2.1. Modelling 17

constraints must be on an eight-dimensional manifold determined by one-forms Wj, and W3 are independent because

tne componentsmax(-.. aYr. and dcp. Let (see Definition13)

to the TIl =

I?

= span{wj,wd and TI2 = = span{Wj.w2.W3}' Aftersome lengthy but elementary calculations. the dimensions of the codistributions in the derived flag are {2.0} (resp. {3, 2. O}) for

I?

(resp. 19).Since the dimension of the last codistribution of the derived flag is 0 in both cases. the lemma follows from Definition l4. D

The kinematics corresponding toqbeing trivial,we are interested asso-ciated to the kinematic constraints (2.20)-(2.22) which evolve on a submanifold ofMA • given by the variables(/;0=(cp.B.1jJ).x~ and Y~'

Two driftless systems will be associated to the kinematic constraints (2.20)-(2.2]) and (2.22) using Definition 15. The driftless system whose vector fields annihilate the one-forms given by the constraints (2.20)-(2.21) is referred to as the case whereas the driftless system whose vector fields annihilate all the three one-forms is to as the non-spinning case. The linearly independent vector fields

(2.23) g3= 1 g2=

R

R

o

cose. sincptanB 1 gj=

Ii

gives the driftless for the spinning case. For the

of the associated are onlygland The

these vector fields areul U2 =iJ~andU3=w'~= .o -I'IJSilltt, constraint (2.22) eliminates preciselyU3equaling

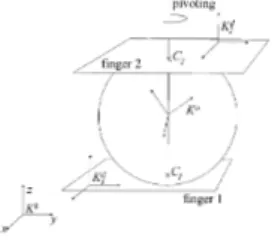
Example 2 (ball between two parallel planes). This example. illustrated in Figure 2.6 (together with the preceding one) is popular in the robotics literature and in the literature of the non-holonomic systems in general [5.45.54]. 1 has the same properties as the finger in the preceding example. Finger2. parallel with one. has a unique translational joint along thezaxis ofKb_{The same modelling processus is followed as in the preceding example.} The surface equations are

=0 (2.24)

and their derivatives read

1=1.2. (2.25)

The direct geometry of the fingers read

[ T 21

1

T22 =p~ q21

18 Chapter 2. Robotic manipulation with permanent rollingcOil/acts

Figure 2.6: Ball between two parallel planes

(2.26)

(2.27) (2.28) 1=1.2.

uon-nenetrru ron constraint (2.6) results

=0 tWs:Illc;J-rtPi.Jc')Sc;JCOSI!-r','J;'.=O.

The' relative angular velocity w' '" "'" u,cc" n'.""borh lingers is already given by Equation (2.18) Lthe

TIlP relative velocity at the contact point C2reads

(2.29)

Using (2.3) together with (2.26). we haw

2,1,Mode lling

Since

w

f.c,

=(LO,Ofand

1I4

c,=

(0.Lof the kinematicconstraints(2.8)read 19

Thekinemat icconstraints

}W , oo ~

+

}lw,in~,c"O+i~> ~0 =0,

(2.30) (2.311 nonholonoruicbecause (2.28)with (2.31)we obr.a.in

.i~,

+

i~,=0 whichca nbe integra ted as

I~,+3t=T~,(O)+X~,(O) !J~,

+Y~,

=Y~L(0)

+

!J~,(OJ. (2.32) These Int egra te dkinem aticconstra int sca nbeusedto eliminate

Then. and withtbe twoaddittonellyobtained

",om"'i,,'oat''''''nt' whichcan bealso to elim inate

=46-38-2=6.He nce ",, 10""coordinatesof a canbegivenbythe q4=('P. &,JiJ,X~L ' y~"q21)

I'he remainingtwo nonholono mk-kinematicequations onI\4Aaresimilartothose obtained inthe preced ing exam ple:

-

niJ cos <p

-

RW>in , ocot,e

+x~, ~

0

-HBsin<p =0.

Toaddthenon-pivotingconstraintwe determine thelinear map T/first

(2 33) (2.3-1-)

20 Chapter2,HoboticIniliJipult:ltion\Vitllperman entrollingcomecrs Thekinemat ic constraintsdonOIinclude allthevariables of

M

-4

[i.e.thevariable'hIis not involved).Thusthe associateddriftless systemsevolveagainallafive-dimensional snb manifold ofMit anddefinedby the vector fields(2.23)of ExampleI

The driftlesssystemforthespin ningcase is givenby

wherea sthe dnnl esssystemassociated to the non-spinnin g cast'reads

withtJ)

=It:.

111=

f/I:

and113=w~

=.p

-

tVsin8 ,

Example3 (ballbetweentwoobliqueplanes }, The set up(set'Figure 2.7)is thesameas inthe precedi ng exampl e.butthetwoplanes representing thefingersareno longerparallelbut obliquewit hanangle remainingconstant during themanipulation.

Ftgure2.7: Ballbetweentwo obliqueplanes

The surfaceequationsarealreadygiven by(2.24)intheprecedi ng exampletoget her with theirderivatives(2.25). Thetran slationaldegree offreedom of ling!'!"2ispar allel totile

v

=

(

x

t

.lI.:,

z

t?

of the planeofthefinger. We supposethatv is suchthat

i-

0{notethat(I~)2

+(

y~)2=0 would givethesetupst udied inExampl e2).The geometryofthefingersrends

[

~

"

J(~ )'+M l '

2.1 I\Jodelling

Constraint (2.6) for the second finger gives

21

(2.36) =

~(pcJTn(Q())TI!(O~)

=

-De~(p~'2)

=[0 0 L] Mulr iplying both sides byRS2(r,b3)1 and taking the transpose, we get

n(d;'»)p,/-,o=-Tt» which relation can be also read form Figure '2.7

The kinematic constraints at the contact between the object and fingerJare already given by Equations(2.27)and(2.28)(we simplify for readability's sake):

-R'.V~=0

+

RuJ.~=

o.

(2.37) (2.38) The relatiw velocity at the contact pointC2is obtained using (2.3). (2.7). and thatd(!,\~)1)=0:

W~.C2=(0, 1.0jT Since. by the direct geometry of the finger 2(2.:3G) we haw

I!(O~?j)~

=

(i2In(Q~)Tu

= [

;~

] -q21 the kinematic constraints corresponding to (2.8) for finger 2 read:

which canIwintegrated to obtain

p~.r7,z~

+p~y~z~~

+

p~((.rl:)2

+

(.IJ~)~)-Y~'I!J~-.r~, x~

=p~({)):r~z~

+

p~({))y~z:;

+p~(O)(CT~)2

+

(.IJ~)~)-

.IJ[j

({))Y~ - xi:](O)xe. (2.41)

lW111Il"".!" " I I \)1U1l11Cll~1VllUlllllnA- 46-38-1=7 and (2.:39)

22 Chflpte r 2.Roboticmanip ulationwith permanentrolling('oll (a(' ts

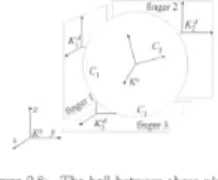
Figure 2.8: Theballbetweenthreeplanes

Exa m p le4(b all be t wee n threeperpen dicu lar plan es).Thesetup isillust ratedinrig.

ure 2.8.Thefingersareagainta ngentplan estoabull ofrad iusR.par alleltothe threerespective Cartesianplanesof theinertialreference frame,definedbyy6=0,x6=0 and::6=O.Alljoin t s aretra nslat ionalandtheirdisplac ementsarerestrictedalongthe co rres po ndin gdirections.

The frames fixedtotheplaneshavethesameonenreuonsas thebaseframe.The posit ions of their aredenoted by

p

1

0==

(

xf. y1

,

Z1)TI=1.2,3 Till;' origmofthespher e and its orientation given byp"=(.1'''.y'' . z'' f and$"- (,."B,w)(RPYangles)3.5 intheprevious examples.Th esurfac e equat ions an>givenas

4

3=0

and theirderivativesread

Drf> (pc, )

=

2(Pc.)]' D4(p~,)=(0. LO) Dc~(p~, )

=

(1,0,0) UC~(P~3 )

=

(0, 0,1). Thedirec t geometryofthe fingers aregivenby

q,=p~ 1=1,2,3,

hencen(4)~)

=

O(rpO).

SinceIIUc"(p:;',l 1l=2RforI=1. 2,3. Constraint(2.6 )forthetangent planes gives

O(!P")Pc ,=-Re2. O(¢O)PCI=-Rei fl(al)pc,=-Re].

withel=(I,o,a f es=(O.l,OlTandea=(D.O.If Thus thegeo metric'const rai nt sco rre-sponrling to (2.3) '

1=1.2.3,

canbe'Simplifiedbythe\1St'oftheaboveex pressions .Isola tingthecoordina tesofthe origi nof thefra me fixed tothe objectoneob ta ins

XO=.I'f+L'~, yO=y~+R ZO=

z

f

+:::-~, xO= x~ +R yO= y~ +y~.

z"=

:1+Z~, X" = I~+ X~3 !I'=yt +JIc. z"=zg+fl. (2.42)

2.1. Modelling

Therelativevelocit yatthecontac t point C,reads

I""1.2.3 23 R~ + .i"-j;t=O -Rw~

+

t"

-

ill=0 -~+iJ" -yq=o Rw~ +i" - iJ=O -R.,)~+j;"-

±1

=

0 Rw·~+if'-iA=O. Thesekinematicconstraintsare notfully uonholonomlc.FOL observethat eliminatingRw~one gets

-t"+

if=

//

-

!If

.

(2.43)

Diffe rl'nt iatingthe geome tric constr aints z"=

z1

+

z~,and

if

=

14

+

Y'!::,obtai ned in(2.42). and repo rti ngthemin(2A3)wegeti.~,=

-if!:.,

whichcanbe integrat ed as

z,/::

,

- z,/::

,

(0)=

-y'l::,

+

!fcl( O).Onemaygetsimilar relationsbyeliminating...:and~ This givesthree integr atedconstraint s:

=-1J~,

+

Y~J (O) =-.r~)

+

x~J(O) =-yt,~

+

11,/:::(0)

(2.44)

wherex~,(O),X'!::2(O;.Y'!::~ (O).Y'/::J(O).4, (0)and:,/::,(U)ateinitialconditi ons. Usingthese express ionstoge therwiththegeomet ricconst ra ints (2.42) and the expression ofi finthe-RPY representa tion:2.18),theremainingkinemat ic constraintsread:

[

' 0

R 0 cos'f'

o

sin'P

{2.45j

Sincethehandhasthreefingers.theconditionsof CorollaryJan' sat isfied.lienee,there are no spinningmotionstoeliminateby additionalkinemu tie constra int

Tables2.2 and 2.3 show thatthe geometricconstrain t s and the integrat.edkine ma tic om's

f.

::

I':.l:\~.t~.e;~,l~~~:~:~

,

v:;:~~

IJ

~sl}:t

of

69. Hence.

thedimens ion of MAequa lstodimAlA=

Chf!prer2. Rohoti cl1JanipulaUolJ wit h permanentrollingcont acts Lemma2. Thl'('odlstnbutwlt11.spmmedhythe one-forms obtamed from theconstramts (2.45) .namely'

tvl ""Rdep-Hsinfld lj}

+

dI~, w2 ""ReosepdO-tRsin cpcosfl d1lJ +dz'f.:2

tv3=Rsin epdO-Heos cpcosf!diP

+d

4 ,

tsfullynonho lonoiru c

Proof.Afterthe elimination of vari ablesusingthe geometricandtheintegrated kinematiccon -straints.tho remaining kinematicconstraints (2.15) mustbesatisfied on the nine-d imensional manifold AlA.The one-formstv),!V2.andtv]arelinear lyindepe nde nt because oftheircom -ponentsindy'b"dZ~" find

d4

t,The dimensionsofthecod tstnbuno ns, inthe derived Hag of [J= [0=span ]!:v't,tv.,tv3}are{3.OJ,Since thedimension ofthelast codistr ibutioninthe derivedHagis0,theclaimfollows fromDefinition14 0 The kinema ti c constraints(2.45) involve onlythefirst sixvariablesofqA-Observe that the last threecoor dinatesqt.,Q21'q31inqAdetermtnethe position ofthe ball, sinceWI"have(using the geometr ic constraints(2.42) and thedirectgeometryofthe fingers)

y"- 912+R z"= qu rH.

Infact , due to thetranslat ionaljoints of thefingers, the tra nsla tional motionsoftheballare docoupled from thekinematics(2.45)which determinestill"orientationof the hall.

Therefore.the associateddriftlesssystemiscalculatedon a submemfcldM~ofMA, bythevaria blesI{).n,l/J.I~" z~"

zt,.involved in

the kinemat icconstrai nts.Thevector annihilatingthecodistributionspannedby the one-forms(2.46) ontheman ifoldAI~are

-I -sin iptan B cos..ptll.tl f) 0 -cos,p -sin ,p 1 0 1 _-~ 1

_~

91

=

il

_R

rn

-="R

₀ 93:;

H

0 0 R 0 0 0 R

givingthe driftless system

(2.47) wheretheinpu tsareUI=i:~" U2=i~, andU3=

i

,!:,

Notetha t byLem ma2.this syst emis locallycommendable{i.e.the involutive closureof thedistribution spannedby 91.9'landQ3. hasdimensionfiwhichequalsto the dimensionof ,\1.~)

2.1. ModellilJg

2

.

1.4

D

yn amic

s

25

Thenotationsint roduc ed in Seeton2.1.1arcreused

'I'hedynamic equationsare obtainedseparatelyforeach fingerand theobject.Thesee qua-tions!U"('connectedbymean s of the contact forces.The contact force appliedby thefingerI

totlJ!~objectisdenoted by the\'('C'tOI'

I

,

E1R"1such thatits coordinatesareexpressed inthe inertialrf'[('reneeframeJ(b

For thefingers,contact forces aretreuslormedtoexte rior torquesin thejoi ntspace(see Figure2.0).

ill

I KY'

b.

C2

I

.

Afg

J object

Figure2.9: COlltadforces

Letusintroduce the inert ial parametersgivenby Table 2.4 (recall thatq,isthe vector of joint ccordlnetesof the fingerI).Thedynam ics of the object are givenby the Newton-Euler

notation definition

H,(q,) inert ia matrixof thefingerl

e

iner tiamatrixofthe object

AI mass ofthf'object

Table 24 Inertia parameters

equati ons

Mp·~M g+L>

_,.,

(2.48)

(2.49)

26 Chapt er2. Roboticmanipulati onwith permallentro/JingCOntacts

obtain ed usingthe LagrangianHO.;)21of thecorrespo ndi ng man ipulators;

H,(q,)ij,

+

h,(q"q,)=T,-T•.w '''''I, (2.50) when 'h,contai nsthe gravitationalandquadraticterms w.r.t.thejointvelocitie s

Thetor'1.l1f'.~rif'1in~rf'<!hy the motorsat the joints areconsidered as the inputvariablesof theHO S. Thevecto rofthesejoint torques of the finger1is denotedby7,.Asmentionedabove, contact forces aretran sformed into exteriorjointtorques.denotedby thevectorT' n lforthe fingerI.

In orderto precise the relation betweenthecontactforce

I

,

andthe vector ofexterior torquesT"HI.we deter minefirstthe equivalentwre nch(force andmomenttakentoge ther ]

corres pond ing tothe contact forceat theorigin of theframef{~,fixed to thelastsegme nt of the fingerI.

Thistransformat ionis linear foranyfixedfingerconfig urati on and contact point and given by the relation

(2 51) whereJTis the transposedjaco bian ofthefingerI(defined by(2.10))and thematrixGTread s

o:

_

[

-I ]

,- -[n(¢1)p~,xl

TIl(>contactis saidtobenon-singu larif the matrix

i

r

e:

can be inverted. Thisallowsto eliminate the contactforces

f,

an dtheexteriortorq uesT,.~tandtoreportEqua tion s(2.50) and(2.51)in the dyna micsoftheobje ctresulting

,

1I1pn"",A19-I-~( J;e:rl [T,

-

JI,Q,-h,(q"q ,)]

a

e";"Q

=

~{O(tfl°)pc,x(J,TCn-I[T,-H,q, -h,(q"q,J]}-WOx8,,,,0

Remar-k7 Inthecase of redundan tfiugers(f.e.such thatthe num berof joints exceedsthree)

thep.~eu.do-mverseofJ,1'C ; ShOlllri bellsed

2.

1.

5

I

n

equ

al i

t

y c

o

nst

ru l

nts

The contactforces appliedto theobjectbytill;' fingers mustorientedinwardstheobject.This requirementis expressedbythe inequality

(2.52) Since we supposepermanent rollmgcontac ts(Le.there is no slip, set' Assumptio nA'l),tI,e forces must also remaininsidethe so called frictioncone.SupposingCoulombfriction model,

2.1. Modelling ₂₇ thevolumeof thisfrictionCOliCis dctcnuincd b.11thefrictio n coefficientJ.I.and thecorrespondi ng constraintreads:

where

1m.

(resp. fll)give thenormal (reep.tangent)component of the contact forcebetween thefinger1andthe object

Other inequalityconstraint may alsobe presen tin ordertodescribethe limits ofthehand's work ingapace and to avoidcollisionsbetweenthe fingers.These constra intsarenot add resse d here and willberelaxed inthesoquel.

2

.1.6

P

la na r h

and- obj

ect

.

s

t

r u

ct ur

es

Ass umptionsAI-A6re main unchangedforplanarHOSs.However,impo r ta nt simp lificatio ns cnnbemad ew.r.t.thegeneralthree-dimens ionalC81;e. \Ve proceed thesameway as for the modelling of three-d imensional HOSs. namelywe sta rtwiththe equa tionsdefining the geometry andthekinem atics and thenwe continuewiththe dynamics

Recall thatthe framesfixed tother-th lingerand totheobjec-tare/(~and /(0and we denoteby thevecto r

P;

EiR?and by th .. angleiP~ e Stheirrela tiveposit ionandorientation. Recal lalsothatthecoordinatesof the contactpoint

P'c.

=

lxt;,.

Yb.]T )E [o.d)areexpressed inrbc fra meKOand /(: ,respectively.

Since 41°and¢'~are scalar.all orientationmat riceshave thefor m

n

ib)

e

[COO

"

sm

e

andwe simply haveWO'""'-

Jp

and

w;

=d>; In particular.therela tive position andorienta tion ofthe object andfingerI.corresponding ro(2.2). isdefinedas

(2.53) Observetha tthe geometry of the contactbetween theobjectand theathfinge risdefinedby theconstr aints

c~ (p~J=0 (2.54)

CO(PcJ=0 (2.55)

p~,~

P:

-

D(10 pc,.=.0 (2.56)

del(

D

C:

(

p~,)

)=O. (2.57)

Dc"(Pc,J.D(¢~)T

correspondingto theequations respectively. These constraints

depen dexcluelvclvon the therela tivesituationofthe

Chllpr(,1"2.Roboticmanipu lat ion withpeunenentrollingcontact s Since kerDc'f(p~,)is one-dimensional. itisspannedby

w'

C,

~

[0

I

-

0

I]

1Jc"(p'-,

o;

)T

Takingintoaccountthefacttha t therelativevelocity oftheobjectandthefingertatthe contactpoint is

'

Vc

,

=p

~

+

[¢.~ )(1(p~,

-

p~ )

thekinematicconstra intcorrespondingto(2.8)reeds

(

w~

,rr

(v

:

+

[

ti:

xl

(p

~,

-

p~)

)

=0 where

(2.58)

Todefine the geometryoffinger1.recall thatF,gives the set inwhichthevector q, getsits values.Thedefinitionoftile direct geometryfunctiond,offingerIintilt' plant"issimilar to(2.9)but with adifferentrange space:

d,:F,---tIR2XR/211'Z, d,(q,) ....(p~,¢~) (2.59)

wecannowgive theinventory of rhovariablesandcons train tsdefiningthe geo metryand thekinematicsofplanarHOSs.similarlyto Tables 2.2 and2.3referringto the generalthree -dimensiona lcase.

varia b les I desr-r-iption _~

q"j- 1. ,m jointcoordinates

I:

::'

..

I(t k

p" , dP position&orientationofthe objec t 3 p~.¢~. I

=

I, ,m positio ns&one nta rionsofthe fingertips 3m p;.¢{.1=1, ,m relative posit ions&orie-ntations 3m p~, .1=I, ,m contact pointsonthe object surface 2m

p

'/:

.?

=1. ,m contac t pointsonthe fingers surface 2m Table2.5: Variab lesintwo dimensions

H.(~IIlR rk8.Itssshownlater(seePropositsori SmSccnon2.2)thaI thekinemati c constnun t 15IllU10!l5mte.lJ'1YlhirI'llthepla1lar case

Thedynamicalequations of the objectandthe fingers for the two-d imensionalcaseread

mr

l=fg+

L

it

1~1 H,(q,)q, t-h,(q,. q,)=r,

i

;

c

;

t.

(2.60) (26 1) (2.62)

2.1. Modelling

I

constraint type numberofequationperfinger

(2.53) geometric 3 (2.56) gecunctrtc 2 (2.5-1)-(2.5;1) geomcmc 2 (2.57) geo met ric l (2.59) geometric 3 (2.58) kinematic I

Table2.6: Constra intsin two dimensions

The following exampleillus tra testhe modelling ofa.planarHaS

Example5.Considerthe110 5giveninFigure 2.10,Thehand

(translat iona l)jointsandfingertipsof radiusr.,I.=L 2.The

radiusR.Thepositionof theobjectis by thecoordina tesXO itsorientationisdetermin edbythe

29 wit hpr ismatir-isadiscof point()and

q

"

Figure2.10: PIMarHOS.

30 Chap ter2,Roooticmanip ulatiollwithperman entrottingconmc ts

Thegeometricconstraints(2.54H2.57)rea d

(I~Y

+

(

yl-Y

-

r

?

::00 (2.63)

(IcY

+

{YcY

-

R

'

=

0 (2.64)

[

g

,,]_

[

x:

-

x~

,

]

_[co.s

0

: -

sin

~o]

[

x

c

,

]

~

0

q" y"

-

111.,

,

mo"

,O',"" Yc, (2.65)

det[

4:,

_

!/

~,

]

-=0 (2.66)

IC

,

cos¢<J-

YC.

Sinql'

I

C

,

sin<pc

+

Y~:.cosrj)0 .

for1=:1,2.The kinematic const raint (2.58)rends

The dynamic equa tionsofthe objectaregivenby(2.60)-(2.6 1),whilethe dynamic s of the

fingerLcorrespondin g,to(2.62) Tt'OOS

[

m d

+

m" 0]

[

g

...

,

,]

,

[

-

(

m"

+

m

,,

)

g

]

~

[Td]

_

[

f

,'

_

.'

,

]

O m" g" 0 T" (-I)

I,

(2.68)

where m'Jgives themass ofthe jthsegmentoffingerI.

2

.

1.

7

H

an

d- o b j

e

ct

st

r

uc

tu

r es

w

i

t h

s

p e ci

a

l

m

orp

hol

o g

y

Conside rarobotichandwit h3fingers, each with 5joint s,Supposethat the following proper t ies

aresatisfied(seeFignTr2.11),

J Thelastsegm ent softhefingersMespheressuchthatthey canbe rotatedaroundtwo indep endentsymme tryaxes.Theserot a tions correspondtothe joints4and 5

2 For each finger,thejointcoordinates corr esponding tothejointsnumber'1and 5 are

cycliccoo rdi nat es[65J:

i=I. .3

where

C.

istheLagrangi an oftheuhfinger).

3.The orient at ion ofthe las tjointaxisdoesnot dependonQ'4(I=J, ,3)

Itt-m a rk9.The lastcondltlOncorrespondstospeCialmectuuncel de1J1ct:s.roughly~pt:uJ.,;l7l.q, SimIlar- tothe ones usedjor trackballsand[orthet71fchant cal mteqrotorpresen tedl1i[56.Ch ap Ie"if. Theresult scon ccrm n osuc h hand~/.ructUT"t:scur;be east/yextendedto hlghe,.lIIJmlle,. jiTlf]t;1'Sand jorn ts,Wehave restrictedoll1.~ dt'estothe lillllp les !caseforreadability'ssake.

2.1. !\Iodc11ing

Figur« 2. [1. Finger with symmetries satisfyingthe conditions

.n

SInce the liru-nr nelocii.u

Ii':~

quies the velocity ofC,which1,Salso a pmnt nf the enlarged surface. the relaiuie velocity quics

proeed nrc presented at the section.

Example 6. Consider the HOS depicted in of radiusR.The coordinates and its orient.at.ion

= 1.2.:3) give' the

to the centers of the last segmeut» arc givell hy

2.12. The rnanipnlat cd object is a [rarne/(0.fixed to the sphere arc angles(i:,o=

Imse points in The

fingers.The' geometric constraints

with derivatives

32 Cha pler2. Robotic mallirm/ati ollwithpermanent rollingcomacrs

(dd: 'J.d' JI

f"'!i", j

Figure2.12: HOS inthree dimensions

Since

II

Dc"

(Pc

,

l

ll

=2RandI~Dc~(p~,)1I=21",Constraint(2.6)reads

P

'b.

=

-

~

n

(,p~)p(" .

Repor tingthisin(2.3),and multiplyingbothsidesfromleft by

n

(4'1l

we get

(270)

Th e rela t ive velocityis nowexp ressed inKb multip liedfro mleftby 0(<14):

Thisis sim ply obt aine difEquation (2.7 )is

The vectors spanningthe tan gentplaneatthecont actpointere

wt.

c.

=l-z~

..

O, I~.Vand

wt

.c. = (

-Yt.. ,

x

'b

..O

jT

Finally,sincethestruct ure ofthe inertiamatrir-es Menot specified neith..rforth e finge rs nor fortheobject,thedyn a mic equat ionsof the objectandthe fingenl aregiw-n illthcirgeneral form by(2..l8)-(2.49) and by(2.50).

2.2

H

ol o n o m

y

,

fl

a tne

s s

a

n d Li

ou villi

au

p

r o

p

e

r

t

i

e s

The nouon of holonomyis defined inAppendix A.The definitions of (different ial)flatnessand Liouv rllian systemsarerecalledhere .Note thatthertlt orderlimederivat ive of afunct ionI(t)

2.2. Holonomy, flatnessiWc!Liouvilluu: properties

Definition 4 (flatness). The system .1:=f(x,u)

33

I~2.71) unih:£ERnand uEjRm c/1JJerentwllyflat ifone can find a set of uaruibles, calledfie:output,

unih r jinite mteqer. sucli that

}; =n(y,Y.;ij, 1L=(i(y,y,y,

unili q a fiiute uueqer, and sucli that the system equations

are idenucallu satisfied:

(2.72)

(2.73)

The weaker notion of l.iouvillian systems is definedin [1OJ using differential algebra. We adopt here a slightly different definition.

Definition 5 (Liouvillian a set oIvanables defined as

(2.74) such that x=n(y,tj,j). 11.=(3(y,y,j), ,ylq),(i,1 ,?/Q+l),(i,,-1

Ji;p-')

.(::" 1), (2.75)

unib.(;,-L=(~"~,'

c:

1)),and such that a and(3ulenticolu)satisfi; the system equations:

~=f(n,.8).

(2.76)

34 Chapte r2.lloboticmallip tila tiollwh hperma nent rollingcont act s

2.

2.

1

H

o

lon

om

y

and fl

a tn

es s

of pl

an a r

s

t r

u

ct

u res

IIcanbe shownthat are holonomic.Wealsoshowthar.suchconfigu -rationsaredifferent ially withmorethan onefingersaslong:as eachfinger bas atleast two

joints.

Prop ositi on 3.Inthe thetxnemouccons traintsbetween

otncctarehotono nuc. planarHOSs. withan arbitrary

bolcnonuc.

Itis toshowthattheconstraintsarcholono micfora single fingerin contact objec t, thesubscript1correspondingto the finger's indexis omitted in the proof

Notethatthe configuration manifold and

afinger incontactis seven-dimens ional. and

observe thatthe con straints (2,54)-(2.38) onlyon

Theone-form s corr espondi ngtothe geometricandkinematiccons traintsread

i':Vj=d(cd(pi, ))=0 (2.77)

i':V2=d(cO(pc))=0 (2.78)

[::]

=d

(p~

~

p

'

·!1(<p')pc )=0 (2.79)

m,

~

+

"

(D,,(~;;

I

P~:&'

)

T))

~

0 12.'0) t:V6=

(wt

,

r

(dp'

+

[ddl x](p~-p'))=0 (2,81)

Propo sition4.PlanarHOS,~w-<th atleasttwofingers. eachlunnnqat leasttwoJomts, dtfJerentw llyfiat

.m, at2:2)thenumber thataflat output is .qt,a,(i=1. ,m)and by y, = g, (/t , ./ ",) 1=1, .2m-3.

2.2. Hoionomy, ttsu.ecs and Liouvillian proper ties 35 with arbitra rybut fixedcombinationsofthecontactfor ces Letus denot ebyYtheCOIT

e--:L

::I

a,dimensionalvector

of the fingerlcan be alllocally calculatedas Considerthe fingert:and

integrat edto getridofp~and

Using Pro positi on 3, thekinematicequatio n can be a setof six algebraicinde pendent rclatrvc Denottce bv 0'.,'th,,,i,ctatio" andposit ion of theframefixed to the finger . the absolute posit ionand orientat.ion of allthefingerst=1. .Inare givenby

(2.82) 1=1 , .m,

givesthe contact

ThecontactforcesandY.

Y

,

Y

allowthen tocalcula tethe vectorsofjointtorquesofthe

fingers r,.(I=1, .m) using(2.62).

Sincewe haveshown tha t all variablescanbe expressedas functionsofYandits

derivat ives we haveproved that a flat outputandthe systemisflat 0

2.2.2

F

la

t n ess

st

u

dy of t

h

e

kinematics (exa m p

le

s

1

and 2)

\Ve wish to concludeabout the

ExamplesIand2.Forboth

allowingpivotingn-otions.then kine matics.

ofthe kinematics studiedin two cases,Fist,we the model

suchmotionsare to the

Kiuem at icswith pi vot ingmotio ns

This is the case of ExamplesIand2without the noo:pi,oci"gconstraints(2.22), samefor bothexamples.Introd ucethe matrixAand

A=

[

~

Hcos.p R~in.p Rsin.p cosB -Rcos.pcos() -1

o

(2.83)

36 Chapter2. Roboti cmanipulationwith permanentrollingcon i ecss

where,for Example2. we identify

onthe firs t Hence 1(reep read AX= O coor dinatesofthe contac t [resp (2.27) -( 2.2 8))of (2.84)

Thefollowingdrift.lesssystemwas associatedto Equa tio n (2.84) usingthevectorfieldsdefined

by(2.23) , <t=]tSin.ptMO- U3

e=~

cos .p

+7;s

i

lL 'f'

(2.85 )

ib

=til iJ~=1l2. Propositio n5. puu:UJ=i:~.112 1m/It

(-= -psin-p cos (}+iJ~'ospsina AX

Proof. Introd ucetilevariablesYland yzas

[

y

tn

,

]~

AX

and

(2.86)

(2.87)

'" ,m d( arefun c t.ions of thesys t e m varrabies(2.S4)includingt.heinputs1<1=I~. Differentiating(.using (2.86)and (2.87) ,one obtains

aYl

+

/;Y']= (:

+

O

,;}co

s

e

with

<I=,ps in<pcos O

+

(i l

+

(

2_{)cos epcos {)-2.jiJs in.psi n(J}

₊

_{Bcos <psin(J}

b=-.j!cos'Pr:osBI-(.p2T(2_{)sin+,cos B t-2¢Ocos <psin0t8sin <psinB}

2.2. HolotJOmy,flatn essandLio uvttlion propert ies 37 Observe nowtha t(2.8B)together with(2.86)constitutesalinearsys temw.r.t.tothe var ia bles

Ylandy~

[.pSin'PCOSf}:JcoslpsinB

henceYland111 areobtai nedasfunction sof(. (,8.

O

.

8

.

-p..p.and

;p

InordertoobtainWas functionof (.<P.(Jand their successivetimederiva tives ,WE'differ -cntiatcEquation(2.87)with(2.84):

["Yl.']

-

d

~(

f

A

X

)

-

(

~

n

t

A)

A

'

-R

_

[

-'

Orp

';'

t·os <p

'''

9

r

+''

<J

'

(

(

iP ~

';

'0

in

'

lp

9

CO

,

"" - 0"

s

e

+

e

co

s

n9,

'P

s

i

,n&)]

n

l)

)

thus yield ingrjJ:

~

+/1;asinep W"" Ii .

.pcos<pcos {l-Osin ipsinO

~

-Orj;cosr.p

.psin.pcos f}+ OcosepsinO (2.89) Sinc ewe have alreadyshown tha t Yl and Ylarefun c t ion sofYandits derivatives.thesame holdsfor!,V.

Finally.by(2.87). wehaw

,t:~""Yl-R(Ocosop

+

wsin<prosO)

Y~""Y'J-R(Bsin op-IPcos.pcosO)

proving thatI~and

11/:

are alsofunct ionsofYenditstimerlerlva nv es.Sincettl=

±'f:

.

tt2 ""iJ~,

tt3-:=....,~=.p -J.sin8.the inputsarealso funct ionsofl'and der tva uv es which achievesthe

~~[. 0

Remark11.Thethl1Il component (oJl'fJ1'1It'f1r-Sqmt,. Inooltled aTld

us

physlcallllterpretahon

ISfar JromobVIOUS.Ithasbeenobtainedby mtegra/l0ntecbmqueswhlch are notreport ed here and tis expressionrxpltcltlycontaul.Sthe Input vanahles WhlCh/.Snot usual.Asimpler fiat Olltput/.SnothlOumat present.Noncethatthe flatnesspropert y oj the dnftless system (2.84) Withthreempufsreslilts(JL~ofromatheorem of !46j.

Casewitheliminatedsptnn lng motio ns

Theintrodu cti on of thenon-pivot ingconstr a int (2.22) {sameforExamplesIand 2)thatelim -inatesspinning motions result s adifferentkinem at ics LetU~del111E'thematrixA'as

A'_[ A ]

38 Cnooior2. RoboticmallipuliUiollwitllpermanI'mtoilingcontacts Thekinema tics ofthissystemreads

A' ..\,=0 (2.00)

whereAandXhavebeenalreadydefined by(2.83) . Usinga result of [46]thenon-flatnessof

the kinematics(2.90)canbeshown.

For complete ness . the following theorem of[461is recalled.

Theorem1.Letthe codlst n butlOll

n

be spanned by11-2nuiependentone-formson a mnmjoid AIof dlm ens IOIln.Thef/-tsoclated dnftless ISfeedback/nwanzable atellcry pomt of an open and dens e subsetIfandDillyIf the of

n

=/0 sousfies

dimf~=n-2-k k=O, ,n- 2

The one-formsspannmgthe codlstr ibutlon defining the kinematicscan bo[Padfromthe rows ofthematri xA'

rot

=

cos.pdB

+

sinopcos 8dt/J-dr~. lV2=sin.pdO- cos<pcos{}dw-dtfc:

l:VJ=d..p- sinOdd,.

giving thecodis tri buuon

onafive-d imensionalmanifold.hence the numberof inputsoftheassociateddrift.lees system is two.Observe thaltheone-for ms&..:'\_02,andtvJme linearlyindependent everywh ere since WI1\W,1\wJhasa constantnonzerocomponentindxt ·1\d!l!:Adp. Thisallows toapply Theorem1.

Pro p osit ion6.The kmemahcs definedby

n

IS notdlfJerent wllyflat

Proof.App lyingTheorem1.thenecessaryandsuffir-icntconditionofflatnessreads dim !\;<2 dim,2

=

L dim/J

; <0

whereII12and13_{areth e codt st nbuuons}in the derivedflagof

n

=JfJSinCE'ccr.1412.and 'tVJMt'ind cl' cn dentone-For msitisenough to co nsid er the irexteriordcrivatsves

dWj

=

-

sin.pdpAdO

+

COS8 cosvx£p1\dlP -sin (}sin.pdO1\dw dw ,=cos.pd.p1\d8

+cos8

sincpd..p1\dlP

+

sin8 cos <pd(}Adl/J dWJ=-cos8dB1\dw.

and observewhich onescanbe obtained asexter iorproductshaving theform1]1II7/2wit h 1/1EIII (A/) . and '12E1° Notetha t allext erior prod uc tshavin gtheformWIItv,(tv EIII(AI).

2.2. lIo/an omy , ttouie....s8/ldLiO ll ~'j1Jj8 IJproperti es ₃₉ componentnorin

1=1,2,.1=1,2.3).It

neitherin i\dy~ . thisimplies thatdw)

¥

tiJl\ro,(wEAI(A!),

to examinetheexterio rproductscr AW3.Since (sin<pdO-cos<pcos fldliJ)i\W3=dOl

(-('Ospdl)-sin<pcosOdl/J)1\W:l=dW2.

onegetsthatIJ_{=span('Wt. cs},so dimIt=2}

Tho precedi ngdiscussio nhas shownthatdw ,

¥

wAw,(0EAl (AI),I=1,2) Hence d'W,

¥

0modItt

=

t,2,thusdim12

₌

₀

_¥

_{1whichshowsthatthe nece}

ssa ryan dsufficient

conditionofTheorem1isnotsat isfiedandthe propositionfollows. U

2

.2 .3

Liouv

illi

an

k

in

e

m

at ic

s

Letusshowthatall dnft.lesssystem sobtainedinthe examplesofSection2.1.3which on.' not

flat areindeedLiouvillian Proposit.ion7 The dnjtle$ssystem

..p

=

7i

sin<pt.llll(I

-

]j

rnscptan(I

iJ=7icos<p+ 7f sin <p

UISlllcp U2COS",

1P=R CQs 8 - R cos8

I~=III

iJ~=U2.

(2.DI)

(obtamedmExample1and2WIththe non-pnmtlll9C01l-~tmvlt(2.22)meludedmthemodel and

proven tobenotflat by Proposition6)ISl.w umillan With Y=(",,0)aspart~allyfiat output

and x'/::.

yt

.,

1f;as mtegmlvanables

Proof.Bythe firsttwo equat ionsof(2.91).theinputsIIJand1t2canbecalculat ed from the tr ajecto ryofYandY

-

,oo

(

~

)

,"n(B

)

] [

~

l

sin:l?I) 0 (2.92)

Hence,the variablesI~,y~.and1Pcallbe obta inedfrom

~= ~ Slll<P_~COS.p Rws8 Rcoe

s

i:~""Ul

y~=u2.

bysimpleintegralsprovided thattheirinitial condit jonsan'knownwhichprovesthatYis a

partialfy Ra toutput andth at

:r

1·,

"f.

.

If'arcintegra lvariables.Thesystemisthusproven tobe

40 Cha p te r 2. Hobot ic manipu/atiollwitIJpemla/lentroJliJJ8 contacts Propositiou S.Tticdnftlcss system

rp

=

-

}i

-

~

sin'{Jlan(}

+

]i

C060Ptau0

0

=

-

7i Cos.p

-

7i ~in<p

tl2sm op U3COS<P lP=-/i cosO+ R cos (} i~,=Ul

ii-

1=U2 i~,=UJ

lobtal1ledInRxample./asthe (.p,8.w)aspartIallyflat OUtP1lt

to(2.45))1.5LlauvllI,all with Y= as IntegralvarudJles.

Proof.TheinputsClH'obtai nedusfunctionsofYandY

[

"

U

,

2

]

=

R

[

-

0

I

'<3 0 -cosp -sin p ,;nO ] [,,] -sin.p cos O ~ cosopcos0 lb

andtheintegral variablesareobt ainedasintegrals oftheinputs.

o

2.

2.4

Ll

ou v

il

fi

u

u

d

y

n a m ic

s

o

f h

and-o

bj

ect s

tr

u

ct

u

re

s

w

i

t

h

s

p

e

c

i

a

l

mor-ph

ol o

g

y

Pro posit.lon9.Con.Slder aHOS $uchthaiCondsuons1-3ofSectlOTI2.1.7holdtrueIIIlth three fingers.jit'Cdrgrees of freedom each.TinssystemISLiouuduonand adrmtsa partwlly flat oulpt lf

poSitionan dol1cnlatuJ1l oj tI'eo'J'"an dcoordvu aesojthecontactpomt s onlheobjectbou nd-ary;,withthree com bm atlons contact forces: y,=q.(/J,h , fJ ),I=1,2.3.Moreover.Q,4,

q,~.1=1, 2,3,thelast coomma tesojthe fingers arr mtegmlMn(ll!les.

Proof.Withoutloss ofgenerality. we may assumetha t eachfinge rt ip hasrad iusf

FixtheframeJ(~to the fingertipofthenhfinge rwithits origin at thecent erofthe sphere.

Hence thevect o r

p1

givingtheoriginofI<~de pends on thejointcoordinate sq,l. ,q,3and doesn 't depend011the lastjoint coordinatesq,~and qiS'Thus the direc tgeometry(2.9 )is given by

p~=P: (Qd .q,2,q,3 )

2.2. Hotonc my.flatness and Liol1vilJillllproperties 41 Moreover.due toCondlt.ion 3, theangularvelocity of thefingerw~doesn'tdependonq.~and

qi~(it depends onq,l, .q'3and4,1. ,4'5):

12.94) Thusthegeometricconstrai nts ofthe unique contactpoint between theobjectandthenh

finger(2.6 ) and the kinematic ofrolling without slipp ing(2.8)can beformula ted

wit houtt.hevariablesQ,4'q,~,and

The geometricconstr aint (2.3)expressed intheinertialreferencefra me1\"1>read s 12.951 Rut,dueto ConditionL hence(2.95)become s , , 0(" )(

°

Dc"(pc,fr) 0 Pi-P- "" Pc,

+

rUD(~(p(J II '= . We makeuseofEquati o n(2.4) (2.96) (2.97) Similarlyto the vectorswf.c.andw{e,JetIlSdenotebywf.c,andwlc,the vec tors spa nning

kellJcO(pt.,),i.e.thetangentplane tothe object atthecontactpoint.

Therelati ve velocity at thecontactpoint between the nhfinger and theobject is ex pressed in the basis ofKI>·

V

c

,

=:

v

e

,

-ll~,=

pO

+

[w" x ]D(itl)p,!::,-p~

-

[w~ x](l1{tP")pc• ...p" -p~) (2.98) thusthe kinematicconstraintsarcgiven by

w[c

,V

c,

=

0 u'ic,V(:.=0 (2.99)

Le tUI;provetha t~c.,p1. qt!'

oa-

q,;\,1'4 '1,5 call beex pressed asfunctionsofY,}' First, by(2.97)and by the implicitfuncti ontheorem. onernn expr ess

z&.

as

zc

,

""'-Z

c,(xc,.yc

.

)

.

l'= 1, 2,3. Then.replacmg

zc

.

in(2.96).

p1

canbeobtumedas function of Y The first(vectorte l) equa tionof(2.93)can be locally solvedforq<!.Q,2,Q'3'givingthese

three variablesas functions of}'

Sincethekern elofDC:is3functionofY the sameholds tru efo rwr.c"w~.c, Moreover.

byEqu ation(2.94).w~depends011\',\',andq,~ ,

q..

s. Using(2.98),Equat io n (2.99)reads