HAL Id: tel-00011866
https://tel.archives-ouvertes.fr/tel-00011866
Submitted on 9 Mar 2006
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
Werner Krauth
To cite this version:
Werner Krauth. Physique statistique des réseaux de neurones et de l’optimisation combinatoire. Analyse de données, Statistiques et Probabilités [physics.data-an]. Université Paris Sud - Paris XI, 1989. Français. �tel-00011866�
DE
L’ECOLE NORMALE
SUPERIEURE
UNIVERSITE DEPARIS-SUD
CENTRE
D’ORSAY
THESE
présentée
Pourobtenir
Le
Titre
deDOCTEUR
ENSCIENCE
par
M. Wemer KRAUTH
SUJET :
Physique
statistique
desréseaux
de neurones etde
l’optimisation
combinatoire
Soutenue
le 14
juin
1989
devant la
Commission d’examen
M. Gérard TOULOUSE Président
M. Bernard DERRIDA
Rapporteur
M.
Nicolas SOURLASRapporteur
M. Hendrik Jan HILHORST
UNIVERSITE
DEPARIS-SUD
CENTRE
D’ORSAY
THESE
présentée
Pour
obtenir
Le Titre de DOCTEUR
ENSCIENCE
par
M. Werner KRAUTH
SUJET :
Physique statistique
des réseaux de
neurones etde
l’optimisation
combinatoire
Soutenue le
14juin
1989 devant la Commission d’examen
M. Gérard TOULOUSE Président M. Bernard DERRIDA
Rapporteur
M. Nicolas SOURLASRapporteur
M. Hendrik Jan HILHORSTREMERCIEMENTS
Cette thèse a été
effectuée
auDépartement
dePhysique
de l’EcoleNormale
Supérieure,
dontje
voudrais remercier ledirecteur,
EdouardBrézin,
et l’ensemble de ses membres. J’aifait
partie
du Laboratoire dePhysique Statistique
dès son début en1988,
et j’ai
bénéficié d’échanges
fructueux
avec ledirecteur,
PierreLallemand,
et laplupart
de sesmembres.
Mon
premier
contact avec l’ENS date du moisde juin
1986,
à l’occasionde la
conférence
deHeidelberg
sur les verres despin.
Là,
j’ai
oséparler
àGérard Toulouse de mon
projet
defaire
une thèse en France. Je lui suisprofondément
reconnaissant de m’avoirécouté,
et ensuite d’avoiraccepté
d’être mon Directeur de thèse auDépartement
dePhysique
de l’ENS.Tout au
long
de mon parcoursj’ai beaucoup
estimé saconfiance
et sesconseils.
Si
j’ai
eu la rare chance de progresserpendant
mes années de thèse àun
rythme
égal
à celui de mespremières
années dephysique
àl’Université, je
le dois enpremier
lieu à Marc Mézard. C’est luiqui
a eula
charge
deguider
mes recherches et de m’initier auxproblèmes
de laphysique
dessystèmes
désordonnés. J’aitoujours
estimé songrand
talent,
sagentillesse
et sapatience.
J’ai
également
entretenu les relationsfructueuses
et amicales avecJean-Pierre
Nadal,
aveclequel
j’ai
eu des discussionsquotidiennes
pendant
unelongue
période.
Tous les travaux
présentés
dans cette thèse sont lesfruits
de collaborations avec M.Mézard,
J.-P. Nadal et M.Opper.
Ungrand
nombre derésultats,
auxquels
je
merefère
dans la thèse comme ’nosrésultats’,
sont l’aboutissement de leurs idées.Qu’ils
voient dans cettethèse un
signe
de ma reconnaissance pour leurapport -
souventdécisif.
scientifiques
avec B.Derrida,
E.Gardner,
H.Gutfreund,
D.d’Humières,
N.
Sourlas,
J.Vannimenus,
G. Weisbuch et J. Yedidia. Je remercieH. J. Hilhorst pour avoir
accepté
defaire partie
de monjury
de thèse etB. Derrida et N. Sourlas pour m’avoir
fait
l’honneur d’en être lesrapporteurs.
Je tiens aussi à remercier Cécile
Combier,
laresponsable
du centre de calcul duDépartement
dePhysique,
pour des relations sansfaille,
et pour ses conseilstoujours
bénéfiques.
Je salue ici la sagesse duDépartement
dePhysique
de s’être doté de moyens considérables pour le calcul vectoriel.Enfin,
je
voudrais remercier J. Vannimenus pour son aide dans larecherche d’un
logement,
S.Großmann
pour ses bonsoffices auprès
del’ENS et les
organisations
debourse,
I. Gazan et M. Manceau pour letirage
de cettethèse,
et lesfondations
C.Duisberg Stiftung
etStudienstiftung
des DeutschenVolkes,
pour m’avoirpermis
depoursuivre
mes études.AVANT-PROPOS
Cette thèse s’inscrit dans le cadre d’une ’industrie de
pointe’
essayant
de pousser
plus
loin les limites de laphysique
statistique.
En
physique
statistique,
les modèles abondent. Ils sontparfois
assezréalistes
(comme
le modèle deHeisenberg
pour lesaimants),
parfois
caricaturaux
(comme
le modèled’Ising),
souvent très loin de lâ réalitéphysique
(caricatures
decaricatures).
Unexemple
de la dernière classeest le modèle
gaussien
de Berlin et Kac[1].
Les auteurs en disent: ’It isirrelevant that the models may be
far
removedfrom physical
reality
if
they
can illuminate someof
thecomplexities of
the transitionphenomena’[1].
Une universalitésous-jacente
(une
sorte de continuitédans un espace
hypothétique
demodèles)
lie les modèles entre eux ; ellerend
pertinente
l’étude dessystèmes
simples.
Dans le cas du modèle deBerlin et
Kac, d’ailleurs,
lacompréhension spectaculaire
de cetteuniversalité est venue d’une révolution bien
postérieure,
la théorie dugroupe de renormalisation.
Ces dernières années un
grand
intérêt a étéporté
à des modèlescollectifs dans d’autres sciences que la
physique,
notamment enéconomie,
enneurobiologie,
ou eninformatique.
Nous avons, pour cettepeuvent
être vus comme des modèlessimples
ducomportement
ducerveau, ou comme modèles d’une classe d’ordinateurs
parallèles.
Le
système particulier
que nousappellerons
’modèle deHopfield’
consiste en un
grand
nombre de processeurs extrêmementsimplifiés
sans mémoire et avec une seule instruction.Chaque
processeurinteragit
avec les autres par descouplages plus
ou moins forts et se met àjour
enfonction de la somme de tous les
signaux
reçus. Le modèle a surtout étéétudié comme modèle d’une mémoire associative
[2].
Par desmodifications successives des
couplages
il estpossible
(dans
un sensqui
sera défini par lasuite)
de stocker un certain nombre de’patterns’
dansle réseau.
Après
cetapprentissage,
le réseau serappelle
les’patterns’
etleur associe des états du réseau
qui
sont peu différents de l’un d’entreeux.
Ce
modèle, qui
est par nature collectif etparallèle,
offre une vue d’unprocessus de calcul
antithétique
de celle de la célèbre machine deTuring
[3]
qui,
elle,
est par constructionséquentielle.
Cette vue est aussibeaucoup plus
proche
de ce que nousimaginons
être le fonctionnementde notre cerveau.
S’il existe une
correspondance
exacte entre la machine deTuring
et tout ordinateur sériel[4],
les réseaux de neurones de nosjours
sontdavantage
des modèles dans le sens de laphysique
statistique
indiqué
audébut,
c’est-à-direallégoriques, potentiellement
capables
d’éclaircir lescomplexités
du cerveau ou d’un futur ordinateurcellulaire,
capables
denous faire concevoir de nouvelles idées
générales.
J’espère
que le lecteurPour ce texte
j’ai
essentiellementreproduit
lespublications auxquelles
j’ai
été associé durant mon travail dethèse ; je
les ai en outreaugmentées
d’introductions et de commentaires.
Le texte est
organisé
en deuxchapitres
de volumesinégaux,
dont lepremier
regroupe les travaux sur les réseaux de neurones, le deuxième lesquelques
travaux sur desproblèmes
provenant
del’optimisation
CHAPITRE I
RESEAUX
DENEURONES
1.
Introduction
Le
système
modèle(fig.
1)
d’une mémoire associative que nousétudions est constitué d’un nombre N de processeurs que, suivant
l’usage,
nous
appellerons
’neurones’.Chaque
neurone ipeut
prendre
deux valeurs03C3
i
=+1
(neurone
’actif)
ou03C3
i
=-1
(neurone
’inactif).
Le neurone ipeut
communiquer
son état à chacun des autresneurones j
par uncouplage
’synaptique’
depoids
Jji.
fig. 1
Système
modèle d’unréseau de neurones, constitué de neurones
i=1,...,N (ici
N=6).
Le neurone i
peut
communi-quer son état
03C3
i
=±1
au neuronej
par uncouplage
’synaptique’
J
Les deux
régimes
dusystème,
l’apprentissage
et lerappel,
sontséparés
l’un de l’autre(c’est-à-dire
que les échelles detemps
de leursdynamiques
sontsupposées
différentes).
Dans lerégime
derappel,
la matrice descouplages
estfigée.
L’état du réseaupendant
laphase
derappel
est donc décrit par le vecteur à N dimensions 03C3 donnant les états detous les neurones
La
configuration
03C3=03C3(t)
du réseau évolue aux intervalles detemps
discretst=0,1,...,
selon ladynamique
suivante:Ceci est une
dynamique (parallèle)
de Monte Carlo àtempérature zéro,
qui
segénéralise
facilement à destempératures
non-nulles[2].
Pendant
l’apprentissage,
un nombre p de’patterns’ 03BE03BC,03BC=1,...,p
sontprésentés
au réseau. Lespatterns
sont desconfigurations possibles
dusystème (correspondant
à un état donné(actif
ouinactif)
dechaque
neurone):
dans la
phase
derappel.
Par définition lepattern 03BE03BC
est mémorisé par le réseauquand
il est unpoint
fixe de ladynamique
éq.
(1.2):
mémoire:
On dit que la mémoire est en
plus
associative,
si un état initial 03C3proche
de03BE03BC
(dans
un sensqui
seraprécisé
par lasuite),
est ramené versle
pattern 03BE03BC
associativité:
c’est-à-dire si le
pattern 03BE03BC
peut
êtrerécupéré
àpartir
de données( 03C3(t=0))
incomplètes.
Lesparadigmes
(1.4)
et(1.5)
sont essentiellement dus aHopfield
[2].
Evidemment,
les définitions de la mémoirepeuvent
facilement être
généralisées
pour tenircompte
d’un taux d’erreur dans lerappel.
Afin de
quantifier
lespossibilités
de ces réseaux et de comparer diversesrègles d’apprentissage,
un cas d’étude extrêmementimportant
est celui des
patterns
aléatoires. Lespatterns
03BE03BC
sont ditsaléatoires,
sileurs
composantes
sont tirées au hasardle
paramètre
m est le biais despatterns.
L’introduction d’une distribution deprobabilité
pour lespatterns
rendpossible
l’étude des réseaux deneurones dans la limite
N~~,
la limitethermodynamique.
La
règle d’apprentissage
est choisie afin de mémoriser(c’est-à-dire
stabiliser)
lespatterns
03BE03BC,
et afin de les entourer de bassins d’attractionaussi
grands
quepossibles
(c’est-à-dire
deramener
leplus
deconfigurations
vers lespatterns
03BE03BC).
L’analyse
que nousprésentons
dans cechapitre s’appuie
engrande
partie
sur la notion de la stabilité. Cettenotion,
qui
sera introduite dansla section suivante
(I.2), permet
une discussion unifiée de lamémorisation et de l’associativité dans le réseau de
Hopfield.
Plus encore, la stabilité donne un critère à la fois clair etsimple
pourconstruire des
algorithmes d’apprentissage
avec de très bonnespropriétés
associatives.Toujours
dans la sectionI.2,
unalgorithme
destabilité
optimale -
le ’minover’ - seraprésenté.
Nous discuterons lesliens de ce nouvel
algorithme
avecl’algorithme
duperceptron
(de
vingt
ans sonaîné).
La stabilité donne un
critère,
une fonction decoût,
qui
peut
êtreattribuée à toute
règle d’apprentissage possible.
Ceci estl’origine
d’uneapproche
due à E.Gardner, qui
a introduit des calculsanalytiques
surl’espace
desrègles d’apprentissage.
La section I.3 est une introduction àcette
approche
propre à laphysique statistique.
Les calculs à la Gardnerpermettent
enparticulier
de détermineranalytiquement
lesperformances
del’algorithme
’minover’. La section I.4 sera consacrée àl’étude
(numérique
etanalytique)
durégime
derappel.
Nous tâcheronssurtout
d’étayer l’hypothèse
initiale selonlaquelle
la stabilité doit êtreoptimisée
afind’optimiser
lespropriétés
associatives du réseau.l’apprentissage,
mais cette fois-ci dans le cas où les efficacitéssynaptiques
sont contraintes àprendre
deux valeursJ
ij
=±1.
Pour cesystème,
le rôle de la stabilité resteinchangé
parrapport
auxsystèmes
àcouplages
J
ij
continus. Lesanalyses
sur laphase
derappel
dans lasection I.4 restent donc valables. En
revanche,
le calcul de la stabilitéoptimale
estprofondément
changé.
D’unepart,
leproblème
del’algorithme qui
cherche un réseau de stabilitéoptimale
(résolu
par le’minover’ dans le cas
continu)
est à cejour
sans solution véritable : nousutilisons un
algorithme
d’énumération pour estimer les valeurs de lastabilité
optimale
dans la limitethermodynamique.
D’autrepart,
lecalcul à la Gardner sur
l’espace
desrègles
d’apprentissage
discrètes secomplique
nettement par l’existence d’unephase
verre despin.
Celle-cinécessite l’inclusion d’effets dits de brisure de la
symétrie
desrépliques.
Néanmoins la double
approche numérique
etanalytique
fournit des résultatsprécis
et cohérents.2.
Règles d’apprentissage
Pour les
patterns
aléatoires non-biaisés(m=0),
Hopfield
[2]
aproposé
unalgorithme d’apprentissage
selon larègle
de Hebb[5]:
Il se trouve
qu’avec
cetterègle,
pour le cas depatterns aléatoires,
onarrive à mémoriser un nombre considérable de
patterns
p=0.14
N avecun très faible nombre d’erreurs.
Depuis
laproposition
deHopfield,
cemodèle,
utilisant despatterns
aléatoires,
a été étudié engrand
détail[6].
Cette étude est facilitée par lefait
qu’avec
le choix de larègle
de Hebbéq. (1.7),
la matrice(J
ij
)
desconnections
synaptiques
estsymétrique.
Enconséquence,
ladynamique
de Monte-Carloéq. (1.2) peut
s’écrire comme unedynamique
derelaxation à la
température
T pour unsystème
décrit par unHamiltonien;
le réseau de neurones devient alors un ’vrai’système
physique.
Toujours
à propos de ceproblème
d’apprentissage,
ungrand
nombred’algorithmes
différents ont étéproposés [7,8,9,10]
afin d’améliorer à la fois le nombre depatterns
que le modèle estcapable
de mémoriser et lespropriétés
associatives du réseau.Finalement,
la connexionprofonde
duproblème d’apprentissage
sur leété révélée. En
fait,
la condition de stabilité despatterns (voir
éqs.
(1.2)
et(1.4))
s’écrit comme(la
notation03A3
j(~i)
indique
une sommationuniquement
sur l’indicej,
excluant le terme
j=i). L’équation
(1.8)
équivaut
àDans la formule
(1.9)
lespatterns
03BE
i
03BC
sont desparamètres,
tandis que lespoids
synaptiques
J
ij
sont les variablesdynamiques
del’apprentissage.
Pour
chaque
neuronei,
la condition de stabilité de tous lespatterns
ne faitintervenir que les connexions
J
ij
,
j=1,...,N,
c’est-à-dire le vecteur de laième
ligne
de la matrice(J
ij
).
Les conditions de stabilitééq.(1.9)
sur lamatrice
(J
ij
)
sedécouplent
donc en Nsystèmes
autonomes(à
l’intérieurdes
parenthèses
{})
si les différenteslignes
de la matrice(J
ij
)
sontindépendantes
(voir
l’article[I]).
Ainsi,
leproblème complet
éq.
(1.9)
del’apprentissage
sedécompose
enN
systèmes
avec N-1 unités d’entrée et une seule unité desortie,
c’est-à-dire N
systèmes
dutype perceptron :
L’éq.
(1.10)
peut
s’écrire commeéquation
vectorielle entre le vecteur deligne
J =(J
i1
,J
i2
,...,J
iN
Il est
important
de réaliser quel’éq.
(1.11)
offre une formulationgéométrique
de la mémoireéquivalente
à la définitiondynamique
initiale(éq
.(1.4)) :
un vecteur J mémorise(au
neuronei)
tous lespatterns 03BE03BC
si etseulement s’il a un recouvrement
positif
avec lespatterns
’auxiliaires’~03BC
(voir
fig.
2).
fig.2
L’image
géométrique
del’apprentissage
(voir éq. (1.11)).
Unpattern
03BE03BC
estappris
par le vecteur J si le recouvrement de J avec lepattern
’auxiliaire’~03BC
estpositif.
En termesgéométriques
l’apprentis-sage consiste à trouver un vecteur Jayant
un recouvrementpositif
avectous les vecteurs
~03BC. J
1
est un telvecteur,
J
2
ne l’est pas.Si elle
existe,
une telle solution Jpeut
être trouvée par le célèbrealgorithme
duperceptron
[11] :
commençant
par un vecteur J =J(t=O) =
(0,0,...,0)
oncherche,
àchaque
instant dutemps
d’apprentissage
t=0,1,...,
un
pattern
~03BC qui
n’est pas encoreappris
J(t) ·
~03BC
< 0 et onl’ajoute
à lasolution du pas de
temps
précédent: J(t+1)=J(t)+~03BC.
L’apprentissage
est terminé(t=M)
s’il n’existeplus
depatterns
avec recouvrementnégatif,
leproblème
(1.11)
étant alors résolu. Le théorème de convergence duperceptron [11]
assure que letemps
d’apprentissage
avecl’algorithme
duperceptron
est fini si et seulement si leproblème
(1.11)
a une solution J.(Il
existe des méthodes basées sur laprogrammation
linéaire([12],
I)
qui
permettent
de décider en untemps
fini(qui
croît comme une fonctionpolynomiale
de la taille N dusystème)
si leproblème
del’apprentissage
n’a aucunesolution).
En
conséquence,
l’algorithme
duperceptron
serait une bonneextension de la
règle
de Hebb dans le modèle deHopfield
[8], [13] :
pour unproblème donné,
il estpossible
de déterminer une matrice(J
ij
)
(par
Napplications
del’algorithme
duperceptron) qui,
stabilise tous lespatterns,
à conditionqu’il
existe au moins une telle solution. Cetalgorithme
(comme
sesvariantes)
converge engénéral
vers des matricesnon-symétriques
(J
ij
~J
ji
).
Unsigne
de sa robustesse estqu’il
peut
êtremodifié pour
préserver
lasymétrie
de la matrice(J
ij
)
[8]
(à
conditionqu’il
existe une matrice
symétrique
stabilisant tous lespatterns).
Si les méthodes
classiques
permettent
déjà
de donner uneréponse
algorithmique
auproblème
de lamémorisation,
latranscription
d’unautre résultat connu
depuis
les années 60[14] permet
d’établir unrésultat d’une
grande importance
théorique :
le nombre maximal depatterns
aléatoires et sans biaisqui
peuvent
être mémorisés sans erreursdans le modèle de
Hopfield
secomporte
dans la limite N~~ commep~2N.
Ce résultat est
important
en cequ’il
fournit une valeur de lacapacité
de mémorisation de
patterns
aléatoires dans le modèle deHopfield,
règles
ont desperformances
restant très endeçà
de cettelimite,
lesrègles
élaborées àpartir
del’algorithme
duperceptron
permettent
d’atteindre la limitethéorique
de Cover(car
ellesconvergent
à conditionqu’il
existe unesolution).
Notonsenfin,
que la limite de mémorisation de Covers’applique
à la mémorisation despatterns
stricto sensu, la limite demémorisation avec un faible taux d’erreurs n’étant pas connue.
Jusqu’ici
nous nous sommespréoccupés
duproblème
de lamémorisation
(éq.
(1.4))
despatterns
03BE03BC,
laissant de côté la condition del’associativité
(éq. (1.5)), qui
est d’uneégale
importance.
Apremière
vue, ceci semble être unproblème beaucoup plus compliqué.
La mémorisation(éq.
(1.4))
des ppatterns 03BE03BC
implique
(sur
chaque
neurone)
p conditionssur la
dynamique
à un pas detemps
àpartir
de cespatterns
(ceci
est lecontenu de
l’équation
(1.8)).
L’associativitééq. (1.5),
aucontraire,
correspond
à ungrand
nombre de conditions sur ladynamique
àplusieurs
pas detemps
àpartir
de touteconfiguration
03C3proche
d’un despatterns.
Nous avons
proposé
dans
ce contexte[15],
[I]
deconsidérer
desvecteurs J dé norme fixée
(comme
|J
ij
| ~
1,
j=1,...,N;
ou03A3
j
J
ij
2
~
N)
vérifiant les conditions :
avec une stabilité 03BA aussi
grande
quepossible
(pour
des vecteurs J denorme
bornée):
pour la norme du maximum(
|J
ij
| ~
1,
j=1,...,N)
on voitfacilement
[I]
quechaque configuration
initiale 03C3qui
diffère dupattern
03BE03BC
en moins de03BA~N/2
positions
est ramenée vers cepattern
en un pas detemps.
Regardons
sans restriction degénéralité
le cas où seuls les spremiers
éléments
de 03C3 diffèrent de03BE03BC (03C3
i
= -
,
03BC
i
03BE
i=1,...,m ;
03C3i=03BE
i
03BC
,
i=m+1,...,N).
La condition de convergence en un pas detemps
est(voir
éqs. (1.8), (1.9))
(à
cause de lacondition
|J
ij
|
~1).
Pour assurer la convergence on a doncla condition m <
03BA~N/2.
Apartir
d’un telargument
on est conduit à rechercher desalgorithmes d’apprentissage optimisant
lastabilité,
pourl’une ou l’autre définition de la norme du vecteur J.
L’algorithme
’minover’ que nous proposons dans[I]
estcapable
dedéterminer la solution
J
opt
avec stabilitéoptimale
03BA
opt
parmi
tous lesvecteur J de norme euclidienne fixée
03A3
j
J
ij
2
=N ,
c’est-à-dire de trouverun vecteur maximisant une stabilité renormalisée
où
|J | est
la norme euclidienne de J. Cetalgorithme
est d’une certaineimportance,
car il se trouve que la stabilité039403BC’ = J·~03BC / |J|
correspondant
à la norme euclidienne est leparamètre
pertinent
pour ladynamique
du réseauproche
d’unpattern 03BE03BC
(voir
la section1.4)
L’algorithme
’minover’ converge vers la solutionoptimale
(c’est-à-dire
un vecteur de stabilité minimaleoptimale)
pour tout ensemble defig.
3L’algorithme
’minover’ en action. Achaque
itération t, onajoute
au vecteurJ(t)
lepattern
auxiliaire~03BC
ayant
un recouvrementpatterns
pourlequel
une solution avec stabilitépositive
existe. Il est reliéà
l’algorithme
duperceptron
en cequ’il
est de nature itératif(voir
fig.
3).
A
chaque
instant dutemps
d’apprentissage
le vecteurJ(t)
est mis àjour
suivant
J(t+1)=J(t)+c·~03BC(t),
où~03BC(t)
est lepattern ayant
un recouvrementminimal avec la solution
J(t) (dans
leperceptron
~03BC(t)
était unpattern
quelconque
ayant
un recouvrement inférieur àzéro).
Le critère d’arrêtest aussi différent de celui du
perceptron (voir I).
Comme nous le verrons
plus
loin,
l’algorithme
’minover’ donne uneréponse
satisfaisante auproblème
d’unerègle d’apprentissage
créant des3.
Apprentissage :
Calculs
analytiques d’après
Gardner
L’algorithme
’minover’ est unegénéralisation
directe(algorithmique)
du
perceptron.
Il estégalement possible
[15,16,17],
sur leplan
théorique,
de
généraliser
d’une manière substantielle les résultats’classiques’
de Cover[14]
sur leperceptron,
utilisant des méthodes propres à laphysique
statistique.
La voie menant vers ces calculsaujourd’hui
assezrépandus
a été ouverte par E. Gardner[15].
Nous traitons dans cette section-ci les idéesprincipales
de ce calcul et de sesgénéralisations,
qui permettent
dedéterminer pour des
patterns
aléatoires(même
biaisés)
la valeur de lastabilité
optimale
03BA
opt
(03B1)
[15],
la distribution deschamps
039403BC=J~03BC
/
|J|
[III,18],
ainsi que letemps
de convergence del’algorithme
[19].
Dans laprochaine
section(I.4)
nous traiterons du rôle exact de la stabilité dansla
dynamique.
La solution
J
opt
,
qui
se calcule avecl’algorithme
’minover’ a, eneffet,
deux
propriétés :
a)
sa stabilité est la stabilitéoptimale 03BA
opt
b)
c’est la seule solution de stabilité03BA
opt
Nous nous sommes
appuyés
sur lapremière
de cespropriétés
pourconstruire le vecteur
J
opt
,
enproposant
deschangements
successifsqui
faisaient
augmenter
la stabilité.Dans un travail tout à fait
remarquable,
E. Gardner montre que ledeuxième critère
(b))
peut
être utilisé pour calculeranalytiquement
lastabilité pour le cas des
patterns
aléatoires. Plusprécisément,
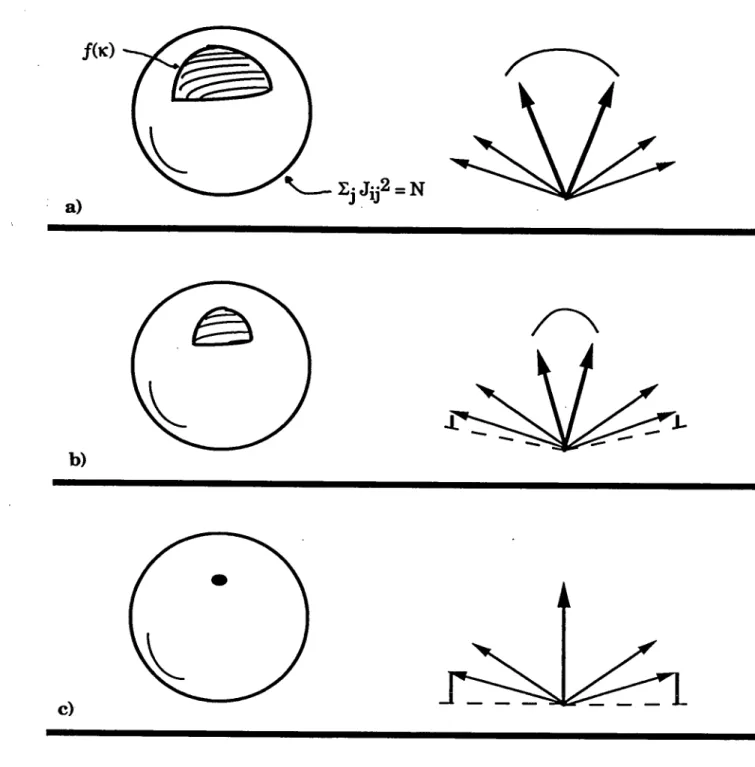
le travailfig. 4 L’espace f(03BA)
surl’hypersphère
03A3
j
J
ij
2
=N
pour 03BA=0(a).
f(03BA)
est un domaine connexe(03BA>0),
étendu sur lasurface
de lasphère ;
lerecouvrement de
deux
solutionsJ
03B1
etJ
03B2
estpetit. L’espace
f(03BA)
serétrécit comme 03BA
augmente (b).
f(03BA
opt
)
n’estqu’un
point,
le recouvrement entre deux solutions est 1(solution
unique)
(c).
03A3
j
J
jj
2
=N,
c’est-à-direl’espace
de tous les vecteurs J avec|J
|
2
=N.
Danscet espace, le sous-espace
f(03BA)
de vecteurs Jqui
stabilisent tous lespatterns
avec une stabilité ~ 03BA(voir
l’éq.
(1.12) )
est connexe. Pour unevaleur de 03BA en dessous de la stabilité
optimale,
lerapport V(03BA)
entre le volume du sous-espace
f(03BA)
et le volume del’hypersphère
est fini(v.
fig.
4a).
Enconséquence,
le recouvrementtypique
de deux solutionsJ
03B1
et
Jp
vérifiant tous les deux cette condition(1.12)
est
plus
petit
que 1(c’est-à-dire
queJ
03B1
etJp
ne sont pasidentiques,
voirfig.
4a).
Le recouvrementtypique
entre deux solutions serapproche
de 1quand
la stabilité 03BA serapproche
de la stabilitéoptimale
03BA
opt
(v.
fig.
4b).
Pour un ensemble de
patterns,
comme despatterns
aléatoires(éq.
(1.6)),
il est intéressant de connaître les valeurstypiques
du volume def(03BA).
Un résultat fondamental de laphysique statistique
[20,
21]
prescrit
dans ce cas de moyenner sur des
quantités
extensives dusystème.
Ici ilfaut donc calculer la moyenne du
logarithme
deV(03BA)
sur un ensemble depatterns.
(log
V(03BA)
a la dimension d’uneentropie;
enphysique statistique
c’est
l’entropie qui
est unequantité thermodynamique
extensive. Nousreviendrons sur cette
question
à la fin de cettesection.)
Pour le calcul de la moyenne < > du
logarithme
deV(03BA)
sur lespatterns
avec
où l’indice a varie de 1 à n ; dans la limite N~~ on trouve
avec
Dans
l’éq.
(1.19)
l’hypothèse
de lasymétrie
desrépliques
estprise,
c’est-à-dire
que tous lesparamètres
d’ordreq03B103B2
sontsupposés
égaux
q03B103B2=q
[15]
(voir
plus
loin).
Le résultat du calcul donne dans la limite q ~1(solution
unique)
pour lacapacité optimale
Le calcul de Gardner
qui
vient d’êtreprésenté
enquelques
motspermet
donc de
déterminer,
pour despatterns
aléatoires,
levolume
typique
dessous-ensembles
f(03BA)
comme fonction de 03BA, ou03BA
opt
,
dans la limite N~~.Le passage de
l’équation
(1.17)
àl’équation
(1.20)
est loin d’êtretrivial,
ets’appuie
engrande partie
sur lesprogrès
des dixdernières
années enphysique statistique
dessystèmes
désordonnés : la méthode desrépliques
[22] (ici
le désordre est réalisé par lespatterns
03BE03BC,
qui
sont différents d’unsystème
àl’autre,
maisqui
sontengendrés
àpartir
de la mêmedistribution de
probabilité).
Ce sont desdéveloppements
assez récentsqui
ont
permis
de contrôler leshypothèses
contenues dans la méthode desrépliques,
surtout l’ansatz de lasymétrie
desrépliques.
Dans le calcul de Gardner cettehypothèse
est cohérente[15]
et le résultat sans doute exact(dans
la limitethermodynamique).
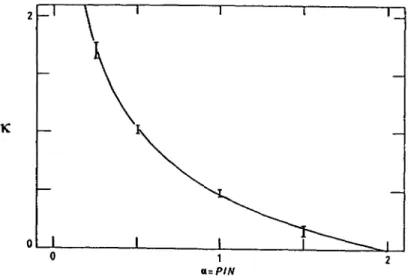
fig. 5
Stabilitéoptimale
pour despatterns
aléatoires non-biaisés. Icion compare la solution
analytique
de Gardner(éq.
(1.20))
avec desDans la
fig.
5 nous montrons le résultatthéorique
(éq.
(1.20))
et celuides simulations
numériques.
Les deuxapproches
sont enbon
accord. Lastabilité minimale devient zéro à la valeur de la
capacité 03B1=p/N=2 prédite
par Cover
[14].
La valeur de 03BA sera reliée à la taille(minimale)
desbassins d’attraction dans la section I.4.
Si
l’éq.
(1.20)
détermine la valeur de la stabilitéoptimale 03BA
opt
,
c’est-à-dire duplus
petit
deschamps,
03BA=min
03BC
(
039403BC = J~03BC/|J|),
ladistribution de
probabilité
deschamps
039403BCpeut,
elleaussi,
être déterminépar un calcul de
répliques
[III, éq. (4.10)],
[18] .
Cette distribution estimportante
car elle gouverne lespropriétés
d’associativité(l’attractivité
près
dupattern 03BE03BC
étant déterminée par la stabilité039403BC).
Un autre résultatconcerne la durée de
l’apprentissage,
c’est-à-dire le nombre d’itération del’algorithme
à une certaineprécision
du résultat. La durée del’apprentissage
utilisantl’algorithme
’minover’ a été calculée parOpper
[19]
pour un échantillontypique,
améliorant la borne valable pourchaque
échantillon
[I,
éq.(A1.5)]
par un facteurnumérique.
Même si la méthode des
répliques
permet
de calculer un certainnombre de
propriétés
de la matrice decouplages
ayant
la meilleurestabilité,
lesquantités
serapportant
àplusieurs lignes
de la matrice(J
ij
)
en mêmetemps
restent hors deportée.
Une desplus
élémentaires de cesCette
symétrie
de la matriceoptimale
doit donc engénéral
êtredéterminée
numériquement,
apartir
de simulations utilisantl’algorithme
’minover’. Pour des valeurs faibles de lacapacité
03B1, ondémontre facilement
(III, éq.
18)
quel’algorithme
’minover’ donne la même solutionqu’une
autrerègle
d’apprentissage,
où la matrice(Jij)
estsymétrique :
lapseudo-inverse
[9,10].
Dans la limite03B1~0,
la matrice(J
ij
)
del’algorithme
optimal
estdonc,
elleaussi,
symétrique.
Pour des valeursde a
s’approchant
de la valeurcritique
on trouvenumériquement
que lasymétrie ~
reste élevée(voir
lafig.
6 pour le résultatnumérique).
fig.6
La valeur de lasymétrie ~
de la matrice(J
ij
)
calculée avecl’algorithme
’minover’ enfonction
de lacapacité
apour des
patterns
aléatoires.
Notons enfin que la valeur de la
capacité
optimale,
elleaussi,
est unequantité
serapportant
à toutes leslignes
de la matrice(Jij)
en mêmetemps
et ,
à cetégard,
la seule tellequantité
facilement accessible. En touterigueur,
il aurait fallu définir le volume V sur toutes leslignes :
donc on aurait
avec
La moyenne < > sur les
patterns 03BE03BC
donne alorspuisque
le volume<log
Vi>
nedépend plus
de l’indice i. De ce fait(sous
condition que le volume
typique puisse
s’obtenir enmoyennant
lelogarithme
duvolume)
lacapacité
03B1 pour uneligne
estégale
à lacapacité
pour toute la matrice
(Jij),
même si les vecteurs~
03BC
=03BE
i
03BC
03BE
03BC
ne sont pasindépendants
d’uneligne
à l’autre.4. Dynamique
du réseau
dans le
régime
de rappel
La
dynamique
dans laphase
derappel
(l’évolution
au cours dutemps
d’un état
03C3)
est au coeur des réseaux de neurones, pourlesquels
ils’agit
de modéliser un processus de calcul comme
dynamique
d’unsystème
physique
[2].
D’habitude,
lessystèmes
considérés enphysique statistique
sont dotés d’une fonction
d’énergie
(car
lescouplages
sontsymétriques).
Pour cessystèmes,
l’étude despropriétés d’équilibre
estprimordiale.
Leur
dynamique
est fortement contrainte par le faitqu’elle
est
unedynamique
de relaxation. Parcontre,
lessystèmes
que nous considéronssont en
général privés
depropriétés
d’équilibre
(la
matrice(Jij)
n’étantpas
symétrique),
et ne sont définis que parleurdynamique.
On
pourrait
donc s’attendre que ladynamique
des réseaux deneurones
(asymétriques)
soit trèscompliquée.
Nousmontrons,
toutefois,
que ceci n’est pas le cas, au moins
près
d’unpattern.
Naturellement,
ladynamique
durappel
est étroitement liée à celle del’apprentissage.
Nous avionsindiqué
que le lien leplus important
était donné par lastabilité,
qui à
la fois ’ancre’ lespatterns
03BE03BC
dans le réseauet ’creuse’ de
grands
bassins d’attraction. C’est cettehypothèse qui
était àla base de la
partie
surl’apprentissage,
etqui
sera au centre de notre intérêt dans laprésente
section.Une démonstration très claire du rôle de la stabilité dans le réseau de
Hopfield
a été obtenue dans des simulationsnumériques
de Forrest[23].
Dans ces simulations on
regarde
l’évolution au cours dutemps
d’étatset on s’intéresse
principalement
à leurprobabilité
de converger vers cepattern.
Forrest acomparé,
pour un réseau et un ensemble depatterns
donné
03BE03BC,
03BC=1,...p,
larègle
de Hebb avec unalgorithme
dutype
perceptron [8]
pour deux valeurs différentes de la stabilité.fig. 7
Bassins d’attractionpour trois
règles
d’appren-tissage
(schématiquement,
après
Forrest[23]).
La
fig.
7 est basée sur les résultatsnumériques
deForrest,
que nousretraçons
schématiquement.
Il se trouve que les bassins d’attraction pourla
règle
de Hebb sont trèspetits.
Pour lesrègles
à stabiliténon-nulle,
lataille du bassin d’attraction est d’autant
plus grande
que la stabilité estgrande. L’analyse
de taille finie de Forrestindique
que dans la limitethermodynamique
N~~ laprobabilité
P(q
0
)
de converger vers lepattern
03BE03B3
devient une fonction en escalier : pour tout recouvrement q0 inférieur à une valeurcritique
qc laprobabilité
P(q
0
)
estzéro,
tandis que pour q0dépassant
qc,P(q
0
)
estégal
à 1 : lepattern
03BE03B3 est
reconnu avecprobabilité
d’attraction,
puisque
ceux-ci sont essentiellementsphériques.
La valeur de qc ne tend pas vers 1 dans la limite N ~ ~. Ce dernier résultat est trèssurprenant :
il contraste avecl’analyse
de la section I.2(voir
éq. 1.13)
oùla convergence
après
un pas detemps
n’était assurée que pour desconfigurations
ayant
un recouvrement initial de l’ordre de 1 -O(1/~N).
Bien
entendu,
la convergence considéré ici est une convergencequi
n’estpas
sûre,
même si elle a lieu avec uneprobabilité
1.Le modèle de
Hopfield
apparaît
donc comme unsimple
discriminateurde distances
(recouvrements).
Ceci est une force - lesystème
reconnaît avecprobabilité
1 un état 03C3 suffisammentproche
dupattern 03BE03BC -
et enmême
temps
une faiblesse : ladynamique
du modèle semble assezrigide,
elle
permet
peu de structure.Nous étudieons ensuite l’évolution au cours du
temps
deconfigurations
initiales 03C3 tirées au sort àpartir
d’unpattern 03BE03BC
de lamanière
suivante :
(Dans
la limite N~~ le recouvrement q0(éq.(1.26))
est alorségal
au biaisq vers le
pattern
(éq.
(1.27)) -
à un terme de l’ordre de1/~N
près.
Pour Nfini,
comme dans toute simulationnumérique,
il estpréférable
deapporte
moins debruit
statistique.)
Il se trouve que la
dynamique
à un pas detemps
est soluble exactementdans le modèle
(1.27)
[III].
Prenons un état initial 03C3 selonl’éq.
(1.27).
Pour une convergence vers le
pattern
nous cherchons à satisfaire à lacondition
pour ramener la
configuration
03C3 vers lepattern
(voir
l’éq.
(1.8)).
Cecin’est en
général
paspossible
(en
un pas detemps), puisque
l’informationque
porte
le vecteur 03C3 sur lepattern
esttrop
faible. Nous pouvonscependant
[III]
déterminer la distribution deprobabilité
parrapport
auxconditions initiales du
champ
sans avoir à moyenner sur les matrices
(Jij)
ou lespatterns
03BE03BC.
De cettedistribution nous allons ensuite calculer la
probabilité
quel’éq.
(1.28)
soitvérifiée,
et en déduire le recouvrement à l’instant t=1.Le
champ
h* est une somme de variablesindépendantes.
A conditionque tous les éléments de la matrice
(J
ij
)
soient du mêmeordre,
lethéorème de la limite centrale montre que h* est une variable
gaussienne
et d’écart
quadratique
moyenvoir
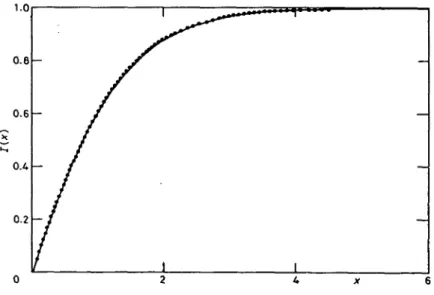
fig.
8(les
moyennes < > sontprises
parrapport
à la distributionéq.(20)). Puisque
l’échelle desJ
ij
,
donc celle deschamps h*,
est sansimportance
pour ladynamique
éq. (1.2),
leparamètre pertinent
pour ladynamique
est lerapport
de la moyenne de la distribution de h* à salargeur
fig.8
Distribution deprobabilité
duchamp
h*=03BE
i
03BC
03A3
j
J
ij
03C3
j
(t=0).
Aupremier
pas de
temps
h* est unegaussienne
dont lerapport
moyenne
/ largeur dépend
dela stabilité et de la norme
euclidienne du vecteur J.
où
q’
est donné parfig.9
Recouvrement aupas de
temps
t=1 commefonction
du recouvrementq=q(t=0)
pour deux valeurs dela stabilité 03BA. Une
configuration
s(t=0) ayant
unrecouvrement
supérieur
àq
c
(t=0)
serapproche
dupattern
aupremier
pas detemps
avecprobabilité
1(q
c
(t=0)=0
pour 03BA >~2/03C0).
L’éq.
(1.32)
est d’uneimportance
fondamentalepuisque
nous yretrouvons la stabilité
039403BC
i
,
avec une normalisation euclidienne duvecteur J. Le recouvrement
q’
à t=1 est une fonction croissante de 03BA et de q(voir
fig.
9).
Comme nous l’avons vu c’est avecl’algorithme
’minover’ que nous pouvonsoptimiser
laplus petite
de ces stabilités0394
i
03BC.
Cependant,
l’approche
qui
vient d’êtreprésentée
n’est valablequ’au premier
pas detemps,
et elle nepeut
pas être réutilisée aux pas detemps
suivants. Laraison en est que les activités des neurones
03C3
i
(t>0)
et03C3
j
(t>0)
sont engénéral corrélées,
et non pasindépendantes ;
donc la distribution duchamp
h* ne seraplus gaussienne.
Nous ne pouvons donc pas itérerl’équation
(1.34)
et l’intersection de la fonctionq’(q)
avec ladiagonale q’=q
(le
point
q
c
(t=0 )
dans lafig.
9)
ne nous donneraqu’une
première
approximation
pour la valeur du recouvrementcritique
qc. Ceci est dûaux corrélations des
lignes
de la matrice(Jij)
et, comme nous l’avons vu,nous ne savons pas déterminer
analytiquement
ces corrélations dans lecadre d’un calcul à la Gardner
(c’est-à-dire
pourl’algorithme
’minover’).
Dans
l’impossibilité
apparente
de faire desprogrès
décisifs sur cepoint
du calcul du rayon des bassins
d’attraction,
plusieurs
démarches restenttoutefois
possibles :
D’unepart
il estpossible
de calculerexplicitement
l’évolutiontemporelle
pour desrègles d’apprentissage
pourlesquelles
une formule
explicite
desJij
est connue. Un tel calcul a été fait pour larègle
deHebb,
où ladynamique
des deuxpremiers
pas a été déterminéepar Gardner et al
[24].
D’autre
part
on aessayé
de considérer des réseauxmodifiés,
pourlesquels (après
moyenne sur lespatterns)
l’indépendance
des états03C3
i
(t)
reste valable : ceci est le réseau dit ’fortement dilué’ de Derrida et al
[25].
Cette
indépendance
est aussi assurée pour un réseau où les corrélationsdes
lignes
de la matrice ont été détruites ’à la main’[II].
Enfin on aessayé
de trouver desstratégies approximatives,
voirephénoménologiques
[18],
qui
permettent
de donner des formulesII nous
poursuivons
une telleapproche :
nous considérons leslignes
dela matrice
(Jij)
commeindépendantes
et y introduisons les corrélations àla main par le
paramètre
desymétrie ~ qui
doit être déterminéindépendamment.
Ceci est une méthodeplutôt simple
qui
nous apermis
toutefois de donner une bonne formule
approchée
de la taille des bassins5. Le
modèle de
couplages
binaires
Jij=
±1
Les
développements précédents
ont étégénéralisés
enplusieurs
directions : d’une
part,
des ensembles différentsd’objets
à mémoriser(patterns)
ont étéétudiés,
comme despatterns
biaisés[15],
hiérarchiques
[26],
ou despatterns
àplusieurs
états. D’autrepart
on s’est intéressé auxcas où les
couplages
synaptiques
(Jij)
sont contraints. Nous avonsdéjà
fait allusion aux réseaux dilués
(où
laplupart
descouplages
sont mis àzéro),
ou à un autre cas où seulement la normalisation estdifférente,
comme par
exemple
|J
ij
| ~
1,
j=1,...,N.
Ce dernierproblème
[KrM]
nedonne pas vraiment lieu à des effets très nouveaux : le calcul à la
Gardner donne une fonction
03B1
crit
(03BA)
légèrement
différente del’éq.(1.20)
(03B1
crit
(0)
vaut évidemmenttoujours
2) ;
lasymétrie
desrépliques
estvérifiée et les résultats
théoriques
sont en bon accord avec les simulations[I],
qui
utilisent unalgorithme
deprogrammation
linéaire.Une extension bien différente est celle des
couplages
discrets,
binairesJij=±1.
Ce cas est leprototype
même des réseaux où laprécision
desJij
est
fixée,
et ne croît pas avec la taille dusystème.
Pour lespatterns
aléatoires,
le formalisme deGardner,
ou lesalgorithmes
dutype
perceptron
nes’appliquent
que si on s’autorise de coderchaque
couplage
Jij
avec un nombre de bits mqui
augmente
avec la taille N du réseaucomme m ~
O(logN).
Ceci est uneconséquence
du fait que, dans ce cas, lacomplexité
del’algorithme
pour un échantillontypique
est une fonctionpolynomiale
deN).
Le modèleJ
ij
=±1
pose donc leproblème
de lamémorisation
économique.
d’algorithme
d’apprentissage
et de calculthéorique
de lacapacité.
Premièrement,
lesalgorithmes
dutype perceptron
ne semblent pass’appliquer
dans le cas descouplages
binaires ;
tous cesalgorithmes
sontde nature
itératifs,
car une solution initiale est améliorée au cours del’apprentissage.
Cette amélioration successive de la valeur desJ
ij
n’est paspossible
si lescouplages
nepeuvent
prendre
que deux valeurs. Leproblème
d’apprentissage,
à cejour,
n’a pas été résolu d’une manièresatisfaisante. Un
algorithme
itératifpermettrait
d’établir facilement lacapacité optimale
du réseau ou la fonction03B1
crit
(03BA)
de manièrenumérique.
fig.10 Algorithme
élémentaire(énumération
complète)
pour lecalcul de la stabilité
optimale
du modèleJ
ij
=±1.
Cetalgorithme
estd’une
complexité
03B1N
2
2
N
(l’évaluation
des 039403BC enligne
3 nécessitep·N
opérations)
Dans
l’impossibilité
d’utiliser unalgorithme
polynomial,
nous avons eu recours à laplus
élémentaire des méthodesnumériques :
l’énumération exhaustive