Higher order (A+E)⊗e pseudo-Jahn–Teller coupling

HAL Id: hal-01118370

https://hal.archives-ouvertes.fr/hal-01118370

Submitted on 10 Jul 2017

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Higher order (A+E)

⊗e pseudo-Jahn–Teller coupling

Wolfgang Eisfeld, Alexandra Viel

To cite this version:

Wolfgang Eisfeld, Alexandra Viel. Higher order (A+E)

_{⊗e pseudo-Jahn–Teller coupling. Journal of}

Chemical Physics, American Institute of Physics, 2005, 122 (20), pp.204317. �10.1063/1.1904594�.

�hal-01118370�

Higher order

„

A

+

E

…‹

e

pseudo-Jahn–Teller coupling

Wolfgang Eisfelda兲

Lehrstuhl für Theoretische Chemie, Department Chemie, Technische Universität München, D-85747 Garching, Germany

Alexandra Vielb兲

LPQ-IRSAMC, Université Paul Sabatier, 118 route de Narbonne, F-31062 Toulouse, France

共Received 3 December 2004; accepted 17 March 2005; published online 25 May 2005兲

The pseudo-Jahn–Teller共PJT兲 coupling of a nondegenerate state A with a twofold degenerate state

E by a degenerate vibrational mode e is studied for a general system with a C3main rotational axis.

The PJT coupling terms up to sixth order are derived by symmetry considerations for this general

共A+E兲丢e case. The obtained expression for the 3⫻3 diabatic potential energy matrix is found to

be closely related to the expression recently developed for the higher order Jahn–Teller case关A. Viel and W. Eisfeld, J. Chem. Phys. 120, 4603共2004兲兴. The dynamical PJT coupling, which can arise for states of appropriate symmetry if one of the vibrational modes induces a change of the nuclear point group between D3h, C3v, C3h, and C3, is discussed. The effect of the higher order PJT coupling is

tested by a two-dimensional model study based on the e bending mode of NH₃+. The models are analyzed by fitting the two-dimensional potential energy surfaces. The significance of the higher order terms on the nonadiabatic dynamics is demonstrated by quantum wave packet propagations. © 2005 American Institute of Physics.关DOI: 10.1063/1.1904594兴

I. INTRODUCTION

Vibronic coupling, i.e., the interaction of energetically close-lying electronic states, induced by the vibrational mo-tion of the nuclei, often plays a very important role in spec-troscopy and nuclear dynamics. This is particularly true for radicals, which are usually characterized by a high density of electronic states, and molecules with high symmetry, result-ing in multiply degenerate states. Such vibronic interactions can induce nonadiabatic transitions among electronic states and thus may have a strong influence on the time evolution of the system.1,2A prominent example of such an interaction is the well-known Jahn–Teller共JT兲 effect.3,4In this case, the symmetry-induced degeneracy of an electronic state is lifted by distortions along modes of the appropriate symmetry and thus a conical intersection is formed. A conical intersection is characterized by the breakdown of the Born–Oppenheimer 共BO兲 approximation because the adiabatic wave functions of the interacting states cease to be continuously differentiable functions with respect to the nuclear coordinates and the symmetry point constitutes a pole of the nonadiabatic cou-pling elements.5

However, even without the existence of a conical inter-section the BO approximation may be invalid if two states become sufficiently close in energy and the nonadiabatic coupling elements become large. Besides the countless cases of general avoided crossings, the so-called pseudo-Jahn– Teller effect 共PJT兲 is particularly interesting for analyzing such nonadiabatic interactions. The PJT interaction is

char-acterized by a degenerate mode, coupling a degenerate with a nondegenerate electronic state.1,6–9Such a situation can arise for any molecule with a main rotational axis C_n with n艌3. In the present study, the case of n = 3 is investigated.

For the theoretical treatment of the nonadiabatic dynam-ics of PJT systems, it is beneficial to change to the diabatic representation of the electronic states.10,11 Although it was shown to be impossible to uniquely define strictly diabatic states,12,13 in practice a large number of diabatization schemes has been developed and successfully applied.14–19 Due to the high symmetry of the PJT problem, a “diabatiza-tion by ansatz” is particularly efficient and will be used throughout this study. The elements of the diabatic potential matrix are expanded as simple Taylor series of properly sym-metrized nuclear coordinates and group theory is used to determine general relations of the expansion coefficients. The diabatic and adiabatic potential matrices are related by the unitary transformation that diagonalizes the diabatic ma-trix. Thus, the parameters of the diabatic matrix can be ob-tained by fitting its eigenvalues to the adiabatic energies which are available, e.g., from ab initio calculations.

Such an approach, which usually includes only the first 共sometimes also the second兲 nonvanishing coupling terms, is widely used for the treatment of JT and PJT problems 共see, e.g., Ref. 1 for an overview兲. From the dynamical point of view, the limitation to second-order terms along with using harmonic oscillator basis sets for the nuclear motion has the advantage that all terms of the Hamilton matrix can be evalu-ated analytically. However, the disadvantage is that for sys-tems displaying strong anharmonicity this method will give poor results for properties determined by more extended re-gions of the potential energy surfaces. Zgierski and Pawlikowski already noticed that for systems with both JT

a兲_{Electronic mail: wolfgang.eisfeld@ch.tum.de}

b兲_{Present address: PALMS-SIMPA, UMR 6627 du CNRS, Université de}

Rennes 1, Campus de Beaulieu, F-35042 Rennes, France; Electronic mail: alexandra.viel@univ-rennes1.fr

and PJT couplings, the second-order JT coupling needs to be included to obtain reasonable results when the first-order PJT coupling is considered.8In our previous study on the higher order JT couplings, we have shown that higher order cou-plings can have a drastic effect on the time evolution of such a system.20This suggests that higher order PJT coupling may also make significant contributions, particularly if higher or-der JT coupling is included.

The aim of the present study is to derive the higher order PJT coupling terms as was previously undertaken for the JT case. The method to determine the form of the coupling el-ements is based on the crude adiabatic approximation by Longuet-Higgens21 and was already used in the previous work on the JT couplings.20An alternative approach, based on the same fundamental considerations, was recently out-lined by Köppel.22

II. SYMMETRY CONSIDERATIONS

In the following, the diabatic potential matrix for the

共A+E兲丢e pseudo-Jahn–Teller system up to sixth order is

derived for a general molecule with a C3 main rotational

axis. Some general symmetry properties of the correspond-ing point groups D_3h, C_3v, C_3h, and C₃with respect to JT and PJT coupling are outlined in the following.

Common to systems of all four point groups are nuclear coordinates belonging to a doubly degenerate vibrational mode e and doubly degenerate electronic states E. The in-variance of the total Hamiltonian under all symmetry opera-tions of the point group along with simple application of group theory leads to selection rules for the possible cou-pling patterns. Thus it can be shown that only the two com-ponents of an e mode can couple the two comcom-ponents of a doubly degenerate E state共JT coupling兲. It is also easily seen that motion along a set of e coordinates is necessary to couple a nondegenerate A state with an E state 共PJT cou-pling兲.

While for the C3group these are the only rules共because

there is no distinction between different A and E representa-tions兲 for C3v and D3hfurther considerations apply. The six

irreducible representations of the D3hgroup are A1

⬘

, A2

⬘

, E

⬘

,

A₁

⬙

, A₂

⬙

, and E

⬙

. It follows that the components of an E

⬘

共or

E

⬙

兲 state can be coupled by an e

⬘

mode in any order but only

by even orders of an e

⬙

set of coordinates. For PJT coupling a similar pattern is obtained. A₁

⬘

and A₂

⬘

states can interact with an E

⬘

state by any order in an e

⬘

coordinate and by even orders in an e

⬙

mode. The same is true for interactions be-tween A₁

⬙

and A₂

⬙

states with an E

⬙

state. In contrast, for coupling of A₁

⬘

and A₂

⬘

states with an E

⬙

state coupling can only occur by odd orders in an e

⬙

mode. This is also true for an interaction between A₁

⬙

and A₂

⬙

states with an E

⬘

state.

The rules given above have to be modified when more than one vibrational mode is taken into account. A particu-larly frequent example is when an a₁

⬙

or a₂

⬙

coordinate is physically relevant. In this case, the PJT coupling between pairs of states A_共1,2兲

⬘

/ E

⬙

or A_共1,2兲

⬙

/ E

⬘

, respectively, will strongly depend on the a_共1,2兲

⬙

coordinate共dynamical PJT cou-pling兲. Such a situation is analyzed in more detail in Sec. III B 3.

The degeneracy of the E state means that there exist two linearly independent eigenvectors 兩⌿₁典 and 兩⌿₂典 associated to the same eigenvalue of the electronic Hamiltonian. Any arbitrary, normalized linear combination of these two vectors will again be an eigenvector to the same eigenvalue. This fact will be utilized in the following. However, in the D3h

and C3vcases, there exist two particular linear combinations

兩⌿x典 and 兩⌿y典, which transform like different irreducible

rep-resentations of the subgroups C2v共D3h兲 or Cs 共C3v兲.

III.„A + E…‹e PSEUDO-JAHN–TELLER EFFECT

A. Complex representation

The invariance of the total Hamiltonian under the sym-metry operations of the symsym-metry point group of the system is used to obtain the nonvanishing terms of the potential energy matrix. The complex representation for both the vi-brational degrees of freedom and the electronic states simpli-fies the study of the effect of the Cˆ3symmetry operator. A set

of complex coordinates, corresponding to the e vibrational mode, is obtained from the real coordinates x and y by the transformation,

Q₊= x + iy , 共1a兲

Q−= x − iy . 共1b兲

The two orthogonal components of the electronically degen-erate E state共具⌿1兩 and 具⌿2兩兲 are modified by the

correspond-ing unitary transformation whereas the nondegenerate elec-tronic eigenfunction共具⌿a兩兲 remains unaffected,

U†⌿_共a12兲=

_冑

1 2

冢

冑

2 0 0 0 1 i 0 1 − i

冣

冢

具⌿a兩 具⌿1兩 具⌿2兩

冣

=

冢

具⌿a兩 具⌿+兩 具⌿−兩

冣

=⌿_共a+−兲. 共2兲 In this complex representation both the coordinates Q+, Q−

and the state functions 具⌿+兩, 具⌿−兩 are eigenfunctions of the

symmetry operator Cˆ₃ with eigenvalues e±2i␲/3_{. In contrast,}

the具⌿a兩 state function is invariant with respect to this

opera-tion. Thus, a rotation of 2␲/ 3 transforms the complex coor-dinates as

Cˆ3Q+= e+2␲i/3Q+, Cˆ3Q−= e−2␲i/3Q−, 共3兲

and the electronic state functions as

Cˆ₃具⌿_a兩 = 具⌿_a兩, Cˆ₃兩⌿_a典 = 兩⌿_a典, 共4a兲

Cˆ3具⌿+兩 = e−2␲i/3具⌿+兩, Cˆ3兩⌿+典 = e+2␲i/3兩⌿+典, 共4b兲

Cˆ3具⌿−兩 = e+2␲i/3具⌿−兩, Cˆ3兩⌿−典 = e−2␲i/3兩⌿−典. 共4c兲

The representation of the electronic Hamiltonian in the

兵兩⌿a典,兩⌿+典,兩⌿−典其 basis is given by

Hˆel=⌿_共a+−兲 † H_共a+−兲⌿_共a+−兲=

兺

i,j 兩⌿i典Hij具⌿j兩 共i, j = a, + ,− 兲, 共5兲 and the matrix elements H_ij=具⌿_i兩Hˆ_el兩⌿_j典 共i, j=a, + ,−兲 are expanded as Taylor series up to sixth order in Q+ and Q−.

Each term of the expansion for each element of Eq.共5兲 has to fulfill the invariance condition when applying the 2␲/ 3 ro-tation operator. For example,

Cˆ₃兩⌿_a典Q₊pQq₋具⌿₊兩 = 1 ⫻ e共+p兲2␲i/3e共−q兲2␲i/3e−2␲i/3

⫻兩⌿a典Q+

p_Q − q_具⌿

+兩 共6兲

can contribute only for共p,q兲 combinations which fulfill the condition 共p−q−1兲共mod 3兲=0. The nonvanishing terms of the matrix Hijare given in Table I in which the Jahn–Teller

terms obtained in Ref. 20 have been reported again for com-pleteness. Note that the nonvanishing terms of the matrix element Ha+are the same as the ones of H+−.

23

Next, the invariance of the nonvanishing terms with re-spect to the other symmetry operations of the symmetry group needs to be tested. To this end, the obtained Hamil-tonian matrix is transformed back to the real representation.

B. Real representation

The real representation for both the electronic state func-tions and the nuclear coordinates are often preferred for the

ab initio computation of electronic energies and for the

dy-namics studies. The matrix representationH of the electronic Hamiltonian in the real representation, including all Jahn– Teller and pseudo-Jahn–Teller couplings up to sixth order, is obtained by the back transformation,

Hˆel=⌿_共a+−兲 †

U†UH_共a+−兲U†U⌿_共a+−兲=⌿_共a12兲† H⌿_共a12兲. 共7兲 This results in the factorized expression:

H = UHU†₌

兺

n=0 6 1 n!

冦冢

VA共n兲 0 0 0 V_E共n兲 0 0 0 VE共n兲

冣

+

冢

0 0 0 0 WJT共n兲 ZJT共n兲 0 Z_JT共n兲 −W_JT共n兲

冣

+

冢

0 W_PJT共n兲 −Z_PJT共n兲 WPJT共n兲 0 0 −Z_PJT共n兲 0 0

冣冧

=

兺

n=0 6 1 n!兵Vdiag 共n兲 _{+ V} JT 共n兲_{+ V} PJT 共n兲_{其. 共8兲}

The diagonal matrices V_diag共n兲 represent the potentials of the corresponding states in absence of any coupling. The matri-ces V_JT共n兲 are responsible for the splitting of the degenerate state due to the Jahn–Teller effect whereas V_PJT共n兲 are the pseudo-Jahn–Teller coupling matrices. The explicit param-etrized expressions for the diagonal V共n兲 elements and the coupling elementsW共n兲andZ共n兲are given by

V共0兲_{= a} 1 共0兲_{, 共9a兲} V共1兲_{= 0, 共9b兲} V共2兲_{= a} 1 共2兲_关x2_{+ y}2_{兴, 共9c兲} V共3兲_{= a} 1 共3兲_关2x3_{− 6xy}2_{兴, 共9d兲} V共4兲_{= a} 1 共4兲_关x4_{+ 2x}2_y2_{+ y}4_{兴, 共9e兲} V共5兲_{= a} 1 共5兲_关2x5_{− 4x}3_y2_{− 6xy}4_{兴, 共9f兲} V共6兲_{= a} 1 共6兲_关2x6_{− 30x}4_y2_{+ 30x}2_y4_{− 2y}6_兴 + a₂共6兲关x6+ 3x4y2+ 3x2y4+ y6兴, 共9g兲 W共0兲_{= 0, 共10a兲} W共1兲_=␭ 1 共1兲_{x, 共10b兲} W共2兲_=␭ 1 共2兲_关x2_{− y}2_{兴, 共10c兲} W共3兲_=␭ 1 共3兲_关x3_{+ xy}2_{兴, 共10d兲} W共4兲_=␭ 1 共4兲_关x4_{− 6x}2_y2_{+ y}4_{兴 + ␭} 2 共4兲_关x4_{− y}4_{兴, 共10e兲} W共5兲_=␭ 1 共5兲_关x5_{− 10x}3_y2_{+ 5xy}4_{兴 + ␭} 2 共5兲_关x5_{+ 2x}3_y2_{+ xy}4_兴, 共10f兲 W共6兲_=␭ 1 共6兲_关x6_{− 5x}4_y2_{− 5x}2_y4_{+ y}6_兴 +␭₂共6兲关x6+ x4y2− x2y4− y6兴, 共10g兲 Z共0兲_{= 0, 共11a兲} Z共1兲_=␭ 1 共1兲_{y , 共11b兲} Z共2兲_{= − 2␭} 1 共2兲_{xy , 共11c兲}

TABLE I. Nonvanishing terms of the 3⫻3 Hamiltonian matrix in complex representation. Order Diagonal Haa= H++= H−− Off-diagonal Ha−= H+a= H−+ =共Ha+兲*=共H−a兲*=共H+−兲* 0 Q+ 0 Q− 0 — 1 — Q+ 0_Q − 1 2 Q+ 1 Q− 1 Q+ 2 Q− 0 3 Q+ 3_Q − 0_{and Q} + 0_Q − 3 _Q + 1_Q − 2 4 Q+ 2 Q− 2 Q+ 0 Q− 4 and Q+ 3 Q− 1 5 Q+ 4_Q − 1_{and Q} + 1_Q − 4 _Q + 2_Q − 3_{and Q} + 5_Q − 0 6 Q+ 6 Q− 0 and Q+ 3 Q− 3 and Q+ 0 Q− 6 Q+ 1 Q− 5 and Q+ 4 Q− 2

Z共3兲_=␭ 1 共3兲_关x2_{y + y}3_{兴, 共11d兲} Z共4兲_=␭ 1 共4兲_关4x3_{y − 4xy}3_{兴 + ␭} 2 共4兲_{关− 2x}3_{y − 2xy}3_{兴, 共11e兲} Z共5兲_=␭ 1 共5兲_{关− 5x}4_{y + 10x}2_y3_{− y}5_{兴 + ␭} 2 共5兲_关x4_{y + 2x}2_y3_{+ y}5_兴, 共11f兲 Z共6兲_=␭ 1 共6兲_关4x5_{y − 4xy}5_{兴 + ␭} 2 共6兲_{关− 2x}5_{y − 4x}3_y3_{− 2xy}5_兴. 共11g兲 It is worth noting that the elements of the JT and PJT cou-pling matrices are of identical form and are only distin-guished by different coupling constants␭_m共n兲. It now needs to be tested whether the Hamiltonian in the real representation fulfills the invariance condition with respect to the remaining symmetry operations of the nuclear point group.

1. D3hSymmetry

The most restrictive rules apply in the case of D3h

sym-metry. Besides the Cˆ₃rotation, this group is characterized by the operators Cˆ2,␴ˆv, ␴ˆh, and Sˆ3. The Sˆ3 operator is special

insofar that it corresponds to a successive application of Cˆ3

and␴ˆ_h. However, the Hamiltonian derived in the preceding section is constructed to be invariant under the Cˆ3operation

and thus the symmetry properties with respect to Sˆ3are fully

equivalent to those with respect to␴ˆ_h. Similarly, the Cˆ₂ ro-tation can also be achieved by successive application of␴ˆ_v

and␴ˆ_h and thus it is sufficient to test the invariance of the Hamiltonian under the latter two operations. The symmetry properties of the x and y nuclear coordinates as well as the ones resulting for the V, W, and Z functions are given in Table II. The characters for the electronic state functions are also presented in Table II. Here the fact is used that the components E_x

⬘

and E_y

⬘

can be chosen to transform as A1and

B2in the subgroup C2vwhile Ex

⬙

and Ey

⬙

transform as B1and

A2. The same correspondence is used for the degenerate

co-ordinates e

⬘

and e

⬙

.

For a general D3h symmetric molecule there may exist

coordinates of e

⬘

as well as e

⬙

character, though in the most common examples of AB3molecules only e

⬘

coordinates are

present. The e

⬘

and e

⬙

sets of coordinates are distinguished by their transformation under␴ˆ_h. It follows that for e

⬘

coor-dinates all orders of V, W, and Z are invariant under ␴ˆ_h

operation. In contrast, for an e

⬙

mode only even orders ofV,

W, and Z are invariant while all odd orders are

antisymmet-ric. For the␴ˆ_voperator there is no distinction between the e

⬘

and e

⬙

case but it is found thatV and W are invariant and Z changes sign under this operation.

The total Hamiltonian is invariant if each term of the

form 兩⌿_i典H_ij典⌿_j兩 with i, j苸兵a,1,2其 is totally symmetric

with respect to the operations given in Table II. Thus the imposed symmetry of the matrix elements H_ij depends on the symmetry of the electronic states involved in the cou-pling. It is easily seen that the condition

␹共Hij兲 =␹共⌿i兲␹共⌿j兲 共12兲

must be fulfilled for the ␴ˆ_h and ␴ˆ_v operations where the characters␹can be taken from Table II.

A first trivial result is that all diagonal elements Haa,

H11, andH22 must be totally symmetric. The elementH12,

for which the symmetry is given by ⌫_⌿

1丢⌫⌿2丢⌫Z, is

al-ways invariant for arbitrary assignments 兵⌿1,⌿2其↔

兵⌿x,⌿y其. The only limitation applies to coupling through an

e

⬙

mode in which case only even orders ofZ共n兲are possible. ForHa1andHa2the explicit form of the coupling elements

depends on the symmetry of the A state and the assignment

of兵⌿1,⌿2其. The PJT coupling elements for all possible

com-binations of states are given in Table III. Depending on the symmetry of the coupling mode 共e

⬘

/ e

⬙

兲, certain couplings vanish or are limited to even or odd orders of the coupling functionsW共n兲andZ共n兲which is also indicated in the table. Table III along with Eq.共8兲 enables us to construct di-abatic potential matrices for any combination of state sym-metries and coupling modes which fulfill the invariance con-dition of the total Hamiltonian. As an example, for coupling of an A₁

⬘

with an E

⬘

state by an e

⬘

mode it is found that the

E state components have to be assigned as 兩⌿1典=兩⌿x典 and

兩⌿2典=兩⌿y典. All orders n are allowed which result in 32 free

coupling parameters for a full sixth-order coupling matrix. If the A₁

⬘

state is replaced by A₂

⬘

, only the assignment of兩⌿1典

and 兩⌿2典 needs to be interchanged while the form of the

diabatic matrix remains the same.

TABLE II. Symmetry properties of the nuclear coordinates, of the nonzero matrix elements共n⬎0 for W and Z兲 and of the possible electronic state functions in D3hsymmetry. ␹Cˆ₂ ␹␴ˆv ␹␴ˆh x共ex⬘, ex⬙兲 +1, −1 +1 +1, −1 y共ey⬘, ey⬙兲 −1, +1 −1 +1, −1 V共n兲_{共e⬘兲 +1 +1 +1} W共n兲_{共e⬘兲 +1 +1 +1} Z共n兲_{共e⬘兲 −1 −1 +1}

V共n兲_{共e⬙兲 +1共even n兲; −1 共odd n兲 +1 +1共even n兲; −1 共odd n兲} W共n兲_{共e⬙兲 +1共even n兲; −1 共odd n兲 +1 +1共even n兲; −1 共odd n兲} Z共n兲_{共e⬙兲 −1共even n兲; +1 共odd n兲 −1 +1共even n兲; −1 共odd n兲}

Ex⬘ +1 +1 +1 Ey⬘ −1 −1 +1 A1⬘ +1 +1 +1 A2⬘ −1 −1 +1 Ex⬙ −1 +1 −1 Ey⬙ +1 −1 −1 A1⬙ +1 −1 −1 A2⬙ −1 +1 −1

TABLE III. Nonvanishing coupling elementsHij, i, j苸兵a,x,y其 in the real

representation for D3hsymmetry. Given in parentheses are the possible order

of the coupling elements for coupling by e⬘/ e⬙modes.

Ex⬘ Ey⬘ Ex⬙ Ey⬙

A1⬘ W共n兲共all/even兲 Z共n兲共all/even兲 W共n兲共—/odd兲 Z共n兲共—/odd兲

A2⬘ Z共n兲共all/even兲 W共n兲共all/even兲 Z共n兲共—/odd兲 W共n兲共—/odd兲

A1⬙ Z共n兲共—/odd兲 W共n兲共—/odd兲 Z共n兲共all/even兲 W共n兲共all/even兲

A2⬙ W共n兲共—/odd兲 Z共n兲共—/odd兲 W共n兲共all/even兲 Z共n兲共all/even兲

2. C3v, C3h, and C3symmetry

C3v, C3h, and C3 are subgroups of D3h for which the

diabatic matrices can be easily obtained from the derivation of the D3hcase. In C3v the only symmetry operator besides Cˆ3 is␴ˆvand the resulting irreducible representations are A1,

A2, and E. The Ex and Ey components can be chosen to

transform like A

⬘

and A

⬙

of the subgroup Cs. Thus, the A1/ E

coupling is described by the same diabatic matrix as the

A₁

⬘

/ E

⬘

pair of states coupled by an e

⬘

mode in D3h. The

coupling of A2/ E corresponds to the 共A2

⬘

+ E

⬘

兲丢e

⬘

case.

The C3h group is characterized by the symmetry

opera-tors Cˆ3,␴ˆh, and Sˆ3 which yields the four irreducible

repre-sentations A

⬘

, E

⬘

, A

⬙

, and E

⬙

. The distinction between x and

y components for the degenerate electronic states is useless

because there is no operator available to decide about the assignment. Thus the coupling patterns are the same as for the C3v case, neglecting the distinctions related to the

sub-scripts 1 and 2.

In C3, Cˆ3is the only operator and there is no distinction

between different A states. Here also no operator can dis-criminate between the Ex and Ey components. Again, this

case is described by the same diabatic matrix as for C3v

symmetry, just without any reference to Exand Eyand to the

subscripts 1 and 2.

3. D3hsymmetry and dynamical pseudo-Jahn–Teller

effect

As indicated in Table III, PJT coupling between states having different characters共

⬘

versus

⬙

兲 with respect to the␴ˆ_h

operator can only occur by displacement along an e

⬙

mode. However, many systems of interest, for which JT and PJT couplings are likely, are AB3 molecules for which no e

⬙

mode exists. For example the A₂

⬙

electronic ground state of NH₃+is not coupled to the A˜ E

⬘

excited state by the e

⬘

mode since A₂

⬙

丢E

⬘

丢E

⬘

does not contain A₁

⬘

. However, this picture is only valid if coupling by only a single vibrational mode is considered. In fact, these two states are coupled by simulta-neous motions in the a₂

⬙

mode, which pyramidalizes the mol-ecule, and an e

⬘

mode because A₂

⬙

丢E

⬘

丢A₂

⬙

丢E

⬘

傻A₁

⬘

. By allowing nonplanar geometries, the effect of the a₂

⬙

bending can be seen as switching on the PJT coupling caused by displacement along the degenerate e

⬘

mode. Thus, this situ-ation can be called a dynamical pseudo-Jahn–Teller effect. The electronic Hamiltonian, introducing the coupling due to the umbrella coordinate Qa

2

⬙at first order, is given by

H =

兺

n=0 6 1 n!兵Vdiag 共n兲 _{+ V} JT 共n兲_{+ Q} a 2 ⬙VPJT共n兲其 +

冢

UA 0 0 0 UE 0 0 0 UE

冣

. 共13兲

U are even functions of the umbrella coordinate only and

represent the unperturbed potentials of the A and E states along the a₂

⬙

mode. In a multidimensional study of NH₃+, which is a prototype example for dynamical PJT coupling, such a significant variation of the PJT coupling with the um-brella mode must be taken into account.

IV. APPLICATION

The derived diabatic matrix is applied to the representa-tion of a two-dimensional cut along the e bending mode of the two lowest electronic states of the NH₃+cation. These two states correspond to 2A₂

⬙

symmetry for the ground state and

2_E

_⬘

_{symmetry for the excited state. Although the ground}

state geometry of the cation is trigonal planar, the pyramidal

C3v ground state geometry of the neutral NH3 is chosen as

reference geometry for the cuts. In C3vthe state symmetries

are 2A₁ and2E. This pyramidal structure is indeed relevant

when treating, for example, the ionization process. We also investigated cuts for different pyramidalization angles which influences the strength of the PJT coupling by the discussed dynamical effect. Cuts along the other e vibrational

共stretch-ing兲 mode have also been considered. The presented

two-dimensional cut has been found to be the most suitable to perform the following model study.

The reference data for the adiabatic potential energies along the two components of the e bending coordinate are obtained by multireference configuration interaction共MRCI兲 calculations, using the augmented cc-pVQZ basis set. Since the structure is pyramidalized, the bending angles are defined by the projection of the three N–H bonds onto the plane which is normal to the trisector, i.e., the line that forms equal angles with all three N–H bonds. Using these projected angles, the e coordinates are defined by displacements from the C3v reference geometry as x = 6−1/2共2⌬␣1−⌬␣2−⌬␣3兲

and y = 2−1/2共⌬␣2−⌬␣3兲. All calculations have been

per-formed by the MOLPROprogram.24

The calculated potential cuts show very strong anharmo-nicity, so that a higher order expansion is necessary to accu-rately describe the system. In order to decide to which order the expansion has to be done, a stepwise scheme is chosen. We first investigate the influence of the Jahn–Teller coupling order on the description of the potentials, setting the pseudo-Jahn–Teller coupling to zero. To this end, the parameters of the diabatic matrix have to be optimized such that the error between the eigenvalues of the matrix and the ab initio en-ergies is minimized. This is achieved by nonlinear least-squares fitting which is performed by a combination of a standard Marquardt–Levenberg procedure embedded into a genetic algorithm.

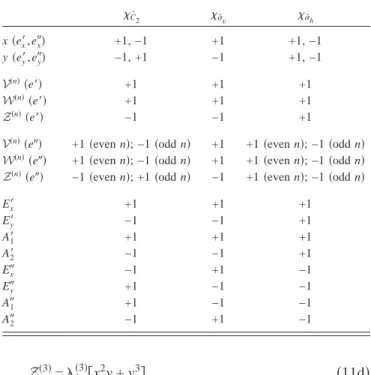
In Fig. 1 the ab initio data are displayed together with the fitting results for the models JT2, JT4, and JT6 along the

x coordinate. The notation JTNmax corresponds to

expan-sion up to n = Nmax for the diagonal V共n兲 and Jahn–Teller coupling matrix elements W_JT共n兲,Z_JT共n兲in Eq.共8兲. In these cal-culations, all PJT couplings are set to zero. It is immediately evident that the second-order model 共JT2兲 gives very poor results for all three potentials, except for a very narrow re-gion around the reference geometry. The fourth-order ap-proximation 共JT4兲 improves the results drastically, though deviations with respect to the reference data are clearly ob-servable. Finally, the sixth-order expansion 共JT6兲 yields po-tentials which are virtually indistinguishable from the ab

ini-tio data.

Though such a good agreement in general is very desir-able, one has to keep in mind that in the real system

pseudo-Jahn–Teller coupling also contributes to the shape of the po-tentials. Thus, the question arises to which degree the anharmonicity has to be accounted for by JT or PJT cou-pling, respectively. For example, the almost perfect JT6 fit indicates that adding further correction terms by the PJT cou-plings could render the fitting function too flexible. Thus, the obtained parameters may loose part of their physical signifi-cance. In such a case, a careful analysis of the obtained po-tential matrix, e.g., by using properties of the electronic wave functions, can help to decide about the suitable coupling

or-ders共see below兲.

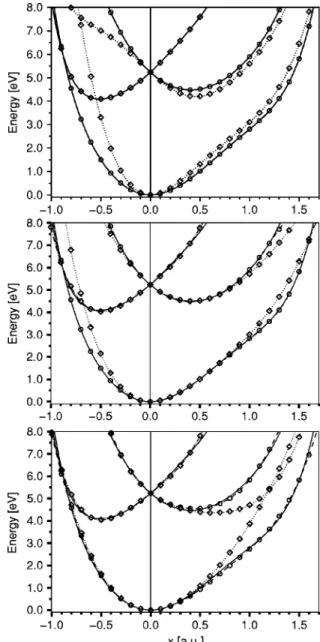
We tested all different combinations of JT and PJT cou-pling and depict characteristic results in Fig. 2. The lower panel of Fig. 2 shows a combination of JT4 and PJT1 which is comparable to the JT4/PJT2 result 共not depicted兲. The adiabatic energies 共indicated by dashed lines with open circles兲 still deviate somewhat from the reference data. Char-acteristic is that two diabatic energy curves 共indicated by

dotted lines with open diamonds兲 cross at a displacement of roughly 1.2 a.u. The middle panel represents the results for the JT4/PJT4 model. The agreement of the adiabatic energies is significantly improved and deviates only very slightly for the Eystate component for negative x 共the Ey state

compo-nent presents a minimum at negative x兲. The JT4/PJT6 model共not depicted兲 shows no significant improvement over the JT4/PJT4 combination. However, the JT6/PJT4 model yields almost perfect adiabatic energies while the shape of the diabatic potentials is not qualitatively different from the JT4/PJT4 or JT4/PJT6 results. For these three models, no crossing of the diabatic surfaces at positive x is obtained. As a third example, the JT6/PJT6 model is presented in the up-per panel of Fig. 2. The adiabatic energies are now in almost perfect agreement with the reference data. The interesting difference to the other models is that a crossing of diabatic potentials is found at about −0.7 a.u.

It is also helpful to compare the coupling coefficients

FIG. 1. Adiabatic energies in eV along x for the pure Jahn–Teller models of order 2共lower panel兲, 4 共middle panel兲, and 6 共upper panel兲 共dashed lines with open circles兲 compared to the ab initio reference data 共solid line兲.

FIG. 2. Adiabatic共dashed lines with open circles兲 and diabatic 共dotted lines with open diamonds兲 energies in eV along x for JT4/PJT1 共lower panel兲, JT4/PJT4共middle pannel兲, and JT6/PJT6 共upper panel兲 models compared to the ab initio reference data共solid line兲.

obtained for the different models. The values for the PJT and JT couplings for some characteristic cases are collected in Table IV共all parameters are given in atomic units兲. The lin-ear coupling constant␭₁共1兲is present in all models and Table IV shows that for all models except JT6/PJT4 and JT6/PJT6 the values are rather similar. It also becomes apparent that the coefficients for the higher couplings are all of significant magnitude. However, one should keep in mind that the fac-torial factor in Eq. 共8兲 reduces the actual coupling strength for the higher order couplings. Comparison of the higher order parameters shows that the values for different models are in the same order of magnitude but in some cases change sign. Particularly the JT4/PJT6 and JT6/PJT6 values show a significantly different behavior. It is likely that in the JT6/ PJT6 case the model is already too flexible to yield param-eters of physical significance. This will be illuminated from a different view point in the following.

The fitting error with respect to the adiabatic energies itself is not a suitable measure because JT6/PJT4 and JT6/ PJT6 result in comparably small errors. However, the diaba-tic states vary strongly with the order of the JT and PJT model and thus a criterion is needed to decide which model is relevant. One can obtain useful information from the elec-tronic wave functions of the ab initio calculations. The CI vectors of complete active space self-consistent field 共CASSCF兲 or MRCI calculations clearly show whether or not the character of two electronic states is interchanged upon distortion along a given coordinate. A maximum-overlap criterion can be applied to the CASSCF molecular orbitals with respect to a reference wave function in which no coupling of the states in question can occur共e.g., due to symmetry兲. In the basis of these so-called diabatic orbitals, the CI coefficients of the treated states reflect their coupling.16 The results of such a calculation for displace-ments along the x coordinate is depicted in Fig. 3.

Since only the2A₁and2E_xstate components are coupled

along x, it is sufficient to monitor the CI coefficients of the corresponding two main electron configurations. The result-ing 2⫻2 matrix is reorthonormalized and the obtained CI coefficients are plotted against the displacement in x. From this plot it can be seen that the2A₁and2E_xstate components start to mix significantly for positive x displacements and to a lesser extent along negative x distortions. However, most important is the finding that apparently no intersection of the configurations is observed. Thus, the two state components keep their main character throughout the whole range of the displacement without a crossing of the diabatic states as well. On the grounds of this analysis it is seen that the best

TABLE IV. PJT and JT coupling coefficients共a.u.兲 determined for different models.

JT2/PJT1 JT4/PJT1 JT4/PJT4 JT6/PJT4 JT4/PJT6 JT6/PJT6 ␭1 共1兲_{共PJT兲 0.0441 0.0548 0.0549 0.1061 0.0467 0.1648} ␭1 共2兲_{共PJT兲 −0.2037 −0.2689 −0.2926 −0.3989} ␭1 共3兲_{共PJT兲 −0.2756 0.1521 0.8040 −0.2183} ␭1 共4兲_{共PJT兲 −0.1482 0.1925 0.2888 0.4670} ␭2共4兲共PJT兲 1.3420 0.3858 1.6040 3.3783 ␭1 共5兲_{共PJT兲 −1.1990 −8.2329} ␭2 共5兲_{共PJT兲 −9.9024 1.7840} ␭1 共6兲_{共PJT兲 7.6403 2.4826} ␭2 共6兲_{共PJT兲 2.4144 −3.7752} ␭1共1兲共JT兲 0.1485 0.1293 0.1337 0.1427 0.1358 0.1433 ␭1 共2兲_{共JT兲 0.0765 −0.1559 −0.1507 −0.0384 −0.1332 0.0347} ␭1 共3兲_{共JT兲 0.6423 0.2933 −0.3355 0.1271 −0.7872} ␭1 共4兲_{共JT兲 1.0700 1.5370 −3.7935 1.4357 1.9497} ␭2 共4兲_{共JT兲 0.5387 0.4516 2.5467 0.7422 −2.3722} ␭1 共5兲_{共JT兲 −1.3896 2.2688} ␭2 共5兲_{共JT兲 7.5791 8.1847} ␭1共6兲共JT兲 97.0116 −13.1908 ␭2 共6兲_{共JT兲 −55.8532 62.5649}

FIG. 3. CI coefficients along x from reorthogonalized 2⫻2 CI coefficient matrix obtained in the diabatic orbital basis. Main configurations . . .共1ex兲2共1ey兲2共3a1兲1of2A1state and . . .共1ex兲1共1ey兲2共3a1兲2of2Exstate

coin-cide共open circles兲; contribution of main2A1configuration in 2

Exstate共open

triangles兲 and of main 2Exconfiguration in

2

A1state共open diamonds兲 are

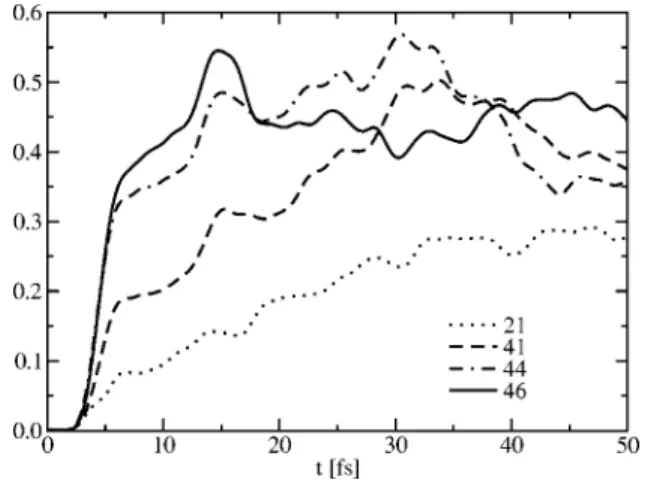
representations of the JT and PJT problem for this system, which yield diabatic states in agreement with the above analysis, are obtained from the JT6/PJT4 and JT4/PJT4 com-binations. Both models result in similarly small fitting errors. The effect of the orders of the diabatization scheme on the nuclear dynamics is investigated by wave packet propa-gations. The dynamics after a vertical excitation onto one of the two excited diabatic surfaces has been studied using a standard propagation scheme based on Fourier transforma-tion. The initial Gaussian wave packet was centered at 共x,y兲=共0,0兲 with a width of 40.8 a.u. A constant mass of 1943.38 amu is assumed for the kinetic part of the Hamil-tonian, leading to an energy of around 5.6 eV for the wave packet. Figure 4 presents the evolution of the ground state adiabatic electronic population for different orders of the model. Large differences are observed during the first 50 fs with a much slower population transfer to the ground state for the lower PJT order 共models JT2/PJT1 and JT4/PJT1兲. The populations obtained with the higher order models JT4/ PJT4 and JT4/PJT6 are similar and only differ in details. For longer propagation time 共up to 500 fs兲, oscillations of the population around 30% for the model 21 and 40% for the other models are observed. The differences obtained for this low dimensionality problem共two vibrational degrees of free-dom on three coupled electronic states兲 indicates that larger differences will be observed for higher dimensional systems because of the increased possibility for the energy to flow from one vibrational mode to another one.

V. CONCLUSION

In this paper, the diabatic Jahn–Teller and pseudo-Jahn– Teller Hamiltonian matrix is presented up to sixth order in both the complex and real representation for a general sys-tem with a C3symmetry axis. The different possible

symme-try groups 共D_3h, C_3v, C_3h, and C₃兲 and coupling mode sym-metries共e

⬘

and e

⬙

兲 have been investigated. Furthermore, the

dynamical pseudo-Jahn–Teller effect is discussed. In such a

case, the strength of the PJT coupling depends upon distor-tion along an addidistor-tional coupling mode.

Application to the representation of a two-dimensional cut of the ground and first exited state of the ammonia cation is presented. Based on the analysis of both the fitting errors to the adiabatic ab initio energies and of the evolution of the CI coefficients along the x vibrational coordinate, the com-bination of Jahn–Teller coupling up to sixth order and pseudo-Jahn–Teller coupling up to fourth order is found to be the most suitable one. It is shown that the higher order JT and PJT expansion developed here can represent the strongly anharmonic potentials of the model system with excellent accuracy. The analysis of dynamical properties and, in par-ticular, of the adiabatic populations underlined the significant role of the coupling order. Application to the NH₃+system in full dimensionality is in progress.

ACKNOWLEDGMENTS

The BFHZ-CCUFB is acknowledged for financial sup-port. The authors thank Alexis Viel for checking the calcula-tions. Stefanie Neumann is acknowledged for assistance with the ab initio calculations.

1

H. Köppel, W. Domcke, and L. S. Cederbaum, Adv. Chem. Phys. 57, 59 共1984兲.

2

I. B. Bersuker, Vibronic Interactions in Molecules and Crystals共Springer, Berlin, 1989兲.

3

H. A. Jahn and E. Teller, Proc. R. Soc. London, Ser. A 161, 220共1937兲.

4

R. Englman, The Jahn-Teller Effect in Molecules and Crystals 共Wiley-Interscience, New York, 1972兲.

5

Conical Intersections: Electronic Structure, Dynamics, and Spectroscopy,

edited by W. Domcke, D. R. Yarkony, and H. Köppel共World Scientific, Singapore, 2004兲.

6

M. H. Perrin and M. Gouterman, J. Chem. Phys. 46, 1019共1967兲.

7

J. H. van der Waals, A. M. D. Berghuis, and M. S. de Groot, Mol. Phys.

13, 301共1967兲. 8

M. Z. Zgierski and M. Pawlikowski, J. Chem. Phys. 70, 3444共1979兲.

9

H. Köppel, L. S. Cederbaum, and W. Domcke, J. Chem. Phys. 89, 2023 共1988兲.

10

W. Lichten, Phys. Rev. 164, 131共1967兲.

11

F. T. Smith, Phys. Rev. 179, 111共1969兲.

12

C. A. Mead and D. G. Truhlar, J. Chem. Phys. 77, 6090共1982兲.

13

C. A. Mead, J. Chem. Phys. 78, 807共1983兲.

14

H. Werner and W. Meyer, J. Chem. Phys. 74, 5802共1981兲.

15

G. Hirsch, R. J. Buenker, and C. Petrongolo, Mol. Phys. 70, 835共1990兲.

16

W. Domcke and C. Woywod, Chem. Phys. Lett. 216, 362共1993兲.

17

J. Jensen and D. R. Yarkony, J. Chem. Phys. 89, 975共1988兲.

18

D. R. Yarkony, Rev. Mod. Phys. 68, 985共1996兲.

19

T. Pacher, L. S. Cederbaum, and H. Köppel, Adv. Chem. Phys. 84, 293 共1993兲.

20

A. Viel and W. Eisfeld, J. Chem. Phys. 120, 4603共2004兲.

21

H. C. Longuet-Higgins, Adv. Spectrosc.共N.Y.兲 2, 429 共1961兲.

22

M. Döscher, H. Köppel, and P. Szalay, J. Chem. Phys. 117, 2645共2002兲.

23

The convention used in Ref. 20 is兩␺1典=兩␺x典 and 兩␺2典=−兩␺y典.

24

MOLPROis a package of ab initio programs written by H.-J. Werner and P. J. Knowles, with contributions from R. D. Amos, A. Berning, D. L. Coo-per et al..

FIG. 4. Adiabatic ground state population as a function of time in femto-seconds for the models JT2/PJT1共dotted line兲, JT4/PJT1 共dashed line兲, JT4/ PJT4共dot-dashed line兲, and JT4/PJT6 共full line兲.