J
OURNAL DE
T
HÉORIE DES
N
OMBRES DE
B
ORDEAUX
H
ENRI
L
AVILLE
B
RIGITTE
V
ALLÉE
Distribution de la constante d’Hermite et du plus court
vecteur dans les réseaux de dimension deux
Journal de Théorie des Nombres de Bordeaux, tome
6, n
o1 (1994),
p. 135-159
<http://www.numdam.org/item?id=JTNB_1994__6_1_135_0>
© Université Bordeaux 1, 1994, tous droits réservés.
L’accès aux archives de la revue « Journal de Théorie des Nombres de Bordeaux » (http://jtnb.cedram.org/) implique l’accord avec les condi-tions générales d’utilisation (http://www.numdam.org/conditions). Toute uti-lisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit conte-nir la présente mention de copyright.
Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques
Distribution de la
constanted’Hermite
etdu
plus
court vecteur
dans les
réseaux
de dimension deux
par HENRI LAVILLE et BRIGITTE
VALLÉE
RÉSUMÉ - En utilisant la géométrie du demi-plan de Poincaré et des familles de disques classiques - disques de Ford, disques de Farey - nous décrivons
les domaines de niveau associés à la constante d’Hermite et au plus court vecteur d’un réseau. Nous en déduisons une évaluation très précise des
fonc-tions de répartition correspondantes, en particulier au voisinage de l’origine.
Introduction
Un réseau est l’ensemble des combinaisons linéaires entières de vecteurs
linéairement
indépendants.
Plusprécisément,
si b =(b1,...,
bn)
désigne
un
système
de n vecteurs linéairementindépendants
deRP,
le réseau Rengendré
par b est défini parLe
système
b estappelé
une base duréseau,
et il y a, pour un réseaufixé,
une multitude de basespossibles;
la définition d’un réseau n’est donc pasintrinsèque.
Cependant,
ilexiste,
dans unréseau,
desobjets intrinsèques,
indépendants
de la baseparticulière
qui
a servi à définir le réseau. Parmi eux, deuxobjets
ont uneimportance
particulière.
Cesont,
d’unepart,
lepremier
minimum duréseau,
et d’autrepart
le déterminant du réseau. Le déterminant du réseau est le volume n-dimensionnel duparallélotope
construit sur une base du
réseau;
il estindépendant
de la base et notéd(R).
Cettequantité
est aisément calculable en fonction de la matrice de GramM (b)
associée à une base bquelconque
de R. Pardéfinition,
si( . ~ . )
désigne
le
produit
scalaire euclidien deRP,
la normeassociée,
on aLe
premier
minimum du réseau R est par définition lalongueur
d’unplus
court vecteur non nul du réseau :Il semble que le
premier minimum
du réseau soit très difficilement calcu-lable : il est engénéral
admis,
bien que cela ne soit pasprouvé,
que ladétermination de
À(R)
est unproblème
NP-dur[VEB].
La constante d’Hermite
~y(R)
du réseau R relie ces deuxquantités;
pardéfinition,
-. 1 -B,>
, ’l’’’’B’B?
et le théorème de Minkowski montre l’existence d’une borne
supérieure
"ln -pour toutes les constantes d’Hermite relatives à des réseaux R de dimensionn. On a ainsi
- - 1
- w /
On montre que yn est inférieur à n. Peu de résultats
précis
sont connus suret seules les huit
premières
valeurs de la suite qn ont été déterminées.En
particulier,
la valeur q2 estégale
à2 / v$,
et donc: pour tous les réseaux R de rang 2.
Ici nous nous intéressons à la distribution de ces deux
grandeurs
À(R)
et¡(R)
pour des réseaux R "aléatoires". Enparticulier,
il est trèsimportant
dans les
applications
à lacryptographie
depouvoir
travailler sur des réseauxR pour
lesquels
la constante d’Hermiteq(R)
n’est pastrop
petite.
Dansce cas, il existe un
parallélotope
fondamental du réseauqui
est suffsam-ment"régulier"
pour être enpremière
approximation
assimilé à une bouleeuclidienne.
Beaucoup
de résultats decryptanalyse,
comme le cassage dugénérateur
linéairecongruentiel
[St],
le cassage du "sac à dos"[F], RO],
[F],
[JS], [CLOS],
le cassage dusystème
d’Okamotoreposent
sur lefait que des familles de réseaux
cryptographiques
sont formés de réseauxassez
réguliers.
Unepremière
question importante
est donc la suivante : ya-t-il,
parmi
les réseauxaléatoires,
unegrande
proportion
de réseauxsuffisamment
réguliers ?
Par
ailleurs, l’analyse
de lacomplexité
desalgorithmes
de réductionde réseaux fait intervenir de manière essentielle la
longueur
duplus
court vecteur d’un réseau. Enparticulier,
la distribution dupremier
minimumA(R)
semble jouer
un rôle essentiel dansl’analyse
en moyenne del’algori-thme LLL
[LLL] .
Daudé et Vallée[DV]
ont obtenu unpremier
résultat dansce sens, en travaillant dans un modèle naturel :
D’autre
part,
il est clair que l’on aLa seconde
question
peut
se formuler ainsi :quel
est lecomportement
précis
de la fonction derépartition
dupremier
minimum,
enparticulier
auvoisinage
del’origine ?
Ici,
nous choisissons unpoint
de vuealgorithmique :
un réseau est définidans la
pratique
algorithmique
par unebase;
nous travaillons donc surles bases des réseaux et non sur les réseaux
eux-mêmes,
contrairement aumodèle usuel étudié par
exemple
parSiegel
[Si].
Les variables aléatoires_ que
nous considérons ne
dépendent
pas seulement d’un réseau R mais d’unebase b
qui
a servi à définir ce réseauR;
nousdésignerons
ces variables par’Y(b)
eta(b).
Par
ailleurs,
cesproblèmes posés
en dimensionquelconque
semblent trèsdifficiles;
nous nous limitons ici à la dimension2,
et nous travaillons dans un modèleprobabiliste simple, déjà
utilisé dans l’étude de lacomplexité
moyenne de
l’algorithme
de Gauss[VF] :
les basespossibles
sont de la forme( 1, z)
où z est unpoint
duplan complexe
C choisi uniformément dans ledemi-disque
unité. Les variablesaléatoires y
et a relatives au réseauR(z)
engendré
par(1, z)
sont alors des fonctions de la seule variable z, et serontdésignées
pary(z)
eta(z).
Nous décrivons
précisément
les fonctions derépartition
de ces deuxvariables aléatoires. En utilisant la
géométrie
classique
dudemi-plan
dePoincaré,
nous caractérisons les domaines~y(z) _
r eta(z) _ t
en fonctionde deux familles de
disques
bien connus : lesdisques
de Ford et lesdisques
deFarey.
Nous obtenons enparticulier
une évaluationprécise
des fonctionsL’article est
organisé
comme suit.Après
avoir défini dans leparagraphe
1un modèle
probabiliste
complexe
pour leproblème,
nousrappelons
lespro-priétés
del’algorithme
deGauss,
dont laconfiguration
de sortiepermet
decalculer les deux variables étudiées dans le
problème.
Puis nous décrivonsprécisément
le domaine de niveau associé à la constante d’Hermite. Cettedescription
fait intervenir de manière naturelle lesdisques
de Ford. Lesdisques
deFarey,
eux, interviennent dans leparagraphe
3,
lors de lade-scription
du domaine de niveau dupremier minimum.
. Lequatrième
et dernierparagraphe
permet alors d’obtenir les résultats annoncés sur lesfonctions de
répartition
de chacune des deux variables considérées.1. Le modèle
complexe
etl’algorithme
de Gauss1.1. Le modèle
probabiliste
complexe
En dimension
2,
un réseau R est déterminé par la donnée d’une base b =(u, v)
de C x C. Lalongueur
de la baseb, qu’on désigne
parIbl,
est alors le maximum des normesjuj
etlvl.
Rappelons
que nous voulons étudier lesprobabilités
lorsque
la base b est choisie uniformémentparmi
les basespossibles
delongueur
inférieure ouégale
à un réelpositif
M.D’abord,
la base b =(u, v)
peut
toujours
êtresupposée
directe et or-donnée de sorte que l’on aitlvl
_jul.
Ensuite,
les deux événementsqui
interviennent dans(5)
sont invariants parsimilitude;
pour une similitudeW de
C,
derapport
ppositif,
on a en effet :On
peut
donc choisir le vecteur u,qui
est leplus grand
des deux vecteursu
et v,
fixe etégal
à 1 et travailler ainsi dans ledemi-disque
défini par l’intersection du
disque
unité et dudemi-plan
dePoincaré,
etmuni de la
probabilité
uniforme. Si Fdésigne l’application
définie parl’égalité
F(u,
v)
=v/u,
alors F induit surla
probabilité
uniforme;
ainsi,
le modèleprobabiliste complexe,
clairementsimplicité
et de sa richegéométrie.
Eneffet,
les calculs sur lecouple
(u, v)
setransportent
agréablement
sur lecomplexe z
=v/u;
par
exemple :
1.2. La
configuration
de sortie del’algorithme
de GaussA
partir
d’une base b =(u,
v)
engendrant
un réseauR,
l’algorithme
deGauss construit une base b* =
(u* , v* )
satisfaisant les deux conditionsLa base b* est alors minimale - elle contient deux vecteurs minimaux
suc-cessifs du réseau - et, en
particulier,
le vecteur u* est unplus
court vecteurnon nul de
R;
on a donc :lu*1
=C’est la formulation de cet
algorithme adaptée
au modèle choisi dudemi-plan complexe
qui
sera utilisée ici.L’algorithme prend
en entrée un nombrecomplexe z
=v/u
dudemi-disque
C et construit le nombrecomplexe
z* =IV* /u*.
Latranscription
donnée par(6),
et lesinégalités
(7)
satisfaites par la base de sortie b* montrent alors que le nombrecomplexe
z*produit
parl’algorithme
de Gauss est un élément du domaine fondamentalComme le déterminant est un invariant du
réseau,
il n’est pas modifiédurant l’exécution de
l’algorithme;
grâce
aux relations(1)
et(6),
les deuxquantités
à étudierlez)
etÀ(z)
se calculent donc àpartir
ducouple
(z, z*)
1.3. Les transformations construites par
l’algorithme
de GaussLa formulation
complexe
del’algorithme
de Gauss se décrit à l’aide del’opérateur
dedécalage
U défini par la relationIci S
désigne
l’inversion-symétrie
définie parS(z) _ -1/z
et[x]
désigne
Algorithme
de Gauss Entrée : z e C Sortie : z G 7Tant
que z 0
.~’ faire z :=U(z).
Ainsi cette
application
U est-elle lacomposée
de deux transformations par-ticulières :l’inversion-symétrie
Sdéjà
mentionnée et la translation entièreT défiae par
T(z)
:= z + 1qui,
à ellesdeux, engendrent
le groupe ’H deshomographies
unimodulairesPar
conséquent,
au cours de sonexécution,
l’algorithme
de Gausscon-struit une
homographie h
permettant
de transformer z en z*. Toutes leshomographies
ne sont pas construites parl’algorithme
de Gauss. Nousnous intéresserons ici aux
homographies
de x effectivement utilisées parl’algorithme,
décrit en sens "inverse" : ce sont donc leshomographies
de 7fqui
envoient le domaine;: défini en(8)
dans ledemi-disque
unitéC;
nousles
appelons
homographies
de Gauss et nousdésignons
par 9
leurensemble,
n est connu par ailleurs que le
demi-disque
unité C s’écrit comme uneréunion
quasi-disjointel
de transformés de 7 par le groupe M. Par définition alors del’ensemble g
des transformations de Gauss donnéen 10),
onpeut
écrire
2. Domaines de niveau associé à la constante d’Hermite et
disques
de FordD’après
les relations(9)
et(10),
l’ensembler(r)
des nombres z de C vérifiant-y(z) :5 r
s’exprime
en fonction des transforméspar g
de l’ensemble1
on appelle quasi-disjointe une réunion d’ensembles dont les intersections deux à
sous la forme
Il est
plus
facile de considérer de manièreglobale
~’ et sestranslatés,
et ledomaine f:,.,.
1s’introduit alors
naturellement; puisque
est l’intersection avecLr,
on obtientOr,
les transformés de la bande~Cr
par leshomographies
sont desdisques
bien connus dans lagéométrie
dudemi-plan
de Poincaré : ce sont desdisques
de Ford.2.1. Les
disques
de FordLe lemme
géométrique
suivant est essentiel pour la suite :LEMME 1. Le
transformé
de la baude£r
située au-dessus de la droiteÙ(z)
=1/r
-par une
homographie
h de laforme
h(z) = (az
-I-b)/(cz
+d)
est ledisque
D,.(a,
c)
de centre(a/c)
+ir/(2c’)
et de rayonr/(2c2)
dontl’équatiorc
estCe
disque Tr(a, c)
esttangent
à la droite réelle aupoint
a/c.
Pour r =1 on retrouve le
disque
de Fordusuel;
ledisque
Tr(a,
c)
est ainsi unegénéralisation
dudisque
deFord,
onl’appelle r-disque
de Ford d’indice(a,
c).
Preuve. Posant s =
1 /r,
on considère le transformé z’ =h(z)
d’unpoint
z = x + is de la droite = s. On utilise
l’égalité
En
posant
h(z)
=z’,
onet on en déduit que
et donc
On vérifie ensuite que les transformés des
points
de.C,.
sont intérieurs audisque.
2.2.
Propriétés
desdisques
de FordNous décrivons maintenant
quelques propriétés
de cesdisques
que nousutiliserons
largement
dans la suite. Nous avonsrappelé
en(2)
qu’en
di-mension
2,
la constante d’Hermite-y(z)
a une valeur maximaleégale
à2/JÔ.
Parconséquent,
seuls lesr-disques
deFord,
avec une valeur de rinférieure à
2/.J3
interviendront ici.Soient deux nombres a et c
premiers
entre eux et r un réelpositif
inférieur ouégal
à2/ V3.
Lesr-disques
de Ford vérifient lespropriétés
suivantes :(Fol)
Pourjal
> c, cesdisques
sont extérieurs audemi-disque
unité C.Dans toute la
suite,
on considère donc descouples
(a, c)
d’entierspremiers
entre eux et vérifiant
lai
:5 c. Ondésignera
par 7~ leur ensemble(Fo2)
Pour 0la
l
c, les rdisques
de Ford d’indice(a,
c)
sont inclus dansle
demi-disque
unité C.(Fo3)
Pour a =0,
ler-disque
de Ford est inclus dans C si et seulement si rest inférieur à 1. Pour
lai
= c =1,
lesr-disques
de Fordcoupent
ledemi-disque
C.(Fo4)
Pour r1,
lesr-disques
de Ford sontdisjoints
deux à deux.(Fo5)
Pour1 _
r2/~,
deuxr-disques
de FordD(a, c)
etD(b, d)
sontsécants si et seulement si on a
ad -
bc)
= 1.La définition des
disques
de Ford et leursprincipales
propriétés
permettent
alors de décrire le domaine de niveau associé à la constante d’Hermite. 2.3.Description
du domaine de niveau associé à la constante d’HermitePROPOSITION 1. L’ensemble
r(r)
des norribres z de Cvérifiant
~(z) _
rPreuve. La relation
(13),
le lemme1,
et lapropriété
(Fol)
montrent lesinclusions suivantes
Réciproquement,
considérons un nombrecomplexe z
dudemi-disque
unitéC
appartenant
à unr-disque
de Ford d’indice(a, c) .
Alors,
puisque z
ap-partient
àC,
il existe unélément g
de 9
pourlequel
appartient
à . Parailleurs,
puisque z appartient
àDr (a,
c),
il existe unehomogra-de 7- pour
laquelle
h- 1 (z)
appartient
à la bandeLr.
Encomposant
éventuellement avec une translation on en déduit l’existence d’une
ho-m.ographie h
de 1£ pourlaquelle
t-1 (z)
appartient
à la bandeZ3,.,
partie
de la bande fondamentale située au-dessus de la droited’équation
E1§(z)
=1/r.
Deux caspeuvent
alors seprésenter :
- ou bien
h-1 (z)
est élément de7r,
alors z est élément der(r);
c’est d’ailleurs nécessairement le cas pour r 1puisque 13,.
et sontégaux.
- ou bien n’est
pas élément de mais alors r est nécessairement strictement
plus
grand
que1,
et pour un tel r, on a,[voir
Figure
1],
l’inclusion .
Figure
1.c Jflr
pour r > 1.On en déduit
qu’alors
est élément deAinsi,
dans tous les cas, il existe une transformation h de 1t pourlaquelle
h-1 (z)
est élément de et aussi unetransformation 9
de 9
pourlaquelle
est élément de .~’. On en déduit
qu’il
existe unetransformation
deg
pourlaquelle
est élément de et donc que zappartient
àr(r).
o
La
figure
2 montre le domainer(r)
pour trois valeurs duparamètre
r,correspondant
à r =1/2,
r = 1 et r =(2/~).
3.
Demi-disques
deFarey
et domaines de niveau associés aupre-mier minimum
La
description
des domaines de niveau associés aupremier
minimum sedéduit
de celle des domaines de niveau associés à la constante d’Hermite. Elle faitapparaître
desdemi-disques
construits sur les intervalles deFarey.
Les intervalles de
Farey
d’ordre t sont, pardéfinition,
les intervallesc)
de centrea/ c
et de rayontic
où a et c sont des entierspremiers
entre eux vérifiant la condition
lai
c. Onrappelle qu’en
(15)
on adésigné
par 7~ l’ensemble de tels
couples.
On considère ici les
demi-disques
construits sur les intervallesc)
lorque
(a, c)
décritP;
on lesappelle
dest-demi-disques
deFarey
et on lesdésigne
par
c).
Quand
lecouple
(a, c)
décrit l’ensembleP,
on obtient unefamille
qui
va intervenir dans la détermination des domaines de niveauassociés à
a(z) _
t.3.1. Relation entre les
demi-disques
deFarey
et le domaine de niveau associé aupremier
minimumLEMME 2. L’ensemble
A(t)
descomplezes z vérifiant
a(z)
t estégal
à la réunion det-demi-disques
deFarey.
Plusprécisément :
où P est l’ercsemble
défini
parPreuue. Pour un nombre
complexe z
departie imaginaire
y =£t(z)
les deux conditions suivantes sontéquivalentes
en vertu de la relation(9) :
z est élément de
A(t),
z vérifie
l’inégalité
~y(z) _
Or,
le domaine de niveauleZ) :5
r est défini àpartir
desr-disques
de Fordd’équation
Lorsque
(a, c)
décritP,
on obtient ainsi lesdemi-disques
deFarey
de centrea/c’
et de rayont/c
dont onprend
l’intersection avecLorsque
(a, c)
décritP,
la famille desdemi-disques
de centrea/c
et de rayontic
forme une réunion "redondante". Oncherche
donc unensemble
Q(t)
fini,
leplus
petit
possible,
pourlequel
On cherche
aussi,
afin d’obtenir une minorationsimple
de l’aire de laréunion
(17),
un sous-ensembleQ’(t) de Q(t),
leplus
grand
possible,
pourlequel
la réunion,-,-,-- ,-,
soit une réunion
disjointe
ou au moinsquasi-disjointe.
Un
problème
similaire se poseclassiquement
pour les intervalles deFarey,
et nous
rappelons
maintenant la solutionqui
en est donnée dans ce cas etqui
fournit desanalogues
P(t)
etP’(t)
aux ensembles définis en(17)
et(18).
3.2. Les intervalles de
Farey
On considère deux rationnels
a/c
etb/d
vérifantbel
= 1. Tous lesrationnels de l’intervalle
] (a/c), (bld) [ sont
de la formeavec m et rt strictement
positifs
etpremiers
entre eux. Pour m = n =1,
on obtient le
médian,
qui
est donc le rationnel deplus
petit
dénominateurde l’intervalle
] (a/c), (b/d) [.
On considère l’ensemble
P(t)
défini comme suit(Fal)
Deux rationnelsa/c
etb/d
sont consécutifs dansP(t)
si et seulements’ils vérifient les deux conditions :
(Fa2)
Deux intervalles’h(a, c)
etTz(b, d)
associés à des éléments desont sécants si et seulement s’ils sont consécutifs.
Deux intervalles
It (a, c)
et associés à des éléments deP(2t)
sonttoujours
quasi-disjoints.
Parmi tous les rationnels
e/ f
compris
entre deux rationnels consécutifsa/c
et
bld
deP(t),
le médianjoue
un rôleparticulier;
en effet :(Fa3)
Sie/ f
n’est pas le médian dea/c
etbld,
alors l’intervalleassocié au rationnel
e/ f
estcomplètement
inclus soit dansIt(a, c)
soit dans1t(b, d).
(Fa4)
L’intervalleIt (e, f )
associé au médian coupe chacun des deuxinter-valles
It (a, c)
etIt(b,
d);
il est inclus dans la réunionIt (a,
c)
U It (b, d)
et contient l’intersection
c) n It (b, d).
Tout ce
qui
précède
montre que l’ensembleP(t)
est solution minimale duproblème posé :
Par
ailleurs,
lapropriété
(Fa2)
montre que~(2t)
peut
être choisi commeensemble
analogue
à(18)
puisque
c’est un sous-ensemble deP(t)
pourlequel
la réunion
Notons l’existence d’un
algorithme
simple
qui
permet
de construirel’ensem-ble
P(t)
àpartir
des troiscouples
(-1,1), (0,1), (1, 1)
enrajoutant
lesmédians d’éléments consécutifs :
Algorithme
construisantP(t)
(1)
Audépart,
S:={(-1,1), (0,1),
(1,1)}.
(2)
Tantqu’il
existe un médian de deux éléments consécutifs de s dont ledénominateur est inférieur à
1/t,
l’ajouter
à S.(3)
P(t)
:= S.3.3. Les
disques
deFarey
On cherche maintenant à décrire les ensembles
Q(t)
etQ’(t)
définis pour lesdemi-disques
c)
en(17)
et(18).
L’ensembleP(2t)
convient pour former une sous-réuniondisjointe :
on choisira dans toute la suitemais l’ensemble
P (t)
lui-même ne convient pas pourQ(t)
car ledemi-disque
associé au médian de deux rationnels consécutifs
de P (t)
n’estplus
engénéral
inclus dans la réunion des deuxdemi-disques
etd) .
II est clair par
ailleurs,
d’après
lapropriété
(Fa3)
que l’ensemble obtenu enrajoutant
à tous les médians des éléments successifsconvient,
mais n’est sans doute pas minimal. .Finalement,
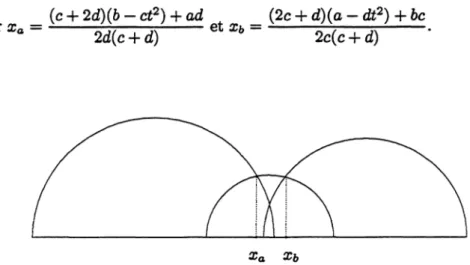
seuls des médians doiventLEMME 3. Pour deux rationnels
consécutifs
alc
etbld
deP(t),
les deux conditions suivantes sontéquivalentes
Preuve. On suppose par
exemple
quea/c
est inférieur àb/d,
et ondésigne
par Xa
[resp xb]
l’abscisse dupoint
intersection du cercle frontière deDt (a,
c)
avec celui de
Dt(a
+b,
c +d)
[resp.
de2Y(b, d)
avec +b,
c +d)].
Lacondition
(i)
est alorséquivalente
à xb,[voir
Figure
3J.
Figure
3. Deuxdisques
deFarey
et leurdisque
médian.On en déduit
l’équivalence cherchée.
Pour obtenir un recouvrement de
A(t),
il faut ainsirajouter
à l’ensembleP(t)
lescouples
(e, f )
vérifianta b , . 2 1
(e, f) = ( a + b, c -- d)
avec c
et -
consécutifs ett2
°c û t
Mais,
àpart
les troiscouples
exceptionnels
( -1,1 ) , ( ©,1 ) , (1, 1),
chaque
couple
(a, c)
de l’ensemble’P(t)
est lui-même un médian de deux élémentsde
P (t) .
L’ensemblecherché Q(t)
est alorségal
à la réunion de deuxensem-bles : un ensemble
exceptionnel
formé des troiscouples
( -1,1 ) , (o,1 ) ,
Il y a alors deux cas à considérer suivant que le dénominateur e = c + d est
celui d’un élément ou non; remarquons que
et donc :
(i)
ou bien e vérifiee
1/t
et tous lescouples
(a,
c)
et(b, d)
vérifiantsont par définition dans
P(t)
et donc dansQ(t) .
(ii)
ou bien e >1/t;
alors c et e vérifient les trois conditions suivantesComme on a
toujours
c(c - e)
e2/4
pour 0 c e, on en déduit une, borne
supérieure
pour les dénominateurs des rationnels de~(t),
et donc ladouble inclusion suivante
Il existe
aussi,
comme c’était le casprécédemment
pourP(t),
unecon-struction
algorithmique
pourQ(t),
qui
s’effectue parajouts
successifs de médians d’éléments consécutifs.Algorithme
construisantQ(t)
(1)
Audépart,
s :={(-1,1), (0,1), (1,1)}.
(2)
Tantqu’il
existe uncouple
(c,
d)
formé par les dénominateurs c et d de deux éléments consécutifs(a/c)
et(b/d)
qui
vérifieEnonçons
maintenant lespropriétés
décrivant l’intersection des demi-dis-ques de lafamille,
analogues
auxpropriétés
(Fal)
et(Fa2)
des intervallesde
Farey.
(Fal’)
Deux rationnelsa/c
etb/d
sont consécutifs dansQ(t)
si et seulements’ils vérifient les deux conditions :
(Fa2’)
Deuxdemi-disques
Dt (a,
c)
etd)
associés à des éléments(a, c)
et
(b, d)
deQ(t)
peuvent
être sécants dans les deux seuls cassuivants,
ou bien ces éléments sont deux éléments deP(t)
consécutifs dansQ(t) :
leur médian n’a donc pas été
rajouté,
ou bien ils ne sont
plus
consécutifs dansQ(t),
mais ils l’étaient danspet) :
ils ont étéséparés
par l’arrivée de leur médian.Dans ce dernier cas, il existe une intersection commune entre les trois
demi-disques
[voir
Figure
3];
mais lapropriété
(Fa4)
des intervalles deFarey
montre que le
demi-disque
+b, c
+d)
contient dans ce casl’intersection
Dl (a,
c)
d) .
L’aire de la réunion des troisdemi-disques
s’ exprime
uniquement
avec l’aire des troisdemi-disques
et l’ aire des deux intersections de chacun des deuxdemi-disques
d’indice(a, c)
et(b,
d)
avecleur
disque
médian commun,[voir
Figure
3j .
Finalement,
dans chacun des deux casprécédemment décrits,
l’aire dela réunion
s’exprimera
en fonction de l’aire desdemi-disques
et de l’aire del’intersection de
disques
consécutifs dont les indices(a, c)
et(b, d)
vérifient donc la relation(24).
3.4.
Description
du domaine de niveau associé aupremier
mini-mumTout ce
qui
précède
permet
de donner unedescription
de l’ensembleQ(t)
cherché,
et d’en déduire une caractérisation minimale de l’ensembleA(t).
PROPOSITION 2. L’ensemble
A(t)
des noTnbres z de Cvérifiant
B(z) :5
test
égal
d la réunion dest-demi-disques
deFarey
prise
sur l’ensemblefini
Q(t)
.avec i
La
figure
4 montre le domaineA(t)
pourcinq
valeurs duparamètre
t,
cor-respondant
iFigure
4. L’ensembleA(t)
pour t
=1/-/3,
1/2, 1/4,
5/22, 5/24.
4. Fonctions de
répartition
des variables étudiéesLes fonctions de
répartition
des deux variables étudiées se calculent à l’aidedes aires des domaines
r(r)
etA(t).
Ondésigne
respectivement
parG(r)
et
L(t)
les aires der(r)
etA(t)
Le
principe
adopté
dans ces deux calculs est le même.D’après
lesproposi-tions 1 et
2,
les deux aires à calculer sont des aires de réunions nondisjointes;
on calcule donc àpart
l’aire desintersections,
et onsépare
l’aire restante endeux,
selonqu’il s’agit
d’une aire"apportée"
par les troisdisques
exception-nels,
d’indice(-1,1 ) , ( ~,1 ) ,
et( 1,1 )
ou d’une aire "ordinaire" . Chacunedes
quantités
Gr(r)
ouL(t)
s’exprimera
comme la somme d’une aireordi-naire,
indicée par o, àlaquelle
on retranchera l’aireexceptionnelle,
indicéepar e et l’aire des
intersections,
indicée par i.Au
voisinage
del’origine,
dans les deux cas, le termeprincipal
proviendra
de l’aire ordinaire.
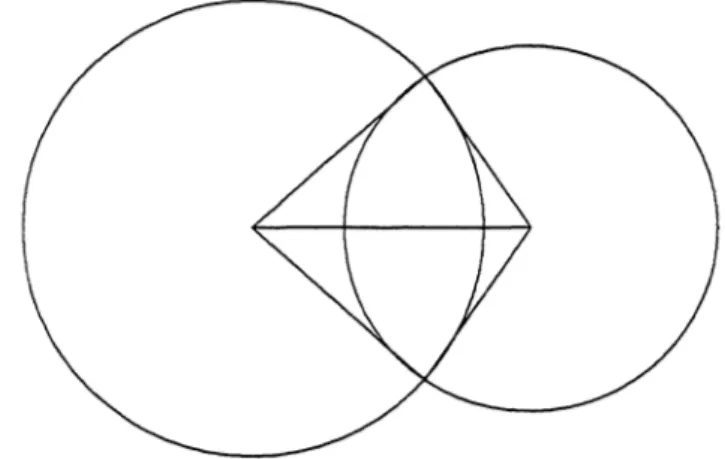
4.1. Calcul des aires d’intersection
On a
besoin,
dans tout cecalcul,
de l’aire de l’intersection de deuxdisques
sécants;
comme le montre lafigure
5,
une telle aires’exprime
comme la somme des aires de deux secteurscirculaires,
àlaquelle
on retire l’aire d’untriangle.
Figure
5. L’aire de l’intersection de deuxdisques.
L’aire J de l’intersection de deux
disques
VI
etD2
sécantss’exprime
uniquement
en fonction des deux rayons ri et r2 et de la distance des centres ô :avec
Dans chacun des cas où ce résultat
(25)
s’applique,
pour l’intersection dedeux
demi-disques
deFarey
ou de deuxdisques
de Ford d’indices(a, c)
et(b, d),
lescouples
(a, c)
et(b,
d)
vérifient la relationet les trois
paramètres - les
deux rayons, et la distance des centres -s’expri-ment
uniquement
en fonction des dénominateurs c et d. On aainsi,
pourl’aire de l’intersection de deux
r-disques
de Fordavec
De
même,
pour l’aire de l’intersection de deuxt-demi-disques
deFarey,
.
avec
Or,
pourchaque
couple
non ordonné(c, d)
d’entierspositifs
premiers
en-tre eux, il existe exactement
quatre
couples
(a, b)
vérifiant(26),
et doncquatre
intersectionspossibles;
àchaque couple
ordonné(c, d),
ilcorrespond
finalement deux intersections
possibles.
Ainsi,
lapropriété
(Fo5)
desdisques
de Fordpermet
d’écrireet, de
même,
lapropriété (Fa2’)
desdisques
deFarey
permet d’écrireoù 7l(t)
est défini comme étant l’ensemble descouples
ordonnés(c, d)
formésde deux dénominateurs de rationnels consécutifs de
Q(t)
et caractérisé par(24).
Comme,
parailleurs,
les deux fonctions pet p
sont des fonctionssymétri-ques de c et
d,
la sommation des deuxpremiers
termes dechaque
expression
J(r,
c,d)
ouJ’(t,
c,d)
fait intervenir la mêmesérie,
et on obtientfinalement,
d’après
(27), (28),
(29),
(30) :
4.2. Calcul de l’aire ordinaire
Dans chacun des cas, la famille d’indices sur
laquelle
on somme les airesordinaires fait
intervenir,
de manière directe ouindirecte,
lescouples
(a, c)
d’entiers
premiers
entre eux et vérifiantlai
:5 c. Dans cetensemble,
les troiscouples
( -1,1 ) ,
( o,1 ) ,
( 1,1 ) j ouent
un rôleexceptionnel puisqu’ils
donnentlieu à des
disques
de Ford ou desdemi-disques
deFarey qui
ne sont pascomplètement
inclus dans ledemi-disque
unité C. On considérera commeordinaire l’aire
apportée
par lecouple
(0,1)
et la moitié de l’aireapportée
par chacun des deux autres
couples.
Ainsi, si cp
désigne
la fonctiond’Euler,
il y aexactement,
pourchaque
valeur de l’entier c, y
compris
la valeur c =1,
telscouples. Comme,
parailleurs,
le rayon nedépend
que du dénominateur c, on est amené auxséries de terme
général
pour les valeurs entières s = 4 et s = 2. On utilise alors les résultatsclassiques
suivants(voir
parexemple
[HW]).
La série de termegénéral
associée à la fonction d’Euler cp a uncomportement
lié à lafonction (
définie pour s > 1 parPour s >
2,
la série de termegénéral
cp(n)fn8
converge et sa somme estégale
à~(s -1)/~(s).
Enparticulier,
pour s =4,
on obtientadmet,
pour N >2,
l’encadrement suivantoù yo est la constante d’Euler.
4.3. Fonction de
répartition
de la constante d’Hermite.On
peut
alors déterminer la valeur de l’aireG(r)
du domaine de niveau associé à la constante d’ Hermite.THÉORÈME 1. La
surface
G(r)
du domazner(r)
s’exprime
comme la som-me de trois termesavec
où
Preuve.
L’expression
deGo {r)
se déduit clairement duparagraphe
4.2,
plus
particulièrement
del’égalité
(33).
Onrappelle qu’on
rajoute
fictivementdans
Go(r)
lepremier
terme pour c= 1, quitte
à le retirer dansGe{r).
L’expression
deGe (r)
est évaluée enremarquant
que les deuxdisques
D,. ( -1,1 ) , Dr(1, 1)
sont tous deuxorthogonaux
audemi-disque
unité C.Selon la valeur de r, le
disque
Vr(O, 1)
est inclus ou non dans C.avec
Comme la
fonction p
est une fonction ducouple
(c,
d)
homogène
dedegré
-2
la fonction sous l’arcsin est
homogène
dedegré
0.Ainsi,
chacune des deuxséries a un terme
général
homogène
dedegré
-4,
et onpeut
transformerla sommation en une sommation sur tous les indices
(c,
d),
quitte
à diviserpar
~(4).
On déduit de cequi
précède
le résultat annoncé pourGs(r).
COROLLAIRE 1. Au
voisinage
del’origine,
on aPreuve. En effet
quand
r tend vers0,
le termeGe (r)
est de l’ordre der3,
car
C’est donc
Go(r)
qui
donne le termeprincipal
auvoisinage
del’origine.
COROLLAIRE 2. La série S =
8(2/-13),
de laforme
peut
s’exprimer
enfonction
de~(3)
sous laforme
suivantePreuve.
Puisque
la valeur2/B/3
est la valeur maximalepossible
pour-I(z),
on déduit que
-ce
qui
permet
d’obtenir le résultatcherché.
4.4. Fonction de
répartition
dupremier
minimumOn
peut
maintenant déterminer la valeur de l’aireL(t)
du domaine de niveau associé aupremier
minimum.THÉORÈME
2. La surfaceL(t)
du domainesA(t)
s’exprime
comme la sommede trois termes
-1., T / iB r 1. B T t ,’B
avec
où et
net)
sont les ensembles définisrespectivement
en(22)
et(24),
et où
~(t,
c,d)
estégal
àCette
expression
exacte est peu maniable et on en cherche donc unen-cadrement.
LEMME 4. Pour tout réel t de l’intervalle
[0, 1],
l’aireL(t)
admetl’encadre-ment suivant
où la
fonction
T(u)
estégale
pardéfinitions
àPreuve. L’encadrement de
Q(t)
obtenu en(23)
permet
d’obtenir lamajo-ration
(35).
La minoration(36)
est obtenue àpartir
de la caractérisationCOROLLAIRE
3. Auvoisinage
de0,
lafonctiorc
derépartition
dupremier
minimum admetl’équivalent
suivant :duec
6(t)
restant bornée sur l’interualle[0,1] .
Preuue. L’encadrement de la fonction L obtenu dans le lemme 4 et celui de la fonction T obtenu dans
l’inégalité
(34)
permettent
deconclure.
Conclusion.
Ainsi,
nous avonsétudié,
dans un modèleprobabiliste
na-turel,
les fonctions derépartition
de deux variables aléatoiresfondamen-tales dans la théorie et la
pratique
algorithmique
des réseaux. Les résultatstrès
précis
que nous avons obtenus sont renduspossibles
par l’efîectivitédu
problème
en dimension 2 : le domainefondamental,
aussi bien que lestransformations
qui
permettent
d’ y arriver sont totalementexplicités
dansce cas. L’obtention de tels résultats est aussi
grandement
facilitée par lapossibilité technique
de travailler dans Cplutôt
que danscC2
et d’utiliser ainsi lagéométrie
dudemi-plan
de Poincaré.Il est sans doute illusoire
d’espérer
obtenir des résultats aussiprécis
endimension
générale.
Ce n’estpeut-être
pas exclu en dimension3,
puisqu’il
existe encore une caractérisation du domaine fondamental
[Ga],
[Di],
etun
algorithme
de réductiongéométriquement
naturel[Va].
En dimensiongénérale,
il n’existeplus
de caractérisationexplicite
d’un domainefonda-mental ;
sans doute est-il tout de mêmepossible
alors depréciser
parex-emple
lecomportement
dupremier minimum,
en affnant l’encadrementobtenu en
(3)
et(4) ...
BIBLIOGRAPHIE
[CMOS]
M. J. Coster, B. A. LaMacchia, A. M. Odlyzko, C. P. Schnorr, An improvedlow-density subset sum algorithm, Comptes-Rendus du congrès Eurocrypt’91,
Lecture Notes in Computer Science 547 (1991), 54-67.
[Di]
G. L. Dirichlet, Über die Reduction der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen, J. reine angew. Math. 40(1850),
209-227.[DV]
H. Daudé, B. Vallée, An upper bound on the average number of iterations of the LLL olgorithm, Theoret. Comput. Sci. 123(1994),
95-115.[FHFLS]
A. M. Frieze, J. Hastad, R. Kannan, J. C. Lagarias, A. Shamir, Recowtructingtruncated integer variables satisfying linear congruences, SIAM J. Comput. 17
[Ga]
C. F. Gauss, Recherches arithmétiques, traduction française de DisquisitionesArithmeticae, Blanchard, Paris, 1953.
[HW]
G. H. Hardy, E. M. Wright, An introduction to the theory of numbers, OxfordScience Publications, 1989.
[JS]
A. Joux, J. Stern, Improving the critical density of the Lagarias-Odlyzko attackagainst subset sum problems, Comptes-Rendus du congrès FCT’91, Lecture
Notes in Computer Science 529
(1991),
258-264.[LLL]
A. K. Lenstra, H. W. Lenstra, L. Lovász, Factoring polynomials with rationalscoefficients, Math. Ann. 261
(1982),
515-534.[LO]
J. C. Lagarias, A. M. Odlyzko, Solving low-density sum problems, J. Assoc.Comput. Mach. 32
(1985),
229-246.[Si]
C. L. Siegel, Lectures on the geometry of numbers, Springer-Verlag, 1989.[St] J. Stern, Secret linear congruential generators are not cryptographically secure,
Comptes-Rendus du 28e congrès IEEE-FOCS
(1987),
421-426.[Va]
B. Vallée, An affine algorithm for minima finding in integer lattices of threedimensions, Rapport de Recherche A3L 1989-9, Département de mathémati-ques, Université de Caen, 1989.
[VEB]
P. van Emde Boas, Another NP-complete partition problem and the complexityof computing short vectors in a lattice, Report 81-04, Department of
Mathe-matics, University of Amsterdam, 1981.
[VF]
B. Vallée, P. Flajolet, The lattice reduction algorithm of Gauss: an average case analysis, Comptes-Rendus du 31e congrès IEEE-FOCS(1990),
830-839.[VGT]
B. Vallée, M. Girault, P. Toffin, How to guess l-th roots modulo n by reducinglattices bases, Comptes-Rendus du congrès AAECC-88, Rome, juillet 1988, Lecture Notes in Computer Science 357 (1989), 427-442.
Henri LAVILLE
GRAL, Département de Mathématiques, Université de Caen,
14032 Caen Cedex
Brigitte
VALLÉE
.LAIAC, Département d’Informatique, Université de Caen et ISMRa,