HAL Id: tel-02580978
https://hal.inrae.fr/tel-02580978
Submitted on 14 May 2020HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
une utilisation adaptée des équations de Saint Venant
André Paquier
To cite this version:
André Paquier. Modélisation des écoulements en rivière en crue : pour une utilisation adaptée des équations de Saint Venant. Sciences de l’environnement. Habilitation à diriger des recherches, Uni-versité Claude Bernard Lyon 1, 2002. �tel-02580978�
N° d’ordre : 52 2002
Université Claude Bernard Lyon 1
Document de synthèse en vue de l’obtention d’une
habilitation à diriger des recherches
Partie 1 : Synthèse des activités scientifiques
Sujet :
Modélisation des écoulements en rivière en crue : pour une
utilisation adaptée des équations de Saint Venant
Soutenue le 5 novembre 2002 à Lyon
par
André Paquier
Jury composé de :
Bernard GAY, président
Denis DARTUS, rapporteur
Vladan MILISIC, rapporteur
Yves ZECH, rapporteur
Philippe BELLEUDY
Michel DESBORDES
Robert MOREL
Introduction... 1
Contexte... 1
Les équations de Saint Venant... 1
1 Onde de rupture... 7
1.1 Utilisation des équations de Saint Venant 1D pour modéliser la propagation ... 7
1.2 Autres modélisations de la propagation... 10
1.3 Modélisation de la rupture ... 12
2 Modélisation bidimensionnelle ... 14
2.1 Schéma de résolution... 14
2.2 Structure du maillage... 14
2.3 Utilisation pour les écoulements débordants ... 16
2.4 Inondations en milieu urbanisé... 17
3 Description de plusieurs lits... 20
3.1 Lit composé ... 20
3.2 Couplage de modèles 1D et 2D ... 21
3.3 Jonction de plusieurs biefs de rivière ... 23
4 Transport de sédiments ... 24
4.1 Modification de la résistance à l’écoulement ... 24
4.2 Transport de sédiments et morphologie du lit ... 25
4.3 Modélisation unidimensionnelle de l’évolution du fond ... 28
4.4 Modélisation bidimensionnelle... 31
Conclusions sur les perspectives de recherches ... 33
Introduction
Contexte
Depuis 1989, j'exerce la fonction de chercheur à l'Unité de Recherches Hydrologie - Hydraulique du Cemagref à Lyon. Mon activité scientifique est organisée au sein du T. R. (Thème de Recherches) Transfeau qui est axé sur les "transferts dans le bassin versant et le réseau hydrographique" dont un des objectifs principaux est de développer des méthodes et outils pour la gestion des eaux sur un bassin versant. Ce T.R. que j’anime depuis 1999 regroupe plus de 20 chercheurs appartenant à trois Unités de Recherches du Cemagref situées à Antony, Lyon et Montpellier et oeuvrant essentiellement dans les domaines de l’hydrologie statistique et de l’hydraulique fluviale. On peut mettre en exergue les deux axes : « influence humaine sur le régime des eaux » et « lutte contre les inondations ». Je situe mes recherches surtout dans ce second axe avec un accent mis sur le seul réseau hydrographique et l’estimation des zones inondées.
Le Cemagref, établissement public à caractère scientifique et technique (EPST) regroupe plus de 1000 personnes dont près de 500 ingénieurs et chercheurs oeuvrant en recherche appliquée, principalement dans l'ingénierie des milieux naturels. De ce fait, mon activité de recherche qu'on peut situer principalement dans le domaine de l'hydraulique fluviale est plutôt axée sur la construction et la validation de méthodes destinées à l'ingénierie que sur la compréhension et la modélisation des processus. L'échelle de travail est celle du bief de rivière de quelques kilomètres et la validation finale se situe uniquement à cette échelle, sur des cas de terrain. Les expérimentations en canal de laboratoire sont utilisées uniquement comme étapes intermédiaires de validation ou pour déterminer les éventuels processus dominants.
Les équations de Saint Venant
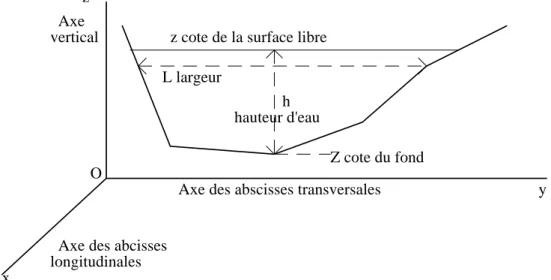
Les écoulements en rivière sont modélisés de manière simplifiée par les équations de Saint Venant (unidimensionnelles) qui permettent de simuler l’évolution dans le temps et le long de l’axe hydraulique de la rivière des deux variables débit Q et niveau de la surface libre z. Ce type de modélisation voit son origine dans les travaux de Barré de Saint Venant qui écrivit ces équations quasiment sous la forme actuelle (Barré de Saint-Venant, 1871).
y Axe des abscisses transversales
Axe des abcisses longitudinales
z
Z cote du fond h
hauteur d'eau z cote de la surface libre Axe
vertical
L largeur
x
O
Lorsque l’écoulement s’effectue dans un milieu invariant dans le temps (ce qui est une hypothèse à la base des équations de Saint Venant), il est possible de remplacer le débit Q par la vitesse moyenne dans la section en travers V et le niveau z par la section mouillée S ou le tirant d’eau h (défini comme la hauteur ou profondeur d’eau maximale dans la section en travers). On dispose des relations élémentaires : V = Q/S ; S= S0 (z, x) et h = h0 (z, x). Pour
une abscisse x longitudinale donnée sur l’axe hydraulique, les fonctions S0 et h0 sont des
fonctions bijectives de z ; dit autrement, à x donné, la connaissance de S, z ou h est équivalente à la connaissance du triplet (S, z, h). Ceci explique que les équations de Saint Venant soient écrites sous différentes formes (équivalentes) en fonction des auteurs ou des modes de résolution. Je privilégie ci-dessous (équations (0.1) et (0.2)) l’écriture en fonction des variables S et Q qui permettent de faire apparaître chacune des équations en terme de conservation d’une quantité : masse (ou plus exactement volume mais on suppose que la masse volumique de l’eau est constante) et quantité de mouvement.
(0.1) q x Q t S = + ∂∂ ∂ ∂ (0.2) S Q kq gSJ x z gS S Q x t Q + =− + +∂∂ β ∂∂ ∂ ∂ 2
où t le temps, x l'abscisse longitudinale, S la section mouillée, Q le débit, q le débit d'apport latéral, z la cote de la surface libre, g l'accélération de la pesanteur, J pente de frottement, k est le ratio entre la composante longitudinale de la vitesse de l’apport et la vitesse de l’écoulement principal, β coefficient de quantité de mouvement ou de Boussinesq. β est un coefficient correcteur (valeur proche de 1) qui prend en compte la répartition réelle des vitesses à l’intérieur de la section en travers.
Les équations (0.1) et (0.2) doivent être complétées par une relation explicitant la pente de frottement, en général, à partir du seul frottement au fond. J’utiliserai en général la relation de Manning - Strickler qui donne ce frottement sous la forme :
(0.3) R S K s Q Q J 2 4/3 2 = c’est-à-dire D KsSR 3 / 2 =
où D est la débitance, K le coefficient de Strickler (frottement), R le rayon hydraulique.
Dans le cas d’un lit composé (où la section de lit mineur ou lit principal est bien identifiable par rapport à un second lit dit lit moyen ou lit majeur utilisé uniquement lors des crues), on peut utiliser la formulation Debord (Nicollet et Uan, 1979) pour estimer β et D : (0.4)
(
)
(
)
β = + + = + − S H S H S H K S S S A R K S A R m M M M m M M m m m 2 2 2 2 2 3 2 3 1 1 1 avec / / (0.5)D = K S A Rm m 2 3m/ +KM S2M+S Sm M(
1− A2)
R2 3M/où les indices m (resp. M) correspondent au lit mineur (resp. moyen), A étant donnée par la formulation suivante (0.6), (0.7) (pour KM≤Km seul cas envisagé et seul présent dans le
milieu naturel) : (0.6) = = − K M K m A A 6 / 1 0 0,9 pour ≥0,3 R R m M (0.7) pour 0< 0,3 2 1 3 , 0 cos 2 1− 0 ∏ + + 0 < = R R A R R A A m M m M
L'hypothèse A = 1 redonnerait la formulation classique la plus simple pour un lit composé pour laquelle la débitance totale est somme des débitances partielles supposées
proportionnelles aux débits partiels.
Le débit latéral q regroupant les échanges (pertes ou apports) latéraux correspond aux différents affluents (ou défluents) et aux différentes pertes (ou apports) diffuses (infiltration à travers le fond et les berges, évaporation, ruissellement latéral, pluie, etc). Ces échanges peuvent ajouter ou retrancher une certaine quantité de mouvement ; en cas de perte, l’hypothèse la plus simple est de supposer soit une vitesse égale à la vitesse moyenne de l’écoulement c’est à dire un coefficient k égal à 1 (défluence par exemple), soit une vitesse nulle (infiltration par exemple). Pour les autres cas, des valeurs de k comprises entre -1 et 1 sont les plus probables, la valeur généralement choisie est 0 qui correspond à négliger l’échange de quantité de mouvement (dans la direction de l’axe de la rivière). Dans le cas d’un déversement au-dessus d’une digue, le débit d'apport latéral peut être exprimé à partir d'une formule de déversoir dénoyé sous la forme (0.8) :
(0.8) q x t
( ) ( )
, =µ x t, 2g z z(
− d( )
x)
m x( )où µ coefficient de débit (valeur standard 0,4), zd cote de la crête de la digue et m exposant (valeur standard 1,5) sont des fonctions linéaires par morceaux et z est la cote de la surface libre dans l’écoulement principal.
L’équation (0.2) peut aussi être écrite sous la forme (0.9) :
(0.9) B R S K Q Q g x Z gS P S Q x t Q =− − + + + 3 4 2 2 ∂ ∂ β ∂∂ ∂ ∂
qui sépare le terme
x z gS∂∂ en trois termes : • x P ∂
∂ qui représente la variation de pression dans l’espace avec P pression définie par
(
) ( )
P=
∫
hg h− y L x y dy,0 où h la hauteur d'eau, L la largeur,
• B pression latérale qui correspond aux variations de largeur de l’écoulement définie
par B g h
(
y)
L xdy h =∫
− ∂ ∂ 0 ,• et gSI un terme lié à la pente générale de la rivière
x Z
I=−∂∂ avec Z la cote du fond, L’analyse du système d’équations (0.1) et (0.2) en supposant β=1 fait apparaître deux caractéristiques de vitesses V-c et V+c où c= gS L est la célérité des ondes. Si les deux vitesses caractéristiques sont positives (forte vitesse relativement à la célérité), le régime de l’écoulement est torrentiel et l’information se propage uniquement de l’amont vers l’aval. Toutefois, en rivière, le régime est, en général, fluvial (nombre de Froude défini par V/c inférieur à 1) ; ceci implique que la résolution des équations de Saint Venant sur un bief de rivière exigera une condition à la limite amont et une condition à la limite aval. A l’amont, on donne, en général, un hydrogramme (débit en fonction du temps). A l’aval, ce sera plutôt une relation entre le débit et le niveau d’eau (courbe de tarage déterminée, par exemple, aux stations hydrométriques) ; on rappelle toutefois que cette relation n’est en général pas univoque, le niveau à débit donné étant le plus souvent différent entre crue et décrue comme montré par (Jain, 1993).
∂ ∂ + − + ± S S V L S g V β β β β 2 2
(Paquier, 1995b) mais l’analyse peut être menée de manière
similaire.
L’utilisation des équations de Saint Venant pour une rivière suppose donc, en premier lieu, une description globale du cours d’eau correspondant à la représentation 1D à savoir des dimensions de la section en travers (horizontale et verticale) faibles devant la dimension longitudinale (longueur de bief voire pas d’espace). Ceci a pour conséquence qu’un certain nombre de processus morphologiques dont la périodicité est de l’ordre de quelques largeurs de rivière (bancs, méandres, alternance de seuils et de mouilles, etc) est difficilement modélisable par cette voie. Parmi les hypothèses de base qui permettent de passer des équations de Navier Stockes aux équations de Saint Venant (voir par exemple (Gerbeau et Perthame, 2000)), je citerai :
• la pente longitudinale doit être faible
• les courbes doivent être peu accusées
• les accélérations verticales doivent être faibles
• la vitesse longitudinale doit être homogène dans la section en travers même si le coefficient β permet en partie de prendre en compte l’hétérogénéité de la vitesse longitudinale.
Le premier chapitre traite de la propagation des ondes de rupture de barrage. Ce cas est représentatif des crues extrêmes et montre l'utilisation des équations de Saint-Venant à la limite de leur domaine de validité dans des cas où le régime peut être successivement torrentiel et fluvial. Les problèmes spécifiques aux ruptures de barrage sont aussi abordés.
Pour la plupart des écoulements en rivière (le mot rivière excluant, en particulier les torrents, suppose une pente moyenne ne dépassant pas 2%), ces hypothèses peuvent être considérées comme vérifiées, en particulier, lorsque le tracé et la section ont été rectifiés par l’homme. Une des limites clairement identifiée est la présence de lits multiples ou d’îles. Cette limitation peut être dépassée par une représentation par un réseau de plusieurs biefs maillés où chaque bief est simulé en une dimension et où, en chaque jonction (considérée comme ponctuelle) entre 3 biefs (ou plus), sont appliquées des relations entre débits et niveaux d’eau (en général, égalité des niveaux et somme algébrique des débits nulle). Il est alors possible de résoudre des problèmes d’écoulement dans des réseaux complexes où le caractère transitoire est un aspect fondamental (Paquier et al., 1996).
Toutefois, pendant les crues, la topologie d’un tel réseau peut évoluer progressivement (disparition d’une île, formation de nouveaux bras, fusion de plusieurs biefs, etc), ce qui pose des problèmes de modélisation difficiles à résoudre dans le cadre 1D. Lors des inondations, ce même cadre apparaît aussi inadapté si on souhaite modéliser les débordements lors des phases où une part notable du débit n’est plus orientée selon l’axe hydraulique de la rivière ; dans ces cas, les hauteurs d’eau restant relativement faibles, il est normal de passer aux équations de Saint Venant bidimensionnelles qui conservent l’ensemble des hypothèses précédentes sauf l’écoulement selon un axe privilégié ; c’est la résolution des équations qui donnera alors l’orientation de l’écoulement dans le plan horizontal. J’écrirai ces équations sous la forme (0.10) + (0.11) + (0.12) : (0.10) P y Q x Q t h+ x+ y = ∂ ∂ ∂ ∂ ∂ ∂
(0.11) ( )W P x F x y h Q x h y x h Q x h x D h K Q y Q x Q x g x Z gh y h Q y Q x x h g h Q x t Q x + + + + + − − = + + + ∂ ∂ ∂∂ ∂ ∂ ∂∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ 3 / 7 2 2 2 2 2 2 (0.12) ( )W P y F y y h Q y h y x h Q y h x D h K Q y Q x Q y g y Z gh y h g h Q y x h Q Q t Q y x y + + + + + − − = + + + ∂ ∂ ∂∂ ∂ ∂ ∂∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ 3 / 7 2 2 2 2 2 2
où h est la hauteur d'eau, Z la cote du fond, Qx le débit selon l'axe Ox égal au produit de la vitesse par la hauteur, Qy le débit selon Oy, g l'accélération de la pesanteur, K une constante de viscosité (ou diffusion), Ks le coefficient de Strickler pour le frottement au fond, W la
vitesse du vent, Fx et Fy les contraintes dues au vent (exprimées, par exemple, (Falconer et al., 1991) sous la forme 0,6x10-6 Wx W3/2 et 0,6x10-6 Wy W3/2), Px et Py les composantes du
frottement à la paroi (verticale), P l’apport local correspondant à la pluie.
Le chapitre 2 traite de la résolution de ces équations bidimensionnelles et de leur utilisation pour la simulation des inondations.
Ce type de modélisation n'est toutefois pas optimal, par exemple, dans le cas d'écoulements dans des lits marqués où l'approche unidimensionnelle peut être suffisante. Pour les applications en ingénierie, il importe de ne détailler la modélisation hydraulique que dans les zones où soit la complexité des processus soit l’importance des enjeux l’exigent. Se pose alors le problème des liaisons entre modélisations de différents types ou à différentes échelles.
Ce point est abordé au chapitre 3 avec, en particulier, les questions liées à la simulation couplée d'écoulements dans des lits différents. Dans ces cas, est nécessaire une représentation spécifique des échanges aux interfaces qu'il s'agisse de berges ou de confluences, de modélisations unidimensionnelles ou bidimensionnelles.
Pendant les crues mais aussi, à un degré moindre, pendant le reste de l’année, la rivière transporte un ensemble d’éléments dissous ou non. En général, la majeure partie des éléments non dissous est constituée par les sédiments. Ces derniers sont principalement transportés :
• soit au sein de l’écoulement. Je parlerai de matériaux en suspension en distinguant l’autosuspension où les sédiments ne touchent que très rarement le fonds et se comportent de manière similaire aux matières dissoutes et la suspension proprement dite où les sédiments interagissent avec le fond, ce qui se traduit par un gradient de concentration positif en allant vers le fond
• soit à proximité du fond. Je parlerai de charriage que le processus principal soit un roulement ou une saltation. La quasi totalité des sédiments (de diamètre souvent plus grand que celui des matériaux en suspension) se situe à une distance du fond inférieure à une distance caractéristique égale à quelques diamètres lorsque le fond reste plat (Yalin et Ferreira da Silva, 2001).
En pratique, lorsque le transport s’intensifie, il devient difficile de distinguer le mode de transport, voire la position du fond. Le fond souvent constitué des mêmes sédiments que ceux transportés est amené à se déformer selon des ondulations (rides, dunes, etc) qui elles mêmes ne sont plus identifiables en cas de fort transport où l’ensemble du fond du lit se déplace en masse. Ce déplacement peut concerner jusqu’à plusieurs mètres d’épaisseur (Ramette et Roult, 1998). On comprend aisément qu’il est donc nécessaire de prendre en compte ces processus de transport de sédiments pour modéliser de manière convenable l’écoulement lors de tels événements. Par ailleurs, ces événements induisent, par dépôt ou érosion, une modification de la topographie du lit de la rivière qui, elle même, aura des conséquences sur les écoulements. Pour une rivière peu anthropisée, en dehors des événements catastrophiques capables d’engendrer une modification brutale du tracé en plan, l’évolution moyenne est régulière et, souvent, de faible ampleur ce qui permet, en première approximation, de la négliger lorsqu'on souhaite modéliser une crue.
Le chapitre 4 traite des effets du transport de sédiments sur, d'une part, les écoulements en crue et, d'autre part, l'évolution du fond du lit. En rivière, la modélisation unidimensionnelle du lit principal est privilégiée mais j'examine aussi une approche bidimensionnelle qui apparaît nécessaire pour des crues largement débordantes.
1 Onde de rupture
1.1 Utilisation des équations de Saint Venant 1D pour modéliser la propagation
L’onde de rupture de barrage se distingue d’une crue naturelle par un temps de montée et un temps de décrue plus faibles (au moins à proximité du barrage). Le débit de pointe de la crue est liée aux caractéristiques du barrage, aux circonstances de la rupture et à la distance au barrage et peut donc être très supérieure aux débits de crue naturelles ; cette relative indépendance de la morphologie de la rivière rend les ondes de rupture atypiques avec, par exemple, de vastes zones inondées au-delà du lit majeur et des ouvrages de franchissement sous-dimensionnés (donc susceptibles de se rompre). En outre, en cas de rupture de barrage rapide,
• d’une part, un front d’eau peut se former et se propager tel un mascaret en diminuant d’amplitude progressivement ;
• d’autre part, les vitesses très fortes peuvent engendrer un régime torrentiel ; les zones de front et de ressaut engendrent des problèmes de modélisation spécifiques.
Au-delà, ces fortes vitesses sont susceptibles d’engendrer un transport solide intense avec des érosions importantes des berges et du fond.
Sur le plan de la recherche, la modélisation de la propagation de l’onde de rupture de barrage pose donc d’une manière extrême, l’ensemble des questions soulevées par la modélisation des crues naturelles. La validité des équations de Saint Venant, en particulier, dans la zone du front où les accélérations verticales sont importantes, peut être remise en question (Mackie, 1984). (Basco, 1989) après comparaison avec un modèle incluant cette accélération verticale, conclut à une représentativité convenable (et quasiment équivalente) des équations de Saint Venant. (Mohapatra et al., 1999) arrive à une conclusion identique par comparaison avec des calculs au moyen d'un modèle 2D vertical. La comparaison sur des expériences de laboratoire entre mesures et résultats de calculs à partir des équations de Saint Venant confirme ce point (Bellos et al., 1992; CADAM, 2000; Chervet et Dalleves, 1970; Gharangik et Chaudhry, 1991) au moins en l’absence de réflexions multiples (Mohapatra et al., 2000). La démonstration sur des cas complexes reste toutefois à établir. Pour les applications en ingénierie, une erreur de l’ordre du % reste négligeable vis à vis des incertitudes sur les principaux paramètres (géométrie, Strickler, conditions initiales). La stabilité du schéma numérique résolvant les équations de Saint Venant 1D y est un point clé. Prenant la suite des travaux menés au Cemagref de 1985 à 1990 à partir des travaux (Vila, 1984; Vila, 1988), j’ai développé le code RUBAR 3 qui résout ces équations par un schéma explicite du second ordre de type Godunov. Ce schéma qui résout les équations sous la forme conservative (0.1), (0.9) (assurance d'une bonne conservation des volumes) s'appuie sur la notion de variation totale décroissante (schéma TVD) et la résolution de problèmes de Riemann, ce qui permet de traiter les discontinuités (ressauts, mascarets) comme des points courants (Paquier, 1995b). Il est, en ce sens, proche des nombreux schémas présentés ces 15 dernières années pour traiter les problèmes d'ondes de rupture de barrage (Fennema et Chaudhry, 1987; Garcia-Navarro et al., 1992; Jha et al., 1994; Zhang et al., 1992), etc .
Les principaux travaux que j’ai menés ont porté sur le traitement du second membre des équations écrites sous la forme (0.1), (0.9) afin d’assurer, en particulier, une stabilité numérique suffisante dans le cas où la variable S est fortement variable (en temps et en espace). La validation de la méthode de résolution n’a pu être démontrée mathématiquement dans le cas général et a donc été effectuée en comparant les résultats numériques soit à des solutions analytiques (géométrie simple, régime transitoire), soit aux solutions obtenues par d’autres méthodes de résolution sur l’équation du régime permanent, soit à des mesures
expérimentales (canaux de laboratoires).
Figure 1.1 Hauteurs d’eau à t=50s (pour un canal rectangulaire à fond plat sans frottement avec à t=0, une hauteur amont de 6 m et une hauteur aval nulle).
0 100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 Abscisse (m) 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0 6.2 6.4 6.6 6.8 Hauteur (m) RUBAR 3 REFERENCE
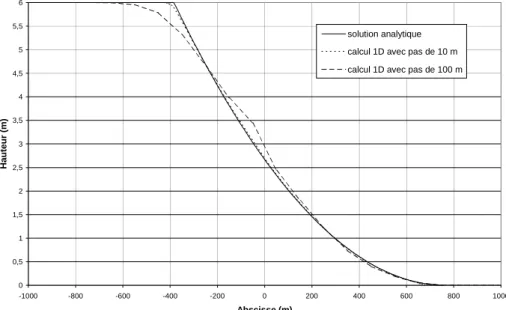
Figure 1.2 Hauteurs d'eau en régime permanent (canal rectangulaire, largeur de 1 mètre pour x<900 et de 0,1 mètre pour x > 1000, pente de 0,3%, débit de 0,1 m3/s).
0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5 5,5 6 -1000 -800 -600 -400 -200 0 200 400 600 800 1000 Abscisse (m) Hauteur (m) solution analytique calcul 1D avec pas de 10 m calcul 1D avec pas de 100 m
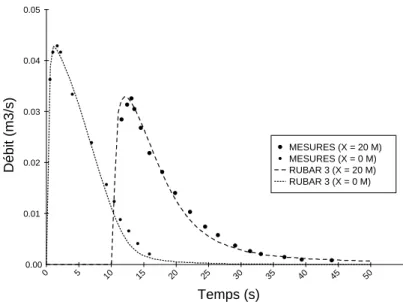
0 5 10 15 20 25 30 35 40 45 50 Temps (s) 0.00 0.01 0.02 0.03 0.04 0.05 Débit (m3/s) MESURES (X = 20 M) MESURES (X = 0 M) RUBAR 3 (X = 0 M) RUBAR 3 (X = 20 M)
Figure 1.3 Hauteurs d’eau pour un canal rectangulaire de 30 cm de large, de pente 4 %, de Strickler de 72 m1/3/s avec une hauteur amont (x<0) de 30 cm à t=0 (expériences de (Chervet
et Dalleves, 1970))
Pour des cas plus complexes, outre la vérification de la stabilité au pas d’espace et au pas de temps, seule la comparaison avec des codes résolvant les mêmes équations est possible car l’écart entre résultats numériques et observations, écart déjà constaté sur les expérimentations est difficilement interprétable : l’incertitude sur les observations et l’écart entre équations de Saint Venant et processus réels pouvant l’emporter sur l’erreur dans la résolution numérique. Sur ce thème, un groupe de travail de l’Association Internationale de Recherches en Hydraulique (A. I. R. H.) relayé par un projet soutenu par l’Union Européenne (CADAM : Action concertée pour la modélisation de la propagation des ondes de rupture de barrage (1998-2000)) a permis de nombreuses comparaisons entre codes. Cette action devrait être poursuivie dans les années à venir (par le projet européen IMPACT (2001-2004) en particulier) en se portant sur des cas plus représentatifs des situations réelles et donc, plus complexes, en particulier, en ce qui concerne la topographie.
Dans ces situations réelles, existent des ouvrages de franchissement des rivières ou des vallées qui forment obstacles à l'écoulement. Ce dernier n'a plus alors des caractéristiques unidimensionnelles et, même s'il les conserve, les accélérations verticales et les courbures de la surface libre et du fond sont fortes en cas de déversement au-dessus de l'ouvrage. Il est alors nécessaire de passer à une modélisation différente. Ce problème est usuellement traité par des lois d'ouvrage définies comme des relations entre niveau (ou charge) amont, niveau (ou charge) aval et débit. Les relations sont définies empiriquement selon le type d'ouvrage et font, en général, intervenir un coefficient de débit variant selon les caractéristiques géométriques et l'implantation de l'ouvrage dans le lit. Ce coefficient doit le plus souvent être calé sur des mesures in situ. Les types d'ouvrages les plus usités sont les déversoirs et les vannes. L'introduction de ces modèles différents pose un problème de couplage avec deux difficultés essentielles :
• au niveau de la résolution numérique, le schéma doit éviter les instabilités qui apparaissent souvent lors des déversements. L'utilisation d'un temps intermédiaire permet plus facilement d'éviter ces instabilités. Il reste toutefois essentiel de définir de manière appropriée les conditions aux limites de l'ouvrage et le pas de temps.
• au plan pratique, les limites du tronçon modélisé par la loi d'ouvrage doivent correspondre aux sections régulières respectivement suffisamment en amont et en aval
de l'ouvrage pour être cohérent avec le type de modélisation concerné. Ceci renforce d'ailleurs la stabilité numérique.
Dans certains cas où la modification de l'écoulement au droit de l'ouvrage est faible (cas d’un seuil noyé, par exemple), on peut préférer conserver une modélisation de type Saint Venant et introduire une perte de charge singulière. Le terme J de l'équation (0.2) est alors remplacé par
J + Js où Js, perte de charge singulière, est égal à
x g V ∆ 2 2
ξ avec ξ coefficient de perte de charge, V vitesse moyenne, g accélération de la pesanteur, ∆x longueur de la singularité.
L’exemple du seuil noyé montre que le type de représentation pour un ouvrage (et plus généralement pour toute singularité) dépend de la gamme de débits simulés : définir les choix optimaux (type de représentation, paramètres a priori) et le mode de passage d’un type de représentation à un autre reste une question importante, en particulier, pour les ondes de rupture où les débits varient rapidement et dans de larges proportions.
Pour l'estimation des risques sur des cas réels, il est nécessaire d'analyser les effets du transport des sédiments (voir chapitre 4) en se penchant sur la spécificité des crues extrêmes (Yang et Greinman, 1999)(ce point sera développé dans le projet IMPACT) et des débris divers qui peuvent jouer un rôle local (au niveau des ouvrages par exemple) ou global (Khan et al., 2000b).
1.2 Autres modélisations de la propagation
Les recherches sur la propagation des ondes de rupture de barrage ne sont pas limitées à la seule résolution des équations de Saint Venant 1D. Certaines situations exigent le passage à une modélisation bidimensionnelle de la propagation ; toutefois les caractéristiques se rapprochent souvent de celles des crues naturelles (largement débordantes et donc rares). Je traite cet aspect dans le chapitre 2 consacré aux équations de Saint Venant 2D. A l’opposé, dans le cas de retenues de faible volume ou de vallées faiblement occupées, il n’est pas utile d’effectuer des calculs complexes pour identifier les risques (en général, l’absence de risque fort) liés à la rupture d’un barrage. La question peut alors être formulée ainsi : trouver une méthode de calcul plus simple que la résolution des équations de Saint Venant 1D qui permette une estimation du niveau d’eau maximal atteint et du temps de propagation pour une onde de rupture de barrage. On ajoutera que, pour évaluer le risque, une estimation chiffrée n’est nécessaire qu’aux points vulnérables de la vallée situés à l’aval du barrage.
Le logiciel CASTOR (Paquier, 1994) que nous avons mis au point au début des années 1990 a permis une première avancée et une nette amélioration par rapport aux modèles simplifiés existant alors (Robin, 1990; Wurbs, 1987). Il repose sur une réduction approximativement exponentielle (la courbe réelle a été tabulée en fonction des résultats obtenus par résolution des équations de Saint Venant 1D sur des vallées types) du débit de pointe (adimensionnalisé par le débit de pointe au barrage) en fonction de la distance au barrage (adimensionnalisée par la racine cubique du volume de la retenue). La courbe d’amortissement peut être paramétrée par le seul paramètre IK2, produite de la pente de la vallée par le carré du coefficient de Strickler représentant le frottement moyen au fond de la vallée. L’équation du régime uniforme (I=J) est ensuite utilisée pour déterminer le tirant d’eau maximal (d’où le niveau maximal) et la vitesse maximale dont on déduit le temps de propagation. La validation de la méthode a reposé sur une comparaison des résultats de CASTOR avec les résultats de RUBAR 3 sur environ 500 points répartis sur 15 vallées (Paquier et Robin, 1995; Paquier et Robin, 1997).
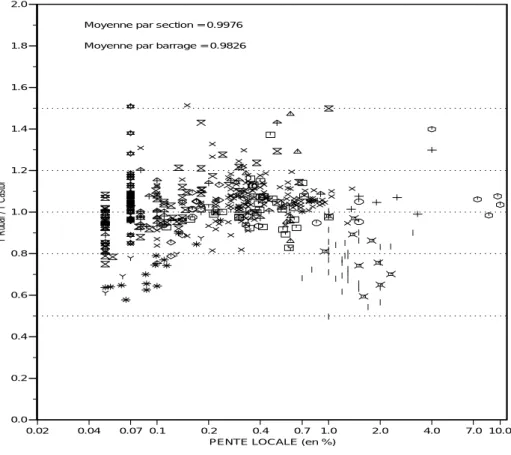
0.02 0.04 0.07 0.1 0.2 0.4 0.7 1.0 2.0 4.0 7.0 10.0 PENTE LOCALE (en %)
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 Y Rubar / Y Castor
Moyenne par barrage = 0.9826 Moyenne par section = 0.9976
Figure 1.4 Validation de Castor par rapport à Rubar 3 – résultats pour les hauteurs d’eau.
Nous poursuivons les recherches afin de mieux tenir compte des singularités (en particulier, lorsqu’il s’agit d’ouvrages de franchissement), de la forme de l’hydrogramme au barrage, des crues venant se surajouter à la rupture du barrage. Ces aspects acquièrent, en effet, de l’importance quand on s’intéresse à des retenues de faible volume (quelques centaines voire quelques dizaines de milliers de m3) pour lesquelles les autorités ou la population posent de plus en plus la question de la sécurité.
En parallèle, le problème de surinondation due à la rupture des digues le long des rivières lors des crues est apparu à la suite des crues sur les grands fleuves (Mississipi, Rhin, Rhône) au cours desquelles de tels événements ont eu lieu. Une résolution détaillée de ce problème passe par l’utilisation de modèles bidimensionnels telle que présentée dans le chapitre 2 consacré à ces modèles. Une estimation plus sommaire dans le même esprit que les méthodes utilisées dans le logiciel Castor est aussi un objectif de mes recherches. Les processus physiques mis en jeu sont les mêmes mais la description simplifiée en est plus complexe car deux phases sont à distinguer :
• une phase de formation de la brèche et d’expansion des eaux : de manière similaire à la rupture d’un barrage, la brèche s’élargit et le débit croît en même temps qu’une onde se propage vers l’aval.
• une phase d’écoulement quasi permanent où la brèche cesse de s’agrandir et où le niveau de l’eau présente à l’aval de la brèche constitue une limitation à l’écoulement par la brèche.
Si la crue est brève ou la brèche tardive, cette seconde phase peut être inexistante et alors une description simplifiée se ramène à une rupture de barrage où la retenue est constituée par le bief amont de la rivière. Dans le cas général, la distinction entre les deux phases n’est pas évidente et est, en partie, conditionnée par des paramètres locaux (par exemple, facilité
d’écoulement en amont et en aval de la brèche). La phase de recherche préliminaire qui vient de débuter (Jarrin, 2000) devra donc s’appuyer sur un examen détaillé des quelques cas réels bien documentés, sur une description des processus physiques mis en jeu, en particulier, à proximité de la digue, et sur une modélisation moins simplifiée de ces processus (en particulier, modélisation bidimensionnelle des écoulements) permettant de balayer l’ensemble des situations pouvant être rencontrées sur le terrain.
1.3 Modélisation de la rupture
L’estimation des conséquences d’une rupture de barrage repose bien évidemment en premier lieu sur la modélisation du processus de rupture lui-même et la formation de l’écoulement au droit de la digue. Les barrages sont des ouvrages complexes. Pour chaque type de digue (voûte, contreforts, béton compacté au rouleau, enrochements, terre, etc) ainsi que pour les ouvrages annexes (évacuateur de crue, vidange, tour de prise, etc), des règles de construction et des méthodes de calcul de stabilité existent. La rupture provient, en général, d’une erreur de conception (sous-dimensionnement de l’évacuateur de crue, surestimation de la résistance des fondations, etc) ou de réalisation (drainage ou compactage insuffisants, matériaux non conformes, etc) ou encore de vieillissement non maîtrisé, le plus souvent en conjonction avec un événement aléatoire (crue forte, glissement de terrain, gestion erronée, etc). Pour estimer le risque, il ne s’agit donc pas de décrire le scénario le plus probable de rupture pour lequel des mesures de contrôle préventif seront étudiées (et mises en oeuvre au cas où la probabilité serait relativement forte) par les spécialistes de la sécurité des barrages mais de définir des scénarios possibles et leurs conséquences en terme d’écoulement vers l’aval. De ce fait, j’ai limité mon objet de recherche à l’obtention d’un hydrogramme au droit du barrage. La simplification de base (reprise des règles recommandées par le Comité Technique Permanent des Barrages et régulièrement rappelées) consiste à distinguer deux types de rupture :
• les ruptures instantanées appliquées à l’ensemble des ouvrages en béton qui peuvent, dans certaines circonstances particulières (glissement d’un appui pour un barrage voûte par exemple), s’effondrer en quelques secondes. Le modélisateur supposera alors qu’à l’emplacement de la brèche (dont il choisit les caractéristiques), le barrage n’existe plus ; la ligne d’eau à cet instant présente alors un dénivelé brutal correspondant à la différence entre niveau d’eau dans la retenue et niveau d’eau à l’aval du barrage. L’hydrogramme au droit du barrage résulte alors directement du calcul d’évolution de l’écoulement. Ainsi, RUBAR 3 permet par la méthode de résolution des équations de Saint Venant 1D, d’estimer cet hydrogramme en tenant compte de la section de la brèche et des éventuelles influences amont et aval. Il s'agit bien évidemment d'une approximation puisque, dans cette phase initiale, les accélérations verticales et la pente de la surface libre sont si fortes qu'on se trouve bien au-delà des conditions d'établissement des équations de Saint Venant.
• les ruptures progressives appliquées aux ouvrages en remblais. A partir d’un point de faiblesse, un écoulement naît entraînant une érosion du corps de digue, érosion qui peut s’amplifier jusqu’à provoquer la ruine totale de l’ouvrage. L’obtention de l’hydrogramme suppose alors une résolution couplée de l’évolution de l’écoulement et de la forme de la brèche. Les codes de transport de sédiments en rivière (tels que ceux présentés au chapitre 4) peuvent être utilisés mais on se trouve en dehors des conditions d’applicabilité. De multiples méthodes plus simplifiées spécifiquement dédiées à ce problème ont, de ce fait, été développées (Singh, 1996).
J’ai repris le code RUPRO développé par le Cemagref antérieurement pour modéliser un renard (érosion interne de la digue) ou une surverse (déversement au-dessus de la crête) pour un barrage en terre homogène. La modélisation est simplifiée : la brèche est représentée par
une section en travers moyenne dont la forme est définie a priori (cercle pour une érosion par renard et rectangle pour une érosion par surverse ou après l’effondrement du toit du renard) et les dimensions évoluent en fonction du débit de sédiments transitant par la brèche (calculé à partir de la formule de Meyer Peter et Müller)(Paquier et al., 1998). Les variables hydrauliques moyennes sont calculées en appliquant l’équation de Bernoulli entre le plan d’eau de la retenue et l’aval de la digue où le régime est supposé critique (nombre de Froude égal à 1). Les développements les plus récents ont porté sur la prise en compte d’une forme de brèche plus réaliste (trapézoïdale au lieu de rectangulaire), l’intégration d’une crue incidente et des débits évacués par les ouvrages annexes du barrage ainsi que la prise en compte des lignes d’eau en amont et en aval de la brèche (Belrhalia, 1996). Ce dernier point a conduit à la définition d’un ouvrage hydraulique particulier intégré dans le code RUBAR 3 et représentant la brèche évoluant avec le temps. Ceci permet alors, en rupture progressive, comme en rupture instantanée, de bâtir un seul modèle pour le calcul d’onde de rupture de barrage, modèle qui intègre la retenue, la digue et la vallée à l’aval. Ce type de modèle a été utilisé lors d’études (Debar et Paquier, 1999) et lors d’un test de comparaison intermodèles du projet CADAM (Paquier, 1998b) où il a montré sa robustesse et son utilité (Paquier, 2001). En parallèle à des recherches menées par ailleurs (au Cemagref et par d’autres partenaires de CADAM) pour bâtir des modèles plus complexes susceptibles de mieux représenter les processus lors de l’érosion de la digue (érosion prioritaire du talus aval, éboulements des parois, etc), les futurs développements que je mènerai consisteront à trouver les méthodes pour définir a priori (en fonction des matériaux) une forme de brèche convenable et les valeurs des principaux paramètres contrôlant le rythme d’érosion dans le modèle (diamètre, porosité, coefficient de frottement) pour une digue réelle dont le matériau n’est que rarement homogène et monodisperse.
2 Modélisation bidimensionnelle
2.1 Schéma de résolution
Les équations de Saint Venant bidimensionnelles (0.10), (0.11) et (0.12) ont été résolues par un schéma explicite en volumes finis similaire à celui utilisé pour les équations unidimensionnelles. La résolution du code RUBAR 20 ainsi bâti est effectuée en plusieurs étapes (Paquier, 1995b; Paquier, 1998a). A partir des variables aux centres de mailles, on reconstitue une solution approchée sur l’ensemble du domaine, solution linéaire sur chaque maille. Une estimation par maille à un temps intermédiaire permet ensuite de poser un problème de Riemann en chaque milieu d'arête. La résolution approchée de ce problème donne alors les flux traversant chaque arête ce qui permet finalement d'obtenir les valeurs moyennes par maille. Comme en 1D, mon effort de recherche a porté principalement sur le calcul des gradients par maille et le traitement du second membre. Il apparaît toutefois que l'obtention d'un régime permanent est difficile à obtenir compte tenu des réflexions multiples sur les limites du domaine qui génèrent des oscillations s'atténuant peu. Une recherche complémentaire est à accomplir pour séparer les oscillations d'origine purement numérique et celles d'origine physique, en particulier, dans le cas d'écoulements torrentiels. Par ailleurs, le traitement des conditions aux limites doit être amélioré et l'éventail des types de conditions aux limites augmenté.
Les autres méthodes de résolution existantes qu'elles soient bâties sur des schémas explicites en volumes finis relativement similaires (Alcrudo et Navarro, 1994; Brufau et Garcia-Navarro, 1998; Fennema et Chaudhry, 1990; Fraccarollo et Toro, 1995; Jha et al., 2000; Nujic, 1995; Tchamen et Kahawita, 1994; Wang et al., 2000; Zhao et al., 1994) ou sur des schémas fondamentalement différents (éléments finis par exemple)(Alam et Bhuyian, 1995; Bates et al., 1999; Hervouet et Janin, 1994; Molls et Molls, 1998; Szymkiewicz, 1993; Tucciarelli et Termini, 2000) ne nous ont pas paru supérieurs à ce jour comme l'ont, en partie, montré les comparaisons effectuées dans le cadre du projet CADAM (CADAM, 2000). Une implicitation du schéma (Fennema et Chaudhry, 1989; Panagiotopoulos et Soulis, 2000) (ou toute autre solution permettant de s'affranchir de la limitation à 1 du nombre de Courant (Leveque, 1988)) reste une voie à explorer dans le cas de phénomènes lentement variables afin de gagner du temps de calcul. Toutefois, il ne semble pas que les gains à attendre soient très importants du fait d'une limitation du nombre de Courant assez basse même avec un schéma implicite (Molls et Zhao, 2000). La déformation du maillage en cours de calcul (maillage adaptatif) pour suivre un front ou un ressaut ne semble pas non plus apporter d'avantage décisif (Akanbi et Katopodes, 1988; Louaked et Hanich, 2000; Rahman et Chaudhry, 1995; Rahman et Chaudhry, 1997).
2.2 Structure du maillage
Afin de simuler les inondations, il importe de pouvoir prendre en compte les digues et remblais qui dévient les écoulements en lit majeur. Ceci peut être modélisé soit en topographie, ce qui implique de disposer d’un schéma numérique stable sur de fortes pentes alors que les équations ne sont pas strictement valides soit par des lois d’ouvrages de type déversoir si on ne souhaite pas se retrouver avec des petites mailles sur lesquelles se produisent de fortes vitesses, ce qui tend à augmenter non seulement le nombre de mailles mais aussi le temps de calcul, le pas de temps étant limité par la condition de Courant sur ces mailles. Comme en modélisation unidimensionnelle, selon la taille de maille, l'ouvrage pourra être ponctuel (localisation sur une arête où le débit de l'ouvrage peut venir s'ajouter ou remplacer le flux à travers l'arête) ou s'étaler sur plusieurs mailles.
Dans chaque modélisation, un paramètre est à caler (soit le coefficient de Strickler, soit le coefficient de débit) qu’il est difficile de définir a priori compte tenu de l’écart avec les situations de base ayant servi à la définition des équations. La représentation par ouvrages est aussi nécessaire pour modéliser les passages sous les remblais mais, de la même façon, il est difficile, en pratique, de trouver le ou les types d'ouvrage correspondant précisément à la situation présente sur le terrain, en particulier, si les niveaux d'eau évoluent fortement ou rapidement. L’intégration de ces lois d’ouvrage dans le schéma de résolution pose des problèmes particuliers de stabilité du même type que ceux posés aux limites externes du modèle lorsque les hypothèses sous jacentes d’homogénéité des écoulements et de quasi-stationnarité ne sont pas vérifiées. On notera aussi que les lois d'ouvrages représentent un écoulement unidimensionnel. Dans la modélisation actuellement programmée, il n'est ainsi pas possible de transférer une quantité de mouvement transversale alors que selon le type d'ouvrage, une partie est transférée (c'est le cas, par exemple, pour un déversoir) : le problème clé de recherche est la définition de ce taux de transfert qui dépend non seulement de l'ouvrage proprement dit mais aussi des écoulements dans les zones d'amenée et de déversement.
Outre ce problème, dans le cas du déversement au-dessus d'un remblai, des instabilités peuvent apparaître si la lame d'eau est faible sur un déversoir. Mais, de manière équivalente, une représentation en topographie présente des instabilités du fait des fortes pentes et faibles hauteurs d'eau. Dans les deux cas, une réduction de la taille de maille et du pas de temps est nécessaire. Des travaux restent toutefois à effectuer pour définir plus précisément les conditions d’application du code. Un des problèmes clés pour l’utilisation du code sur des cas réels est la définition d’un maillage adapté. Les travaux passés ont conduit à adapter le schéma pour prendre en compte à la fois des mailles triangulaires et des quadrilatères (Paquier, 1998a; Paquier, 1999a). Ceci permet plus facilement de définir le maillage à partir des lignes directrices correspondant soit aux traits caractéristiques du relief soit aux principaux ouvrages linéaires, lignes qui peuvent se croiser, se confondre, etc (Paquier, 1999b) (voir aussi (Secretan et al., 2001)). Ces lignes qui constituent des limites de l’écoulement à des moments clés des crues doivent être présentes comme arêtes des mailles, la topographie étant définie aux sommets des mailles. J’ai montré (Paquier et al., 1999) que si la discrétisation n’est pas très fine, ce qui est, le plus souvent, le cas dans les études d'ingénierie, les résultats en terme de ligne d’eau peuvent être fortement modifiés selon le maillage et l’interpolation de la topographie. Des méthodes pour définir le (ou un) maillage optimal restent à trouver.
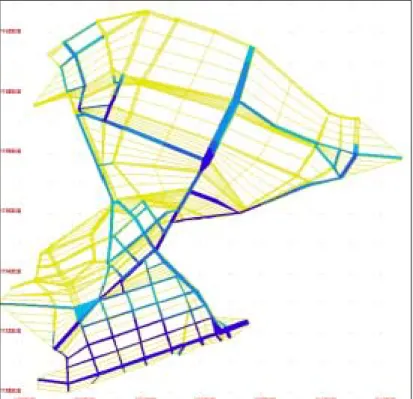
Figure 2.1. Exemple de maillage utilisé pour une étude (avec emplacement des ouvrages modélisés par des lois de déversoirs ou orifices).
2.3 Utilisation pour les écoulements débordants
Lors d'une inondation, l'écoulement s'effectue à la fois dans le lit mineur et dans le lit majeur. Si les écoulements dans les deux lits sont parallèles, une représentation unidimensionnelle en lit composé telle que présentée ci-après au §3.1 est envisageable. Il existe toutefois de nombreuses situations géographiques où la division de l'écoulement est tel qu'une modélisation bidimensionnelle est a priori préférable (Paquier et al., 2001c). Il en est de même pendant les phases de débordement ou de retour au lit mineur où les écoulements hors du lit mineur peuvent avoir momentanément une direction transversale à celui-ci ; le passage à un modèle 2D (Keller et Rodi, 1988) ne résout toutefois pas tous les problèmes. Outre la prise en compte des remblais explicitée ci-dessus au §2.2 et les problèmes particuliers des zones urbanisées abordés au §2.4 ci-dessous, je mentionne quelques questions de recherche qui restent largement ouvertes :
• lorsque les écoulements dans le lit mineur et le lit majeur sont parallèles mais avec des vitesses bien différenciées, à l'interface, sont générées des structures turbulentes tridimensionnelles(Anderson et al., 1996). De même, des obstacles transversaux créent de telles structures difficilement modélisables en 2D. L'évaluation du cisaillement dans cette zone permet une estimation de l’énergie dissipée et peut être à la base d'une modélisation. Les méandres du lit mineur qui conduisent à la superposition d'écoulements de directions différentes (axe du lit mineur d'une part et axe de la vallée d'autre part) constituent une autre circonstance défavorable (Thornton et al., 2000).
• dans le cas où les hauteurs de débordement sont faibles, les structures tridimensionnelles ont un développement plus réduit mais les irrégularités du terrain naturel ont alors des hauteurs comparables aux hauteurs d'eau, ce qui remet en cause l'application de loi de frottement de type Strickler même si quelques résultats existent pour généraliser à des écoulements sur des macro rugosités (Ranga Raju et Garde, 1970).
• la végétation présente dans le lit majeur souvent selon une répartition très hétérogène joue un rôle de frein à l'écoulement qui est également plus sensible pour les faibles hauteurs d'eau. Si le problème est très étudié (Christensen, 1996; Darby, 1999; Fathi-Maghadam et Kouwen, 1997; Fischer-Antze et al., 2001; Kutija et Hong, 1996;
Stephan et Wibmer, 2001; Stern et al., 1998; Tsujimoto et Kitamura, 1998), l'utilisation des résultats en ingénierie reste lointain.
• la présence de bourrelets de berge, digues ou remblais qui peuvent s'éroder pendant l'inondation induit une double difficulté:
! la prise en compte d'une géométrie évolutive. Ceci peut être traité de manière spécifique et simplifiée par exemple à travers un ouvrage de type particulier (pour nous, selon les principes du logiciel Rupro décrit au §1.3) ou être renvoyé au problème général du transport de sédiments en crue traité au chapitre 4.
! le caractère aléatoire d'une telle érosion. La situation locale, topographie mais aussi effet de la végétation en place ou de débris transportés est souvent prépondérante dans l'initialisation de l'érosion. Ceci implique que plusieurs simulations sont nécessaires pour estimer le risque lié à une crue de débit donné (Paquier et Farissier, 1996). Cela peut aussi remettre en question le calage à partir d'observations locales à moins que des informations complémentaires sur ces ruptures soient collectées (par exemple, à partir de photos aériennes (Raclot et Puech, 1999)).
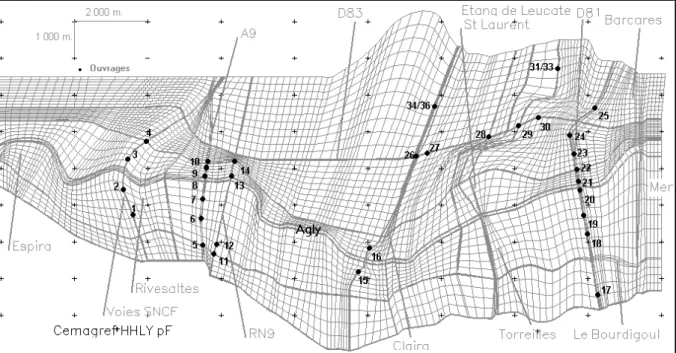
• même sans tenir compte du point précédemment mentionné, l'application d'un modèle 2D à un cas pratique se heurte aux difficultés de calage (Bates et al., 1998). Les principales causes sont la multiplication des paramètres de calage, la rareté des crues utilisables pour ce calage (il faut des événements avec forts débordements souvent avec une période de retour supérieure à 30 ans) et l'incertitude de la topographie (le plus souvent, quelques dizaines de centimètres hors levé au sol, ce qui se traduirait par une incertitude du même ordre sur les niveaux (Aronica et al., 1998)). A titre d'exemple, notre expérience sur l'inondation de novembre 1999 dans la basse plaine de l'Agly a conduit à un écart moyen de l'ordre de 40 cm (Paquier et al., 2002). Définir des méthodes de calage efficaces qui tiennent compte de ces incertitudes sur les données et sur les observations est fondamental pour l'utilisation de modèles bidimensionnels en ingénierie. Si l'optimisation directe (Khaladi, 1992) semble exclue, logique floue ou système à base de connaissance sont-ils des voies plus prometteuses?
2.4 Inondations en milieu urbanisé
Des essais ont été effectués pour appliquer le code dans un milieu urbain (Haider, 2001; Paquier et Haider, 2001). Les premiers résultats sur Nîmes montrent la faisabilité mais aussi la difficulté. En particulier, des questions de stabilité numérique et de définition du maillage se posent de manière forte : les contrastes topographiques y sont plus marqués, les processus physiques plus complexes. Ainsi, aux croisements de rues, deux (ou plus) écoulements peuvent se rencontrer (avec éventuellement un choc) puis se séparer dans un espace réduit de topographie parfois complexe ; des zones d’eaux mortes sont souvent créées mais semblent n’influer que peu sur les lignes d’eau hormis à proximité du carrefour. Dans le cas d'expériences en canal rectangulaire, une jonction avec un angle droit (Best et Reid, 1984) (Gurram et Karki, 1997; Hsu et al., 1998; Ramamurthy et al., 1994; Schumate et Weber, 1998; Weber et al., 2001) génère une contraction de l'écoulement qui conduit localement à une recirculation et, éventuellement un passage en régime torrentiel. Dans le cas d'une bifurcation (Barkdoll et al., 1998; Neary et Sotiropoulos, 1996; Shettar et Murthy, 1996), des résultats similaires sont observés. Malgré le caractère fortement tridimensionnel du phénomène à proximité du carrefour, (Khan et al., 2000a) conclut à la validité de calculs utilisant les équations de Saint Venant 2D.
Figure 2.2 Hauteurs d’eau maximales et maillage de calcul pour un calcul sur un quartier de Nîmes (crue d’octobre 1988).
Dans le cadre du projet "estimation des écoulements de surface pour une crue extrême en milieu urbanisé" du programme RIO (Risques d’inondation) du MATE (2001-2003), nous avons prévu des expériences sur un carrefour à 4 rues. Les premières expériences (Vayssière, 2001) effectuées dans un canal de 1,2 m de large au Laboratoire de Mécanique des Fluides de l'INSA de Lyon ont montré, d'une part, la complexité des écoulements, en particulier, en régime torrentiel où des ondes sont générées et mal rendues par les équations de Saint Venant et, d'autre part, l'apparition de contractions latérales de l'écoulement très similaires à celles décrites pour 3 branches, par exemple, par (Shettar et Murthy, 1996) et semblant peu affectées par les interactions entre carrefours. Ces expériences devraient être poursuivies.
En parallèle, il apparaît nécessaire de définir la taille de maille optimale pour le calcul selon qu'il est souhaité de bien simuler les différences de niveaux au voisinage des carrefours ou de seulement estimer le niveau moyen dans une rue et la dynamique globale de la crue. Pour représenter l’inondation sur l’ensemble d’un quartier, il faut, en effet, choisir une taille de maille suffisamment grande pour rester à un nombre de mailles et un temps de calcul raisonnables. Cette taille ne permettra pas de présenter tous les détails de l’écoulement. Il est donc nécessaire de prévoir une résolution multi-échelle ou un maillage de taille de maille très variable. Cette résolution doit chercher à exploiter les bases de données urbaines (Heping et al., 1999; Hingray, 1999; Rodriguez et al., 2000; Xiaotao et al., 2001) qui apportent des détails utiles pour bâtir le MNT (Modèle Numérique de Terrain) nécessaire comme base du maillage ; ceci suppose aussi des méthodes efficaces pour extraire ces informations. En outre, dans ce milieu, les échanges avec le milieu souterrain (constitué en majeure partie par le réseau d’assainissement) et les apports par la pluie peuvent jouer un rôle majeur alors qu’ils sont négligeables quand on considère les inondations dans un lit majeur de rivière en zone rurale. Des recherches spécifiques sont nécessaires pour intégrer ces échanges dans la simulation des écoulements de surface : choix de l’échelle, lois d’échange, couplage éventuel des écoulements dans le réseau d’assainissement avec l’écoulement de surface. Localement, les effets en terme de niveau d’eau peuvent ne pas être négligeables. D’autres points doivent
être modélisés ou, au moins, étudiés : influence de la structure 3D de l’écoulement au voisinage des carrefours, influence d’obstacles tels que véhicules, mobilier urbain, etc. Le nombre et le caractère aléatoire de ces détails impliquent une prise en compte spécifique. Les test effectués (Haider, 2001; Haider et Paquier, 1999) sur le modèle physique de Toce comprenant des blocs dispersés représentant des bâtiments ont bien montré la difficulté pour optimiser la représentation de détails de taille inférieure à la dimension moyenne des mailles. Le passage des équations de Saint Venant classiques à une forme simplifiée (Blade et al., 1994; Hingray et al., 2000; Smith, 1992), l'introduction d'une porosité (Defina et al., 1994; Hervouet et al., 2000) ou de frottement additionnel (Testa et al., 1998) sont des solutions possibles selon les cas à traiter.
On notera aussi le lien entre ces recherches et celles concernant l'écoulement de surface sur une parcelle (Esteves et al., 2000; Tayfur et al., 1993) ou un versant (Laura et Wang, 1984; Liong et al., 1994) (en particulier, au sein d'un modèle hydrologique distribué) qui portent aussi sur l'échelle de représentation des détails, le type de d'équations à utiliser pour l'écoulement (équations de Saint Venant plus ou moins simplifiées) et l'infiltration (Lal, 2001).
3 Description de plusieurs lits
En crue, la rivière s’étend sur plusieurs lits de caractéristiques (tirant d’eau, vitesse, occupation du sol, etc) éventuellement différentes. La modélisation 1D est souvent insuffisante à rendre compte de l’interaction entre lits ; même en cas de maillage adapté, la modélisation 2D ne tient pas compte de cette structuration en lits qui a pour corollaire, l’existence de transition entre les écoulements. Ces zones de transition où les écoulements sont souvent fortement 3D impliquent donc soit une description détaillée support d’une modélisation 3D soit une description globale spécifique du problème rencontré.
3.1 Lit composé
Le cas le plus courant est le lit composé dans lequel le lit principal a une vitesse plus forte que celle du ou des lits secondaires. Dans les configurations simples de deux lits rectilignes parallèles, l’interaction se traduit par des courants hélicoïdaux à la transition ce qui permet un échange de quantité de mouvement (Anderson et al., 1996). Dans ce cas simple, de nombreuses méthodes (Samuels, 1989) ont été proposées pour se ramener à une modélisation 1D basée sur une perte de charge moyenne. En général, l’hypothèse de base est un niveau horizontal dans le sens transversal, ce qui permet de définir une correspondance entre le niveau de la surface libre et les variables section mouillée, périmètre mouillé et tirant d’eau dans chacun des lits. Une des formulations les plus simples est la méthode DCM (divided channel method) qui considère deux lits séparés, la seule liaison étant le même niveau dans les deux lits. La formulation Debord (Nicollet et Uan, 1979) (voir introduction) utilisée dans RUBAR 3 considère une perte de charge supplémentaire liée à la différence de vitesses et de frottements (modélisés éventuellement par deux Stricklers différents) entre les deux lits ; elle est traduite par la modification du coefficient de quantité de mouvement β et de la débitance. Ces relations sont, en général, valides pour une hauteur relative (hauteur dans le lit majeur sur hauteur dans le lit mineur) bornée entre une valeur haute correspondant au retour à un lit unique et une valeur basse au-dessous de laquelle la hauteur d’eau sur le lit majeur est très faible. En particulier, se pose un problème de modélisation au voisinage du débordement du lit principal. Si on va au-delà de la situation simple de deux lits rectilignes parallèles, se posent des problèmes supplémentaires lors des méandrements (Ervine et al., 2000; Lambert et Sellin, 2000) ou lors des variations de largeur du lit majeur qui impliquent un échange de masse entre les deux lits ; un problème du même type peut se poser en cas de variation de la débitance du lit principal. Nous avons commencé des recherches pour résoudre les problèmes de modélisation en liaison avec l’Université Catholique de Louvain qui a proposé l’EDM (Bousmar et Zech, 1999), un modèle qui a pour but de tenir compte à la fois des échanges de masse et de quantité de mouvement.
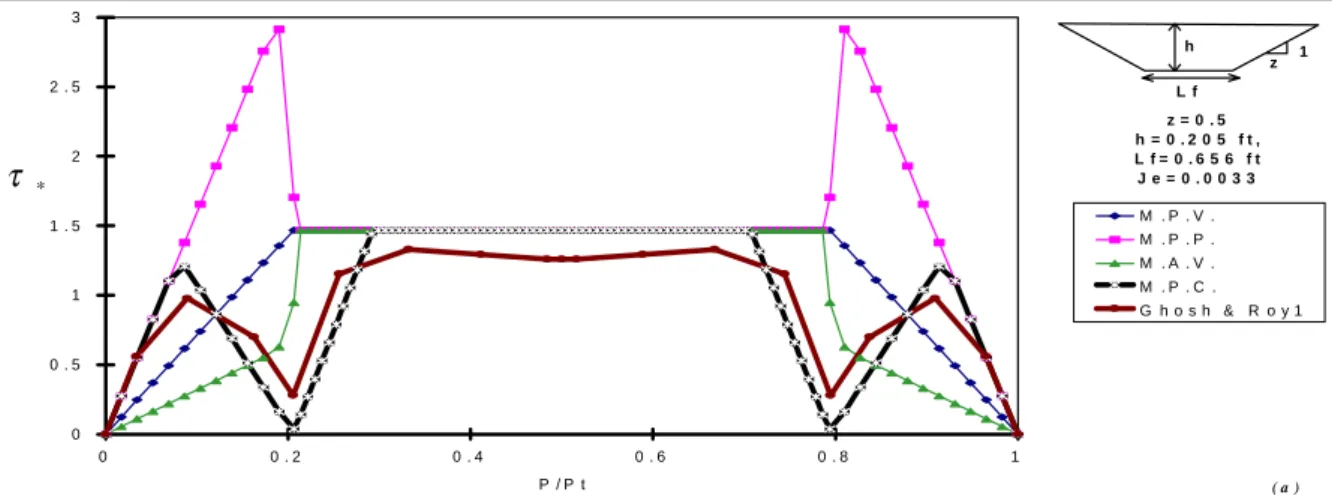
Notre recherche (thèse de S. Proust en cours) est centrée sur les cas de variation brutale de la largeur du lit majeur telle qu’on peut l’observer, par exemple, lors du franchissement de la vallée par un pont prolongé par un remblai. Avec le soutien du Programme National de Recherches en Hydrologie (PNRH), dans le cadre de projets communs avec le Laboratoire de Mécanique des Fluides et Acoustique (LMFA de Lyon) et le Laboratoire d’Essais de la Compagnie Nationale du Rhône (CNR), plusieurs séries d’expériences représentant cette situation ont été effectuées ou prévues. L’objectif de ces expériences est de pouvoir disposer d’un champ détaillé des vitesses au voisinage d’un obstacle barrant partiellement l’écoulement afin de comprendre les processus dominants selon les configurations (Paquier et al., 2001b; Paquier et al., 2000). Nous chercherons ensuite à en déduire comment un modèle intégré sur la verticale (2D ou 1D à lit composé) peut rendre compte de cette configuration : estimation des paramètres clés, addition de paramètres, etc. (Paquier et al., 2001a)
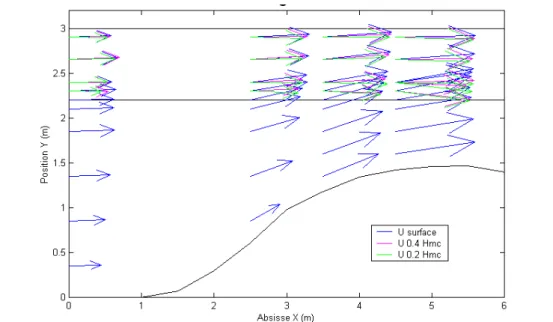
Figure 3.1. Résultats de mesures de vitesse sur une des expériences du projet PNRH99-04.
3.2 Couplage de modèles 1D et 2D
Lors des crues, il apparaît souvent que la majeure part du débit continue à emprunter le lit principal où une modélisation 1D parvient à bien rendre compte des variables hydrodynamiques principales (niveau d’eau, vitesse moyenne, contrainte moyenne, etc) tandis qu’une partie plus faible est dérivée vers le lit majeur en des écoulements éventuellement multiples aisément modélisables en 2D mais difficilement en 1D dès que l’organisation en biefs indépendants évolue avec le temps. Cette configuration conduit à proposer une modélisation 1D pour le (ou les) lit principal et 2D pour le lit majeur. La modélisation 2D du lit majeur permet de gérer aisément les obstacles linéaires (tels que les remblais) ou locaux (tels les bâtiments) qui souvent y sont présents. En revanche, le problème de définition des lois d’échange (de masse et de quantité de mouvement) à la transition entre le lit majeur et le lit principal demeure et justifie les travaux décrits précédemment au paragraphe 3.1. Le principe de mise en œuvre de ce couplage à partir des codes de calcul Rubar 3 et Rubar 20 a été défini (Paquier, 1995b). L’implémentation dans un code de calcul a été tentée en 1997 dans le cadre d’un projet du Pôle Grenoblois des Risques intitulé « Simulations de crues débordantes en rivière par couplage 1D-2D. Etude d'un cas test sur la Bourbre à l'aval de l'Isle d'Abeau ». Ce thème a aussi servi de support à un stage (Sigrist, 1996). La comparaison des résultats sur des cas tests simples entre modèle couplé et modèle 2D a montré l’influence des hypothèses de transfert de quantité de mouvement (Paquier et Sigrist, 1997a; Paquier et Sigrist, 1997b). Une des solutions choisie était l’estimation de la vitesse transversale à la transition entre lit mineur (1D donc sans estimation de la vitesse transversale) et lit majeur directement à partir d’une interpolation linéaire de la vitesse sur les deux premières mailles du lit majeur. De manière similaire, la vitesse longitudinale était estimée à partir d’une moyenne pondérée entre la vitesse dans le lit mineur (1D) et l’interpolation linéaire des vitesses dans les deux premières mailles du lit majeur. Selon les cas, ce n’était pas le même facteur de pondération qu’il était nécessaire d’utiliser pour retrouver des résultats similaires au 2D. Ces travaux devraient donc être poursuivis pour identifier les causes de cette variation. Dans le cas de l’inondation de la Bourbre, la complexité du cas n’a pas permis de déterminer exactement l’origine des différences entre modèle couplé et modèle 2D bien que la courbure des axes des deux lits principaux près de la confluence semble avoir été l’élément déterminant. Notons que ce modèle couplé est certainement plus adapté que le modèle 2D total dans le cas où le lit principal est bien délimité, par exemple, par des endiguements ; les problèmes d’échanges
sont alors limités à des problèmes de déversement au-dessus de remblais ou d’interruptions (ouvrages construits ou brèches) dans ces endiguements. D’un point de vue théorique, il apparaît essentiel de définir une méthode d’estimation des vitesses de transfert qui soit valide pour tous les types d’interface et ne dépende pas du maillage de calcul.
D’autres configurations pourraient être modélisées par un modèle couplé. Il s’agit des cas où on passe d’un écoulement dans un lit bien délimité à un lit à bras multiples ou une jonction de plusieurs biefs, mieux décrits par un modèle 2D. La transition n’est plus parallèle à l’écoulement mais transversale : on passe d’un bief amont décrit par un type de modèle à un bief aval décrit par un autre type de modèle. Si la transition est effectuée dans une zone où l’écoulement est suffisamment régulier et rectiligne, aucun processus particulier n’intervient et une surface libre transversale horizontale est une estimation acceptable tandis que la répartition transversale des vitesses qui manque au modèle 1D peut aisément être approchée : par exemple, extrapolation de la répartition dans la zone proche du modèle 2D ou répartition standard (par exemple par le biais d’une fonction puissance) (Belaud et Paquier, 2000). Ce cas idéal peut ne pas être trouvé dans les applications, ce qui rend alors la complexification du problème incontournable. Par ailleurs, dans toutes les configurations, sauf cas extrêmement rare d’un écoulement totalement torrentiel, il y a influence de l’amont sur l’aval et réciproquement ce qui oblige à un couplage effectif entre les deux modèles, ce qui pose des problèmes informatiques d’échanges de données et d’organisation de ces échanges mais aussi mathématiques de stabilité des codes.
Une autre possibilité de couplage que je n’ai pas abordé est la représentation des écoulements dans le lit mineur par un modèle 1D jusqu’au point de débordement et celle des écoulements dans le lit majeur et dans le lit mineur après débordement par un modèle 2D. Dans le lit mineur, il y a alors superposition d’un écoulement à plein bord modélisé en 1D et d’un écoulement au-dessus modélisé en 2D. La justification de cette modélisation peut être trouvée dans (Patra et Kar, 2000) où il est observé que, dans un lit composé rectiligne, selon le niveau d’eau, la séparation entre l’écoulement dans le lit majeur et l’écoulement dans le lit mineur, séparation identifiée à la ligne (surface si on considère le bief et pas seulement une section en travers) de contrainte nulle n’est jamais une verticale mais une oblique dont l’inclinaison varie et peut aller jusqu’à une horizontale voir au-delà. On trouve aussi une telle justification à cette description dans le cas d’un lit mineur méandrant dans un vaste lit majeur ; alors, le courant principal dans le lit majeur peut couper le lit mineur et le traverser complètement s’il est assez puissant. On a bien entendu, dans ce cas, une zone de fort cisaillement à l’interface qui donne lieu à des courants hélicoïdaux et à une forte turbulence (Shiono et Muto, 1998). On voit bien qu’une difficulté est de définir les pertes d’énergie dans cette zone ; si on souhaite rester dans une modélisation classique de type Saint Venant, il faut définir une contrainte de frottement à la surface pour le 1D (comme cela est effectué parfois pour le vent à la surface libre) et une contrainte de frottement au fond pour le 2D qui représente ce même frottement entre les deux masses d’eau. En outre, compte tenu des irrégularités d’un lit naturel, des échanges de masse s’effectuent à travers cette interface. Ce dernier point n’est pas sans rappeler le transfert d’eau qui peut se produire en fond de rivière par infiltration ou remontée de nappe.
La plupart de ces problèmes de couplage (sur les plans hydraulique, mathématique et informatique) font l’objet d’un volet du projet de l’Action Concertée Incitative Prévention des Catastrophes Naturelles « Modélisation des processus hydrauliques à surface libre en présence de singularités » (2000-2003) auquel je participe.