by
SYLVAIN LE VESQUE
B.Ing. in Mechanical Engineering, Universit6 de Sherbrooke (1987) S.M. in Mechanical Engineering, Massachusetts Institute of Technology (1989)
Submitted to the Department of Mechanical Engineering in Partial Fulfillment of the Requirements
for the Degree of
DOCTOR OF PHILOSOPHY
at the
MASSACHUSETTS INSTITUTE OF TECHNOLOGY
September 1993
@ Massachusetts Institute of Technology All rights reserved
Signature of Author
Signature Redacted
Signature Redacted
Department ofMechanical Engineering
Certified by Professor Derek Rowell
Professor Derek Rowell
Thesis Supervisor
Signature Redacted
Accepted byProfessor Ain A. Sonin Chairman, Department Committee on Graduate Studies
SYLVAIN L* VESQUE
Submitted to the Department of Mechanical Engineering on June 17, 1993 in partial fulfillment of the requirements for the
Degree of Doctor of Philosophy in Mechanical Engineering
ABSTRACT
Acoustical imaging is perhaps the most commonly used medical imaging modality. In conventional B-scan imaging methods, a major assumption is that ultrasonic energy propagates in tissue along straight rays and that distance may be inferred from propagation delay. In general, acoustic wave radiation undergoes refraction as it passes through various tissue types and therefore cannot be modeled as straight-propagating rays. The velocity of sound in tissue varies; therefore wave properties such as refraction, reflection, and diffraction must be modeled if one hopes to avoid the pitfalls of ray tracing imaging method.
The broad goal of this research is the theoretical and experimental study of a tomographic image reconstruction method termed Wave Propagation Tomography (WPT). The imaging task is to produce a spatial distribution of the complex wave number inferred from a set of measurements made at the periphery of an object space. WPT attempts to derive images directly from the acoustic wave equation itself, with the only approximations resulting from numerical discretization of the image space. The imaging problem is thus formulated as an inverse solution of the Helmholtz wave equation.
A wave propagation forward model that combines the Finite Element Method (FEM) and the Bound-ary Element Method (BEM) was implemented and validated. The forward model inversion was formu-lated using the Bayesian paradigm which, under the assumption of Gaussian uncertainties, provides tools for making inferences about the wave number distribution and errors in the solution. Simulations showed empirically that, while resolution at scales smaller than the wavelength is possible with analyt-ical data, previous claims of super-resolution on the order 1/10 of the wavelength are not accurate. Further, an error analysis estimated the resolution of WPT to be of the order of a wavelength for a sig-nal to noise ratio of 54 dB. Comparisons with linear Diffraction Tomography showed that Wave Prop-agation Tomography remains robust in the presence of strong scatterers.
An experimental scanning and data acquisition system was designed which provided the first experi-mental verification of WPT. Successful image reconstruction of a glycerine tube submerged in water was achieved. The Bayesian paradigm proved essential for the stable inversion of data with experimen-tal uncertainties.
Thesis Supervisor: Derek Rowell, Ph.D.
Dr. Derek Rowell Professor
Department of Mechanical Engineering
Dr. Harri KytSmaa Associate Professor
Department of Mechanical Engineering
Dr. Robert W. Mann
Whitaker Professor Emeritus of Biomedical Engineering Department of Mechanical Engineering
Dr. Henrik Schmidt Associate Professor
Special thanks to Professor Derek Rowell for his continual support. During these past four years, you have always offered me friendly advice and guidance, incited me to work toward high standards, and taught me a lot about engineering. Along the way, I picked up some sailing skills and I got tutored in the language of Shakespeare.
Thanks to Professor Robert W. Mann for developing a laboratory environment like the Newman Laboratory. I have benefited greatly from your experience, insight, guidance and support.
Thanks to Professor Henrik Schmidt who was my teacher and mentor in the field of numerical acoustics. You not only taught me the fundamentals but also gave me the insight necessary to apply them in a sensible way. Your readiness to offer advice and criticism was most appreciated.
Thanks to Professor Kyt5ma for his expert advice on a wide range of technical issues, his always friendly support, and at times some parenting tips.
Thanks to Bill Rodi for patiently introducing me to the field of inverse theory. Thanks to Professor Robert Fricke who entrusted me with his hydrophones which made my experiment possible. He also introduced me to the underwater acoustic group which was always a source of ideas and insight.
Thanks to all the past and present members of the Newman Laboratory for your willingness to help and all the insightful discussions. A lot of the learning and fun of being at M.I.T. occurred in "The Lab". Taking the risk of forgetting someone, I especially thank Crispin, Denis, Gerald, Greg, Joe, John, Justin, Karon, Keita, Marc, Michael, Mike, Norm, Pat, Pete, and Tony for your friendship and help. My only regret is that I do not seem to have convinced anyone that my homeland is "so much better".
Thanks to my parents and sister, Jacqueline, Victor and Annie, for their support, love, encouragement.
Susan, thanks do not even begin to repay the debt I have accumulated. During this doctoral degree, we got engaged, we got married and we had our fist child, Philippe. Your help, companionship, and love have made the difference for the completion of this thesis as well as keeping some sort of balance in my life. I love you.
This research was performed in the Eric P. and Evelyn E. Newman Laboratory for Biomechanics and Human Rehabilitation at MIT. Student support was provided by the 1967 Science and Engineering Scholar-ship through the Natural Science and Engineering Council of Canada, by the Fonds Canadiens pour l'Aide A la Recherche, by the Poitras Fellowship through Withaker College, and by the National Institute on Disabil-ities and Rehabilitation Research of the U.S. Department of Education.
Chapter 1
1.1 1.2 1.3Chapter
2
2.1 2.2 2.3 TITLE PAG E ... 1A BSTRACT ...
3
ACKN OW LED G M ENTS ... 7
CO NTEN TS ... 11 INTRO D U CTIO N ... 15 The Issues... . 15 Summary ... . 16 Thesis Overview ... 17
FRA M EW ORK ...
19
Approach... . 19Imaging and Inverse Theory... . 21
12
2.3.2 Simple Wave Fields...25
2.3.3 Non-Uniqueness of Source Characterization from Field Solution...27
2.3.4 Attenuation... 28
Chapter 3 FORWARD MODEL OF WAVE PROPAGATION IN
TW O DIM ENSIONS ...
31
3.1 Introduction ... 31
3.2 FEM Formulation in the Internal Space ... 34
3.2.1 Weighted Residual Formulation of the Helmholtz Equation... 34
3.2.2 Discretization of the Object Space Into Finite Elements ... 37
3.3 BEM Formulation in the External Space...42
3.3.1 Integral Formulation of BEM ... 42
3.3.2 Discretization into Boundary Element ... 47
3.4 Combination of FEM and BEM Formulation...49
3.5 Analytical Verification of Forward M odeling...51
3.5.1 Scattering by a cylinder insonified by a cylindrical source ... 51
3.5.2 Numerical model... 53
3.6 Summary... 56
Chapter 4 INVERSE M ODELING ...
59
4.1 Introduction ... 59
4.2 M inimization of Forward M odel Approach ... 60
4.3 Inverse Problem Using Bayesian Inference ... 61
4.3.1 Background ... 61
4.3.2 Explicit Forward Model d=g(m) ... 62
4.4 M ethod of Resolution ... 66
4.4.1 Introduction ... 66
4.4.2 Gauss-Newton Method...67
4.5 Characterization of the Inverse Solution ... 68
4.5.1 Summary... 69
4.6 Analysis of Error and Resolution... 69
4.6.1 Posterior Covariance ... 69
4.6.2 Resolution Operator ... 70
4.7 Summary... 71
Chapter 5 IM AGING SIM ULATION ... 73
5.1 Introduction ... . 73
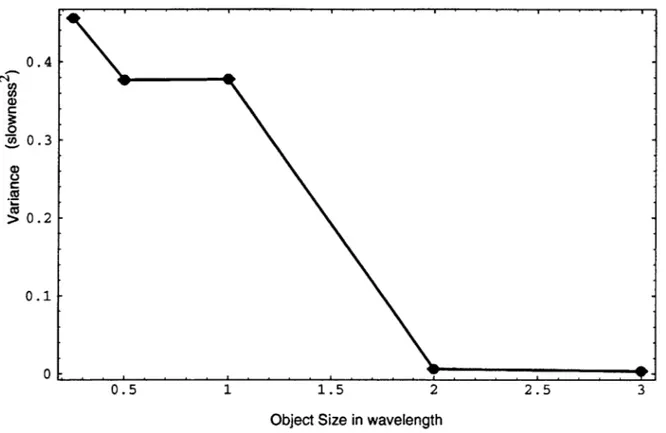
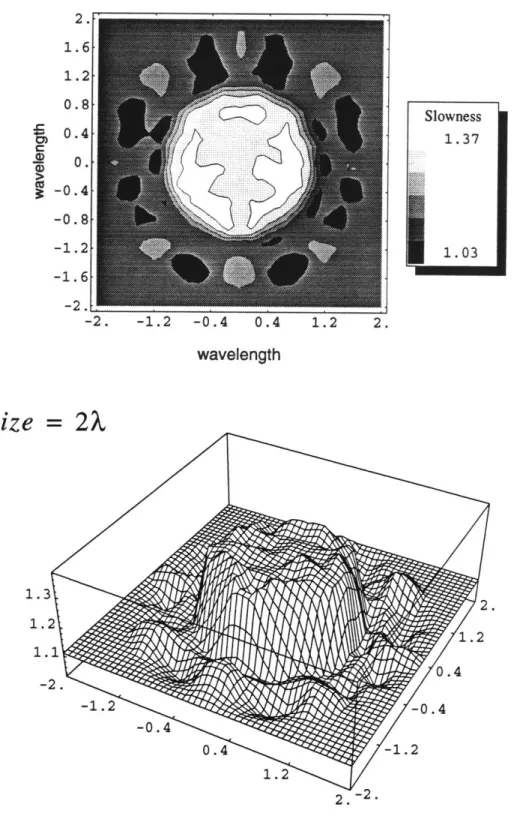
5.2 Is Super-Resolution Feasible?... .74
5.2.1 Appearance of Super-Resolution ... 74
5.2.2 Simulated Data and Inversion Calculated with Different FEM/BEM Mesh ... 78
5.2.3 Adding Noise on Simulated Data ... 79
5.3 Inversion of Noise Free Analytical Data... . 82
5.3.1 Objective Function ... 82
5.3.2 Disk Imaging from Analytical Data ... 84
5.4 Comparison with Linear Diffraction Tomography ... 91
5.5 Summary ... 92
5.6 Figures ... 93
Chapter 6 EXPERIMENTAL INVESTIGATION: DESIGN...131
6.1 Background...131
6.2 Hardware...135
6.2.1 Tank, Transducers and Positionning ... .135
6.2.2 Data Acquisition System and Protocol... .140
6.3 Signal Processing and Calibration...141
Chapter 7
7.1 7.2 7.3 7.4 7.5 7.6 7.7Chapter 8
8.1 EXPERIMENTAL INVESTIGATION:RESULTS ... 157Object Design Considerations ... 157
Experiment, Data Acquisition and Signal Processing ... 159
Objective Function ... 160
Images W hich Do Not Include a M odel of Absorption ... 162
7.4.1 Images using Coarse FEM/BEM Mesh ... .162
7.4.2 Images using Fine FEM/BEM Mesh ... .166
Images which Include an Absorption Coefficient...167
Summary and Discussion ... 169
Figures...171
CONCLU SIONS ...
205
14 8.2 Conclusions ... 207
Appendix A
Appendix B
Appendix C
BIBLIOGRAPHY ...
209
SCATTERING BY A CYLINDER INSONIFIED BY
A LINE SOURCE ...
213
BAYESIAN INFERENCE FOR AN IMPLICIT
M O D E L ...
221
OMNIDIRECTIONAL TRANSDUCER
SPECIFICATIO N S...
231
INTRODUCTION
1.1 The Issues
Ultrasonic imaging is perhaps the most commonly used medical imaging modality. Conven-tional imaging methods are based upon detection of back-scattered, or reflected energy and therefore produce images of acoustic discontinuities in the object space. A major assumption is that ultrasonic energy propagates in tissue along straight-line "rays" and that distance may be inferred from propagation delay. In general, acoustic wave radiation cannot be modeled as straight-propagating rays and undergoes refraction as it passes through various tissue types. In contrast to X-rays, acoustic wavelengths used in medical imaging are usually larger than the discontinuity in the material properties (ultrasound at 500kHz has a wavelength X of approximately 3mm, while for X-ray radiation X =0.012pm). The velocity of sound varies between tissue types [29], therefore wave properties such as refraction, reflection, and diffraction must be modeled if one hopes to achieve high resolution images. The availability of powerful and low cost computers now makes feasible the incorporation of more complex wave propagation models in the reconstruction of acoustic images. In the past 15 years, ultrasonic tomographic imaging techniques that attempt to model these phenomena have been developed.
I-16 CHAPTER 1: INTRODUCTION
Two approaches, termed wave propagation methods, offer a possibility of improved image formation. Mueller, Kaveh and Wade [23] first proposed Diffraction Tomography in the 1970's. This method uses a weakly diffracting model of the acoustic propagation by applying a Born or Rytov approximation to the wave equation to yield a Fourier-based image reconstruction method. The primary limitation of this method is that the amplitude of the scattered field is assumed to be restricted to a few percent of the incident field from an exter-nal sound source. More recently Miyashita [20-22] developed a theoretical approach, termed Wave Propagation Tomography, which offers the prospect of improved resolution in acousti-cal images even in the presence of a strong scattered field. To our knowledge there has been no attempt to provide a practical demonstration of this method.
1.2 Summary
This thesis investigates and characterizes the Wave Propagation Tomography imaging method both theoretically and experimentally. A rigorous development of the method pro-posed by Miyashita is presented. Computer based simulations are used to validate and char-acterize the method. In particular, special attention is placed on the issue of super-resolution since it has been inferred in the literature [20-22] that resolution to very small scale can be achieved. In the process, the error propagation from analytical measurements into image for-mation is examined and used evaluate the sesolving power of Wave Propagation Tomogra-phy.
An experimental study is used to explore the performance of the algorithm as a practi-cal imaging technique in the presence of noise and biased error in measurements. An imag-ing experiment with a submerged thin film tube filled with glycerine was performed. The goal was develop a near optimal and flexible algorithm for the estimation of the object image. The best reconstruction was sought based on knowledge of the true image and issues relating to errors in the image estimate.
To summarize, this thesis describes a theoretical study and an experimental verifica-tion of a new imaging method. The aim was to formulate an algorithm in a rigorous
work such that results and performances can be evaluated and interpreted with standard metrics.
1.3 Thesis Overview
The thread of the thesis follows a logical sequence that goes from wave propagation model formulation to experimental study. In Chapter 2, a scenario for an hypothetical ideal experiment is laid out. Then some background on acoustic propagation and inverse theory is given to introduce notation and terminology. Chapter 3 presents the formulation wave propa-gation using Finite Element Method (FEM) and Boundary Element Method (BEM). This model allows the direct calculation acoustic pressure field, given material properties, at any point within an FEM mesh. An analytic verification of the model is also presented. In Chap-ter 4, a theoretical framework for the inversion of the FEM/BEM wave propagation model is presented. This framework, termed Bayesian inference, also provide a methodology for image error analysis. Chapter 5 integrates the wave propagation model and the inversion method and presents imaging simulations with noise free data that elucidate the performance and limitation inherent to the wave propagation tomography method. In Chapter 6, the design of experimental hardware is presented. The design objective is the simulation in three-dimensions of a two-dimensional fictitious experiment in an infinite space. Final design is presented with the results of a calibration experiment in water only. Chapter 7 pre-sents experimental results for a glycerine cylinder submerged in water. Image reconstruc-tions for different parameter are presented as well as an error analysis. Finally, Chapter 8 gives a overview of the results.
18 CHAPTER 1: INTRODUCTION
Chapter 2
FRAMEWORK
2.1 Approach
In general, the imaging task is to estimate the spatial distribution of a given material property as inferred from a set of measurements, usually made at the periphery of the object space. Wave Propagation Tomography [20-22] attempts to derive images directly from the acoustic wave equation itself, with the only approximations resulting from numerical discretization of the image space. The imaging problem is formulated as an inverse solution of the acoustic Helmholtz equation, which is defined as follows:
V2pQ) +k 2 r -(-r (2.1)
where k (r) = kon (r) - ia (r) is the complex wave number, 8 (r, - r) is a point source term, and i is the position vector. Here, n(r) is the index of refraction (or normalized slow-ness) and a (Q) is the absorption coefficient of the material. The image to be reconstructed is the spatial distribution of k(P).
To visualize a Wave Propagation Tomography imaging experiment, consider a mea-surement geometry as shown in Figure 2.1. A monochromatic sinusoidal source, that can be
20 CHAPTER 2: FRAMEWORK
receiver at each node Source
on the boundary E ms
Figure 2.1: Schematics of Wave Propagation Tomography experiment an numerical modeling (adapted from Miyashita [22]).
moved to different positions, irradiates an object. The acoustic field p (r) on a closed circu-lar boundary around the object is measured for each location of the source. Knowing the acoustic field p (r) on the boundary for many positions of the source, the goal is to solve for the complex wave number distribution k (r) inside the circular boundary. For this, the method combines the Finite Element Method (FEM) and the Boundary Element Method (BEM).
To discretize the Helmholtz equation, the infinite two-dimensional space is divided into two regions. One is the area within a circular boundary, where the FEM is used to model the wave propagation through the non-homogeneous object space (i.e., where k = k(r)). Within this space a mesh is created and the image will be formed at the nodes of this mesh. The other region is the infinite space outside the circular boundary, where a point source lies, and where the BEM is used to model the wave propagation through the homogeneous mate-rial (i.e. where k (r) = ko, a real constant). The two solutions techniques, FEM and BEM, lead when combined algebraically to a matrix equation of the form:
LA]
[]
E (2.2)S = I _ BJ s -5s
where Pi is the field in the interior of the boundary (unknown), PB is the field on the boundary (measured), A is the propagation matrix which depends on the complex wave
numbers (the unknown imaging parameters), and S is a vector which depends on the source strength and phase. The subscript s of vectors P and S indicates that they are a function of the source position. In this equation the right hand side, E, tends to zero when all the param-eters are known exactly. Thus, the inverse problem becomes an iterative search for the distri-bution of wave number that minimizes E. In practice a functional based on the wave propagation model of Equation 2.2 is constructed and then iteratively minimized. This is a computationally intensive iterative minimization procedure during which the wave numbers are updated at each iteration in order to calculate a new FEM/BEM solution.
This project involves in its first phase the development of a wave propagation simula-tion program in order to optimize the signal analysis methods. This includes: formulasimula-tion and programming of the FEM and BEM for the Helmholtz wave equation; formulation of an inversion method based on a Bayesian point of view which result in a well-posed minimiza-tion principle; computer based imaging simulaminimiza-tion; and a study of parameters including mesh fineness and mesh-sources configuration. In a second phase, experiments will be per-formed with objects for which the wave number distribution is known. This includes the selection of transducers, choice of optimal frequency; design of tissue-like phantom objects; data acquisition; and performance analysis. Issues such as sensitivity of the reconstruction method to noise and spatial sampling; and disturbance effect introduced by the presence of finite size receivers in the field will be investigated.
2.2
Imaging and Inverse Theory
In general, the goal of imaging is to estimates and display a set of spatially varying parame-ters that describe a physical system as completely as possible. The most common form of display is a two-dimensional still frame, such as a photograph taken from a camera, a trans-lucent film chest x-ray, or a cathode ray tube displaying an x-ray tomogram. In mathematical terms, a two dimensional image translates an underlying image function rn(r) as a matrix of pixels that can be seen by the human eye. This function ^(x, y), in a 2-D Cartesian coordi-nate frame, estimates the spatial distribution of a physical property that describes the system under study. The so-called true distribution m(r) of the physical property is usually three dimensional and perhaps time dependent. For example, a planar x-ray is a two dimensional
A
22 CHAPTER 2: FRAMEWORK
map of the line integral of the three-dimensional x-ray absorption coefficient along the ray path. Another example is a color photograph which maps the ambient light reflectivity of objects in the camera's field of view. In acoustical imaging, spatial distributions of acoustic wave velocity and acoustic wave energy absorption are of interest.
Backus and Gilbert [6] were the first to formalize the fact that the true distribution of a physical parameter can never be obtained. The estimate ^(x, y) is a filtered version of m(r) and the relationship between r^(x, y) and m(r) can be written formally as:
mz(x, yO) = R(x, y, x0, yo)m(x, y)dS (2.3) S
where R is a resolution operator. The goal of an imaging protocol is to make the filtering process as close as possible to a dirac function such that
t5n(xo, yo) = 8(x - x0, y - yo)m(x, y)dS. (2.4)
S
While this is impossible to achieve, this equation illustrates the concept of a perfect resolu-tion operator. The cases where this can almost happen are when rmn can be obtained directly by instrument measurements.
In this thesis we are looking for distributions of the acoustic wave velocity and acous-tic wave absorption coefficient. These are properties of the material through which the wave propagates and therefore cannot be measured directly. In an acoustical imaging experiment, field parameters such as pressure can be measured at the periphery of the object to be imaged. Fortunately the pressure field depends on wave velocity distribution in the object space and that dependence will be the foundation for the imaging algorithm.
At this point, this discussion is formalized into definitions and notation. Parameters such as wave speed and absorption are termed model parameters, with the letter m used as a generic notation for these parameters. Parameters such as pressure field are termed observ-able parameters or data, with the letter d used as the generic notation. The data usually depends explicitly on the model parameter such that
d = g(m) (2.5)
where g is in general a non-linear function. The data and model parameters can also be related implicitly such that:
f(d, m) = 0 (2.6)
Solving aforward problem is to predict the values of observable parameters given a set of arbitrary values for the model parameters. Solving an inverse problem is to infer the val-ues of the model parameters from given observed valval-ues of the observable parameters. It is clear in this context that acoustical imaging is an inverse problem.
In the following, background material on the physics of wave propagation in fluid is presented. This will be the foundation to build a forward model that fall into the category of either Equation 2.5 or Equation 2.6.
2.3 Acoustic Theory Background
2.3.1 Wave Equation
The wave equation for a fluidic system in terms of the pressure disturbances is as follows:
v2P(P ) - 0 (2.7)
c2() at2
where we assume that the phase speed c(P) is a function of position. This equation, derived from conservation of mass and from conservation of momentum in a fluid, expresses a bal-ance between compressibility and inertia.
Several assumptions are made in order to obtain Equation 2.7 from first principle. a) fluid medium (zero shear modulus)
b) inviscid fluid
c) no conduction or radiation of heat d) small disturbances
e) fluid of a single phase and continuous f) zero mass addition
24 CHAPTER 2: FRAMEWORK
i) zero current and turbulence
k) ambient conditions steady in time
In the context of medical imaging, and of day to day understanding of acoustical phenom-ena, most of these assumptions are valid but some are violated to different degrees.
Living tissue, with the exception of bone, can be regarded as a fluid medium with regards to acoustic propagation. If waves propagate through tissue that includes bone, it is necessary to model elastic wave behavior as well.
Viscosity and heat loss conduction are also neglected in the derivation of Equation 2.7. At the wavelength scale, the pressure represents a far greater stress field than that induced by viscosity. The ratio of the two stresses, as expressed by the Reynolds number,
,
(OX2
(2.8)
where X is the wavelength and v is the fluid kinematic viscosity, is for most applications very large. Viscosity, thermodynamic effects and others dissipative phenomenon become rel-evant to explain attenuation over propagation distances of many wavelengths. Attenuation will be addressed later in this section.
Disturbances (pressure, velocity, density) from a state in which a fluid is at rest with a uniform pressure and density are assumed to be weak, such that products of those distur-bances (i.e. second order effect) may be neglected. Under such condition the response of the acoustic field is linear, which has two major consequences. First, several waves can propa-gate simultaneously without distorting one another, and their fields add linearly. Second, each of the flow variables associated with the propagation of acoustic energy (pressure, den-sity, velocity) is linearly related to any other.
A general solution of the wave equation for the pressure p' is
p'Q(, t) = fit - r/c) + g(t + r/c) (2.9)
where
f
and g are functions. In this thesis, only harmonic solution are considered such that:p'(, t) = p(r)e(t (2.10)
Acoustic Theory Background 25
where o is the angular frequency of the pressure field p. Replacing Equation 2.10 into Equation 2.9 yields the Helmholtz equation:
W2
V2p(r) +
PG.)
= 0 (2.11)cI(O) where the time dependence has been removed.
Harmonic solutions are convenient. Since acoustic field are linear, Fourier analysis decomposes any general wide band acoustic process into a sum of linearly independent har-monic functions that can be analyzed or solved separately. Note that Equation 2.11 implic-itly assumed that the density of the medium can be approximated as constant.
2.3.2
Simple Wave Fields
These simple wave field solution will be used for the FEM/BEM formulation of wave propa-gation and for calibration of the experimental apparatus. A spherical wave centered at the origin of a homogeneous fluid (e.g. c() = c0) is the simplest acoustic field beside a plane wave field. In this case, the pressure depends on the radial distance r only. The Helmholtz equation in spherical coordinate reduces to:
(02 2P 2 a = r 2 ( r - ) 2(rp) -k (rp) = 2__(.2 0 ~ ar2
where ko = .o/c is a constant wave number. The general solution of Equation 2.12 for out-going waves (i.e. waves that satisfy the Sommerfeld radiation condition or causality) is:
ftkor)
r) = r (2.13)
where
f
is a generic function. For a spherically symmetric wave the solution is:ik r e0
p(r) - r (2.14)
-1
26 CHAPTER 2: FRAMEWORK
Equation 2.14 is a solution to the homogeneous Helmholtz Equation 2.11 in a domain that excludes the origin (r = 0) where the solution has a singularity. To elucidate the behav-ior of the solution around the origin, Equation 2.14 is substituted in Equation 2.12 and its integral is calculated over a vanishingly small volume surrounding the origin, that is:
iker (ik r lim (V2+k )e r dV= lim 2 eVe dV rn -4i r V r-+ v r V lim ik ,JdS r-+ an( r S -ik r = lim 4nr2 _ e 2 _ k -ikor r -40 r2 r - 4n (2.15)
Using the following definition of the delta function
J4ir6(r)dV
= 4n if V includes r = 0V
= 0 otherwise (2.16)
and comparing Equation 2.15 and Equation 2.16 we reach the important result that
iker
(V2+ k ) - -42(5-) (2.17)
0)r
Therefore, the solution to the non homogeneous Helmholtz equation
(V2+ k)p( ) =
-6()
(2.18)is
1 -ikor
p(r) = e (2.19)
for a symmetric wave field in an unbounded domain.
For a cylindrically symmetric field in two-dimensions the solution to Equation 2.18 is
p(r) = H (kor) (2.20)
where HO (z) is an Hankel function of zero order and second kind. In the limit when z is large, it can be approximated by
H (r) -ei(Z /4) when (r -+ oo) (2.21)
where the characteristic 1/ (,Fr) geometric spreading factor for 2-D wave is more evident.
2.3.3 Non-Uniqueness of Source Characterization from Field Solution
This section is relevant to the issue of estimating material property of an object (i.e. the com-plex wave number k) from a sound field p. Devaney [11] rigorously showed that even if the sound field was known in all space outside an object, the object material property cannot be uniquely determined from the sound field. In the following proof [12], which illustrates the main ideas of Devaney's proof, it shown that a source of sound cannot be determined uniquely from knowledge of the field that originates from it. Since in an imaging experiment an object can be considered as the source of a scattered field [11,16], this simpler proof helps making the argument that an inverse scattering problem is mathematically ill-posed.Equation 2.11 must be satisfied for any acoustic disturbance in a fluid. However, Equation 2.11 says nothing about where the acoustic field originate. Taking the view that no sound can exist without the presence of a source, a generic sound source q() is usually defined such that [12]:
2
V2p() + 2p(r) = q(J) (2.22)
c
where q is non-zero in a volume V and where q vanishes in the sound field since the sound field p must satisfy Equation 2.11 .The pressure field p does not contain enough information about the source to determine it. To illustrate this, consider the pressure field p + q which is identical to p since by definition q = 0 in the pressure field. However the source of these two fields are different. From Equation 2.22, the source of p is q and for the field p + q
28 CHAPTER 2: FRAMEWORK
22
(p+q) + 2 (p+q) =q+ V2q+ q, (2.23)
C C
which shows that the source of (p + q) is q + V2 q + (o2/c 2) q. This demonstrate that the
field does not contain enough information about the source to be characterized and that the source characterization problem from field data is ill-posed. This mathematical proof might appear discouraging but it does not mean that meaningful source characterization cannot be achieved. It will be shown in Chapter 4 how an ill-posed problem can be transformed into a well-posed extension.
2.3.4 Attenuation
In the prior discussion of simple wave filed, mechanism by which acoustic energy is dissi-pated into heat have been neglected. Instead of considering all the possible dissipative mech-anisms such as viscous damping, chemical relaxation, or others, a law based on an exponential reduction in amplitude over distance is stated. The same law could be arrived at analytically by careful consideration of viscous dissipative processes. [18].
If the geometric spreading is ignored (i.e. assume that we are in the far field), the change in pressure amplitude over a distance dr is assumed to be:
diPi- -adr,
(2.24)
1p1
where a is termed the attenuation coefficient. The integral of Equation 2.24 is simply:
-ar
pI = Poe , (2.25)
where P0 is some calibrated constant. For spherical symmetric fields this is equivalent to:
p(r) = -- Ie i(kia)r (2.26)
4nr
which include a quadrature correction to the wave number k0.
In general, when c = c(r) and cx = (xr), we will solve the following Helmholtz equation
V2p() + k2(P)p() = -8(r' - r,1) (2.27)
where k() = (o/c(r)) - ia() is a complex wave number that incorporates the attenuation coefficient and ir is the origin or a compact monopole source. In practice, Equation 2.27 is solved assuming that the wave number is real, and then the complex value is substituted in the solution.
1
30 CHAPTER 2: FRAMEWORK
FORWARD MODEL OF WAVE
PROPAGATION IN TWO DIMENSIONS
3.1 Introduction
This chapter describes the development of a numerical model for 2-D wave propagation. This forward model is later used as the basis for an objective function in the iterative image reconstruction algorithm.
There are several methods that may be used to form a numerical model of wave propa-gation. In Chapter 2 the problem was constrained to the Helmholtz equation. The bias here is to make no approximation in the numerical model other than those required by discretization of a continuous domain. This disqualifies ray tracing models and Fourier based diffraction tomography methods which are based on linear models with a weak scattering assumption. [16,23].
The spatial domain of a physical differential equation, such as the Helmholtz equation, can be discretized for numerical calculation in two ways. One consists of partitioning the whole spatial domain of interest and performing numerical solutions over the discretized domain. The other consists of partitioning the boundary of the differential equation domain
32 CHAPTER 3: FORWARD MODEL OF WAVE PROPAGATION IN TWO
receiver at each node Source
on the boundary FMms
Figure 3.1: Wave CT schematics
able when the physical parameter or coefficients of the differential equation are constant within the bounded domain.
As described in Chapter 2, the proposed imaging experiment is to be performed in an assumed infinite domain where the Helmholtz equation applies. The physical parameter k (e.g. wave number) is assumed to be constant everywhere with the exception of the space occupied by the object to be imaged. Consequently, the infinite domain may be partitioned into two parts: one which encloses the object (where a spatial partition will be used); and one that surrounds the previous one (where a boundary partition will be used).
The simplest way to discretize a domain over which a differential equation applies is to use finite difference equations. The method approximates differentiates by finite differ-ences; transforming a set of differential equations into a set of simultaneous algebraic equa-tions, which then can be solved. One constraint with finite differences is that one is constrained to use a uniform square grid. This would force us in an experiment to acquire data on a rectangular path, which would necessitate different hardware than what we pro-pose. The main problem with finite differences is that the grid used must be uniform. If there
are highly localized gradients of a function in parts of the domain, one must use a fine grid everywhere to adequately sample those high gradients. This makes the algebraic equation harder to solve.
Finite Element Methods (FEM) [8] have the same advantages as the finite difference method but not the disadvantages. The basic concept of the finite element method in func-tional analysis is that the function domain can be represented by an equivalent mathematical model which consists of a discrete number of finite domain elements. The functional behav-ior of each of these elements may be described by different sets of functions which are cho-sen such that some degree of continuity is ensured throughout the domain. The disadvantage of finite element methods compared to finite difference methods is the increased complexity of the formulation implementation. Nevertheless, FEM advantages outweigh its disadvan-tages and is used in this thesis to model wave propagation over the object domain. However, FEM cannot be used to map an infinite two dimensional domain because it would obviously require an infinite number of elements. The domain of an FEM formulation must be bounded and a set of boundary conditions must be prescribed.
In the proposed imaging geometry, we have a two-dimensional localized object in a constant background (e.g. a infinite region wiht homogeneous properties). Solutions of wave propagation in the homogeneous domain, which exclude the object, can be written in terms of boundary (or contour) integrals around that domain. That is where Boundary Element Methods (BEM) [9] enters. Continuous boundary integrals can be discretized over boundary elements which lead to an algebraic formulation. The method is very similar to the FEM method.
Consider the geometry shown in Figure 3.1. A BEM algebraic equation is used to describe the wave propagation solution on the boundary of the FEM mesh. An FEM alge-braic equation is formulated to describe the wave propagation solution in the 2-D domain of the triangular mesh. The BEM and FEM solutions are combined algebraically by matching the boundary conditions to lead to the forward model.
FEM and BEM are well documented in the literature, and several commercial software packages exist that implement these methods. However none were flexible enough to accom-modate the Helmholtz equation or the combination of FEM and BEM. Therefore a FEM and
34 CHAPTER 3: FORWARD MODEL OF WAVE PROPAGATION IN TWO
Lnormal
ninternal domain S
object
boundary FB
Figure 3.2: Coordinate system and sign convention for FEM modeling
BEM computer program had to be implemented from the ground up. In the remainder of this chapter, the forward model theoretical foundation and implementation are explained in detail. The FEM formulation is based on Bathe [8] and the BEM formulation is based on Brebbia [9].
3.2 FEM Formulation in the Internal Space
3.2.1 Weighted Residual Formulation of the Helmholtz Equation
The Helmholtz equation for an internal closed space S without a source is defined as follows:
V2po (r) + k2 (r)po(r) = 0 (3.1)
with a natural boundary condition defined as:
apo (ix)
a =N', (r) on the boundary FB of the closed space (3.2)
an
where:
po (r) is the exact pressure field of sound;
k (r) = kon (r) - ia (r) is the complex wave number;
ko is the wave number of reference (usually that of water);
n (r) is the refractive index or normalized slowness;
cc (P) is the absorption coefficient.
In general, the exact solution po is impossible to find. In practice, the exact solution po is approximated by a function p. The form of p will be discussed in subsequent sections. Substituting p in Equation 3.1 results in a "residual" function R such that
R = V2p () + k2 0)p () 0. (3.3)
In the weighted residual method, the residual R is distributed over the domain S by multiplying it by a weighting function w such that on average the error introduced by the approximating function is zero, i.e.
JjRwdS = ff(aip (r) +k 2(r)p (r) )w(b)dS = 0. (3.4)
S S
Nothing is said about at this point whether or not the function p satisfies the boundary condi-tion of Equacondi-tion 3.2. To investigate this further, we integrate Equacondi-tion 3.4 by parts once, and invoke Green's identity ,
if
[Q (waip)
-apaw + k2pw] dS = 0 (3.5) Sf[- aipaiw + k2pw] dS+ wd = 0. (3.6)
S rB
Replace (Dp) / (a n) in Equation 3.6 by XVB (Note that this is an approximation if the function p does not satisfies the boundary condition exactly). To see the effect of this substi-tution, we try to get back to Equation 3.4 by integrating Equation 3.6 by parts:
fJ(a p (r) +k2 (r)p (r)) wdS = f J (waip) dS - f WB wdF (3.7)
S S r
1. Given two scalar functionf and g, Green's identity in tensor notation for a domain such as in Figure 3.2 is given by
36 CHAPTER 3: FORWARD MODEL OF WAVE PROPAGATION IN TWO
JJ(ap (r) + k2 (r)p (r) ) wdS = ( j- B) wdF. (3.8)
S r
If we were to choose the approximating function p such that the boundary condition would be satisfied exactly, the right hand side of Equation 3.8 would be zero. However, in our problem we will choose a p that does not necessarily exactly satisfy the boundary condi-tion in Equacondi-tion 3.2. Thus Equacondi-tion 3.8 becomes the appropriate weighted residual state-ment for the Helmholtz equation, and can be rewritten as
JjRwdS = f Rewdf, (3.9)
s rB
where R is the residual of the homogeneous Helmholtz equation and RB is the residual of the natural boundary condition. Thus in Equation 3.9 the weighted residual errors are averaged to zero over the surface S and the boundary TB. Given these conditions, we wish to
charac-terize further the weighting function w using the method of Galerkin.
In the method of Galerkin, the weighting function belongs to the same set as the approximating function p. That is, we use a family of functions qk such that
N
P = Pk'k (3.10)
k =0
where the Pk's are coefficients to be determined. Therefore, the weighting function can be written as
N
W I k (3.11)
k =0
where the $k's are arbitrary non-zero coefficients. Since the same function gk's are used for p and w and the P's are arbitrary, it is common to write the w function as a variation of p, that is
N
8P= (81pk) ;k (3.12)
k = 0
These variations are often associated with virtual quantities which in this case is the virtual pressure. Using Equation 3.12 and integrating Equation 3.8 by parts we get a more useful form for FEM discretization
f[a pa; (p) - k2p5p] dS - f i(Sp) df = 0 (3.13) S or f a (5p) ap a (8p) ap 2 fJ ax) a + ay a"-k PSp - dS - f 1BSpdT = 0. (3.14) S rB
3.2.2 Discretization of the Object Space Into Finite Elements
Derivation of discrete finite element integral of weighted residual formulation
In the previous section, Equation 3.14 describes an approximate formulation of wave propa-gation in a continuous two-dimensional domain S enclosed by a closed contour 0F. The approximation stems from the use of the function p to approximate the exact solution p0 .
The main point here is that Equation 3.14 are still continuous equations.
In this finite element formulation the continuous domain is approximated by an assem-blage of triangles interconnected at three nodal points on the triangle's vertices. The field p "M within each triangle (m) is approximated as a function of the field P(M) at 3 nodal points defined by the vertices of a triangular finite element. Using appropriate linear interpo-lation functions, we have for element (m)
p (n) - (3.15)
where H is the interpolation vector and P(i) is defined as
P2
p fl") =
p
2 ~ (3.16)P3
38 CHAPTER 3: FORWARD MODEL OF WAVE PROPAGATION IN TWO pi P2 P = ** '(3.17) pn PN
where the p,,'s are the nodal field of the assemblage. Note that for P (i) the nodal field
num-bering is local to a particular triangular element while for P, the numnum-bering corresponds to the assemblage of triangular elements. There is a one to one relationship between these two numbering schemes and the compatibility is kept by the programmer.
Since the method of Galerkin is used, the field variation are defined in the same man-ner
8P ('" = H (8P) ("m)
SP(m) = [P, 8P2 8P]
(3.18) The derivatives of these quantities involve calculating the derivative of the vector H which we will define in the next section.
Using the field approximation of Equation 3.15 and Equation 3.18 within each trian-gular element, Equation 3.13 can be approximated as a sum of integrals over the areas of all the triangular elements:
mM rm 2 (in)Pn)8p07 m f fi [ (
L
(5p) i) i)- (k) ~(n 6' i)dS~n) M I "'V, (5p) "'drd' M = I ,("I) B (3.19)where terms such as (a)p) "I and (Di (Sp)) (") are still to be defined. In order to define
these terms more precisely and further simplify Equation 3.19 into a matrix equation, the lin-ear triangular finite element is developed is the next subsection.
Derivation of the linear isoparametric triangular element
The isoparametric formulation of finite element is based on the use of a local natural coordi-nate system (rs). Thus the interpolation of nodal coordinate and state variables (i.e. the com-plex acoustic field) is performed with the same interpolation functions. The generic triangular element is shown in Figure 3.3 with its respective local and global coordinate sys-tem. y S s=1 2 r r=O r=1,/
Figure 3.3: Isoparametric triangular element
With this configuration, the global coordinates of any point within the element is expressed as
x = (1 - r -s)x, + rx2+sx3
y = (1 -r-s)yl+ry2+sy3 (3.20)
or alternatively as
3 3
x =( ix =H.2(" ~~ h~X,=Hy' y = h~y = h HA y"(n
i= 1 i=1 (3.21)
-4
40 CHAPTER 3: FORWARD MODEL OF WAVE PROPAGATION IN TWO
hi = (1 -r-s)
h2 = r
h3 = S and
H = [h h2 h3] = (1- r-s) r s]
Similarly, any variable within each element can be written as
(m " h((nm) = H (, .
i = 1
(3.22)
(3.23)
(3.24)
The derivatives of the state variables with respect to x and y are calculated with the fol-lowing matrix equation
ax
(ya
r~a1
as(3.25)
where the Jacobian J is defined, using Equation 3.21, as
ax
ay]
ax ay as as - -j (-x1+x2) (-y+ (-xl+x3) (~Yl+Therefore, for a generic variable 4, we have
ax
a45
(M) =J-i Dar = _ -1 102 as 93L
_i
= B ", (3.27)where the superscript (m) indicate that the values are local to a particular element (m).
Finally, the matrix B is further defined as the combination of two matrices such that
Massachusetts Institute of Technology
Y2) Y3)_
(3.26)
FEM Formulation in the Internal Space 41
-g(' m ( )a (in) ( n) )
() B ( , and (FY) = Y (3.28)
Derivation of matrix formulation using triangular elements
With the triangular element isoparametric formulation of Equation 3.21, Equation 3.24 and Equation 3.28, Equation 3.19 can be rewritten as
(SP)T [JJS(M) (BJB +B B -H HkH) dS"'] P=
[
M (i)(8p)
X
f,m) (HBHB) TB (3.29).i= 1
Since (8P) are non-zero arbitrary variations, we can eliminate them, thus:
M
-() M T )
f f (B B -HTH kH) dSI"" P = (HBHB) (330)
m=1 S(J) . = J
This equation can be rewritten in matrix notation as
LP = MBPB. (3.31)
Finally, in order to differentiate between nodes on the boundary and nodes in the inte-rior surface, Equation 3.31 can be rewritten as
L1 LI P _0
0 0
[
[ LMB]] ^ (3.32)LBI LBB PB M B
where the subscripts I indicate elements involved with interior nodes and the subscripts B indicate elements involved with boundary nodes.
Matrices L and M are symmetric and sparse, with most elements concentrated along the diagonal. Furthermore, matrix L depends non-linearly on the wave numbers k which are the parameters that will be used to form images. There are as many parameters ki as there are internal nodes in the FEM mesh.
42 CHAPTER 3: FORWARD MODEL OF WAVE PROPAGATION IN TWO
hn \0
/n
Figure 3.4: External domain convention. The external space extends from to infinity represented by
3.3 BEM Formulation in the External Space
3.3.1 Integral Formulation of BEM
The appropriate form of the Helmholtz equation in the external space (see Figure 3.4) is:
V2p (r) + k p (r) = -8(r, -r) (3.33)
with the natural boundary condition defined as
ap (r)
= XV (r) (3.34)
on the closes contour FB of the internal space, and the Sommerfeld radiation condition
= ikop (3.35)
at infinity ..
Note here that ko is the constant wave number of the homogeneous external space and that the boundary F is composed of the closed curve FB enclosing the internal domain and a closed curve F. at infinity. An appropriate weighted residual statement (equivalent to Equation 3.8 in the FEM formulation) for the BEM is:
v2p (r) + k p (r) + (Ir - r)wdS = Saa
f
-VB) wdf + ( - ikop)wdTrB F.. (3.36)
In this equation, w is the weighting function which will be appropriately chosen. The terms in parentheses are three residuals. In the method of Galerkin, the same set of functions is chosen for the weighting function and for the function approximating the field. In the BEM, the aim is to eliminate the domain integrals in order to obtain only boundary integrals. For this, different functions are used for the weighting and for the approximating functions. To choose these functions, we must first obtain an inverse formulation. Replacing w by p* and integrating Equation 3.36 by parts once, we have
f
[k p+8(|r,-rI)]p*dS+ a, (p*a p) dS- (Dip* Dp)dS =S S S
f (V-VB)p df+f (F -ikop)p dF
FB . (3.37)
Invoking Green's identity on the second integral and rearranging terms, we get
[k p+5(1rs-r)] p*dS- (Dip* ip)dS =
S S
- jVp*dr - (ikopp*) dF
r B . (3.38)
Integrating by parts once more yields
fJ(aip* + kop ) dS - =
(p3 p dS
S S
- * (|r- - f ,p*dF - (ikopp*) dT
rB r. (3.39)
44 CHAPTER 3: FORWARD MODEL OF WAVE PROPAGATION IN TWO
(aiip* +k 2p ) dS =
S
-P
(r,-r)
+ f (pV-* -p )dF+ (* ikop*)4drr B .C (3.40)
Inspection of Equation 3.40 shows that if p' satisfies the governing Helmholtz equation, i.e.
( k2 p) = -5 (1- - i|) = -(341)
the left hand side surface integral can be eliminated. Note that p* is a function of two points: the source point r, at which we have the singularity of the delta function, and the observation point r which is the variable involved in the differential equation. A weighting function that satisfies Equation 3.41 is termed a fundamental solution. For the two-dimensional Helm-holtz equation
P* _H(2)
p = H (kor) (3.42)
and
=-H (kor) (3.43)
where r =
jI
- r;j is the distance from the source point to the point of observation. H 0(2)isthe Hankel function of the second kind of zero order, i.e.
Ho (kor) = JO (kor) - iY0 (kor) (3.44)
where J0 is a Bessel function of the first kind, and Yo is of the second kind. The Hankel function of order one is
H I (kr) = J I (kor) - iYI (kor) . (3.45)
Also, note that the fundamental solution satisfies the Sommerfeld radiation condition such that
an" -ikop }dfT -+0 for r-+oo. (3.46)
Therefore, for a point i, Equation 3.40 reduces to
point
Figure 3.5: Point on the boundary
p (i ) = -P' (| S-" |) +
[p(r) y(r -ril) -p * (1r - rg|) W '0]
B (3.47)
where ri is the position of the point under observation and r, is the position of the point source in the external space.
For the purpose of combining the FEM and BEM formulation, where the observation point i is on the boundary FB [5], special attention must be given to the contour integrals near point i. Using Figure 3.5 as reference, Equation 3.47 can be rewritten as
$g+ lim
E0
(r-BOf
E [PVd -P* fB]d+ f -pN* ]P d]rE
= pF ( l (3.48)
The limit for the first integral is:
lim
5
[p1I* ]f] = [* -P I ] dBS(rB
-rE) Bwhile the limit for the second integral can be written as:
(3.49)
(3.50) lim S0 r
fr
-)d] n = e 0 lim ah7T pi46 CHAPTER 3: FORWARD MODEL OF WAVE PROPAGATION IN TWO
lim
(
E-0 f (p* XVB) d]
(3.51)
To calculate the limits in Equation 3.50 and Equation 3.51, the following approximation of the fundamental function is used:
p* =
-[
7
+
(3.52)(3.53)
a*
Dr 2itr
where y is the Euler's constant (y = 0.577216...). The substitution of Equation 3.53 into Equation 3.50 yields: lim rE ap * an
]
a = im0 {- d9}= --0 (3.54)where a is the angle at point i as defined in Figure 3.5. Similarly, substituting Equation 3.52 into Equation 3.50 gives
a
=lim
{-E 0
1
2n(y+ log-i-)f
Therefore, the boundary integral formulation for a point i on the boundary can be writ-ten as:
c rp(|1;|) + p (I-|I) V* (Iiu -ri)dF = B
p* (Il- - _-g1) VB d+P ( I rip rs -r J)
r B (3.56)
(3.57)
Massachusetts Institute of Technology
a c= 1- n lim P dF E-+0 EdO] = 0. (3.55) log ( r)] - i - 4-
}
Sylvain LUvesque, Ph.D. = lim
' s . E PM d (VJ r E IIn Equation 3.56, the weighting function is chosen to be the fundamental solution of the Helmholtz equation but nothing is said about the approximating function p. In the next section, a boundary element analog to the triangular element is developed.
3.3.2 Discretization into Boundary Element
Isoparametric boundary element formulation
The isoparametric boundary element formulation is in principle very similar to the triangular element case. One must remember that the nodal points on the boundary are used both for the boundary elements and the finite elements. Therefore, we use the same node numbering
for the boundary element and for the finite elements.
Using Figure 3.6 as reference, any points (x, y) on the element can be interpolated as
1 1
x = (1+r)xl+ r)x2
1 1
y = I(1+ r)y+ (l-r)y2
2 2 (3.58)
or similarly for any variable 4
(i+ r) (1-r)] = HBa (3.59)
where the superscript (p) designates a particular boundary element. Also, in order to calcu-late the integrals in Equation 3.56, the differential boundary length expressed in the r natural coordinate system of the element is needed. Taking dI? as the differential length,
2 2(L/2
df = det J Bdr; when det J ( ) + ( (3.60)
With these definitions Equation 3.56 can now be discretized.
Discrete Integral BEM equation and matrix formulation
With the boundary element defined as in Figure 3.6 and Equation 3.59 and Equation 3.60; the continuous boundary integral (Equation 3.47) can be written in discrete form:
48 CHAPTER 3: FORWARD MODEL OF WAVE PROPAGATION IN TWO
y
2
> x
Figure 3.6: Isoparametric boundary element
P
~~f(P
dr=
ci;$ + P (I r-) V* (Ir - r ) det J dr
P 1r(P)
P (3.61)
P' (r -ry Il det J drp((P,)i|
p= lp(P)
B
where P is the number of boundary elements. Replacing XVB and p by their discrete ver-sions: P - - (P) c;$ + xV (I r- det J dr h h h])
-I
fLP2 P = (P) - B P ~ ~ (P(3.62)pr'-i -;) det J dr [h Ih2]() +p' (|, - ;i
p = pP) ( -2B
where hl, h2 correspond to the interpolation function of Equation 3.59, and the index i
indi-cates that a function is evaluated at ri on the boundary. In the BEM, rg is chosen to corre-spond to the nodal points on the boundary elements. Thus, after calculating the boundary integrals for each boundary element, Equation 3.62 can be written for each boundary node i:
P (p) -( P. (p)
cpj+ q (P]PI ([q2() = I[g (P) g(p]
KI
+ Si, (3.63)P= - B L= -
-where the numbering of the variables is local to the elements. If the summations are per-formed and global numbering of p and V is used, Equation 3.63 becomes
P1
cp + [q' i q'i2 --- Pg ='iN 1 i 2 -.. iN 2 + ; (3.64)
-I B B -NB B where
q'ij = q W + qf - and gj = gg1 +g
(365)
By including ci4, in the q's, Equation 3.64 becomes
NB NB q pj= Ig 1 + Si, (3.66) j=1 j where qij = q'j if i *j q = q' + c if i =
j.
(3.67) Finally Equation 3.66 can be written in its final matrix formQPB = G'B + PSB (3.68)
where Q and G are full matrices.
3.4 Combination of FEM and BEM Formulation
In Section 3.2 we developed an FEM formulation of the acoustic field inside a closed bound-ary. FEM allows us to model acoustic propagation through non-homogeneous material whose properties are mapped onto element nodes. This formulation led to Equation 3.32.