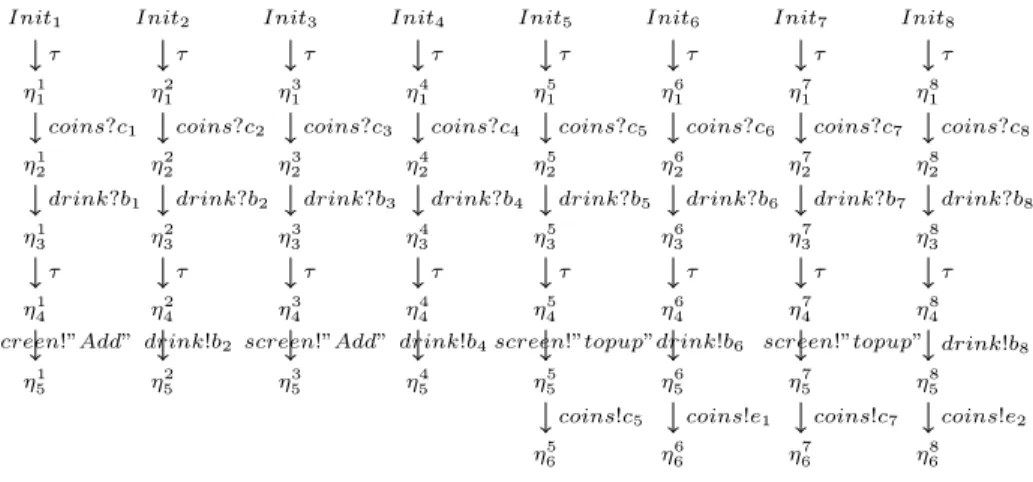HAL Id: hal-01191890
https://hal.archives-ouvertes.fr/hal-01191890
Submitted on 4 Sep 2015
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of
sci-entific research documents, whether they are
pub-lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diffusion de documents
scientifiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
Input Output Symbolic Transition Systems Enriched by
Program Calls and Contracts: a detailed example of
vending machine
Imen Boudhiba, Christophe Gaston, Pascale Le Gall, Virgile Prévosto
To cite this version:
Imen Boudhiba, Christophe Gaston, Pascale Le Gall, Virgile Prévosto. Input Output Symbolic
Tran-sition Systems Enriched by Program Calls and Contracts: a detailed example of vending machine.
[Research Report] Laboratoire MAS - CentraleSupelec. 2015. �hal-01191890�
Enriched by Program Calls and Contracts:
a detailed example of vending machine
Imen Boudhiba1, Christophe Gaston2 and
Pascale Le Gall1 and Virgile Prevosto2
1 Laboratoire MAS, CentraleSupelec, 92195 Chˆatenay-Malabry, France
email: {imen.boudhiba,pascale.legall}@centralesupelec.fr
2 CEA LIST, Point Courrier 174, 91191, Gif-sur-Yvette, France
email: {virgile.prevosto, christophe.gaston}@cea.fr
Abstract. An Input Output Symbolic Transition System (IOSTS) spec-ifies all expected sequences of input and output messages of a reactive system. Symbolic execution over this IOSTS then allows to generate a set of test cases that can exercise the various possible behaviors of the system it represents. In this paper, we extend the IOSTS framework with explicit program calls, possibly equipped with contracts specifying what the program is supposed to do. This approach bridges the gap between a model-based approach in which user-defined programs are abstracted away and a code-based approach in which small pieces of code are sep-arately considered regardless of the way they are combined. First, we extend symbolic execution techniques for IOSTS with programs, in or-der to re-use classical test case generation algorithms. Second, we explore how constraints coming from IOSTS symbolic execution can be used to infer contracts for programs used in the IOSTS.
Keywords: Input Output Symbolic Transition Systems, Program Con-tracts, Model-based Testing, Symbolic Execution, Feasibility.
1
Introduction
Symbolic transition systems, such as Input Output Symbolic Transition Systems (IOSTS) [10] are a classical reference modeling framework for model-based test-ing of reactive systems. They provide a convenient abstraction of the behaviors of such systems by modeling system state evolution using variable assignments. The symbolic execution tree of an IOSTS characterizes the different classes of numeric executions. Each path defines a sequence of symbolic inputs and out-puts, and a path condition which is a formula constraining the values exchanged (inputs or outputs) with the environment of the system. It is possible to use such paths as reference symbolic behaviors to be tested (i.e. as test purposes). In [10], we have proposed a framework to analyze IOSTS both to extract such test purposes and to solve the oracle problem thanks to a fully on-line algorithm. However, this kind of framework is limited by the symbolic treatment of func-tions. Indeed, IOSTS variables are assigned by terms built on funcfunc-tions. In order
to be able to reason on the symbolic values assigned to variables, the symbolic execution engine is equipped with constraint solving techniques able to analyze those functions. As long as one deals with basic arithmetic or boolean functions, it is generally tractable, but as soon as one deals with user-defined or ad-hoc functions, solving techniques may fail to scale, or even, due to undecidability results, such techniques may not exist. Analyzing such functions (later referred as ”programs”) may require both to deal with sophisticated data structures and to explore their (arbitrarily complex) control graph.
In this paper we propose an approach to overcome this limitation by abstract-ing program behaviors by means of contracts [17]. A contract for a program con-sists in a collection of couples, also called behaviours, formed of a pre-condition that specifies constraints that the caller must enforce at the call site, and a post-condition which is a property guaranteed at the program return. We enrich the basic IOSTS framework to deal with program calls equipped with contracts. We show how to extend symbolic execution mechanisms to reason about IOSTS equipped with program calls by analyzing those calls through their contracts. Thus, we avoid analyzing the actual behavior of the program and replace it by abstract constraints on its formal parameters. Our framework allows computing symbolic paths that can be used as test purposes. It may happen that guards and contracts are incompatible so that some symbolic paths are infeasible (i.e. they have no associated trace). In practice it means that there exists no pro-gram that can both satisfy its associated contracts and compute values allowing to follow the whole symbolic path. We show how to use symbolic techniques to check that a given set of symbolic paths is consistent with respect to program calls.
Moreover, since guards occurring on transitions of an IOSTS interact with contracts associated to programs, we present an approach to extract new con-tracts for each of the program exercised. Such concon-tracts reflect constraints on the program that make the path feasible. As such, they represent new contracts that can be used at the unitary level, to evaluate the correctness of actual program used to implement the system under test.
The remaining of the paper is organized as follows. In Section 2, we give ba-sic definitions about many-typed first order logic. Section 3 presents programs and their contracts. In Section 4, we introduce IOSTS with programs. Section 5 defines symbolic execution of an IOSTS with programs and the associated fea-sibility condition. Usage of symbolic execution for testing purposes, including contract inference for unitary testing is introduced in Section 6. In Section 7, we give a detailed example of a vending machine modelled by an IOSTS enriched by program calls: in particular, it includes a program in charge of computing the giving of change in function of coins inserted by the user and of the machine reserve.
2
Preliminaries
For two sets A and B, BAdenotes the set of mappings f : A → B from A to B
and idAis the identity mapping on A. For a mapping f : A → B, f [ai7→ bi]i∈1..n
is the mapping associating bi to ai for all i in 1..n and f (a) to a not belonging
to {ai | i ∈ 1..n}. By convention, [ai 7→ bi]i∈1..n stands for idA[ai 7→ bi]i∈1..n.
For two mappings f : A1 → B and g : A2 → B with A1∩ A2 = ∅, f ∪ g :
A1 ∪ A2 → B is the mapping defined by: ∀a ∈ A1, (f ∪ g)(a) = f (a) and
∀a ∈ A2, (f ∪ g)(a) = g(a). A∗(resp. A+) denotes the set of words on A provided
with the concatenation operator ’.’ and the empty word ε (resp. deprived of the empty word ε). For an ordered list l = (a1, . . . , an) of n elements of A, {{l}}
denotes the set {a1, . . . , an} of elements occurring in l.
We use classical multi-typed first order logic to handle data. A data signature is a pair (S, F ) where S is a set of so-called types and F is a set of functions provided with a profile s1...sn−1→ sn with each si∈ S. For V =`s∈SVsa set
of variables typed in S, the set TF(V ) = `s∈STF(V )s of so-called functional
terms over V is defined as usual over (S, F ). Moreover, each set Vscontains an
identified subset, denoted Vf ro
s , whose elements are called frozen variables and
we denote Vf ro = `
s∈SV f ro
s the subset of V of all frozen variables. The set
SenF(V ) of formulas is built over Boolean constants > and ⊥, equalities t = t0
for t and t0terms in TF(V ) of same type and usual Boolean connectives (∧, ∨, ¬,
. . . ). Substitutions over V are applications σ : V → TF(V ) that preserve types
and are such that all elements of Vf roare frozen for σ (i.e. ∀v ∈ Vf ro, σ(v) = v). Thus, as frozen variables cannot be substituted, they may be considered as new special constants. Substitutions can be canonically extended to TF(V ). For a
term t in TF(V ), for a formula ϕ in SenF(V ), Occ(t) and Occ(ϕ) will denote
the set of variables occurring in respectively t and ϕ. A F -model is a set of typed variables M =`
s∈SMs provided with a
func-tion f : Ms1 × · · · × Msn−1 → Msn for each f : s1· · · sn−1 → sn in F . An
interpretation is an application ν : MV that preserves types and can be canon-ically extended to TF(V ). The satisfaction of a formula ϕ in SenF(V ) by an
interpretation ν ∈ MV, denoted M |=
νϕ, is defined as usual by considering the
meaning of the equality predicate, Boolean constants and connectives. A formula ϕ in SenF(V ) is valid if and only if for all interpretations ν : V → M , M |=ν ϕ.
In the sequel, data signature (S, F ) and F -model M are supposed given.
3
Programs and contracts
Programs. User-defined functions, called programs, are identifiers provided with an interface specifying their formal parameters used to store input and output data. We only consider here programs with no side effect and one output variable.
Definition 1 (Program). Let X = `
s∈SXs be a set of typed variables. A
– a list InOut(p) = (x1, · · · , xn+1) ∈ Xn+1, called the interface of p, with
n ≥ 1 and ∀i 6= j, xi 6= xj. In(p) (resp. Out(p)) denotes the list (x1· · · xn)
(resp. (xn+1)) of input (resp. output) formal parameters of p.
– and a mapping Sem : M{{In(p)}}→ M{{InOut(p)}}, called the semantics of p,
verifying the so-called semantic condition: ∀ν ∈ M{{In(p)}}, ∀x
j ∈ {{In(p)}}, Sem(ν)(xj) = ν(xj).
Depending on the values associated to In(p) through the interpretation ν, Sem associates a value to the formal parameter xn+1in Out(p). The semantic
condition ensures that a program call has no effect on its input formal param-eters. By extrapolation, given a list l = (x1, · · · , xn+1), In(l) and Out(l) will
resp. denote (x1, · · · , xn) and (xn+1).
A signature Σ is a tuple (S, F, X, P ) where (S, F ) is a data signature and P is a set of programs defined over the set of typed variables X.
Let V =`
s∈SV be a set of typed variables. The set TΣ(V ) =
`
s∈STΣ(V )s
of typed terms over V contains: – all functional terms of TF(V )
– all elements p(t1, · · · , tn) with p ∈ P of interface (x1, · · · , xn+1), ∀1 ≤ i ≤
n, xi∈ Xsi, and ti∈ TF(V )si. If xn+1∈ Vs, p(t1, · · · , tn) ∈ TΣ(V )s.
Any interpretation ν : V → M can be canonically extended on TΣ(V ) as follows:
for any program p in P defined by its interface (x1· · · xn+1) and its semantics
Semp, let us consider µpν : {{In(p)}} → M an interpretation such that ∀1 ≤ i ≤
n, µpν(xi) = ν(ti), we have ν(p(t1, · · · , tn)) = Semp(µpν)(xn+1).
Contracts. Contracts specify what programs are expected to compute, as op-posed to how they compute their result. They have been introduced in the pio-neering work of Floyd [9] and Hoare [11], and form a key ingredient of the Eiffel programming language [17]. In short, a contract describes what a program re-quires from its caller (the pre-condition) and what it guarantees when it returns (the post-condition). We use here a slightly refined notion where a contract can be split in a set of behaviors [2, 4]. In this setting, pre-condition of a behavior indicates a possible case in which the program may be executed. As before, when a behavior is active, its post-condition must hold at the end of the execution.
Most of the times, pre and post conditions of a program are simply formulas in resp. SenF({{In(p)}}) and SenF({{InOut(p)}}). However, contracts can involve
other variables representing the global state of the system. The latter will be frozen variables whose associated values are conditioned by axioms and cannot be modified. These variables will be useful for inferring contracts from symbolic execution tree, as shown in Section 6.2.
Definition 2 (Program contract). Let l = (x1, . . . , xn+1) be a list of variables
with ∀i ≤ n + 1, xi∈ X. Let W be a subset of frozen variables verifying X ∩ W =
∅. A program contract for l and W is a set:
such that ∀ i ≤ k, P rei ∈ SenF({{In(l)}} ∪ W ) and P osti∈ SenF({{l}} ∪ W ).
A program contract is said to be:
– disjoint if for all i, j ≤ k with i 6= j, the formula ¬(P rei∧ P rej) is valid.
– complete if the formula W
i≤kP rei is valid.
Disjointness requires that at most one behavior of the contract is applicable for any considered input data, i.e. the pre-conditions are mutually exclusive. For simplicity purpose, we only consider disjoint contracts in this paper. Complete-ness indicates that for any input at least one behavior is applicable. In practice, programs are often partially defined over their input domain. We thus allow incomplete contracts, rejecting input data outside the scope of preconditions. Example 1. Let us consider a program P rice of interface (x1, x2) where x1 is
of type Drink, an enumerated type with two values {0, 1} and x2 is of type
Integer. x1is the input parameter indicating the selected beverage and x2is the
output parameter corresponding to its price. An example of contract for P rice is Cr= {(P re1, P ost1), (P re2, P ost2)} (both disjoint and complete), with:
– P re1: x1= 0, P ost1: x2≥ 100 ∧ x2≤ 200
– P re2: x1= 1, P ost2: x2≥ 200 ∧ x2≤ 300
Definition 3 (Contract satisfaction). Let l = (x1, · · · , xn+1) be an interface,
W a set of frozen variables provided with Ax ⊆ SenF(W ) and C a contract for
l and W . Let us consider an interpretation ν ∈ MW such that M |=
νAx and a
mapping Sem : M{{In(l)}}→ M{{l}} satisfying the semantic condition.
Sem satisfies C up to ν, denoted Sem |=νC, if and only if:
∀(P re, P ost) ∈ C, ∀µ ∈ M{{In(l)}}, M |=ν∪µP re ⇒ M |=ν∪Sem(µ)P ost
Semν(C) = {Sem : M{{In(l)}} → M{{l}} | Sem |=ν C} denotes the set of
semantics satisfying C up to ν.
For each interface l, we consider the trivial contract C∅,l = {}, simply denoted C∅, defined on l that does not restrict behaviors of programs, that is p ∈ Sem(C∅) for all programs p of interface l. Similarly, we consider the contract C>,l =
{(>, >)}, simply denoted C>, defined on l that requires that the program is
defined for every well-typed input data tuple.
Given a signature Σ = (S, F, X, P ), a set of frozen variables W with its set of axioms Ax ⊆ SenF(W ), and an interpretation ν ∈ MW verifying M |=ν
Ax, we consider families C = (Cp)p∈P of contracts indexed by P , in particular
C∅ = (C∅)p∈P and C> = (C>)p∈P. M odν(C) is the set of all families Sem =
(Semp)p∈P such that ∀p ∈ P, Semp|=ν Cp. Sem is then called a P -model.
4
IOSTS
Input Output Symbolic Transition Systems (IOSTS) represent behaviors of re-active systems as sequences of emissions or receptions of values through com-munication channels conditioned by guards expressed on some attribute values.
An IOSTS-signature Γ is a couple (A, Ch), where A =`
s∈SAsis a set of types
variables, called attribute variables, such that for all s in S, As∩ Xs = ∅ and
where Ch is a set of communication channel names.
An IOSTS communicates with its environment through communication ac-tions. The set of symbolic actions over Γ , denoted Act(Γ ), is I(Γ ) ∪ O(Γ ) ∪ {τ } where: I(Γ ) = {c?x|x ∈ A, c ∈ Ch} is the set of inputs, O(Γ ) = {c!t|t ∈ TΣ(A), c ∈ Ch} is the set of outputs and τ is an internal action.
Values of attribute variables can be modified in two ways: by receiving a value from the environment or by assigning a value from some internal process. Definition 4 (IOSTS). An IOST S (Q, q0, T r) over Σ and Γ = (A, Ch) is
a triple where Q is a set of states, q0 ∈ Q is the initial state and T r ⊆
Q × SenF(A) × Act(Γ ) × TΣ(A)A× Q is a set of transitions tr of the form
(q, ψ, act, ρ, q0) where:
– q and q0 are resp. the source (source(tr)) and target state (target(tr)) of tr, – ψ ∈ SenF(A) is a guard
– act ∈ Act(Γ ) is a communication action;
– ρ ∈ TΣ(A)A is a substitution associating a term to attribute variables;
Remark 1. We can always consider an IOSTS in which guards only contain con-junctions. If not, for a transition tr of guard ψ, it suffices to use a disjunctive normal formWn
i=1ψiequivalent to ψ and to split the transition into n transitions
having the same source, target and communication action as tr and ψi as guard.
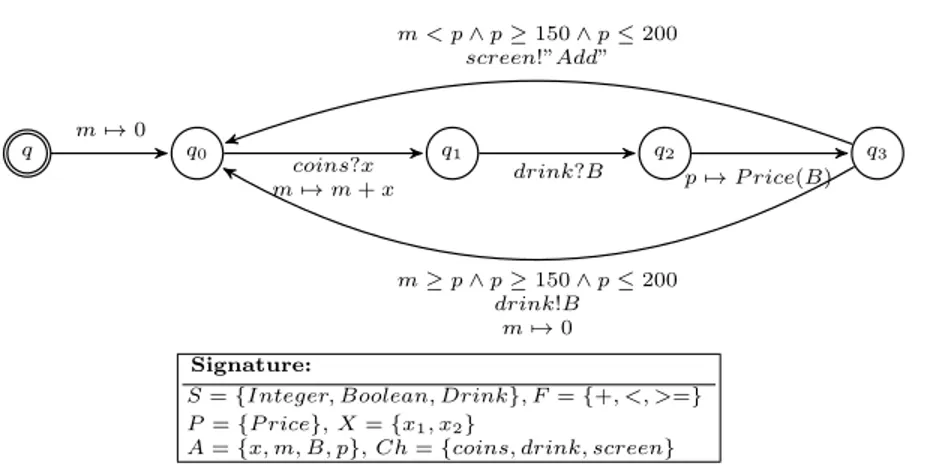
Example 2 (Drink vending machine). We consider a very simple drink vending machine. Its behavior is specified by the IOSTS in Fig. 4. An initialization step (q → q0) sets the amount to zero. Then, in q0, the machine waits for an amount
(x) of coins introduced by the user, and updates the amount m. The user then chooses his/her beverage (0 or 1 for ”Tea” or ”Coffee”). The choice is stored in variable B. In the transition q2→ q3, the program P rice computes the price of
the chosen drink. Two cases are possible here. If the introduced amount is lower than the price (m < p), then a message ”Add” appears on the screen and the machine returns to q0. Otherwise (m ≥ p), the drink is delivered, the amount
is reinitialized to zero and the machine goes back to q0. Note that transitions
outgoing from q3constrain the value (p) computed by P rice (p ≥ 150 ∧ p ≤ 200).
For a transition tr = (q, ψ, act, ρ, q0) ∈ T r and a P -model Sem, the semantics of tr, denoted as Run(tr, Sem) ⊆ MA× ActM(Γ ) × MA, is defined as the set of
triple (νi, actM, νf) verifying:
– if act is of the form c!t (resp. τ ), then M |=νi ψ, νf = νi◦ρ and actM = c!νi(t)
(resp. actM = τ )
– if act is of the form c?x, then M |=νi ψ, there exists νasuch that νa(z) = νi(z)
for every z 6= x, νf = νa◦ ρ and actM = c?νa(x),
Note that the definition of semantics of transitions is very classical and does not explicitly refers to Sem. In fact, semantics of programs are taken into account when defining νffrom the extensions of νior νato TΣ(A) as defined in Section 3.
q q0 q1 q2 q3 coins?x m 7→ m + x p 7→ P rice(B) m 7→ 0 drink?B m < p ∧ p ≥ 150 ∧ p ≤ 200 screen!”Add” m ≥ p ∧ p ≥ 150 ∧ p ≤ 200 drink!B m 7→ 0 Signature:
S = {Integer, Boolean, Drink}, F = {+, <, >=} P = {P rice}, X = {x1, x2}
A = {x, m, B, p}, Ch = {coins, drink, screen}
Fig. 1: IOSTS of the drink vending machine.
For a run r = (νi, actM, νf), we note source(r), act(r) and target(r) resp.
for νi, actM and νf. νi and νf are the interpretation of attribute variables resp.
before and after executing the transition. Let us observe that, given a transition tr and an interpretation νi, the set Run(tr, Sem) does not necessarily contain a
run of the form (νi, actM, νf) due to the fact that νimay not satisfy ψ.
The set of paths of an IOSTS G = (Q, q0, T r), denoted P ath(G), are all
finite sequences tr1. · · · .trn of transitions with source(tr1) = q0 and ∀i, 1 ≤ i <
n, target(tri) = source(tri+1). The set of runs of a path pa = tr1. · · · .trn in
P ath(G), denoted as Run(pa, Sem), are sequences r1. · · · .rn such that ∀i ≤ n,
ri ∈ Run(tri, Sem) and ∀i < n, target(ri) = source(ri+1). Similarly, the set of
traces T races(pa, Sem) of pa is the set of sequences act(r1). · · · .act(rn) for all
r1. · · · .rn∈ Run(pa, Sem), act(r) being equal to ε if act(r) = τ .
In general, it is not guaranteed that there exists at least a run for a given path pa, as it depends on the semantics associated to programs involved in pa. Definition 5 (Path feasibility condition). Let G = (Q, q0, T r) be an IOSTS
over Γ = (A, Ch) and pa a path of G. pa is a feasible path if and only if: ∃ Sem ∈ M od(C∅), T races(pa, Sem) 6= ∅
Let W be a set of frozen variables provided with Ax ⊆ SenF(W ) and ν ∈ MW
an interpretation satisfying M |=ν Ax. Let us consider C = (Cp)p∈P a family of
contracts indexed by P . pa is a feasible path up to (ν, C) if and only if: ∃Sem ∈ M odν(C), T races(pa, Sem) 6= ∅
5
Symbolic Execution and path feasibility condition
Symbolic execution consists in executing an IOSTS for symbolic values (taken from a dedicated set of frozen variables F r =`
ones, and computing constraints on those values for all possible IOSTS execu-tions. The main novelties with respect to [10] are twofold: substitutions occurring in transitions may include program calls and a renaming mechanism ensures that a given frozen variable can not appear in two distinct paths.
To store information concerning an execution, we use structures called sym-bolic states. A symsym-bolic state is a tuple of the form (q, π, λ, κ) where q ∈ Q, π ∈ SenF(F r), λ : A → TF(F r) is an application preserving types and κ ⊂
P × TF(F r)∗ × F r. For a symbolic state η = (q, π, λ, κ), q (or q(η)) denotes
the state reached after an execution leading to η, π (or π(η)) is a constraint on variables in F r called path condition that should be satisfied for the execution to reach η, λ (or λ(η)) denotes terms over variables in F r that are assigned to vari-ables of A and κ (or κ(η)) denotes the set of tuples of the form (p, (t1, · · · , tn), x)
indicating that a program call has been performed for the program p with the arguments (t1, · · · , tn) and that its result is stored in the variable x in F r.
In our approach we do not have the code of programs. Instead, we reason on their contracts. Since the input formal parameters associated to a call are represented symbolically by functional terms t1, · · · , tn, different pre-conditions
may hold depending on the way those terms will be interpreted. At the symbolic execution level, we thus consider a sub-case for each of those pre-conditions. More precisely, the symbolic execution of a transition tr from a given symbolic state η will consist in a set of symbolic transitions, one for each possible combination of pre-conditions for all program calls occurring in tr. We now introduce some notations aiming at tracing program calls: for a substitution ρ : A → TΣ(A) and
for p ∈ P , Res(p, ρ) is the set of variables y ∈ A such that ρ(y) is of the form p(t1, · · · , tn) and for such an y, Arg(y, ρ) is then (t1, · · · , tn) and P rog(y, ρ) = p.
We also denote Res(ρ) forS
p∈PRes(p, ρ).
Definition 6 (Symbolic execution of transitions). Let G = (Q, q0, T r) be
an IOSTS over Σ and Γ = (A, Ch), tr = (q, ψ, act, ρ, q0) ∈ T r be a transition and η = (q, π, λ, κ) be a symbolic state over G.
If act is of the form c?x, λi= λ[x 7→ f ], f fresh in F r. Otherwise, λi= λ.
λ0 is the substitution such that for all y ∈ Res(ρ), λ0(y) is a fresh variable of
F r and for all y ∈ A \ Res(ρ), λ0(y) = λ
i◦ ρ(y).
The symbolic execution SE(tr, η) of tr from η is the set defined as follows: – if Res(ρ) = ∅ then SE(tr, η) = {(η, λi(act), η0)} with η0= (q0, π∧λ(ψ), λ0, κ).
– if Res(ρ) 6= ∅, for any mapping Beh : Res(ρ) → S
p∈PCp such that for
y ∈ Res(p, ρ), Beh(y) = (P rey, P osty) ∈ Cp.
For y ∈ Res(p, ρ) with InOut(p) = (x1, · · · , xn, xn+1) and Arg(y, ρ) =
(t1, · · · , tn), we have (η, λi(act), η0) ∈ SE(tr, η) with
• η0 the symbolic state (q0, π ∧ λ(ψ) ∧V
y∈Res(ρ)∆(y), λ 0, κ0)
• ∆(y) = (P rey∧ P osty)[x17→ λi(t1) · · · xn7→ λi(tn), xn+17→ λ0(x)]
• κ0 the set κ ∪S
y∈Res(ρ){(P rog(y, ρ), (λi(t1), · · · , λi(tn)), λ0(y))}
Elements of SE(tr, η) are called symbolic transitions. We denote F r(η0) the set of all fresh variables of F r occurring in its definition.
Example 3. In order to illustrate Definition 6, let us consider a transition tr of the form (q, ψ, c?x, ρ, q0) with ρ = [y 7→ p1(t1, t2), z 7→ t01+ t02] with p1 a
program and t1, t2, t01, t02functional terms. Let us observe that Res(p1, ρ) = {y},
Arg(y, p1) = (t1, t2), P rog(y, ρ) = p1 and Res(ρ) = {y}.
Let η = (q, π, λ, κ) be a symbolic state. Let us suppose that the program p1is
provided with an interface (x1, x2, x3) and with a behavior (P re1, P ost1). Then
SE(tr, η) contains the symbolic transition (η, c?f1, η0) with f1 a fresh variable
of F r and η0 the symbolic state defined as: ( q0,
π ∧ λ(ψ) ∧ (P re1∧ P ost1)[x17→ λ[x 7→ f1](t1), x27→ λ[x 7→ f1](t2), x37→ f2]
[x 7→ f1, y 7→ f2, z 7→ λ[x 7→ f1](t01+ t02)],
κ ∪ {(p1, (λ[x 7→ f1](t1), λ[x 7→ f1](t2)), f2})
F r(η0) is then {f1, f2}.
Definition 7 (IOSTS symbolic execution). Given an IOSTS G, the sym-bolic execution SE(G) = (Init, ST ) of G is minimally defined by:
– Init = (q0, Ax, λ0) with ∀x ∈ A, λ0(x) ∈ F r and ∀x 6= y ∈ A, λ0(x) 6= λ0(y),
– for tr ∈ T r and η symbolic state with source(tr) = q(η), SE(tr, η) ⊆ ST . – for any distinct SE(tr1, η1) SE(tr2, η2) that are defined, F r(SE(tr1, η1)) ∩
F r(SE(tr2, η2)) = ∅.
Definition 8 (Paths and distinguished paths). The set P aths(SE(G)) of paths of SE(G) is the set of all sequences tr1· · · trnwith ∀i ∈ 1..n, tri∈ ST such
that source(tr1) = Init and for any j < n, q(target(trj)) = q(source(trj+1)).
For a non-empty sequence δ = tr1· · · trn, we note End(δ) = target(trn) and
F r(δ) = ∪i∈1..nF r(target(tri)). By convention, End(ε) = Init and F r(ε) = ∅.
Given a finite subset ∆ of P aths(SE(G)), DP aths(∆) is a set of paths δ∗ such that there exists an unique path δ in ∆ such that δ and δ∗ are isomorphic up to a renaming of variables of F r and such that for two distinct paths δ1∗ and δ∗2 in DP aths(∆), F r(δ∗1) ∩ F r(δ∗2) = ∅.
We say that DP aths(∆) is a set of distinguished paths issued from SE(G). Generally speaking, a set ∆ of P aths(SE(G)) represents a tree whose tran-sitions issued from the root Init can be shared by several paths of ∆ while DP aths(∆) consists in applying a variable renaming mechanism in order to du-plicate shared transitions to completely separate paths. Distinguished paths can still share common variables, namely those in W .
Example 4. The drink vending machine of Fig. 4 has two possible paths from q to q0with exactly one cycle on q0. They share a transition with a call to program
P rice defined by its contract Cr as seen in Ex. 1. We thus get 4 distinguished
paths shown in Fig. 5. Associated path conditions are the following:
pc1: B1= 0 ∧ p1≥ 100 ∧ p1≤ 200 ∧ v1< p1∧ p1≥ 150 ∧ p1≤ 200
pc2: B2= 0 ∧ p2≥ 100 ∧ p2≤ 200 ∧ v2≥ p2∧ p2≥ 150 ∧ p2≤ 200
pc3: B3= 1 ∧ p3≥ 200 ∧ p3≤ 300 ∧ v3< p3∧ p3≥ 150 ∧ p3≤ 200
Init1 η1 1 η1 2 η31 η41 η1 5 screen!”Add” τ drink?B1 coins?v1 τ Init2 η2 1 η2 2 η23 η24 η2 5 drink!B2 τ drink?B2 coins?v2 τ Init3 η3 1 η3 2 η33 η43 η3 5 screen!”Add” τ drink?B3 coins?v3 τ Init4 η4 1 η4 2 η43 η44 η4 5 drink!B4 τ drink?B4 coins?v4 τ
Fig. 2: Symbolic paths.
A path condition is a formula over the frozen variables built by accumulating constraints from the guards of the IOSTS transitions and from constraints of called programs contracts. The path is infeasible if its path condition is not satisfiable. In addition, this feasibility depends on the fact that if a program is called twice with the same arguments, it returns the same value (semantic condition of Definition 1). Since this is not enforced by the path condition alone, we consider another set of constraints accounting for this condition:
Definition 9 (Feasibility of a set of paths). Let G be an IOSTS over Γ = (A, Ch) and let ∆∗ be a set of distinguished paths issued from SE(G).
For any program p of interface (x1, · · · , xn, xn+1), for (p, (t1, · · · , tn), f ) and
(p, (t01, · · · , t0n), f0) two distinct elements of ∪δ∗∈∆∗κ(End(δ∗)) we introduce the
deterministic program condition relating to these two program calls as the for-mula φ{f,f0} defined byVni=1ti= t0i⇒ f = f0.
The deterministic program condition related to ∆∗ is then Φp =V φ{f,f0},
for all f and f0 appearing as return variable of a call of p in ∆∗.
Finally, the feasibility condition of ∆∗ is
^
δ∗∈∆∗
π(End(δ∗)) ∧ ^
p∈P
Φp
If this feasibility condition holds, it is possible to implement the programs occurring in the IOSTS so that all paths of ∆∗ will complete successfully. Note that the contracts of the programs are taken into account in the path condition, and have thus an impact on the paths that are feasible or not.
Example 5. In the context of the drink vending machine, we now want to check the feasibility condition of the distinguished paths associated to the paths de-scribed in Ex. 4 according to two distinct contracts for P rice, denoted resp. Cw
and Cr (in Example 1). Both Cw and Cr include two behaviors resulting in 4
distinguished paths. Path conditions are given in Tab. 2.
– With the contract Cw, no distinguished path is feasible because of
contradic-tions between guards of the IOSTS transicontradic-tions and post-condicontradic-tions of Cw.
– With the contract Cr, all distinguished paths are feasible. P rice can return
anything between 150 and 200 for an argument equal to 0 and must return 200 for an argument equal to 1.
Cw: {(x1= 0, x2≥ 0 ∧ x2≤ 100), (x1= 1, x2≥ 250)} pc1: B1 = 0 ∧ p1≥ 0 ∧ p1≤ 100 ∧ v1< p1∧ p1≥ 150 ∧ p1≤ 200 pc2: B2 = 0 ∧ p2≥ 0 ∧ p2≤ 100 ∧ v2≥ p2∧ p2≥ 150 ∧ p2≤ 200 pc3: B3= 1 ∧ p3 ≥ 250 ∧ v3< p3∧ p3≥ 150 ∧ p3≤ 200 pc4: B4= 1 ∧ p4 ≥ 250 ∧ v4≥ p4∧ p4≥ 150 ∧ p4≤ 200 φ{p1,p2}: B1= B2⇒ p1= p2 φ{p1,p3}: B1= B3⇒ p1= p3 φ{p1,p4}: B1= B4⇒ p1= p4 φ{p2,p3}: B2= B3⇒ p2= p3 φ{p2,p4}: B2= B4⇒ p2= p4 φ{p3,p4}: B3= B4⇒ p3= p4 Feasibility: No Cr : {(x1 = 0, x2 ≥ 100 ∧ x2 ≤ 200), (x1= 1, x2≥ 200 ∧ x2≤ 300)} pc1: B1 = 0∧p1≥ 100∧p1≤ 200∧v1< p1∧ p1≥ 150 ∧ p1 ≤ 200 pc2: B2 = 0∧p2≥ 100∧p2≤ 200∧v2≥ p2∧ p2≥ 150 ∧ p2 ≤ 200 pc3: B3 = 1∧p3≥ 200∧p3≤ 300∧v3< p3∧ p3≥ 150 ∧ p3 ≤ 200 pc4: B4 = 1∧p4≥ 200∧p4≤ 300∧v4≥ p4∧ p4≥ 150 ∧ p4 ≤ 200 φ{p1,p2}: B1= B2 ⇒ p1= p2 φ{p1,p3}: B1= B3 ⇒ p1= p3 φ{p1,p4}: B1= B4 ⇒ p1= p4 φ{p2,p3}: B2= B3 ⇒ p2= p3 φ{p2,p4}: B2= B4 ⇒ p2= p4 φ{p3,p4}: B3= B4 ⇒ p3= p4 Feasibility: Yes
Table 1: Feasibility according to different contracts
6
Testing
6.1 Model-based testing of IOSTS with program calls and contracts
In a previous work [10], we have proposed an online testing algorithm to test Systems Under Test (SU T ) with respect to a basic IOSTS (without program calls). The algorithm is based on the ioco conformance relation [20] and on the use of test purposes (T P ) to select some behaviors to be tested. A T P is a finite sub-tree of the symbolic execution structure (SES) derived from the IOSTS of reference so that any execution trace constructed by interacting with SU T and leading to a leaf of T P will be considered as covering T P . The testing process is implemented as a simultaneous traversal of both SES and T P . Verdicts depend on whether the observed execution trace does or does not belong to T P and SES: W eakP ASS when the execution trace covers T P and belongs to at least one path of SES which does not end at a leaf of T P , P ASS when the execution trace covers T P and does not belong to another path of SES, IN CON C (for inconclusive) when the execution trace belongs to SES but does not cover T P , F AIL when the execution trace does not cover T P and goes outside SES.
In Section 5, we have associated to any IOSTS with contracts a symbolic tree structure in order to be able to use it both as the SES input of the algorithm given in [10] and as a carrier to extract a finite sub-tree to play the role of T P . We can use the work described in [10] with the following slight modifications:
– Unlike [10], we allow unobservable τ transitions. Under the assumption that there does not exist a cycle of τ transitions, we can replace any sequence of consecutive τ transitions by a transition carrying the input/output action just located at the end of the τ sequence. Furthermore, in [10], quiescence
conditions are expressed by enriching the reference IOSTS with transitions carrying the special label δ denoting the intended absence of reaction. Be-cause the presence of τ transitions makes such a direct enrichment tricky, it becomes more appropriate to perform this enrichment at the level of the τ -reduced symbolic execution itself. Once the operations of τ -reduction and δ-enrichment are applied to the symbolic execution of the IOSTS with con-tracts, we can then apply the algorithm of [10] for free.
– In [10], path conditions for paths that are part of test purposes are satisfi-able by construction. In our setting, we have to take into account the notion of feasibility, i.e, the existence or not of programs that meet their associ-ated contracts and that are compatible with considered paths. Indeed, if the considered set of distinguished paths constituting the test purpose is unfea-sible, then the application of algorithm is meaningless. In other words, the feasibility of the targeted set of paths plays the role of a testing hypothesis.
6.2 Contracts Inference
As we have seen in Section 5, the feasibility condition checks whether a given program contract preserves the feasibility of a symbolic path or not. In this section, we focus on the inference of contracts based on path conditions. Such contracts can then be used to define unit tests for the programs. More precisely, we start with an IOSTS G calling programs without associated contract. We then show that we can infer contracts such that feasible paths of G are guaranteed to verify the feasibility condition of the IOSTS augmented with contracts. The generated contract for a program p contains one behavior per call to p in SE(G). For that, we use the parts of the final condition of the path on which the call occurs that are related to the return variable and to the arguments.
Given a formula F , we define inductively the set RelF(X) of variables related
to a set X of variables, as the smallest set satisfying the following conditions – X ⊂ RelF(X)
– Occ(t1= t2) ∩ Relt1=t2(X) 6= ∅ ⇒ Occ(t1= t2) ⊂ Relt1=t2(X)
– RelF1(X) ∪ RelF2(X) = RelF1∧F2(X) = RelF1∨F2(X)
– RelF(X) = Rel¬F(X)
Similarly, for a formula F and a set of variables X, CleanX(F ) is defined as
follows. As noted in remark 1, we can assume that the path condition only has conjunctions, and is in negation-normal form.
– CleanX(>) = > – CleanX(⊥) = ⊥ – CleanX(t1= t2) = t1= t2 if Occ(t1= t2) ∩ X 6= ∅ – CleanX(t1= t2) = > if Occ(t1= t2) ∩ X = ∅ – CleanX(¬t1= t2) = ¬t1= t2 if Occ(t1= t2) ∩ X 6= ∅ – CleanX(¬t1= t2) = > if Occ(t1= t2) ∩ X = ∅
Remark 2. If F is satisfiable, then CleanX(F ) is also satisfiable, as we only
remove atomic propositions from the conjunction.
Definition 10 (Contract inference). Let G be an IOSTS , ∆∗ a set of dis-tinguished paths from SE(G). We note κ(∆∗) = ∪δ∗∈∆∗κ(End(δ∗)).
For any f such that (p, (t1, · · · , tn), f ) ∈ κ(∆∗), with In(p) = (x1, ..., xn)
and Out(p) = xn+1, we define a behavior (P ref, P ostf) for p, as well as a set
of frozen variables Gf and axioms Axf.
We pose φ = π(End(δ∗)) the final condition for the path containing the call and Y = Occ(t1, · · · , tn) ∪ {f } the variables occurring in the call. Then
– Gf is Relφ(Y ) – Axf is CleanRelφ(Y )(φ) – P ref isV n i=1xi= ti – P ostf is xn+1= f
Finally, the inferred contracts for ∆∗ are defined as follows. – G is S
(p,(t1,··· ,tn),f )∈κ(∆∗)Gf
– Ax is V
(p,(t1,··· ,tn),f )∈κ(∆∗)Axf
– ∀p ∈ P, Cp= ((P ref, P ostf))(p,(t1,··· ,tn),f )∈κ(∆∗)
Example 6. Let us consider here a symbolic path δ∗ of our drink vending ma-chine’s specification (Figure 6) that calls twice the program P rice of interface (x1, x2). The first call leads to the appearance of a message ”Add” on the screen
and the second call permits the drink delivery, such that:
π(End(δ∗)) : v1< p1∧ p1≥ 150 ∧ p1≤ 200 ∧ (v1+ v2) ≥ p2∧ p2≥ 150 ∧ p2≤ 200 coins ? v1 τ dr ink ? B1 τ scr een !” Add ” coins ? v2 dr ink ? B2 τ dr ink !B 2 Init η1 η2 η3 η4 η5 η6 η7 η8 η9
Fig. 3: Symbolic path.
From the path condition φ = π(End(δ∗)), two behaviors will be generated according to Def. 10. For p1 the result of the first call (P rice, (B1), p1) we have:
Y : {B1, p1}
Gp1 : {B1, p1, v1, p2, v2}
Axp1 : v1< p1∧ p1≥ 150 ∧ p1≤ 200 ∧ (v1+ v2) ≥ p2∧ p2≥ 150 ∧ p2≤ 200
P rep1 : x1= B1
For p2 the result of the second call (P rice, (B2), p2) we have: Y : {B2, p2} Gp2 : {B2, p2, v1, p1, v2} Axp2 : v1< p1∧ p1≥ 150 ∧ p1≤ 200 ∧ (v1+ v2) ≥ p2∧ p2≥ 150 ∧ p2≤ 200 P rep2 : x1= B2 P ostp2 : x2= p2
Finally, the inferred contract for our program P rice in δ∗ is: – G = Gp1∪ Gp2
– Ax = Axp1∧ Axp2
– C = ((P rep1, P ostp1), (P rep2, P ostp2))
We can now define the IOSTS G0 with the same signature and transitions than G and equipped with the inferred contracts for the programs in P . Then, for every path δ∗ in ∆∗ that is feasible, there exist paths δ∗ in G0 similar to δ∗
except that the path conditions π are augmented with axioms and behaviors. For each (p, (t1, ..., tn), f ) ∈ κ(End(δ∗)), Axf is satisfiable by remark 2 and the
behavior (P ref, P ostf) becomes trivially true: one of the behaviors of p makes
the corresponding transition feasible. Since this is true for any call in δ∗, there exists thus a path in δ∗ that is feasible. This leads to the following theorem. Theorem 1 (Feasibility preservation). Let G be an IOSTS, ∆∗ a set of feasible distinguished symbolic paths of G. G0 is the IOSTS obtained by adding to G the inferred contracts of Definition 10. For any path δ∗in ∆∗, there exists a symbolic path δ∗0 for G0 having the same transitions as δ∗ and which is feasible.
7
A detailed example of a vending machine with a
program call for giving the change
In this section, we consider a more realistic drink vending machine example in order to introduce a rather complex user-defined program. The program call will help us to calculate the giving of change according to the coins inserted by the user and to the machine reserve.
The machine allows the user to order a coffee or a tea and returns money. The machine accepts only three different types of coins:e0.20, e0.50 and e1.
A counter (variable m) is used for calculating the total amount inserted by the user in the machine. According to the drink chosen by the user, as for Example 2, the price of the selected drink is given by the program P rice of interface (x1, x2)
where x1is of type Drink, an enumerated type with two values {0, 1} and x2 is
of type Integer. x1 is the input parameter indicating the selected beverage and
x2 is the output parameter corresponding to its price. An example of contract
for P rice is Cr = {(P re1, P ost1), (P re2, P ost2)} (two behaviors both disjoint
and complete), with:
– P re2: x1= 1, P ost2: x2≥ 200 ∧ x2≤ 300
When the desired amount is inserted, the selected beverage will be delivered to the user. If the inserted amount is more than the beverage’s cost and if the reserve contains enough change, the drink will be delivered to the user and the extra change will be returned to him. If the reserve does not contain enough change, the inserted coins will be returned to the user and he/she will be asked to top up the amount. The inserted money is specified as an array C (has three cases C[0], C[1] and C[2]) that contains respectively the number ofe0.20, e0.50 ande1 coins. More precisely, we consider four such arrays, C for storing the cu-mulated amount inserted by the user, X for storing the current inserted amount (that the user is likefy to top up if the amount is not sufficient for covering the beverage price), E for storing the giving of change and R for storing the machine reserve.
If the cumulated inserted amount 20∗C[0]+50∗C[1]+100∗C[2] is greater than the cost and the reserve has enough change, then a program Return calculates the extra change to be returned to the user as an array (E). The program Return of interface (x01, x02, x03, x04) where
– x01 represents the beverage price (positive integer),
– x02 represents the amount (positive integer) , – x0
3represents the reserve (as an array storing separately the number ofe0.20,
e0.50 and e1 coins),
– and x04 is the program output variable (an array that contains the number of different coins to be returned to the user)
We associate with the Return program a contract: (P re, P ost) such that: – Pre: x01> 0 ∧ x02≥ x01
– Post: (((x04[0] ∗ 20 + x04[1] ∗ 50 + x04[2] ∗ 100) = x02− x0
1) ∧ x04[0] ≤ x03[0] ∧ x04[1] ≤
x03[1] ∧ x04[2] ≤ x03[2]).
The contract specifies that under the conditions that the beverage price (x01) is strictly positive and that the cumulated inserted amount (x02) is greater that the beverage price (x01), then the amount (x04[0] ∗ 20 + x04[1] ∗ 50 + x04[2] ∗ 100) represented by the output variable (x04) is equal to the difference (x02−x0
1) and the
array variable (x04) is less than or equal to the reserve, component by component. Let us notice than the considered contract cannot be achieved in any situa-tion: in particular, if the difference is equal to 20 and if x03[0] is equal to 0, there is no way to give back an array x04 making the postcondition true.
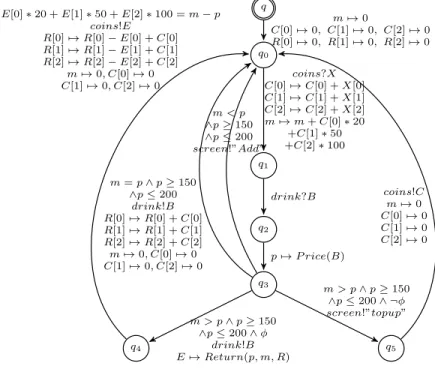
The machine’s behavior is specified by the IOSTS in Figure 4. An initializa-tion step (q → q0) sets C cases and the amount m to zero. Then, in state q0, the
machine waits for coins (X) introduced by the user, updates C and the amount m. The user then chooses his/her beverage (0 or 1 for ”Tea” or ”Coffee”). The choice is stored in the variable B. In the transition q2→ q3, the program P rice of
interface (x1, x2) computes the price of the chosen drink. Four cases are possible
q q0 q1 q2 q3 q4 q5
E[0] ∗ 20 + E[1] ∗ 50 + E[2] ∗ 100 = m − p coins!E R[0] 7→ R[0] − E[0] + C[0] R[1] 7→ R[1] − E[1] + C[1] R[2] 7→ R[2] − E[2] + C[2] m 7→ 0, C[0] 7→ 0 C[1] 7→ 0, C[2] 7→ 0 coins!C m 7→ 0 C[0] 7→ 0 C[1] 7→ 0 C[2] 7→ 0 coins?X C[0] 7→ C[0] + X[0] C[1] 7→ C[1] + X[1] C[2] 7→ C[2] + X[2] m 7→ m + C[0] ∗ 20 +C[1] ∗ 50 +C[2] ∗ 100 m > p ∧ p ≥ 150 ∧p ≤ 200 ∧ ¬φ screen!”topup” m > p ∧ p ≥ 150 ∧p ≤ 200 ∧ φ drink!B E 7→ Return(p, m, R) m = p ∧ p ≥ 150 ∧p ≤ 200 drink!B R[0] 7→ R[0] + C[0] R[1] 7→ R[1] + C[1] R[2] 7→ R[2] + C[2] m 7→ 0, C[0] 7→ 0 C[1] 7→ 0, C[2] 7→ 0 m < p ∧p ≥ 150 ∧p ≤ 200 screen!”Add” Such that φ is ∃n1, n2, n3, 0 ≤ n1≤ R[0] ∧ 0 ≤ n2≤ R[1]∧ 0 ≤ n3≤ R[2] ∧ m − p = n1∗ 20 + n2∗ 50 + n3∗ 100 m 7→ 0 C[0] 7→ 0, C[1] 7→ 0, C[2] 7→ 0 R[0] 7→ 0, R[1] 7→ 0, R[2] 7→ 0 drink?B p 7→ P rice(B) Signature:
S = {Integer, Boolean, Drink, Array}, F = {+, −, <, >, =} P = {P rice, Return}, X = {x1, x2, x01, x 0 2, x 0 3, x 0 4} A = {X, C, R, E, m, B, p}, Ch = {coins, drink, screen}
Fig. 4: IOSTS of the drink vending machine.
– If the introduced amount is lower than the price (m < p), then a message ”Add” appears on the screen and the machine returns to q0;
– if the user has introduced exactly an amount equal to the price (m = p), the drink is delivered, the reserve is updated, the amount and C cases are reinitialized to zero and the machine goes back to q0;
– if the user has introduced an amount strictly greater than the beverage price and if the reserve has enough change (m > p ∧ φ), then the program Return calculates the extra change to be returned to the user and the machine goes to the state q4in order to return extra coins, set up the reserve and initialize
m and C. The formula φ defined as:
∃n1, n2, n3, 0 ≤ n1≤ R[0] ∧ 0 ≤ n2≤ R[1] ∧ 0 ≤ n3≤ R[2]∧
m − p = n1∗ 20 + n2∗ 50 + n3∗ 100
specifies that with the current reserve (R), there is at least a possibility of giving the expected change (m − p).
– otherwise (the user has introduced an amount strictly greater than the bev-erage price and the reserve does not permit to return back the extra to the user (m > p ∧ ¬φ)), the user is asked to refill the machine (if possible, with the exact amount) and from the state q5, the introduced coins are returned
to the user.
Note that to be triggered, guards on transitions outgoing from q3 to q4 and
q5 contain the φ formula that checks the reserve’s availability. The φ formula
expresses that there is at least a combination of coins among the coin reserve that permits to give back to the user a correct change. Note also that the φ formula is stronger than the postcondition P ost previously associated to the program Return: in particular, φ makes explicit that giving change is possible, without explaining how it is calculated.
7.1 Symbolic execution: distinguished paths
The drink vending machine of Figure 4 has 4 possible paths from the state q to state q0 with exactly one cycle on q0, with a common transition (q0 → q1)
including a call to the program P rice defined by its contract Cr that has two
behaviors (coffee or tea). The symbolic execution of the IOST S gives rise to a set of 8 distinguished paths. They are shown in Figure 5, taken into account the renaming mechanism ensuring that fresh variables occurring in two distinct paths are distinct.
screen!”Add” drink!b2 screen!”Add” drink!b4screen!”topup”drink!b6 screen!”topup” Init1 η11 η12 η1 3 η1 4 η1 5 τ drink?b1 coins?c1 τ Init2 η12 η22 η2 3 η2 4 η2 5 τ drink?b2 coins?c2 τ Init3 η13 η23 η3 3 η3 4 η3 5 τ drink?b3 coins?c3 τ Init4 η41 η42 η4 3 η4 4 η4 5 τ drink?b4 coins?c4 τ Init5 η51 η52 η5 3 η5 4 η5 5 η5 6 coins!c5 τ drink?b5 coins?c5 τ Init6 η16 η26 η6 3 η6 4 η6 5 η6 6 coins!e1 τ drink?b6 coins?c6 τ Init7 η17 η27 η7 3 η7 4 η7 5 η7 6 coins!c7 τ drink?b7 coins?c7 τ Init8 η81 η82 η8 3 η8 4 η8 5 η8 6 coins!e2 drink!b8 τ drink?b8 coins?c8 τ
The associated path conditions are the following: pc1: b1= 0 ∧ p1≥ 100 ∧ p1≤ 200 ∧ m1< p1∧ p1≥ 150 ∧ p1≤ 200 pc2: b2= 0 ∧ p2≥ 100 ∧ p2≤ 200 ∧ m2= p2∧ p2≥ 150 ∧ p2≤ 200 pc3: b3= 1 ∧ p3≥ 200 ∧ p3≤ 300 ∧ m3< p3∧ p3≥ 150 ∧ p3≤ 200 pc4: b4= 1 ∧ p4≥ 200 ∧ p4≤ 300 ∧ m4= p4∧ p4≥ 150 ∧ p4≤ 200 pc5: b5= 0 ∧ p5≥ 100 ∧ p5≤ 200 ∧ m5> p5∧ ¬(∃n1, n2, n3/ 0 ≤ n1≤ r5[0] ∧0 ≤ n2≤ r5[1] ∧ 0 ≤ n3 ≤ r5[2] ∧ m5− p5= n1∗ 20 + n2∗ 50 + n3∗ 100) ∧p5≥ 150 ∧ p5≤ 200 pc6: b6= 0 ∧ p6≥ 100 ∧ p6≤ 200 ∧ m6> p6∧ ∃n1, n2, n3/ 0 ≤ n1≤ r6[0] ∧0 ≤ n2≤ r6[1] ∧ 0 ≤ n3 ≤ r6[2] ∧ m6− p6= n1∗ 20 + n2∗ 50 + n3∗ 100 ∧p6> 0 ∧ m6> p6∧ ((e1[0] ∗ 20 + e1[1] ∗ 50 + e1[2] ∗ 100) = m6− p6) ∧e1[0] ≥ r6[0] ∧ e1[1] ≥ r6[1] ∧ e1[2] ≥ r6[2] ∧ p6≥ 150 ∧ p6≤ 200 pc7: b7= 1 ∧ p7≥ 200 ∧ p7≤ 300 ∧ m7> p7∧ ¬(∃n1, n2, n3/ 0 ≤ n1≤ r7[0] ∧0 ≤ n2≤ r7[1] ∧ 0 ≤ n3 ≤ r7[2] ∧ m7− p7= n1∗ 20 + n2∗ 50 + n3∗ 100) ∧p7≥ 150 ∧ p7≤ 200 pc8: b8= 1 ∧ p8≥ 200 ∧ p8≤ 300 ∧ m8> p8∧ ∃n1, n2, n3/ 0 ≤ n1≤ r8[0] ∧0 ≤ n2≤ r8[1] ∧ 0 ≤ n3 ≤ r8[2] ∧ m8− p8= n1∗ 20 + n2∗ 50 + n3∗ 100 ∧p8> 0 ∧ m8> p8∧ ((e2[0] ∗ 20 + e2[1] ∗ 50 + e2[2] ∗ 100) = m8− p8) ∧e2[0] ≥ r8[0] ∧ e2[1] ≥ r8[1] ∧ e2[2] ≥ r8[2] ∧ p8≥ 150 ∧ p8≤ 200
The four path conditions (from pc1to pc4) are associated with paths when the inserted
amount is lower than the price and when the introduced amount equal to the price (for different choices of drink: coffee or tea). pc5and pc7are associated with symbolic paths
issued from the numeric path where the reserve is not enough to return change. pc6
and pc8 are resulted from the symbolic execution of the path that contain the program
Return
7.2 Feasibility
In the context of the drink vending machine, we now want to check the feasibility con-dition of a set of distinguished paths ∆∗having {pc1, pc2, pc3, pc4} as path conditions,
the first four paths described in Figure 5, according to two distinct contracts for P rice, denoted respectively Cw and Cr and already discussed in Example 5 . Both Cw and
Cr include two behaviors resulting in 4 distinguished paths. Path conditions and the
feasibility decision are given in Tab. 2.
– With the contract Cw, no distinguished path of ∆∗ is feasible because of
contra-dictions between guards of the IOSTS transitions and post-conditions of Cw.
– With the contract Cr, all distinguished paths are feasible. P rice can return
any-thing between 150 and 200 for an argument equal to 0 and must return 200 for an argument equal to 1.
7.3 Contract Inference
Let us consider here a symbolic path δ∗ of our drink vending machine’s specification (Figure 6) that calls twice the program P rice of interface (x1, x2) and the program
Return of interface (x01, x 0 2, x 0 3, x 0
4) without associating contracts with programs. The
first call of P rice leads to the appearance of a message ”Add” on the screen and the second call permits the drink delivery and the return of the extra, such that:
Cw: {(x1= 0, x2≥ 0 ∧ x2≤ 100), (x1= 1, x2≥ 250)} pc1: b1= 0 ∧ p1≥ 0 ∧ p1≤ 100 ∧ m1< p1∧ p1≥ 150 ∧ p1≤ 200 pc2: b2= 0 ∧ p2≥ 0 ∧ p2≤ 100 ∧ m2= p2∧ p2≥ 150 ∧ p2≤ 200 pc3: b3= 1 ∧ p3≥ 250 ∧ m3< p3∧ p3≥ 150 ∧ p3≤ 200 pc4: b4= 1 ∧ p4≥ 250 ∧ m4= p4∧ p4≥ 150 ∧ p4≤ 200 φ{p1,p2}: b1= b2⇒ p1= p2 φ{p1,p3}: b1= b3⇒ p1= p3 φ{p1,p4}: b1= b4⇒ p1= p4 φ{p2,p3}: b2= b3⇒ p2= p3 φ{p2,p4}: b2= b4⇒ p2= p4 φ{p3,p4}: b3= b4⇒ p3= p4 Feasibility: No Cr : {(x1 = 0, x2 ≥ 100 ∧ x2 ≤ 200), (x1= 1, x2≥ 200 ∧ x2≤ 300)} pc1: b1= 0∧p1≥ 100∧p1≤ 200∧m1< p1∧ p1≥ 150 ∧ p1 ≤ 200 pc2: b2= 0∧p2≥ 100∧p2≤ 200∧m2= p2∧ p2≥ 150 ∧ p2 ≤ 200 pc3: b3= 1∧p3≥ 200∧p3≤ 300∧m3< p3∧ p3≥ 150 ∧ p3 ≤ 200 pc4: b4= 1∧p4≥ 200∧p4≤ 300∧m4= p4∧ p4≥ 150 ∧ p4 ≤ 200 φ{p1,p3}: b1= b3⇒ p1= p3 φ{p1,p4}: b1= b4⇒ p1= p4 φ{p2,p3}: b2= b3⇒ p2= p3 φ{p2,p4}: b2= b4⇒ p2= p4 φ{p3,p4}: b3= b4⇒ p3= p4 Feasibility: Yes
Table 2: Feasibility according to different contracts
π(End(δ∗)) : m1 < p1∧ p1 ≥ 150 ∧ p1 ≤ 200 ∧ (m1+ m2) > p2∧ p2 ≥ 150 ∧ p2 ≤ 200 ∧ ∃n1, n2, n3/ 0 ≤ n1≤ r[0] ∧ 0 ≤ n2 ≤ r[1] ∧ 0 ≤ n3≤ r[2] ∧ (m1+ m2) − p2 = n1∗ 20 + n2∗ 50 + n3∗ 100 ∧ ((e1[0] ∗ 20 + e1[1] ∗ 50 + e1[2] ∗ 100) = (m1+ m2) − p2) coins ? c1 τ dr ink ? b1 τ scr een !” Add ” coins ? c2 dr ink ? b2 τ dr ink !b2 coins !e1 Init η1 η2 η3 η4 η5 η6 η7 η8 η9 η10
Fig. 6: Symbolic path.
From the path condition φ = π(End(δ∗)), we will generate a contract for the Return program and P rice program according to3 Definition 10. For e1 the result of
3
In fact, Definition 10, and in particular the function Clean, should be adapted to take into account the case of quantifier in formulas.
the program call (Return, (p2, m1+ m2, r), e1) we have: Y : {p2, m1+ m2, r, e1} Ge1 : {e1, m1, m2, p2, r, p1} Axe1 : m1< p1∧ p1≥ 150 ∧ p1≤ 200 ∧ (m1+ m2) > p2∧ p2≥ 150 ∧ p2≤ 200 ∧∃n1, n2, n3, 0 ≤ n1 ≤ r[0] ∧ 0 ≤ n2≤ r[1] ∧ 0 ≤ n3≤ r[2] ∧(m1+ m2) − p2= n1∗ 20 + n2∗ 50 + n3∗ 100 ∧ ((e1[0] ∗ 20 + e1[1] ∗ 50 +e1[2] ∗ 100) = (m1+ m2) − p2) P ree1 : x 0 1= p2∧ x02= m1+ m2∧ x03= r P oste1 : x 0 4= e1
The inferred contract for our program Return in δ∗is C = (P ree1, P oste1).
In the same way, from φ = π(End(δ∗)), two behaviors (a behavior par call) will be generated for the P rice program according to our inference Definition. For p1 the
result of the first call (P rice, (b1), p1) we have:
Y : {b1, p1} Gp1 : {b1, p1, m1, p2, m2, r, e1} Axp1 : m1< p1∧ p1≥ 150 ∧ p1≤ 200 ∧ (m1+ m2) > p2∧ p2≥ 150 ∧ p2≤ 200 ∧∃n1, n2, n3, 0 ≤ n1≤ r[0] ∧ 0 ≤ n2≤ r[1] ∧ 0 ≤ n3≤ r[2] ∧(m1+ m2) − p2= n1∗ 20 + n2∗ 50 + n3∗ 100 ∧ ((e1[0] ∗ 20 + e1[1] ∗ 50 +e1[2] ∗ 100) = (m1+ m2) − p2) P rep1 : x1= b1 P ostp1 : x2= p1
For p2 the result of the second call (P rice, (b2), p2) we have:
Y : {b2, p2} Gp2 : {b2, p2, m1, p1, m2, r, e1} Axp2 : m1< p1∧ p1≥ 150 ∧ p1≤ 200 ∧ (m1+ m2) > p2∧ p2≥ 150 ∧ p2≤ 200 ∧∃n1, n2, n3, 0 ≤ n1≤ r[0] ∧ 0 ≤ n2≤ r[1] ∧ 0 ≤ n3≤ r[2] ∧(m1+ m2) − p2= n1∗ 20 + n2∗ 50 + n3∗ 100 ∧ ((e1[0] ∗ 20 + e1[1] ∗ 50 +e1[2] ∗ 100) = (m1+ m2) − p2) P rep2 : x1= b2 P ostp2 : x2= p2
Finally, the inferred contract for our program P rice in δ∗is: – G = Gp1∪ Gp2
– Ax = Axp1∧ Axp2
– C = ((P rep1, P ostp1), (P rep2, P ostp2))
8
Related Work
In the context of reactive systems verification, IOSTS and symbolic execution have been used in many works [1,10,13] for different purposes. They use IOSTS with atomic actions and substitutions whereas, in our case, we enrich IOSTS with programs specified by contracts. Our purpose is to define an integration framework and analyze in one hand the impact of programs contracts on a whole system and in the other hand elicit accurate contracts for our programs.
Our work is quite close to [12], that augments a SOA’s BPEL business model with pre- and post-condition contracts defining essential component traits, and derive a suite of feasible test cases, taking into account contracts that are provided for some of the opaque components of their system. On the other hand, they do not infer contracts from the constraints expressed directly in the BPEL model as is done in section 6.2.
The use of symbolic execution and path feasibility analysis are studied in [3,21] but this is limited to the analysis of programs themselves and does not take in consideration as we do the impact of the program calls on the feasibility of the system as a whole. Similarly, symbolic execution techniques over the code have been used to infer program annotations. More specifically, such approaches concentrate on generating invariants. This is for instance the case in the KeY verification framework [19], for the DySy tool [6], or for the iDiscovery tool [23]. Those invariants are meant to help the formal verification of the code against its specification, while we are aiming at generating a specification that the programs must meet in order to be usable in the context of the system under test.
The problem of inferring contracts for programs has been studied differently in other works that do not rely on symbolic execution. In particular, [5] derives pre-conditions from assertions already present in the code using abstract interpretation. [22] uses dy-namic analysis to augment simple programmer-written contracts with candidate post-conditions that describes precisely what the code is doing, building upon techniques developed initially in the Daikon tool [8] for proposing likely invariants. This kind of inference is dual to ours, in the sense that we infer contracts in a top-down approach, in order to express what conditions individual components should fulfill inside a broader system, while the works mentioned above are bottom-up, encapsulating the behavior of actual code in contracts in order to check whether callers can use this particular implementation. The same can be said of works that aim at generating transition sys-tems modeling the behavior of programs, either as message sequence charts as in [15], or as scenarios expressed under the form of live sequence charts, as in [16].
9
Conclusion
In this work, we extended the IOSTS framework with programs which are specified with contracts and we adapted symbolic execution techniques to deal with them. This gives rise to two main results. First, we study how contracts impact path conditions and describe the feasibility condition of the entire symbolic execution tree. Second, we show that path conditions can be used to infer contracts for programs in order to specify what these programs should do in the context of the system under test. Such contracts can then be used for unitary testing purposes, while feasibility preservation theorem gives some guarantees that program calls will not get in the way during integration testing. Implementation of the technique presented in this paper is currently under development in the Diversity [7] symbolic execution tool and the Frama-C [14] C code analysis framework using the ACSL specification language [2] as target for contract inference.
Future work include in particular integrating programs and contracts into vari-ous IOSTS extensions. From an implementation point of view, UML Sequence Dia-grams [18], a widely used formalism for describing transition systems, would be a good input language from a practical point of view. Sequence diagrams are already sup-ported by Diversity, but program calls and contracts need to be added to the UML
subset supported by Diversity. On a more theoretical level, we have so far examined pro-gram and contracts in one single component. IOSTS are nevertheless meant to model whole systems consisting in various components interacting with each other through communication actions. Path conditions can then be projected on the internal state of a single component to define constraints on this component. It would be interesting to examine how to compose such projections with contract inference.
References
1. B. Bannour. Symbolic analysis of scenario based timed models for component-based systems: Compositionality results for testing. PhD thesis, Ecole Centrale Paris, CEA, 2012.
2. P. Baudin, J.-C. Filliˆatre, T. Hubert, C. March´e, B. Monate, Y. Moy, and V. Pre-vosto. ACSL: ANSI/ISO C Specification Language, v1.9, March 2015.
3. N. Bjørner, N. Tillmann, and A. Voronkov. Path feasibility analysis for string-manipulating programs. In 15th Int. Conf., TACAS, volume 5505 of Lecture Notes in Computer Science. Springer, 2009.
4. P. Chalin, J. R. Kiniry, G. T. Leavens, and E. Poll. Beyond assertions: Advanced specification and verification with JML and esc/java2. In 4th Int. Symposium, FMCO, volume 4111 of Lecture Notes in Computer Science. Springer, 2006. 5. P. Cousot, R. Cousot, and F. Logozzo. Precondition Inference from Intermittent
Assertions and Application to Contracts on Collections. In Proc. VMCAI, 2011. 6. C. Csallner, N. Tillmann, and Y. Smaragdakis. Dysy: Dynamic symbolic execution
for invariant inference. In Proceedings of ICSE, 2008.
7. J. Deltour, A. Faivre, E. Gaudin, and A. Lapitre. Model-based testing: An approach with SDL/RTDS and DIVERSITY. In 8th Int. Conference, SAM 2014, volume 8769 of Lecture Notes in Computer Science. Springer, 2014.
8. M. D. Ernst, J. Cockrell, W. G. Griswold, and D. Notkin. Dynamically discovering likely program invariants to support program evolution. Trans. Soft. Eng., 27, 2001. 9. R. W. Floyd. Assigning meanings to programs. Proc. AMS Symp. on Applied
Mathematics, 19, 1967.
10. C. Gaston, P. Le Gall, N. Rapin, and A. Touil. Symbolic execution techniques for test purpose definition. In Testing of Communicating Systems, Int. Conference, TestCom, volume 3964 of Lecture Notes in Computer Science. Springer, 2006. 11. C. A. R. Hoare. An axiomatic basis for computer programming. Communications
of the ACM, 12(10), 1969.
12. S. Jehan, I. Pill, and F. Wotawa. Functional SOA Testing Based on Constraints. In Automation of Software Test, 2013.
13. J. C. King. Symbolic Execution and Program Testing. Comm. ACM, 17, 1976. 14. F. Kirchner, N. Kosmatov, V. Prevosto, J. Signoles, and B. Yakobowski. Frama-C,
A Software Analysis Perspective. Formal Aspects of Computing, 27, 2015. 15. S. Kumar, S.-C. Khoo, A. Roychoudhury, and D. Lo. Inferring class level
specifi-cations for distributed systems. In Proc. ICSE, 2012.
16. D. Lo and S. Maoz. Scenario-based and value-based specification mining: better together. Autom. Softw. Eng., 19, 2012.
17. B. Meyer. Applying ”design by contract”. IEEE Computer, 25(10), 1992. 18. Object Management Group. OMG Unified Modeling LanguageTM (OMG UML),
version 2.5 edition, 2013.
19. P. H. Schmitt and B. Weiß. Inferring invariants by symbolic execution. In VERIFY Workshop, volume 259 of CEUR Workshop Proceedings, 2007.
20. J. Tretmans. Conformance Testing with Labelled Transition Systems: Implemen-tation Relations and Test Generation. Computer Networks and ISDN Systems, 1996.
21. Y. Wang, Y. Xing, and X. Zhang. A Method of Path Feasibility Judgment Based on Symbolic Execution and Range Analysis. International Journal of Future Gen-eration Communication and Networking, 2014.
22. Y. Wei, C. A. Furia, N. Kazmin, and B. Meyer. Inferring better contracts. In Proc. ICSE, 2011.
23. L. Zhang, G. Yang, N. Rungta, S. Person, and S. Khurshid. Invariant discovery guided by symbolic execution. In The Java PathFinder Workshop, 2013.