Etude de l'influence de nombre de Richardson sur la convection mixte dans une cavité carrée

RESUME

Dans ce travail, nous avons étudié numériquement la convection mixte dans une cavité carrée ayant des parois latérales mobiles. Celle de droite chaude et se déplace vers le bas. Celle de gauche froide se déplace vers le haut, Les autres parois sont supposées adiabatiques.

Les équations régissant ce phénomène ont été discrétisés par la méthode des volumes finies. L’approche numérique est basée sur l’algorithme simple et résolut par un code commercial FLUENT. Les champs dynamiques et thermiques ainsi que le coefficient de transfert thermique (nombre de Nusselt) ont été déterminés pour différents nombres de Richardson.

Les résultats obtenus montrent l’existence d’écoulements complètement différents en fonction de la valeur du nombre de Richardson et du sens de déplacement des parois latérales. De plus, l’augmentation du nombre de Richardson signifie une augmentation d’apport de chaleur dans la cavité. Cettedernière a pour effet d’intensifier le mouvement du fluide et donc l’augmentation du nombre de Nusselt moyen.

Mots clés : Convection mixte, cavité carrée, Méthode des volumes finis.

REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE MINISTÈRE DE L'ENSEIGNEMENT SUPÉRIEUR ET

DE LA RECHERCHE SCIENTIFIQUE

DEPARTEMENT DE GENIE MECANIQUE

N° d’ordre : …/Master/2016. Série :…………/GM/2016

MEMOIRE

Présenté pour l’obtention du diplôme de Master en Génie Mécanique Ayant pour Thème :

OPTION :

Mécanique Energétique

Réalisé par : Encadré par : Mr. Messai.T • KERNOU Lamine

• BELLATRACHE Fayçal

Soutenu le : 29 /06 /2016

Devant le jury composé de :

Président : Mr. LEKHAL .R MAA Examinateurs : Mr. MOUSSAOUI.M MAA Mme. BAGHDADI .F MAB Rapporteur : Mr. MESSAI .T MAA

Année universitaire : 2015-2016

Etude de l’influence de nombre de Richardson sur la convection

mixte dans une cavité carrée

Nous tenons à remercier tout d’abord le bon Dieu qui nous a

donné la volonté de réaliser ce travail.

Toutes nos infinies gratitudes à notre promoteur, Monsieur

Messai.Tpour son encadrement et ses aides précieuses.

Nous remercions aussi les membres de jury qui nous ont fait

l’honneur d’accepter le jugement de notre travail.

Enfin, nous remerciens tous ceux qui nous a aidé de près ou de

loin, que ce soit par leur amitié, leurs conseils ou leurs soutien

moral, trouveront dans ces quelque lignes l’expression de notre

remerciements les plus vifs.

Lamine - Fayçal

Dédicace

Je dédie ce modeste travail a :

 Mes très chères parents qui m’ont aidés et m’encouragés

durant toutes mes études.

 Mon cher frère Reda et mes chères sœurs Yasmine et

Chahra.

 tous mes amis (es) avec lesquels (les) j’ai partagés mes

meilleurs moments.

Je dédie ce modeste travail a :

 Mes très chères parents qui m’ont aidés et m’encouragés

durant toutes mes études.

 Mes chers frères, et Leurs enfants «SALSABILE, ADAM ».

 toute la famille BLLETR ACHE ainsi que tous mes proches.

 tous mes amis (es) avec lesquels (les) j’ai partagés mes

meilleurs moments.

RESUME

Dans ce travail, nous avons étudié numériquement la convection mixte dans une cavité carrée ayant des parois latérales mobiles. Celle de droite chaude et se déplace vers le bas. Celle de gauche froide se déplace vers le haut, Les autres parois sont supposées adiabatiques.

Les équations régissant ce phénomène ont été discrétisés par la méthode des volumes finies. L’approche numérique est basée sur l’algorithme simple et résolut par un code commercial FLUENT. Les champs dynamiques et thermiques ainsi que le coefficient de transfert thermique (nombre de Nusselt) ont été déterminés pour différents nombres de Richardson.

Les résultats obtenus montrent l’existence d’écoulements complètement différents en fonction de la valeur du nombre de Richardson et du sens de déplacement des parois latérales. De plus, l’augmentation du nombre de Richardson signifie une augmentation d’apport de chaleur dans la cavité. Cettedernière a pour effet d’intensifier le mouvement du fluide et donc l’augmentation du nombre de Nusselt moyen.

ABSTRACT

In this work, we study numerically the mixed convection in a square cavity with mobile lateral walls (right: Move to the bottom and hot, and the left wall is cold), the other walls are supposed adiabatics. Thegoverning equations ofthe phenomena have been discretize by the finite volume method. The numerical approach is based on the simple algorithm and resolve by a commercial code FLUENT. Dynamic fields and thermal as well as the coefficient of thermal

transfer (the Nusselt number)were represented for different numbers of Richardson. The results obtained show the existence of flows completely different function of the value of the Richardson number and the direction of moving of the side walls. In addition, the increase in the number of Richardson means an increase of heat input in the cavity. The latter has the effect of intensifying of the movement of the fluid movement and thus is increase in the number of average Nusselt.

م

صخل

ا ايييييي دب ب ييييييردب ييييييلردب ايييييي د ا ماييييييقر اييييييلب لم اييييييال اداييييييردب ايييييياحلا اييييييف ييييييللدب ييييييخبد اييييي ب يييييل ب هيييييرس يييييا( خايييييل يييييل( ب اييييياماس اا يييييقم اايييييم را( ااييييي رساي اب ليييييي ايييييرد هيييييجف يييييق(لاب ب يييييييييييييييييي ب اييييييييييييييييي م اب ييييييييييييييييير ايييييييييييييييييف يييييييييييييييييحا ب يييييييييييييييييدب لءييييييييييييييييي ( د ايييييييييييييييييرف ء يييييييييييييييييد ه . ج اس م دبلاإم اال الم ا راالدبماجرلاب ا ( ط الءالب مت ا دام اصاخدب تلاداءلدب تلت الب لدب . هج دب خبد ب ردب ع(زهت حا ه ردب اااك زلدها( دلا ت رثام 011 دلءد ا حاخ م لا .اهلد اشا( دهييييييييهلدب بهيييييييرحد اييييييي ك اا(لدب ب اييييييي( ب ردب اييييييي خدب اب ييييييييله( اييييييير حا ييييييي رالدب ج اييييييياادب ييييييي حرت .اهييييييييييييييييييييلد اشا( دلييييييييييييييييييييا اييييييييييييييييييييل م يييييييييييييييييييي رم كييييييييييييييييييييشم س ييييييييييييييييييييات هييييييييييييييييييييج دب ييييييييييييييييييييخبد :ةيحاتفملا تاملكلا ب ردب لردب – ب ا ( ط ماجرلا ا راالدب FLUENT

Nomenclature

Liste des figures

Liste des Tableau

CHAPITRE I : ETUDE BIBLIOGRAPHIQUE

I.1Contenu du mémoire...………….………...1

I.2 Introduction générale…...………..……….2

I.3 Etude bibliographique………….………....3

CHAPITRE II : MODELE MATHEMATIQUE

II.1 Présentation du problème………...………8

II.2 Équations générales………...………..………..8

II.3 Hypothèses simplificatrices………..……… .9

II.4 Approximation de Boussinesq………9

II.5 Formulation du problème………..………10

II.5.1 Equations de gouvernante .…………..………...……….10

II.5.2 Conditions aux limites………..……..………...11

II.6.1 Principales grandeurs physiques et variables adimensionnelles...…….12

II.6.2 Equations adimensionnelles………...13

CHAPITRE III : MODELISATION NUMERIQUE

III.1 Introduction……….14

III.2 Principe de la méthode des volumes finis……….………..14

III.3 Maillage……….………..16

III.4 La discrétisation….………..17

III.4.1 Intégration du flux total….………...20

III.4.2 Intégration de terme source….……….21

III.4.3 Discrétisation spatiale………..……….22

III.4.3.1 Schéma aux différences centrées (CDS)………..………..22

III.4.3.2 Schéma Upwind (UPS)……….……….24

III.4.3.3 Schema Hybrid (HDS : hybrid-differencing scheme)..………..25

III.5 Formulation générale du problème……….……….27

III.6 Procédure de Résolution……….……….28

III.6.1 Equation algébrique de pression……...………….………..29

III.6.2 Algorithme SIMPLE…………...……….………31

III.6.3 Résolution des systèmes d’équations linéaires….………..…….32

IV.2 Propriétés physique………….………...36

IV.3 Choix de maillage………….………..37

IV.4 validation du code de calcul.………...38

IV.5 résultats et discussions…….………..41

IV.5 .1 Le Champ thermique………41

IV.5.2 Le Champ dynamique………...………45

IV.5.3 Le Profil de vitesse………48

IV.5.4 Nusselt local………..49

IV.5.5 Nusselt moyen………..50

CONCLUSION GENERALE………..…….51

Nomenclature

A Surface de la partie chauffée [m²]

Cp Chaleur spécifique à pression constante [J/k𝑔.k]

g Accélération de la gravité, [m/s²]

Gr Nombre de Grashof [ - ]

i,j Coordonnées indicielle des nœuds [ - ]

k Conductivité thermique [W/m. K]

L Longueur de la cavité [m]

Nu Nombre de Nusselt local [ - ]

P Pression [𝑃a]

Pr Nombre de Prandt [ - ]

Ri Nombre de Richardson [ - ]

Ra Nombre de Reynolds [ - ]

T Température [K]

u,v Composantes des vitesses [m/s]

Vp Vitesse des parois latérale [m/s]

V,U Composantes adimensionnelles des vitesses [ - ]

x,y Coordonnées d’espace dimensionnelles [m] X,Y Coordonnées d’espace adimensionnelles [ - ] Indice Supérieur * : valeur estimée ’ : Valeur corrigée Indice Inferieur h : surface chaude c : surface froide

α Diffusivité thermique [m²/s]

β Coefficient d’expansion thermique à pression constante [1/ K] 𝜃 Température adimensionnelle [ - ] ∅ Variable dépendante générale [ - ] 𝜈 Viscosité cinématique [m²/s]

μ Viscosité dynamique [kg /m².s] 𝜌 Masse volumique [kg/ m3]

φ «Fonction de dissipation» puissance locale des forces de viscosité [w/ m3] 𝜌 Masse volumique à T [kg/ m3] 𝜓 Fonction de courant adimensionnelle [ - ]

ω Vorticité adimensionnelle

Liste des figures

Figure. II.1 : Schématisation du problème physique et conditions aux limites………8

Figure III.1 : Volume de contrôle bidimensionnel………...15

Figure III.2 : Schéma du maillage………...16

Figure III.3 : Maillage de la cavité………..17

Figure III.4 : Volume de contrôle………....19

Figure III.5 : Domaine de calcul……….32

Figure III.6 : L’algorithme SIMPLE………...35

Figeur.IV.1 : Influence du nombre de nœuds sur la valeur du nombre de Nusselt moyen….37 Figure.IV.2 : Maillage 100x100 utilisé pour la simulation……….38

Figeur.IV. 3 : Comparaison entre les vecteurs de vitesse……….39

Figeur.IV. 4 : Contours de Stream Fonction………39

Figeur.IV. 5 : Calcul les données expérimentales pour vitesse suivant (x) et (y)………..…...

40

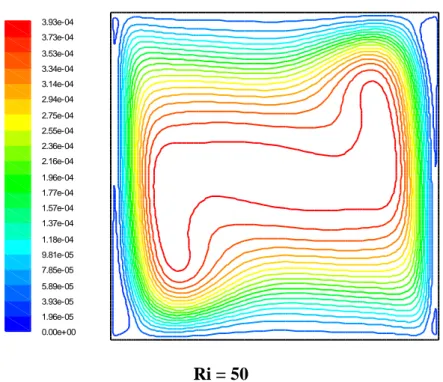
Figure IV.6 : les lignes des isothermes pour différentes valeurs de nombre de Richardson...44

Figure IV.7 : les lignes de courant pour différentes valeurs de nombre de Richardson……..48

Figure IV.8 : Evolution de Profils de vitesse à X=0.005 (m)………..49

Figure IV.9 : Evolution de nombre de Nusselt local..……….50

Figure IV.10 : nombre de Nusselt moyen en fonction de nombre de Richardson………...…50

Tableau III.1 : Les termes de l’équation de transport……….18

Tableau III.2 : La fonction A(|pee|) pour différents schémas………..28

Tableau IV.1 : Influence de la taille du maillage sur le Nusselt moyen………..37

Tableau B-1 : Propriétés d’air à la pression atmosphérique………...56

Tableau C-1 : code (CFD)………...59

Tableau C-2 : Récapitulatif des équations régissantes l’écoulement………..61

Tableau C-3 : les différentes formes de maillage des faces [24]…...………..……63

CHAPITRE

I

Page 1

I.1 Contenu du mémoire

Le travail présenté dans ce mémoire est constitué de quatre chapitres :

Le premier chapitre, présente une introduction générale sur la convection mixte, ainsi que les objectifs ont réalisé. On a cité quelques travaux numériques concernant la convection dans une cavité.

Le deuxième chapitre constitué modèle physique choisi, à savoir les équations gouvernantes ainsi que les conditions aux limites associées à ce modèle.

Le troisième chapitre est consacré à la présentation de la méthode des volumes finies et sa mise en œuvre pour la discrétisation des équations du problème.

On a rassemblé, dans le quatrième chapitre, le choix du maillage, la validation de notre programme de calcul et les principaux résultats numériques de cette étude. Les commentaires, l’interprétation et l’analyse des divers résultats de cette étude paramétrique sont également présentés.

Enfin nous avons terminé ce travail par une conclusion générale qui résume les principaux résultats obtenus.

CHAPITRE I ETUDE BIBLIOGRAPHIQUE

Page 2

I.2 Introduction générale

Le transfert de chaleur est un processus d’une grande importance dans le domaine de l’industrie et des technologies. Bien qu’il se manifeste sous diverses formes (rayonnement, conduction et convection), cette dernière est la plus visée dans certains domaines bien spécifiés tels que le refroidissement des processeurs et des composantes électroniques, les radiateurs et les échangeurs de chaleurs, etc.

La convection est un mode de transport d'énergie par l'action combinée de la conduction, et de l'accumulation de l'énergie et du mouvement du milieu. La convection est le mécanisme le plus important du transfert d'énergie entre une surface solide et un liquide ou un gaz. Le transfert d'énergie par convection d'une surface dont la température est supérieure à celle du fluide qui l'entoure s'effectue en plusieurs étapes.

D'abord la chaleur s'écoule par conduction de la surface aux particules fluides adjacentes, L'énergie ainsi transmise sert à augmenter la température et l'énergie interne de ces particules. Ensuite ces dernières vont se mélanger avec d'autres particules situées dans une région à basse température et transférer une partie de leur énergie, celle-ci est à présent emmagasinée dans les particules fluides et elle est transportée sous l'effet de leur mouvement.

La transmission de chaleur par convection est désignée, selon le mode d'écoulement du fluide, par convection libre et convection forcée. Lorsqu'il se produit au sein du fluide des courants dus aux différences de densité résultant des gradients de température, on dit que la convection est naturelle ou libre. Par contre si le mouvement du fluide est provoqué par une action externe, telle que une pompe ou un ventilateur, le processus est appelé convection forcée. Si les deux causes existent, sans que l'une soit négligeable par rapport à l'autre, la convection est dite mixte.

Page 3

I.3 Etude bibliographique

Cette partie est consacrée à la revue des principales investigations effectuées par le Passé sur la convection mixte dans les cavités.

Oztop et Dagtekin [1] et Basak [2] qui ont étudié le transfert thermique en mode de convection

mixte dans une cavité carrée avec des parois mobiles, et l’étude numérique entreprise par

Mitsouliset Zisis [3]

T. Basak et S. Roy[4]se sont intéressés au sujet de la convection mixte dans une cavité carrée

où la paroi inférieure est soumise à haute température non-uniforme par contre les deux autres latérales sont froides et celle qui est supérieure est supposée en mouvement avec une vitesse constante. Leur étude a porté sur l’effet de divers paramètres de contrôle tels que 𝑃𝑟, 𝑅𝑒 et𝐺𝑟. Ils ont observé que la convection naturelle est dominante pour 𝑅𝑒=10 et 𝐺𝑟=105, mais si 𝑅e est supérieure à cette valeur ; celle qui est forcée sera devenue la dominante.

Prasad et Koseff[5] qui ont présenté une étude expérimentale de la convection mixte

tridimensionnelle de l’air dans une enceinte allongée chauffée différentiellement par les parois verticales, alors que les autres parois sont adiabatiques. La technique TLC (Thermo Liquids Crystals) est utilisée pour visualiser simultanément les champs thermiques et dynamiques. Les résultats montrent que le nombre de Richardson influe sur le coefficient de transfert de chaleur (nombre de Nusselt). Ils ont proposé une corrélation qui tient compte de l’influence du nombre de Richardson sur le nombre de Nusselt moyen.

Sharif [6] a considéré la convection mixte laminaire au sein d’une cavité rectangulaire inclinée,

dont le rapport d’aspect est égal à 10. La cavité est remplie d’eau dont les conditions aux limites sont celles de la configuration géométrique étudiée par Torrance et al [1971]. Le nombre de Reynolds est fixé à la valeur de 408 et le nombre de Rayleigh varie de 105 à 107. L’angle d’inclinaison varie de 0 à 30°. Un comportement intéressant de l’écoulement est observé en augmentant l’angle d’inclinaison.

CHAPITRE I ETUDE BIBLIOGRAPHIQUE

Page 4

Hakan et Ihsan [7] qui ont examiné numériquement la convection mixte stationnaire dans une

cavité rectangulaire. Les parois gauche et droite sont en mouvement et maintenus à des températures différentes, tandis que les autres parois sont adiabatiques. Trois cas ont été considérés selon le sens du mouvement des parois mobiles. L’étude a porté sur une gamme du nombre de Richardson (0.01 – 100). Les résultats obtenus montre que le transfert de chaleur est maximum dans le cas où le mouvement des parois est ascendant.

T.S. Cheng et W.H. Liu[8]ont repris numériquement la convection mixte dans une cavité

carrée, dont la paroi supérieure est mobile. Quatre cas sont distingués selon la direction du gradient de la température imposée. L’échauffement différentiel des parois supérieures et inférieures se traduit par l’attraction gravitationnelle stable et les gradients de température instable, alors que l’échauffement différentiel des parois latérales gauche et droite favorise et controverse les effets de flottabilité. En utilisant les paramètres de contrôle 𝑃𝑟=6.2 et 𝑅𝑖=0.1, 1 et 10, ils ont constaté que le nombre de Richardson et la direction du gradient de température affectent les types d’écoulement et l’évolution du transport de chaleur dans la cavité. De plus, ils ont montré que le taux de transfert de chaleur augmente avec la diminution du nombre de Richardson indépendamment de l’orientation du gradient de température imposée.

Torrance et al [9] Ont présenté une étude numérique concernant l’écoulement d’un fluide dans

une cavité rectangulaire, dont la paroi supérieure est supposée mobile et chauffée, tandis que les autres sont froides. Les trois cas traités montrent que la convection naturelle prédomine aux grands nombres de Grashof (± 104).

M.A.R. Sharif [10]a étudié numériquement la convection mixte dans une cavité rectangulaire

bidimensionnelle à l’aide de l’algorithme SIMPLER. La surface supérieure de la cavité rectangulaire est maintenue à plus haute température et la surface inférieure à basse température, tandis que les deux surfaces gauche et droite sont considérées adiabatiques. L’étude numérique est faite pour un nombre de Rayleigh varié de 105 _{à 10}7_{, le nombre de}

Reynolds 𝑅𝑒 = 408.21. Les résultats montrent que le nombre de Nusselt local augmente avec l’augmentation de l’angle de l’inclinaison pour la convection forcée dominante.

Page 5

Aussi, le nombre de Nusselt local et moyen augmentent avec l’augmentation de l’angle d’inclinaison dans le cas (𝑅𝑖 0.1), tandis qu’il augmente plus rapidement pour (𝑅𝑖 =10).

P. Kandaswamy, J.Lee et M. Muthtamilselvan[11]ont rapporté des conditions aux limites

que celles sont de la configuration géométrique étudiée par Aydin et Yang qui ont considéré une température fixe alors que Guo et Sharif ont imposé un flux de chaleur constant. La partie restante de cette paroi est supposée adiabatique. Les effets de la longueur de la source de chaleur ainsi que du nombre de Richardson ont été examinés. Ici, les effets de la convection forcée et de la convection naturelle étant couplé, aucune bifurcation vers une solution non symétrique n’a été observée.

Arpaci etLarson [12] ont présenté une étude numérique du transfert de chaleur par convection

mixte dans cavité, qui a une verticale du côté latérale mobile, les limites verticales à différentes températures, et limites horizontales sont adiabatique.

Moallemi et Jang [13] ont étudié numériquement la convection mixte dans un boîtier carré

chauffé par le bas Ils ont étudié l'effet du nombre de Prandtl sur le processus d’écoulement et de transfert thermique. Ils ont constaté que les effets de flottabilité sont plus prononcés pour les valeurs plus élevées de nombres de Prandtl, et ils ont aussi une corrélation dérivée pour le nombre de Nusselt moyen en termes de nombre de Prandtl, nombre de Reynolds et nombre de Richardson.

Moallemi et Jang [14]. Ils ont étudié les effets d'une variation du nombre de Prandtl (0 :01 <

Pr <50) sur l'écoulement et le transfert de chaleur dans la cavité. La température et le champ des vitesses sont calcules et présentes pour illustrer l'influence du nombre de Prandtl. Les nombres de Nusselt, local et global, sont rapportés pour différentes valeurs de Re, Ri et Pr.

Guo et Sharif [15].Ils ont étudié la convection mixte laminaire bidimensionnelle dans une

cavité carrée avec une paroi supérieure adiabatique et des parois verticales froides se déplaçant vers le bas à une vitesse constante. Les effets de la longueur de la source de chaleur ainsi que du nombre de Richardson ont été représentés.

CHAPITRE I ETUDE BIBLIOGRAPHIQUE

Page 6

B. Dahdi[16]a repris numériquement la convection mixte dans une cavité carrée en considérant

la même configuration que celle d’Aydin avec une direction de déplacement des parois latérales inversée. Les résultats obtenus montrent l'existence de trois écoulements complètement différents en fonction de la valeur du nombre de Richardson. Dans une première phase, l'écoulement est constitué de deux cellules contrarotatives et parfaitement symétriques lorsque la convection forcée est dominante.

Ogut [17] à présente une étude numérique sur la convection mixte dans une cavité carrée avec

un angle d'inclinaison en utilisant la technique différentielle quadrature(DQ). Les parois verticales sont maintenues adiabatiques. Cette cavité a une paroi qui se déplace avec une vitesse constante tandis que les autres parois sont immobiles.

L’étude numérique est faite pour des nombres de Richardson allant de 0;1 jusqu'à 100. Il a examiné les effets de l'angle d'inclinaison

H.F. Oztop et I. Dagtekin [18] ont étudié numériquement la convection mixte

bidimensionnelle stationnaire dans une cavité carrée portant deux parois mobiles verticales et chauffées différentiellement. Les parois horizontales sont adiabatiques. Trois cas ont été considérés qui dépendent de la direction du mouvement des parois. Toutes les simulations ont été réalisées avec les valeurs des nombres de Richardson (0.01≤ 𝑅𝑖≤100)et du nombre de Prandtl (Pr = 0.7). Les résultats montrent que le nombre de Richardson influe sur l’écoulement du fluide et le transfert thermique pour Ri > 1, et par conséquent, le transfert de chaleur est assez meilleur.

O. Aydin et W.J.Yang [19] ont rapporté une étude numérique de la convection mixte laminaire

bidimensionnelle dans une cavité carrée avec une paroi supérieure adiabatique. Les parois verticales froides se déplacent vers le bas à une vitesse constante. Une source chaude est placée au centre de la paroi inférieure (température fixe). La partie restante de cette paroi est supposée adiabatique. Les effets de la longueur de la source de chaleur ainsi que du nombre de Richardson ont été étudiés. Les résultats montrent que l’effet de la convection forcée et de la convection naturelle étant coopérant, aucune bifurcation vers une solution non symétrique n’a été observée.

Page 7

K.M.Khanafer et al[20] ont rapporté une étude numérique sur le transfert de chaleur par

convection mixte laminaire instable dans une cavité carrée. La paroi supérieure est maintenue à une température froide 𝑇𝑐 soumise à une vitesse horizontale sinusoïdale, tandis que la paroi inférieure est maintenue à une température chaude ; les autres parois sont adiabatiques. La discrétisation des équations gouvernant le problème est obtenu à l’aide des éléments finis basée sur la méthode de Galerkin. Les caractéristiques de l’écoulement du fluide et de transfert de chaleur sont examinés pour une gamme de Reynolds (102≤ 𝑅𝑒 ≤103), de Grashof (102≤ 𝐺𝑟 ≤105), d’une fréquence sans dimensions d’oscillation du couvercle 0.1≤𝜔≤5 et un nombre de Prandtl de 0.71. Ils ont montré que le nombre de Nusselt moyen augmente avec l’augmentation du nombre de Grashof, tandis qu’il diminue avec l’augmentation du nombre de Reynolds et de la fréquence de vitesse du couvercle.

Y.S.Prasad et M.K.Das [21] ont étudié la convection mixte dans une cavité rectangulaire avec

la méthode des volumes finis. Les parois verticales sont maintenues à une température froide tandis que la paroi supérieure chaude et la paroi inférieure froide pour un premier cas et inversement pour le deuxième cas. L’étude numérique est faite pour des nombres de Grashof allant de 0 jusqu’à 106_{, un nombre de Reynolds égale à 100 et un rapport d’aspect égale à 0,5.}

Les résultats sont donnés sous forme des isothermes, iso courants, ainsi que la variation du nombre de Nusselt.

CHAPITRE II

Page 8

II.1 Présentation du problème

La configuration géométrique étudiée est présentée sur la Figure (II.1), il s’agit d’une cavité carrée avec des parois latérales mobiles remplie d’air. Celle de droite chaude et se déplace vers le bas. Celle de gauche froide se déplace vers le haut, les autres parois sont supposées adiabatiques.

Figure. II.1 : Schématisation du problème physique et conditions aux limites.

II.2 Équations générales

L’analyse de la convection thermique se base sur l’application des trois lois fondamentales de la physique générale :

 Équation de conservation de la masse (équation de continuité) :

𝜕𝜌

𝜕𝑡+ 𝑑𝑖𝑣(𝜌𝑣 ⃗⃗⃗ ) = 0 (II-1)

Équation de la conservation de la quantité de mouvement :

𝜕𝑣⃗

𝜕𝑡+ 𝑣 𝑔𝑟𝑎𝑑 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑣 = −1

CHAPITRE II MODELE MATHEMATIQUE

Page 9

Équation de la conservation de l’énergie : 𝜌 𝐶𝑝 (𝜕𝑇_𝜕𝑡+ 𝑣 𝑔𝑟𝑎𝑑 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑇) = 𝛽𝑇(𝜕𝑃

𝜕𝑡 + 𝑣 𝑔𝑟𝑎𝑑 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑃) + 𝑃𝑠+ 𝜑 + 𝑑𝑖𝑣(𝐾 𝑔𝑟𝑎𝑑 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑇) (II-3)

II.3 Hypothèses simplificatrices

La modélisation du système étudié prend en considération les hypothèses suivantes : L’écoulement est bidimensionnel.

Le fluide est newtonien et incompressible. L’écoulement est laminaire.

le transfert de chaleur par rayonnement est négligeable.

le travail, induit par les forces visqueuses et de pression, est négligeable.

Les propriétés physiques du fluide sont constantes hormis la masse volumique qui obéit à l’approximation de Boussinesq dans le terme de la poussée d’Archimède.

II.4 Approximation de Boussinesq

Pour des configurations d’écoulement dans une cavité, la résultante des forces externes est limitée aux forces gravitationnelles de sorte que l’influence de la convection naturelle provoquée par des gradients de la température soit évidente. Quand les forces de flottabilité se produisent dans l’écoulement, la conception des propriétés physiques fixes n’assortit plus le comportement de l’écoulement du fluide. L’effet de la convection naturelle est pris en considération dans l’équation de quantité de mouvement par la variation de la masse volumique.

Si en prenant un état thermodynamique de référence (masse volumique 𝜌₀ et température T0)

l’équation d’état pour la masse volumique ρ devient en utilisant le développement de Taylor 𝜌 = 𝜌0(1 −

𝑇−𝑇0

𝑇0 + ⋯ )

Page 10

En se limitant à un développement du premier ordre :

𝜌 = 𝜌0 (1 − 𝛽(𝑇 − 𝑇0) (II-5)

Le terme 𝛽de l’équation (II.5) est le coefficient de dilatation isobare du fluide, soit : 𝛽 = −1

𝜌( 𝜕𝜌

𝜕𝑇)_{𝑝=𝑐𝑡𝑒} (II-6)

En effet, c’est la variation de la masse volumique du fluide qui est à l’origine du phénomène de convection naturelle, créant une force motrice volumique (Archimède) à laquelle s’oppose notamment une force de frottement visqueux

II.5 Formulation du problème

II.5.1 Equations gouvernantes

Le système des équations qui gouvernent l'écoulement laminaire en convection mixte et le transfert de chaleur en coordonnées cartésiennes après simplifications s'écrivent comme suit :

●

Equation de continuité

𝜕𝑈 𝜕𝑋

+

𝑑𝑉

𝑑𝑌

= 0

(II-7)

●

Equations de quantités de mouvement Selon (ox)

𝑢

𝜕𝑈 𝜕𝑋

+ 𝑣

𝑑𝑉 𝑑𝑌

= −

1 𝜌 𝜕𝑃 𝜕𝑋

+ 𝑣 (

𝜕2𝑈 𝜕𝑋2

+

𝜕2𝑈 𝜕𝑌2

)

(II-8) Selon (oy)

𝑢

𝜕𝑈 𝜕𝑋

+ 𝑣

𝑑𝑉 𝑑𝑌

= −

1 𝜌 𝜕𝑃 𝜕𝑌

+ 𝑣 (

𝜕2𝑉 𝜕𝑋2

+

𝜕2𝑉 𝜕𝑌2

) − [1 − 𝛽(𝑇 − 𝑇

∞

)]g

(II-9)

CHAPITRE II MODELE MATHEMATIQUE

Page 11

●

Equation d'énergie

𝑢

𝜕𝑈 𝜕𝑋

+ 𝑣

𝑑𝑉 𝑑𝑌

= 𝑎 (

𝜕2𝑇 𝜕𝑋2

+

𝜕2𝑇 𝜕𝑌2

)

(II-10)

Où :

𝑎 =

𝑘

𝜌𝑐

_𝜌 𝒂: diffusivité thermique K : conductivité thermique

𝒄_𝝆 : Chaleur spécifique à pression constante

II.5.2 Conditions aux limites

𝟎 < 𝒀 < 𝟏

𝑋 = 0 𝑈 = 0 𝑉 = 𝑉0 𝑇 = 𝑇

_𝐶

(II-11)

𝟎 < 𝒀 < 1

𝑋 = 1 𝑈 = 0 𝑉 = −𝑉

₀

𝑇 = 𝑇

_𝐻

(II-12)

𝟎 < 𝑿 < 𝟏

𝑌 = 0 𝑈 = 0 𝑉 = 0

𝜕𝑇 𝜕𝑌

= 0

(II-13)

Page 12

𝟎 < 𝑿 < 𝟏

𝑌 = 1 𝑈 = 0 𝑉 = 0

𝜕𝑇

𝜕𝑌

= 0

(II-14)

II.6 Formulation adimensionnelle

L'emploie de la variable adimensionnelle permet d'exprimer la réalité des phénomènes physiques indépendamment des systèmes de mesures, qui permet d'avoir des informations généralisées à une variété des problèmes ayant les mêmes grandeurs de coefficient de similitudes d'un côté, et d'un autre côté, réduire le nombre de paramètres d'un problème. En effet, pour faire apparaître les paramètres de contrôle du problème étudié, il est nécessaire d’introduire les grandeurs de référence.

II.6.1 Principales grandeurs physiques et variables adimensionnelles

Le nombre de Reynolds local, le nombre de Prandtl et le nombre de Grashof sont définis par : 𝑅𝑒_𝐿 =𝜌∞u∞𝐿 𝜇 𝑃𝑟 = 𝜇𝐶𝑝 𝑘 𝐺𝑟𝐿 = 𝑔𝛽𝐿3_(𝑇 𝐶 −𝑇𝐻) 𝑉2 (II-15) 𝑅𝑖_𝐿 = |𝐺𝑟𝐿|

𝑅𝑒𝐿2 (Le nombre de Richardson)

Le nombre de Nusselt local est défini par : 𝑁𝑢𝑥 = ℎ𝑥 𝑘 = −𝑘[𝜕𝑢(𝑥)_𝜕𝑦 ] 𝑦=0 (𝑇_{𝐶 −}𝑇𝐻) ∙ 𝑥 𝑘 (II-16)

Les variables adimensionnels choisis sont : 𝑋 =𝑋 𝐿 𝑌 = 𝑌 𝐿 𝜃 = (𝑇−𝑇𝐻) (𝑇_{𝐶 −}𝑇_𝐻) 𝑈 = 𝑢 u∞ 𝑉 = 𝑣 u∞ (II-17)

CHAPITRE II MODELE MATHEMATIQUE

Page 13 P=𝑃−𝜌(𝑔𝑥𝑋+𝑔𝑦𝑌) 𝜌𝑢2 ∞ 𝑔𝑥 Où :

𝐮∞ : représente la vitesse caractéristique de l'écoulement de convection forcée.

II.6.2 Equations adimensionnelles

Les équations adimensionnelles de continuité, de quantités de mouvement et d'énergie qui gouvernent le phénomène de la convection mixte s'écrivent alors :

● Equation de continuité :

𝜕𝑈 𝜕𝑋+

𝜕𝑉

𝜕𝑌 = 0 (II-18)

● Equations de quantités de mouvement :

Selon (OX) 𝑈𝜕𝑈 𝜕𝑋+ 𝑉 𝜕𝑈 𝜕𝑌 = − 𝜕𝑃 𝜕𝑋+ 1 𝑅𝑒( 𝜕2_𝑈 𝜕𝑋2+ 𝜕2_𝑈 𝜕𝑌2) (II-19) Selon (OY) 𝑈𝜕𝑉 𝜕𝑋+ 𝑉 𝜕𝑉 𝜕𝑌 = − 𝜕𝑃 𝜕𝑌+ 1 𝑅𝑒( 𝜕2𝑈 𝜕𝑋2+ 𝜕2𝑈 𝜕𝑌2) + 𝑅𝑖 𝜃 (II-20) ● Equation de l'énergie : 𝑈𝜕𝜃 𝜕𝑋+ 𝑉 𝜕𝜃 𝜕𝑌= 1 𝑃𝑟𝑅𝑒( 𝜕2𝜃 𝜕𝑋2+ 𝜕2𝜃 𝜕𝑌2) (II-21)

CHAPITRE III

CHAPITRE III MODELISATION NUMERIQUE

Page 14

Dans ce chapitre nous décrivons la méthode numérique utilisée pour résoudre les équations de base formulées dans le chapitre II.

Le système d'équations aux dérivées partielles est résolu numériquement par la méthode des volumes finis où la correction de la pression et de la vitesse est obtenue par l'algorithme SIMPLE [21]. Cette discrétisation donne un système matriciel tridiagonal dont la résolution est obtenue par l'application de l'algorithme de Thomas. Le domaine de calcul est divisé en un nombre fini de volumes de contrôle ou mailles. Le maillage est uniforme, les équations de base sont intégrées sur chaque volume de contrôle. Pour éviter la divergence de la solution, le schéma en loi de puissance est utilisé pour évaluer les flux aux interfaces des volumes de contrôle.

III.1. Introduction

La discrétisation des équations présentées dans le chapitre précédent traduisant le phénomène de convection mixte est l'opération de transformer ces équations différentielles en un système d'équations algébriques.

Plusieurs méthodes de discrétisation des équations différentielles aux dérivées partielles sont utilisées actuellement telles que : la méthode des volumes finis, des différences finies et des éléments finis, etc., ... Parmi ces méthodes, nous avons choisi la méthode des volumes finis.

III.2. Principe de la méthode des volumes finis

La méthode des volumes finis a été décrite pour la première fois en 1971 par Patankar et Spalding et publiée en 1980 par Patankar. Le principe de méthode des volumes finis baser sur une technique de discrétisation qui convertit les équations de conservation aux dérivées partielles en équations algébriques qui peuvent être résolues numériquement.

Dans la simulation par la méthode des volumes finis, le domaine de calcul est divisé en un nombre fini de sous-domaines élémentaires, appelés volumes de contrôle. La méthode des volumes finis consiste à intégrer les équations aux dérivées partielles, décrites au chapitre II, sur chaque volume de contrôle. Chacun de ces derniers (volumes de contrôle) contenant un nœud dit : "nœud principal". Comme indiqué dans la Figure III-1.

Page 15

La technique des volumes de contrôle consiste dans l’intégration des équations aux dérivées partielles sur chaque volume de contrôle pour obtenir les équations discrétisées qui conservent toutes les grandeurs physiques sur un volume de contrôle.

Les différentes étapes de la méthode des volumes finis sont :

 La discrétisation du domaine considéré en volume de contrôle ;

 La formulation intégrale des équations différentielles aux dérivées

partielles ;

 Écriture des équations algébriques aux nœuds du maillage ;

 Résolution du système algébrique linéaire obtenu.

Un exemple de volume de contrôle est montré dans la figure ci-dessous. Pour un nœud principal (P’), les points E et W (E : Est, W : West (ouest)) sont des voisins dans la direction X, tandis que N et S (N : Nord), (S : Sud) sont ceux dans la direction Y. Le volume de contrôle entourant (P’) est montré par les lignes discontinues.

Les faces du volume de contrôle sont localisées aux points (e) et (w) dans direction X, (n) et (s) dans la direct

CHAPITRE III MODELISATION NUMERIQUE

Page 16

III.3. Maillage

Le maillage est la subdivision du domaine d’étude en grilles longitudinales et transversales dont l’intersection représente un nœud.

La discrétisation du domaine est obtenue par un maillage constitué d’un réseau de points (Nœuds). Ainsi un élément de volume (volume de contrôle) est défini autour de chaque nœud. Les grandeurs scalaires (pression, température) sont stockées dans le nœud (P’) du maillage, tandis que les grandeurs vectorielles (U et V) sont stockées aux milieux des segments reliant les nœuds. L’équation générale de transport est intégrée sur le volume de contrôle associé aux variables scalaires et les équations de quantité de mouvement sont intégrées sur le volume de contrôle associé aux composantes de la vitesse.

Le volume de contrôle de la composante longitudinale (U) est décalé suivant la direction (X) par rapport au volume de contrôle principal, celui de la composante transversale (V) est décalé suivant la direction (Y). Ce type de maillage dit : «maillage décalé» permet une bonne approximation des flux convectifs et une meilleure évaluation des gradients de pression ainsi qu’une stabilisation numérique de la solution.

Page 17

Dans ce mémoire nous avons opté pour un maillage non uniforme dans les deux directions, horizontal et vertical comme le montre la (Figure III-3). On a construit plusieurs maillages de différent nombre nœuds,

Figure III.3 : Maillage de cavité.

III.4. La discrétisation

Les équations de conservation présentées au chapitre précédent peuvent être écrites sous une forme commune. Cette formulation permet de ne pas répéter le travail de discrétisation pour chaque équation. Chacun des équations peut être réduite à une seule équation générale, en coordonnées cartésiennes. ∂ ∂t⏟ (ρ∅) 𝑇 + ∑ ∂ ∂𝑋𝑗 j=1 (ρu𝑗∅) ⏟ C = ∑ ∂ ∂𝑋𝑗 j=1 (Γ∅ ∂∅ ∂𝑋𝑗) ⏟ D + 𝑆⏟_∅ S (III-1)

CHAPITRE III MODELISATION NUMERIQUE

Page 18 Avec : T : Terme transitoire. C : Terme de convection. D : Terme de diffusion. S : Terme source.

Nous venons de voir que, pour chaque variable Ф, l’équation de transport s’écrit dans le cas stationnaire, bidimensionnel : 𝜕 𝜕𝑡(ρu∅) + 𝜕 𝜕𝑦(ρv∅) = 𝜕 𝜕𝑥(Γ 𝜕∅ 𝜕𝑥) + 𝜕 𝜕𝑦(Γ 𝜕∅ 𝜕𝑦) + 𝑆∅ (III-2)

Où Ф est la propriété transportée, Γ indique le coefficient de diffusion et SФ le terme source. Tous ces termes sont listés dans le tableau suivant :

Grandeur transportée ∅ Γ 𝑆∅

Conservation de masse 1 0 0 Quantité de mouvement selon x

U Pr

−𝜕𝑃 𝜕𝑋

Quantité de mouvement selon y V Pr

−𝜕𝑃

𝜕𝑋+ Ra Pr 𝜃

Energie 𝜃 1 0

Tableau (III.1) : Les termes de l’équation de transport.

Cette équation (III.2) est discrétisée et le système d’équation aux dérivées partielles est résolu pour chaque valeur successive de Ф. Le système prend alors la forme d’une équation très condensée.

Page 19

L’équation (III.2) peut être écrite sous la forme :

∂ ∂X(jx) + ∂ ∂y(jy) = S∅ (III-3) Avec :{𝑗𝑥= 𝜌𝑢∅ − Γ 𝜕∅ 𝜕𝑥 𝑗_𝑦 = 𝜌𝑣∅ − Γ𝜕∅ 𝜕𝑦 } (III-4)

𝑗𝑥Et 𝑗𝑦sont les flux totaux (convection et diffusion) par unité de surface dans les directions

x et y.

La discrétisation consiste à transformer l’équation différentielle de transport en un système d’équation algébrique. L’équation (III.3) est d’abord intégrée sur le volume de contrôle Figure (III.4) : ∫ ∫ (∂J_∂xx+∂Jy ∂y) dxdy e w n s ⏟ 𝐼 = ∫ ∫ 𝑆∅ 𝑒 𝑤 n s dxdy ⏟ 𝐼𝐼 (III-5)

CHAPITRE III MODELISATION NUMERIQUE

Page 20

Pour pouvoir l’approximation de l’équation sous forme algébrique, on considère les hypothèses suivantes :

- La variable généralisée Ф varie linéairement entre les nœuds principaux dans les deux directions.

- Les termes convectifs et diffusifs sont uniformes à travers les faces correspondantes. - Le terme source est uniforme sure le volume de contrôle.

III.4.1. Intégration du flux total

L’intégration du terme convectif et diffusif (terme (I) de l’équation (III.5)) sur tout le .Volume de contrôle est :

𝐼 = ∫ ∫ (∂Jx ∂x + ∂Jy ∂y) dxdy e w n s (III-6)

𝐼 = ∫ ∫_sn _we_∂x∂ (J_x)dxdy + ∫ ∫_𝑠𝑛 _𝑤𝑒_∂y∂ (J_y)dxdy (III-7)

I = ((J_x)_e− (J_x)_w) ∫ dy + ((Jy)n− (Jy)s) n

s ∫ dx e

w (III-8)

I = (Jx)e∆y − (Jx)w∆y + (Jy)n∆x − (Jy)s∆x (III-9)

Si on pose :

J_e = (J_x)_e∆y J_n = (J_y)_n∆x J_w= (J_x)_w∆y J_s = (J_y)_s∆x

Donc l’expression de terme (I) devient :

Page 21

III.4.2. Intégration du terme source

L’intégration du terme source (terme (II) de l’équation (III.5)) sur tout le volume de contrôle est : II = ∫ ∫ 𝑆∅ 𝑒 𝑤 n s dxdy = ∫ [∫ 𝑆∅dx 𝑒 𝑤 ] 𝑛 𝑠 dy (III-11) Donc : H = 𝑆̅̅̅ ∆𝑥 ∆𝑦 _∅ (III-12)

Où 𝑆̅̅̅est la valeur moyenne du terme source sur le volume de contrôle. Quand le terme source _∅ dépend de la variable dépendante. Cette dépendance doit être exprimée par une relation linéaire, ceci permettra d’utiliser les méthodes de résolution des systèmes linéaires. La linéarisation est l’évolution de la valeur moyenne 𝑆̅̅̅qui peut être fonction de la variable dépendante, leur valeur _∅ est donc calculée à chaque itération à partir des nouvelles des variables dépendantes.

Suite à la résolution des équations algébriques adoptées, le terme source sera linéarisé de, façon à forcer la convergence, de sorte que :

𝑆∅

̅̅̅ = 𝑆𝑐+ 𝑆𝑝∅𝑝 (III-13)

Où

𝑆_𝑐: Est la partie constante qui ne dépend pas explicitement de𝑆_𝑝. 𝑆_𝑝: est la pente de ∅_𝑝.

Il est nécessaire que le coefficient 𝑆𝑝soit inférieur à zéro pour que la solution soit

CHAPITRE III MODELISATION NUMERIQUE

Page 22

III.4.3. Discrétisation spatiale

Discrétiser une équation différentielle aux dérivées partielles revient à remplacer l’information continue exacte, contenue dans cette équation par une information discrète contenue dans une équation algébrique.

L’approximation de la variable généralisée Ф. aux interfaces du volume de contrôle se fera donc avec le choix du schéma de discrétisation approprié. Le rôle du schéma intervient pour expliquer comment évaluer les flux de diffusion et de convection sur les faces du volume de contrôle après intégration. On a l’équation (III.5) qui devient :

(J_e− J_w+ J_n− J_s) = ( 𝑆_𝑐+ 𝑆_𝑝∅_𝑝)∆x∆y (III-14)

Où Ji (i= e, s, n, w) est le flux total évalué sur chaque face du volume de contrôle. Ce flux est

composé de deux parties : flux convectif et diffusif. Par exemple :

J_e = (𝜌𝑢∅ − (𝜕∅

𝜕𝑥)) ∆𝑦 (III-15)

On peut utiliser les schémas suivants :

III.4.3.1 Schéma aux différences centrées (CDS)

Pour évaluer le flux convectif à l’interface, la variation de la variable Ф entre deux nœuds adjacents doit être exprimée par un profil linéaire. On suppose que les faces (e, w, n, s) se trouvent au milieu des nœuds (E, W, N, S) respectivement, les termes convectifs des variables généralisées Ф se présentent par une interpolation comme suit :

{ ∅𝑒 = 1 2 (∅𝐸 + ∅𝑃) ∅𝑤 = 1 2 (∅𝑃 + ∅𝑊) ∅_𝑛 = 1 2 (∅𝑁 + ∅𝑃) ∅𝑠 = 1 2 (∅𝑃 + ∅𝑆) (III-16)

Page 23

Les parties diffusives sont évaluées en approximant les dérivées par les différences, ce qui donne : { Γ𝑒( 𝜕∅ 𝜕𝑥)_𝑒 = Γ𝑒 ∅𝐸−∅𝑃 (𝛿𝑥)𝑒 Γ_𝑤(𝜕∅ 𝜕𝑥)_𝑤 = Γ𝑤 ∅𝑃−∅𝑊 (𝛿𝑥)𝑤 Γ𝑛( 𝜕∅ 𝜕𝑥)_𝑛 = Γ𝑛 ∅𝑁−∅𝑃 (𝛿𝑥)𝑛 Γ_𝑠(𝜕∅ 𝜕𝑥)_𝑠 = Γ𝑠 ∅𝑃−∅𝑆 (𝛿𝑥)𝑠 (III-17)

Nous remplaçons les formules (III.16) et (III.17) dans l’équation (III.14), on obtient :

𝑎𝑃∅𝑃 = 𝑎𝐸∅𝐸 = 𝑎𝑊∅𝑊= 𝑎𝑁∅𝑁 = 𝑎𝑆∅𝑆+ 𝑏 (III-18) Ou : 𝑎_𝑃 = 𝑎_𝐸+ 𝑎_𝑊+ 𝑎_𝑁+ 𝑎_𝑆− 𝑠_𝑝∆𝑥 ∆𝑦 { 𝑎𝐸 = 𝐷𝑒− 𝐹𝑒 2 𝑎𝑊= 𝐷𝑤− 𝐹𝑤 2 𝑎_𝑁 = 𝐷_𝑛−𝐹𝑠 2 𝑎_𝑆 = 𝐷_𝑠−𝐹𝑠 2 (III-19) b = 𝑆𝑐∆𝑥∆𝑦 , 𝐷𝑖 = Γ𝑖

𝛿𝑥𝑖 : Est La conductance de la diffusion toujours positive et 𝐹𝑖 = (𝜌𝑢𝑖)

la force de convection peut être, positif ou négatif, selon le sens de l’écoulement. Les coefficients de discrétisation 𝑎_𝑖(i=E, W, N, S) rassemblant le flux convectifs et diffusifs. Les coefficients𝑎𝑖 Doivent avoir le même signe positif (la deuxième règle de base pour la méthode

de volume finis), mais la relation (III.19), peut créer des coefficients négatifs.

CHAPITRE III MODELISATION NUMERIQUE

Page 24

Les coefficients de l’équation (III.19) écrits en terme du nombre de Peclet(Pe) sont donnés

par : { 𝑎E = De(1 − pee 2 ) 𝑎W= Dw(1 + pew 2 ) 𝑎N = Dn(1 − pen 2 ) 𝑎_S = D_s(1 +pes 2 ) (III-20) Avec : P𝑒_𝑖 = 𝐹𝑖 𝐷𝑖= (𝜌𝑢𝑖)(𝛿𝑥𝑖) Γ𝑖 P𝑒𝑖 = 𝐹𝑖 𝐷𝑖 = (𝜌𝑢𝑖)(𝛿𝑥𝑖) Γ𝑖 (III-21)

Pour que ces coefficients soit positifs, le nombre de Pe doit être dans l’intervalle [-2,2]. L’application de ce schéma n’est avantagée que si|pe| ≤ 2, ceci est réalisé pour des maillages fins.

III.4.3.2 Schéma Upwind (UPS)

Dans ce schéma, la valeur de la variable Ф à l’interface n’est pas interpolée. Il est appliqué pour les écoulements à dominance convective. Si on considère la figure (III-4), on voit que ce schéma assigne directement Фi (i=e, w, n, s), par exemple :

{ ∅e= ∅P si Fe> 0 ∅_e= ∅_E si F_e> 0 ∅_w = ∅_W si F_w > 0 ∅_w = ∅_P si F_w> 0 ∅n = ∅P si Fn > 0 ∅n= ∅N si Fn> 0 ∅_s = ∅_S si F_s > 0 ∅_s = ∅_P si F_s > 0 (III-22)

Les valeurs de ∅_w, ∅_n𝑒𝑡∅_ssont exprimées de la même façon. Cette condition peut être exprimée par l’opérateur :

Page 25

Le schéma Upwind s’écrit donc :

{ F_𝑒∅_e = ∅_P‖F𝑒, 0‖ − ∅E‖−F𝑒, 0‖ F𝑤∅w = ∅W‖F𝑊, 0‖ − ∅P‖−F𝑤, 0‖ F𝑛∅n = ∅P‖F𝑛 , 0‖ − ∅N‖−F𝑛 ,0‖ F_𝑠∅_s = ∅_S‖F𝑠, 0‖ − ∅P‖−F𝑠, 0‖ (III-23)

En substituant les expressions (III.23) dans l’équation (III.14), l’équation de discrétisation devient 𝑎_𝑃∅_𝑃 = 𝑎_𝐸∅_𝐸 = 𝑎_𝑊∅_𝑊= 𝑎_𝑁∅_𝑁= 𝑎_𝑆∅_𝑆+ 𝑏 𝑎𝑃 = 𝑎𝐸+ 𝑎𝑊+ 𝑎𝑁+ 𝑎𝑆− 𝑆𝑝∆𝑥 ∆𝑦 ; 𝑏 = 𝑆𝑝∆𝑥 ∆𝑦 𝐴𝑣𝑒𝑐: { 𝑎𝐸 = 𝐷𝑒+ ‖−F𝑒, 0‖ 𝑎𝑊= 𝐷𝑤 + ‖F𝑤, 0‖ 𝑎𝑁 = 𝐷𝑛+ ‖−F𝑛 , 0‖ 𝑎_𝑆 = 𝐷_𝑠 + ‖F_𝑠, 0‖ (III.24)

Tous les coefficients de discrétisation de ce schéma sont positifs, ce qui fait ce schéma est inconditionnellement stable, il introduit une erreur nommée fausse diffusion, et de ce fait il donne une mauvaise représentation du phénomène physique réel.

III.4.3.3 Schéma Hybrid (HDS: hybrid-differencing scheme)

Ce schéma mis au point par Spadling (1972). Le schéma HDS est la combinaison des deux schémas (centré et Upwind).

En appliquant ce schéma, la variable généralisée Ф aux différentes interfaces du volume de contrôle prend la forme suivante :

CHAPITRE III MODELISATION NUMERIQUE

Page 26 { ∅_𝑒 = 𝑎_𝑒∅_𝑃+ (1 − 𝑎_𝑒)∅𝐸 ∅_𝑤 = 𝑎_𝑤∅_𝑊+ (1 − 𝑎_𝑤)∅𝑃 ∅_𝑛 = 𝑎_𝑛∅_𝑃+ (1 − 𝑎_𝑛)∅𝑁 ∅_𝑠 = 𝑎_𝑠∅_𝑆+ (1 − 𝑎_𝑠)∅𝑃 (III-25)

Où les coefficients 𝑎𝑖 (i = e, w, n, s) sont définis par :

𝑎_𝑖 = { 0 𝑠𝑖 𝑃_𝑒 < −2 → 𝑠𝑐ℎé𝑚𝑎 𝑢𝑝𝑤𝑖𝑛𝑑 1 2 𝑠𝑖 |𝑃𝑒| ≤ 2 → 𝑠𝑐ℎé𝑚𝑎 𝑐𝑒𝑛𝑡𝑟é 1 𝑠𝑖 𝑃_𝑒 > 2 → 𝑠𝑐ℎé𝑚𝑎 𝑢𝑝𝑤𝑖𝑛𝑑 (III-26)

En substituant les valeurs prises par la variable Ф à l’équation (III.14), on aura : 𝑎_𝑃∅_𝑃 = 𝑎_𝐸∅_𝐸 = 𝑎_𝑊∅_𝑊= 𝑎_𝑁∅_𝑁= 𝑎_𝑆∅_𝑆+ 𝑏 𝑎𝑃 = 𝑎𝐸+ 𝑎𝑊+ 𝑎𝑁+ 𝑎𝑆− 𝑆𝑝∆𝑥 ∆𝑦 ; 𝑏 = 𝑆𝑝∆𝑥 ∆𝑦 { 𝑎𝐸 = ‖−F𝑒, 𝐷𝑒− 𝐹𝑒 2 , 0‖ 𝑎𝑊= ‖−F𝑤, 𝐷𝑤− 𝐹𝑤 2 , 0‖ 𝑎_𝑁 = ‖−F_𝑛, 𝐷_𝑛−𝐹𝑛 2 , 0‖ 𝑎_𝑆 = ‖−F_𝑠, 𝐷_𝑠−𝐹𝑠 2, 0‖ (III-27)

On peut distinguer que le nombre de Peclet est l’élément essentiel pour caractériser le comportement d’un schéma numérique. La limitation des schémas précédents se situe comme suit :

 Schéma centré : par les valeurs |pe| ≤ 2

 Schéma Upwind : surestime la diffusion pour les grands nombres de Peclet ;  Schéma Hybride : son inconvénient est l’erreur maximale lorsque |pe| = 2 ;  Schéma PLDS : stable et donne une bonne approximation de la solution exacte.

Page 27

III.5. Formulation générale du problème

L’intégration de l’équation de transport (III.2) donne :

(J_e− J_w+ J_n− J_s) = ( 𝑆_𝑐+ 𝑆_𝑝∅_𝑝)∆x∆y (III-28) Où : J_i = (𝜌𝑢_𝑖)∅_𝑖− Γ_𝑖(𝜕∅𝑖 𝜕𝑥_𝑖) , 𝑎𝑣𝑒𝑐: {𝑠𝑖 𝑖 = 𝑒, 𝑤 𝑎𝑙𝑜𝑟𝑠 𝑢𝑗 = 𝑢 𝑒𝑡 𝑥𝑗 = 𝑥 𝑠𝑖 𝑖 = 𝑛, 𝑠 𝑎𝑙𝑜𝑟𝑠 𝑢𝑗 = 𝑣 𝑒𝑡 𝑥𝑗 = 𝑥 (III-29)

L’intégration de l’équation de continuité sur le volume de contrôle donne :

Fe− Fw+ Fn− Fs = 0 (III-30)

Où : Fi (i=e, w, n, s) sont les débits massiques à travers les faces du volume de contrôle.

Si on multiplie l’équation (III.30) par ∅_𝑝 et on la retranche de l’équation (III.28), on obtient : (J_𝑒− F_e∅_𝑝) − (J_𝑤 − F_w∅_𝑝) + (J_𝑛− F_n∅_𝑝) − (J_𝑠− F_s∅_𝑝) = ( 𝑆_𝑐+ 𝑆_𝑝∅_𝑝)∆x∆y (III.31)

On peut écrire les termes entre parenthèses de l’équation (III.33) comme suit :

{ 𝑗𝑒− 𝐹𝑒∅𝑝 = 𝑎E(∅𝑝− ∅𝐸) 𝑗𝑤−𝐹𝑤∅𝑝 = 𝑎W(∅𝑤− ∅𝑝) 𝑗_𝑛−𝐹_𝑛∅_𝑝 = 𝑎_N(∅_𝑝− ∅_𝑁) 𝑗_𝑠−𝐹_𝑠∅_𝑝 = 𝑎_s(∅_𝑆− ∅_𝑝) (III-32) Avec: { 𝑎_E = D_e𝐴(|𝑝𝑒_𝑒|) + ‖−𝐹_𝑒,0‖ 𝑎_W = D_w𝐴(|𝑝𝑒_𝑤|) + ‖𝐹_𝑤,0‖ 𝑎_N = D_n𝐴(|𝑝𝑒_𝑛|) + ‖−𝐹_𝑛 ,0‖ 𝑎_S = D_s𝐴(|𝑝𝑒_𝑠|) + ‖𝐹_𝑠,0‖ (III-33)

CHAPITRE III MODELISATION NUMERIQUE

Page 28

L’équation de discrétisation s’écrit sous la forme :

𝑎𝑃∅𝑃 = 𝑎𝐸∅𝐸 = 𝑎𝑊∅𝑊= 𝑎𝑁∅𝑁= 𝑎𝑆∅𝑆+ 𝑏

𝑎_𝑃 = 𝑎_𝐸+ 𝑎_𝑊+ 𝑎_𝑁+ 𝑎_𝑆− 𝑆_𝑝∆𝑥 ∆𝑦 ; 𝑏 = 𝑆_𝑝∆𝑥 ∆𝑦 La fonction 𝐴(|𝑝𝑒𝑒|)est choisie d’après le tableau suivant :

Schéma La fonction 𝐴(|𝑝𝑒_𝑒|) Différences centrées 1 − 0.5|𝑝𝑒_𝑒|

Upwind 1

Hybride ‖0 , (1 − 0.5|𝑝𝑒_𝑒|)‖

Tableau (III.2) : La fonction A(|pe_e|)pour différents schémas.

Où Pe est le nombre de Peclet qui représente le rapport local de la convection à la diffusion.

P𝑒_𝑖 = (𝜌𝑢𝑖)(𝛿𝑥𝑖)

Γ𝑖 , i = (e, w, n, s) (III-34)

III.6. Procédure de Résolution

Le résultat de la discrétisation des équations différentielles de transport est un ensemble d’équations algébriques non linéaires. Si on divise le domaine de calcul en N mailles selon x et en M mailles selon y, on aura un système de N×M équations algébriques non linéaire pour chaque variable Ф considérée. Rappelons que les variables Ф, dans notre problème, sont la température T, les deux composantes de la vitesse u et v. Un problème subsiste du fait qu’il n’existe pas d’équation donnant directement le champ de pression. Il faut faire à une méthode itérative. On utilise un algorithme de correction de pression appelé SIMPLE (Semi- Implicit Method for Pressure-Linked).

Page 29

III.6.1. Equation algébrique de pression

Lorsque le champ de pression est connu, le champ de vitesse est obtenu directement par la résolution des équations de quantité de mouvement. Dans le cas où ce champ est inconnu, l’établissement d’une équation de pression est nécessaire.

Dans l’équation de quantité de mouvement, le terme Ф représente les composantes de la vitesse u et v, qui doivent satisfaire l’équation de continuité. Le but est de chercher des champs corrects de pression dans le volume de contrôle. L’intégration de l’équation générale de transport pour u et v sur les deux volumes de contrôle spécifiques aux composantes de vitesse donne les équations suivantes :

𝑎_𝑒𝑢_𝑒 = ∑ 𝑎_𝑛𝑏𝑢_𝑛𝑏+ 𝑏_𝑒+ 𝐴_𝑒(𝑃_𝑃 − 𝑃_𝐸) (III-35)

Avec e b contient tous les termes source de l’équation, sauf ceux de la pression, Le terme 𝐴𝑒(𝑃𝑃 − 𝑃𝐸)Représente les forces de pression et Ai sont les surfaces i= (e, w, n, s).L’étape de

prédiction consiste à donner un champ de pression p* pour obtenir des valeurs estimées de la vitesse u* et v* à partir des équations suivantes :

𝑎𝑒𝑢∗𝑒 = ∑ 𝑎𝑛𝑏𝑢∗𝑛𝑏+ 𝑏𝑒+ 𝐴𝑒(𝑃∗𝑃 − 𝑃∗𝐸) (III-36)

Les vitesses u obtenues à partir de l'équation (III-35) en utilisant la distribution correcte de la pression p (mais généralement inconnue) satisferait la condition de continuité, alors que les vitesses u* de l'équation (III-43) en général violent cette condition. La correction de la pression estimée par p' = p − p* est donc nécessaire pour corriger le champ u* par u' = u − u*. La relation entre p' et u' est obtenue par soustraction d'équation (III-36) d'équation (III-35) :

𝑎_𝑒𝑢′_𝑒 = ∑ 𝑎_𝑛𝑏𝑢′_𝑛𝑏𝐴_𝑒(𝑃′

CHAPITRE III MODELISATION NUMERIQUE

Page 30

La pression p et les vitesses u qui satisfont les équations de la masse et de quantité de mouvement sont :

𝑢 = 𝑢′+ 𝑢∗ (III-38)

𝑝 = 𝑝′_{+ 𝑝}∗ _(III-39)

L'attention est maintenant tournée sur la méthode employée pour trouver p'. L'équation exacte pour p', dérivée d'équations (III.37) et (III.38) et la condition de continuité, est compliqué et peu convenable pour des calculs économiques. Le procédé SIMPLE donne une équation plus appropriée, en négligeant le terme souligné dans l'équation (III.37).

La Combinaison entre l'équation simplifiée (III.37) et l'équation (III.38) donne :

𝑎_𝑒 = 𝑢_𝑒∗+ 𝑑_𝑒(𝑝′_𝑝− 𝑝_𝐸) (III-40)

Ou : 𝑑_𝑒 =𝐴𝑒

𝑎𝑒

L'équation de continuité pour le volume de contrôle montré dans la Fig. III.2 est :

(𝜌𝑢𝐴)_𝑤 − (𝜌𝑢𝐴)_𝑒+ (𝜌𝑢𝐴)_𝑠−(𝜌𝑢𝐴)_𝑛 = 0 (III-41)

En regroupant les différents termes de cette équation peut être finalement mise sous la forme standard :

𝑎_𝑒𝑝′_𝑝 = 𝑎_𝐸𝑝′_𝐸+ 𝑎_𝑤𝑝′_𝑤+ 𝑎_𝑁𝑝′_𝑁+ 𝑎_𝑠𝑝′_𝑠+ 𝑏 (III-42)

Avec :

{𝑎𝐸 = (𝜌𝐴𝑑)𝑒 ; 𝑎𝑊= (𝜌𝐴𝑑)𝑤 𝑎_𝑁 = (𝜌𝐴𝑑)_𝑛 ; 𝑎_𝑆 = (𝜌𝐴𝑑)_𝑠

Page 31

𝑎𝑒 = 𝑎𝐸 + 𝑎𝑤 + 𝑎𝑁+ 𝑎𝑠

(𝜌𝑢∗_𝐴)

𝑤 − (𝜌𝑢∗𝐴)𝑒 + (𝜌𝑣∗𝐴)𝑠 − (𝜌𝑣∗𝐴)𝑛 (III-43)

Cette équation est appelée équation de correction de la pression.

III.6.2. Algorithme SIMPLE

L’algorithme SIMPLE est une procédure de prédiction correction, avec laquelle il nous sera possible de tirer un champ de pression et de vitesse vérifiant à la fois les équations de quantité de mouvement et celle de continuité.

Cet algorithme résume la résolution du problème posé dans les séquences suivantes : .Estimer le champ de pression p*,

.Calculer les coefficients pour les équations de quantité de mouvement et déterminer les vitesses u* et v*,

.Calculer les coefficients pour l’équation de pression et obtenir le champ de pression, .Évaluer la source de masse b [l’équation (III.42)] et résoudre l’équation (III.43) pour p'. .Corriger le champ de vitesse, en utilisant des équations comme équation (III.40). Corriger le champ de pression en utilisant équation (III.39), avec la modification discutée dans le paragraphe suivant (le paragraphe ci-dessous).

.Résoudre les autres équations de Ф ; mettre à jour les propriétés, les coefficients, etc… . Employant le p trouvé dans l'étape 4 comme nouveau p*, revenir à l'étape 2. Faire un cycle par cette boucle jusqu'à ce que la convergence soit réalisée. Pour obtenir équation (III.40) de l’équation (III.37), le terme ∑ 𝑎𝑛𝑏𝑢′𝑛𝑏.doit être négligé. Cette approximation résulté des

valeurs de p' trop grandes, et ceci cause une convergence lente ou divergence du cycle décrit ci-dessus. Pour traiter ceci, Patankar a supposé une valeur de αp dans la gamme de (0.3-0.8), et une sous-relaxation de la correction de pression en remplaçant l’équation (III.39) par :

CHAPITRE III MODELISATION NUMERIQUE

Page 32

III.6.3. Résolution des systèmes d’équations linéaires

Considérons la notation indicielle, utilisée en raison de faciliter la programmation des étapes de calcul. La forme de l’équation de discrétisation de l’équation générale de transport sous la nouvelle notation est :

(𝐴_𝑖,𝑗− 𝑆_{𝑝𝑖,𝑗})∅_𝑖,𝑗− 𝐴_{𝑖,𝑗−1}∅_{𝑖,𝑗−1}− 𝐴_𝑖,𝑗+1∅_𝑖,𝑗+1 = 𝐴_𝑖+1,𝑗∅_𝑖+1,𝑗 + 𝐴_{𝑖−1,𝑗}∅_{𝑖−1,𝑗}+ 𝑆_𝑐 (III-45)

Avec 1 ≤ 𝑖 ≤ 𝑁 𝑒𝑡 1 ≤ 𝑗 ≤ 𝑀

Figure III.7 : Domaine de calcul.

Les coefficients de l’équation précédente sont fonction des variables de transport Ф, une méthode de résolution itérative doit être utilisée à cause de la non-linéarité. Le système (III-45) est écrit sous la forme matricielle suivante :

[A][∅]= [S] (III-46)

Page 33

La technique de balayage permet de transformer le système (III.46), en un système tridiagonal qui peut être résolu par l’algorithme de Thomas TDMA (Tri Diagonal Matrix Algorithme). Considérons le balayage Ouest-Est :

On attribue à la variable Ф pour les lignes (i-1) et (i+1), ses valeurs obtenues lors de l’itération précédente, on aboutit au système suivant :

𝑑𝑖∅𝑖 = 𝐶𝑖 + 𝑏𝑖 ∅𝑗− 1 + 𝑎𝑗 ∅𝑗+1 (III-47) Où : { 𝑎𝑗 = 𝐴𝑖,𝑗+1 𝑏_𝑗 = 𝐴_{𝑖,𝑗−1} 𝐶𝑗 = 𝐴𝑖+1,𝑗 ∅𝑖−1,𝑗+ 𝐴𝑖−1,𝑗 ∅𝑖−1,𝑗+𝑆𝑐 𝑑_𝑗 = 𝐴_𝑖,𝑗−𝑆_𝑐 (III-48)

Cette technique de balayage permet une convergence plus rapide. Le choix de la direction de balayage exigé par les conditions aux limites. La méthode TDMA est utilisée après le balayage pour résoudre les systèmes d’équations correspondantes. Dans l’équation (III.47), Фj est fonction on de Фj+1 et Фj-1, or une équation correspondante au nœud (i, j) peut être écrite de la manière suivante :

∅_𝑗 = 𝑃_𝑗∅_𝑗+1+ 𝑄_𝑗 (III-49)

Une équation correspondante au nœud (i, j-1) est de la forme :

∅_𝑗 = 𝑝_𝑗∅_𝑗−1+ 𝑄_𝑗−1 (III-50)

En introduisant l’expression précédente dans l’expression (III.47), nous aurons : ∅_𝑗 = 𝑎𝑗

𝑑𝑗 −𝑏𝑗𝑃𝑗−1∅𝑗+1+

𝑐𝑗+𝑏𝑗𝑄𝑗−1

𝑑𝑗−𝑏𝑗𝑃𝑗−1 (III-51)

De telle façon que : ∅𝑗 =

𝑎𝑗

𝑑𝑗 −𝑏𝑗𝑃𝑗−1 𝑒𝑡 𝑄𝑗 =

𝑐𝑗+𝑏𝑗𝑄𝑗−1

𝑑𝑗−𝑏𝑗𝑃𝑗−1 (III-52)

Donc il faut calculer P1 et Q1, ensuite P2 et Q2 jusqu’à PN et QN. P₁ = 𝑎1

𝑑₁ , P1 = 𝑐₁

𝑑₁ , 𝑃𝑁= 0 , 𝑄𝑁 = ∅𝑁

La valeur de ФN étant connue d’après les conditions aux limites, on déterminera par retour en arrière ФN-1, ФN-2, …, Ф2 (Ф1 étant connue aux limites), nous balayons dans le sens inverse.