Constructing two-qubit gates with minimal couplings
The MIT Faculty has made this article openly available.
Please share
how this access benefits you. Your story matters.
Citation
Yuan, Haidong et al. “Constructing two-qubit gates with minimal
couplings.” Physical Review A 79.4 (2009): 042309.(C) 2010 The
American Physical Society.
As Published
http://dx.doi.org/10.1103/PhysRevA.79.042309
Publisher
American Physical Society
Version
Final published version
Citable link
http://hdl.handle.net/1721.1/51007
Terms of Use
Article is made available in accordance with the publisher's
policy and may be subject to US copyright law. Please refer to the
publisher's site for terms of use.
Constructing two-qubit gates with minimal couplings
Haidong Yuan,1,
*
Robert Zeier,2 Navin Khaneja,2and Seth Lloyd1 1Department of Mechanical Engineering, MIT, Cambridge, Massachusetts 02139, USA
2
School of Engineering and Applied Science, Harvard University, Cambridge, Massachusetts 02138, USA
共Received 27 July 2008; published 7 April 2009兲
Couplings between quantum systems are frequently less robust and harder to implement than controls on individual systems; thus, constructing quantum gates with minimal interactions is an important problem in quantum computation. In this paper we study the optimal synthesis of two-qubit quantum gates for the tunable coupling scheme of coupled superconducting qubits and compute the minimal interaction time of generating any two-qubit quantum gate.
DOI:10.1103/PhysRevA.79.042309 PACS number共s兲: 03.67.Lx
I. INTRODUCTION
Superconducting systems are among the leading candi-dates for the implementation of quantum information pro-cessing applications关1兴. Due to the ubiquitous bath degrees
of freedom in the solid-state environment, the time over which quantum coherence can be maintained remains lim-ited, although significant progress in lengthening that time has been achieved. A key challenge is how to produce accu-rate quantum gates and how to minimize their duration such that the number of operations within T2 meets the error cor-rection threshold. Concomitantly, progress has been made in applying optimal control techniques to steer quantum sys-tems in a robust, relaxation-minimizing 关2,3兴, or time
opti-mal way 关4–6兴.
In order to perform multiqubit operations, one needs a reliable method to perform switchable coupling between the qubits, i.e., a coupling mechanism that can be easily turned on and off. Over the past few years, there has been consid-erable interest in this question, both theoretically关7–11兴 and
experimentally 关12–22兴. As a practically relevant and
illus-trative example, we consider the tunable coupling scheme for flux qubits and considering building two-qubit gates using minimal coupling time. This is an extension of previous stud-ies of time optimal control关4兴, which considers constructing
quantum gates using one coupling Hamiltonian, to the prob-lem of constructing quantum gates using two or more cou-pling Hamiltonians.
II. SYNTHESIZATION OF TWO-QUBIT GATES In this paper, we will take the tunable coupling scheme proposed in 关23兴 as our main model for superconducting
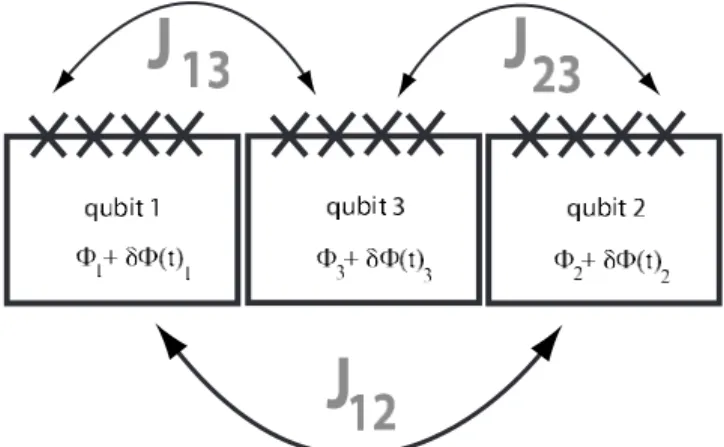
quantum computing, but the methods can be easily general-ized to the other schemes. The tunable coupling scheme in 关23兴 uses an extra high-frequency qubit to obtain the
para-metric ac-modulated coupling, as shown in Fig. 1. As dis-cussed in 关23兴, this coupling scheme has some useful
fea-tures including an optimal point for the effective coupling energy. At such a point the effective coupling energy is in-sensitive to low-frequency flux noise, so two-qubit
oscilla-tions can be expected to be long lasting. This coupling scheme has been recently realized experimentally 关24兴.
The effective Hamiltonian of this system is关23兴
H = −1 2
兺
j=1 2 关⌬jz j− uj共t兲 x j兴 − J 12共t兲x 1 x 2 . 共1兲In this Hamiltonian, the coupling J12共t兲 is modulated
sinusoi-dally at the angular frequency⫾=共⌬2⫾⌬1兲. The essence of the coupling scheme is seen by considering a general modu-lation of the form
J12共t兲 = g0+ g+共t兲cos共+t兲 + g−共t兲cos共−t兲. 共2兲
To perform single-qubit operations we use Rabi oscillations driven by a resonant microwave control field,
uj共t兲 = 2⍀j共t兲cos关⌬jt +j共t兲兴. 共3兲 In this setup all the temporal dependence of the Hamiltonian is assumed to arise from the time-dependent flux of the ap-plied fields. The rotating wave approximation, which is also valid if cross couplings are taken into account, results in a rotating frame Hamiltonian of the form
*haidong@mit.edu
FIG. 1. By modulating external magnetic field on qubit 3, we can turn on and off the effective coupling between qubit 1 and qubit 2.
Hrot=1 2
兺
j=1 2 ⍀j共t兲关cosj共t兲x j − sinj共t兲y j兴 −g+共t兲 4 共x 1 x 2− y 1 y 2兲 −g−共t兲 4 共x 1 x 2+ y 1 y 2兲.Here, g+共t兲 and g−共t兲 are the effective coupling strengths in
the rotating frame when we apply magnetic field with fre-quencies +and−, respectively, on the auxiliary qubit.
The problem of using one given coupling Hamiltonian and local operations to simulate another Hamiltonian has been extensively studied in 关4,5兴. What is different here is
that instead of one given coupling Hamiltonian, we have two tunable coupling Hamiltonians:
H1=x 1 x 2 −y 1 y 2 , H2=x 1 x 2 +y 1 y 2 . 共4兲
Combining with local controls, we want to find out the mini-mal coupling time synthesizing any given two-qubit gate. Note that our result can be easily generalized to simulating Hamiltonian using two general coupling Hamiltonians or multiple coupling Hamiltonians.
We first review some background materials.
Proposition 1 (Canonical decomposition [4,25]). Any two-qubit nonlocal Hamiltonian H =兺i,jMij共t兲i丢j, i , j 苸兵x,y,z其 can be written in the form
H =共A丢B兲†共H1x丢x+2 H y丢y+3 H z丢z兲共A丢B兲 共5兲 and any two-qubit unitary U苸SU共4兲 may be written in the form
U =共A1丢B1兲e−i共1
U x 丢x+2 U y 丢y+3 UZ 丢Z兲共A 2丢B2兲. 共6兲
Here A, A1, A2, B, B1, and B2are single-qubit unitaries and
1 Hⱖ 2 Hⱖ 兩 3 H兩, 4 ⱖ1 Uⱖ 2 Uⱖ 兩 3 U兩. 共7兲 We call 1Hx丢x+2 H y丢y+3 H z丢z and e−i共1 U x 丢x+2 U y 丢y+3 U
z 丢z兲 the canonical form of H and U, respectively, and ជHand ជU the canonical parameters of H and U, respectively.
For an element x =共x1, x2, x3兲TofR3, introduce the vector
xˆ =共兩x1兩,兩x2兩,兩x3兩兲Tand define the s-order version xs of x by
setting x1s= xˆ1↓, x2s= xˆ2↓, and x3s= sgn共x1x2x3兲xˆ3↓, where 共xˆ1↓, xˆ2↓, xˆ3↓兲 is a permutation of xˆ which arranges the entries in
decreasing order, i.e., xˆ1↓ⱖxˆ2↓ⱖxˆ3↓.
Definition 1 [26–30]. The vector x苸R3is s majorized by
y苸R3 共denoted xⱮsy兲 if
x1sⱕ y1s,
x1s+ x2s+ x3sⱕ y1s+ y2s+ y3s,
x1s+ x2s− x3sⱕ y1s+ y2s− y3s. 共8兲
Remark 1. xⱮsy means that x lies in the convex hull of 兵共⑀1y共1兲,⑀2y共2兲,⑀3y共3兲兲兩⑀1,2,3=⫾1, 兿i=13 ⑀i= 1 , is permu-tation on兵1,2,3其其.
From now on, when we say constructing a gate in time T, we mean constructing the gate with coupling time less or equal to T, aided by local operations.
Theorem 1 [5]. A unitary gate U苸SU共4兲 can be generated in coupling time T if and only if we can simulate a Hamil-tonian H˜ in coupling time T, such that ជUⱮsជH˜ or ជU +2共−1,0,0兲ⱮsជH˜. For a given Hamiltonian H共t兲, the Hamil-tonians that can be simulated within time T using H共t兲 and local control are the Hamiltonians with the canonical forms of the following:
再
1x丢x+2y丢y+3z丢z兩 共1,2,3兲Ɱs冕
0 T ជH共t兲dt, 1ⱖ2ⱖ 兩3兩冎
.This theorem reduces our problem to the integration of the canonical form of
H共t兲 = g+共t兲共x1x2−1yy2兲 + g−共t兲共x1x2+y1y2兲 =„g+共t兲 + g−共t兲…x1x2+„g−共t兲 − g+共t兲…y1y2 共9兲 while we absorbed the constant 14 into g+共t兲 and g−共t兲 and
here g+共t兲 and g−共t兲 are both non-negative. We need to find
out the boundary of 兰0TជH共t兲dt, as all the Hamiltonians that can be simulated within time T is s majorized by one of the points on the boundary. We study the problem in two cases: Case 1. The magnetic fields of frequencies+and−can
be generated power independently, i.e., g+ and g− are
con-strained independently. Let us say they take values indepen-dently in the ranges of关0,A兴 and 关0,B兴.
Using Proposition 1, we get the canonical parameter of the Hamiltonian共9兲, which is
„g+共t兲 + g−共t兲,兩g−共t兲 − g+共t兲兩,0….
We will see that it is actually s majorized by 共A + B,兩A − B兩,0兲 since g+共t兲 + g−共t兲 ⱕ A + B, g+共t兲 + g−共t兲 + 兩g−共t兲 − g+共t兲兩 = max兵2g+共t兲,2g−共t兲其 ⱕ max兵2A,2B其 = A + B +兩A − B兩,
so (g+共t兲+g−共t兲,兩g−共t兲−g+共t兲兩,0)Ɱs共A+B,兩A−B兩,0兲 for all t.
Then given a unitary matrix U苸SU共4兲, the minimal cou-pling time needed to generate U is the minimal T such that
ជUⱮs„共A + B兲T,兩A − B兩T,0… or
YUAN et al. PHYSICAL REVIEW A 79, 042309共2009兲
ជU+
2共− 1,0,0兲Ɱs„共A + B兲T,兩A − B兩T,0… holds.
For example, suppose we want to generate a
controlled-NOT共CNOT兲 gate, CNOT= exp
冋
− i4
冉
z丢x−z丢I − I丢x+ 1 2I冊
册
. The canonical parameter of CNOT is 共4, 0 , 0兲. The two in-equalities coincide in this case, so the minimal coupling time needed is the minimal T such that冉
4,0,0
冊
Ɱs„共A + B兲T,兩A − B兩T,0…, which is 4共A+B兲 .Case 2. The magnetic fields of frequencies⫾are gener-ated power correlgener-ated, i.e., g+and g−are jointly constrained,
g+2+ g−2ⱕM2. In this case the situation is more subtle as there
is no single point, like共A+B,兩A−B兩,0兲, that s majorizes all the points in the region.
Since xជⱮsDxជwhen Dⱖ1, to be at the boundary, g+共t兲 and
g−共t兲 should take maximal values. Let g+共t兲=M sin␣共t兲 and
g−共t兲=M cos␣共t兲, where ␣共t兲苸关0,4兴 共as ␣ and
2−␣ give
the same canonical parameter, we will just consider ␣ 苸关0,4兴兲, then integration of these canonical parameters give
a set of boundary points,
冉
冕
0 T g+共t兲 + g−共t兲dt,冕
0 T 兩g−共t兲 − g+共t兲兩dt,0冊
.In the case that␣ is constant, we obtain
冉
冕
0 T g+共t兲 + g−共t兲dt,冕
0 T 兩g−共t兲 − g+共t兲兩dt,0冊
= TM共sin␣+ cos␣,cos␣− sin␣,0兲 = TM
冠
冑
2 sin冉
␣+4
冊
,冑
2 cos冉
␣+
4
冊
,0冡
. 共10兲 In the general case where␣ varies in time, we get冉
冕
0 T g+共t兲 + g−共t兲dt,冕
0 T 兩g−共t兲 − g+共t兲兩dt,0冊
=冉
冕
0 T M sin„␣共t兲… + M cos„␣共t兲…dt,冕
0 T M cos„␣共t兲… − M sin„␣共t兲…dt,0冊
共11兲 =冉
兺
i=1 T/␦tM共sin„␣共ti兲… + cos„␣共ti兲…兲␦t,
兺
i=1 T/␦t
M共cos„␣共ti兲… − sin„␣共ti兲…兲␦t,0
冊
共12兲=
兺
i=1 T/␦t ␦t TTM冠
冑
2 sin冉
␣共ti兲 + 4冊
,冑
2 cos冉
␣共ti兲 + 4冊
,0冡
. 共13兲 This is just the convex combination of the points we ob-tained by constant␣, and lies in the interior of those points, so all the boundary points are achieved by constant␣.So given a unitary matrix U苸SU共4兲, the minimal time needed to generate U is the minimal T such that ∃␣ 苸关0,4兴, ជUⱮs TM
冠
冑
2 sin冉
␣+ 4冊
,冑
2 cos冉
␣+ 4冊
,0冡
or ជU + 2共− 1,0,0兲ⱮsTM冠
冑
2 sin冉
␣+ 4冊
,冑
2 cos冉
␣+ 4冊
,0冡
. Again taking CNOT, for example, the minimal time needed to generate it is the minimal T such that冉
4,0,0冊
ⱮsTM冠
冑
2 sin冉
␣+ 4冊
,冑
2 cos冉
␣+ 4冊
,0冡
holds for one ␣苸关0,4兴. It is obvious that ␣=4 gives the minimal time T =4冑2M. So to generate CNOT, we should take g+共t兲=g−共t兲=冑2M
2 , turning on the coupling for a time 4冑2M.
This control sequence generates the term exp关−i4x丢x兴, which is locally equivalent to the CNOT gate.
III. CONCLUSION
To perform large-scale quantum information processing, it is necessary to control the interactions between individual qubits while retaining quantum coherence. To this end, su-perconducting circuits allow for a high degree of flexibility. In this paper, we found the minimal coupling time required to generate arbitrary two-qubit quantum gate in the super-conducting quantum computing scheme. We reduced this problem to the problem of simulating a desired Hamiltonian using two Hamiltonians and single-qubit operations and de-rived explicit forms to compute the minimal time needed to control the system. The results of this work might be useful for guiding the design of pulses in superconducting quantum computing experiments. Minimizing the time taken to per-form an operation is certainly helpful in the presence of finite decoherence times. If one were able to take into account the specific form and time dependence of the environmental cou-pling, one might be able to devise more robust schemes. While it lies outside the scope of the current paper, it might be interesting to combine the time optimal control techniques with methods that take advantage of correlations in the noise, e.g., implementing refocusing sequences to counteract the effects of 1/ f noise 关31,32兴. Such optimization in the face of
the combination of several different types of constraints is a challenging problem in both classical and quantum control theories.
关1兴 For recent reviews on the subject, see, e.g., J. Q. You and F. Nori, Phys. Today 58 共11兲, 42 共2005兲; G. Wendin and V. Shumeiko, in Handbook of Theoretical and Computational
Nanotechnology, edited by M. Rieth and W. Schommers共ASP,
Los Angeles, 2006兲.
关2兴 N. Khaneja, B. Luy, and S. J. Glaser, Proc. Natl. Acad. Sci. U.S.A. 100, 13162共2003兲.
关3兴 D. Stefanatos, N. Khaneja, and S. J. Glaser, Phys. Rev. A 69, 022319共2004兲.
关4兴 N. Khaneja, R. Brockett, and S. J. Glaser, Phys. Rev. A 63, 032308共2001兲.
关5兴 H. Yuan and N. Khaneja, Phys. Rev. A 72 040301共R兲 共2005兲. 关6兴 N. Khaneja, B. Heitmann, A. Spoerl, H. Yuan, T. Herbrueggen,
and S. J. Glaser, Phys. Rev. A 75, 012322共2007兲.
关7兴 Y. Makhlin et al., Nature 共London兲 398, 305 共1999兲; J. Q. You, J. S. Tsai, and F. Nori, Phys. Rev. Lett. 89, 197902 共2002兲; Phys. Rev. B 68, 024510共2003兲; D. V. Averin and C. Bruder, Phys. Rev. Lett. 91, 057003共2003兲; B. L. T. Plourde, J. Zhang, K. B. Whaley, F. K. Wilhelm, T. L. Robertson, T. Hime, S. Linzen, P. A. Reichardt, C. E. Wu, and J. Clarke, Phys. Rev. B
70, 140501共R兲 共2004兲.
关8兴 C. Rigetti, A. Blais, and M. Devoret, Phys. Rev. Lett. 94, 240502共2005兲.
关9兴 Y. X. Liu, L. F. Wei, J. S. Tsai, and F. Nori, Phys. Rev. Lett.
96, 067003共2006兲.
关10兴 P. Bertet, C. J. P. M. Harmans, and J. E. Mooij, Phys. Rev. B
73, 064512共2006兲; M. Grajcar, Y. X. Liu, F. Nori, and A. M.
Zagoskin, ibid. 74, 172505共2006兲.
关11兴 S. Ashhab, S. Matsuo, N. Hatakenaka, and F. Nori, Phys. Rev. B 74, 184504共2006兲.
关12兴 Yu. A. Pashkin et al., Nature 共London兲 421, 823 共2003兲. 关13兴 P. R. Johnson, F. W. Strauch, A. J. Dragt, R. C. Ramos, C. J.
Lobb, J. R. Anderson, and F. C. Wellstood, Phys. Rev. B 67, 020509共R兲 共2003兲.
关14兴 A. J. Berkley et al., Science 300, 1548 共2003兲. 关15兴 T. Yamamoto et al., Nature 共London兲 425, 941 共2003兲. 关16兴 A. Izmalkov, M. Grajcar, E. Ilichev, T. Wagner, H. G. Meyer,
A. Y. Smirnov, M. H. S. Amin, A. Maassen van den Brink, and A. M. Zagoskin, Phys. Rev. Lett. 93, 037003共2004兲. 关17兴 H. Xu et al., Phys. Rev. Lett. 94, 027003 共2005兲. 关18兴 R. McDermott et al., Science 307, 1299 共2005兲.
关19兴 J. B. Majer, F. G. Paauw, A. C. J. ter Haar, C. J. P. M. Har-mans, and J. E. Mooij, Phys. Rev. Lett. 94, 090501共2005兲. 关20兴 B. L. T. Plourde, T. L. Robertson, P. A. Reichardt, T. Hime, S.
Linzen, C. E. Wu, and J. Clarke, Phys. Rev. B 72, 060506共R兲 共2005兲.
关21兴 T. Hime et al., Science 314, 1427 共2006兲.
关22兴 S. H. W. van der Ploeg, A. Izmalkov, A. M. van den Brink, U. Hubner, M. Grajcar, E. Ilichev, H. G. Meyer, and A. M. Za-goskin, Phys. Rev. Lett. 98, 057004共2007兲.
关23兴 A. O. Niskanen, Y. Nakamura, and J.-S. Tsai, Phys. Rev. B 73, 094506共2006兲.
关24兴 A. O. Niskanen, K. Harrabi, F. Yoshihara, Y. Nakamura, S. Lloyd, and J. S. Tsai, Science 316, 723共2007兲.
关25兴 B. Kraus and J. I. Cirac, Phys. Rev. A 63, 062309 共2001兲. 关26兴 R. Bhatia, Matrix Analysis 共Springer-Verlag, New York, 1997兲. 关27兴 A. Horn, Am. J. Math. 76, 620 共1954兲.
关28兴 C. H. Bennett, J. I. Cirac, M. S. Leifer, D. W. Leung, N. Linden, S. Popescu, and G. Vidal, Phys. Rev. A 66, 012305 共2002兲.
关29兴 G. Vidal, K. Hammerer, and J. I. Cirac, Phys. Rev. Lett. 88, 237902共2002兲.
关30兴 K. Hammerer, G. Vidal, and J. I. Cirac, Phys. Rev. A 66, 062321共2002兲.
关31兴 H. Gutmann, F. K. Wilhelm, W. M. Kaminsky, and S. Lloyd, Quantum Inf. Process. 3, 247共2004兲.
关32兴 K. Shiokawa and D. A. Lidar, Phys. Rev. A 69, 030302共R兲 共2004兲.
YUAN et al. PHYSICAL REVIEW A 79, 042309共2009兲