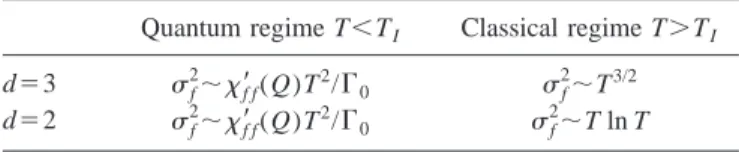Critical phenomena near the antiferromagnetic quantum critical point of heavy fermions

HAL Id: hal-01896145

https://hal.archives-ouvertes.fr/hal-01896145

Submitted on 16 Oct 2018

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Critical phenomena near the antiferromagnetic quantum

critical point of heavy fermions

M. Lavagna, Catherine Pepin

To cite this version:

M. Lavagna, Catherine Pepin. Critical phenomena near the antiferromagnetic quantum critical point of

heavy fermions. Physical Review B: Condensed Matter and Materials Physics (1998-2015), American

Physical Society, 2000. �hal-01896145�

Critical phenomena near the antiferromagnetic quantum critical point of heavy fermions

M. Lavagna1,*and C. Pe´pin2

1

Commissariat a` l’Energie Atomique, DRFMC /SPSMS, 17, rue des Martyrs, 38054 Grenoble Cedex 9, France 2_{Department of Physics, University of Oxford, 1 Keble Road, Oxford OX1 3NP, United Kingdom}

共Received 18 January 2000; revised manuscript received 27 April 2000兲

We present a paper of the critical phenomena around the quantum critical point in heavy-fermion systems. In the framework of the S⫽1/2 Kondo lattice model, we introduce an extended decoupling scheme of the Kondo interaction, which allows one to treat the spin fluctuations and the Kondo effect on an equal footing. The calculations, developed in a self-consistent one-loop approximation, lead to the formation of a damped collective mode with a dynamic exponent z⫽2 in the case of an antiferromagnetic instability. The system displays a quantum-classical crossover at finite temperature depending on how the energy of the mode, on the scale of the magnetic correlation length, compares to kBT. The low-temperature behavior, in the different regimes separated by the crossover temperatures, is then discussed for both two- and three-dimensional systems.

I. INTRODUCTION

A central issue in the thermal properties of heavy-fermion

compounds is the discovery of a non-Fermi liquid 共NFL兲

behavior in systems close to an antiferromagnetic quantum

phase transition.1 Such a behavior has been discovered in a

series of compounds containing cerium or uranium, for

example, CeCu6⫺xRx (R⫽Au,Ag),

2

CeIn3, CePd2Si2, 3

CeNi2Ge2,4 U1⫺xYxPd3,5 and CexLa1⫺xRu2Si2.6 In

CeCu5.9Au0.1, the specific heat C depends on T as C/T

⬃⫺ln(T/T0), the magnetic susceptibility as␹⬃1⫺␣

冑

T, and

the T-dependent part of the resistivity as⌬␳⬃T 共instead of

C/T⬃␹⬃const and ⌬␳⬃T2 in the Fermi-liquid state兲. Most interestingly, the breakdown of the Fermi-liquid behavior

can be tuned by alloying共chemical pressure兲 or by applying

a hydrostatic pressure or a magnetic field. The origin of this NFL behavior is a problem of current debate.

Different scenarios have been proposed in order to

eluci-date the NFL behavior at the quantum critical point 共QCP兲.

On the one hand, there are scenarios involving strong disor-der to account for the non-Fermi liquid properties, including

共i兲 a distribution of the Kondo temperature P(TK) 共Ref. 7兲

induced by disorder following a distribution of the local density-of-states, and共ii兲 the possibility of the formation of a

Griffiths phase at the quantum critical point.8,9On the other

hand, starting from a clean or rather weakly disordered

sys-tem, there is a scenario 共iii兲 referring to the proximity of a

quantum critical point in a theory of itinerant

antiferromagnetism,10–17 in which the Fermi surface is

coupled to critical collective antiferromagnetic excitations.

An alternative possibility has been recently put forward18on

the basis of an analysis of the neutron scattering

measure-ments in CeCu5.9Au0.1. The unusual spin dynamics that has

been observed suggests 共iv兲 the existence of critically

screened local magnetic excitations due to the formation of

local moments. Finally, 共v兲 a variant of the quadrupolar

Kondo effect19 in which the interactions of the rare-earth

共actinide兲 internal degrees of freedom with the conduction

electrons are reduced to a single impurity multichannel

Kondo effect has been proposed. As it stands, the situation remains highly controversial.

In this paper, we adopt the point of view共iii兲 of the

prox-imity to a quantum critical point. The effect of a nonzero temperature on quantum critical points is a long-standing problem encountered in itinerant magnetism. We refer to the

papers of Hertz20 and Millis11 using renormalization-group

techniques, and of Moriya21 introducing a self-consistent

renormalization 共SCR兲 theory of spin fluctuations. These

theories yield a rich phase diagram with, in addition to the

ordering temperature TN, a series of crossover temperatures

separating different regimes of behaviors. They are well adapted for the treatment of spin fluctuations as present in the single-band Hubbard model but essentially do not ac-count for the Kondo effect.

Indeed, the model that is believed to describe the physics

of heavy fermions is the Kondo lattice model22derived from

the periodic Anderson model in a given limit. The large N

expansions,23which have been carried out for these models

共where N represents simultaneously the degeneracy of the

conduction electrons and of the spin channels兲 give a good

description of the Kondo effect. But, unlike the above-mentioned spin-fluctuation theories, they fail to account for the spin fluctuations since the Ruderman-Kittel-Kasuya-Yosida interactions only appear at the order 1/N2_.24

Hence our motivation to set up an approach of the S

⫽1/2 Kondo lattice model (N⫽2) that enlarges the standard

1/N expansion theories up on the spin-fluctuation effects.

Our previous paper25 presented such an approach by

per-forming a generalized Hubbard-Stratonovich transformation on the Kondo interaction term of the Hamiltonian, which

makes three types of fields 共magnetization densities and

Kondo type兲 appear on an equal footing. The dynamical spin

susceptibility was derived in a one-loop expansion associated with the Gaussian fluctuations of the magnetization density fields around their saddle-point values.

With the aim to describe the critical phenomena around the quantum critical point of the heavy-fermion systems, we

propose to push the treatment of the S⫽1/2 Kondo lattice

model in a self-consistent one-loop approximation in

com-PRB 62

plete analogy with the SCR theory of spin fluctuations

de-veloped for the Hubbard model.21,26,27As in itinerant

mag-netism, we will show how the system displays a quantum-classical crossover at finite temperature depending whether the temperature is lower or higher than the characteristic en-ergy scale of the collective mode associated with the mag-netic instability. The low-temperature behavior in the differ-ent regimes essdiffer-entially depends on the value of the dynamic exponent z of the mode and on the dimensionality d of the problem. In the case of an antiferromagnetic instability, z is found to be equal to 2. Heavy-fermion systems are usually believed to be three dimensional. However, a recent

proposal28 based on the neutron-scattering data obtained in

CeCu6⫺xAux, stipulates that the critical magnetic

fluctua-tions, which the quasiparticles are coupled to, are simply two

dimensional. So both situations d⫽2 and d⫽3 will be

con-sidered.

The rest of the paper is organized as follows. In Sec. II, we introduce the self-consistent one-loop approximation method for the Kondo lattice model using a generalized Hubbard-Stratonovich transformation on the Kondo interac-tion term. The approach combines both aspects of the 1/N expansion and of the self-consistent renormalization theory of spin fluctuations. The calculations, presented in the func-tional integral formalism, closely follow the presentation

made by Hertz and Klenin27for the Hubbard model. Hence,

we extract the general expression of the dynamical spin

sus-ceptibility extending the results of the previous paper25 to a

self-consistent treatment. Section III gives a discussion on the nature of the damped collective mode associated to the proximity of the magnetic transition with a dynamic

expo-nent z⫽2 in the antiferromagnetic case. In Sec. IV, we

de-rive the resulting quantum-classical crossover. This occurs at a finite temperature T, which depends on how the energy of

the mode, on the scale of the magnetic correlation length ␰

compares to kBT. The low-temperature behavior of the

sys-tem in the different regimes, separated by the crossover sys- tem-peratures, is then discussed in Sec. V. Concluding remarks follow in Sec. VI.

II. SELF-CONSISTENT ONE-LOOP APPROXIMATION TO THE KONDO LATTICE MODEL

This section extends the approach introduced in our

pre-vious paper25 to a self-consistent one-loop approximation.

Our starting point is a path-integral treatment of the Kondo lattice model Hamiltonian

H⫽

兺

k␴ ␧k c_k†_␴ck␴⫹J

兺

i Sf i•

兺

␴␴⬘ci␴ † _␶ ␴␴_⬘ci␴⬘ ⫺␮

冉

兺

i␴ c_i†_␴ci␴⫺ncNS

冊

, 共1兲

where Sf i represents the spin (S⫽1/2) of the impurities

dis-tributed on the sites共in number NS) of a periodic lattice; ck␴ †

is the creation operator of the conduction electron of

momen-tum k and spin quanmomen-tum number␴ characterized by the

en-ergy ⑀k⫽⫺兺具i, j典ti jexp(ik•Ri j); ␶ are the Pauli matrices

(␶x,␶y,␶z) and␶0the unit matrix; J is the antiferromagnetic

Kondo interaction (J⬎0). The Hamiltonian is written in the

grand canonical ensemble with the introduction of a

chemi-cal potential ␮ in order to guarantee an average number of

conduction electrons per site nc⬍1. The spin of the

impuri-ties is treated within the Abrikosov pseudofermion represen-tation Sf i⫽兺␴␴⬘fi␴

† _␶

␴␴_⬘fi␴⬘ where the local constraint Qi ⫽兺_␴f_i⫹_␴f_i␴⫺1⫽0 is implemented in the usual way, by

in-troducing a time-independent Lagrange multiplier ␭_i. The

local Kondo interaction is decoupled using a Hubbard-Stratonovich transformation, which introduces four auxiliary fields ⌽i(␶), ⌽i*(␶), and ␰f_i(␶), ␰c_i(␶). We are then left

with the effective action

Se f f⫽

冕

0

␤

d␶关L0共␶兲⫹HJ共␶兲兴,

whereL0(␶) is the Lagrangian in the absence of the

interac-tion J and HJ共␶兲⫽

兺

i␴␴⬘ 关ci␴ †_共␶兲f i␴ † _共␶兲兴 ⫻

冉

⫺JS i␰f_i共␶兲•␶␴␴⬘ JC⌽i*共␶兲␶_␴␴⬘ 0 J_C⌽_i共␶兲␶_␴␴ ⬘ 0 _⫺J Si␰c_i共␶兲•␶␴␴⬘

冊

⫻

冉

ci␴⬘共␶兲 f_i␴⬘共␶兲

冊

⫹JC

兺

i ⌽i *_共␶_兲⌽i共␶兲 ⫹JS

兺

i ␰fi共␶兲•␰ci共␶兲, 共2兲

with JS⫽J/4 and JC⫽J/3. Details on the saddle-point

solu-tion and the Gaussian fluctuasolu-tions can be found in our

pre-vious paper.25The saddle-point solution transposes to N⫽2

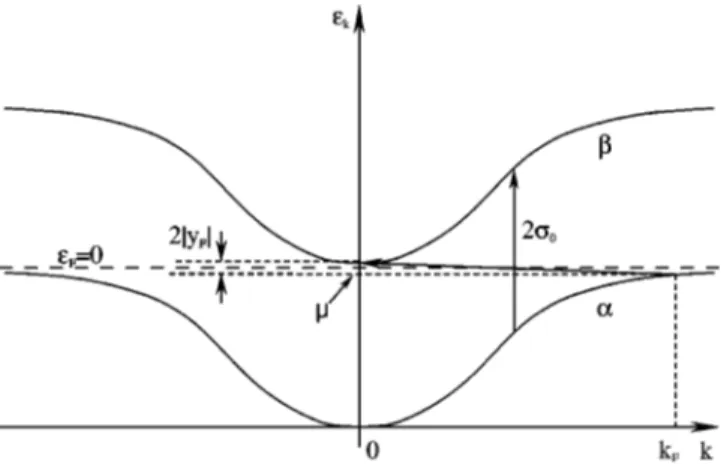
the large-N results obtained within the slave-boson mean-field theories. It gives rise to the formation of a Abrikosov-Suhl resonance pinned at the Fermi level and split by a

hy-bridization gap defining two bands ␣ and␤. The one-loop

approximation is then obtained by considering the Gaussian fluctuations of the bosonic fields around their mean-field val-ues. As in the conventional approaches to critical phenom-ena, the approach consists to integrate out the fermion fields and thereby reduce the problem to the study of an effective bosonic theory describing fluctuations of the ordering fields.

But contrary to Hertz20and Millis,11who considered a single

field corresponding to the magnetization density of one type of electron, the approach, starting from a different micro-scopic model, extends the description to the case of several fields, i.e., the Kondo fields on the one hand, and the f- and c- magnetization densities on the other hand.

We now propose to include the self-consistent effects in the one-loop approximation. We do it in a variational way and replace the full expression Se f f⫺Se f f

(0) _{共where S} e f f (0)

and F(0)are the zeroth order effective action and the related free energy兲 by a trial quadratic form ⌬S˜e f f

(2)_⫽S˜ e f f (2)_⫺S e f f (0) in the fields␦rq,␯, ␦␭q,␯, ␦␰f_q,␯, and␦␰c_q,␯working in the radial

gauge for the Kondo parameters29 using Fourier transform

notations

⌬S˜e f f (2)_⫽1 ␤ q,i

兺

␻_␯

冋

共␦ rq,␯␦␭q,␯兲D˜C⫺1共q,i␻␯兲

冉

␦r_⫺q,⫺␯ ␦␭⫺q,⫺␯

冊

⫹共␦␰f q,␯ z _␦␰ cq,␯ z _兲D˜ S 储⫺1_共q,i␻ ␯兲

冉

␦$xiz_f⫺q,⫺␯ ␦␰c⫺q,⫺␯ z

冊

⫹共␦␰⫹f q,␯␦␰cq,⫹ ␯兲D˜⬜⫺1S 共q,i␻␯兲

冉

␦␰f⫺⫺q,⫺␯ ␦␰c⫺⫺q,⫺␯

冊

⫹共␦␰⫺f q,␯␦␰cq,⫺ ␯兲D˜⬜⫺1S 共q,i␻␯兲

冉

␦␰f⫹⫺q,⫺␯ ␦␰c⫹⫺q,⫺␯

冊册

, 共3兲

where the indices q and ␯, respectively, stand for the wave

vector q and the bosonic Matsubara frequencies i␻_␯

⫽2␯i␲/␤. Note that Eq.共3兲 is written using the radial gauge

in which the phase of the fields ⌽i and⌽i* is incorporated

into the Lagrange multiplier␭i, which turns out to be a field.

The elements of the matrices D˜_C⫺1(q,i␻_␯), D˜_S储⫺1(q,i␻_␯)

and D˜⬜⫺1_S (q,i␻_␯) are determined variationally by minimiz-ing the free energy or, more precisely, the upper bound to the free energy according to the Feynman variational principle F⭐F˜_{e f f}(2)⫹1/␤

具

Se f f⫺S˜e f f

(2)

_典

where F˜_{e f f}(2) represents the free en-ergy related to S˜_{e f f}(2) and

具

A

典

means the average of the quan-tity A over the distribution of fields exp(⫺⌬S˜_{ef f}(2)), i.e.,

具

A

典

⫽

冕

DriD␭iD␰f_iD␰c_iA exp共⫺⌬S˜e f f (2)_兲

冕

DriD␭iD␰f_iD␰c_i)exp共⫺⌬S˜e f f (2)_兲 . 共4兲

After minimization, one can show that关D_C⫺1(q,i␻_␯)兴r_␭is

equal to (1/2)⳵2Se f f/(⳵rq,␯⳵␭⫺q,⫺␯) averaged over the

mentioned distribution of fields 共and equivalent expressions

for the other elements兲. Explicitly we obtain,

D˜_C⫺1共q,i␻_␯兲⫽

冉

JC关1⫺JC共

具

␸¯2共q,i␻␯兲

典

⫹

具

¯␸m共q,i␻␯兲

典

兲兴 ⫺JC

具

␸¯1共q,i␻␯兲

典

⫺JC

具

␸¯1共q,i␻␯兲

典

⫺

具

␸¯f f共q,i␻␯兲

典

冊

, 共5兲

D˜_S储⫺1共q,i␻_␯兲⫽

冉

J_S2

具

␸_cc储 共q,i␻_␯兲

典

JS关1⫹JS

具

␸储f c共q,i␻␯兲

典

兴

J_S关1⫹J_S

具

␸_{c f}储 共q,i␻_␯兲

典

兴 J_S2

具

␸_{f f}储 共q,i␻_␯兲

典

冊

,

and an equivalent expression for the transverse spin part D˜⬜⫺1_S (q,i␻_␯). The different bubbles

具

␸(q,i␻_␯)

典

in the latter

expressions represent the susceptibilities ␸(q,i␻_␯) 共cf.

appendix兲 averaged over the distribution of fields

exp(⫺⌬S˜_{ef f}(2)). At that point, the problem is highly complex and cannot be solved exactly. Therefore, we introduce a local and instantaneous approximation that is equivalent to

aver-aging over Gaussian distributions of local fields

(r_i,␭_i,␰_f

i,␰ci) with variances␴r, ␴␭, ␴f, and ␴cdefined

as ␴f 2_⫽3

兺

q,i␻_␯ 关D ˜ S 储_共q,i␻ ␯兲f f兴, 共6兲

and similar expressions for the three other variances. Equa-tion 共6兲 is obtained from Eq. 共3兲 by letting the summation

over (q,i␻_␯) act on the matrix elements only, hence defining

the local and instantaneous fluctuations of the various de-grees of freedom. One expects that at low temperatures, the fluctuations of ri, ␭i, and␰c_i only bring T2 corrections to

their saddle-point values. Those corrections are negligible compared to the T dependence brought by the fluctuations of

␰f_iand will not be considered here. So we will neglect, in the

following, the fluctuations of ri, ␭i, and ␰c_i, and focus on

the fluctuations of␰f_i only. Then

具

␸(q,i␻␯)

典

is simply given

by

具

␸共q,i␻␯兲

典

⫽

冉

冕

D␰f_i␸共q,i␻␯兲exp关⫺␰f_i 2 /共2␴2_f兲兴

冊

冉

冕

D␰f_iexp关⫺␰f_i 2_/共2␴ f 2_兲兴

冊

. 共7兲

Equations 共6兲–共7兲 are the basic equations of the paper

from which the dynamical spin susceptibility is extracted and the critical phenomena around the QCP are studied. Let us note that, when the averages acting on the various bubbles

␸(q,i␻_␯) in Eq.共5兲 are omitted, one recovers the standard

results of the random-phase approximation. As pointed out

by Lonzarich and Taillefer,30 the corresponding

self-consistent renormalized spin fluctuation SCR-SF procedure can be analyzed within the Ginzburg-Landau formalism in which the local free energy is expanded in terms of a small

and slowly varying order parameter m(r) as f (r)⫽ f0

⫹1 2a兩m(r)兩 2_⫹1 4b兩m(r)兩 4_⫹1 2c兺i兩“m i_(r)兩2_{⫹O(6) and}

the following approximation is made 兩m(r)兩4

⫽

具

兩m(r)兩2

_典

_兩m(r)兩2_{. Hence}

_具

_兩m(r)兩2

_典

_{is evaluated via the}

fluctuation-dissipation theorem.

The expression of the dynamical spin susceptibility is then derived in the usual way, by adding a source term

⫺2Sf•B to the Hamiltonian. In the Matsubara

␹f f共q,i␻␯兲⫽

具

␸f f共q,i␻␯兲

典

1⫺J_S2

冋

具

␸f f共q,i␻␯兲

典具

␸cc共q,i␻␯兲

典

⫺

具

␸f c共q,i␻␯兲

典

2⫺

2

J_S

具

␸f c共q,i␻␯兲

典

册

. 共8兲

In the low-frequency limit, one can easily check that the dynamical spin susceptibility may be written in terms of intra- and interband suceptibilities corresponding,

respec-tively, to particle-hole pair excitations within the lower ␣

band and from the lower␣ to the upper␤ band

␹f f共q,i␻␯兲⫽

具

␹¯_{␣␣共q,i␻␯兲}

_典

_⫹

_具

¯_{␹␣␤共q,i␻␯兲}

_典

1⫺J_S2

具

␹_␣␣共q,i␻_␯兲

典具

␹¯_␣␤共q,i␻_␯兲

典

. 共9兲

The expressions of the susceptibilities ␹_␣␣(q,i␻_␯) and

␹

¯

␣␤(q,i␻␯), corresponding to intra- and interband

particle-hole excitations are given in the Appendix. The latter expres-sion is reminiscent of the behavior proposed by Bernhoeft

and Lonzarich31to explain the neutron scattering observed in

U Pt3 with the existence of both a ‘‘slow’’ and a ‘‘fast’’

component in␹

⬙

(q,␻)/␻due to spin-orbit coupling. Also in

a phenomenological way, the same type of feature has been suggested in the duality model developed by Kuramoto and

Miyake.32 To our knowledge, the proposed approach

pro-vides the first microscopic derivation from the Kondo lattice model of such a behavior. Expanding the various

suscepti-bilities ␸ up to the second order in ␰f_i, and making use of

Eq.共7兲, one can draw from Eq. 共9兲 the following expression

of the dynamical spin susceptibility 共taking the analytical

continuation i␻_␯→␻⫹i␦) ␹f f共q,␻兲⫽ ␹␣␣共q,␻兲⫹¯␹␣␤共q,␻兲 1⫺JS 2_␹ ␣␣共q,␻兲␹¯␣␤共q,␻兲⫹␭␴f 2, 共10兲

where␭ is a constant which can be evaluated from the

ex-pansion of

具

␹_␣␣(q,i␻_␯)

典

and

具

¯␹_␣␤(q,i␻_␯)

典

up to the second order in␴2_f. The variance␴_f2defined by Eq.共6兲 can as well be expressed as a function of␹_{f f}(q,i␻_␯)

␴f 2_⫽

兺

q,i␻_␯ ␹f f共q,i␻␯兲⫽ 3 ␲

兺

q

冕

0 ⫹⬁ coth␤␻ 2 ␹f f

⬙

共q,␻兲d␻. 共11兲

The two last equations 关Eqs. 共10兲–共11兲兴 provide a

self-consistent determination of␴2_f and hence of the spin

suscep-tibility. We will successively present now共i兲 in Sec. III, the

result for the dynamical spin susceptibility in the

random-phase approximation共RPA兲 giving information on the nature

of the collective mode that is involved;共ii兲 then in Sec. IV,

the implications of that mode in the critical phenomena around the quantum critical point.

III. RPA-DYNAMICAL SPIN SUSCEPTIBILITY NEAR THE ANTIFERROMAGNETIC WAVE VECTOR:

DISCUSSION ON THE NATURE OF THE COLLECTIVE MODE

As pointed out in Sec. II, the RPA corresponds to the absence of any averaging in the different equations. Thereby the expression of the dynamical spin susceptibility at the

RPA level is given by Eq. 共10兲 taking␴_f2⫽0. We now

dis-cuss the q and ␻ dependence of the RPA dynamical spin

susceptibility around the antiferromagnetic wave vector Q.

The bare intraband susceptibility ␹_␣␣(Q⫹q,␻) is well

approximated at 兩q兩Ⰶ兩Q兩 by a Lorentzian ␹_␣␣(Q⫹q,␻)

⫽␳␣␣/(1⫺i␻/⌫0⫹bq

2_{) where ␳}

␣␣⫽␹␣␣

⬘

(Q,0) and ⌫0 is

the relaxation rate of order 兩y_F兩⫽T_K. As expected for the

antiferromagnetic case, the relaxation rate remains finite when q goes to zero reflecting the fact that the fluctuations of the order parameter are not conserved. The bare interband susceptibility¯␹_␣␤(Q⫹q,␻) can be considered as purely real

and frequency independent equal to ␳_␣␤ in the

low-frequency limit. Due to the presence of the hybridization gap in the density-of-states, the continuum of the interband

particle-hole excitations displays a gap ranging from 2␴0,

the value of the direct gap for the wave vector 0, to 2兩yF兩,

the value of the indirect gap at Q. The RPA dynamical spin susceptibility is given by ␹f f R PA⬙_{共Q⫹q,␻兲⫽␻}␹f f

⬘

共Q⫹q兲⌫共q兲 ␻2_{⫹⌫共q兲}2 共12兲 with ␹f f

⬘

共Q⫹q兲⫽ ␳␣␣⫹␳␣␤ 共1⫺Iq兲 , ⌫共q兲⫽⌫0共1⫺Iq兲,

where Iq⫽I⫺bq2 and I⫽JS

2

␳␣␣␳␣␤ 共of order 1 near the

antiferromagnetic instability兲.

The bulk staggered susceptibility ␹_{f f}

⬘

(Q) diverges at I

⫽1. The frequency dependence of ␹f f R PA⬙

(Q⫹q,␻) is a

Lorentzian with a vanishing relaxation rate⌫(0) at the

anti-ferromagnetic transition. The corresponding excitation can be analyzed as an antiferromagnetic paramagnon mode that

softens at the magnetic transition. Equation共12兲 provides us

with the dispersion of that mode. The corresponding dynami-cal exponent z is found to be equal to 2 due to the

overdamp-ing of the mode when enters the continuum of the ␣-␣

particle-hole excitations. We will show how the dynamic ex-ponent z strongly affects the static critical behavior. This is

due to the fact that, contrary to the T⬎0 phase transitions,

statics and dynamics are intimately linked in quantum (T

⫽0) phase transitions. We turn now to the resulting

quantum-classical crossover occurring at finite temperature.

IV. CRITICAL PHENOMENA AROUND THE ANTIFERROMAGNETIC QUANTUM

CRITICAL POINT„AF-QCP…

The parameter which controls the temperature depen-dence of the thermodynamical variables near the AF-QCP is

␴f

2_{, which expresses the thermal local fluctuations of the}

staggered magnetization. Using Eqs.共11兲 and 共12兲

␴f 2_⫽

兺

q

S共Q⫹q兲⬃

冕

S共Q⫹q兲qd⫺1_{dq, 共13兲}

where S(Q⫹q) is the static form factor

S共Q⫹q兲⫽3

␲

冕

0

⬁

coth共␤␻/2兲␹

⬙

f f共Q⫹q,␻兲d␻. 共14兲

Depending on the temperature scale considered, quantum or classical behavior is observed. In general, the thermal

fluctuations ␴_f2 of the magnetization should depend on the

total self-consistent renormalized dynamical spin susceptibil-ity␹

⬙

f f(Q⫹q,␻) as defined in Eq.共9兲. However, in practice,

we will be content with its truncated form ␹R PA_{f f} ⬙(Q⫹q,␻) derived at the RPA level. The temperature dependence of the

static form factor S(Q⫹q) is given by

S共Q⫹q兲⫽6T

␲ ␹

⬘

f f共Q⫹q兲tan⫺1

冉

T

⌫共q兲

冊

. 共15兲

A first crossover temperature TI⫽2⌫0(1⫺I) appears, which

separates the quantum from the classical regime.

共i兲 T⬍TI: quantum regime. One can show that the static

form factor S(Q⫹q) exhibits a quadratic temperature

depen-dence S共Q⫹q兲⫽6 ␲ ␹

⬘

f f共Q⫹q兲 ⌫0共1⫺Iq兲 T2, 共16兲

The thermal local fluctuations ␴f2 of the magnetization are

also quadratic as a function of the temperature. They can be

easily evaluated from Eq.共15兲. Taking advantage of the fact

that the integrand S(Q⫹q)qd⫺1 is peaked at q1

⫽

冑

(1⫺I)/b, the temperature dependence of ␴_f2 is also found to be quadratic ␴f2⫽ 3 2␲ ␹

⬘

f f共Q兲 ⌫0共1⫺I兲 T2, 共17兲

The physics is quantum in the sense that the fluctuations on

the scale of the magnetic correlation length ␰ have energy

much greater than the temperature k_BT.

共ii兲 T⬎TI: classical regime. In this regime, the static

form factor S(Q⫹q) shows a linear temperature

depen-dence. As long as q is smaller than the thermal cutoff q*

defined by␻max(q*)⫽T, S(Q⫹q) takes the following form

S共Q⫹q兲⫽3␹

⬘

_{f f}共Q⫹q兲T. 共18兲

The thermal local fluctuations ␴f2 of the magnetization are

deduced from Eq. 共15兲. The main contribution arises from

the integration over 关q1,q*兴. The result depends on the

di-mensionality d. One finds ␴_f2_⬃T3/2 _{at d⫽3 and ␴}

f 2

⬃T ln T at d⫽2. This classical regime corresponds to the

case where the energy of the mode on the scale of␰becomes

less than k_BT.

Table I recapitulates the expressions that we get for the

thermal local fluctuations ␴2_f of the staggered magnetization

depending on the temperature scale and on the

dimensional-ity. Following Eq. 共10兲, the staggered spin susceptibility is

given by

␹Q

⬘

⫽

␹f f 0⬘_共Q兲

1⫺I⫹␭␴_f2, 共19兲

where ␹_{f f}0⬘(Q)⫽␳_␣␣⫹␳_␣␤. Incorporating the values of the

thermal local fluctuations ␴_f2 reported in Table I, we are

able to identify a second crossover temperature TII. Above

TII, ␴f2 becomes larger than (1⫺I) and all the physical

quantities are controlled by the temperature only. TII⬃(1

⫺I)2/3_{at d⫽3 and T}

II⬃(1⫺I) at d⫽2. As expected in the

two-dimensional case, the T⫽0 transition is at its upper

critical dimension since z⫹d⫽4 in the antiferromagnetic

case characterized by a dynamic exponent z⫽2. That

corsponds to the marginal case for which the intermediate

re-gime TI⬍T⬍TIIis squeezed out of existence. The results for

the d⫽3 and d⫽2 cases are, respectively, summarized in

Figs. 1 and 2, which picture the different regimes of behav-iors reached depending on the values of the temperature T

and of the control parameter I⫽J2␳_␣␣␳_␣␤. When I⬎1,

long-range antiferromagnetic order occurs when T is smaller

than the Ne´el temperature TN. TN⬃(I⫺1)2/3 at d⫽3 and

TN⬃(I⫺1) at d⫽2.

V. DISCUSSION

The low-temperature physics is dominated by the pres-ence of an antiferromagnetic paramagnon mode that softens at the magnetic transition. The results depend crucially on

the value of d⫹z, where d is the spatial dimension and z is

the dynamic exponent associated to that mode. Due to the overdamping of the mode when it enters the continuum of intraband particle-hole excitations, the dynamic exponent z is found to be equal to 2 in the antiferromagnetic case. As far as the dimensionality is concerned, there is no doubt about the dimensionality associated with the heavy quasiparticles in those systems that are clearly of 3. However the question about the dimensionality of the critical magnetic fluctuations, which the quasiparticles are coupled to, is still an open problem. Up to now, it has been assumed that the critical

fluctuations of the quantum phase transition 共QPT兲 are

dominated by the three-dimensional antiferromagnetic

TABLE I. Predictions for thermal local fluctuations ␴f 2

of the staggered magnetization depending on the temperature T and on the dimensionality d. TI⬃(1⫺I) represents the first crossover tempera-ture separating the quantum from the classical regime in the vicinity of the antiferromagnetic-quantum critical point共AF-QCP兲.

Quantum regime T⬍TI Classical regime T⬎TI d⫽3 ␴_f2⬃␹⬘_{f f}(Q)T2/⌫0 ␴f 2 ⬃T3/2 d⫽2 ␴f 2_⬃␹ f f ⬘(Q)T2/⌫0 ␴f 2_{⬃T ln T}

correlations. This would impose a description by a quantum

critical theory with d⫽3, z⫽2. Recently Rosch et al.28

pro-posed, on the basis of the neutron-scattering data in CeCu6⫺xAux, that the critical magnetic fluctuations are two

dimensional, which leads to a QCP with d⫽2 and z⫽2. Let

us summarize the different regimes of behaviors that we get

in each of those two cases (z⫽2, d⫽3 or 2兲 depending on

the values of the temperature T and of the control parameter I⫽J2␳_␣␣␳_␣␤. As one can see, the results that we obtain are

very similar to those established by Hertz20and Millis11

us-ing renormalization-group approaches in the spin-fluctuation theory.

共i兲 Case d⫽3. A long-range antiferromagnetic phase

oc-curs when I⬎1 below the Ne´el temperature T_N⬃(I⫺1)2/3_.

A first crossover temperature TI⬃(1⫺I) separates the

quan-tum from the classical regime. In the regime I(I⬍1) and T

⬍TI), the physics is quantum in the sense that the energy of

the relevant mode on the scale of ␰ is greater than the

tem-perature kBT. Since d⫹z⬎4, the T⫽0 phase transition is

above its upper critical dimension and the various physical quantities depend upon the parameter I. The magnetic

corre-lation length diverges at the magnetic transition ␰

⬃1/

冑

(1⫺I) and the staggered spin susceptibility behaves as

␹Q

⬘

⫽␹f f 0⬘

(Q)/(1⫺I⫹aT2). Regimes II and III are both

classical regimes characterized by large thermal effects since

the fluctuations on the scale of␰ have energy much smaller

than kBT. In regime II关TI⬍T⬍TIIwith TII⬃(1⫺I)2/3兴, the

magnetic correlation length ␰⬃1/

冑

(1⫺I) is still controlled

by (1⫺I) even though modes at the scale of␰have energies

less than k_BT. On the contrary, the staggered spin

suscepti-bility is sensitive to the thermal fluctuations ␹Q

⬘

⫽␹f f 0⬘

(Q)/(1⫺I⫹aT3/2). In regime III(T⬎TII), the thermal

dependence of physical quantities becomes universal and

both ␰ and␹Q

⬘

are controlled by the temperature: ␰⬃1/T3/4

and␹Q

⬘

⫽␹f f 0⬘

(Q)/T3/2.

共ii兲 Case d⫽2. Then, since z⫽2, z⫹d⫽4 and the T ⫽0 phase transition is at its upper critical dimension. The

physics is qualitatively similar to the case d⫽3 with stronger

fluctuation effects particularly in the classical regime. A

long-range antiferromagnetic phase occurs when I⬎1 below

the Ne´el temperature TN⬃(I⫺1). For d⫽2, the two

cross-over temperatures TI and TII coincide so that regime II of

Fig. 1 is squeezed out of existence. Regime I 关T⬍TI with

TI⬃(1⫺I)兴 is the quantum regime in which the thermal

fluctuations are negligible : ␰⬃1/

冑

(1⫺I) and ␹_Q

⬘

⫽␹f f

0⬘_{(Q)/(1⫺I⫹aT}2_{). Regime III (T⬎T}

I) is the unique

classical regime characterized by very strong fluctuation ef-fects since kBT is larger than the energy of the relevant mode

on the scale of ␰. Both the magnetic correlation length and

the staggered spin susceptibility are then controlled by the temperature:␰⬃1/

冑

T ln T and␹_Q

⬘

⫽␹_{f f}0⬘(Q)/(T ln T).

VI. CONCLUDING REMARKS

We considered the S⫽1/2 Kondo lattice model in a

self-consistent one-loop approximation starting from a general-ized Hubbard-Stratonovich transformation of the Kondo in-teraction term. The model exhibits a zero-temperature magnetic phase transition at a critical value of the Kondo coupling. The transition is usually antiferromagnetic but it may be incommensurate depending on the band structure considered. The low-temperature physics is controlled by a collective mode that softens at the antiferromagnetic transi-tion with a dynamic exponent z equal to 2.

A quantum-classical crossover occurs at a temperature TI

related to the characteristic energy scale of that mode. Heavy-fermion systems are usually believed to be three-dimensional. However, since some recent

inelastic-neutron-scattering experiments performed in CeCu6⫺xAux show that

FIG. 1. Phase diagram in the plane (T,I) for dimension equal to 3. The shaded region represents the long-range antiferromagnetic phase bordered by the Ne´el temperature TN. The unshaded region

marks the magnetically-disordered regimes I, II, and III, associ-ated to different behaviors of the system. Regime I is the quantum regime in which the energy of the relevant mode on the scale of␰ is much greater than kBT. The magnetic correlation length is ␰ ⬃1/

冑

(1⫺I) and the staggered spin susceptibility is ␹Q⬘ ⫽␹f f

0⬘

(Q)/(1⫺I⫹aT2_{). Regimes II and III are both classical}

re-gimes in which the thermal effects are important since the fluctua-tions on the scale of ␰ have energy much smaller than kBT. In

Regime II,␰⬃1/

冑

(1⫺I) is still controlled by (1⫺I) but the stag-gered spin susceptibility is sensitive to the thermal fluctuations:

␹Q⬘⫽␹f f

0⬘

(Q)/(1⫺I⫹aT3/2_{). In Regime III, both␰ and ␹}

Q

⬘ are con-trolled by the temperature:␰⬃1/T3/4and␹Q⬘⫽␹f f

0⬘

(Q)/T3/2.

FIG. 2. Phase diagram in the plane (T,I) for dimension equal to 2. The shaded region represents the long-range antiferromagnetic phase bordered by the Ne´el temperature TN. The unshaded region

marks the magnetically-disordered regimes I and III. In that d⫽2 case, the equivalent of regime II in Fig. 1 is squeezed out of exis-tence since TI⫽TII. Regime I is the quantum regime in which the

thermal fluctuations are negligible: ␰⬃1/

冑

(1⫺I) and ␹Q⬘ ⫽␹f f

0⬘

(Q)/(1⫺I⫹aT2). Regime III is the unique classical regime in which both the magnetic correlation length and the staggered spin susceptibility are controlled by the temperature:␰⬃1/

冑

T ln T

and␹Q⬘⫽␹f f

0⬘

(Q)/(T ln T).

the critical magnetic fluctuations, which the quasiparticles are coupled to, are two-dimensional, we both considered the

cases d⫽2 and d⫽3 with z⫽2. The low-temperature

behav-ior of the system is deduced, with predictions for the tem-perature dependence of the physical quantities such as the

magnetic correlation length␰and the staggered susceptibility

␹Q

⬘

. A second crossover temperature TII appears above

which the thermal dependence of␰ and␹_Q

⬘

becomes

univer-sal and is uniquely controlled by the temperature. It would be very interesting now to study the temperature behavior of other physical quantities as the specific heat or the transport properties.

A number of significant issues remain to be addressed. Among others, we will mention the possibility of getting a

different value of the dynamic exponent for instance z⫽1 if

nesting effects are considered corresponding to an absence of damping of the mode when located in the gap of excitations around the antiferromagnetic vector. Disorder is expected to play a crucial role in this problem. In that direction, some

recent works33,17 pointed out the formation of some ‘‘hot

lines,’’ i.e., points at the Fermi surface linked by the mag-netic Q vector. On the hot lines, the quasiparticle scattering rate is linear in temperature while, away from the hot lines, it

acquires the standard Fermi liquid form in T2_{. At low}

tem-perature, the ‘‘cold’’ regions are shown to short circuit the

scattering near those lines, and induce a T2 behavior of the

resistivity. The disorder is found to emphasize the contribu-tion of the hot lines, eventually leading to a non-Fermi liquid behavior. It would be worthy to study the effects of the ‘‘hot lines’’ in the presence of disorder within the critical phenom-ena description presented in this paper.

ACKNOWLEDGMENTS

We would like to thank Nick Bernhoeft, Piers Coleman, Mucio Continentino, Jacques Flouquet, Patrick A. Lee, and Gilbert Lonzarich for very useful discussions on this work.

APPENDIX EXPRESSIONS OF THE DIFFERENT BUBBLES

The expressions of the different bubbles appearing in the

expression of the boson propagators 关cf. Eq. 共5兲兴 are given

here共with i⫽1, 2, m, or ff兲

␸

¯

i共q,i␻␯兲⫽␸i共q,i␻␯兲⫹␸i共⫺q,⫺i␻␯兲, 共A1兲

␸1共q,i␻␯兲⫽⫺

1

␤ k␴,i␻

兺

_n

Gc f␴₀共k⫹q,i␻n⫹i␻␯兲G␴f f₀共k,i␻n兲,

␸2共q,i␻␯兲⫽⫺ 1 ␤ k␴,i␻

兺

_n G_cc 0 ␴ _{共k⫹q,i␻} n⫹i␻␯兲G␴f f₀共k,i␻n兲, ␸m共q,i␻␯兲⫽⫺ 1 ␤ k␴,i␻

兺

_n G_{c f} 0 ␴ _{共k⫹q,i␻} n⫹i␻␯兲Gc f␴₀共k,i␻n兲, ␸储f f共q,i␻␯兲⫽⫺ 1 ␤ k␴,i␻

兺

_n G_{f f} 0 ␴ _{共k⫹q,i␻} n⫹i␻␯兲Gf f␴₀共k,i␻n兲, ␸cc储 共q,i␻␯兲⫽⫺ 1 ␤ k␴,i␻

兺

_n G_cc 0 ␴ _{共k⫹q,i␻} n⫹i␻␯兲 ⫻Gcc␴₀共k,i␻n兲, ␸f c 储 _共q,i␻ ␯兲⫽⫺ 1 ␤ k␴,i␻

兺

_n G_{f c} 0 ␴ _{共k⫹q,i␻} n⫹i␻␯兲G␴f c₀共k,i␻n兲, ␸⬜f f共q,i␻␯兲⫽⫺ 1 ␤ k␴,i␻

兺

_n

G↑f f₀共k⫹q,i␻n⫹i␻␯兲G↓f f₀共k,i␻n兲,

␸⬜cc共q,i␻␯兲⫽⫺ 1 ␤ k␴,i␻

兺

_n G_cc 0 ↑ _{共k⫹q,i␻} n⫹i␻␯兲 ⫻Gcc↓ ₀共k,i␻n兲, ␸⬜f c共q,i␻␯兲⫽⫺ 1 ␤ k␴,i␻

兺

_n G_{f c} 0 ↑ _{共k⫹q,i␻} n⫹i␻␯兲G↓f c₀共k,i␻n兲, where G_cc 0 ␴ _(k,i␻

n), Gf f␴₀(k,i␻n), and Gf c␴₀(k,i␻n) are the

Green’s functions at the saddle-point level obtained by in-versing the matrix G₀␴(k,␶) defined in Eq. 共2兲.

The different bubbles ␸f f(q,i␻␯), ␸cc(q,i␻␯), and

␸f c(q,i␻␯) can be expressed as a function of the Green’s

functions associated with the eigenoperators ␣k␴

† and␤k␴ † Gf f共k,i␻n兲⫽uk 2_G ␣␣共k,i␻n兲⫹vk 2_G ␤␤共k,i␻n兲, 共A2兲 Gcc共k,i␻n兲⫽vk 2 G_␣␣共k,i␻n兲⫹uk 2 G_␤␤共k,i␻n兲, Gc f共k,i␻n兲⫽Gf c共k,i␻n兲

⫽⫺ukvk关G␣␣共k,i␻n兲⫺G␤␤共k,i␻n兲兴,

where G_␣␣(k,i␻n) and G␤␤(k,i␻n) are the Green’s

func-tions associated to the eigenstates␣_k†_␴兩0

典

and␤_k†_␴兩0

典

. In the low-frequency limit, one can easily check that the dynamical spin susceptibility may be written as

␹f f共q,i␻␯兲⫽

␹␣␣共q,i␻␯兲⫹¯␹␣␤共q,i␻␯兲

1⫺J_S2␹_␣␣共q,i␻_␯兲␹¯_␣␤共q,i␻_␯兲, 共A3兲 for both the longitudinal and the transverse parts.

␹␣␣共q,i␻␯兲⫽ 1 ␤

兺

k n_F共E_k⫺兲⫺n_F共E_k⫺_⫹q兲 i␻_␯⫺E_k⫺_⫹q⫹E_k⫺ ␹ ¯_{␣␤共q,i␻} ␯兲⫽ 1 ␤

兺

k 共uk 2 vk⫹q 2 _⫹v k 2_u k⫹q 2 _兲 ⫻nF共Ek ⫺_兲⫺n F共Ek⫹_⫹q兲 i␻_␯⫺E_k⫹_⫹q⫹E_k⫺ .

*_{Also at the Center National de la Recherche Scientifique共CNRS兲.} 1_{For reviews see H. von Lohneysen, J. Phys.: Condens. Matter 8,} 9689共1996兲; D. A. Gajewski, N. R. Dilley, R. Chau, and M. B. Maple, ibid. 8, 9793共1996兲; F. Steglich, B. Buschinger, P. Ge-genwart, M. Lohmann, R. Helfrich, C. Langhammer, P. Hell-mann, L. Donnevert, S. Thomas, A. Link, C. Geibel, M. Lang, G. Sparn, and W. Assmus, ibid. 8, 9909共1996兲.

2_{H. von Lo¨hneysen, A. Schro¨der, M. Sieck, and T. Trappmann,} Phys. Rev. Lett. 72, 3262共1994兲; H. von Lo¨hneysen, J. Phys.: Condens. Matter 8, 9689共1996兲; O. Stockert, H. V. Lo¨hneysen, A. Schro¨der, M. Loewenhaupt, N. Pyka, P. L. Gammel, and U. Yaron, Physica B 230-232, 247共1997兲.

3_{N. D. Mathur, F. M. Grosche, S. R. Julian, I. R. Walker, D. M.} Freye, R. K. W. Haselwimmer, and G. G. Lonzarich, Nature

共London兲 394, 39 共1998兲, and references therein.

4_{F. Steglich, B. Buschinger, P. Gegenwart, M. Lohmann, R.} Hel-frich, C. Langhammer, P. Hellmann, L. Donnevert, S. Thomas, A. Link, C. Geiber, M. Lang, G. Sparn, and W. Assmus, J. Phys.: Condens. Matter 8, 9909共1996兲.

5_{C. L. Seaman, M. B. Maple, B. W. Lee, S. Ghamaty, M. S.} Torikachvili, J.-S. Kang, L.-Z. Liu, J. Allen, and D. L. Cox, Phys. Rev. Lett. 67, 2882共1991兲.

6_{S. Kambe, S. Raymond, L. P. Regnault, J. Flouquet, P. Lejay, and} P. Haen, J. Phys. Soc. Jpn. 65, 3294共1996兲.

7_{E. Miranda, V. Dobrosavljevic, and G. Kotliar, J. Phys.: Condens.} Matter 8, 9871共1996兲.

8_{A. H. Castro-Neto, G. Castilla, and B. A. Jones, Phys. Rev. Lett.}

81, 3531共1998兲; M. C. de Andrade, R. Chau, R. P. Dickey, N.

R. Dilley, E. J. Freeman, D. A. Gajewski, M. B. Maple, R. Movshovich, A. H. Castro Neto, G. Castilla, and B. A. Jones, ibid. 81, 5620共1998兲.

9_{R. Narayanan, T. Vojta, D. Belitz, T. R. Kirkpatrick, Phys. Rev.} B 60, 10 150共1999兲; T. R. Kirkpatrick and D. Belitz, Phys. Rev. Lett. 76, 2571共1996兲.

10_{B. Andraka and A. M. Tsvelik, Phys. Rev. Lett. 67, 2886共1991兲.} 11_{A. J. Millis, Phys. Rev. B 48, 7183共1993兲.}

12_{T. Moriya and T. Takimoto, J. Phys. Soc. Jpn. 64, 960共1995兲.} 13_{M. A. Continentino, Phys. Rev. B 47, R11 587共1993兲.} 14_{P. Schlottmann, Phys. Rev. B 59, 12 379共1999兲.} 15

P. Coleman, Physica B 259-261, 353共1999兲.

16_{Q. Si, J. L. Smith, and K. Ingersent, Int. J. Mod. Phys. B 13, 2331}

共1999兲.

17_{A. Rosch, Phys. Rev. Lett. 82, 4280共1999兲.}

18_{A. Schro¨der, G. Aeppli, E. Bucher, R. Ramazashvili, and P.} Cole-man, Phys. Rev. Lett. 80, 5623共1998兲.

19_{D. L. Cox, Phys. Rev. Lett. 59, 1240共1987兲; D. L. Cox and M.} Jarrell, J. Phys.: Condens. Matter 8, 9825共1996兲.

20_{J. A. Hertz, Phys. Rev. B 14, 1165共1976兲.}

21_{T. Moriya and A. Kawabata, J. Phys. Soc. Jpn. 34, 639共1973兲; H.} Hasegawa and T. Moriya, ibid. 36, 1542共1974兲.

22_{S. Doniach, Physica B 91, 231共1977兲; C. Lacroix and M. Cyrot,} Phys. Rev. B 20, 1969共1979兲; D. M. Newns and N. Read, Adv. Phys. 36, 799共1987兲; and for a recent review see H. Tsunetsugu, M. Sigrist, and K. Ueda, Rev. Mod. Phys. 69, 809共1997兲 and references therein.

23_{A. J. Millis and P. A. Lee, Phys. Rev. B 35, 3394共1987兲; A.} Auerbach and K. Levin, Phys. Rev. Lett. 57, 877 共1986兲; M. Lavagna, A. J. Millis, and P. A. Lee, ibid. 58, 266共1987兲. 24_{A. Houghton, N. Read, and H. Won, Phys. Rev. B 37, 3782}

共1988兲.

25_{C. Pe´pin and M. Lavagna, Phys. Rev. B 59, 2591共1999兲.} 26_{P. Nozie`res共unpublished兲.}

27_{J. A. Hertz and M. A. Klenin, Phys. Rev. B 10, 1084共1974兲; J. A.} Hertz and M. A. Klenin, Physica B 91, 49共1977兲.

28_{A. Rosch, A. Schro¨der, O. Stockert, and H. von Lo¨hneysen, Phys.} Rev. Lett. 79, 159共1997兲.

29_{N. Read and D. N. Newns, J. Phys. C 16, 3273共1983兲.} 30_{G. G. Lonzarich and L. Taillefer, J. Phys. C 18, 4339共1985兲.} 31_{N. R. Bernhoeft and G. G. Lonzarich, J. Phys.: Condens. Matter}

7, 7325共1995兲.

32_{Y. Kuramoto and K. Miyake, J. Phys. Soc. Jpn. 59, 2831共1990兲.} 33_{R. Hlubina and T. M. Rice, Phys. Rev. B 51, 9253共1995兲.}