New bounds on the length of finite pierce and Engel series

J

OURNAL DE

T

HÉORIE DES

N

OMBRES DE

B

ORDEAUX

P. E

RDÖS

J. O. S

HALLIT

New bounds on the length of finite pierce and Engel series

Journal de Théorie des Nombres de Bordeaux, tome

3, n

o

_{1 (1991),}

p. 43-53

<http://www.numdam.org/item?id=JTNB_1991__3_1_43_0>

© Université Bordeaux 1, 1991, tous droits réservés.

L’accès aux archives de la revue « Journal de Théorie des Nombres de Bordeaux » (http://jtnb.cedram.org/) implique l’accord avec les condi-tions générales d’utilisation (http://www.numdam.org/conditions). Toute uti-lisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit conte-nir la présente mention de copyright.

Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques

New

bounds

on

the

Length

of

Finite

Pierce

and

_Engel

Series.

par P.

ERDÖS

AND J.O. SHALLIT*

ABSTRACT. _Every real number x, 0 x 1, has an _{essentially unique}

expansion as a Pierce series:

1

1 1

x = + - ...

x1 x1x2 x1 x2x3

where the xi form a strictly increasing sequence of positive integers. The

expansion terminates if and _only if x is rational. Similarly, every positive

real _{number y} has a unique expansion as an Engel series:

1 1 1

y = + + + ...

y1 y1 y2 y1 y2 y3

where the _yi form a _{(not necessarily} strictly) _increasing sequence of positive

integers. If the _expansion is _infinite, we _require that the _{sequence yi} be not

eventually constant. _Again, such an _expansion terminates if and only if y

is rational. In this paper we obtain some new _upper and lower bounds on the lengths of these series on rational _inputs a/b. In the case of the _Engel

series, this answers an _{open question} of Erdös, Rényi, and Szüsz. However, our _upper and lower bounds are _{widely separated.}

1. Introduction.

Let

_{a, b}

be

_integers

with 1 a

_b,

and define

Since _a,+, ai,

eventually

we must have an+1 = 0. Put

P(a, b)

= n. We ask: how

_big

can

P(a, b)

be as a function of a and b?

This

_question

seems to be much harder than it first _appears. Shallit

_[11]

proved

that

_{P(a, b)}

_2~;

also see

Mays

[6].

1980 Mathematics Subject Classification

(1985 Revision).

11A67.

Key words and _phrases. Pierce _{series, Engel} series.

* _Research

supported in _{part by} NSF _grant CCR 8817400 and a Walter Burke Award from Dartmouth College.

In this _paper we

improve

the bound to

P(a,b)

=

O(b1/:1+f)

for _every

E &#x3E; 0.

_(This

is still a weak

result,

as we believe that

P(a, b)

=

O((log

b)2).)

We can also ask about the _average behavior of

P(a, b).

We define

In this paper we _prove

Q(b)

=

Q(Iog

log

b). (Again,

this result is rather

weak,

as it seems

likely

that

Q(b)

=

S2(log b).)

There is a connection between the

algorithm given by

(1)

and the

fol-lowing

expansion,

called the Pierce series:

Let 0 x 1 be a real number. Then x _may be

expressed

uniquely

in the form

, , ,

1 1 1

where 1 Xl X2 X3 .. . We sometimes abbreviate eq.

(2)

by

The

_expansion

terminates if and

_only

if x is rational. If the

_expansion

does

terminate,

with

as the last

_term,

then we also must have zn-i Xn - 1.

Let

_{P’(a, b)}

denote the number of terms in the Pierce series for

_a/b.

Then we have the

following

OBSERVATION 1.

This follows

_easily,

as _a2 = b mod _a, means b = _{qi ai + a2;} hence

Similarly,

from b =

Continuing,

we find

In

_fact,

the

_algorithm

₍₁₎

has the same

relationship

with

expansions

into

Pierce series as the Euclidean

algorithm

for the

_greatest

common divisor

has with continued fractions.

A similar

_algorithm

is as follows: let 1 a b and define

Again,

we must

eventually

have _an+1 = 0. Put

E(a, b)

= n .

Erd6s,

Renyi,

and Szusz

_[4]

asked for a nontrivial estimate for

E(a,

b).

In this

paper we _prove the first such

estimate, namely

E(a, b)

=

O(b1/3+f) for

all

E &#x3E; 0.

The

_algorithm

₍₃₎

is related to

_expansion

in

_{Engel series,}

as follows:

Let _y be a

_positive

real number.

_{Then y}

_may be

_{expressed uniquely}

in

the form

-1 , ,

11 1

where 1

_y2

.... If the

expansion

does not

terminate,

then we

require

that the _{sequence yi} be not

_eventually

constant. Such an

expansion

terminates if and

_only

if _y is rational.

Let

_{E’(a, b)}

denote the number of terms in the

_expansion

for

_a/b.

As

above,

it is _{easy to} see that

E(a, b)

=

E’(a, b).

For more information about the Pierce

_series,

see

[7,8,11,13,14].

The

results in Section 3 were announced

previously

in

[12].

For more information about

_{Engel’s series,}

see

[1,2,3,4,9,13].

2.

_Upper

bounds.

Note that for 1 ~ n.

Without loss

_{of generality}

we _{may assume ql} =

1,

for if _not, then :

Choose k such that

_qk

v6

and &#x3E;

Vb.

_(If

no such k

exists,

then

Then,

as

the qi

are

strictly increasing,

we have k

Vb.

Now since

b,

we have _ak+i

Vb.

Since the _ai are

_{strictly decreasing,}

we

have n - k

Vb.

Hence we find n

2Vb.

We now show how to

_modify

this

_argument

to

_get

an

_improved

bound:

THEOREM 2.

Proof.

We first observe that for _any fixed r, we cannot have _ai+l = r too

often. For

_if,

_say, we have

then b + r is divisible

by

each of _{ai2 , ... ,}

ai,. Since the a’s are all

distinct,

we

have j

d(b

₊

r),

where

d(rn)

is the number of divisors of n. Now it is well known

_(see

[5])

_that

_d(m)

=

0(m)

for

all E &#x3E;

_0,

so

j

d(b

+

_r)

=

O(b’).

Now as above we can assume _{ql =} 1. Choose i such that qi and

1 &#x3E;

b~ ~~~ .

(If

no such i

exists,

then _qi

b 1/3

for all i and hence n

b~

1/3 .)

Note that

,"

Let us count the number

_{of j’s, i -f-1 j}

_n, such that r =

aj -

b1/3. By

the

_argument

_above,

there are

such j

for each _r, 1 ~ r

bi ~‘~ .

Now let us count the number

of j’s,

i +

I j n

such that _{aj -} &#x3E;

b .

Since

_b2/3,

it is clear that there can be at most such

J.

Hence all

_together

there are

j’s

in the

_{range i}

+

_{1 j}

n,

and we conclude

Adding

(5)

and

_(6),

we conclude

P(a, b)

= n =

O(b~~’~+f~.

0

We now show how to

_modify

this

_argument

to

_get

an _upper bound for

E(a, b).

We write a, = a and

Note

_{that qi}

=

In what

_follows,

we assume 1 a

_b;

such a restriction ensures that

Note that

_akqk

2b for 1 k n. The _ai are

strictly decreasing.

In the case of

Engel

series,

the _qi form an

increasing

_sequence that is not

necessarily strictly

increasing.

However,

it is not difficult to show that we

cannot have _{too many} consecutive

_quotients

that are the same:

LEMMA 3.

Proof.

By

induction on i. The result is

clearly

true when i

= j.

Now assume it

true for

_i;

we _prove it for _{i + 1.} We have b = and b = _{qai+l ai+2}

-Subtracting,

we find _{ai+i -} = As _ai+l

by

COROLLARY 4.

Let 1 ~ a b and

_{q &#x3E;}

2. In the

Engel

series for

a/b,

there cannot be

more than 1 ₊

_log

a

quotients

_q. that are

equal

to q.

We _may now

apply

the same

_argument

used _{to prove} Theorem 2 to

_get

a similar result for

E(a, b):

,

THEOREM 5.

Proof.

Again,

we choose i such that _qi

b1/3

and

b1/3.

.

(If

no such i

exists,

then _qi

b~ ~‘~

for all i and hence

_{by Corollary}

_4,

n

b1/3(1+10g2

b) . )

Note that i =

O(b1/3Iogb),

by

Corollary

4. Since

b~ ~‘~,

and the

ai are

_{strictly decreasing,}

we have

2b 2/3

for i +

1 j

n. Now an

argument

similar to that in the

_proof

of Theorem 2 shows that there can

be at most

O(b~ ~‘~+~)

_{subscripts j &#x3E;}

i + 1 such that _{aj -}

2b~ f ‘~ .

Similarly,

there can be at most

o(b~ ~‘~ )

subscripts j &#x3E;

i + 1 such that

2b~ ~~ .

We conclude that there are

O(b~ ~‘~+f )

subscripts j

in

the range i +

1 j

n, and hence n - i =

o(b~ ~~+f ).

Adding

our estimates for i and n -

_i,

we conclude that

E(a, b) =

n =

. 0

3. Lower bounds for

_{P(a, b)}

and

_Q(b).

In this section we _prove some lower bounds for

P(a, b)

and

Q(b).

In

_[11],

it was

proved

that

infinitely

often.

_Actually,

a _very

simple

_argument

gives

a better result:

THEOREM 6.

There exists a constant c &#x3E; 0 such that

_{P(a, b)}

&#x3E;

_{c log b}

_infinitely

often.

Proo f.

so

P(a, b)

= n.

_However,

where

_{~(x) _}

_Epk5x

_logp

and we have used an estimate from

[10].

This

proves the theorem with c =

(1.03883)-l.

D

REMARK.

It is trivial to find a similar lower bound for

_Engel’s

_series,

as

E(2"

-1, 2’)

= n.

We now _prove a result on the average

complexity

of the

_algorithm

(1).

THEOREM 7.

Q(b)

=

Q(log

log

b).

Proof.

Let

_Tb(j)

be the total number of times

_{that j}

_appears as a term in the Pierce

_expansions

of

_{1/6, 2/b, ... , (b - 1)lb,}

1.

Clearly

The idea is to find a lower bound for this last sum. More

precisely,

we find a bound for

Fix

_{a j, 1 j}

_log

b. Now _every real number in the _open interval

has a Pierce series

expansion

that

begins

~x~ , x2, ... , xk, j, ... )

provided

Xk

j.

(Actually,

the

endpoints

of the open interval

given

in

(8)

should

be reversed if k is

_even.)

There are

bill

₊

0(1)

rationals with denominator b contained in the interval

_I,

and the interval I is of size

Now let us sum

blil

+

₀₍₁₎

over all

possible

values for _{Xl, X2, ... , Xk;} this

_gives

us an estimate for

Tb(j).

We find

Now,

using

the observation that

we

_get

Now consider We

_get

Thus,

using

(7),

we see

4. Worst cases: numerical results.

In this section we

_report

on some

computations

done to find the least b such that

_{P(a, b)}

= n and

E(a, b)

= _n, for some small values of n.

The

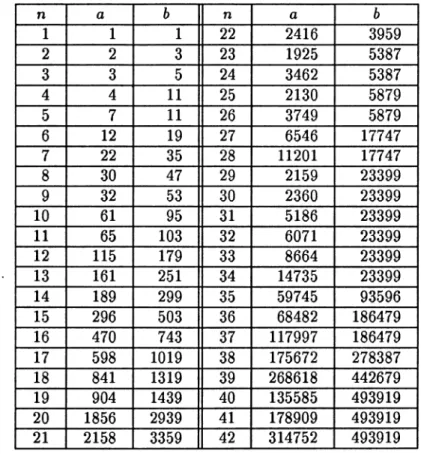
_following

table

_gives,

for each n

_42,

the least b such that there exists an _a, I a

_b,

with

_{P(a, b)}

= n. If there is more than one such a for a

particular b,

the smallest such a is listed. This table extends one

given

in

_Mays

_[6].

Table I: Worst Cases for Pierce

_Expansions

[Note

added in

_proof:

the

_following

_entry

_extending

Table I has

_recently

been discovered

_by

_{computer :}

n =

43,

a =

490652,

b =

830939.]

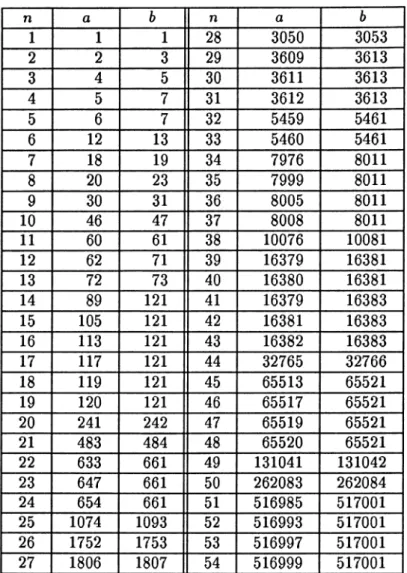
Table II: Worst Cases for

_{Engel Expansions}

v.

_{Acknowledgments.}

Part of this work was done while the second author was at Dartmouth

College.

REFERENCES

1. A. _{Békéssy, Bemerkungen} zur _{Engleschen Darstellung} reeler _Zahlen, Ann. Univ. Sci.

Budapest. Eötvös Sect. Math. 1

_(1958),

143-151.

2. P. _Deheuvels, L’encadrement _asymptotique des elements de la série _d’Engel d’un nombre _réel, C. R. Acad. Sci. Paris 295

_(1982),

21-24.

3. F. _{Engel, Entwicklung} der Zahlen nach _{Stammbrüchen, Verhandlungen} der 52.

Ver-sammlung deutscher _Philologen und Schulmänner in Marburg, 1913, pp. 190-191. 4. P. _Erdös, A. _Rényi, and P. _Szüsz, On _Engel’s and _{Sylvester’s} series, Ann. Univ. Sci.

Budapest. Eötvös Sect. Math. 1 _(1958), 7-32.

5. G. H. Hardy and E. M. _Wright, An Introduction to the Theory of Numbers, Oxford

University Press, 1985.

6. M. E. Mays, Iterating the division algorithm, Fibonacci _Quart. 25

_(1987),

204-213.

7. T. A. _Pierce, On an _algorithm and its use in _{approximating} roots _{of algebraic}

equa-tions, Amer. Math. _Monthly 36

_(1929),

523-525.

8. E. Ya. Remez, On series with alternating signs which may be connected with two

algorithms of M. V. _{Ostrogradskii for} the approximation of irrational _numbers,

Us-pekhi Mat. Nauk 6

_{(5) (1951), 33-42, (MR #13,444d).}

9. A. _Rényi, A new approach to the _{theory of Engel’s series,} Ann. Univ. Sci. _Budapest. Eötvös Sect. Math. 5

_(1962),

25-32.

10. J. B. Rosser and L. _{Schoenfeld, Approxamate formulas for} some _{functions of prime}

numbers, Illinois J. Math. 6

_(1962),

64-94.

11. J. O. _Shallit, Metric theory of Pierce _expansions, Fibonacci _Quart. 24

_(1986),

22-40.

12. J. O. _Shallit, Letter to the _editor, Fibonacci _Quart. 27 _(1989), 186.

13. W. _Sierpinski, O kilku _algorytmach dla _rozwijania liczb _{rzeczywistych} na szeregi,

C. R. Soc. Sci. Varsovie 4 _{(1911), 56-77,}

_(In

_{Polish; reprinted} in French transla-tion as Sur quelques algorithmes pour développer les nombres reéls en _séries, in W.

Sierpinski, Oeuvres _Choisies, Vol. I, PWN, Warsaw, 1974, pp.

236-254.).

14. K. G. Valeyev and E. D. Zlebov, The metric theory of an _{algorithm of} M. V.

Os-trogradskij, Ukrain. Mat. Z. 27

_(1975),

64-69.

P. ERD 0 S

Mathematical Institute

Hungarian Academy of Sciences Realtanoda u. 13-15 H-1364 Budapest HUNGARY

et

J.0. SHALLIT

Department of _Computer Science

University of Waterloo

Waterloo, Ontario N2L 3Gl CANADA.