From Planck to Ramanujan : a quantum $1/f$ noise in equilibrium

J

OURNAL DE

T

HÉORIE DES

N

OMBRES DE

B

ORDEAUX

M

ICHEL

P

LANAT

From Planck to Ramanujan : a quantum 1/ f

noise in equilibrium

Journal de Théorie des Nombres de Bordeaux, tome

14, n

o

_{2 (2002),}

p. 585-601

<http://www.numdam.org/item?id=JTNB_2002__14_2_585_0>

© Université Bordeaux 1, 2002, tous droits réservés.

L’accès aux archives de la revue « Journal de Théorie des Nombres de Bordeaux » (http://jtnb.cedram.org/) implique l’accord avec les condi-tions générales d’utilisation (http://www.numdam.org/conditions). Toute uti-lisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit conte-nir la présente mention de copyright.

Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques

From Planck

to

_Ramanujan:

a

_quantum

1/f

noise in

equilibrium

par MICHEL PLANAT

RÉSUMÉ. J’introduis un nouveau modèle de bosons

_thermiques

sans masse ; il

prédit,

pour les

fluctuations,

un _spectre

hyper-bolique

aux basses

fréquences.

On trouve que la fonction de par-tition par mode est la fonction

_{génératrice}

d’ Euler _pour le

nom-bre de

_partitions

_p(n).

Les

_quantités

_{thermodynamiques}

ont une structure

_{arithmétique profonde :}

elles sont données _par des

_séries,

dont les coefficients de Fourier sont les fonctions sommatoires

03C3k(n)

des

_puissances

des diviseurs de n, avec k _{= 20141 pour}

_l’énergie

libre,

k = 0 _pour le nombre de

particules,

_et k = 1 pour

l’énergie

interne. Les contributions de basse

_fréquence

sont calculées par

l’usage

de transformées de Mellin. En

_{particulier, l’énergie}

interne

par mode

diverge

comme E/kT =

03C02/6x,

avec x =

h03BD/kT, au

contraire de

l’énergie

de Planck E = kT. La théorie _est

_appliquée

à la correc-tion de la loi de _rayonnement du _corps noir et au solide de

_Debye.

Les fluctuations fractionnaires de

_{l’énergie présentent}

un _spectre

en

1/v

aux basse

fréquences.

On en déduit un modèle satisfaisant

pour les fluctuations d’un résonateur à quartz. On

rappelle

aussi

les résultats essentiels de la théorie

_{mathématique}

des

_partitions

de

_{Ramanujan-Rademacher.}

ABSTRACT. We describe a new model of massless thermal bosons

which

_predicts

an

_hyperbolic

fluctuation _spectrum at low

frequen-cies. It is found that the

_partition

function _per mode is the Euler

generating

function for unrestricted

_partitions

_p(n).

Thermody-namical

_quantities

carry a _strong arithmetical structure:

_they

are

given by

series with Fourier coefficients

equal

to _summatory

func-tions

_03C3k(n)

of the power of

divisors,

with k = -1 for the free

energy, k = 0 for the number of

_particles

and k = 1 for the

in-ternal energy. Low

frequency

contributions are calculated

_using

Mellin transform methods. In

_particular

the _{internal energy per} mode

_diverges

as

E/kT=03C02/6x

with x

=h03BD/kT

in contrast to the Planck

energy

E

= kT. The

theory

is

_applied

_to calculate corrections

in black

_body

radiation and in the

_Debye

solid. Fractional

low

_frequency

_range. A

_satisfactory

model of

_frequency

fluctua-tions in a _quartz

crystal

resonator follows. A sketch of the whole

Ramanujan-Rademacher theory

of

_partitions

is reminded as well.

1. Introduction

According

to the

_{equipartition}

law of statistical

_mechanics,

the available noise _power

P

in the

_frequency

interval dv is

_equal

to

_[15]:

this result is

_{essentially Nyquist’s}

theorem for the

_voltage

noise

_v2

at a resistor

_R,

,

P -

= kTdv where _means the _{avera e} value. Since

-

kT is

i.e.,

_4R

=

kTdv,

where

()

_means the

average value. Since 2? = kT is

the mean _{energy per}

_{mode, Nyquist proposed}

to add

_quantum

corrections

as

E

=

p(x),

with the Planck factor

p(x) =

which x =

hv/kT .

kT

_ exp (

-1

This result was

_generalized

as

FT-

= p(x)

₊

to account for the zero

_point

energy. There are still controversies

_concerning

the

_physical

relevance of

these relations: the Planck factor removed the ultraviolet

_divergence

but this was

reincorporated

in the frame of

_quantum

electrodynamics

~1~,~4~.

At the

_present

_stage,

_quantum

statistical mechanics does not include infrared corrections of the

_1/v

_type.

The infrared

_catastrophe

was studied

previously

in

_{non-stationary}

processes such as the

scattering

of electrons in an atomic field

[3],[9].

Here we derive an alternative

_approach

in which

_1/v

noise is a

_property

of

_{non-degenerate}

bosons in

_equilibrium.

We first observe that the

_quantum

mechanical

_partition

function of a boson _gas, with

equally spaced energy

levels,

is the Euler

_generating

function

_{of p(n) :}

the number of indiscernible collections of the

_integer

n. It relates to

_elliptic

modular functions which

are _{very exactly} known. As a result the main contribution in the mean

energy per mode is the infrared term

t - M2-

instead of

unity.

The new

kT -

6

law also leads to fractional _{energy fluctuations of the whole gas.}

Using

the new

_approach

and the

_density

of states of the conventional

ap-proach

we calculate the corrections to

_black-body

radiation

_laws,

_including

the

_density

of

_photons,

the

_emissivity

and infrared fluctuations. We also

apply

the calculations to the

_phonon

_gas in a

_quartz

resonator.

The

_partition

function Z of a non

degenerate

boson _gas is

_given

from

where the summation is

_performed

over all the states s of the

_assembly.

In the conventional

_approach

it is thus considered that the

_partition

function Z per mode of

frequency

es =

hvs

is such that ln Z = -

In

_black-body

radiation one accounts for the wave character of the

quan-tum states

_by

_counting

the number I of

_wavelengths

in a cubic box of size L

where the summation

₍₁₎

should be

_performed

over all

_{integers II, 12,}

13

obeying (2).

This can be achieved

by removing

the discreteness of _energy levels and

replacing

the sum

(1)

by

an

integral

with

_{D(v) =}

2 x the

_density

of states

_[11]:

the factor 2 occurs due to the two

_degrees

of freedom of

_{polarization,}

c is the

light velocity

and

V =

L3

the volume of the

cavity.

From now we consider that with each mode is associated a set of

_equally

spaced

energy levels

nhv, n integer,

so that the

partition

_per mode becomes

As shown in Section

_(2.1)

this accounts for new

multiparticle

microstates

not considered so far.

The summation above is well known in number

_theory

and can be _very

accurately

described

_{using elliptic}

modular functions. At is will be

_shown,

there are drastic _consequences in the low

frequency

_part

of the

_spectrum,

while the

_{high frequency}

_part

is left

_unchanged.

In the

_following

the

_{thermodynamical}

_quantities

will be defined as usual

the

_occupation

_number,

the internal energy, the

_entropy,

-, the

spectral

energy density,

, the free energy,

the _{fluctuations of the internal energy.}

In all the _paper the

_{subscript -}

will indicate that we restrict the calculation

2.

_{Thermodynamics}

of the Euler gas

2.1. Euler

_generating

function. The

_partition

function per mode Z in

(4)

can be written in the Euler form

[14]

with _y = and 2? = This is

equivalent

to the Boltzmann

summation

where

_p(n)

is the

_degeneracy

_parameter

of the _energy level nhv. It is known in number

_theory

as the number of unrestricted

_partitions

of the

_integer

_n,

that is the number of different ways of

calculating n

as a sum of

integers.

For

_example

with n = 4 we have

p(4)

= 5 and the

corresponding

indis-cernible collections are

This can be

_pictured

in terms _{of the energy levels. The collection}

_(a)

means one

particle

on the level of index 4 and the three

_{remaining particles}

on the

_ground

state of index

_0,

i.e. 4hv = 1 x 4hv + 3 x Ohv. This

collection is the

_only

one considered in the conventional

approach.

The

other microstates from

_(b)

to

_(d)

_correspond

to different

_{possibilities}

of

bunching

of the

_particles.

Collection

_(b)

means the four

particles

on the

level of index

_1,

i.e. 4hv = 4 x

_hv,

collection

_(c)

means two

_particles

on the

level 2 and two

_particles

on the

_ground

_state,

i.e. 4hv = 2 x 2hv + 2 x

_Ohv,

and so on.

Properties

of Euler

_generating

function were studied in full details

_by

Ramanujan

[10]

in 1918 and

_{completed by}

Rademacher

_[14]

in 1973. An

important

result is the

_asymptotic

formula

2.2. Riemann zeta function and the _{free energy of the Euler gas.} The

_partition

function

_2(x)

defined in

₍₄₎

is related to the Riemann zeta

function

_((s)

_through

the Mellin transform as follows

(Ref.

[12],

_Eq.

_(6.3)

Introducing

as the sum of

kth

_powers of the divisors of n and the

Dirichlet series

and

_computing

the inverse Mellin transform one obtains

([12],

_p.

467)

the

free

_{energy F}

as follows

with =

Ql(n)/n.

There is thus a close

relationship

between the

arithmetic of and that of divisors. This will be confirmed in the derivation of the other

_{thermodynamical quantities.}

Since the main contributions to

Z(x)

are

_{given by}

the

poles

at s = 0 of

r(s)

and

_~(s+1)

and at s = 1 of

C (s),

the free _{energy may} be

approximated

in the low

_frequency

_part

of the

_spectrum

_([5],

_p.

₅₈₎

with the error term

_{ln(1 -}

2.3. Dedekind eta function and the internal _energy of the Euler gas. One

easily

shows that the Mellin transform of the

occupation

number is

_r(s)~(s)2.

A similar derivation to the one

performed

in Section

(2.2)

leads to

In the low

_{frequency region}

one

_gets

(see [6],

_p.

27)

where 0.577 is Euler constant.

The Mellin transform of the internal energy is

_{r(s)~(s)~(s -1)}

and from the same method than above

An alternative derivation involves

_elliptic

modular

_aspects.

_According

to

Ninham

_[12]:

All rrcathematics is a

tautology,

and all

physics

uses

mathe-matics to look in

_different

_ways at a

fundamental

problem

of philosophy

The link between the modular _group and the Euler

_generating

function

is from the

_equality

_[14]

where the domain of

_integration

of

_Z(y)

is taken to be the upper half

complex plane

of the new variable T

Here we have

As shown in Section

₍₅₎

Dedekind eta function acts on the full modular

group

SL(2,

Z).

At this

stage

we do not enter into the full ramifications of the

_theory

and

_{only emphasize}

the connexion to the modular Eisenstein function

where the summation is

_performed

over all non-zero relative

_integers

m and n and

9(r)

&#x3E; 0. It can be shown

([16],

_p.

29)

that

G2(T)

connects to the

logarithmic

derivative of

_q(T)

- - I I , , , ’"

with the Fourier

_expansion

Using

(22), (23)

and

_(25)-(27)

the relation

₍₂₁₎

is

_easily

recovered. The low

_frequency

_expansion

_{of internal energy is} as follows

instead of the Planck result E - kT.

One can also

_compute

the

_entropy

S

from

At _very low

_frequency

it results that the internal _{energy equals} the

3.

_Application

to

_black-body

radiation

3.1. Stefan-Boltzmann constant revisited. The Stefan-Boltzmann

constant is an

integrated

measure of the

emissivity

of a black

body

[11].

In the conventional

_approach

the

_partition

function is calculated from the

integral

(3)

using

the

_density

of states

_D(v)

= 8~

that is

with

_{((4) =}

_{7r4 /90}

and we used the Mellin

_integral

formula

The Stefan-Boltzmann constant CRSB is defined from the free energy

If instead of

₍₃₀₎

one uses the

general

formula

the

_interchange

of the

_integral

and the sum leads to

As a result we find a free _energy

(and

a modified Stefan-Boltzmann

con-stant)

in excess with a factor =

((3) ~

1.20. If _{one uses} the

alternative derivation in terms of

the divisors

one recovers the

mathemati-cal formula

₍₁₆₎

with s = 3 and k = -1.

3.2. The

_density

of

_photons.

The number of

_photons

in the bandwidth dv is

with the

_occupation

number

_N(v,

_{T) =}

in the conventional

In the

_{general approach}

the

_occupation

number is defined from the

sum-mation

₍₁₉₎

and we need to evaluate

This is in excess of a factor

((3) ~

1.20 as for the free energy. If one

compares the calculation in terms of divisors one recovers the mathematical

formula

₍₁₆₎

with s = 3 and = 0.

3.3. Planck radiation formula revisited. _{The energy within the}

band-width dv is defined as

with

E(v,T)

= in the conventional

approach

and with

u(v,T)

the _energy

_{spectral density.}

We

_get

the Planck radiation formula

The

_{black-body emissivity}

is defined as

At _very low

_frequency

the conventional result leads to the

_{Rayleigh-Jeans}

formula

which is

_independent

of Planck constant and is

_proportional

to the inverse of the _square of

_wavelength

A =

c/v.

In the new

approach

the

_emissivity

is

At _very low

_frequency

one uses

(28)

with the result

Thus the

_{v2T dependence}

is

_{replaced by}

the

vT 2

_dependence,

the low

frequency

emissivity

now

depends

on the Planck constant and on the inverse

wavelength;

there is a ratio

7’2between

the new result and the one

predicted

s

3.4. Radiative atomic transitions. Let us now consider the

equilibrium

between atoms and a radiation

field, allowing

the emission or

_absorption

of

photons

of

_frequency

where 62 =

hv2

is the _{energy in} the _upper state and _{f¡ =} in the lower

state.

The conventional

theory,

as derived for the first time

_by

Einstein[l 1],

states that the rate at which atoms make a transition 1 --3 2 in which one

photon

is absorbed is

_equal

to the rate at which atoms emit

_photons,

so

that

where

Nl

and

N2

are the

occupation

numbers of atoms in levels 1 and

_2,

A21

is the

_spontaneous

_absorption

_rate,

B12

is the induced emission rate

and

_u(v)

is _{the energy}

_density

in the radiation field as

_given

in

(39).

In thermal

_equilibrium

the

_occupation

numbers in states 1 and 2

_obey

the Boltzmann law

Using

(46)

and

₍₃₉₎

one

_gets

the well known formulas

where A =

c/v

is the

wavelength

of the radiation field.

If one uses the

general

formula one

_gets

low

frequency

corrections in

the

_spontaneous

to stimulated emission ratio.

_Using

the low

_frequency

expression

(28)

for the internal _energy this

_yields

The

_A/B

low

_frequency

ratio now

depends

on the inverse of the _square of

wavelength

A and is

_independent

of the Planck constant

_~,

in contrast to

the

_{hi À3 dependence}

of the standard ratio. The _spontaneous to stimulated

absorption

rate is enhanced a

factor ’ 2over

the conventional one.

6x

3.5. Einstein’s fluctuation law revisited.

_According

to the

conven-tional Einstein’s

_approach

_[13]

the _energy fluctuations of a

_system

in

One can reformulate this relation for the fluctuations of the energy dE =

u(v,T)dv

in the bandwidth dv

with u the _energy

_{spectral density}

and

_{Su (v)}

the _power

_{spectral density}

of the fluctuations of u. One

_gets([13],

p.

429 )

The first term on the

_right

hand side is the one

_{corresponding}

to the

_high

frequency

part

of the

_spectrum

_{(Wien’s law):}

it is of a _pure

_quantum

nature

and is

_{corpuscular-like;}

the second one

corresponds

to the low

_frequency

(Rayleigh-Jeans)

region:

it is

_purely

classical and wavelike. In the low

frequency

part

of the

_spectrum

_they

are fractional _energy fluctuations of

the random walk

_type

In the new

approach

one uses the low

frequency

_energy

_density

u(v,

4~ v~

so that instead of

(52)

one

_gets

This is the announced

_quantum

_1/v

fluctuation

_spectrum.

There is a

re-duced low

_frequency

noise and the ratio between the new result and the

Einstein-Rayleigh-Jeans

one is

~.

4.

_Application

to a

phonon

_gas and to the

_{1/ f}

_frequency

noise of a

_quartz

resonator

4.1. The

_specific

heat of a

_phonon

_gas revisited. The

_properties

of

the

_phonon

_gas are

quite

similar to those of the

_photon

_gas

_except

for the

new form of the density of modes as g(v) -

with

₃

=

2 1

where

cph ph t 1

cph

represents

the average wave

_velocity

and _ct and _cl are the transverse and

longitudinal

velocities for an

_isotropic

solid

[11].

The maximal vibrational

frequency

Vm

(Debye

frequency)

is defined from the total number of allowed

quantum states

In the conventional

theory

[11]

we

_get

The _{internal energy follows from the formula}

and the constant volume

_specific

heat

_Cv

=

equals

the

_{Debye function,}

and xm -

flp,

with

---; the

Debye

characteristic

_temperature.

The case

D(0D) -

1

corresponds

to the

_Dulong-Petit

value

_Cv

-3R. At very low

temperatures

one

_gets

the cubic

_temperature

_dependence

In the new

approach

Debye

results are found

_unchanged

_except

for an extra

_{multiplicative}

factor in the

_specific

heat as was the case for the

integrated emissivity

in Section

(3.1)

that is

At very low

temperatures

the electronic contribution to the

_specific

heat which decreases as

_T,

dominates the lattice

_{contribution,}

which decreases as

T3.

This is accounted for in the conventional _way.

4.2.

_{1 /f}

noise in a

_quartz

resonator.

_Specific

heat is involved in the

energy fluctuations of a canonical ensemble from the relation

The relative _energy fluctuations follows as

2013y ==

_E7 which is of the

3No

order

10-11.

The

_Avogadro

number

_equals

_No

= 6.02 x

1023 .

For _energy fluctuations in the bandwidth

_dv,

the main difference with the conventional

_theory

lies in the low

_{frequency region,}

as was the case of

The method can be used to

_predict

fractional

_frequency

fluctuations in a

quartz

crystal

resonator from the

_{formula ~[7]-[8]}

where a; and

Q

are the

frequency

and

_quality

factor of the resonator.

Using

cph - 3.5 x

103

_m/s,

we find

_{Aph -}

5 x

10-4.

For a 5 MHz P5

_quartz

crystal

resonator with

_{Q -}

2 x

106,

the active

_region

under the electrodes has thickness t =

5A/2 -

3 _mm, and section S N 3

cwn2,

that is V - 1

cm3.

The

_resulting

_1/v

factor is

h-1

=

A h 102

6 X

lO-24.

This is the order of

_magnitude

found in

_experiments

_[7].

5.

_{R.amanujan-R,ademacher theory}

of

_partitions:

a short reminder

Besides the low

_{frequency approximations}

encountered in Section

₍₂₎

there is a an exact method to calculate the number of

_partitions

_p(n)

first discovered

_{by Ramanujan}

_[10]

and

_{improved by}

Rademacher

_[14]

thanks to

an

_integration

_along

Ford circles in the

complex

half

plane.

For

complete-ness we remind here the main

points

of the

theory

from which the results

in Section

₍₂₎

may also be derived .

From well-known mathematical

_arguments

_[10]

_{(p. 113)}

one can

_get

the

leading

term for the case 0 _y 1 _{and y -3} 1 from the

_expression

The use

of y =

exp(-hv/kT)

corresponds

to the low

_frequency

approxima-tion at v -

_0,

that is

_{1 - y}

= 1 -

hvlkt.

This leads to

the

_leading

low

_frequency

term in _{the free energy}

₍₁₈₎

and _{internal energy}

(28).

They

are similar formulas associated with rational

points

which are

lo-cated at

on the unit circle

Iyl

= 1. The

leading

_term in the

_expansion

of

Z(y)

corresponds

to the fundamental

_{mode 2 - 1*}

The

_general

method to

_compute

rational contributions is a master

_piece

of the mathematics of the 20th

_{century([10]),}

_{([14) .}

It uses the connection

of

_Z(y)

to the

_elliptic

modular functions.

I To establish the formula one writes the equation for a _lossy harmonic oscillator and one

5.1. The fundamental contribution. To

_compute

the contribution of the fundamental

_point

_1/1

of the unit circle

_Iyl

= 1 one uses the

_property

((2), p. 96, [5],p.58)

In the low

_{frequency region y}

=

exp( -z) -

1 so

that

= 0

and

_{2(y) ,}

1. Low

_{frequency approximations}

of the free _energy

₍₁₈₎

and of the internal _energy

₍₂₈₎

follow. There are similar formulas associated

with the other rational

points

of the circle as shown below.

To

_get

the

_leading

term in

_p(n)

one uses the

_Cauchy

formula

where i

means an

arbitrary

closed

loop

encircling

the

origin.

Substituting

(65)

in

₍₆₆₎

with

_2(y’)

= 1 one can obtain

This includes

₍₁₄₎

in the limit n - oo but is much more accurate.

5.2.

_Farey

contributions and Ford circles. From now on we extend

the domain of definition of

Z(y)

to the

_{complex plane}

and we introduce the new variable T and the Dedekind eta function as defined in

(22)-(24).

It can be shown that is a modular form of

degree

-1/2

on the

full modular _group. It acts on the

_generators

of such a _group

_through

the

relations

_{[2] 2}

To express the

partition

function one uses the

Cauchy

formula

In the third term above this

_corresponds

to a

path

of unit

length starting

at an

arbitrary

point

in 7~.

2For more _general modular _{transformations,} we have

The choice of the

_{integration path}

comes

_along

in a natural _way

by using

the connection of

_2(y)

to the modular _group. Let us observe that the set

of

_images

of the line T = X ₊

i,

X

real,

under all modular transformations

can be written as

Equation

(71)

defines circles

_C(p,

_q)

centered at

_{points T}

_{= Q}

+ 2~

with radius

_1/2q2.

_They

are named after L. R. Ford who first studied their

prop-erties in 1938

_(14~.

Ford circles are

easily generated by using

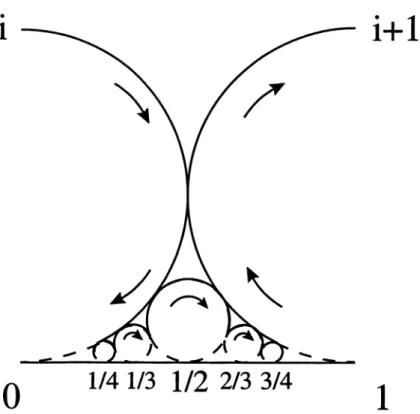
the ordered

Farey

sequence

To

_{each P}

_belongs

a Ford circle in the _upper half

_plane,

which is

_tangent

to the real axis at

_{T - Q .}

It can be observed that Ford circles never

intersect.

_They

are

_tangent

to each other if and

_only

if

_they

_belong

to

fractions which are

_adjacent

in some

Farey sequence.

If

_q

_q

are three

_adjacent

fractions in a

_{Farey sequence}

then 1 q q2

C(p, q)

touches

_C(pl,

_ql)

and

_{C(P2, q2)}

_respectively

at the

_points

where

In Rademacher’s

_approach

_(which

_improves

_{Ramanujan’s}

_one)

the unit

length

path

on 1-£ is chosen so as to _go

_along

Ford circles

where is the upper arc on a Ford circle which connects

_points

of

_tangency

at

_{T 9}

and

_7~.

Each Ford circle

_{C(p, q)}

is labelled

_by

the

_expression

r

= 9

+

_(,

where the

_{variable (}

runs on an arc of the circle

~~-2~~ - 2~.

If one uses z such

that (

=

FIGURE 1. Rademacher’s

_path

of

_integration.

transforms as

where and

_R

follow from

_(73).

5.3.

_Farey

contributions and Dedekind sums. To

_compute

₍₇₆₎

one uses the transformation formula

(22).

After some

_{manipulations}

and

us-ing

z/q

instead of z

_(see

Ref.

_[14],

_p.

_269),

one

_gets

the formula which

generalizes (65)

The so-called Dedekind sums

s(p,

q)

are introduced

by

where

_{[ ] in (79)}

denotes the

_integer

_part.

For the calculation

_{of p(n)}

one uses an

_{approximation}

similar to the one

used in

_(65).

If z is a small

_positive

real

_number,

_{then y}

is near

the modulus at that

_point

= 0 and

2(y’) -

1.

As a result

(76)

can be

_{readily integrated}

and the final result is

The

_physical

_meaning

of these

_higher

modes has still to be understood.

Acknowledgements

A first version of this

_manuscript

was

presented

at the 8th Van der Ziel

Quantum

1/ f

Noise

_Symposium

in St-Louis

_(Missouri),

June 5-6

_(2000).

I thanks P. Handel and C. Van Vliet for their useful comments.

References

[1] D. A. _ABBOTT, B. R. DAVIS, N. J. _PHILLIPS, K. ESHRAGHIAN, Quantum vacuum fluctu-ations, zero _{point energy} and the _{question of} observable noise. In: Unsolved Problems of

Noise in Physics, Biology, Electronic _Technology and Information _Technology, eds Ch. R.

Doering, L. B. Kiss and M. F. _Shlesinger, World _Scientific, 1997, 131-138.

[2] T. M. APOSTOL, Modular Functions and Dirichlet Series in Number _{Theory (Second}

Edi-tion). Springer Verlag, New _York, 1990.

[3] F. BLOCH, A. _NORDSIECK, Note on the Radiation Field _of the Electron. _Phys. Rev. 52

(1937), 54-59.

[4] H. B. _CALLEN, T. A. _{WELTON, Irreversibility} and _generalized noise. _Phys. Rev. 83 _(1951), 34-40.

[5] E. _ELIZALDE, Ten _{Physical Applications of Spectral} Zeta Functions. _{Springer Verlag} Lecture Notes in _Physics Vol. _{m35, Berlin,} 1995.

[6] P. _FLAJOLET, X. _GOURDON, P. _DUMAS, Mellin _transforms and _asymptotics: harmonic

sums. Theoretical _Computer Science 144 _(1995), 3-58.

[7] J.-J. GAGNEPAIN, J. _UEBERSFELD, G. GOUJON, P. H. HANDEL, Relation between _1/f noise

and Q-factor in quartz resonators at room and low _temperature, first theoretical

interpreta-tion. In: Proc. 35th Annual Symposium on _{Frequency Control, Philadelphia, 1981,} 476-483.

[8] P. H. _HANDEL, Nature _{of 1/f frequency} fluctuations in quartz crystal resonators. Solid State Electronics 22 _(1979), 875-876.

[9] P. H. _{HANDEL, Quantum 1/f} noise in the presence of a thermal radiation _backgrnund. In: Proc. II Int. _Symp. on _{1/f Noise,} eds C. M. Van Vliet and E. R. Chenette, Orlando, 1980, 96-110. See also P. H. HANDEL, Infrared divergences, radiative _corrections, and _{Bremsstrahlung}

in the presence of a _{thermal-equilibrium background. Phys.} Rev. A 38 _(1988), 3082-3085.

[10] G. H. _{HARDY, Ramanujan:} Twelve Lectures on _{Subjects Suggested by} his _Life and Work.

[11] J. _KESTIN, J. R. DORFMAN, A Course in Statistical Thermodynamics. Academic Press,

New York, 1971.

[12] B. W. NINHAM, B. D. HUGHES, N. E. FRANKEL, M. L. GLASSER, Möbius, Mellin and mathematical physics. Physica A 186 _(1992), 441-481.

[13] A. PAIS, "Subtle is the Lord... " The Science and the Life of Albert Einstein, Oxford Univ. Press, Cambridge, 1982.

[14] H. RADEMACHER, Topics in Analytic Number Theory. Springer Verlag, New York, 1973.

[15] A. VAN DER _ZIEL, Noise in Measurements. John _Wiley and _Sons, New _York, 1976.

[16] A. WEIL, Elliptic functions according to Eisenstein and Kronecker. _{Springer Verlag, Berlin,} 1976.

Michel PLANAT

Laboratoire de Physique

et _M6trologie des Oscillateurs du CNRS 32, Avenue de 1’Observa,toire

25044 Besanqon Cedex France