Percolation by cumulative merging and phase transition for the contact process on random graphs
Texte intégral
Figure




Documents relatifs
2014 A model based on second rank tensor orientational properties of smectic phases is developed.. The model predicts a second order smectic A-smectic C phase transition
A fragmentation occurs in the random permutation when a transposition occurs between two integers in the same σ-cycle, so tree components in the random graph correspond to cycles in
and [12] in a wave-front tracking scheme and prove that the obtained approximate solution u n converges (up to a subsequence) to a globally defined solution of the constrained
In this note, we prove a law of large numbers for an infinite chemical reaction network for phase transition problems called the stochastic Becker-Döring process.. Under a
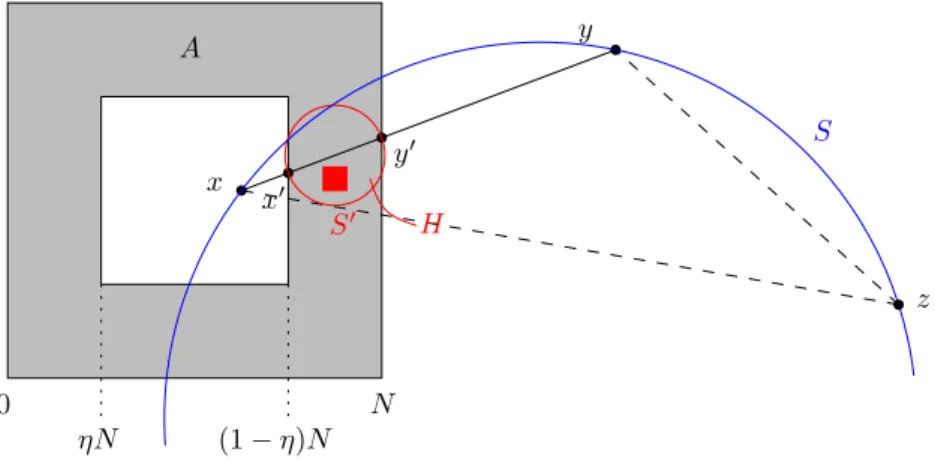
We consider the contact process on the model of hyperbolic random graph, in the regime when the degree distribution obeys a power law with exponent χ ∈ (1, 2) (so that the
The dielectric strength and the critical frequency of the relaxation mechanisms connected with these two modes were obtained throughout the measurement temperature
We also say that the beta distribution with parameter β = −1 is the uniform distribution on the Euclidean sphere S d−1 ; this is justified by the fact that the beta distributions
Though, one remarks conditions of Theorem 2.6 are milder: one can actually show the existence of s 1 in a neater way, assume λ 2 > λ c : without transition ”2 → 3” in
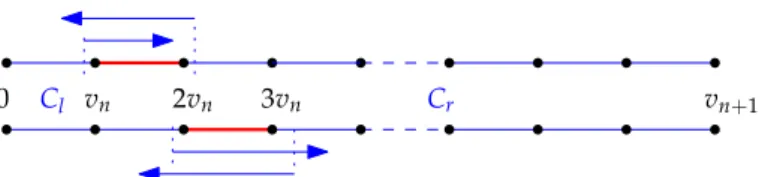
![Figure 7: Illustration of the proof of Proposition 2.12. In this configuration, 0 and L are both in a cluster composed of vertices of [[ 0; L ]]](https://thumb-eu.123doks.com/thumbv2/123doknet/14346001.500039/23.892.254.641.99.157/figure-illustration-proof-proposition-configuration-cluster-composed-vertices.webp)