Variable and Value Elimination in Binary Constraint Satisfaction via Forbidden Patterns

HAL Id: hal-01280349

https://hal.archives-ouvertes.fr/hal-01280349

Submitted on 9 Mar 2016

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Variable and Value Elimination in Binary Constraint

Satisfaction via Forbidden Patterns

David Cohen, Martin Cooper, Guillaume Escamocher, Stanislas Zivny

To cite this version:

David Cohen, Martin Cooper, Guillaume Escamocher, Stanislas Zivny. Variable and Value Elimination

in Binary Constraint Satisfaction via Forbidden Patterns. Journal of Computer and System Sciences,

Elsevier, 2015, 81 (7), pp.1127-1143. �10.1016/j.jcss.2015.02.001�. �hal-01280349�

O

pen

A

rchive

T

OULOUSE

A

rchive

O

uverte (

OATAO

)

OATAO is an open access repository that collects the work of Toulouse researchers and

makes it freely available over the web where possible.

This is an author-deposited version published in :

http://oatao.univ-toulouse.fr/

Eprints ID : 14812

To link to this article : DOI :10.1016/j.jcss.2015.02.001

URL :

http://dx.doi.org/10.1016/j.jcss.2015.02.001

To cite this version : Cohen, David and Cooper, Martin C. and

Escamocher, Guillaume and Zivny, Stanislas Variable and Value

Elimination in Binary Constraint Satisfaction via Forbidden Patterns.

(2015) Journal of Computer and System Sciences, vol. 81 (n° 7). pp.

1127-1143. ISSN 0022-0000

Any correspondance concerning this service should be sent to the repository

administrator:

staff-oatao@listes-diff.inp-toulouse.fr

Variable

and

value

elimination

in

binary

constraint

satisfaction

via

forbidden

patterns

✩

David

A. Cohen

a

_,

_Martin

_{C. Cooper}

b

,

∗

_,

_{Guillaume Escamocher}

c

_,

Stanislav Živný

d

a_{Dept.ofComputerScience,RoyalHolloway,UniversityofLondon,UK} b_{IRIT,UniversityofToulouseIII,31062Toulouse,France}

c_{InsightCentreforDataAnalytics,UniversityCollegeCork,Ireland} d_{DepartmentofComputerScience,UniversityofOxford,UK}

a

b

s

t

r

a

c

t

Variable orvalue elimination in aconstraint satisfactionproblem (CSP)can be used in preprocessing or duringsearch toreduce searchspace size.A variable elimination rule (value elimination rule) allows the polynomial-time identification of certain variables (domain elements) whose elimination, without the introduction of extra compensatory constraints, does not affect the satisfiability of an instance. We show that there are essentially just fourvariable eliminationrulesand threevalue eliminationrulesdefined by forbidding generic sub-instances, known as irreducible existential patterns, in arc-consistentCSPinstances.Oneofthevariableeliminationrulesisthealready-knownBroken TriangleProperty,whereastheotherthreearenovel.Thethreevalueeliminationrulescan allbeseenasstrictgeneralisationsofneighbourhoodsubstitution.

1. Introduction

Constraintsatisfactionhasprovedtobeausefulmodellingtoolinavarietyofcontexts,suchasscheduling,timetabling, planning,bio-informaticsandcomputervision[17,24,29].Dedicatedsolversforconstraintsatisfactionareattheheartofthe programmingparadigmknown asconstraintprogramming. Theoretical advances onCSPscan thuspotentially lead tothe improvementofgenericcombinatorialproblemsolvers.

IntheCSPmodelwehaveanumberofvariables,eachofwhichcantakevaluesfromitsparticularfinitedomain.Certain sets of the variables are constrained in that their simultaneous assignments of values is limited. The generic problem in which thesesets of variables,known asthe constraint scopes, are all of cardinalityat mosttwo, is knownas binary constraint satisfaction. We are required to assign values to all variables so that every constraint is satisfied. Complete solutionalgorithms forconstraintsatisfactionarenot polynomialtime unless P

=

NP,since thegraphcolouringproblem,

which is NP-complete, canbe reducedto binary constraint satisfaction[17].Hence we need tofind ways toreduce the searchspace.

✩ _{Apreliminaryversionofpartofthisworkappearedin}

Proceedingsofthe23rdInternationalJointConferenceonArtificialIntelligence(IJCAI),2013.

*

Correspondingauthor.

Searchalgorithms forconstraintproblemsusually proceedby transformingtheinstance intoaset ofsubproblems,for example,by selectinga variableandassigning to itsuccessively eachvalue fromits domain. Thisnaive backtracking ap-proachisrecursiveandexploresthesearchtreeofpartialassignmentsinadepthfirstmanner.Eventhoughthebacktracking algorithmcantakeexponentialtimeitisofteneffectiveinpracticethankstointelligentpruningtechniques.

Therearemanywaystoimprovenaivebacktrackingbypruningthesearch spaceinwaysthatcannotremovesolutions. Thisisdonebyavoidingsearchingexhaustivelyinallgeneratedsubproblemswhencertainkindsofdiscoveredobstruction tosolution exists.Such techniquesincludeBack-marking, Back-jumping,Conflict-DirectedBack-jumping [6,28].As well as theselook-backtechniquesit isalsopossible tolookaheadby propagating theconsequences ofearlydecisions orofthe discoveredstructure.Oftheselook-aheadtechniquesthemostcommonistomaintainthelocalconsistencypropertycalled generalisedarc-consistency(GAC)[5].Thistechniqueidentifiescertainvaluesforvariablesthatcannotpossiblyformpartof asolution.

Ofcourse, savings can alsobe madeif we are able to eliminate variables from a sub-problem. Since backtracking is of exponential time complexity, the eliminationof variables and values (domain elements) to reduce instance size can inthe bestcasereduce search time by an exponential factor. Tomaintainthe soundnessofsearch we requirethat such eliminationsdonotchangethesatisfiabilityoftheinstance.Invarianceofsatisfiability,whichwestudyinthepresentpaper, isaweakerpropertythantheinvarianceofthesetofsolutionsguaranteedbyconsistencytechniquessuchasGAC.However, detectionofnon-satisfiabilityistheessential role oflook-ahead techniques,sincethisallowspruningduringsearch.Thus satisfiability-preservingreductiontechniques(whichdonotnecessarilypreservesolutions)mayproveusefulevenwhenthe aimistodiscoveroneorall solutions.Infact,we showthat allthetechniquespresentedinthispaper,althoughthey do notpreservesolutions,allowasolutiontotheoriginalinstancetobereconstructedveryefficiently.

1.1. Simplificationbyvariableandvalueelimination

WeconsideraninstanceI oftheCSPviewedasadecisionproblem.Supposethatx isavariableofI andthat,whenever thereissomevalidassignmenttoallvariablesexcept x,thereisasolutiontothewholeinstance;inthiscase,wecansafely removevariablex from I.Oneofthequestionsweaddressinthispaperishowtoidentifysuchvariables?

Variable elimination has been considered before in the literature. It is well known that in an arc-consistent binary CSP instance,a variable x whichisconstrained by onlyone other variable y can be eliminated;by the definitionofarc consistency, each assignment to y is compatible withsome assignment to x. It has been observed that a moregeneral property, calledthe (local)Broken TriangleProperty(lBTP) [11],ifit holds atsome variable, allows usto eliminate that variable.One wayofstatingthelBTPisthatthereisnopairofcompatibleassignmentstotwo othervariables y

,

z which

haveopposite compatibilities withtwo assignments to x. The closure ofa binary CSP instanceunder the eliminationof allvariables thatsatisfy thelBTPis uniqueandcanbe foundin O

(

ncd3

)

time,wheren isthe numberofvariables,c the

numberofconstraintsandd themaximumdomainsize,whichmaywellproveeffectivewhencomparedtotheexponential costofbacktracking.Themoregenerallocalmin-of-maxextendableproperty(lMME)allowsustoeliminatemorevariables thanthelBTP,butrequirestheidentificationofaparticular domainorder.Unfortunately,thisdomainorderisNP-hard to discover[11]forunboundeddomainsize,andsothelMMEislesslikelytobeeffectiveinpractice.

An alternativeto simple variableelimination isused inBucket Elimination [23].In thisalgorithm a variable v is not simplyeliminated.Insteaditisreplacedbyaconstraintonitsneighbourhood(the setofvariablesconstrainedby v).This newconstraintprecisely capturesthose combinations ofassignments to theneighbourhood of v which can be extended toa consistent assignmentto v.Such an approachmaygenerate high-orderconstraints,which areexponentially hard to processandtostore.Thearitycanbeboundedbytheinducedtreewidthoftheinstance,butthisstilllimitstheapplicability ofBucketElimination.Inthepresentpaperwerestrict ourattentiontotheidentificationofvariableeliminationstrategies whichdonotrequiretheadditionofcompensatoryconstraints.

The elimination of domain elements is an essential component of constraint solvers via generalised arc consistency (GAC)operations. GACeliminates domain elements thatcannot be partof anysolution,thus conservingall solutions. An alternativeapproachisthefamilyofeliminationrulesbasedonsubstitution:ifallsolutionsinwhichvariablev isassigned value b remainsolutionswhenthevalue ofvariable v ischangedto anothervalue a,thenthevalue b canbe eliminated fromthedomainofvariable v whileconservingatleastonesolution(iftheinstanceissatisfiable). Themostwell-known

polynomial-timedetectablesubstitutionoperationisneighbourhoodsubstitution[18].Thevalueeliminationrulesdescribed inthispaper gobeyondthe paradigmsof consistencyandsubstitution;we only requirethat theinstance obtainedafter eliminationofavaluefromadomainhasthesamesatisfiabilityastheoriginalinstance.

WestudyrulesforsimplifyingbinaryCSPinstancesbasedonpropertiesoftheinstanceatthemicrostructurelevel.The termmicrostructurewasfirstgivenaformaldefinitionbyJégou[22]:ifI isabinaryCSPinstance,thenitsmicrostructure isa graph

h

A

,

E

i

whereA isthesetofpossiblevariable-valueassignmentsandE isthesetofpairsofcompatiblevariable-value

assignments.Solutions to I arein one-to-onecorrespondencewiththen-cliquesofthemicrostructure of I andwiththe size-n independentsetsof themicrostructurecomplementof I. Thechromaticnumber ofagraphis thesmallestnumber of colours required to colour its vertices so that no two adjacent vertices have the same colour. A graph G is perfect

iffor every induced subgraph H of G, the chromatic number of H is equal to the size of the largest clique contained

in H.Since amaximumcliqueinaperfectgraphcanbefound inpolynomial time [21],theclassofbinary CSPinstances withaperfectmicrostructureistractable [30].Perfectgraphscanalsoberecognised inpolynomialtime [16].Aninstance

of the minimum-cost homomorphism problem (MinHom) is a CSP instance in which weights are associated with each variable-value assignmentandtheaimistofindasolutionwhich minimisesthesumoftheweights.Takhanov[31] gave a dichotomy for tractable conservative constraint languages forMinHom which uses the fact that an instance of binary MinHomcanbesolvedinpolynomialtimeifitsmicrostructureisperfect.ElMouelhietal.[26]maketheobservationthat ifthe microstructure hasa boundednumberof maximal cliques thenthe instancewill be solved inpolynomial time by classicalalgorithmssuchasForwardCheckingorReallyFullLookaheadandhencebyCSPsolvers.

Simple rules forvariable orvalue eliminationbased onproperties ofthe microstructure are usedby Beigel and Epp-stein[4]intheir algorithmswithlowworst-casetimeboundsforsuch NP-completeproblemsas3-COLOURINGand3SAT. Such simplificationoperationsarean essential firststepbefore theuseofdecompositions intosubproblems withsmaller domains. Asimilar approach allows AngelsmarkandThapper [3]toreduce the problemoffinding a minimumweighted independentsetinthemicrostructurecomplementtotheproblemofcountingthenumberofsolutionstoa2SATinstance. Thus, thevariableandvalueeliminationruleswe presentinthispapermayfindnotonlypracticalapplicationsinsolvers butalsotheoreticalapplications.

1.2. Ourcontribution

In thispaperwe characterise thoselocal conditionsunderwhich we caneliminate variables orvaluesin binary CSPs while preserving satisfiability ofthe instance,without theneed to add compensating constraints.Bylocal conditionswe meanconfigurationsofvariables,valuesandconstraintswhichdonot occur.Thatis,wewillidentify(local)obstructionsto variableorvalueelimination.Wewillcallsuchconstructionsvariableeliminationorvalueeliminationpatterns.

Surprisingly we find that there are precisely four (three) essentially different local patterns whose absence permits variable (value) elimination. Searchingfor theselocalpatterns takespolynomial time and needonly be done duringthe pre-processingstage,beforesearch.Any discoveredobstructionstoeliminationcanbeeffectivelymonitoredduring subse-quentsearchusingtechniquesanalogoustowatchedliterals[20].Wheneveravariable(value)nolongerparticipatesinany obstructionpatternsitcansafelybeeliminated.

Weshow thatafterasequence ofvariableandvalueeliminationsit isalwayspossibletoreconstructasolutiontothe originalinstancefromasolutiontothereducedinstanceinlow-orderpolynomialtime.

2. Definitions

WhencertainkindsoflocalobstructionsarenotpresentinabinaryCSPinstance,variableorvalueeliminationis possi-ble.Suchobstructionsarecalledquantifiedpatterns.A patterncanbeseenasageneralisationoftheconceptofaconstraint satisfactioninstancethatleavestheconsistencyofsomeassignmentstopairsofvariablesundefined.

Definition2.1.Apattern isafour-tuple

h

X

,

D

,

A

,

cpt

i

where:

•

X isafinitesetofvariables;

•

D isafinitesetofvalues;

•

A

⊆

X

×

D is the set of possible assignments; the domain of v

∈

X is its non-empty set

_D(

v

)

of possible values:

D(

v

)

= {

a

∈

D

| h

v

,

a

i

∈

A

}

;and

•

cpt is a partial compatibilityfunction from the set of unordered pairs of assignments

{{h

v

,

a

i,

h

w

,

b

i}

|

v

6=

w

}

to

{TRUE,

FALSE

_}

; if cpt

_(h

v

,

a

i,

h

w

,

b

i)

= TRUE

(resp.,

FALSE

) we saythat

_h

v

,

a

i

and

h

w

,

b

i

are compatible (resp., in-compatible).

Aquantifiedpattern isapattern P withadistinguishedvariable,v

(

P

)

andasubsetofexistentialvaluese

(

P

)

⊆

D(

v

(

P

))

.

Aflatquantifiedpattern isaquantifiedpatternforwhiche

(

P

)

isempty.Anexistentialpattern isaquantifiedpattern P for

whiche

(

P

)

isnon-empty.Anexistentialpattern P mayalsohaveadistinguishedvalueval

(

P

)

∈

e

(

P

)

.

When thecontext variable v isclear weusethe valuea to denotetheassignment

h

v

,

a

i

to v. We willoftensimplify

notationbywritingcpt

(

p

,

q

)

forcpt

({

p

,

q

})

.Wewillalsousetheterminologyofgraphtheory,sinceapatterncanbeviewed asalabelledgraph:ifcpt

(

p

,

q

)

= TRUE

(resp.,

FALSE

),thenwesaythatthereisacompatibility (resp.,incompatibility)edge

betweenp and q.

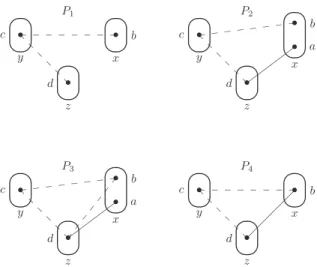
Wewilluseasimplefigurativedrawingforpatterns.Eachvariablewillbedrawnasanovalcontainingdotsforeachof itspossibleassignments.Pairsinthedomainofthefunctioncpt willberepresentedbylinesbetweenvalues:solidlinesfor compatibilityanddashedlinesforincompatibility.Thedistinguishedvariable(v

(

P

)

)andanyexistentialvaluesine

(

P

)

will

beindicatedbyan

∃

symbol.ExamplesofpatternsareshowninFig. 1andFig. 2.

We are neverinterestedinthe namesofvariables northe namesof thedomainvalues inpatterns.So wedefine the followingequivalence.

Definition2.2. Twopatterns P and Q are equivalent if they are isomorphic,i.e. ifthey are identical exceptfor possible injectiverenamingsofvariablesandassignmentswhichpreserve

D,

cpt

,

v,e andval.

Apatterncanbe viewedasaCSP instanceinwhichnot allcompatibilitiesare defined.Wecanthus refinepatternsto giveadefinitionofa(binary)CSPinstance.

Definition2.3. A binaryCSPinstance P is a pattern

h

X

,

D

,

A

,

cpt

i

where cpt is a total function,i.e. the domainof cpt is

precisely

{{h

v

,

a

i,

h

w

,

b

i}

|

v

6=

w

,

a

∈

D(

v

),

b

∈

D(

w

)}

.

•

Therelation Rv,w

⊆

D(

v

)

×

D(

w

)

on

h

v

,

w

i

is

{h

a

,

b

i

|

cpt

(h

v

,

a

i,

h

w

,

b

i)

= TRUE}

.

•

Apartialsolution to P onY

⊆

X isamappings

:

Y

→

D where,forall v

6=

w

∈

Y wehave

h

s

(

v

),

s

(

w

)i

∈

Rv,w.

•

Asolution to P isapartialsolutionon X .

Fornotationalsimplicitywehaveassumedthatthereisexactlyonebinaryconstraintbetweeneachpairofvariables.In particular,thismeansthattheabsenceofa constraintbetweenvariables v

,

w ismodelledby acompleterelation Rv,w

=

D(

v

)

×

D(

w

)

allowing every possible pair ofassignments to v and w. We say that there isa non-trivial constraint on

variablesv

,

w if Rv,w

6=

D(

v

)

×

D(

w

)

.

Inpractice,whensolvingCSPinstancesweprunethedomainsofvariablesinsuchawayastomaintainallsolutions.

Definition2.4.LetP

= h

X

,

D

,

A

,

cpt

i

beaCSPinstance.Anassignment

h

v

,

a

i

∈

A tovariablev iscalledarcconsistent if,for allvariablesw

6=

v in X thereissomeassignment

h

w

,

b

i

∈

A compatiblewith

h

v

,

a

i

.

TheCSPinstance

h

X

,

D

,

A

,

cpt

i

iscalledarcconsistent ifeveryassignmentinA isarcconsistent.

Assignmentsthatarenotarc-consistentcannotbepartofasolutionsocansafelyberemoved.Thereareoptimal O

(

cd2

)

algorithmsforestablishingarcconsistencywhichrepeatedly removesuchvalues[5],wherec isthenumberofnon-trivial constraintsandd themaximumdomainsize.Hence,fortheremainderofthispaperwewillassumethatallCSPinstances

arearc-consistent.

Inthispaperweareconcernedwithvariableeliminationcharacterisedbyforbiddenpatterns.Wenowdefinewhatthis means.

Definition2.5.Wesaythat avariablex canbe eliminated intheCSPinstance

h

X

,

D

,

A

,

cpt

i

if,wheneverthereisapartial solutionon X

\ {

x

}

thereisasolution.

Inordertouse(the absenceof)patternsforvariableeliminationwe needtodefine whatwe meanwhenwesaythat aquantified patternoccursatvariablex ofa CSPinstance.We define occurrencein termsofreductionsonpatterns.The

definitionsofoccurrenceandreductionbetweenquantifiedpatternsextenddefinitionspreviouslygivenfornon-quantified patterns[8].

Definition2.6.LetP

= h

X

,

D

,

A

,

cpt

i

beanypattern.

•

Wesaythat a pattern P′

= h

X′

,

D′

,

A′

,

cpt′

_i

_{isa sub-pattern of P if X}′

_⊆

_X

_,

_A′

_⊆

_{A and}

_∀

_p

_,

_q

_∈

_A′_,eithercpt′

₍

_p

_,

_q

₎

₌

cpt

(

p

,

q

)

orcpt′

(

p

,

q

)

isundefined.

If,furthermore,P′ _{isquantifiedthenwerequirethat P isquantifiedandthatv}

₍

_P′

₎

₌

_v

₍

_P

₎

_ande

₍

_P′

₎

_⊆

_e

₍

_P

₎

_{.If P}′_has

adistinguishedvaluethenwerequirethat P alsohasadistinguishedvalueandthatval

(

P′

₎

₌

_val

₍

_P

₎

_.

•

Valuesa

,

b

∈

D(

v

)

aremergeable inapatternifthereisnoassignment p

∈

A forwhichcpt

(h

v

,

a

i,

p

)

,cpt

(h

v

,

b

i,

p

)

are

bothdefinedandcpt

(h

v

,

a

i,

p

)

6=

cpt

(h

v

,

b

i,

p

)

.Inaquantifiedpattern, fora tobemergedintob,wealsorequirethat

a

∈

e

(

P

)

onlyifb

∈

e

(

P

)

.

Whena

,

b

∈

D(

v

)

aremergeablewedefine themergereduction

h

X

,

D

,

A

\ {h

v

,

a

i},

cpt′

_i

_{,inwhicha ismergedintob,}

bythefollowingcompatibilityfunction:

cpt′

₍

_p

_,

_q

_{) =}

½

_cpt

(h

v

,

a

i,

q

)

if p

= h

v

,

b

i

and cpt

(

p

,

q

)

undefined

,

cpt

(

p

,

q

)

otherwise

.

•

Adanglingassignment p of P isany assignment forwhich thereis atmost one assignment q for whichcpt

(

p

,

q

)

is

defined,andfurthermore(if defined)cpt

(

p

,

q

)

= TRUE

.If P is quantified, thenwe alsorequirethat p

∈

/

v

(

P

)

×

e

(

P

)

.

Foranydanglingassignment p,wedefinethedanglingreduction

h

X

,

D

,

A′

_,

_cpt

_↾

A′_×A′

i

where A′

=

A

\ {

p

}

.

•

Areduction ofapattern P isapatternobtainedfromP byasequenceofmergeanddanglingreductions.Anirreducible pattern isoneonwhichnomergeordanglingreductionscanbeperformed.

Toillustratethenotionsintroduced inDefinition 2.6,considerthepatternsinFig. 1.Pattern P1 isasub-patternof P2

which isitself a sub-pattern of P3.In pattern P2,the values a

,

b

∈

D(

x

)

are mergeable: merging a into b produces the patternP4.InthepatternP3,thevaluesa

,

b

∈

D(

x

)

arenotmergeablesincecpt

(h

x

,

a

i,

h

z

,

d

i)

andcpt

(h

x

,

b

i,

h

z

,

d

i)

areboth definedbutarenotequal.InpatternP2,

h

x

,

a

i

isadanglingassignment:applyingthedanglingreductiontothisassignment

Fig. 1. Examples illustrating the notions of sub-pattern, merging and dangling assignment.

in P2produces P1.LetP′2 beidenticalto P2exceptthat P′2isaquantifiedpatternwithv

(

P′2

)

= {

x

}

ande

(

P′2

)

= {

a

}

.Then

P2 isasub-patternofP2′,butP′2isnotasub-patternofP2.Inthedomainofx inP′2,b canbemergedintoa buta cannot

bemergedintob sincea

∈

e

(

P′

2

)

butb

∈

/

e

(

P′2

)

.Furthermore,theassignment

h

x

,

a

i

isnotadanglingassignmentinP′2 since

a isanexistentialvalueforv

(

P′ 2

)

=

x.

Now wewanttodefine whenaquantified patternoccursatavariableinaCSPinstance,inordertocharacterisethose patternswhosenon-occurrence allowsthisparticularvariabletobeeliminated. Wedefinetheslightlymoregeneralnotion

of occurrence of a pattern in another pattern. Recall that a CSP instance corresponds to the special case of a pattern whosecompatibilityfunctionistotal.Essentiallywewanttosaythatpattern P occursinpattern Q ifP ishomomorphic to a sub-patternof Q viaan injective renamingof variablesanda (possibly non-injective)renaming ofassignments [7]. However,wefinditsimplertodefineoccurrenceusingthenotionsofsub-pattern,reductionandequivalence.Wefirstmake theobservationthatdanglingassignmentsinapatternprovidenousefulinformationsinceweassumethatallCSPinstances arearcconsistent,whichexplainswhydanglingassignmentscanbeeliminatedfrompatterns.

Wecanthendefineoccurrenceintermsofreducedpatterns.

Definition2.7.Wesaythatapattern P occurs inapatternQ (andthat Q contains P )ifsomereductionof P isequivalent toasub-patternofQ .

If Q isa CSPinstance,thenthequantifiedpattern P occursatvariablex ofQ ifsomereductionof P isequivalenttoa sub-patternofQ andx isthevariableofthesub-patternofQ correspondingtov

(

P

)

.

WesaythatthequantifiedpatternP occursatvariablex ofQ withvaluemapping m

:

e

(

P

)

→

D(

x

)

ifthevaluesofvariable x correspondingtoeacha

∈

e

(

P

)

aregivenbythemappingm.

AvariableeliminationpatternisdefinedintermsofoccurrenceofapatterninaCSPinstance.

Definition2.8.Aquantifiedpatternisavariableeliminationpattern(var-elimpattern) if,wheneverthepatterndoesnotoccur atavariablex inanarc-consistentCSPinstance I foratleastoneinjectivevaluemapping,x canbeeliminatedinI (inthe senseofDefinition 2.5).

Anon-quantifiedpattern(i.e.apatternwithoutadistinguishedvariable)isavar-elimpatternif,wheneverthepattern doesnotoccurinanarc-consistentCSPinstance,any variablecanbeeliminatedinI .

The notion of non-quantifiedvar-elim patterns is necessaryfor some of our proofs, butfor practical applications we are interestedinfinding quantified (and,in particular,existential)var-elim patterns.Existentialpatterns mayallow more variablestobeeliminatedthanflatquantifiedpatterns.Forexample,aswewillshowlater,thepatternssnakeand

∃

snake

showninFig. 2arebothvar-elimpatterns,butthelatterallowsmorevariablestobeeliminatedsinceweonlyrequirethat itdoesnotoccuronasinglevalueinthedomainofthevariabletobeeliminated.

Example2.1. Suppose that we can assign value 0 to a subset S of the variables ofan instance, without restricting the assignments toanyothervariables.Furthermoresupposethat,within S,0isonlycompatiblewith0.Thevar-elimpattern

∃

invsubBTP, shown in Fig. 2, allows us to eliminate all variables in S,without having to explicitly search for S. This is becausethepatterndoesnotoccurforthemappinga

7→

0.Theflatvariant(invsubBTP)wouldnotallowtheseeliminations.

Fig. 2. Variable elimination patterns.

Weconcludethissectionwiththesimpleobservationthatvar-elimpatternsdefinetractableclasses.Ittakespolynomial time toestablisharcconsistency andtodetect (byexhaustivesearch)the non-occurrenceofa var-elimpattern. Hence it takespolynomial timeto identifyarc-consistentCSP instancesforwhich allvariables can beeliminated one byone by a var-elimpattern P .Suchinstancesaresolvableinagreedyfashion.

Henceweareabletosignificantlyextendthelistofknowntractable classesdefinedbyforbiddenpatternssinceamong knowntractablepatterns,namelyBTP[11],2-constraintpatterns[8],pivots[7]andJWP[9],only BTP(anditssub-patterns) allowvariableelimination.

Indeed, a general hybrid tractable class can be defined: the set of binary CSP instances which fall in some known tractableclassafterwehaveperformedallvariable(andvalue)eliminationsdefinedbytherulesgiveninthispaper.

3. Variableeliminationbyforbiddenpatterns

Inthispaperwecharacteriseirreduciblevar-elimpatterns.Thereareessentiallyjustfour(togetherwiththeirirreducible sub-patterns):thepatternsBTP,

∃

subBTP,

∃

invsubBTPand

∃

snake,showninFig. 2.Webeginbyshowingthateachofthese fourpatternsallowsvariableelimination.ForbiddingBTPisequivalenttothealready-knownlocalBrokenTriangleProperty (lBTP)[11]mentionedinSection1.1.

Theorem3.1.ThepatternsBTP,

∃

subBTP,

∃

invsubBTPand

∃

snakearevar-elimpatterns.

Proof. Since it is known that BTPis a var-elim pattern[11],we only need to prove the resultfor the three existential patterns:

∃

subBTP,

∃

invsubBTPand

∃

snake.

Everytwo-variable arc-consistentCSP instanceallows eithervariable to beeliminated. So we onlyhaveto prove that thesepatternsallowvariableeliminationinCSPinstanceswithatleastthreevariables.

Wefirstsetup somegeneralmachinerywhichwillbeusedineach ofthethreecases.Consideran arc-consistentCSP instanceI

= h

X

,

D

,

A

,

cpt

i

andlets beapartialsolutionon X

\ {

x

}

.

Fixsomeassignment

h

x

,

d

i

,andlet:

Y

= {

y

∈

X

\ {

x

} |

cpt

(h

y

,

s

(

y

)i, h

x

,

d

i) = TRUE} ,

Y

= {

z

∈

X

\ {

x

} |

cpt

(h

z

,

s

(

z

)i, h

x

,

d

i) = FALSE} .

Forall y

,

z

∈

X

\ {

x

}

,sinces isapartialsolution,cpt

(h

y

,

s

(

y

)i,

h

z

,

s

(

z

)i)

= TRUE

.Thus,ifX

=

Y

∪ {

x

}

thenwecanextend s toasolutionto I bychoosingvalue d forvariablex.So,inthiscasex couldbe eliminated.Soweassumefromnowon thatY

6= ∅

.

Byarcconsistency,forallz

∈

Y ,thereissome

h

z

,

t

(

z

)i

∈

A suchthatcpt

(h

z

,

t

(

z

)i,

h

x

,

d

i)

= TRUE

.

Wenowprovetheresultforeachpatterninturn.

Supposethat

∃

subBTPdoesnotoccuratx inI forthemappinga

7→

d.Consideranyy

∈

Y .Byarcconsistency,

∃

b

∈

D(

x

)

such that cpt

(h

y

,

s

(

y

)i,

h

x

,

b

i)

= TRUE

. Since the pattern

∃

subBTP does not occur, and in particular on the set of

as-signments

{h

y

,

s

(

y

)i

,

h

z

,

s

(

z

)i

,

h

x

,

d

i

,

h

x

,

b

i}

, we can deduce that, forevery variable z

∈

X different from both x and y,

cpt

(h

z

,

s

(

z

)i,

h

x

,

b

i)

= TRUE

. Hence, we can extend s to a solution to I by choosing s

(

x

)

=

b. So, in any case x can be eliminatedand

∃

subBTPisindeedavar-elimpattern.

Fig. 3. Patterns which do not allow variable elimination.

Now instead,suppose

∃

invsubBTPdoesnot occur atx in I forthemappinga

7→

d.Since thepattern

∃

invsubBTPdoes not occur, if both y and z belong to Y then cpt

(h

y

,

t

(

y

)i,

h

z

,

t

(

z

)i)

= TRUE

, otherwise the pattern would occur on the assignments

{h

y

,

s

(

y

)i

,

h

y

,

t

(

y

)i

,

h

z

,

t

(

z

)i

,

h

x

,

d

i}

.Also, if y

∈

Y , z

∈

Y ,then cpt

(h

y

,

s

(

y

)i,

h

z

,

t

(

z

)i)

= TRUE

,otherwise the

patternwouldoccuron

{h

z

,

s

(

z

)i

,

h

z

,

t

(

z

)i

,

h

y

,

s

(

y

)i

,

h

x

,

d

i}

.

So,inthiscasewehaveasolutions′_{toI ,where}

s′

(

v

) =

(

_d if v

₌

_x

_,

s

(

v

)

if v

∈

Y

,

t

(

v

)

otherwise

.

So

∃

invsubBTPisindeedavar-elimpattern.

Forthe final pattern, suppose that

∃

snakedoesnot occur atx in I for themappinga

7→

d.If y

∈

Y , z

∈

Y ,since the pattern

∃

snakedoesnotoccur, we candeducethat cpt

(h

y

,

s

(

y

)i,

h

z

,

t

(

z

)i)

= TRUE

,otherwisethepatternwouldoccur on

the assignments

{h

z

,

s

(

z

)i

,

h

z

,

t

(

z

)i

,

h

y

,

s

(

y

)i

,

h

x

,

d

i}

. If both y and z both belong to Y , then we can deduce first that cpt

(h

y

,

s

(

y

)i,

h

z

,

t

(

z

)i)

= TRUE

(as in the previous case) and then, asa consequence,that cpt

(h

y

,

t

(

y

)i,

h

z

,

t

(

z

)i)

= TRUE

(otherwisethepatternwouldoccuron

{h

y

,

s

(

y

)i

,

h

y

,

t

(

y

)i

,

h

z

,

t

(

z

)i

,

h

x

,

d

i}

).

So,againinthiscasewehaveasolutions′toI ,wheres′isdefinedasabove.So

∃

snakeisalsoavar-elimpattern.

✷

4. Characterisationofquantifiedvar-elimpatterns

Ouraimistopreciselycharacteriseallirreduciblepatternswhichallowvariableeliminationinanarc-consistentbinary CSPinstance.Webeginbyidentifyingmanypatterns,includingallthoseshowninFig. 3,whicharenotvariableelimination patterns.

Lemma4.1.Noneofthefollowingpatternsallowvariableeliminationinarc-consistentbinaryCSPinstances:anypatternonstrictly morethanthreevariables,anypatternwiththreenon-mergeablevaluesforthesamevariable,anypatternwithtwonon-mergeable

incompatibilityedgesinthesameconstraint,Diamond,Z,XL,V(

+−

),Triangle(asym),Triangle,Kite(sym),Kite(asym),rotsubBTP, Pivot(asym),Pivot(sym),Cycle(3).

Proof. Foreachpatternweexhibitabinaryarc-consistentCSPinstancethat:

•

hasapartialsolutiononthesetofallthevariablesexceptaspecifiedvariablex;

•

hasnosolution;

•

doesnotcontainthegivenpattern P atvariablex (if P isaquantifiedpattern)ordoesnot contain P atanyvariable (ifP isanon-quantifiedpattern).

Bydefinition,anysuchinstanceisenoughtoprovethatapatternisnotavar-elimpattern.

•

ForanypatternP whichiseitherDiamond,Z,XL,orTriangle,orhasatleastfourvariables,orhasthreenon-mergeable valuesforthesamevariable.

Let I₃2COL be the CSP instance(corresponding to 2-colouringon 3 variables)withthree Boolean variables, wherethe

constraintbetweenanytwovariablesforcesthemtotakedifferentvalues.

Thisinstancehaspartialsolutionsonanytwovariables,buthasnosolution,anddoesnotcontain P .

•

ForV(

+−

)andTriangle(asym).

Let I∃₄ bethe instanceonfour variablesx1

,

x2

,

x3 andx,wherethe domainsof x1

,

x2 andx3 are all

{

0

,

1

,

2

}

andthe

domainofx is

{

0

,

1

,

2

,

3

}

.Eachpairofvariablesin

{

x1

,

x2

,

x3

}

musttakevaluesin

{h

0

,

0

i,

h

1

,

2

i,

h

2

,

1

i}

.Therearethree

furtherconstraints:fori

=

1

,

2

,

3,wehavethat

(

xi

>

0

)

∨ (

x

=

i

)

.

I∃₄ hasapartialsolutionon

{

x1

,

x2

,

x3

}

buthasnosolution.I∃₄ containsneitherV(

+−

)norTriangle(asym)atvariable x

forthevaluemappingm

(

a

)

=

0.

•

ForKite(sym).

LetI4 betheCSPinstanceonfourvariablesx1

,

x2

,

x3

,

x wherex1

,

x2 andx3 areBooleanand

D(

x

)

= {

1

,

2

,

3

}

,withthe

followingconstraints:x1

∨

x2,x1

∨

x3,x2

∨

x3,xi

⇔ (

x

=

i

)

(i

=

1

,

2

,

3).

I4 hasapartialsolutionon

{

x1

,

x2

,

x3

}

,hasnosolution,anddoesnotcontainKite(sym)atvariablex.

•

ForKite(asym).

LetIZOA₄ betheCSPinstanceonthefourvariablesx1

,

x2

,

x3

,

x eachwithdomain

{

1

,

2

,

3

}

,withthefollowingconstraints:

x1

=

x2,x1

=

x3,x2

=

x3,

(

x1

=

1

)

∨ (

x

=

1

)

,

(

x2

=

2

)

∨ (

x

=

2

)

,

(

x3

=

3

)

∨ (

x

=

3

)

.

•

ForrotsubBTP.

Definethethreebinaryrelations:

R

= {h

0

,

0

i, h

1

,

2

i, h

2

,

1

i},

R0

= {h

0

,

0

i, h

1

,

1

i, h

2

,

1

i},

R1

= {h

0

,

1

i, h

1

,

0

i, h

2

,

0

i}.

LetI7betheCSPinstanceonthesevenvariablesx1

,

. . . ,

x6

,

x where

D(

xi

)

= {

0

,

1

,

2

}

,fori

=

1

,

. . . ,

6,and

D(

x

)

= {

0

,

1

}

, withthefollowingconstraints:

For

(

1

≤

i

<

j

≤

3

)

and

(

4

≤

i

<

j

≤

6

)

,

h

xi

,

xj

i

musttakevaluesin R. For

(

1

≤

i

≤

3

)

,

h

xi

,

x

i

musttakevaluesin R0.

For

(

4

≤

i

≤

6

)

,

h

xi

,

x

i

musttakevaluesin R1.

•

ForthepatternPivot(sym).

Let I₄SAT be the 2SAT instance onfour Boolean variables x1

,

x2

,

x3

,

x with the following constraints: x1

≡

x2, x1

≡

x3,

x2

∨

x3,x2

∨

x,x3

∨

x.

•

ForCycle(3)orPivot(asym),oranypatternwithtwonon-mergeableincompatibilityedgesinthe sameconstraint. LetISAT₆ bethe2SATinstanceonsixBooleanvariablesx1

,

x2

,

x3

,

x4

,

x5

,

x withthefollowingconstraints:x1

∨

x2,x1

∨

x4,

x1

∨

x3,x1

∨

x5,x2

∨

x,x4

∨

x,x3

∨

x,x5

∨

x.

✷

Thefollowinglemmaisthenkeytoprovingthatwehaveidentifiedallpossibleirreduciblequantifiedvar-elimpatterns.

Lemma4.2.TheonlyflatquantifiedirreduciblepatternsthatdonotcontainanyofthepatternslistedinLemma 4.1arecontained in BTP,invsubBTPorsnake(showninFig. 2).

Proof. Considera flatquantified irreduciblepattern P

= h

X

,

D

,

A

,

cpt

i

that doesnotcontain anyofthepatterns listedin Lemma 4.1.Thus P hasatmostthreevariables,eachwithdomainsizeatmosttwo.

Weconsiderfirstthecaseofa2-variablepatternP .ByLemma 4.1, P doesnothavetwonon-mergeableincompatibility edgesanddoesnotcontainZ.Since P isirreducibleandhencedoesnothaveanydanglingassignment,wecandeduceby

exhaustingoverallpossibilitiesthat P doesnothaveanycompatibilityedgeandasingleincompatibilityedge.Hence P is

Fig. 4. The possible negative skeletons of var-elim patterns.

Nowconsiderthenegativesub-pattern P−

_{= h}

_X

_,

_D

_,

_A

_,

_neg

_i

_{wherethecompatibilityfunctionneg iscpt withitsdomain}

reducedtotheincompatiblepairsofassignmentsof P .

Any irreducible pattern on three variables that does not contain an incompatible pair of assignments must contain Triangle.Moreover,ifanyassignmentisincompatiblewithtwootherassignmentsthen P mustcontaineitherPivot(sym)or Pivot(asym),orhavetwonon-mergeableincompatibleedgesinthesameconstraint.Now,sinceP doesnotcontainCycle(3), itfollowsthat P−is I1 orI2,asshowninFig. 4.

We firstconsider thelattercase. Withoutlossof generality,we assume that b iscompatiblewithc,to avoida andb

beingmergeable.

Sincethedomainshaveatmosttwoelements,webeginbyassumingthat

D(

v1

)

= {

c

,

d

}

and

D(

v2

)

= {

e

,

f

}

.Inthiscase

a andd mustbe compatibletoavoidd and c beingmergeable.Alsob and f mustbe compatibletostop e and f being

mergeable.Nowd andb cannotbecompatiblesinceotherwiseZoccursinP .Moreover,d ande cannotbecompatiblesince otherwiseXLoccursinP .Furthermore,d and f cannotbecompatiblesince,whichevervariableischosen forv

(

P

)

,either

Kite(sym)orKyte(asym)occursin P .Itfollowsthatd canberemovedasitisadanglingassignment.

Now we begin again. As before, to avoid e and f being mergeable or Diamond occurring in P , we have that f is

compatible withb and not compatiblewitha. Toavoid Triangleoccurring in P , f cannot be compatiblewith c, which

meansthat f canberemovedsinceitisadanglingassignment.

So, we have

D(

v1

)

= {

c

}

and

D(

v2

)

= {

e

}

.Suppose that thereis a compatibilityedge betweenc and e. If the

distin-guished variable v

(

P

)

is v0 then,whetherornotthereisa compatibilityedge betweena and e,thepatterniscontained in BTP. If v

(

P

)

=

v1 and there is no compatibility edge between a and e, then the patternis contained in invsubBTP.

If v

(

P

)

=

v1 andthereisacompatibilityedgebetweena ande,thenthepatterncontainsrotsubBTP.Ifv

(

P

)

=

v2,thenthe

patterncontains rotsubBTP. Since we havecovered all casesinwhich thereis acompatibilityedge betweenc and e,we assumethatthereisnoedgebetweenc ande.

Whetherornotthereisanincompatibilityedgebetweena ande,thepatterniscontainedinBTPifv

(

P

)

=

v0,andthe

patterniscontainedinsnakeifv

(

P

)

iseitherv1 orv2.

The finalcasetoconsider iswhen P is a3-variablepatternwith P−

₌

_I

1.Anytwo assignmentsforthethird variable

v2 could be merged,so we can assume its domainis a singletonwhich we denoteby

{

a′′

}

.Since P is irreducible,does not contain Diamond, Z,Triangle, Kite(sym)orKite(asym),we can deducethat theonly compatiblepairs ofassignments include a′′_{. Infact, both}

_{

_a

_,

_a′′

_}

_and

_{

_a′

_,

_a′′

_}

_{must becompatiblesince P is irreducible.Butthen P iscontained inBTPif}

v

(

P

)

iseitherv0orv1,andiscontainedininvsubBTPifv

(

P

)

=

v2.

✷

Weneedthefollowingtechnicallemmawhichshortensseveralproofs.

Lemma4.3.IfapatternP occursinavar-elimpatternQ with

|

e

(

Q

)|

≤

1,thenP isalsoavar-elimpattern.

Proof. Suppose that P occurs in the var-elim pattern Q and that

|

e

(

Q

)|

≤

1. By transitivity ofthe occurrence relation, if Q occurs ina binary CSP instance I (at variable x), then so does P . It follows that if(there is an injective mapping

m

:

e

(

P

)

→

D(

x

)

forwhich) P does not occur (at variable x) in an arc consistent binary CSP instance I , then (there is

an injective mapping m′

_:

_e

₍

_Q

₎

_→

D(

x

)

for which) Q does not occur (at variable x) and hence variable elimination is possible.

✷

Thecondition

|

e

(

Q

)|

≤

1 isrequiredinthestatementofLemma 4.3,sinceforaninstanceinwhich

D(

x

)

isasingleton,

if

|

e

(

P

)|

≤

1 and

|

e

(

Q

)|

>

1 theremaybeaninjectivemappingm

:

e

(

P

)

→

D(

x

)

forwhich P doesnotoccuratx butthere canclearlybenoinjectivemappingm′

:

e

(

Q

)

→

D(

x

)

.

AccordingtoDefinition 2.7,aflatquantifiedpatternP isasub-patternofanyexistentialversion Q of P (andhence P

occursin Q ).WestatethisspecialcaseofLemma 4.3asacorollary.

Corollary4.1.LetQ beanexistentialvar-elimpatternwith

|

e

(

Q

)|

=

1.IfP istheflattenedversionofpatternQ ,correspondingto e

(

P

)

= ∅

,thenP isalsoavar-elimpattern.

Lemma4.4.NoirreducibleexistentialpatternP with

|

e

(

P

)|

>

1 isavar-elimpattern.

Proof. Leta1

,

a2 betwo distinctassignments ine

(

P

)

.Since P is irreducible,a1 anda2 arenot mergeable;sothereis an

assignmentb suchthat

h

b

,

a1

i

isacompatibilityedgeand

h

b

,

a2

i

isanincompatibilityedge(orviceversa)in P .

Consider theinstance Ik₄ (where k

= |

e

(

P

)|

+

3) on fourvariables x1

,

x2

,

x3

,

x with domains

D(

x1

)

=

D(

x2

)

=

D(

x3

)

=

{

0

,

1

,

2

}

,

D(

x

)

= {

1

,

. . . ,

k

}

andthefollowingconstraints:x1

=

2

−

x2,x1

=

2

−

x3,x2

=

2

−

x3,

(

xi

6=

1

)

∨ (

x

=

i

)

(i

=

1

,

2

,

3).

Ik

4hasapartialsolution(1,1,1)onvariablesx1

,

x2

,

x3buthasnosolution.Furthermore,forany(arbitrarychoiceof)injective

mappingm

:

e

(

P

)

→

D(

x

)

whichmapse

(

P

)

toasubsetof

{

4

,

. . . ,

k

}

,P doesnotoccuronx sincethevaluesm

(

a1

),

m

(

a2

)

∈

{

4

,

. . . ,

k

}

havethesamecompatibilitieswithallassignmentstoothervariablesinIk₄.

Thereforetherearenoirreduciblevar-elimpatternsP with

|

e

(

P

)|

>

1.

✷

Thefollowingtheoremisa directconsequenceofTheorem 3.1andCorollary 4.1 togetherwithLemma 4.1,Lemma 4.2

andLemma 4.3.

Theorem4.1.Theirreducibleflatquantifiedpatternsallowingvariableeliminationinarc-consistentbinaryCSPinstancesareBTP, invsubBTPorsnake(andtheirirreduciblesub-patterns).

Wearenowabletoprovidethecharacterisationforexistentialpatternsafteralittleextrawork.

Theorem4.2.Theonlyirreducibleexistentialpatternswhichallowvariableeliminationinarc-consistentbinaryCSPinstancesare

∃

subBTP,

∃

invsubBTP,

∃

snake(andtheirirreduciblesub-patterns).

Proof. ByLemma 4.4weonlyneedtoconsiderpatternsP with

|

e

(

P

)|

=

1.

WeknowfromTheorem 3.1that

∃

subBTP,

∃

invsubBTP,

∃

snakearevar-elimpatterns.

Theorem 4.1andCorollary 4.1showthatwhenweflattenanexistentialvar-elimpatternthentheresultingflatquantified patterniscontainedinBTP,invsubBTPorsnake.

In the case of invsubBTP and snake, the existential versions of thesepatterns are var-elim patterns andso there is nothinglefttoprove.Soweonlyneedtoconsiderquantifiedpatternswhichflattenintosub-patternsofBTP.

Let

∃

BTPdenotetheexistentialversion Q ofBTPsuchthat

|

e

(

Q

)|

=

1.Bysymmetry,

∃

BTPisunique.Theonlyremaining

caseiswhen P isanirreduciblesub-patternof

∃

BTPwith

|

e

(

P

)|

=

1.Byastraightforwardexhaustivecaseanalysis,wefind

that,inthiscase, either P containsV(

+−

)orTriangle(asym)or P isasub-patternof

∃

subBTP.Theresultthenfollowsby

Lemma 4.1andLemma 4.3.

✷

CombiningTheorem 4.1andTheorem 4.2,weobtainthecharacterisationofirreduciblequantifiedvar-elimpatterns.

Theorem4.3.Theonlyirreduciblequantifiedpatternswhichallowvariableeliminationinarc-consistentbinaryCSPinstancesare B T P ,

∃

subBTP,

∃

invsubBTP,

∃

snake(andtheirirreduciblesub-patterns).

It is easy to see that variable elimination cannot destroy arc consistency. Hence there is no need to re-establish arc consistencyaftervariableeliminations.Furthermore,theresultofapplyingourvar-elimrulesuntilconvergenceisunique; variable eliminations may lead to new variable eliminations but cannot introduce patterns andhence cannot invalidate applicationsofourvar-elimrules.

5. Valueeliminationpatterns

Wenow considerwhenforbiddinga patterncanallow theeliminationofvaluesfromdomains ratherthan the elimi-nationofvariables.Value-eliminationisattheheartofthesimplificationoperationsemployedbyconstraintsolversduring preprocessingorduringsearch.Incurrentsolverssucheliminationsarebasedalmostexclusivelyonconsistencyoperations: avalueiseliminatedfromthedomainofavariableifthisassignmentcanbeshowntobeinconsistent(inthesensethatit cannotbepartofanysolution).Anothervalue-eliminationoperationwhichcanbeappliedisneighbourhoodsubstitutability whichallowstheeliminationofcertainassignmentswhichareunnecessaryfordeterminingthesatisfiabilityoftheinstance. NeighbourhoodsubstitutabilitycanbedescribedbymeansofthepatternshowninFig. 5.IfinabinaryCSPinstance I,there aretwoassignments a

,

b forthesamevariablex suchthat thispatterndoesnotoccur (meaningthata isconsistentwith all assignments with which b is consistent), then the assignment b canbe eliminated. This is because in any solution

containing b,simplyreplacingb bya producesanothersolution.

Itisworthnotingthatevenwhenallsolutionsarerequired,neighbourhoodsubstitutabilitycanstillbeappliedsinceall solutionstotheoriginalinstancecanberecoveredfromthesetofsolutionstothereducedinstanceintimewhichislinear inthetotalnumberofsolutionsandpolynomialinthesizeoftheinstance[14].

Fig. 5. A value elimination pattern corresponding to neighbourhood substitution.

Fig. 6. Three val-elim patterns.

Definition5.1.Wesaythatavalueb

∈

D(

x

)

canbeeliminated fromaninstance I iftheinstanceI′_{inwhichtheassignment}

b hasbeendeletedfrom

D(

x

)

issatisfiableifandonlyifI issatisfiable.

Definition5.2. Anexistential pattern P with adistinguishedvalue val

(

P

)

isa valueeliminationpattern(val-elimpattern) if

in allarc-consistentinstances I ,wheneverthepatterndoesnot occurata variablex in I foratleastone injectivevalue mappingm,thevaluem

(

val

(

P

))

canbeeliminatedfrom

D(

x

)

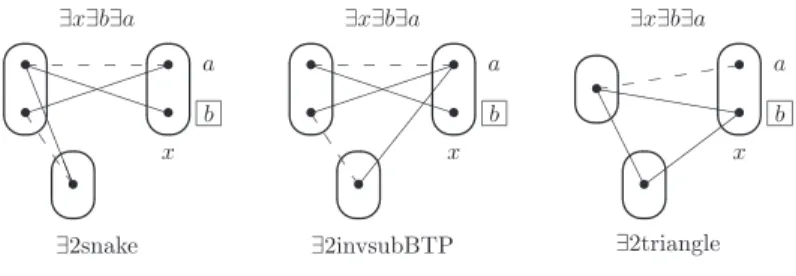
inI .

An obvious question is which patternsallow value eliminationwhile preserving satisfiability? The following theorem givesthreeexistentialpatternswhichprovidestrictgeneralisationsofneighbourhoodsubstitutabilitysinceineachcasethe patternofFig. 5isasub-pattern.Ineachofthepatterns P inFig. 5andFig. 6,thevaluethatcanbe eliminatedval

(

P

)

is

thevalueb surroundedbyasmallbox.

Theorem5.1.TheexistentialpatternsshowninFig. 6,namely

∃

2snake,

∃

2invsubBTPand

∃

2triangle,areeachval-elimpatterns.

Proof. WefirstshowthattheresultholdsforinstancesI withatmosttwovariables.Letx beavariableofI .For

|

D(

x

)|

>

1,

there isclearlyaninjectivemappingm

:

e

(

P

)

→

D(

x

)

forwhichnoneofthepatterns P showninFig. 6occur sincethey all havethreevariables.But,we canalways eliminateall butonevalue in

D(

x

)

withoutdestroyingsatisfiability, sinceby arc consistency the remaining value is necessarily part ofa solution.For

|

D(

x

)|

≤

1, there can be no injective mapping m

:

e

(

P

)

→

D(

x

)

since

|

e

(

P

)

=

2

|

andhencethereisnothingto prove.Intherestofthe proofwe thereforeonlyneedto

consider instances I

= h

X

,

D

,

A

,

cpt

i

withat leastthreevariables.We willprove theresultforeach ofthethree patterns onebyone.

Weconsiderfirst

∃

2snake.Supposethatforavariablex andvaluesa

,

b

∈

D(

x

)

,thepattern

∃

2snake doesnotoccur.Let I′_{beidenticaltoI exceptthatvalueb hasbeeneliminatedfrom}

_D(

_x

₎

_{.Supposethats isasolutiontoI withs}

₍

_x

₎

₌

_b.It

suf-fices to show that I′ hasa solution.Let Y (Y ) be the set ofvariables z

∈

X

\ {

x

}

such that cpt

(h

z

,

s

(

z

)i,

h

x

,

a

i)

= TRUE

(

FALSE

). By arc consistency, there are assignments

_h

z

,

t

(

z

)i

for all z

∈

Y which are compatible with

h

x

,

a

i

. Let z

∈

Y

and y

∈

X

\ {

x

,

z

}

. Since s isa solutionwith s

(

x

)

=

b, cpt

(h

y

,

s

(

y

)i,

h

z

,

s

(

z

)i)

=

cpt

(h

x

,

b

i,

h

z

,

s

(

z

)i)

= TRUE

.Since

∃

2snake doesnot occur on

{h

x

,

a

i,

h

x

,

b

i,

h

z

,

s

(

z

)i,

h

z

,

t

(

z

)i,

h

y

,

s

(

y

)i}

, we can deducethat cpt

(h

z

,

t

(

z

)i,

h

y

,

s

(

y

)i)

= TRUE

.In

partic-ular, we have cpt

(h

y

,

s

(

y

)i,

h

z

,

t

(

z

)i)

= TRUE

for all y

6=

z

∈

Y . Then, since

∃

2snake does not occur on the assignments

{h

x

,

a

i,

h

x

,

b

i,

h

y

,

s

(

y

)i,

h

y

,

t

(

y

)i,

h

z

,

t

(

z

)i}

, we can deduce cpt

(h

z

,

t

(

z

)i,

h

y

,

t

(

y

)i)

= TRUE

. Hence the assignments

h

z

,

t

(

z

)i

(z

∈

Y ) are compatible between themselves, are all compatible with all

h

y

,

s

(

y

)i

(y

∈

Y ) and with

h

x

,

a

i

. Thus, s′ is a solutiontoI′_,where

s′

(

v

) =

(

_a if v

₌

_x

_,

s

(

v

)

if v

∈

Y

,

t

(

v

)

otherwise

.

Wenow consider

∃

2invsubBTP.Suppose thatforavariablex andvaluesa

,

b

∈

D(

x

)

inan instance I ,thepattern

∃

2in-vsubBTP doesnot occur. Let I′ be identicalto I exceptthat value b has beeneliminated from

D(

x

)

.Suppose that s isa

solution to I with s

(

x

)

=

b and againlet Y (Y ) be the setof variables z

∈

X

\ {

x

}

such that cpt

(h

z

,

s

(

z

)i,

h

x

,

a

i)

= TRUE

(

FALSE

).Byarcconsistency, foreach z

∈

Y ,there isanassignment

h

z

,

t

(

z

)i

whichiscompatiblewith

h

x

,

a

i

.Lets′ _be

de-fined asabove.Consider v

∈

X

\ {

x

}

.Weknowthatcpt

(h

x

,

a

i,

h

v

,

s′

(

v

)i)

= TRUE

.Let z

∈

Y .Sincethepattern

∃

2invsubBTP

doesnotoccur on

{h

x

,

a

i,

h

x

,

b

i,

h

z

,

s

(

z

)i,

h

z

,

t

(

z

)i,

h

v

,

s′

₍

_v

_)i}

_{,we candeducethat cpt}

_(h

_z

_,

_t

₍

_z

_)i,

_h

_v

_,

_s′

₍

_v

_)i)

_{= TRUE}

_.Itfollows

Finally,we consider

∃

2triangle. Suppose that inan instance I , forvaluesa

,

b

∈

D(

x

)

, the pattern

∃

2triangle doesnot

occur. Let I′ _{be identicalto I exceptthat value b hasbeen eliminatedfrom}

_D(

_x

₎

_{.Suppose that s isa solutionto I with}

s

(

x

)

=

b.Then

h

x

,

a

i

mustbecompatiblewithallassignments

h

y

,

s

(

y

)i

(y

∈

X

\ {

x

}

),otherwisethepattern

∃

2trianglewould occuron

{h

x

,

a

i,

h

x

,

b

i,

h

y

,

s

(

y

)i,

h

z

,

s

(

z

)i}

forallz

∈

X

\ {

x

,

y

}

.Itfollowsthat s′′ isasolutiontoI′,where

s′′

(

v

) =

½

a if v

=

x

,

s

(

v

)

otherwise

.

✷

Example5.1.ConsideraCSPinstancecorrespondingtoaproblemofcolouringacompletegraphonfourvertices.Thecolours assignedtothe fourverticesare representedby variablesx1

,

x2

,

x3

,

x4 whosedomains are,respectively,

{

0

,

1

,

2

,

3

}

,

{

0

,

1

}

,

{

0

,

2

}

,

{

0

,

3

}

. Notice that the instance is arcconsistent andno eliminations are possible by neighbourhood substitution.

However,thevalue 1canbe eliminatedfromthedomainofx1 sinceforthemappinga

7→

0,b

7→

1,thepattern

∃

2snake

doesnotoccuronx1.Thevalues2and3canalsobeeliminatedfromthedomainofx1 forthesamereason.Afterapplying

arcconsistencytotheresultinginstance,alldomainsaresingletons.

Example5.2.Considerthearc-consistentinstanceonthreeBooleanvariablesx

,

y

,

z andwiththeconstraints z

∨ ¬

x,z

∨

y,

¬

y

∨ ¬

x. Inthisinstancewe caneliminate theassignment

h

x

,

0

i

since

∃

2invsubBTPdoesnotoccur onvariable x forthe mappinga

7→

1,b

7→

0.The assignments

h

y

,

1

i

and

h

z

,

0

i

then havenosupport atx andhencecanbe eliminated byarc

consistency,leavinganinstanceinwhichalldomainsaresingletons.

Example5.3.Consider the arc-consistentCSP instance corresponding to a graphcolouring problemon a completegraph

onthreeverticesinwhichthedomainsofvariablesx1

,

x2

,

x3 areeach

{

0

,

1

}

.Again,noeliminationsarepossibleby

neigh-bourhoodsubstitution.However,thevalue1canbeeliminatedfromthedomainofx1 sinceforthemappinga

7→

0,b

7→

1,

thepattern

∃

2triangledoesnot occuronx1.Applyingarcconsistencythenleads toanemptydomainfromwhichwe can

deducethattheoriginalinstancewasunsatisfiable.

Neighbourhoodsubstitution cannotdestroyarcconsistency[14],buteliminating avaluebya val-elimpatterncan pro-vokeneweliminationsbyarcconsistency,aswehaveseenintheaboveexamples.

Theresultofapplyingasequenceofneighbourhood substitution eliminationsuntilconvergenceisuniquemodulo iso-morphism[14].Thisisnottruefortheresultofeliminatingdomainelementsbyval-elimpatterns,asthefollowingexample demonstrates.

Example5.4. Consider the CSP instance onthree variables x1

,

x2

,

x3, each with domain

{

0

,

1

,

2

}

,and withthe following

constraints:

(

x1

6=

2

)

∨ (

x2

6=

2

)

,

(

x1

,

x3

)

∈

R,

(

x2

,

x3

)

∈

R,where R istherelation

{(

0

,

0

),

(

0

,

2

),

(

1

,

1

),

(

2

,

1

)

,

(

2

,

2

)}

.Wecan eliminatetheassignment

h

x3

,

0

i

since

∃

2snake doesnot occuron x3 withthevalue a mappingto2 andb to0.Butthen

intheresultingarc-consistentinstance,nomoreeliminationsarepossibleby anyoftheval-elim patternsshowninFig. 6. However, in the original instance we could have eliminated the assignment

h

x3

,

1

i

since

∃

2snake doesnot occur on x3

withthevaluea mappingto0 andb to1.Thenwecansuccessivelyeliminate

h

x1

,

1

i

,

h

x2

,

1

i

byarcconsistencyandthen

h

x1

,

2

i

,

h

x2

,

2

i

,

h

x3

,

0

i

by

∃

2snake.Intheresultinginstancealldomainsaresingletons.Thus,forthisinstancetherearetwo

convergentsequencesofvalueeliminationswhichproducenon-isomorphicinstances.

Itisclearthatvariableeliminationbyourvar-elimrulescanprovokenewvalueeliminationsbyourval-elimrules.Value eliminationmayprovoke newvariableeliminations,butmayalsoinvalidateavariableeliminationifthevalue eliminated (orone ofthevalueseliminated bysubsequentarcconsistency operations)istheonlyvalue onwhich anexistential var-elimpatterndoesnotoccur. Thus,tomaximise reductions,variableeliminationsshouldalways beperformedbeforevalue eliminations.

6. Characterisationofvalueeliminationpatterns

Aswithexistential variable-eliminationpatterns,we cangive a dichotomy forirreducibleexistentialval-elim patterns. Wefirstrequirethefollowinglemmawhichshowsthatmanypatterns,includingthoseillustratedinFig. 7(alongwiththe patternsZ andDiamondshownin Fig. 3),cannot be contained inval-elim patterns. InFig. 7,each of the patternsI(

−

), L(

+−

),triangle1, triangle2,

∃

Kite,

∃

Kite(asym)and

∃

Kite1hasa distinguishedvalueb

=

val

(

P

)

whichishighlightedinthe

figurebyplacingthevalueinasmallbox.

Lemma6.1.NoneofthefollowingexistentialpatternsP (withadistinguishedvalueval

(

P

)

)allowvalueeliminationinarc-consistent binaryCSPinstances:anypatternonstrictlymorethanthreevariables,anypatternwiththreenon-mergeablevaluesforthesame variablev

6=

v

(

P

)

,anypatternwithtwonon-mergeableincompatibilityedgesinthesameconstraint,anypatterncontaininganyof Z,Diamond,I(

−

),L(

−

),L(

+−

),triangle1,triangle2,

∃

Kite,

∃

Kite(asym)or

∃

Kite1.