Cristallisation induite par l'écoulement d'un polymère. Cas d'un polymère viscoélastique décrit par des variables moléculaires

HAL Id: hal-01006709

https://hal.archives-ouvertes.fr/hal-01006709

Submitted on 11 Feb 2017

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Distributed under a Creative Commons Attribution| 4.0 International License

Cristallisation induite par l’écoulement d’un polymère.

Cas d’un polymère viscoélastique décrit par des

variables moléculaires

Amine Ammar, Arnaud Poitou

To cite this version:

Amine Ammar, Arnaud Poitou. Cristallisation induite par l’écoulement d’un polymère. Cas d’un

polymère viscoélastique décrit par des variables moléculaires. Mechanics & Industry, EDP Sciences,

2002, 3 (6), pp.525-535. �10.1016/S1296-2139(02)01198-3�. �hal-01006709�

Cristallisation induite par l'écoulement d'un polymère.

Cas d'un polymère viscoélastique décrit par des variables moléculaires

Polymer flow induced crystallization.

Case of viscoelastic pol ymer with molecular variables

Amine Ammar, Arnaud Poitou

Laboratoire de mécanique et technologie, ENS de Cachan, 6! avenue du président Wilson, 94235 Cachan cedex, France

Résumé

Nous présentons dans ce travail un modèle de cristallisation, d'un polymère viscoélastique, induite par son écoulement Dans un travail antérieur [A, Poitou, A. Ammar, Pol ymer crystallization induced by strain or flow : a thermodynamic approach, C. R. Acad. Sei. Mécanique (Janvier 200l) 5-ll], nous avons montré comment le cadre thermodynamique des matériaux standards généralisés pourrait être appliqué

à la cristallisation d'un polymère avec un comportement visqueux. Nous décrivions dans ce cadre les couplages entre le comportement mécanique et le changement de phase. La difficulté relevé dans cet article concerne l'écriture du comportement viscoélastique dans le cadre thermodynamique. Nous nous basons ici sur une vision moléculaire du modèle de Maxwell. Nous écrivons dans ce cadre l'équation de cristallisation induite, qui traduit de façon naturelle l'influence de la sollicitation mécanique sur la cinétique. Cette équation peut s'appliquer pour simuler des sollicitations complexes, sans qu'elle ne soit limitée à un cas d'élongation ou de cisaillement simple. Nous comparons, enfin, les résultats de simulation à un cas expérimental d'élongation plane [M. Vigny, A. Aubert, J.M. Hiver, M. Aboulfaraj, C. G'Sell, Constitutive viscoplastic behaviour of amorphous pet during plane-strain tensile stretching, Polymer Engrg. Sei. 39 (12) (December 1999) 2366]. Abstract

We present in this work a mode! of flow iduced crystallization. In a former work [A, Poitou, A. Ammar, Pol ymer crystallîzation induced by strain or flow: a thermodynamîc approach, C. R. Acad. Sei. Mécanique (Janvier 200 l) 5-11] we showed how the therrnodynamic forrnalism of the standard materials could be applied to the crystallization of a polymer with a viscous behavior. We described within this framework the coup ling between the mechanical behavior and the phase transition. The difficulty raised in this paper relates to the writing of the viscoelastic behavior within the thermodynamic framework. A molecular vision of the Maxwell mode! is used. Within this framework, the equation of flow induced crystallization expresses naturally the influence of the mechanical sollicitation on the kinetics. This equation can be applied to simulate complex sollicitations wîthout limitation to the case of the simple elongation or the simple shearing. We compare finally the results of simulations with an experimental case of plane elongation [M. Vigny, A. Aubert, J.M. Hiver, M. Aboulfaraj, C. G' Sel!, Constitutive viscoplastic behaviour of amorphous pet during plane-strain tensile stretching, Polymer Engrg. Sei. 39 (12) (December 1999) 2366].

Mots-clés: Cristallisation ; Viscoélastique ; Cadre thermodynamique ; Variables moléculaires

Keywords: Crystallization; Viscoelastic; Thermodynamic; Molecular variables

1. Introduction

Il existe différentes lois de cinétique naturelle pour décrire la cristallisation d'un polymère [ 1-3]. On peut écrire

certains modèles sous forme différentielle. Une écriture possible du modèle de Nakamura [3] est celle proposée par Hieber [4,5]

x

a = - = 1-exp(-f),

j

=

_n_

₁

J-1jn

x(T)

(l)

où a est la fraction cristalline relative (rapport du degré de cristallinité X par le degré ultime de cristallinité X00 ), fest

Nomenclature

Opérateurs

tenseur du second ordre en notation matricielle

Xi] tenseur du second ordre en notation indicielle dX jdt

=X

dérivée matérielle par rapport au temps

a x

1

at

dérivée partielle par rapport au temps 8 X/

ot

dérivée surconvectée par rapport au temps

:D

X

/:Dt

dérivée convective (écriture générique) gradX opérateur gradient

div X opérateur divergence Tr X opérateur trace de matrice Tr (X J::.) produit contracté de matrices

:X.

produit contracté de matrices Variables cinétiques et thermiques

X fraction cristalline

X 00 degré ultime de cristallisation

a

fraction cristalline relative

{3 variable duale à la fraction cristallîne relative

f

fraction cristalline du volume infini A variable duale à la fraction cristalline

du volume infini

n indice de morphologie

T

température

Tm température de fusion Variables moléculaires

Ji

vecteur bout à bout de la chaîne

v nombre de chaînes par unité de volume

K raideur élastique de la chaîne c tenseur de conformation

~ tenseur dual au tenseur de conformation

la cristallinité intrinsèque, n est l'exposant d' Avrami et

x

est un paramètre qui dépend de la température.

Ces lois sont valables dans les conditions statiques. Lorsque le polymère est soumis à des sollicitations méca-niques, l'écriture de modèles de cristallisation induite se tra-duit par un ensemble de deux équations :

• la première donne l'influence de la mécanique (tenseur des contraintes ou tenseur des taux de déformation) sur l'évolution de la cristallinité,

• et la deuxième exprime l'influence de la cristallinité sur la viscosité ou plus généralement sur les autres paramètres rhéologiques du comportement

La deuxième équation ne pose pas de difficultés théoriques particulières. Elle est en général donnée par les lois de

mé-Variables mécaniques

D

tenseur identité tenseur des contraintes tenseur des extracontraintes tenseur des taux de déformations tenseur des déformations (hpp)

tenseur des déformations élastiques (hpp) tenseur des déformations anélastiques (hpp) TJ viscosité () temps de relaxation G module élastique .!:!. champ de vitesses p pression Variables thermodynamiques cp~ e s h q L r

c

p k énergie libre

énergie libre spécifique de la phase cristalline énergie libre spécifique de la phase amorphe dissipation mécanique ou intrinsèque dissipation thermique

pseudo-potentiel de dissipation

pseudo-potentiel de dissipation de la cinétique naturelle

pseudo-potentiel de dissipation mécanique énergie interne spécifique

entropie spécifique enthalpie spécifique flux de chaleur chaleur latente génération de chaleur capacité calorifique masse volumique conductivité

lange. Ces lois sont déterminées de manière expérimentale. Cependant la première équation est obtenue de manières dif-férentes selon les modèles utilisés.

L'une des démarches les plus naturelles dans le cas des sollicitations simples (unidimensionnelles) consiste à mo-difier une équation de cinétique naturelle et à identifier la dépendance de ses coefficients au taux de déformation. Par exemple Jay et al. l6] proposent une modification de la ci-nétique d'Ozawa. Cependant, avec ces types d'approches on ne peut pas décrire, avec le même modèle, le comportement sous différentes sollicitations (élongation et cisaillement).

D'autres auteurs, comme Verhoyen 17], distinguent les mécanismes de nucléation et de croissance et n'expriment l'effet de la mécanique que sur la cristallisation primaire.

En dissociant toujours les mécanismes de nucléation et de croissance et en se basant sur les anciens travaux de

Kolmo-goroff [8], Eder utilise le modèle de cristallisation naturelle décrit dans [9] et prend en compte l'effet de la mécanique en introduisant le second invariant du tenseur des taux de défor-mations [ 1 0,11 ] . Contrairement à ce que propose Verhoyen pour la cristallisation primaire, Eder suppose qu'aussi bien la nucléation que les différents mécanismes de croissance (linéaire, surfacique ou volumique) doivent être atiectés par le taux de cisaillement

y.

Cette dépendance doit être quadra-tique pour que le taux de nucléation ne puisse pas dépendre du sens de cisaillement. Pour d'autres auteurs comme Zui-dema [ 12J, les mécanismes de cinétique naturelle et induite sont dissociés et seules la nucléation et la croissance linéaire sont affectées par la sollicitation mécanique.

Enfin Doufas et aL [13] proposent un modèle de cristal-lisation dans lequel les couplages sont introduits grâce au formalisme thermodynamique (des systèmes Hamiltoniens généralisés [14]). Dans ce formalisme, on vérifie les rela-tions d 'Onsager qui traduisent la symétrie des coefficients de réponse. Cependant, les crochets de dissipation qui définis-sent les couplages sont utilisés avec beaucoup de paramètres ajustables.

Notre démarche consiste à utiliser le cadre des matériaux standards généralisés [15]. Nous avons présenté dans une étude antérieure [ 16] comment ce cadre pourrait être utilisé pour décrire naturellement le couplage mécanique-cinétique dans le cadre d'un comportement visqueux. Pour ceci nous avons écrit la cinétique naturelle dans le formalisme thermodynamique en définissant ;

• L'énergie libre

if/(T,œ) = Xif/c(T)+(l X)Vta(T)

=

(1-

exp(-f))XxVtc(T)

(2)

+

(1- (1

exp(- f))Xx)Vta(T) • La variable thermodynamique

f

et sa variable

asso-ciée A ()if/ A= p aj =exp(-j)fJ(T) où T

f3

= -T

1

Xoo L(T') dT' (3) Tm

T rn est la température de fusion et L est la chaleur latente

de changement de phase.

• Le pseudo-potentiel de dissipation convexe

q;;

qui vérifie

(4)

Dans ce cas l'écriture thermodynamique d'un modèle de comportement visqueux ne pose pas de problème particulier. Dans la suite nous nous focalisons sur le comportement viscoélastique.

2. Difficultés liées au comportement viscoélastique

L'écriture des modèles viscoélastiques tels que celui de Maxwell dans un cadre thermodynamique permet principa-lement de traiter le comportement dans des situations aniso-thermes. Nous bénéficions, en conséquence, de la connais-sance de la manière dont les déformations contribuent à la dissipation ou à la génération de la chaleur. Dans les hypo-thèses de petites perturbations, l'écriture du modèle de Max-well, dans le cadre des matériaux standards généralisés, ne pose pas de problème particulier. Dans ce cas, les potentiels sont définis de la manière suivante :

()if/ (§..e) a=p =

=

d§..e

(5)

()cp* (Q:.)

(6)

= - - - =

a

a

Cependant, les modèles de viscoélasticité linéaire ne décri-vent pas le comportement des polymères à l'état fondu qui subissent généralement de très grandes déformations. Afin de bien décrire le comportement de ces polymères, il est essentiel d'analyser l'orientation des chaînes qui les consti-tuent, ainsi que la réponse en grandes déformations, cas de tous les procédés de mise en forme.

Dans ce cas, l'écriture devient moins triviale. De nom-breuses recherches dans différents cadres thermodynamiques ont été menées pour surmonter cette difficulté.

Des visions récentes dans le cadre des polymères mon-trent que le problème viscoélastique peut être décrit avec une seule variable issue de la conformation des chaînes.

Dans un cadre analogue aux matériaux standards généra-lisés, Peters et Baaijens [ 17] utilisent le tenseur de confor-mation des chaînes f

{Ji

ET) comme variable. Dans cette expression, le vecteur bout à bout R suit la loi d'évolution:

dR

-=

= grad v R- QR

dt

= - - _-

(7)

où Q représente un tenseur choisi de telle manière qu'on retrouve l'équation d'évolution du modèle différentiel qui nous intéresse. Le cas particulier Q =

2

correspond à l'hy-perélasticité. Sinon, ditiérentes autres formes aboutissent aux modèles de Maxwell, Phan Tien et Tanner, Johnson-Segalman ... Par exemple, dans le cas du modèle de Max-well surconvecté. on a :

Q

=

_!.__!-

Gr*

= 2()= 2()= ' =vKc

Avec!_= G lie premier principe s'écrit alors : dT

pC-= -divq +8.r:

dt - -

+

(l - 8) 2()

(8)

(9)

(8!. : D) correspond à l'élasticité d'origine entropique. (1--o)Tr.r/20 correspond à l'élasticité d'origine énergé-tique. Il eXIste dans cette écriture deux cas extrêmes, le cas purement entropique ( 8

=

1) et le cas purement énergétique

(o

=

0). Mais cette écriture ne permet pas d'aller plus loin notamment pour la description des phénomènes couplés.

Dans le formalisme à double générateur (GENERIC) Ot-tinger et al. [ 18] proposent une écriture générale de quelques modèles différentiels. Ils choisissent le tenseur de conforma-tion f comme variable pour décrire la viscoélasticité. L'état du système est alors décrit par la masse volumique, la vi-tesse, l'énergie interne, et le tenseur de conformation en chaque point matériel du milieu :

::t

=

(p, Q, e, f) T

Les opérateurs

1

et M de l'équation :

a::t

=L aE +Mas

at

=

ax

=a::t

(10)

où E = j(v2j(2p)

+

e)dQ et S =

J

s(p,e,g)dQ sont choisis tels que :

• la première équation du système (1 0) exprime l'incom-pressibilité,

• la deuxième exprime les équations de Navier et Stokes, • la troisième exprime le premier principe de la

thermo-dynamique,

• et la quatrième exprime 1' équation du comportement viscoélastique.

En définissant la variable~ tel que~=

T(as;açJ

on obtient par identification du terme de dissipation de Ïa deuxième équation 1' expression du tenseur des contraintes Q. = 2~f·

On trouve dans la référence [ 18] d'autres travaux con~er­ nant la thermodynamique des modèles viscoélastiques.

3. Une vision thermodynamique eulérienne des modèles viscoélastiques

Pour surmonter les difficultés liées au transport, notre idée consiste à nous placer en configuration eulérienne et définir, pour le modèle en question, la transformation conservative d'un élément de matière. Cette transformation donne l'expression de la variable conjuguée qui à son tour permet de définir d'une part, le potentiel d'énergie libre et d'autre part, le pseudo-potentiel de dissipation.

Nous illustrons notre démarche premièrement dans le cas du modèle de Maxwell, sachant qu'elle pourrait être facilement étendue pour traiter d'autres modèles K-BKZ ou encore des modèles de Doi et Edwards [19] ou pom-pom [20].

3.1. Modèle de Maxwell 3.1.1. Rappel

Si on désigne par K la raideur élastique de l'haltère, v

le nombre de chaînes par unité de volume, G le module

d'élasticité et

ofot

la dérivée surconvectée, alors l'évolution du tenseur de conformation

{Ji

RT}) est donnée par :

oc

G -

₌

+ - 1

Dt OvK=

oc

(Il)

-

= Dt

Le tenseur des extracontraintes est donné par :

!. = VKf-

Gl

(12)

Et le modèle de Maxwell surconvecté s'exprime par :

DT

e-=

_ot

+

T

₌

=

2nD,

_''=

2n =GO

_.,

(13)

3.1.2. Étape 1 : Choix d'un transport matériel, écriture du tenseur des contraintes

Nous choisissons le tenseur de conformation c comme variable. Nous appelons (comme dans [18]) ~ sa variable associée au travers de l'énergie libre

-al[!

z = p

-=

ac

alors la dissipation intrinsèque s'écrit: <P1 = !. : D ~ :

g

(14)

(15) À ce niveau, nous devons connaître comment est trans-portée la matière, en particulier quand il n'existe pas de viscosité. Si nous admettons que le transport est régi par une dérivée surconvectée, alors la transformation telle que

Of/ lit =

Q

(Fig. 1) correspond à une transformation élastique oÜ encore à une dissipation mécanique nulle. D'ailleurs ceci se confirme en faisant tendre le temps de relaxation vers 1' in-fini dans l'Éq. (11). La dissipation peut s'écrire alors: <P1 =

Tr(:~;JD- Tr(~

· (

:~

+

gradQg

+

ggradQT))

= Tr((,; ·

D)

Tr(~:~)

(16)

Par un raisonnement analogue à celui de Coleman [21], c'est à dire pour tout champ de déformation D une transfor-mation élastique ne doit pas dissiper de l'énergie, on obtient

Fig. 1. Transformation d'un élément de matière sans relaxation : (a) ca<>

la relation entre les extracontraintes et la variable associée au tenseur de conformation

(17) Nous notons également que tout tenseur

r.,

à une pression hydrostatique près, vérifie l'Éq. (16).

3. 1 .3. Étape 2 : Expression de la variable conjuguée et de l'énergie libre

Pour définir maintenant l'expression exacte de

z,

nous supposons que le tenseur de conformations est

inve~sible

1•

À partir des Éqs. ( 12) et ( 17) on obtient ainsi :

1 l

~ =

2vKJ:-2 (18)

Pour satisfaire l'Éq. (14), nous pouvons remonter mainte-nant à l'expression "classique" de l'énergie libre:

1 l

P

!/1

= -vKTr(c)- -Glndet(

2

=

2 (19)

Nous allons écrire maintenant dans cette situation notre premier principe de la thermodynamique. La variation de l'énergie interne s'exprime par

.

.

ae .

pe

=

pCT

+

p - : f (20) avec

ae

a\ll

as

= - + T

aç_

aç_

-

-Dans le cas général (élasticité énergétique-entropique) on a

ae

p -

z-aT

et le premier principe s'exprime par

pCT

=

div q

+

r.:

1:è+T

:i;

=

=

aT

-(21)

(22)

Cette première partie de la démarche est valable pour tous les modèles qui utilisent une dérivée surconvectée et non pas uniquement pour le modèle de Maxwell.

Remarque. A ce niveau il est intéressant d'examiner le cas

particulier de l'élasticité purement entropique. Dans ce cas

r

énergie interne ne dépend pas de la conformation et ;:

s'écrit donc (par la même définition):

-a!/1

a

as

;: p - = p -Ts)=

On retrouve ainsi l'expression de l'équation de la chaleur proposée par Peter et Baaijens [171 dans la même situation entropique :

(23)

1 _{Il n'est pas interdit à ce tenseur d'avoir un déterminant nul mais c'est} une situation qui ne se produit pas à partir de la loi de comportement.

3. 1.4. Étape 3: Dissipation et pseudo-potentiel de dissipation

Reste maintenant à démontrer, dans le cas particulier du modèle de Maxwell, que la dissipation mécanique est positive

<Pt=-

Tr(/g)

_-ot

=

Tr(;:(~f- ~

_{- e-}

1))

vK

e-

(24)

Avec l'Éq. ( 18) on peut écrire <Pt sous la forme:

vK (( G

<Pt=

2 Tr

_e

l-

-vK

(25)

En développant le produit on obtient : <Pt vK (Trc

+

(!}_)

2

Trc-1

2!}_

Tr

1)

(26)

2e

= vK

=

vK

=

Or la trace du tenseur de conformation n'est autre que le premier invariant qui s'exprime comme la somme des valeurs propres Ài. Finalement la dissipation peut se factoriser comme : <Pt 3 K ( G ( G ) 2

1)

2:~ À~-2-+

-

-28

vK vK Àt i=t

t ;e~i

(

Àj -

\)~

r

t=l (27)

Nous en déduisons alors que la dissipation est positive puisque les valeurs propres de f sont positives. Elle est nulle quand À;

=

G

1

(v K), c' esC à dire, quand le tenseur des extracontraintes .I est nul. Nous pouvons alors définir un potentiel convexe,et nul pour~

Q

tel que :

z:

ot

ou encore tel que :

=

(vKe ₁

G

=

z:

(~c- ~~)

=

e=

vK

e=

2e

7)

l G;: G. 1 vKe=

(28)

(29)

Le pseudo-potentiel associé au modèle de Maxwell s'écrit donc:

*

c

1 ( 2)

G

cp (z)

= - -

n det 1 -

z

-=

2e

=

vK= vKe (30)

3.1.5. En résumé

Pour écrire une loi vîscoélastique en grandes déforma-tions, nous nous limitons au cadre formel suivant:

(a) Reconnaître les variables X2 qui, quand elles varient, sont susceptibles de faire varier l'énergie du système. En d'autres termes, il s'agit de répondre à la question: par quelles variables le système est-il capable de stoker de l'énergie?

2 _{X peut représenter plusieurs variables scalaires. vectorielles ou tenso·} rielles.

Dans le cas du modèle Maxwell la variable est le tenseur de conformation (l/1 ( f) ).

(b) Donner l'expression de 1 'énergie libre l/1 (X) et calculer les variables duales par

x:.

=

p

a

l/1

1

a x.

Dans le cas du modèle de Maxwell

1 1 plJ!(fl:_) = 2vKTr(g)-2Glndet(g) et àl/1 1 1 1 z=p-= -vKl-

-Gf-=

ac

2 - 2

-(c) Choisir une dérivée convective TJ jTJt telle que le comportement élastique soit équivalent à TJ X jTJt = Q. Cette dérivée est la dérivée surconvectée pour le modèle de Maxwell et la transformation élastique est telle que

Offot = Q.

-

-(d) Choisir un pseudo-potentiel des dissipations <p*(X:.)

convexe tel que <p

* (

Q) = 03. Pour le modèle de Maxwell

*

G ( 2 ) G

<p (z)

=

--lndet

1-

- z -

--Trz

=

28 - vK= vKB

=

(e) Les équations qui en découlent à partir de l'état du système sont :

• l'expression des extracontraintes .I. en écrivant que la dissipation est nulle pour toute évolution de X, • les lois d'évolution sous la forme

nx o<p* = -TJt

ax:.

• et le premier principe dT .

ar.

pC-= -div q

+

r : D - Y X+ T-= X dt -

:::.___,_..=...

ar-<Pl

Dans le cas du modèle de Maxwell on a :

• J;=2~fi:_=VKfi:.-Gl Of o<p* l G • - = = - - = - - c + - - 1 ot oz e= BvK= oz '•

pCT=-div'l.+J;:D-~:~+T a~:~

3 C'est le cas général, mais il existe des cas où le pseudo-potentiel n'est pas nul à zéro.

4. Application à la cristallisation induite

4.1. Le modèle de cristallisation induite

Nous allons maintenant coupler le modèle de comporte-ment viscoélastique de Maxwell au même modèle de ciné-tique naturelle issu du modèle de Nakamura sous forme dif-férentielle proposé par Hie ber.

Nous faisons l'hypothèse que chacune des deux phases peut être décrite avec un tenseur de conformation suivant le modèle de Maxwell avec une dérivée surconvectée.

Dans notre cas, si on désigne par fe et fa les tenseurs de conformation relatifs à la phase cristalline -et amorphe alors l'énergie libre s'écrit

pl/1 (a, T, fe, fa)

=aXcx{~(vK)e

Tr(fl:_e)-

~Gclndet(gc)

+

pl/lc(T))

+

(1-

aX

00

)(~(vK)a

Tr(ga)

-

~Galndet(fl:_a)

+

pl/la(T)) (31) (a) Afin de simplifier, on décrit les deux phases par le même tenseur de conformation f et nous maintenons

f

comme variable de

cristallisation-:-(b) On obtient alors une approximation de l'énergie libre sous la forme 1 l pl/1(/, T,c) = -vKTr(c)- -Glndet(c)

=

2

=

2

=

+

(1-

exp(- f))XooPlJ!c(T)

+

(1 - (1

-exp(- f) )Xoo)PlJ!a(T) (32) où les paramètres matériaux (par exemple le module d'élasticité) sont calculés avec la règle des segments inverses. En réalité v K et G dépendent de façon plus complexe du taux de cristallinité mais nous supposons que la définition des variables conjuguées (~ et A) reste inchangée.

(c) La dérivée convectée s'exprime ici par

TJ ( f ) ( off or )

TJt

f

=

j

=-df jdt (33)

( d) Pour la dissipation maintenant, qui est à 1 'origine des équations du modèle couplé, le pseudo-potentiel total est obtenu par superposition du pseudo-potentiel de cristallisation naturelle et celui du comportement viscoélastique :

<p*(~,

A)

= -

28

~A)

lndet(l-

v~~)

G - Trz vKB(A)

=

A

+ /[-

x;T)(ln(f)Y-1/n]d/ (34) f3

Ici, c'est toujours la dépendance des paramètres maté-riaux (module d'élasticité, temps de relaxation ... ) au taux de cristallinité qui est à l'origine de la cristallisa-tion induite (à partir du pseudo-potentiel global). Dans cette rédaction nous présentons le cas où la viscosité et l'élasticité varient de la même manière, c'est à dire, que c'est uniquement le temps de relaxation qui dépend de la cristallinité. Ceci est simplement dans le but d'avoir une meilleure compréhension et lisibilité des équations. ( e) On en déduit dans ce cas grâce au couplage :

• l'équation de cristallisation induite :

qui s'écrit:

.

a (

1 )

f

=

aA

B(A) ·

(~Inde{~

2_z)

_vK=

+ _E_

_vK

Trz)

₌

+

n (ln({J(T))) 1-l/n X A(t) • et le premier principe : pCT =-div~+~: - ~:g

az

+~+ra;:g

-Aj (35) (36) (37)

Remarque. En pratique, quand nous voulons identifier de tels modèles de comportement, nous décrivons la viscoélas-ticité par le modèle de Maxwell exprimé avec le tenseur des extracontraintes. Dans ce cas, les seuls paramètres matériaux sont le module d'élasticité G et le temps de relaxation

e.

Nous rappelons que ce type d'écriture ne peut être appliqué qu'une fois l'équation finale (36) est obtenu. Cela veut dire que le tenseur

:r

ne joue aucun rôle de variable thermodyna-mique. En détèfminant la relation entre ~ et ~ :

1

(!. )-1

-vK =

+

1

2 G = (38)

et en substituant la valeur de ~ dans l'Éq. (36), on ob-tient l'évolution de la cristallinité en fonction des extracon-traintes:

.

a (

1 )

.f

= -àA B(A) · (

~

ln det(

~

+

~)

+

~

Tr( (

~

+

~)

-t - 3))

+

n (ln({J(T)))I 1/n X A(t) (39)

Cette dernière équation, associée à celle du modèle de Maxwell

8(11)

8t

+

~

=

21J(A)D (40) dans laquelle la viscosité et le temps de relaxation sont fonc-tions du taux de cristallinité, permettent de résoudre le pro-blème couplé pour tout type de sollicitation tridimension-nelle.

4.2. Exemple d'application à un essai d'élongation plane

Nous allons maintenant appliquer le modèle précédent sur les essais de Vigny et al. [22]. Nous avons ajusté au mieux nos paramètres pour une meilleure corrélation avec un maximum de simplicité. Nous prenons alors :

• G constante à 2 GPa,

• e

80(1

+

7a) avec

eo

= 3000 s.

Nous appliquons sur le modèle la sollicitation plane proposée par les auteurs qui s'exprime sous la forme:

grady_

=

(~ ~s ~)

- 0 0 0

(41)

et nous calculons les contraintes réelles de Cauchy suivant la direction de l'étirement à partir du tenseur des extracon-traintes par : ( a

0 0)

(ru

0 0 0 =-p~

+

0 0 0 0 0 (42)

La résolution du système défini par les Éqs. (39) et (40) et les conditions initiales suivantes :

• a= 0,08 (X00

=

0,5),

• !.

Q,

nous permettent d'obtenir les courbes d'évolution de la con-trainte et du taux de cristallinité en fonction du temps ou encore en fonction de la déformation 8 puisque le taux de

déformation est constant et que 8 = t

s.

Contrairement aux résultats du modèle puissance [ 16], où les contraintes sont établies instantanément, la Fig. 2 montre que la contrainte, nulle au départ, s'établit progressivement, croît dans un premier temps à cause de l'effet mécanique du modèle viscoélastique, ensuite par le durcissement induit par la cristallisation. On reproduit mieux dans ce cas les résultats expérimentaux.

Pour la cristallisation induite, le cas visqueux ne montrait pas de temps d'induction. Mais avec le cas viscoélastique et en utilisant la même loi de mélanges on observe que, durant l'établissement de contraintes, la cristallinité ne commence pas à croître instantaném'ent (Fig. 3).

10

8

6

4

2

cr

(MPa)

0.5

1.5

Fig. 2. Évolution de la contrainte en cours d'élongation.

0.5

1

1.5 2

Fig. 3. Évolution de la cristallinité en cours d'élongation.

2

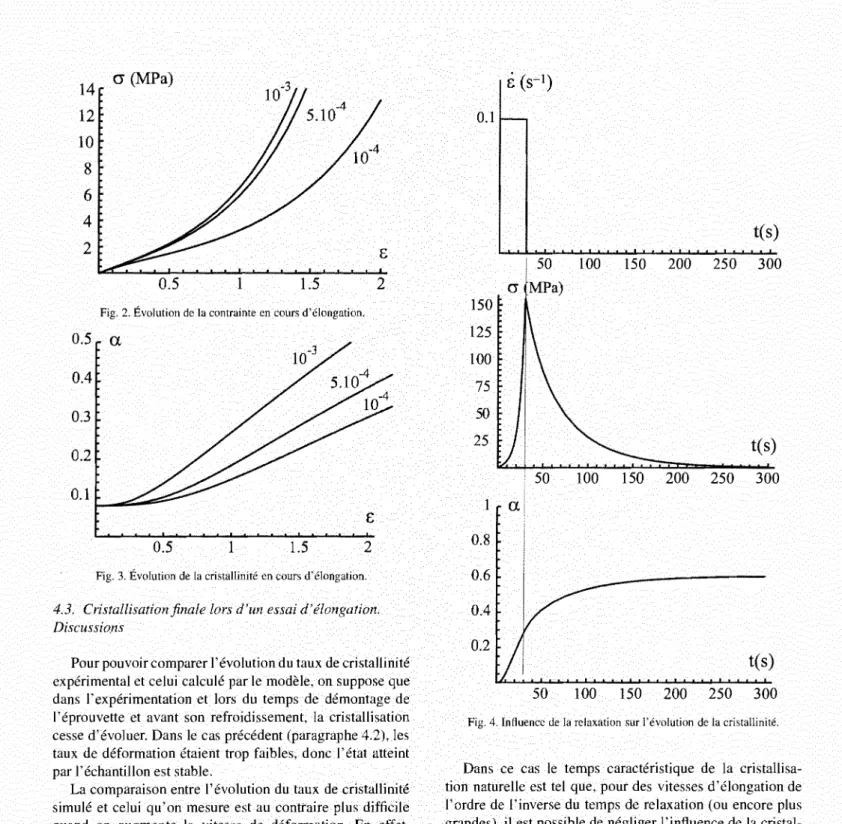
4.3. Cristallisation finale lors d'un essai d'élongation. Discussions

Pour pouvoir comparer l'évolution du taux de cristallinité expérimental et celui calculé par le modèle, on suppose que dans l'expérimentation et lors du temps de démontage de l'éprouvette et avant son refroidissement, la cristallisation cesse d'évoluer. Dans le cas précédent (paragraphe 4.2), les taux de déformation étaient trop faibles, donc l'état atteint par l'échantillon est stable.

La comparaison entre l'évolution du taux de cristallinité simulé et celui qu'on mesure est au contraire plus difficile quand on augmente la vitesse de déformation. En effet, en fin d'essai, si la déformation reste constante, le temps de relaxation des contraintes peut être relativement lent par rapport au temps de l'essai. Pendant cette phase la cristallisation continue à évoluer. Pour mettre en évidence l'évolution du taux de cristallinité après élongation, nous traitons un cas académique dans le quel les paramètres, et notamment le temps de relaxation, ont été choisis pour bien mettre en évidence le phénomène.

On prend:

• G constante à 2 GPa,

• e =eo(I

+7a) aveceo= lOs,

• /3

=

-25 . 10

6 '

• x=

20000s.

0.1

150

125

100 75

50

25

0.8 0.6 0.4 0.2

50

cr

MPa)

50

a

t(s)

100

150

200

250

300

t(s)

100

150

200

250

300

t(s)

150

200

250

300

Fig. 4. Influence de la relaxation sur l'évolution de la cristallinité.

Dans ce cas le temps caractéristique de la cristallisa-tion naturelle est tel que, pour des vitesses d'élongacristallisa-tion de l'ordre de l'inverse du temps de relaxation (ou encore plus grandes), il est possible de négliger l'influence de la cristal-lisation naturelle devant celle induite par la mécanique.

On effectue à plusieurs vitesses d'élongation des simula-tions à déformation finale fixes= 3. Si les vitesses d'élon-gation sont faibles on considère que la cristallisation n' évo-lue plus après le test (car aussi le temps d'essai est impor-tant), on relève donc le taux de crista!Iinité à la fin du test Par contre quand les vitesses d'élongation augmentent, le re-levé du taux de cristallinité juste à la fin du test se fait avant que les contraintes se relaxent. Si on suppose qu'on observe la cristallinité cinq minutes après la fin du test (temps à peu près nécessaire pour le démonta'ge et le refroidissement) on remarque que celle ci continue à évoluer .

L'évolution de la cristallinité finale peut être observée sur la Fig. 5.

a

0.8

_{Cristallisation finale après attente de Smin}

0.6

zone 1

0.4

0.2

Log (s) -4 0 2

Fig. 5. Évolution de la cristallinité finale dans un essai d'élongation à

déformation finale fixe.

Pour illustrer l'influence du temps d'attente, nous nous plaçons à Ê: = 1/

eo

et nous regardons 1 'évolution du matériau lors de la phase d'attente (Fig. 4).

Cette figure montre qu'après la fin d'application de dé-formation, les contraintes ne s'annulent pas instantanément, mais encore plus lentement que s'il n'y avait pas de cristal-lisation. En fait, la cristallisation a modifié le temps de re-laxation. Lors de la relaxation et en présence de contraintes ou encore de déformation élastique, la cristallinité continue à augmenter. Cette valeur tend vers une asymptote horizon-tale qui dépend du temps d'attente (bien évidemment de plus en plus proche de la valeur 1 quand ce temps augmente).

Ceci confirme l'effet mémoire constaté par certains au-teurs comme [23] et [24].

On en déduit alors que ce se sont les orientations des chaînes ou les contraintes qui sont à l'origine de la cristallisation induite ou encore ce sont les déformations élastiques plutôt que les déformations totales ou visqueuses.

Analysons maintenant de près les courbes de la Fig. 5. Celles ci contiennent principalement trois zones :

• Dans la première, les taux d'élongation sont tellement faibles qu'on ne dépasse pas le seuil de vitesse permet-tant d'activer la cristallisation induite par la mécanique. D'ailleurs dans ce cas, la sollicitation est tellement lente que les déformations élastiques sont absentes et le ma-tériau est toujours relaxé. Dans cette zone, c'est la cris-tallisation naturelle qui l'emporte. Il est donc naturel, si le taux d'élongation augmente, que le temps de l'essai diminue (puisqu'on travaille à déformation fixe) et par conséquent la cristallisation naturelle a moins de temps pour se développer, donc elle décroît.

• Dans la deuxième zone, les effets de la cinétique naturelle deviennent négligeables devant ceux de la mécanique. Dans cette zone, se situent la plupart des essais expérimentaux de la littérature. On observe alors une cristallinité finale de plus en plus croissante quand on augmente le taux d'élongation. Le comportement observé ici est appelé classiquement durcissement par cristallisation.

• Une originalité de notre modèle consiste à mettre en évidence la divergence des deux courbes qu'on observe dans la troisième zone quand on sollicite le matériau au delà de son temps de relaxation. Comme dans la zone précédente, la force de cristallisation induite augmente toujours pour les taux d'élongations croissants. Mais, on regarde l'état du matériau juste après 1' élongation, le temps d'observation est très court et la cristallisation n'a pas le temps de se développer. Par contre, si on continue à observer l'évolution de la cinétique (cf. Fig. 4) tout en maintenant la déformation totale, on remarque que, tant qu'il existes des contraintes (ou des déformations élastiques), la cristallisation continue à croître et sa vitesse de croissance est fonction des contraintes résiduelles.

S. Conclusions

Le modèle présenté met en évidence l'origine mécanique de la cristallisation induite par écoulement. Il permet d'ex-pliquer la tendance du comportement à fort taux de déforma-tion.

Par ailleurs, l'écriture dans un cadre thermodynamique avec des variables moléculaires permet de se généraliser avec d'autres comportements mécaniques (K-BKZ, pom-pom ... ) ce qui nous permet de bénéficier, en particulier, de modèles de cristallisation induite avec ces comportements.

Références

[1) M. Avrami, J. Chem. Phys. 8 (1940) 212. [2] T. Ozawa, Polymer 12 (1971) 150.

[31 K. Nakamura. T. Watanabe, K. Katayma, T. Amano, J. Appl. Polymer Sei. 17 (1973) 1031.

[41 C.A. Hieber, Correlation for the quiescent crystallization kinetics

of isostatic polypropylene and poly(ethylene terephthalate), Po1y-mer36(7)(1995) 1455-1467.

[5] C.A. Hieber, Results on crystallization effects, Notes (November 1998).

[6] F. Jay, B. Monasse, J.M. Haudin. Memory effects in crystallization of polypropylene during cast film extrusion. Int. J. Form. Proc. (1998) 75-95.

[7] O. Verhoyen, Crystallization of PolyEthylene Terephthalate in in-jection mou1ding : Experiments, molding and numerical simulation, Thèse de PhD, Université catholique de Louva in, 1997.

[8] A.N. Kolmogoroff, Izv. Akad. Nauk SSSR. Ser. Math. 1 {1937) 355-359.

[9] H. Janeschitz-Kriegl, G. Eder, Basic concepts of structure formation during processing of thermoplastic materials, J. Macromol. Sei. A 27 (13-14) (1990) 1733-1756.

[10] S. Liedauer, G. Eder, H. Janeschitz-Kriegl, P. Jerschow, W. Geymayer. E. lngolic, On the limitation of shear induced crystallization in polypropylene, in: International Polymer Processing VIII, Vol. 3. 1993. pp. 236-244.

[Il] S. Liedauer. G. Eder. H. Janeschitz-Kriegl, On the limitations of shear induced crystallization in polypropylene melts, in : International Polymer Processing X, Vol. 3, 1995, pp. 243-250.

[ 12] H. Zuidema, Flow induced crystallization on polymers. Application to injection moulding, Thèse de PhD, Université technique d'Eindhoven, 2000.

[13] A.K. Doufas, LS. Dairanîeh. A.J. McHugh, A continuum mode! for flow-înduced crystallization of polymer melts, J. Rheol. 43 (1) (JanuaryfFebruary 1999) 85-109.

[14] A.N. Beris, B.J. Edwards, Thermodynamîcs of Flowîng Systems, Oxford, New York, 1994.

[15] J. Lemaître, J.L Chaboche, Mecanique et thermodynamique des milieux continus, Dunod, 1988.

[16] A. Poitou, A. Ammar, Polymer crystallization induced by strain or flow :a thermodynamic approach, C. R. Acad. Sei. Mécanique (Janvier 2001) 5-11.

[17] G.W.M. Peters, F.P.T. Bal\iens, Modeling of non-isothermal viscoelas-tîc flows, J. Non-Newt. Fluid Mech. 68 (1997) 205-224.

118] M. Dressler, B.J. Edwards, H.C. Ottinger, Macroscopic thermodyna-mics offlowing polymerie liquids, Rheol. Acta 38 (1999) 117-136. [19] M. Doi, S.F. Edwards, J. Chem. Soc. Faraday Trans. Il 74 (19751

1789-1818.

[20] T.C.B. McLeish, R.G. Larson, Molecular constitutive equations for a class of branched polymers: the pom-pom polymer. J. Rheol. 42 (1) (1998) 81-llü.

[21] B.D. Coleman, M.E. Gurtin. Thermodynamic with internai variables.

J. Chem. Phys. 47 (1967) 597-613.

[22] M. Vigny, A. Aubert, J.M. Hiver, M. Aboulfaraj, C. G'Sell, Constitu-tive vîscoplastic behaviour of amorphous pet during plane-strain ten-sile stretching, Pol ymer Engrg. Sei. 39 ( 12) (December 1999) 2366. [23] J.A. Pople, G.R MitchelL S.J. Sutton, A.S. Vaughan, C.K. Chai, The

development of organized structures in polyethylene crystallîzed from a sheared melt, analyzed by waxs and tem, Pol ymer 40 ( 1999) 2769-2777.

[24] E. Gorlier, J.M. Haudin, J.F. Agassant, G. Perez, J.L. Lepage. D. Darras, N. Billon, Strain induced crystallization in amorphous pet. in · European Conference on Macromolecular Physics, Guimareas, 2000.