Density matrix approach to the complex heavy ion potential

Density matrix approach

to

the complex

heavy

ion optical potential

R.

Sartor and

Fl.

Stancu

Institut de Physique B5, Uniuersite de Liege, Sart Tilman, B-4000Liege 1,Belgium (Received 28 April 1982)

We extend the applicability ofthe density matrix expansion to a complex effective in-teraction depending both onthe density and the kinetic energy density. A detailed study of the kinetic energy density dependence ofthe density matrix expansion coefficients is given. The corresponding energy density has a parametrized form which is tested in the calcula-tion ofthe optical potential ofthe '

0+

'

0

system at several energies. Exact results are well reproduced bythe complex density matrix expansion.

NUCLEAR REACTIONS Density matrix expansion for acomplex ef-fective interaction; application toheavy ionoptical potential.

J

I.

INTRODUCTION

It

is now common practice' ' to define the heavy ion optical potential at a separation distance

D

as the difference between the expectation value

of

some effective Hamiltonian

H

at distance

D

and the expectation value

of

the same Hamiltonian at infini-ty

V»,

(D)=(H(D))

—

(H(ce))

.

Early computations' used an energy functional or an effective interaction which can be related to G matrix calculations in nuclear matter with a spheri-cal Fermi sea. As a consequence those computa-tions could only determine the real part

of

the opti-cal potential. However,

if

the heavy ion collision is locally described as the collision

of

two nuclear matter systems, one isled to anon-Hermitian

6

matrix '

'

' ' _{which will also enable the}

compu-tation

of

ImV,

_„,

(D)through the use

of

Eq.

(1.

1). The direct computation

of

V», from a finite range effective interaction is, however, cumbersome and time consuming. As a consequence, approxi-mation schemes have been proposed. Aconvenient procedure, extensively used for the real part'

of

V»„

is based on energy functionals. In aprevious work ' weproposed acomplex Skyrme-type interac-tion which generates a complex energy density, to be used in the calculation

of

both the real and imag-inary parts. The imaginary part

of

the Skyrme-type interaction was obtained by multiplying the real Skyrme-interaction used in

Ref.

3by a scaling fac-tor. This was assumed todepend on the local densi-ty

_p

and the intrinsic kinetic energy density v' '_and

found numerically from the finite range complex

ef-fective interaction

of Ref.

12.

In

Ref.

14, more emphasis was put on avoiding the explicit use

of

any wave function in the compu-tation

of

the expectation values appearing in

Eq.

(1.

1). Suitable approximations _{for p} and r'~' have been found toreproduce the exact results at low en-ergies by means

of

a generalized double folding method.

In this paper we extend the density matrix expan-sion (DME)

of

Negele and Vautherin to the com-plex domain in order tojustify the energy function-al introduced in

Ref. 21.

The present paper is organized as follows. In Sec.

II,

we briefly recall the

DME

and single out the peculiar features arising from its application to acomplex effective interaction. In Sec.

III,

we dis-cuss the asymptotic behavior

of

two colliding nu-clear matter systems when the Fermi sea is nearly spherical, and its consequences on the imaginary part

of

the optical potential. In

Sec.

IV,we provide a parametrized form for the

DME

coefficients, and in Sec.Vwe apply it tothe calculation

of

the opti-cal potential

of

the '

0+

'

0

system and compare the present results with the exact calculations

of

Ref.

13.

II.

THE DENSITY MATRIX EXPANSION WITH ACOMPLEX EFFECTIVE

INTERACTION

In this section, we recall the relevant

DME

for-mulas derived in

Ref.

22 and adapt them tothe case

of

a complex effective interaction. The discussion is limited tonuclei having an equal number

of

neu-trons and protons. The effective N-N interaction 1025

1982

TheAmerican Physical Society

component can be written as psL(kFS) is the Slater approximation given by 6 UsT(r) _{( 1 e}

—

2x)2e—3x

~

_g

sT X _m=0 m& PSL(kFS)= 3

J

(kFS) sk~ (2.4) for

r

(1

fm,

(2.

1) 7 (1 —2x)2

_y

ZST m=1 for r

)1

fm,

(2.

2) 1/3

p(R)

(2.5)

In Eqs. (2.3) and (2.4), the local Fermi momentum kF is related tothe matter density

p(R)

by

with

x

=0.

7r, where r isthe separation distance be-tween the interaction nucleons, and Am and Zm"

are complex coefficients depending upon the local density p, the local intrinsic kinetic energy density T' ' _{defined in Sec.}

_III,

_{and the incident energy (see}

Refs. 10

—

14for full details).

The basic approximation

of

the

DME

proposed in

Ref.

22was touse the following truncated Bessel function expansion forthe density matrix:

P

R+

—,

R

—

—

=PSL(kFS)P(R)+

2skp3

Xj,

(kFS)[—,V'P(R)

—

T(R)

Bywriting asimilar expansion for the product

p

R+

—

₂ p

R

——

₂

(H

_)~,

=

f

4

_~,

(R)dR,

(2.6)

where the potential energy density

4

_~,

(R)

reads:

~Pot(R)

VNM

+

2 VD(P~'P

—

I

~P

l

')

which appears in the direct term

of

the expectation value

_(H),

one can express the potential part

of

(H) as":

+

—,kF

_P(R)],

+

Vs( 5kFP

2T+

—,V

—

P)

.

(2.7)

(2.3)

I

The expression

of

P

_p thas two distinct parts

V~M

—

—

f

d

s[3v

(s)+3usa(s)+9v

(s)+Uso(s)]

2

+

f

d sPSL (kFS)[3U

(s)+3U

(s)

—

9U (s)

—

U

(s)]

32 (2.8)

is the potential energy

of

nuclear matter corre-sponding to the local density

p(R),

and V23 and Vs

are the direct (D) and exchange (E) finiteness corrections given by I with 35

g(kFS)=

j3(kFs)

.

2(kFs) (2.11) and VD

—

—

1

Jd

ss

g(kFS)[3u

(s)+3U

(s)

+9u

(s)+U

(s)]

(2.9) Vz

—

—

d

ss

PsL(kFS)g(kFs) 16 X [3v

(s)+3U

(s) (2.12) Negele and Vautherin then proceed to eliminate the V_pterms by an integration by parts. In the case

of

acomplex effective interaction, this implies the ap-pearance

of

U derivatives with respect to both p

and ~. In order to avoid any derivative here we keep the V_pterms.

. We introduce the following notation: '_2/3 A

=V~~+

3 37K s/3 5 2 p

VE,

9~ To(s } Uso(s)

]

(2.10)

B

=

—

_pVE,

1

C=

—

—,_VD, (2.13) (2.14)

FIG.

2. Brueckner-Hartree-Fock contribution to the binding energy ofthe Fermi sea depicted in Fig. 1. The wiggly line depicts the Brueckner reaction matrix G.

22 treats a static case. The replacement

of

~by

r'

' appears as a consequence

of

preserving the Galilean invariance

of

the interaction.

FIG.

1. A deformed Fermi sea used in the local description of a heavy ion collision as the collision of two nuclear matter systems.

III.

THE BINDING ENERGY OFNUCLEAR MATTER FORANEARLY SPHERICAL

FERMISEA

1 1

D

=

_,

p(Vn

+

——,_VE

),

(2.15)

where

_{2, 8,}

C,and

D

are complex quantities, which depend on_p, ~' ',and the incident energy. Then the potential energy density (2.7) becomes

4

_~,

(R)=A+Br'

'+C(Vp)

_{+DV' p . (2.}16) At this point we stress that the potential energy density (2.16)depends on the intrinsic kinetic ener-gy density

r'

' defined in

Eq. (3.

15) instead

of

the kinetic energy density ~ as introduced by Negele and Vautherin. The difference comes from the fact that we deal with a moving system while

Ref.

I

As itwill turn out in Sec. IV, it isuseful to study the ~' ' _dependence

_of

_{the imaginary part}

_of

_the binding energy for a nearly spherical Fermi sea. The present analysis takes place in the momentum space and the density and the incident relative momentum EC, given by the separation distance be-tween the centers

of

the two spheres constituting the Fermi sea shown in Fig. 1 are fixed quantities. The intrinsic kinetic energy density ~' ' is then uniquely determined by the radii

of

the two spheres.

In the Brueckner-Hartree-Fock (BHF) approxi-mation, the potential energy

of

nuclear matter is given by the diagram

of

Fig.

2.

It

can be easily shown that its imaginary part is proportional

to

the integral

ImVEHF cc

f

_dk)dk2dk3dk4

_[

_(k)k2

~G(co&+cop) ~ k3k4)A I @coi+coz

—

co3

—

~4

(3.

1)

where the momenta k~ and k2 are inside the de-formed Fermi sea

F

of Fig.

1,while k3 and k4 are outside it, and G is the Brueckner reaction matrix. The single particle energies co;are defined as

1

where we have shifted from k

=

~ k ~ tocoas

thein-tegration variable. This causes no problem since co(k} is a monotonously increasing function

of k.

Hence, wecan write

A'k,

'

co;

=

+

U(kc),

201 (32) Im

V,

„„fdco~d-co2dco3dcl)4I (co]&c02&c03&c04) where U is a continuous auxiliary potential.

For

any k integration, one has

X

5(co~+cop

—

co3

—

co4) (3.4)

f

dk

=

f

k dk dk

=

f

k (Co} dCodk,

(3.

3) with

I(

„,

,

)=g

k;

f

gdk;

)

(k,

k ~

G(,

+

)~ k k

)„('.

(3 5)

I.

et us consider the Fermi sea

of

Fig. 1and denote by coF~ the energy associated with the momentum kF& and

by

~~~+

g

that

of

E,

+k&2. The quantity

_g

issmall compared toruz~ since the Fermi sea isnearly spherical. Since co3and co4are greater than coF&,the 5function in

Eq. (3.

4)vanishes except when k& or/and k2 lie

in-(3.6) side

it.

Since all the above expressions are symmetrical in k1 and k2, the case in which k1 is inside

Z

and k2 isoutside itwould yield the same result. The contribution to (3.4)is

F1 ~F1+~ 00 00

(ImVBHF)1

—

dco1 dcog dco3 dco4I(co„co2,co3, 4)5(co1~co2

—

co3

—

4

0 F1 ~F1

COF1

—

_g&CO1&COF1, NF1(C02

(COF1+'g,

F1

&3(F1+9

(3.7)

The function I(co1,co2,co3,co4) can thus be

appmxi-where we have specified the integration limits.

It

is, however, clear that the 6 function imposes further restrictions over the range

of

integration

of

co1, co3,

and ~4. One can easily see that in fact, the integra-tion limits are restricted to

mated by l(coF»coF»coF»coF,)and be taken outside the integral sign in

Eq.

(3.6). The remaining in-tegrations arethen straightforward and yield

(ImVBHF)1

I

(COF» COF»COF»COF1)

9

3

I

(COF1~COF1~COF1~

~F

1)

X [co(K,

+

kF2)

—

co(kF1)]'. (3.&)

Case

2.

Both k1 and k2 lie inside

Z.

The contri-bution to (3.4) isnow

~F1+& F1+'9 00 00

(ImVBHF)~- _~F1 dco1 dco2 dco3 dco4J(co1,co~, co3co4)5(co1+co2 co3 co4)

~F1 F1 NF1 (3.9)

and the further restrictions imposed by the 6 func-tion give

I

(3.12)can be written in leading order

ImVBH&-(51+5&)3 . (3.14)

N3&Q)F1+2'g ~

Q)4&COF1+2Y/

.

(3.10)

Therefore the function I(co1,co2,co3,co4)can again be

approximated by I(coF1,coF1,coF1,coF1) and taken outside the integral sign. Explicit integration then yields

VBHF)2 i(COF1 COF1 COF1 COF1)C)3

I

(COF1&NF»COF1~NF1)

=r—

pkG

(2)

(3.15) where _p is the density, ~is the kinetic energy densi-ty given by

We have now to relate 61 and 62to the variation

of

the intrinsic kinetic energy density ~' ' when one goes from the spherical Fermi sea

of

radius kF to the deformed sea

I' of

Fig.

1.

The intrinsic kinetic energy density ~' 'is defined as10

X

[co(K„+

kF~) co(kF,)

]',

—

i.

e., the same as in case

1.

Therefore, one has

ImVBHF [co(Ki

+

kF2) co(kF1)

]—

(3.11)

(3.12)

r=

1

gk—

V-

_kcry

and kG isthe mean momentum per nucleon

(3.16)

(3.17)

kF1 kF 61 ~

K„+kF2

—

—

kF

j62,

(3.13)

where 61and 62are small with respect to kF and the change in the Fermi sea is such as the density remains equal _{to p} (constant volume). Then

Eq.

Let us define kF as the radius

of

the spherical Fer-mi-sea corresponding to the fixed density

p.

One can write

N

—

=p=constant

.

V (3.18)

The intrinsic kinetic energy density ~' ' _defined

In Eqs.

(3.

16) and

(3.

17), the k summations extend over the deformed Fermi sea

F,

o. and ~are the spin and isospin degrees

of

freedom, V is the volume

of

the boxin which the system is contained, while Nis the total number

of

nucleons. As usual Vand N tend toinfinity with

above represents the same quantity as that given by formula (6)

of Ref.

21.

Denoting by

M

the variation

of

any quantity

x

when one goes from the spherical Fermi sea tothe deformed one depicted in

Fig.

1, one has

(3.19)

kF kF

_—

1 5

+

2p+

&r

(3.

24) Hence, when

hp=O,

wehave in the lowest order

because ko

—

—

0

for a spherical Fermi sea (static case). By explicit calculation we obtain up to second order in 5; 2 2) kF kF

—

_{1 52} 3m'

(3.

25) 2 2 1 kF

bp=

—

kp

5)+

kp

3+

5) 2%2

Bycomparing Eqs. (3.14)and (3.25) and taking into account

Eq. (3.

21),we get

kF kF

2n

L

&m~mrF

-~&

(2)

(3.

26)

kF kF

+

—

1

₅₎₅₂₊

(3.20) which is the main result

of

this section and will be

used as abasic argument in the next section.

5)

—

—

0(52 )

.

(3.21)

Hence, up tothird order in 52,a consistent approxi-mation to Ap is provided by

kF

bp=

—

kF

5)+

—

1 ₅₂

2'

p

Equation (3.20) shows that 5~ and 52 cannot be

of

the same order

of

magnitude. The reason is that the density must remain constant and the constraint Ap=O would imply

5;=0,

i.

e., no deformation at all. Therefore, the constraint

Ap=0

imposes

IV. THEPARAMETRIZED FORM OF DME COEFFICIENTS

We have computed the A,

B,

C, and

D

coeffi-cients

of Eq.

(2.16) for

E„=O,

0.

5, and 1

fm '/nucleon and for a series

of

spherical and de-formed Fermi seas. In view

of

possible future

ap-K„=0.5fm kF kF

_—

1 _5)5p r kF

+

2rr' (3.22) C) X QJl K„=1.0fm

The variation

of

the intrinsic kinetic energy density r' ' _{is then related to the variation b,}

p

of Eq.

(3.22) by 20 15 10

h~=kF

bp+

—

1 62 3m-2 0.5

+0(5

)+.

(3.23)

where the term 0(52)also contains the variation

of

k62given by

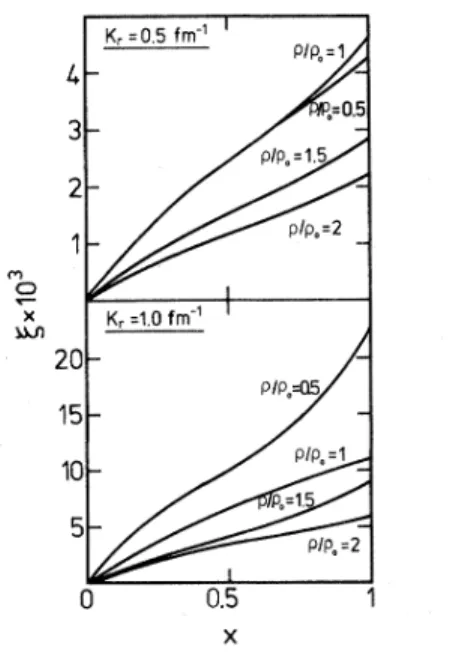
FIG. 3. The ratio (=ImA/ReA for various densities and two K, values as a function of x defined by Eq. (4.1). po

—

—

0.17 nucleon/fm is the normal nuclear rnatter density.

following,

4

will designate any

of

the A,

8,

C, and Dcoefficients.

nomial we take the following expression for Im@':

ImÃ=x(Ii+I2x+I3x

) (4.2)

A. ~' 'parametrization

It

turns out that the dependence on

E„and

r' '

_of

the real part

of

any

4

coefficient is negligible and therefore we only have to discuss the

r'

' parame-trization

of ImÃ. It

isuseful to define the_p depen-dent ratio

(2) (2) (2) (2)

ax VmIII %max Vm

(4.1)

where z'

„and

~',

',

are the minimum and max-imum intrinsic kinetic energies associated with a de-formed Fermi sea

of

a given density

p.

The value

~' _{„corresponds to aspherical Fermi sea and gives}

x

=0.

The other extreme ~ma'x implies

x

=l

and

corresponds to a deformed Fermi sea composed

of

two spheres

of

equal radii having their centers separated by adistance

j:„.

At present we wish to make use

of

the result ob-tained in the previous section.

For

a small defor-mation

of

the Fermi sea,

i.

e._{, small}

x,

expression

(3.

25) indicates that the imaginary part

of

all 4'

and find values

of

the coefficients

I„(n

=1

—

3) which reproduce the exact results within

3/o.

We note that each

I„depends

on

E„and

p.

The p dependence is parametrized below. In Figs. 3

—

6, we plot the ratio

Im@'

Re@

as a function

of

x

for a series

of

values

of

_p and

E,

.

Parametrization (4.2) is used for Im@'. These fig-ures are very much reminiscent

of Fig.

3

of

Ref.

21 where the

x

dependence

of

the entire imaginary part

of

the Skyrme-type interaction had been found nu-merically. The present parametrization is more de-tailed than that

of Ref.

21 and gives an explicit dependence on

r'

'

of

the imaginary part

of

the en-ergy density.

B.

_pparametrization

We now discuss the _p parametrization

of Re@

and

of

the

I„(n

=1

—

3)

coefficients appearing in

Eq.

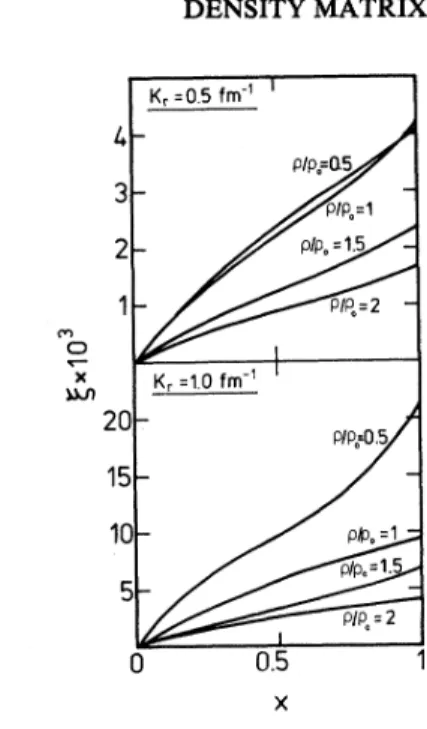
(4.2). As can be seen from Eqs. (2.8), (2.12),

K„=0.5fm '

20-K„=1.0fm" Pl C) X Qdl 20 K„=1,0 fm" 15 10 10 0.5 0.5

K„=0.5fm'

K„=1.0fm "

potential as defined by

Eq.

(1.

1), where we have used the expression (2.16}with the parametrizations found forA,

B,

C,and

D.

The densities _p and v' '_{have been calculated with}

a two center shell model described in

Ref.

3 and equivalent to Fliessbach's model.

In this model the ground state

of

'

0+' 0

is described by a Slater determinant built from the single particle states

20 15 eik[z+(D/2)] Wa(1) Y'a(1)e —ik[z—(D/2)] 'VP(2) 9'P(2)e (51) 10 0

FIG.

6. Same asFig. 3,but for g=ImD/ReD.

(2.13),and _{(2.15), a p factor} can be extracted from the _p dependence

of

A, while _{a p factor} can be ex-tracted from that

of

B

and

D.

Byparametrizing the remaining _p dependence by acubic polynomial, we can write

Owing tothe fact that the single particle states

_g

ii~

and ltipi2~ are not orthogonal, wehave

—1

X

pv), ( ) ( }

C(.

)WP(j) p(j),a(i) (5.3) —1 + Bp(j),a(i) (D)k)V0a(i)Vtkp(q

)(5

4)'

p(j),a(i) and

where Pa~,~ and PP~2~ are eigenstates

of

harmonic

os-cillator wells centered at

—

(D/2)

and

D/2,

respec-tively. The relation between the single particle momentum component k along the z axis and

E,

defined previously is (5.2)

Re@

=

p'(R

)

+R2p+R

3p'+R4p')

I„=p

_{(I„(+I„2p+I„3p+I„4p}

) (4.3} 1

—

1 Bp()a(;) (D, k) P p(j),a(i) X(ga(,;)VQp(;) Vga(i)fpij—)) ~ (5.5)

(5

=1

—

3),

(4.

4) where the exponent

a

is equal to 2, 1,0, and 1 for

the coefficients A,

B,

C, and D,respectively. Densi-ty parametrizations analogous to (4.3) and

(44)

were also used in Refs. 9and 22.

The numerical values

of

Rj

and Iaj (n

=1

—

3;

j

=1

—

4) of

all

4

coefficients are gathered together in Table

I.

For

_E,

=0,

all

_I»

vanish because in the static case the G matrix has no imaginary part.

V. APPLICATION TOTHE OPTICAL POTENTIAL

In order to check the reliability

of

the density matrix expansion applied to

a

complex effective in-teraction, we have calculated the '

0+' 0

optical

where

Bp(j),a(i) ('Pp(j)&Qadi)

)

(5.6)

The results (full curves) are presented in Figs. 7 and 8 for the real and imaginary parts

of

V,

„

respectively.

%e

compare them with the

"exact"

computation

of

Ref.

13 (dashed curves}. The agree-ment for ImV,

_„,

is very good at all separation dis-tances.

For

the discussion

of

the real part it is useful to roughly divide the range

of

the separation distance

R

into two intervals.

I.

et us call R0 the distance at which

ReV»,

has an inflection point.

(a) R

)Rp.

This interval is dominated by the nuclear surface properties

of

the interaction because in the region where the nuclei interpenetrate the

K,

=0.

5

K„=1

~0 K,

=0.

5 K,

=1

~0 K,

=0.

5 K,

=1.

0 K,

=0.

5 K,

=1

RJ

Ii)

I2J I3J

Ii)

I2J I3J RJ

Ii)

I2J Ig)

I))

I2J I3J Ri I)~ Ip) I3J I)~ I2J Ig) RJ I)~ Ig) Ig) I)~ Ip) I3J

j=1

—

519.42

—

1.7061

—

0.0639 1.0509

—

30.761 55.802

—

47.766 178.24 0.89300

—

0.30740

—

0.12053 9.1548

—

14.065 11.292 72.343 0.27056

—

0.06102

—

0.07316 3.9753

—

7.3330 6.2272

—

116.90

—

0.49381 0.13787 0.10329

—

6.2640 10.849

—

9.

0502

J=2

1936.5

—

22.876 38.424

—

36.367 282.88

—

671.27 623.59

—

1058.2

—

1.6991

—

4.2111 6.5022

—

91.

622 163.45

—

141.52

—

385.83 1.6955

—

3.5555 3.5791

—

38.710

91.

173

—

82.406 650.39

—

1.2707 4.6082

—

5.2046 61.615

—

132.03 117.79

J=3

—

5391.2 175.19

—

227.17 191.34

—

950.54 2707.1

—

2649.9 3359.3

—

13.110 34.202

—

36.914 319.86

—

634.96 578.26 1085.1

—

16.537 22.764

—

19.642 136.09

—

374.66 352.60

—

1925.0 19.815

—

31.314 28.871

—

216.05 533.39

—

497.16

j=4

6265.3

—

289.25 349.65

—

2S2.25 1086.1

—

3541.0 3600.5

—

3969.4 32.117

—

57.614 56.152

—

376.59 808.30

—

763.18

—

1184.6 28.762

—

35.986 29.476

—

161.54 496.01

—

480.85 2176.9

—

36.791 50.390 ~

—

43.514 255.68

—

698.08 671.64

density is not higher than the saturation density

of

the nuclear matter. This can be easily seen within the proximity concept. ' _{In this interval the}

DME

results are slightly higher than the exact re-sults. The difference shows that the surface proper-ties

of

the exact interaction have somewhat been al-tered by the

DME.

This is not surprising because the

DME

introduces a truncation

of

the higher or-der or-derivatives

of

the density matrix.

To

find the effect

of

this truncation it would be interesting to calculate the surface energy

of

semi-infinite slabs

of

nuclear matter both with the exact interaction and the energy density resulting from

DME.

(b) R

&Ro.

At such separation distances the overlapping region has reached the nuclear matter density regime and the behavior

of

Re V,

_',

is essen-tially given by the bulk properties

of

the nuclear matter. Owing to the independence

of

Reà on

_E„

and r' ' the discussion given below is valid for any

E,.

For

nuclear matter the

DME

approximation gives

E/A

= —

16.

85MeV and

d

E

=451.

9MeV fm dp2

20-l

'

(1)

-20

-60

_-10

-80

4 D (fm)

D

(fmI

FIG.

8. Same asFig. 3,but for ImVp$.

FIG.

7. A comparison between the density matrix ex-pansion computation ofReV,~& as a function ofD (full lines) and the exact computation of Ref. 13 (dashed lines). The curves marked I, 2, and 3 correspond to

E,

=O, 0.5, and 1 fm ', i.e., E~,b

—

—

0, 83, and 332,

respectively.

overbinding mentioned above. Towards

R

~0,

both potentials are linear, and the difference between their slope is consistent with the values found for

Q2 (jp~

For

the imaginary part, the ~' ' dependence plays the dominant role and thus ImV,

_„,

is insensitive to the saturation density effects described above.

In conclusion, we believe to have found areliable parametrization

of

a complex density functional to be used in the calculation

of

the heavy-ion optical potential. Our results are given at two different en-ergies and can be applied to any pair

of

nuclei once the density and the kinetic energy density

of

the colliding system are known.

One

of

us

(R.S.

) acknowledges financial support from the Institut Interuniversitaire des Sciences Nucleaires.

other hand the exact binding energy is

—

15.59MeV and its second derivative takes the value 575.8 MeVfm at a lower saturation density

p=0.

1752 fm

.

Therefore the

DME

overbinds the nuclear matter, as already noticed in

Ref.

28,and alters the curvature at the saturation point. The changes it produces on the nuclear matter constants can ex-plain the difference between the two results. Name-ly,

ReV,

~, calculated with the

DME

reaches a

deeper minimum at shorter separation distances than the exact

ReV,

&,

.

This is because the

satura-tion Fermi momentum kF

—

—

1.

49fm ' given by the

DME

is larger than the exact one KF 1.37

fm-

—

Hence, in the first case, the saturation density is

reached when the nuclei interpenetrate further, bringing in the extra attraction associated with the

K.

A.Brueckner etal.,Phys. Rev. 171, 1188 (1968).

K.

A.Brueckner et_{al., Phys.} Rev. 173, 944 (1968). D. M. Brink and Fl. Stancu, Nucl. Phys. A243, 175

(1975).

4Fl. Stancu and D. M. Brink, Nucl. Phys. A270, 236

(1976).

5C. Ngo et al._,Nucl. Phys. A240, 353(1975). C.Ngo et al.,Nucl. Phys. A252, 237(1975).

7F. Beck,

K.

H. Muller, and

K.

S.Kohler, Phys. Rev. Lett. 40,837(1978).

C20, 683(1979).

T.

Izumoto, S.Krewald, and A. Faessler, Nucl. Phys. A341, 319(1980).

T.

Izumoto, S.Krewald, and A. Faessler, Nucl. Phys. A357,471(1981).

' _{A. Faessler,}

_T.

_{Izumoto, S.Krewald, and}

_R.

_Sartor, Nucl. Phys. A359,509(1981).

R.

Sartor, A. Faessler, S.

B.

Khadkikar, and S. Krewald, Nucl. Phys. A359,467(1981).

~R. Sartor and A. Faessler, Nucl. Phys. A376, 263 (1982).

~5G.

_R.

Satchler and W.

G.

Love, Phys. Rep. 55, 183 (1979).

'

_J.

_{P.Vary and C.}

_B.

_{Dover, Phys. Rev. Lett. 31,1510} (1973)~

G.

F.

Bertsch, Phys. Rev. C 15, 713 (1977).

SE.S.Hernandez and S.A. Moszkowski, Phys. Rev. C 21, 929 (1980).

2OD._{A. Saloner and C.Toepffer, Nucl. Phys. A283, 208}

(1977).

R.

Sartor and Fl.Stancu, Phys. Rev.C24, 2347(1981).

22J.W. Negele and D.Vautherin, Phys. Rev. C 5, 1472 (1972).

Y.

M.Engel, D.M.Brink,

K.

Goeke, S.

J.

Krieger, and

D.Vautherin, Nucl. Phys. A249,215 (1975).

J.

P.Jeukenne, A.Lejeune, and C.Mahaux, Phys. Rep. 25C, 83(1976).

T. Fliessbach, Z. Phys. 238, 329 (1970); 242, 287 (1971);247, 117(1971).

J.

Mocki,

J.

Randrup, W.

J.

Swiatecki, and C.

F.

Tsang, Ann. Phys. (N.Y.)105, 427(1977).

27D. M. Brink and Fl. Stancu, Nucl. Phys. A299, 321 (1978).

8D.W.L.Sprung, M.Vallieres,

X.

Campi, and Che-Ming Ko,Nucl. Phys. A253, 1(1975).