HAL Id: hal-02947196
https://hal.archives-ouvertes.fr/hal-02947196
Submitted on 23 Sep 2020HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
Dimensionally Homogeneous Extended Jacobian and
Condition Number
Latifah Nurahmi, Stéphane Caro
To cite this version:
Latifah Nurahmi, Stéphane Caro. Dimensionally Homogeneous Extended Jacobian and Condition Number. The 2nd International Conference on Mechanical Engineering (ICOME 2015), Sep 2015, Patra Jasa, Bali, Indonesia. �hal-02947196�
Dimensionally Homogeneous Extended Jacobian and Condition Number
Latifah Nurahmi and Stéphane Caro
Institut de Recherche en Communications et Cybernétique de Nantes, France Emails: {latifah.nurahmi,stephane.caro}@irccyn.ec-nantes.fr
Keywords: screw theory, condition number, dimensionally homogeneous extended Jacobian
matrix, singularities, and parallel manipulators.
Abstract. This paper deals with the formulation of the dimensionally homogeneous extended
Jacobian matrix, which is an important issue for the performance analysis of f degrees-of-freedom (f ≤6) parallel manipulator having coupled rotational and translational motions. By using the f independent coordinates to define the permitted motions and (6-f) independent coordinates to define the restricted motions of the moving platform, the 6×6 dimensionally homogeneous extended Jacobian matrix is derived for non-redundant parallel manipulators. The condition number is computed over the homogeneous extended Jacobian matrix, the homogeneous actuation wrench matrix, and the homogeneous constraint wrench matrix to evaluate the performance of the parallel manipulators. By using these indices, the closeness of a pose to different singularities can be detected. An illustrative example with the 3-RPS parallel manipulator is provided to highlight the effectiveness of the approach and the proposed indices.
Introduction
The input-output relationship of the manipulators is represented by the Jacobian matrix that maps the actuators rates onto the velocity twist of the moving platform. By applying the theory of reciprocal screw, Joshi and Tsai in [1] proposed a systematic procedure to express a 6×6 overall Jacobian matrix that comprises both f linearly independent actuation wrenches and (6-f) linearly independent constraint wrenches. However, the overall Jacobian matrix considers only the instantaneous motions accessible by the moving platform. In [2], Huang et al. developed a methodology to formulate the Jacobian matrix that takes into account the instantaneous motions inaccessible by the moving platform, named the generalized Jacobian matrix.
The Jacobian matrix of parallel manipulators with coupled rotational and translational motions, possess nonhomogeneous physical units. It leads to significant problem in which the computation of the condition number will vary with the scaling of dimensions. Dated back to 1990 [3], Gosselin used the velocities of two points to describe the velocity of the end effector hence the entries of the Jacobian matrix would bear the same units. Stocco et al. in [4] presented the diagonal scaling matrices by separating the task-space forces and the joint-space torques. The characteristic/natural length was introduced in [5-7] to overcome the issue of nonhomogeneous physical units. Kim and Ryu in [8] used three non collinear points on the moving platform and linked the linear velocities of these points with the actuators rates. In [9], Liu et al. introduced a tetrahedron containing five points and specified relevant axes at these points. A set of independent axes are selected which represents the permitted motions of the moving platform. Then, the dimensionally homogeneous Jacobian matrix is derived by combining the linear map between the twist of moving platform with the selected independent coordinates, and the generalized Jacobian matrix defined in [2]. However, this method does not take into account the restricted motions due to the existence of the constraint wrenches on the moving platform, that also affect the performance of the lower-mobility parallel manipulators.
Accordingly, this paper focuses on the formulation of the dimensionally homogeneous extended Jacobian matrix for non-redundant lower-mobility parallel manipulators with coupled rotational and translational motions. By considering a set of linear independent axes which depicts the restricted motions of the moving platform, the 6×6 dimensionally homogeneous extended Jacobian matrix is derived. The method is applied to the 3-RPS (R, P, S denote prismatic, revolute, and spherical joints, respectively) manipulator. The condition number is computed over the homogeneous extended
Jacobian matrix, the homogeneous actuation wrench matrix, and the homogeneous constraint wrench matrix. These indices can measure the closeness of a pose to different singularities, namely the actuation singularity, the constraint singularity, and the compound singularity.
Formulation of the Jacobian Matrix
This section briefly reviews the derivation of the Jacobian matrix for non-redundant parallel manipulators having f-dof . The instantaneous motions of a body must form a six dimensional vector, known as twist space 𝒯, that comprises a permitted twist subspace 𝒯𝑎 and a restricted twist subspace 𝒯𝑐. The subspaces 𝒯𝑎 and 𝒯𝑐 have $𝑡𝑎𝑖 and $𝑡𝑐𝑗 being its elements, respectively. $𝑡𝑎𝑖 is the 𝑖-th permitted twist screw of the moving platform and $𝑡𝑐𝑗 is the 𝑗-th virtual restricted twist screw that is produced by releasing the correspondence 𝑗-th constraint wrench.
On the other hand, the entire set of wrenches exerted in the moving platform forms six dimensional vector space, known as wrench space 𝒲, that comprises an actuation wrench subspace 𝒲𝑎 and a constraint wrench subspace 𝒲𝑐. The subspaces 𝒲𝑎 and 𝒲𝑐 have $̂𝑤𝑎𝑖 and $̂𝑤𝑐𝑗 being its elements, respectively. Therefore, the relationships between all four subspaces are: 𝒲𝑎 = 𝒯𝑐⊥ and 𝒲𝑐 = 𝒯𝑎⊥. The twist of the moving platform at each instant $𝑡 ∈ 𝒯 can be expressed as linear combination of the elements of 𝒯𝑎 and 𝒯𝑐, as:
$𝑡 =$𝑡𝑎𝑖+ $𝑡𝑐𝑗 =∑𝑖=1𝑓 𝑞̇𝑎𝑖 $̂𝑡𝑎𝑖 + ∑(6−𝑓)𝑗=1 𝑞̇𝑐𝑗 $̂𝑡𝑐𝑗 (1)
where 𝑞̇𝑎𝑖 and 𝑞̇𝑐𝑗 are the actuated joints rates and the virtual constrained joints rates, respectively. The twist $𝑡 contains the linear velocity 𝒗𝒐 and the angular velocity 𝝎𝒐 of the moving platform origin. By performing the reciprocal product on both sides of Eq. (1) with $̂𝑤𝑎𝑖 and $𝑤𝑐𝑗, we obtain:
𝐉𝒕 $𝑡= 𝐉𝒒 𝐪̇ (2) 𝐉𝒕 = [𝐉𝐉𝑡𝑎 𝑡𝑐], 𝐉𝑡𝑎= [ $̂𝑤𝑎1 ⋮ $̂𝑤𝑎𝑓 ], 𝐉𝑡𝑐 = [ $̂𝑤𝑐1 ⋮ $̂𝑤𝑐(6−𝑓) ], 𝐉𝒒= [ 𝐉𝑞𝑎 𝐉𝑞𝑐], 𝐉𝑞𝑎 = [ $̂𝑤𝑎1 𝑇 $̂𝑡𝑎1 … … ⋮ ⋱ ⋮ ⋯ ⋯ $̂𝑤𝑎𝑓 𝑇 $̂𝑡𝑎𝑓 ], 𝐉𝑞𝑐 = [ $̂𝑤𝑐1𝑇$̂𝑡𝑐1 … … ⋮ ⋱ ⋮ ⋯ ⋯ $̂𝑤𝑐(6−𝑓)𝑇$̂𝑡𝑐(6−𝑓) ], 𝐪̇ = [𝐪̇𝐪̇𝑎 𝑐], 𝐪̇𝑎 = [ 𝑞̇𝑎1 ⋮ 𝑞̇𝑎𝑓], 𝐪̇𝑐 = [ 𝑞̇𝑐1 ⋮ 𝑞̇𝑐(6−𝑓)], $𝑡= [ 𝝎𝒐 𝒗𝒐]. where 𝐉𝒕 and 𝐉𝒒 are 6×6 Jacobian matrices for non-redundant parallel manipulators. The derivation of the Jacobian matrices defined in Eq. (2) will be employed to formulate the 6×6 dimensionally homogeneous extended Jacobian matrix discussed hereafter.
Formulation of the 6×6 Dimensionally Homogeneous Extended Jacobian Matrix
Theoretically, the rotations and the translations of a body can be sufficiently described by the translations of three non collinear points embedded on it. Let us consider a moving platform as shown in Fig. 1 with the origin 𝑂 and the moving frame 𝛴1 attached to it. It rotates with angular velocity 𝝎𝒐 and translates with linear velocity 𝒗𝒐 with respect to the fixed frame 𝛴0 of the base. If point 𝑃 is embedded at the moving platform with the position vector 𝐩𝟏 (with respect to the moving frame 𝛴
1), its velocity with respect to the fixed frame 𝛴0 can be defined as:
𝒗𝒑𝟎= 𝒗
𝒐+ 𝝎𝒐× 𝐩𝟎 (3)
where 𝐩𝟎 = 𝐌 𝐩𝟏. 𝐌 is a spatial Euclidean transformation matrix 𝐌 ∈ 𝑆𝐸(3) defined in [10]. Place a set of axes at point 𝑃 defined as 𝒆𝑖,𝑗1 . After transforming into 𝒆
𝑖,𝑗
0 , take the dot product on both sides of Eq. (3) with 𝒆𝑖,𝑗0 , it yields:
𝒗𝑝(𝑖,𝑗)0 = [𝐩
𝟎× 𝒆
𝑖,𝑗 0
𝒆𝑖,𝑗0 ] $𝑡 (4)
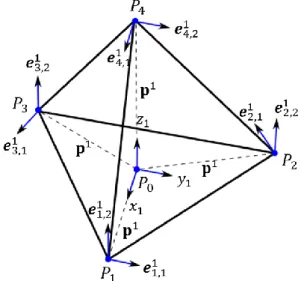
To describe the velocity of the moving platform, a tetrahedron adopted from [9] is defined in Fig. 2. It contains five points (𝑃𝑖, 𝑖 = 0. .4) with an equilateral base and three identical isosceles faces. The orthogonal axes are attached at each point i.e. 𝒆𝑖,11 ⊥ 𝒆
𝑖,2 1 , 𝒆 𝑖,1 1 ⊥ 𝐩1, and 𝒆 𝑖,2 1 ⊥ 𝐩1, (𝑖 = 1. .4). 𝒆1,11 = [0 1 0]𝑇, 𝒆 2,1 1 = [0 −√3 2 − 1 2] 𝑇 , 𝒆13,1 = [0 √3 2 − 1 2] 𝑇 , 𝒆1,21 = [0 0 1]𝑇, 𝒆12,2 = [0 0 1]𝑇, 𝒆13,2 = [0 0 1]𝑇, 𝒆14,1 = [1 0 0]𝑇, 𝒆14,2 = [0 1 0]𝑇, (5) 𝒆0,11 = [1 0 0]𝑇, 𝒆10,2 = [0 1 0]𝑇, 𝒆10,3 = [0 0 1]𝑇.
Transform all the position vectors and the unit vectors in Eq. (5) with respect to the fixed frame 𝛴0 and substitute into Eq. (4), we can obtain in matrix form:
𝒗𝑝0 = 𝐓 $ 𝑡 (6) where 𝒗𝑝0 = [𝒗𝑝0,10 𝒗𝑝0,20 ⋯ 𝒗𝑝4,20 ]𝑻 and 𝐓 = [ (𝐩0 × 𝒆 0,1 0 ) 𝒆 0,1 0 ⋮ (𝐩0× 𝒆 4,2 0 ) 𝒆 4,20 ]
and 𝐓 is a 11×6 matrix. For any f-dof non-redundant parallel manipulators with certain motion type, any f linearly independent row vectors of 𝐓 can be selected to represent the permitted motions of the moving platform. Furthermore, (6-f) linearly independent row vectors of 𝐓 are selected such that it depicts the restricted motions of the moving platform. By substituting Eq. (2) into Eq. (6), we can obtain the linear map from the joint rates 𝐪̇ onto the linear and angular velocities of the moving platform, represented by the selected points (𝑃𝑖).
𝐉𝒑 𝒗𝒑𝟎= 𝐉
𝒒 𝐪̇, 𝐉𝒑 = 𝐉𝒕 𝐓−𝟏, 𝐉𝒑 = [ 𝐉𝑝𝑎
𝐉𝑝𝑐]. (7)
where 𝐉𝒑 is a 6×6 dimensionally homogeneous extended Jacobian matrix for non-redundant parallel
manipulators and it contains a f×6 homogeneous actuation wrench matrix (𝐉𝑝𝑎), and a (6-f)×6 homogeneous constraint wrench matrix (𝐉𝑝𝑐).
Figure 1: Rigid body displacement Figure 2: Points and axes in tetrahedron
Condition Number
The condition number is quite often used as an index to explain the accuracy/dexterity of a parallel manipulator. It is also used to measure the closeness of a pose to a singularity. For a parallel manipulator with mix rotations and translations, the computation of the condition number is in general
not possible due to the inconsistent units. However, after formulating the 6×6 dimensionally homogeneous extended Jacobian matrix, the condition number can be evaluated throughout the workspace, defined as: 𝜅(𝐉𝒑−𝟏). The condition number can also be computed over the f×6 homogeneous actuation wrench matrix (𝐉𝑝𝑎) and the (6-f)×6 homogeneous constraint wrench matrix (𝐉𝑝𝑐), defined as 𝜅((𝐉𝒑𝒂 𝐉𝒑𝒂𝑻)−𝟏) and 𝜅((𝐉
𝒑𝒄 𝐉𝒑𝒄𝑻)−𝟏), respectively.
Consequently, the parallel manipulators are said to be at an actuation singularity if 𝜅((𝐉𝒑𝒂 𝐉𝒑𝒂𝑻)−𝟏) = 0 and at a constraint singularity if 𝜅((𝐉
𝒑𝒄 𝐉𝒑𝒄𝑻)−𝟏) = 0. It also indicates that the actuation wrench matrix and the constraint wrench matrix degenerate, respectively. On the other hand, there is a case in which the parallel manipulators are neither at the actuation singularity nor at the constraint singularity while the system is subjected to a singularity. In this case, the Jacobian matrix degenerates due to the dependency between the actuation wrench matrix and the constraint wrench matrix, hence 𝜅(𝐉𝒑−𝟏) = 0, while 𝜅((𝐉𝒑𝒂 𝐉𝒑𝒂𝑻)−𝟏) ≠ 0 and 𝜅((𝐉𝒑𝒄 𝐉𝒑𝒄𝑻)−𝟏) ≠ 0. This type of singularity is called a compound singularity and the moving platform gains one or more uncontrolled motion. Therefore, larger values of the condition number signify larger distances of a pose to different types of singularities.
Application: 3-RPS Parallel Manipulator
Figure 3: 3-RPS Parallel Manipulator
The 3-RPS parallel manipulator shown in Fig. 3 is a 3-dof parallel manipulator. It is composed of an equilateral triangle base (circumradius ℎ0), an equilateral triangle platform (circumradius ℎ1), and three RPS limbs. The fixed frame 𝛴0 and the moving frame 𝛴1 are located at the origin of the base and at the origin of the moving platform, respectively. The revolute joint in the 𝑖-th limb is located at point 𝐴𝑖, its axis being along vector 𝐬𝑖, while the spherical joint is located at point 𝐵𝑖 (𝑖 = 1. .3). Each pair of vertices (𝐴𝑖𝐵𝑖) is connected by a prismatic joint along the direction 𝐮𝑖.
Due to the manipulator architecture, each limb applies one constraint force, which is perpendicular to the actuated prismatic joint and parallel to the axis 𝐬𝑖 of the revolute joint. By considering that the prismatic joints are actuated, each leg applies one actuation force whose axis is along the direction of the corresponding actuated joint 𝐮𝑖. By collecting all the actuation forces and the constraint forces, the Jacobian matrix 𝐉𝒕 can be obtained.
𝐉𝒕 = [(𝐫𝐵1 0 × 𝐮 1) (𝐫𝐵20 × 𝐮2) (𝐫𝐵30 × 𝐮3) 𝐮1 𝐮2 𝐮3 (𝐫 𝐵10 × 𝐬1) (𝐫𝐵10 × 𝐬2) (𝐫𝐵30 × 𝐬3) 𝐬1 𝐬2 𝐬3 ] 𝑇 𝐉𝒒= 𝐈 (6 × 6 Identity matrix)
Since the 3-RPS parallel manipulator has one pure translation along vertical direction and two rotations, three linearly independent axes can be selected from the tetrahedron to represent 3-dof permitted motions i.e. 𝒆𝑖,21 , 𝑖 = 1. .3. Furthermore, three other independent axes are selected to represent the restricted motions of the manipulators i.e. 𝒆𝑖,11 , 𝑖 = 1. .3. Hence:
𝐓 = [(𝐫𝐵10 × 𝒆1,20 ) (𝐫𝐵20 × 𝒆2,20 ) (𝐫𝐵30 × 𝒆3,20 ) 𝒆1,20 𝒆 2,2 0 𝒆 3,2 0 (𝐫𝐵10 × 𝒆 1,1 0 ) (𝐫 𝐵10 × 𝒆2,10 ) (𝐫𝐵30 × 𝒆3,10 ) 𝒆1,10 𝒆 2,1 0 𝒆 3,1 0 ] 𝑇 Eventually, the 6×6 dimensionally homogeneous extended Jacobian matrix of the 3-RPS parallel manipulator is formulated i.e. 𝐉𝒑 𝒗𝒑𝟎 = 𝐪̇. The Euler angles (azimuth-tilt-torsion) is used to represent
(a) Distribution of κ(𝑱𝒑−𝟏)
(b) Distribution of κ((𝑱𝒑𝒂 𝑱𝒑𝒂𝑻)−𝟏) (c) Distribution of κ((𝑱𝒑𝒄 𝑱𝒑𝒄𝑻)−𝟏) Figure 4: Distribution of the Condition number as a function of the azimuth angle (ϕ) and tilt angle ( θ)
the orientation workspace of the moving platform. It is well known that the orientation capability of the 3-RPS parallel manipulator is defined as the maximum tilt angle 𝜃 for a given azimuth angle 𝜙. Its maximum orientation capability depends mostly on the singularity loci.
The design parameters are assigned as ℎ0 = 2𝑚 and ℎ1 = 1𝑚. Let us consider the moving platform works at altitude 𝑍 = 3𝑚, then the condition number of 𝐉𝑝, 𝐉𝑝𝑎, 𝐉𝑝𝑐 is computed throughout the entire workspace and its distributions are plotted in Fig. 4(a)-4(c). For a given value of azimuth angle 𝜙, the performance of the 3-RPS manipulator reaches its maximum at 𝜃 = 0°. Figure 4(b) shows that the manipulator never reaches the actuation singularity. In [11-12], it reveals that the 3-RPS manipulator has two operation modes and the constraint singularity occurs at the boundary of each operation mode. This condition is explained in Fig. 4(c) when the moving platform is titled by 𝜃 = 180° for any value of azimuth angle 𝜙.
Figure 5 represents the singularity loci of the 3-RPS manipulator and the distribution of the condition number 𝜅(𝐉𝒑−𝟏) over the entire orientation workspace. The performance of the manipulator decreases when the tilt angle is no longer zero and eventually reaches the singularity loci. It reveals that the singularity loci in Fig. 5 corresponds to the compound singularity since neither the actuation wrench matrix nor the constraint wrench matrix degenerates. Likewise (𝐉𝒑−𝟏) = 0, while 𝜅((𝐉𝒑𝒂 𝐉𝒑𝒂𝑻)−𝟏) ≠ 0 and 𝜅((𝐉𝒑𝒄 𝐉𝒑𝒄𝑻)−𝟏) ≠ 0. It means that when the 3-RPS manipulator is in the compound singularity, there is the dependency between the actuation wrench matrix and the constraint wrench matrix.
Figure 5: Atlas of singularity loci and condition number κ(𝑱𝒑−𝟏)
Conclusions
In this paper, the 6×6 dimensionally homogeneous extended Jacobian matrix is derived for non-redundant parallel manipulators. The method can be used for the parallel manipulators with coupled rotations and translations by considering a set of linear independent axes at the points of a tetrahedron, which represents the permitted motions and the restricted motions of the moving platform. The proposed approach is applied to the 3-RPS manipulator and the condition number is computed over the homogeneous extended Jacobian matrix (𝐉𝒑), the homogeneous actuation wrench matrix (𝐉𝒑𝒂), and the homogeneous constraint wrench matrix (𝐉𝒑𝒄). It reveals that at altitude 𝑍 = 3𝑚, the singularity loci of the RPS manipulator corresponds to the compound singularity, in which the 3-RPS manipulator is neither at the actuation singularity nor at the constraint singularity. The 3-3-RPS manipulator reaches the constraint singularity when the moving platform is tilted by 𝜃 = 180° for any value of azimuth angle 𝜙. Accordingly, these indices can measure the closeness of a pose to different types of singularities, namely the actuation singularity, the constraint singularity, and the compound singularity.
References
[1] S. A. Joshi and L.-W. Tsai, Jacobian Analysis of Limited-DOF Parallel Manipulators, ASME Journal of Mechanical Design, 124(2), pp. 254-258, 2002.
[2] T. Huang., H. T. Liu., and D. G. Chetwynd, Generalized Jacobian Analysis of Lower Mobility Parallel Manipulators, Mechanism and Machine Theory, 46, pp. 831-844, 2011.
[3] Clément M. Gosselin, Dexterity Indices for Planar and Spatial Robotic Manipulators, Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, pp.650-655, 13-18 May 1990.
[4] Leo J. Stocco., S. E. Salcudean., and F. Sassani, On the Use of Scaling Matrices for Task-Specific Robot Design, IEEE Transactions on Robotics and Automation, 15(5), October 1999.
[5] M. Tandirci, J. Angeles., and F. Ranjbaran, Characteristic Point and the Characteristic Length of Robotic Manipulators, ASME Des. Eng. Division, 45, pp. 203-208, 1992.
[6] Waseem A. Khan and J. Angeles, The Kinetostatic Optimization of Robotic Manipulators: The Inverse and the Direct Problems, Transactions of the ASME, 128, pp. 168-178, 2006.
[7] Jorge Angeles, Is there a characteristic length of a rigid-body displacement?, Mechanism and Machine Theory, 41, pp. 884-896, 2006.
[8] S.-G. Kim and J. Ryu, New Dimensionally Homogeneous Jacobian Matrix Formulation by Three End-Effector Points for Optimal Design of Parallel Manipulators, IEEE Transactions on Robotics and Automation, 19(4), 2003.
[9] H. Liu., T. Huang., and D. G. Chetwynd, A Method to Formulate a Dimensionally Homogeneous Jacobian of Parallel Manipulators, IEEE Transactions on Robotics, 27(1), 2011.
[10] L. Nurahmi., J. Schadlbauer., S. Caro., M. Husty., and P. Wenger, Kinematic Analysis of the 3-RPS Cube Parallel Manipulator, ASME Journal of Mechanims and Robotics, 7(1), pp. 011008-1-011008-10, 2015.
[11] J. Schadlbauer., L. Nurahmi., M. Husty., P. Wenger., and S. Caro, Operation Modes in Lower-Mobility Parallel Manipulators, In Second Conference on Interdisciplinary Applications of Kinematics, Lima, Peru, pp. 1-9, 2013.
[12] J. Schadlbauer., D. R. Walter., and M. L. Husty., The 3-RPS Parallel Manipulator from an Algebraic Viewpoint, Mechanism and Machine Theory, 75, pp. 161-176, 2014.