Analyse automatique de données par Support Vector Machines non supervisés

Analyse automatique de donnees

par Support Vector Machines non supervises

par

Vincent D'Orangeville

These presentee au Departement d'informatique

en vue de l'obtention du grade de docteur es sciences (Ph. D.)

FACULTE DES SCIENCES UNIVERSITE DE SHERBROOKE

Library and Archives Canada Published Heritage Branch Bibliotheque et Archives Canada Direction du Patrimoine de I'edition 395 Wellington Street Ottawa ON K1A0N4 Canada 395, rue Wellington Ottawa ON K1A 0N4 Canada

Your file Votre reference ISBN: 978-0-494-89639-6 Our file Notre reference ISBN: 978-0-494-89639-6

NOTICE:

The author has granted a non­

exclusive license allowing Library and Archives Canada to reproduce, publish, archive, preserve, conserve, communicate to the public by

telecommunication or on the Internet, loan, distrbute and sell theses

worldwide, for commercial or non­ commercial purposes, in microform, paper, electronic and/or any other formats.

AVIS:

L'auteur a accorde une licence non exclusive permettant a la Bibliotheque et Archives Canada de reproduire, publier, archiver, sauvegarder, conserver, transmettre au public par telecommunication ou par I'lnternet, preter, distribuer et vendre des theses partout dans le monde, a des fins commerciales ou autres, sur support microforme, papier, electronique et/ou autres formats.

The author retains copyright ownership and moral rights in this thesis. Neither the thesis nor substantial extracts from it may be printed or otherwise reproduced without the author's permission.

L'auteur conserve la propriete du droit d'auteur et des droits moraux qui protege cette these. Ni la these ni des extraits substantiels de celle-ci ne doivent etre imprimes ou autrement

reproduits sans son autorisation.

In compliance with the Canadian Privacy Act some supporting forms may have been removed from this thesis.

While these forms may be included in the document page count, their removal does not represent any loss of content from the thesis.

Conformement a la loi canadienne sur la protection de la vie privee, quelques

formulaires secondaires ont ete enleves de cette these.

Bien que ces formulaires aient inclus dans la pagination, il n'y aura aucun contenu manquant.

Le4juin2012

le jury a accepte la these de Monsieur Vincent D'Orangeville dans sa version finale.

Membres du jury

Professeur Andre Mayers Directeur de recherche Departement d'informatique

Professeur Ernest Monga Codirecteur de recherche Departement de mathematiques

Professeur Jean-Pierre Dussault Evaluateur interne Departement d'informatique

Professeur Denis Larocque Evaluateur externe

Service de I'enseignement des methodes quantitatives de gestion HEC Montreal

Professeur Shengrui Wang President rapporteur Departement d'informatique

Sommaire

Cette dissertation presente un ensemble d'algorithmes visant a en permettre un usage rapide, robuste et automatique des « Support Vector Machines » (SVM) non supervises dans un contexte d'analyse de donnees. Les SVM non supervises se declinent sous deux types algorithmes prometteurs, le « Support Vector Clustering » (SVC) et le « Support Vector

Domain Description » (SVDD), offrant respectivement une solution h deux probldmes

importants en analyse de donnees, soit la recherche de groupements homogenes (« clustering »), ainsi que la reconnaissance d'elements atypiques (« novelty/abnomaly detection ») a partir d'un ensemble de donnees.

Cette recherche propose des solutions concretes a trois limitations fondamentales inherentes a ces deux algorithmes, notamment 1) l'absence d'algorithme d'optimisation efficace permettant d'executer la phase d'entrainement des SVDD et SVC sur des ensembles de donnees volumineux dans un delai acceptable, 2) le manque d'efficacite et de robustesse des algorithmes existants de partitionnement des donnees pour SVC, ainsi que 3) l'absence de strategies de selection automatique des hyperparametres pour SVDD et SVC controlant la complexity et la tolerance au bruit des modeles generes.

La resolution individuelle des trois limitations mentionnees precedemment constitue les trois axes principaux de cette these doctorale, chacun faisant l'objet d'un article scientifique proposant des strategies et algorithmes permettant un usage rapide, robuste et exempt de parametres d'entree des SVDD et SVC sur des ensembles de donnees arbitrages.

Remerciements

Je tiens a remercier mes directeurs et codirecteurs de th&se, Andre Mayers et Ernest Monga, pour leur confiance a mon egard et la rigueur scientifique qu'il on su me transmettre au cours des dernieres annees.

Merci infiniment a mes parents, Annie et Christian, pour leur support indefectible, leur comprehension a l'egard de mes absences rep&6es lors de mon exil a Sherbrooke, et pour toute l'aide et l'inspiration qu'ils ont su m'apporter. Je remercie egalement ma belle-famille Monique et Michel pour leurs petites attentions delicates et le simple fait d'avoir une fille aussi formidable.

Je tiens a remercier mon frere Loic et ma soeur Akane pour avoir veille a ce que je maintienne un semblant de sante mentale et de vie sociale, et a petit mon gar9on, Alexandre, pour ses grands sourires qui eclairent chacune de mes journees.

Je remercie mon comite examinateur pour leurs critiques pertinentes et commentaires constructifs.

Je dedicace cette thdse k ma formidable femme, Elizabeth, qui par sa patience infinie, son kernel soutien, ses constants encouragements et son caractere unique, a su me faire garder le sourire et me garder motive au cours des dernieres annees.

Table des matieres

Sommaire

ii

Remerciements

iii

Table des matieres

iv

Liste des abreviations

v

Introduction

1

Contexte 1

Objectifs 3

M6thodologie 4

Structure de la these 5

Chapitre 1 Optimisation rapide de SVDD avec mecanisme d'apprentissage actif.

6

Chapitre 2 Partitionnement efficace des donnees pour SVC

33

Chapitre 3 Selection des hyperparametres pour SVDD

68

Conclusion

104

Contributions 104

Critique du travail 106

Travaux future de recherche 106

Perspective 107

Bibliographie

108

Liste des abreviations

SVM Support Vector Machine SVC Support Vector Clustering

SVDD Support Vector Domain Description AL Active Learning

SV Support Vector

SMO Sequential Minimal Optimization F-SMO Fast SMO

Introduction

Contexte

Les « Support Vector Machines » (SVM) sont une classe d'algorithmes d'analyse de donnees deriv^es des fondements theoriques sur 1'apprentissage statistique formalises par Vapnik dans son ouvrage The Nature of Statistical Learning Theory [5]. Les SVM se declinent sous deux categories d'algorithmes d'apprentissage: les algorithmes dits supervises, adaptes aux contextes de classification (« Support Vector Classifier » - SVM) et de regression (« Support

Vector Regression » - SVR), et ceux dits non supervises, objets de cette these doctorale,

adaptes a la detection d'elements atypiques (« Support Vector Data Description » - S VDD) et

h la recherche de groupements homogenes (« Support Vector Clustering »- SVC).

Les SVM non supervises sont caracterises par un processus d'induction estimant une courbe de niveau de la fonction de densite sous-jacente a un ensemble de donnees, englobant de fa<?on compacte les observations les plus representatives. Ces contours sont estimes par la methode SVDD, en generant une hypersphere de rayon minimal renfermant une proportion contrdlee de points dans un referentiel de projection non lineaire. La projection est r£alis£e implicitement par l'usage de noyaux gaussiens et permet de gendrer, dans le referentiel des donnees, un ensemble de courbes de formes arbitraires dont la complexite est controlee par le parametre a definissant l'etendue du noyau gaussien, et dont la tolerance au bruit est contrdlee par le parametre p definissant la proportion de points exclus des contours.

Le SVDD produit et exploite ces contours afin de differencier les instances normales des instances anormales d'une classe d'observations, et l'algorithme SVC utilise ces memes contours afin d'identifier des groupements homogenes d'observations (« clusters ») associes a des zones de densites eievees.

Les SVDD ont ete utilises avec succes dans des contextes tels que la detection de visages [10], la reconnaissance vocale [3], la detection d'ombres mouvantes en telesurveillance [11], le diagnostic de pathologies cardiaques rares [4] et l'identification de dysfonction dans les reseaux informatiques [5]. Les SVC ont ete employes en segmentation de clientele en marketing [7] et en gestion de relation a la clientele [16], la detection de regies semantiques [14], en groupement des courbes de charges electriques [2] et d'images retiniennes biometriques [12], et en segmentation d'images [6].

Les SVDD et les SVC b6neficient des qualites fondamentales suivantes :

• La surface estimant le domaine jouit d'une grande flexibility lui permettant de s'adapter a des distributions complexes. La complexity de la surface est controlee via un seul param^tre a definissant l'etendue du noyau gaussien;

• La surface beneficie d'une tolerance explicite au bruit controlee par un parametre de penalisation p permettant de definir la proportion de points exclus des contours.

En contrepartie, les SVDD et SVC sont affliges des trois limitations fondamentales suivantes restreignant leur usage dans des contextes concrets d'analyse de donnees :

• L'absence d'algorithme d'optimisation efficace permettant d'executer la phase d'entrainement des SVDD et SVC sur des ensembles de donnees volumineux dans un delai acceptable;

• L'absence de strategies de selection automatique des hyperparametres (<r,p) pour SVDD et SVC controlant respectivement la complexity et la tolerance au bruit des modules gen£r6s;

• Le manque d'efficacite et de robustesse des algorithmes existants de partitionnement des donnees pour SVC en presence de groupements aux formes complexes.

La resolution individuelle des trois limitations mentionnees ci-haut constitue les trois axes principaux de cette these doctorale, chacun faisant l'objet d'un article scientifique proposant des strategies et algorithmes permettant un usage rapide, robuste et exempt de param&res d'entree des SVDD et SVC sur des ensembles de donnees arbitraires.

Objectifs

Les trois limitations pr6c£demment enumerees sont individuellement resolues via l'atteinte des objectifs suivants :

1. Creer un algorithme d'optimisation executant la phase d'entrainement des SVDD sur des donnees volumineuses dans un delai acceptable. L'algorithme developpe doit traiter des observations sequentiellement, afin d'etre compatible avec une strategic d'apprentissage actif.

2. Developper un mecanisme d'apprentissage actif (« active-learning ») identifiant les candidats les plus informatifs dont 1'optimisation par 1'algorithme developpe en (1) minimise le nombre total d'etapes d'optimisation tout en produisant une solution de qualite comparable a celle d'un modele entraine sur la totalite des observations.

3. Developper un algorithme pour SVC permettant un partitionnement robuste et efficace des donnees en groupes homogenes distincts, a partir d'ime solution d'un mod&le SVDD prealablement entraine par l'algorithme developpe en (1). L'algorithme propose doit produire une segmentation exacte en presence de groupements aux formes complexes ainsi qu'en presence de donnees bruitees.

4. Mettre au point un mecanisme non supervise de selection automatique des hyperparametres pour SVDD, resultant en une representation robuste et compacte du domaine d'un ensemble de donnees bruite. La strategie proposee doit etre independante d'un ensemble de validation comportant des instances negatives/anormales de la classe cible.

Methodologie

Nous avons developpe « Fast-SMO » (F-SMO), un algorithme d'optimisation permettant d'accomplir efficacement la phase d'entrainement d'un SVM non supervise (objectif 1) sur un flux d'observations selectionnees par notre strategic d'apprentissage actif (objectif 2). Cette strat^gie est basee sur une mesure hybride offrant un compromis entre un critere de diversity spatiale ainsi qu'un critere d'ambigui'te, et permet de concentrer la phase d'entrainement de I'algorithme F-SMO sur un sous-ensemble d'observations les plus pertinentes.

Nous avons mis au point L-CRITICAL, un algorithme efficace de partitionnement de donnees (objectif 3) pour SVC, base sur un nouveau test ^interconnexion robuste permettant un partitionnement precis et rapide des donnees en presence de groupements aux formes complexes. Ce test ^interconnexion est base sur une analyse des chemins ^interconnexions entre les points critiques de la fonction d{x) definissant les contours. A cet efFet, un algorithme efficace de recherche des points critiques a ete mis au point, jumelant un processus d'optimisation de Quasi-Newton avec un mecanisme de fusion des trajectoires similaires.

Nous avons cree une methode de selection automatique des hyperparametres pour SVDD (objectif 4) dans un contexte non supervise. La methode integre une mesure de surgeneralisation, permettant de rejeter les hyperparametres resultant en une representation trop complexe d'un ensemble de donnees (« overfitting »), et int&gre a la fois une mesure robuste en presence de bruit, permettant d'identifier des representations compactes offrant une estimation juste du domaine d'un ensemble de donnees quelconque.

R6sultats

Tel que discute dans l'article 1, les experimentations revelent que Palgorithme F-SMO permet d'executer la phase d'entrainement 7 fois plus rapidement que Palgorithme usuel

«Sequential Minimal Optimization » (SMO) [9], tout en gen£rant une solution pratiquement

l'algorithme F-SMO permet de resoudre en moyenne la phase d'optimisation 13 fois plus rapidement que l'algorithme SMO, tout en produisant une solution compacte composee de seulement du quart du nombre de supports vectoriels de la solution exacte. L'algorithme F-SMO couple & la strategic d'apprentissage actif rend consequemment possible l'apprentissage d'ensembles de donnees volumineux dans un delai raisonnable sans deteriorer la qualite de la solution SVDD resultante.

Les experimentations decrites dans Particle 2, realisees sur des ensembles de donnees artificiels representant des structures complexes de groupements, m&ient a deux conclusions. En premier lieu, la methode proposee, L-CRITICAL, afFiche un temps d'execution largement plus comp&itif que les methodes competitives [8] [1]. En second lieu, L-CRITICAL gendre un partitionnement parfait sur l'ensemble des simulations realisees, alors que les algorithmes competitifs affichent une proportion moyenne d'erreurs de partitionnement importante sur des groupements de formes complexes.

Les resultats presents dans l'article 3 demontrent que la methode proposee affiche une excellente tolerance au bruit, et permet de discerner efficacement les donnees normales des observations atypiques. L'algorithme SVDD implementant notre strategic de selection des parametres a ete comparee a l'algorithme « abnomaly detection » implements dans le logiciel SPSS Clementine 12.0. Les resultats demontrent la superiorite de la methode proposee sur la vaste majorite des ensembles de donnees et demontrent son efficacite pour un usage pratique et automatique en analyse de donnees reelles.

Structure de la th&se

Cette these doctorale est structuree sous forme de trois articles proposant des solutions a chacun des objectifs pr6c£demment enumeres.

Chapitre 1

Optimisation rapide de SVDD avec mecanisme

d'apprentissage actif

Nous proposons F-SMO, un algorithme rapide permettant d'efFectuer la phase d'entrainement d'un module SVDD sur des ensembles de donnees volumineux et de dimensions elevees. L'algorithme F-SMO a la particularity de pouvoir traiter sequentiellement les observations, et est par consequent compatible avec les strategies d'apprentissage actif. Une nouvelle methode d'apprentissage actif est proposee, permettant d'accelerer la vitesse de convergence de l'algorithme d'optimisation tout en ne requerant qu'un nombre restreint d'observations. Cette strategic est la premiere strategic d'apprentissage actif proposee dans le contexte des SVM non supervises. Les resultats experimentaux confirment que la methode d'optimisation proposee surclasse significativement l'algorithme « Sequential Minimal Optimization » [9] en terme de temps d'entrainement, et que 1'integration du mecanisme d'apprentissage actif decuple la vitesse d'entrainement de F-SMO, rendant possible l'entrainement d'un module SVDD sur des ensembles de donn£es massifs au cout d'une erreur d'approximation fonctionnelle negligeable.

La contribution de l'auteur (V. D'Orangeville) k cet article represente 90% de la charge de travail globale liee au developpement des algorithmes et de la redaction de Particle.

Fast Optimization of Support Vector Data

Description with Active Learning

V. D'Orangeville, A. Mayers, E. Monga and S. Wang

Abstract — We propose F-SMO, a fast algorithm for solving the Support Vector Domain

Description (SVDD) optimization problem that implements a new active learning strategy that accelerates its learning rate by focusing only on the most informative instances of the dataset. The proposed active learning strategy integrates spatial-diversity and distance-based strategies reduce by more than 90% the training time and 70% the model complexity without affecting the solution accuracy. We investigate the computational efficiency of the F-SMO algorithm with active learning on synthetic and real-world datasets of various sizes and dimensions and show that it significantly outperforms the well-established Sequential Minimal Optimization (SMO) algorithm in terms of training time and solution complexity.

1

Introduction

S

cal Learning Theory [18]. The SVMs were introduced in 1995 by Cortes and Vapnik [7] as a

binary classifier algorithm and then extended to the regression problem, providing exceptional generalization performance on many difficult learning tasks. While the literature reveals a high degree of interest in new efficient SVM optimization algorithms in the supervised context over the past decade, few work has been reported on unsupervised SVM counterpart. In fact, to our knowledge, there is only one adaptation of the SVM, known as Support Vector Domain Descrip­ tion (SVDD) [17] for unsupervised learning. Although the SVDD has been successfully applied to perform anomaly detection and cluster analysis, it is not effective on large-scale datasets.

In this paper, we aim to propose an efficient and effective method, named F-SMO, for solving the nonlinear optimization problem associated with unsupervised SVM learning for SVDD for large-scale datasets. This objective will be reached in two stages. First, we develop a fast online algorithm for SVDD. Our approach is inspired by recent advancements proposed by Bordes in 2005 [4] in the context of SVM classifiers. Bordes's online optimization algorithm for SVM classifiers was derived from the Sequential Minimal Optimization (SMO) [15]. It allows learning

sequentially from individual instances as opposed to the conventional SVM algorithm, which requires the prior availability of the entire training dataset. We propose an extension of the SMO to solve SVDD by redefining the KKT optimality conditions that allow defining the selection criterion for KKT violating pairs for joint optimization and Lagrangian updating rules. The new algorithm, named Fast-SMO or F-SMO for short, allows solving efficiently the SVDD optimiza­ tion problem from a stream of individual patterns.

In the second stage, we develop an active learning strategy [6] that selects individual patterns for the F-SMO algorithm. In fact, most of the individual patterns analysed by the F-SMO process do not contain significant information about the borders of clusters. At the same time, they also cause a reduction in the efficiency of the algorithm, especially if we need to deal with very large datasets. The new active learning strategy is designed for selecting the most informative instanc­ es for optimization by F-SMO while reducing significantly the number of training patterns in­ volved for obtaining a good approximation of the SVDD exact solution. The proposed selection scheme is based on a combination of a spatial diversity and distance-based criteria. It allows F-SMO to generate an approximation of the exact solution with a very small error, while dramati­ cally reducing the complexity of the solution and the computational time requirement by an order of magnitude compared to the LIBSVM implementation of SMO for SVDD. The proposed ac­ tive learning strategy is the first selection strategy of its kind in an unsupervised SVM learning context, and allows large scale datasets to be learned within reasonable training time.

In the follows, Section 2 presents adaption of SMO to solving SVDD. Section 3 describes the new active learning strategy for SVDD. Section 4 presents experimental evaluations of the pro­ posed algorithms on real and synthetic datasets. Note that to allow a fair comparison between LIBSVM1 and F-SMO for SVDD optimization, we have chosen to disable all heuristics such as

shrinking and kernel caching. All algorithms are implemented in C++ and are available upon re­ quest to the authors.

2

SVDD sequential optimization

The SVDD is designed to characterize the support of the unknown distribution function of an

input dataset by computing a set of contours that rejects a controlled proportion p of patterns. These contours provide an estimate of a specific level set associated with the probability 1 - p of the distribution function and allow unseen patterns to be classified as normal or abnormal. This section details the SVDD optimization problem, the optimal candidate selection strategy for op­ timization and the F-SMO algorithm for solving efficiently the SVDD optimization problem.

2.1 SVDD optimization problem

Given a set X of training vectors xt e , / = 1,..., n and a nonlinear mapping <f> from X to some

high-dimensional nonlinear feature space <I>, we seek a hypersphere of center a and minimal radius R that encloses most data points and rejects a proportion p of the less representative patterns. This requires the solution of the following quadratic problem:

fe-af <,R

+S„

(1)

£ > 0 , 1 = 1 , . . . , « .

Slack variables are added to the constraints to allow soft boundaries, and $ denotes the coordinate ^(x, ) of xi in the feature space. Points associated with £(. > 0 are excluded from the contours and pe­ nalized by a regularization constant C which controls a proportion p of points lying outside (and on the surface of) the hypersphere.

The optimization problem (1) can be solved by introducing the Lagrangian L as a function of primal variables R2, <£• and a and dual variables a and ft referred as Lagrange multipliers enforcing the two

constraints in (1).

L { l P , i , a ,a, p ) = R2+ c £ & - ' £lal( R ' + {l- yt- 4 ) - £ f i A

(=1 /= 1 1=1

<*,.,#> 0, i = \,...,n.

Define p* as the optimal value of the object function (1), we can verify that

p* = min( max L ( R2,£,a,a,/?)) (4)

R2,f,a\ai O.fiiO V ' /

Moreover, we can define the dual optimal value of the dual objective function

D(a,p) = mmRl^L(R2 ,%,a,a,p) as

p* = max D ( a , B ) = max (m m l ( R2 , E , a , a , B ] \ (4)

aiO.fiiO v ' aiO,fiiO\K2 ^ ')

Setting to zero the partial derivatives of formula (3) with respect to primal variables R2, and a at the

optimal point leads to:

dLp . A ^-i -ai? "*5°" ff:C-a,-A = 0->C = <*,+/), (4) P)j " " " -z*- • -2^ ad + 2a1L ai = 0 ^ a = Z da t! M M

We can deduce from the constraints C = at + P( in (4) and a,,/?, > 0 in (3) that a , < C. The

Karush-Kuhn-Tucker (KKT) complementary slackness conditions [REF] results in:

Af,=o

<r,(*'+£-fo-<»f)=o (5>

It follows from constraints (S) that the image fa of a point x. with et > 0 and ai > 0 lies outside (or on

the surface) the feature-space sphere, and that a point x( with f, = 0 and a, = 0 lies within the sphere.

This indicates that the solution is sparse, only training vectors excluded from the decision surface with

ai > 0 contributes to the SVDD solution. These vectors are referred to as support vectors.

R2, a n d a, turning the Lagrangian into the Wolfe dual form Ld where (•,•) is the inner product of

two possibly infinite vectors.

Ld: max

Jz

(# 4

[ /=l i=1 7=1 J

Z«, = (6)

/=l

0 <a( ^C, I = 1,...,#I.

Details of the derivation of the Lagrangian into to Wolfe dual is provided below:

£, = + ci 4, - £ «, (x2+4, -1|4 - flf ) •- £ M 1=1 1=1 1=1 -> R' + C £$ - «2 jo, - 2>, + )», + Z". k H (=1 1=1 /=1 " £ ' i=l 2 «I ^ - 2 (fl, #,) + (a,«)) i=i -> 2 «, (4 A )~ 2^ a< (fl» $ ) + Z a- (a> a> i=l i=l (=1 1 n ->Z aM*b)-(a*a) 1=1 Z 4 ) - Z Z aiay ) 1=1 »=1 7=1 (7)

The dot product in eq. (7) is replaced by an appropriate Mercer [REF] kernel k ( xt, X j), re­

ferred to as kUj for notation simplicity, overcoming the explicit reference to $ of possible infinite dimen­ sion. The Gaussian kernel is used in this context, adjusting the complexity of the cluster contours with a single parameter a controlling the kernel bandwidth.

*/.7=e (8)

The Wolfe dual is simplified by replacing the dot products (<!>,,by the kernel k( j: Ld ' max \ £ a,ku - Z Z aiajhj <*i [ (=1 /=1 j=\ ^>,=1, (9) /=! 0 < at< C , i = \,...,n.

The SVDD solution can consequently be optimized by maximizing the dual equation (9). Note that the problem remains convex since the kernel matrix K with i,j th entry Ktj = kt J is positive definite.

As described in eq. (4), the center a of the hypersphere is described as a linear combination of the feature space vectors fa.

a = 0°)

J

The square distance r2 (jt,) from an image fa of xt to the sphere center a is defined as:

r\ xl) = \<f>t-af

= ( f a , f a ) -2Z «, )+Z Z a'ai (h'tj) (11)

ia1 1=i y»i

n n _ n

=K ~ 2Z aiK<+Z Z aiaiK)

i=l /=! j=\

Based on eq. (11), the square radius R2 defined in (12) of the hypersphere can be calculated as the aver­

age of distances to center of r2(xu) and r2(xv) of two feature-space vectors <t>u and <f>v both located the

closest of the hypersphere surface and respectively outside and inside the sphere. Theses vectors are iden­ tified during the optimization phase of SVDD described in Section 2.3.

R2 =i(/-2(xB) + r2(xv))

u <-argminr2(xJ) s J . as> 0 (12)

s

v<—argmax r2( xs) s J . as< C

where

Eq. (11) and (12) allows defining the function d ( xt) for evaluating the relative position from any image

xt) to the surface of the hypersphere by comparing its distance r2(xt) to center a to the sphere radi­

u s R2.

d ( xt) = R2- r \ xt)

= h ( r \ x , ) + r\ x, ) ) - r\ x , )

= + i ( K ,+ k . , . ) ~ k u < 1 3 )

i=l i=i i=i

= 2Ot- Os where Oj= J ^ aiki j and Os= ± ( Ou+ Ov)

(=i

The function J(x,) classifies a point xt inside the contours if < 0, on its surface if ) = 0

and outside otherwise. The decision surface is defined as the implicit surface : d(jc) = 0}. Note that t h e G a u s s i a n k e r n e l p r o p e r t y kt t= \ a l l o w e d s i m p l i f i c a t i o n s t o b e m a d e i n e q . ( 1 3 ) . A l s o , v a l u e s o f Ou

and Ov are calculated in the optimization process described in Section 2.3.

2.2 Optimal candidate selection

We describe here the notions of KKT optimality and r -violating pair that will be used to select candidates for joint optimization during the F-SMO learning phase, as well as a stopping criteri­ on during its optimization process.

For a trained SVDD solution, points jc(. associated with a Lagrange multiplier 0 < at < C lie

on the surface of the sphere described by the iso-surface d(x,) = 0. Points such as aj = C are

excluded from the contours (d(xt) > 0) and those associated with a, = 0 are enclosed by the 13

hypersphere («/(*, ) < 0) and do not contribute to the description of the contours. The maximiza­ tion of the Wolfe dual eq. (9) produces a sparse Lagrangian vector a, where a proportion 1 - p of data points lies inside the hypersphere and only a small fraction p of points with a, > 0 and

d(x,)>0 contributes to the definition of the hypersphere surface. Based on the

Karush-Kuhn-Tucker optimality conditions [14], a SVDD solution eq. (9) is optimal if each of the following conditions are fulfilled for each point x of the training set X.

a, = 0 a d ( x ,) < 0

0 <a,<C a rf(x(.) = 0 (14)

ai= C a d (x,) > 0

Conversely, we can state that a point xt violates the KKT conditions in either of the following

two cases:

a , > 0 a * / ( X ) < 0

; C (15)

a(< C a d( X j ) > 0

The KKT violation test of formula (15) allows defining a criterion to test for simultaneous vi­ olation of the KKT conditions by a pair of points (*, ,*, ) referred to as a r -violating pair.

( af> 0 A a

j < c )

(16)

A r -violating pair ( xnx j ) is a pair of points with at > 0 and a} < C which are respectively

misclassified by the decision function d(x) as inside and outside of the hypersphere, within a tolerance factor of r. The absence of any such pair in the training set indicates the convergence of F-SMO and T -optimality of the solution within a tolerance factor r,

The F-SMO implements an efficient selection scheme inspired from Keerthi's improved se­ lection strategy [11] for SVM classifiers and optimizes successively r -violating pairs of formula (16) that locally maximize the gradient of the objective function (9) and induce a maximal step in the objective function's value at each iteration.

The gradient of the objective function (9) is maximized by selecting a r -violating pair

(x.-yXj) for joint optimization according to max|<9,. - Oj|, The optimal selection strategy for the

r -violating pair in the SVDD context can be stated as follows:

The selection of a r-violating pairs is achieved by maintaining a cache of Ofor all active support vectors and by keeping track of <9min, Omax, «min and during the optimization process

in order to allow an immediate identification of the optimal x -violating pair according to formu­ la (17).

2.3 Fast sequential optimization

This section describes the algorithm F-SMO, inspired from the algorithm proposed by Bordes [4] for SVM classification. The F-SMO algorithm offers two important advantages over SMO. First, F-SMO allows the sequential processing of individual training examples, as opposed to the SMO algorithm, which treat patterns in pair and cannot treat them separately. This property is essential, as it makes it possible to implement our active learning strategy for selecting the most informa­ tive individual training patterns for optimization by the INSERT function of the F-SMO algo­ rithm described below. Moreover, F-SMO allows solving the SVDD optimization problem in a single sequential pass over all patterns of the training set, while the SMO requires multiple pass­ es over the dataset. The F-SMO method works by alternating the two following steps.

j <— argmaxOk sJ. ak> 0

k

with max (17)

The first step, INSERT reads an unseen input pattern x^ and seeks an existing sup­

port vector to form a r -violating pair {x^x^) according to the optimal selection strategy eq. (14). It then performs a joint optimization of the pair by updating both multipliers ) as stated in the F-SMO subroutines in Table l.The second step, UPDATE, aims at minimizing the imbalance produced by the recent inclusion of and update of in the solution, by per­ forming a single optimization step on a r -violating pair selected according to [14]. It then pro­ ceeds to a pass to remove all inactive support vectors (a, = 0) fulfilling the KKT optimality condition (0. + r > ). The purpose of this removal pass is to enforce sparseness in the solu­ tion during the optimization process by removing inactive SVs. These two steps are repeated in alternation until all points x(. of the training set X have been evaluated once by the function

INSERT or until no more candidates are selected by the active learning strategy. A finalizing pass is then performed by iterating the function UPDATE over the set of active support vectors, until no more t -violating pair can be identified indicating the convergence of the SVDD solu­ tion.

The sequence of INSERT and UPDATE in step 4 in Algorithm 1 can be considered as a fil­ tering pass over the training set that identifies and optimizes potential support vectors within a single pass through the training set, while step 6 ensures the stabilization of the solution over the selected set of support vectors. It is worth mentioning that the single pass over the training set could fail to select important support vectors during the learning phase on very small datasets. However, the likelihood of this is minimal as the F-SMO algorithm is designed for solving large-scale datasets. Segments of code highlighted in blue in Algorithm 1 and Table 1 represent in­ struction sequences that benefit from multithreaded implementation.

Algorithm 1 - F-SMO. Input parameters

• X c= Rd : input dataset of size N and dimension d

• y: RBF bandwidth (reK+)

• p: rejection rate (pe[0,lj) • r: KKT tolerance factor (r « 0.001)

Initialization:

C = — w i t h p' = min (•*=*•, max (^, p))

« = {"o =•" = «»„-. = C , a „n = - - - = aN_{ =0}

d = {O0,- -,On^} with 0, = £ aiKi

)=\—n„

Selection:

Select an unseen training example xte . X

go to (5) if no unseen pattern remains.

Optimization:

a. INSERT (xf)

b. UPDATE ( ) Return to (3).

Finish:

Repeat UPDATE ( ) until r -convergence.

Table 1 - F-SMO subroutines.

INSERT (jc^) 1. Initialization

Set am = 0

and compute = £ «A,,

1=1 ..B„

2. Check x -optimality of xn

Exit if Onew+r>Onax

3. Optimize Pair

UPDATE( )

1. Check r -optimality of solution Exit if Omin+r>Omax

2. Optimize Pair(ocmin,xmax)

3. Inactive SV removal

Remove any jc, such as ai = 0 and 0 , + T>OW K

4. Update MinMax( )

5- R2 =(Omin+Omax)/2

Optimize Pair(jcj, x , )

1. Joint optimization

mm- °s °' ,C-as,-a,

k , + k , - 2 k , . _{StS (,/ s,t} a , < — Aa as < - as+ Aa

2. Update O (for all active SVs) a) O, <— 0, — Aa( ki s — ku) Vi g {l. Update MinMax ( ) i <— min Ot s i . at< C *c[U„] * * j <— max Ok s i . ak> 0 *e[l,n„]

Omin = On = OJ, xmia = x„ Xmax = XJ

3

Active learning for SVDD

Active learning is the process of actively selecting the most informative patterns during the learning phase according to a sample selection criterion that accelerates the learning rate and minimizes the number of training examples required to achieve a good solution approximation. Active learning has been successfully implemented in the context of classification to enhance the learning rate of neural networks [1], support vector classifiers [8] [10] [12] [18] and statistical models [5][6][16].

Despite its strong theoretical foundations and encouraging results in a classification context, no active learning strategy adapted to unsupervised SVM has yet appeared in the literature, for accelerating the learning phases of SVDD. For this purpose, we propose a new active learning strategy intended to concentrate the learning phase of F-SMO on a small set of the most informa­ tive patterns, in order to improve its learning rate and reduce its solution complexity at the cost of a minimal loss of functional accuracy (compared to a full model trained on the whole training set). The proposed method is a hybrid sampling method which combines a spatial diversity and

distance-based criteria to guide the selection of new candidates within small subsets of po­ tential learning candidates , to be optimized by the function INSERT (jc^) of F-SMO. This sequence of active learning selection and optimization is repeated until every training pattern has been evaluated once by the active learning selection procedure.

3.1 Spatial diversity

The spatial diversity criterion enforces the selection of candidates dissimilar to the current sup­ port vectors set Xn, in order to minimize redundancy among support vectors and focus on the

most informative candidates. The diversity fitness score Sdiv(x/) of a potential candidate

x, e XAL is assessed as the minimal dissimilarity from xt to any support vector x} e Xsv .

(18)

According to the spatial diversity criterion, the best candidate x*^ e XA L is the one which max­

imizes the minimal distance to any support vector of the expansion setZ^.

xdh, = arg max Sdiv (x,)

= arg max

xle^4L

mm(l-*,,)]

(19)

This strategy is analogous to the angle diversity strategy tested in SVM classification [18], where the authors considers the maximal angle between the induced hyperplane h(xt) of a can­

didate x, e XAL in feature space and each hyperplane /?(xy.) associated with each support vector

Xj e . The function h{x,) defines a hyperplane passing through the image <j>t of xt in feature

space and the center a of the hypersphere. The angle diversity fitness score Sang (x,) of a candi­

date xt is evaluated as the minimal angle between /*(*,) for and any /*(*,) for

x , _J e X„,, _sv ^U)=min|cos(z(/I(x(),A(x,)))| where cos|z(/z(x,),/j(jry -I T J I 'II po I.J _{= \k, \ = k.,}

I

'

(20)

According to the angle diversity fitness score of eq. (20), a candidate is chosen according to:

x*ang = arg min Smg (x,)

xls XM

= arg min

x, *XA L

mm

(21)

hypersphere surface with support vectors images <f>j, and is equivalent at encouraging spatial di­ versity in the primal space among support vectors.

xdlv = arg max

= argmin

* le X4 L

(22)

3.2 Distance-based strategy

In the SVM classification context, the distance-based strategy aims at selecting the misclassified candidates located the nearest of the separating plane, which corresponds at choosing ambiguous candidates in order to fine-tune the separating plane. This strategy translates in the SVDD con­ text into focusing on the most ambiguous training patterns located immediately outside the hypersphere, or equivalently, finding the closest candidate to the contours which is excluded from the contours. Recall that only data points located outside the cluster surface contribute to the definition of the contours described by the isosurface of the decision function d(x) of eq.

where d ' ( xt) is the relative position of the surface of hypersphere <j>t, normalized by the value

O, in order to constrain its range between 0 and 1, and defined as follows:

(13).

The distance-based fitness score of a potential candidate xt is calculated as:

S* s , {X, ) = d' {X, ) (23)

d' (x, ) = o ;d(xi ) = l— o ; Z aj k j

j=\..N

(24)

The normalization of </(*,) is intended to control the magnitude of S^, (x,). A training example

xdisi € %AL is then selected according to:

xd«< = arg m,n

* , *XA L

'-iZ

aih> (25)

A more naive approach would favor selecting an input pattern xV^ e XA L located the farthest

away from the contours as xVM = argmaxJ'(x,), resulting in a model more sensitive to outliers.

xI*Xal

3.3 Hybrid selection criteria

We propose a hybrid active learning selection strategy which combines the spatial diversity score (18) and the distance-based score (23) seeking a candidate x, excluded from the contours which simultaneously has simultaneously a minimal (positive) distance d ' ( xt) > 0 to the hypersphere

surface and maximal distance to all existing support vectors.

The existing hybrid selection strategies for SVM classification described in [10] and [18] combine these two selection criteria by defining the following convex combination:

Sa m m [{ x , ) = w - Sd l t( x , ) + ( l - w ) - 1 with we[0,1]

•*<*« (26)

^convex = argmax5_(x,)

xleXAl

One major drawback of this convex combination of fitness scores stems from the fact that the efficiency of a linear combination of fitness scores depends on the appropriate choice of the weighting parameter w which is data dependant and depends on the relative values of Sdiv (x,)

to l/S^, (jc, ). To avoid the unintuitive choice of w, we defined a hybrid score S,^u (x,) (27)

computed as the ratio of the two fitness scores, allowing simultaneous maximization of the di­ versity score Sdiv (x,) as numerator and minimization of distance score SdiJI (x,) as denominator.

(27)

Combining the two selection criteria, the hybrid selection strategy selects training points

x'ai e Xal according to the following criterion:

The indicator function I (</•(*,)>o) returns a value of 1 if d' >0 and 0 otherwise, and enforc­ es the selection of a candidate xa( excluded from the sphere. A candidate xal is selected accord­

ing to eq. (28) from a small subset of potential candidates XAL (20 candidates in our implemen­

tation), then optimized by the F-SMO procedure INSERT (*!/)• The selection and optimization sequence is repeated until each training pattern has been evaluated once.

Experiments have been performed on synthetic and real-world datasets in order to compare the computational efficiency of the F-SMO optimization method with and without active learning, to the standard LIBSVM SMO algorithm, for solving the SVDD training phase. All algorithms are evaluated on 11 well-known UCI benchmark datasets with dimensions ranging from 2 to 60, in order to compare their respective training times, numbers of support vectors of the solutions and functional approximation errors in comparison to a reference exact solution ®rtf. The refer­

ence model (referred to as REF) is generated by training a SVDD model with SMO using a high­ ly restrictive KKT tolerance factor of r = 10-7.

argmax I (</-(*, )>o) (28)

4

Experiments and results

The functional approximation error ^ is assessed by training a model with a looser factor of r = 10"4 on the same training set as &ref, and then evaluating the proportion of points

misclassi-fied by the "approximate" SVDD solution as:

The procedure I(y) is the indicator function returning a value of 1 for any negative value of

y and 0 otherwise. The function (29) evaluates the proportion of points that are (mis)classified

by the approximate model (SMO or F-SMO) to the opposite side of the hypersphere as compared with the reference model.

Two variants of the proposed active learning scheme were tested. F-AL1 refers to the F-SMO method with active learning trained with rejection rate p. F-AL2 is trained with an adjusted

pAL > p to compensate for a phenomenon involving the expansion of the generated contours ob­

tained with active learning, in comparison to SVDD contours obtained without active learning. Values of pobs displayed in Table 2 measure the observed proportion of points excluded from the

contours generated by the models F-AL1 and F-AL2, the expected values of pobs are p = 20%.

All the experiments reported in Table 2 are performed on a 3.6 GHz Intel quad-core CPU, with each test repeated 20 times and the results averaged. Note that the symbols +1 and -1 identify positive and negative class instances of each dataset.

Table 2 - Comparison of SMO, F-SMO. F-AL1 and F-AL2: training times, number of support vectors, functional approximation error in comparison to a reference solution and proportion of points rejected by the trained contours. Rejection rates are

set to p - 20% (for RER SMO, F-SMO and F-AL1) and to pU2 for F-AL2.

Draining time(s) Number of SVs

Mm MU asm H42H MU Mu 11.74* 22.10% Bamra(tl) ! 217C « | imacc (+1) ! un l - l mm 9m7 0.70K io.#o* MM 0.44% S.1S* 5.67* 9.82* 22.79* UJMK . 1S.01K 19.2SK 24.31* 24.34* imm imm 13.01* 21.63* rlngnorm (-1) 2,41* u spile* (-1) 0013 0.013 AM 0.029 a 034 0.139 MB mm w4 0J7* 6.88% wwmrain) r~i 0.505 0.059 0.029 0.030 0.4#* J. 78* 1A2M 21.14* 12M ftiiu aaa

As shown in Table 2, F-ALl and F-AL2 significantly outperform both SMO and F-SMO in terms of average training times, at the cost of increased functional approximation error ^ over SMO and F-SMO. The models F-ALl and F-AL2 exhibit averaged observed rejection rates p^ of 15.39% and 21.42%, respectively, which suggests that a SVDD model trained with active learning requires an adjusted pAL1 in order to minimize the absolute difference between p^ and

P-The increased functional approximation error ^ of F-ALl is caused by the choice of the regularization factor C = l/(p-Af) with p = 20% kept constant for both F-SMO and F-ALl. Because the active learning selection strategy enforces the selection of candidates located near the outer part of the hypersphere, it alters the distribution of training patterns optimized by the INSERT (x) procedure and results in contours of slightly expanded shapes compared to the F-SMO trained on the whole training set for the same value of p.

Figures 3, 4 and 5 summarizes the relative running times, numbers of support vectors, and functional approximation errors ^ of the algorithms discussed in this paper. Based on the ex­ perimental results, F-SMO is far more competitive than SMO for optimizing a SVDD solution (not using an active learning strategy), and F-AL2 is superior to F-ALl in terms of functional accuracy.

As illustrated in Table 2, the functional approximation error ^ can be minimized efficiently by setting an increased value of pAL2 > p to compensate for the contour expansion, also reducing

for F-AL2 compared to F-ALl in all tests performed.

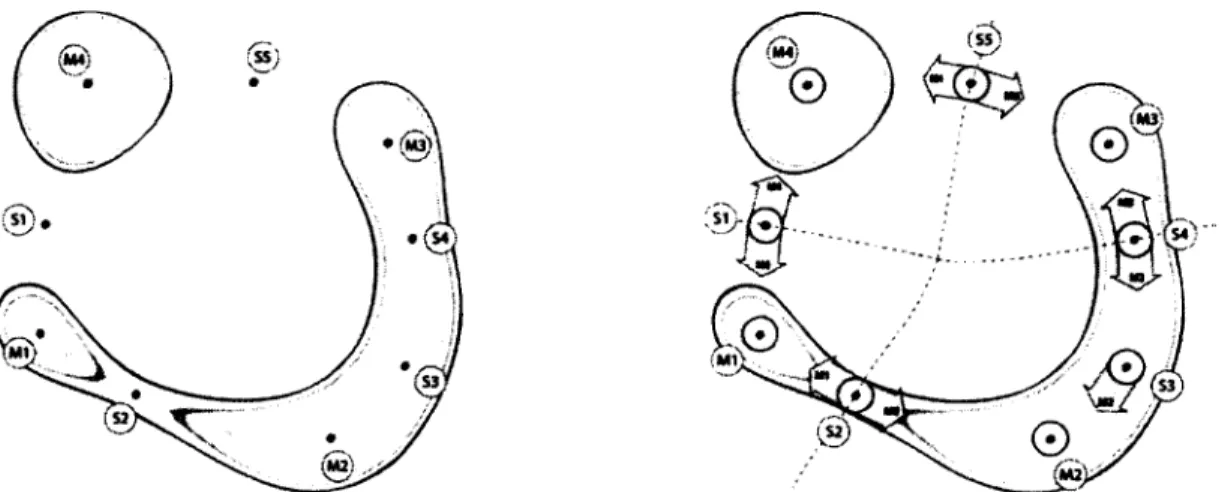
Figures 1 and 2 illustrate two SVDD models trained with F-SMO and F-AL2 on a same train­ ing set of 5,000 points, F-SMO trained with p = 20% and F-AL2 trained with equal kernel bandwidth while increasing p to pAL2 = 27.5%. The two methods produce comparable contours

minimize the functional approximation error ^ remain to be explored in further research.

Figures 1 and 2 (from left to right) - (Figure 1) F-SMO trained with/7 = 20%. (Figure 2)

F-AL2 trained with pAL2 = 27.5% and ^ = 4.95%.

Table 3 - Comparison of F-SMO, F-AL1 and F-AL2 versus SMO: relative training times

and number of support vectors compared to SMO.

Training time (s) Number of SVs

banana (+1) 8.73% 7.96% a _»«WI ick 9.27% 7.11* 6.76% 3.79% 9.65% •MMi 6.83% 21.66% 31.37% 18.00% mam image (+1) 17.45% 8.74% 26.70% 33.87% 25.78* 25.10% 27.02% 28.04% 12.41% ringnorm (-1) 12.58% 5.98% 22.70% 14.20% mmm 13.09% 9.48% 28.05% splice (-1) twonorm(-l) 12.80% 5.81% 22.61% 27.12% u MM. MnHnl 22.26% 27.31% 14.10* waveform (-1) 11.69% 5.65% 5.98%

Table 3 reports the relative training times of F-SMO, F-AL1 and F-AL2 in reference to SMO (with T = 10"), computed from values in Table 2. F-SMO's computing time represents 14.25% of the time required by SMO to optimize the solution, and F-AL1 and F-AL2 benefit from re­ duced average training times and numbers of support vectors in comparison to F-SMO. The re­ duced number of support vectors is responsible for the increase in functional approximation error

^, while significantly reducing at the same time the complexity of the SVDD solution, which in turn allows new data points to be classified far more rapidly.

100.0% 80.0% 60.0% 40.0% 20.0% F-SMO FAL2 • Time 14.3% 100.0% 80.0% 20.0% F-SMO 99.9% 99.9% 24.1% 28.2% F-SMO «%t(fn)

Figures 3,4 and 5 (from left to right) - Comparison of SMO, F-SMO, F-AL1 and F-AL2.

(Figure 3) Relative training time compared to SMO with r = 10~4, (Figure 4) Relative

number of SVs compared to the exact solution, (Figure 5) Functional approximation error

The hybrid selection strategy was evaluated on synthetic 2D datasets of sizes ranging from 10,000 to 90,000 training patterns, in order to assess the asymptotic behavior of the training times of the F-SMO algorithm implementing an active learning strategy (F- AL1 and F-AL2) rel­ ative to training set size.

U 1L0 15.1 1M

• F-SMO 0J

0.7 Of

at 03 0.4 1.1

at OJ 05 as u 1.7 2.1

Figure 6 - Comparison of training times (s) for F-SMO, F-AL1 and F-AL2, as a function of

Table 4 - Training times, number of support vectors and functional approximation errors

^ of F-SMO (p = 10%), F-AL1 (p = 10%) and F-AL2 (pAL2 = 23%) for increasing train­

ing set size (N) with fixed kernel bandwidth <r = 0.05.

10,000 30,000 •UUP 50,000 70,000 Time (s) ~F-ALI F-AI4 006 0.17 0.31 QJ90 0.75 IM 1.35 1.72 2.14 SVs

F-SMO F-AU F-AJL2 1,010 £007 3,008 4,007 5,007 7,005 64 117 169 221 272 9,006 373 423 475 124 239 355 470 584 700 814 929 1,044 8.41% 3.28% 1*9% 1.76%

!&*

As expected, the proposed hybrid selection schemes (F-AL1 and F-AL2) show dramatically improved training times compared with the F-SMO algorithm: indeed, the asymptotic relation­ ship of their training times to training set size is almost linear (R2 = 0.9821 for AL1 and

R2 = 0.9632 for AL2).

Note that F-SMO with active learning can be effectively used in an online context on a con­ tinuous flow of training points, by dynamically adapting the number of candidates \XAL\ evaluat­

ed in each active learning pass according to the availability of processing power and the speed of data acquisition.

5

Conclusion

We have proposed F-SMO, an efficient algorithm for SVDD that optimizes a stream of individu­ al patterns during its learning phase. The development of F-SMO requires defining the KKT op-timality conditions, the selection criterion for KKT-violating pairs for joint optimization and the Lagrangian updating rules in the unsupervised SVM context.

We have proposed a new active learning strategy that identifies the most informative instances for optimization by F-SMO, and reduces the overall number of training patterns required to ob­ tain a good approximation of the SVDD solution. The hybrid candidate fitness measure is based

on diversity and ambiguity criteria that allow F-SMO to generate an approximation of the exact solution with small approximation error, while dramatically reducing the complexity of the solu­ tion and the computational burden - by more than 10 times compared to SMO. The proposed active learning strategy is the first selection strategy adapted to SVDD learning, and makes it possible to optimize large-scale datasets within reasonable training time.

We have compared the effectiveness of the proposed method F-SMO with active learning to the standard LIBSVM SMO implementation on several synthetic and real-world datasets. Exper­ iments suggest that F-SMO solves the same problem in less than 15% of the time spent by SMO and that F-SMO with active-learning in less than 8%, proving their vast superiority in terms of computational cost on all experiments performed.

References

[1] A. Adejumo, A. Engelbrecht, A Comparative study of neural networks active learning algorithms, Proceedings of the International Conference on Artificial Intelligence. (1999) 32- 35.

[2] A. Ben-Hur, D. Horn, H.T. Siegelmann, V. Vapnik, A support vector clustering method, Proceedings 15th International Conference on Pattern Recognition. 2 (2000) 724-727.

[3] Benchmark repository. [Online] [Cited: 11 11, 2009.]

http://ida.first.fraunhofer.de/projects/bench/.

[4] A. Bordes, S. Estekin, J. Weston, L. Bottou, Fast kernel classifiers with online and active learning, Journal of Machine Learning Research. 6 (2005) 1579-1619.

[5] D. A. Cohn, Minimizaing statistical bias with queries, Advances in Neural Information Processing Systems. 6 (1997).

[6] D. A. Cohn, Z. Ghahramani, M. I. Jordan, Active learning with statistical models, Journal of Artificial Intelligence Research. 4 (1996) 129-145.

[7] C. Cortes, V. Vapnik, Support-vector networks, Machine Learning. 20 (1995) 273-297. [8] C. K. Dagli, S. Rajaram, T. S. Huang, Utilizing information theoric diversity for SVM

active learning, 18th International Conference on Pattern Recognition. (2006) 506-511. [9] B. Scholkopf, J. C. Piatt, J. Shawe-Taylor, A. J. Smola, R. C. Williamson, Estimating the

support of a high-dimensional distribution, Microsoft Research. (1999) 30.

[10] J. Jiang, H. H. S. Io, Dynamic distance-based active learning with SVM, Proceedings of the 5th international conference on Machine Learning and Data Mining in Pattern Recog­ nition. (2007) 13.

[11] S. S. Keerthi, S. K. Shevade, C. Bhattacharyya, K. R. K. Murthy, Improvements to Piatt's SMO algorithm for SVM classifier, Neural Computation. 13 (2001).

[12] M. I. Mandel, G. E. Poliner, D. P. W. Ellis, Support vector machine active learning for music retrieval, Multimedia Systems. 12 (2006) 3-13.

[13] W. Karush, Minima of functions of several variables with inequalities as side constraints, M.Sc. Dissertation, Dept. of Mathematics, Univ. of Chicago. (1939).

[14] H. W. Kuhn, A. W. Tucker, Nonlinear programming, Proceedings of 2nd Berkeley Sym­ posium (1951) 481-492.

[15] J. C. Piatt, Fast training of support vector machines using sequential minimal optimiza­ tion, Advance in Kernel Methods. (1999).

[16] N. Roy, A. McCallum, Toward optimal active learning through sampling estimation of error reduction, Proceeding 18th International Conference on Machine Learning. (2001) 441-448.

[17] D.M.J. Tax, R.P.W. Duin, Support vector domain description, Pattern Recognition Let­ ters. 20(1999)1191-1199.

[18] V. Vapnik, The Nature of Statistical Learning Theory, Springer, New York, (1995). [19] Q. Wang, Y. Guan, X. Wang, SVM-Based spam filter with active and online learning,

Chapitre 2

Partitionnement efficace des donn€es pour SVC

Cet article propose L-CRITICAL, un algorithme de partitionnement des donnees en sous-groupes homogenes disjoints pour la methode « Support Vector Clustering ». L'objectif de cet algorithme est d'identifier l'ensemble de groupements intrinseques a un ensemble de donnees arbitraire, et de produire un partitionnement robuste et precis des observations en fonction des sous-groupes d&ectes. L'algorithme repose sur une analyse topologique fonctionnelle de la solution d'un SVDD decrivant les contours des segments, et cherche a caract6riser les chemins d'interconnexion entre les points critiques situes a l'interieur des contours, permettant ainsi de distinguer les segments. Les resultats experimentaux confirment que l'algorithme propose ameliore significativement la precision du processus de partitionnement des donnees dans un contexte de SVC comparativement aux competitifs, tout en minimisant significativement le temps de calcul nScessaire sur tous les ensembles de donnees analyses.

La contribution de l'auteur (V. D'Orangeville) h cet article represente 90% de la charge de travail globale liee au developpement des algorithmes et de la redaction de l'article.

Efficient Cluster Labeling for

Support Vector Clustering

V. D'Orangeville, A. Mayers, E. Monga and S. Wang

Abstract — We propose a new efficient algorithm for solving the cluster labeling problem

in Support Vector Clustering (SVC). The proposed algorithm analyzes the topology of the function describing the SVC cluster contours and explores interconnection paths between critical points separating distinct cluster contours. This process allows distinguishing disjoint clusters and associating each point to its respective one. The proposed algorithm implements a new fast method for detecting and classifying critical points while analyzing the interconnection patterns between them. Experiments indicate that the proposed algorithm significantly improves the accuracy of the SVC labeling process in the presence of clusters of complex shape, while reducing the processing time required by existing SVC labeling algorithms by orders of magnitude.

1

Introduction

^^LUSTER analysis is a learning procedure aimed at discovering intrinsic group structure in unlabeled patterns in order to organize them into homogeneous groups. Clustering analysis is a key area of data mining for which computationally efficient and accurate methods are needed to deal with very large-scale datasets in terms of data volume, data dimensionality and clusters complexity.

Support Vector Clustering (SVC) is a clustering algorithm proposed in 2000 by Ben-Hur [1] that uses the solution of the Support Vector Domain Description (SVDD) [2] model to group data points into clusters. While the SVDD algorithm produces contours that estimate a level set of the unknown distribution function of a dataset, the SVC method interprets these contours as cluster cores and assigns each data point to its nearest core to generate the final clusters.

The SVDD generates cluster boundaries by projecting a dataset into a nonlinear feature space via the use of Gaussian kernels, and by defining a sphere of minimal radius which encloses most data points. In the input space, the hypersphere surface defines a set of contours that can be regarded as an estimate of the dataset domain exploited by the SVC algorithm. While providing a

description of the cluster cores, the SVDD method lacks information that connects each individual point to its membership cluster, hereby necessitating algorithms such as the one proposed in this paper to solve the cluster labeling process.

From a cluster analysis perspective, the SVC method has attractive properties. It allows controlling the number of clusters and their shape complexity by simply varying the Gaussian kernel bandwidth a. It also allows controlling the sensitivity to outliers with a single parameter

p representing the rejection rate for cluster boundaries. Finally, it defines clusters based on the

structural risk minimization principles that are more robust to outliers.

Ben-Hur proposed a simple labeling algorithm [1] (referred to as BENHUR in this paper) based on an interconnection test that assumes that a pair of patterns belongs to the same cluster if both can be connected by a virtual segment located within a common contour. This test verifies the inclusion of test points along the connecting segments, and is repeated for every combinations of pairs of points. This exhaustive test allows creating an adjacency matrix that is used to partition data points into distinct clusters. As described in Section 5, experiments show that the method suffers from intractable processing time on moderately sized datasets. Moreover, the interconnection test is inaccurate when dealing with high rejection rates p as it results in data points being excluded from the contours and thus considered wrongly as singleton clusters as they cannot be interconnected internally.

Lee partially addressed the high processing requirements of Ben-Hur's method by proposing an algorithm referred to here as LEE [3]. It simplifies the labeling process by first grouping together data points distributed aroung a same local minimum of the function describing the cluster contours. It then tests the interconnection between each pairs of local minima (similarly to BENHUR interconnection test) to deduce the inner partitioning of the dataset. Although less time consuming than BENHUR, Lee's method still suffers from high computational complexity due to the repetition of gradient descents starting from each point of the dataset. In addition, experiments presented in Section 5 show that Lee's method produces high labeling error rates when dealing with complex datasets displaying narrow or curved cluster contours.