Faculté des Sciences, 4 Avenue Ibn Battouta B.P. 1014 RP, Rabat – Maroc Tel +212 (0) 37 77 18 34/35/38, Fax : +212 (0) 37 77 42 61, http://www.fsr.ac.ma
THÈSE DE DOCTORAT
Présentée par
Hajar SAHBANI
Discipline : Sciences de l’ingénieur
Spécialité : Informatique et Télécommunications
Étude de la Complexité des Réseaux Planaires par l’Évaluation du
Nombre d'Arbres Couvrants.
Soutenue le 19/11/2016 Devant le jury
Président :
Pr. Driss ABOUTAJDINE PES, Faculté des Sciences de Rabat Examinateurs :
Pr. Mohamed EL MARRAKI PES, Faculté des Sciences de Rabat Pr. Abdellah IDRISSI PH, Faculté des Sciences de Rabat
Pr. Abdelah ADIB PES, Faculté des Sciences et Techniques, Mohammedia Pr. Ahmed HAMMOUCH
Invités :
PES, ENSET de Rabat
Pr. Noussaima EL KHATTABI PA, Faculté des Sciences de Rabat
A
VANT-
PROPOSLes travaux pr´esent´es dans ce rapport ont ´et´e r´ealis´es dans le cadre de mon docto-rat effectu´e au sein du Laboratoire de Recherche en Informatique et T´el´ecommunications (LRIT), `a la Facult´e des Sciences de Rabat, Universit´e Mohammed V de Rabat, sous la direction du Professeur Mohamed EL MARRAKI et le Co-Encadrement du Professeur Mohamed ESSALIH.
Je tiens tout d’abord `a remercier mon directeur de th`ese, Pr Mohammed EL MAR-RAKI, pour avoir toujours ´et´e disponible pour m’apporter son aide et mener `a bien ce travail de th`ese. Je le remercie aussi pour sa confiance, ses encouragements, et sa gen-tillesse. Je profite de cette occasion pour lui exprimer tous mes sentiments de respect et d’estime. Ces quelques mots ne sauraient exprimer mon sentiment de reconnaissance `a son ´egard.
Je remercie mon Co-encadrant, Pr Mohamed ESSALIH,Professeur assistant `a l’´Ecole Sup´erieur de Technologie de Safi pour ses aides et ses conseils durants ces trois ann´ee de th`ese.
Je remercie ´egalement Pr Driss ABOUTAJDINE, professeur de l’enseignement sup´ e-rieur `a la facult´e des Sciences de Rabat, membre de l’Acad´emie Hassan 2 des Sciences et Techniques, et directeur du Centre National pour la Recherche Scientifique et Technique, pour m’avoir fait l’honneur d’accepter de pr´esider mon jury de th`ese, d’avoir ouvert les portes de son laboratoire et m’avoir accept´e au sein de son ´equipe. Je voudrais lui expri-mer toute ma gratitude, et lui souhaite un tr`es bon r´etablissement.
Mes remerciements vont ´egalement `a Pr Abdellah IDRISSI professeur habilit´e `a la Facult´e des Sciences de Rabat, pour avoir accept´e d’ˆetre rapporteur de ma th`ese et pour ses conseils pr´ecieux.
Je remercie vivement Pr Abdellah ADIB professeur de l’enseignement sup´erieur `a la facult´e des Sciences et Techniques de Mohammedia pour l’int´erˆet qu’il a port´e `a cette th`ese en acceptant de la rapporter et `a assister en tant que membres de jury. Je le remer-cie aussi pour son temps et pour les conseils et remarques tr`es constructives qui m’ont aid´e `a am´eliorer ce rapport.
Je remercie aussi Pr Ahmed HAMMOUCH, professeur de l’enseignement sup´erieur `a l’´ecole Normale Sup´erieure de l’Enseignement Technique de Rabat(ENSET), pour m’avoir fait l’honneur d’examiner cette th`ese et d’assister `a la soutenance en tant que membre du jury.
Je remercie aussi Pr Noussaima EL KHATTABI, Professeur assistant `a la Facult´e des Sciences de Rabat, pour m’avoir fait l’honneur d’appartenir au jury de th`ese en tant que invit´ee.
Je tiens `a remercier ´egalement mon p`ere, ma m`ere, pour m’avoir soutenu tout au long de mes ´etudes, je ne saurais jamais ˆetre reconnaissante pour toute leurs confiance en moi, leurs affection, mais aussi leurs soutien ind´efectible. Merci `a vous. Je remercie par la mˆeme occasion ma grand-m`ere, mes soeurs Nawal, Sanaa, Saida et Ouafae ; mes beaux parents, mes beaux fr`eres et ainsi que toute ma famille pour leurs encouragements. Enfin, je remercie mon cher ´epoux pour son soutien quotidien ind´efectible et son enthousiasme contagieux `a l’´egard de mes travaux comme de la vie en g´en´eral. Notre couple a grandi en mˆeme temps que mon projet scientifique.
Un grand merci ´egalement `a tous les membres du laboratoire de recherche en Infor-matique et t´el´ecommunications, professeurs, docteurs et coll`egues doctorants, pour leurs soutien, encouragements. C’´etait un plaisir de partager ces ann´ees de th`ese avec vous.
R´
ESUM´
ELe domaine des r´eseaux a envahi tous les aspects de la vie : les r´eseaux de communi-cation, ´electriques, et sociaux sont devenus indispensables dans notre vie quotidienne. Les r´eseaux peuvent ˆetre consid´er´es comme des syst`emes compos´es d’un grand nombre d’enti-t´es qui interagissent entre elles, et qui peuvent ˆetre repr´esent´es par des graphes o`u chaque entit´e constitue un nœud du r´eseau et chaque interaction un lien entre deux nœuds. Il est donc important de souligner que les r´eseaux peuvent ˆetre consid´er´es comme des graphes dont nous pouvons calculer la complexit´e, la fiabilit´e et bien d’autres mesures que nous verrons dans cette th`ese.
La plupart des ´etudes sur les r´eseaux se basent sur les mesures de fiabilit´e. La fiabilit´e d’un r´eseau peut ˆetre mesur´ee par divers moyens. Dans le cas pratique, il faut imp´ erative-ment construire ce r´eseau, le programmer, et le faire fonctionner pour obtenir son temps de diffusion. Malheureusement, dans ce cas, le temps de calcul est une mesure impar-faite, car il d´epend de la machine, du langage de programmation, du compilateur utilis´e (constructeur, la version, compiler options choisies), et des donn´ees envoy´ees.
Il est donc pr´ef´erable d’avoir un moyen plus direct pour mesurer la fiabilit´e d’un r´eseau. L’un des moyens repose sur l’´enum´eration du nombre d’arbres couvrants dans la topo-logie `a ´evaluer. Ce nombre, appel´e complexit´e, du r´eseau ne d´epend pas des param`etres techniques du r´eseau, et peut ˆetre ´evalu´e de fa¸con th´eorique.
Cette th`ese porte sur l’´evaluation du nombre d’arbres couvrants d’un graphe d´ecrivant un r´eseau planaire. La difficult´e dans un r´eseau provient principalement du grand nombre de nœuds, ainsi que de la fa¸con dont ils sont interconnect´es.
e-rale qui permet le calcul de la complexit´e du r´eseau ´electrique ”Ligth”, cette formule combine l’utilisation des m´ethodes de suppression-contraction et ceux de d´ecomposition. Nous avons ensuite trait´e la cat´egorie des graphes planaires maximales ”Lantern” en uti-lisant le principe de dualit´e, apr`es avoir d´elimiter la classe de ces graphes en 3 cat´egories en prouvant qu’un graphe maximal ne peut contenir plus de deux sommets complets. Par la suite, nous nous sommes bas´es sur le nombre d’arbres couvrants pour ´etudier la robustesse de diff´erentes topologies de r´eseaux sociaux `a chaˆınes ferm´ees, ces topologies sont constitu´ees d’une s´erie de sous-graphes connect´es de mani`eres diff´erentes, afin d’en d´eduire quelle topologie r´esiste le plus `a la d´efaillance d’une connexion ou des suppressions de nœuds (ou liens), et par cons´equent celle qui peut ˆetre adopt´ee pour un acheminement plus fiable.
Il est `a noter que les travaux qui pr´ec`edent, traitent le cas des graphes simples, bien que de nombreux probl`emes `a int´erˆet pratique avec des connections multiples entre ses com-posants se repr´esentent par des graphes avec multiple arˆetes. Dans ce sens, nous avons d´evelopp´e une g´en´eralisation de la formule de Feussner pour traiter les graphes larges avec de multiples connections.
Mots-cl´es : R´eseau, graphe planaire, complexit´e, fiabilit´e, robustesse, arbre couvrant, suppression-contraction, d´ecomposition, graphe maximale, multiple arˆetes.
A
BSTRACTThe world surrounding us includes many networks that have invaded all aspects of life : communication networks, electrical networks and social networks, have become indis-pensable in daily life. Networks can be considered as systems composed of many entities interacting with each other. Each entity is represented by a network node and each inter-action by a link between two nodes. It is therefore important to stress that networks can be modeled by graphs of which we can compute the complexity, the reliability and other measures that we will see in this thesis.
Most networks studies are based on the reliability measures, It may be measured by va-rious means. In practice, it is imperative to construct this network, program it and operate it to get its broadcasting time. Unfortunately, in this case, computing time is an imperfect measure, as it depends on the machine, the programming language, the used compiler and sent data.
Therefore it is better to have a more direct means to measure the reliability of a network. One of the means relies on the enumeration of the number of spanning trees in the topo-logy to evaluate. This number, known as network complexity does not depend on network technical parameters and can be evaluated theoretically.
This thesis focuses on the evaluation of the number of spanning trees of a graph descri-bing a complex network. The difficulty in a complex network comes mainly from the large number of entities and the way they are interconnected.
We are interested first on the derivation of a general formula to compute the complexity of the electrical network ”Ligth”, this formula combines the use of deletion-contraction method and those of decomposition. Then we treated the category of the maximal planar
graphs ”Lantern” using the principle of duality, after having demonstrate that a maximal planar graph can not contain more than two complete vertices. Afterward, we based on the number of spanning trees to study the robustness of different topologies of closed chains social networks, these topologies are constituted by a series of sub-graphs connected in various ways, in order to deduce which one resists more to the failure of a connection or to deletions of nodes (or links), and consequently which can be adopted for a more reliable routing.
Note that previous works in computing spanning trees treat simple graphs (without loops or multiple edges), although numerous problems at practical interest with multiple connec-tions between its components are represented by graphs with multiple edges. In that sense, we developed a generalization of Feussner formula to treat large graphs with multiple connections.
Keywords : Complex network , planar graph, complexity, reliability, robustness, spanning tree, deletion-contraction, decomposition, maximal graph, multiple edges.
T
ABLE DES MATI`
ERESR´esum´e iii
Abstract v
Liste des figures xvi
Liste des tableaux xviii
Introduction g´en´erale 1
Liste des publications 7
Chapitre 1 : Les concepts de base de la th´eorie des graphes . . . 9
1.1 Origine de la notion de graphe . . . 10
1.2 D´efinition des graphes . . . 11
1.2.1 Notations . . . 11 1.2.2 Terminologie . . . 12 1.2.3 Isomorphismes et graphes . . . 13 1.2.4 Degr´es . . . 14 1.2.5 Graphes r´eguliers . . . 15 1.2.6 Graphes complets . . . 15 1.3 Sous-graphes . . . 16 1.3.1 Notations courantes . . . 16
1.4 La Connexit´e . . . 17
1.4.1 Chaˆınes et cycles, ´el´ementaires et simples . . . 17
1.4.2 Chemins et circuits, ´el´ementaires et simples . . . 18
1.4.3 Graphes connexes . . . 18
1.5 Graphes Planaires . . . 19
1.5.1 Relation d’Euler . . . 20
1.5.2 Crit`eres de graphes planaires . . . 21
1.5.3 Caract´erisation des graphes non planaires . . . 22
1.5.4 Caract´erisation des graphes planaires . . . 23
1.5.5 Graphe planaire maximal . . . 23
1.5.6 Graphe planaire ext´erieur . . . 24
1.6 Repr´esentation non graphique . . . 25
1.6.1 Matrice d’adjacence . . . 25
1.6.2 Matrice d’incidence . . . 27
1.6.3 Matrice des degr´es . . . 27
1.6.4 Matrice laplacienne . . . 28
1.7 Arbres et forˆets . . . 28
1.7.1 Arbres . . . 29
1.7.2 Forˆets . . . 30
1.7.3 Arbres couvrants d’un graphe . . . 31
1.7.4 Int´erˆet des arbres couvrants . . . 32
1.7.5 La complexit´e d’un graphe planaire . . . 35
1.8 Conclusion . . . 36
Chapitre 2 : M´ethodes d’´enum´eration des arbres couvrants d’un graphe planaire . . . 37
2.0.1 Probl´ematique . . . 38
2.1 Enum´eration d’arbres couvrants des graphes de mani`ere alg´ebrique . . . . 38
ix
2.1.2 M´ethode des valeures propres . . . 42
2.2 Enum´´ eration d’arbres couvrants des graphes de mani`ere combinatoire . . . 42
2.2.1 Formule de Cayley . . . 42
2.2.2 M´ethode de suppression et de contraction . . . 44
2.2.2.1 Formule de Feussner et sa g´en´eralisation . . . 44
2.2.3 La m´ethode de d´ecomposition . . . 46
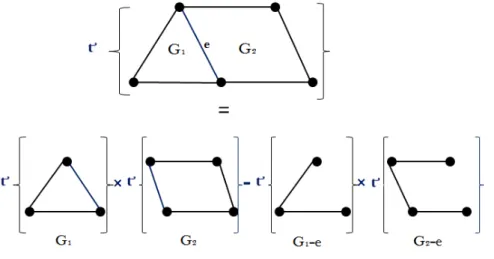
2.2.3.1 Les graphes planaire de type G = G1•G2 . . . 46
2.2.3.2 Les graphes planaire de type G = G1:G2 . . . 47
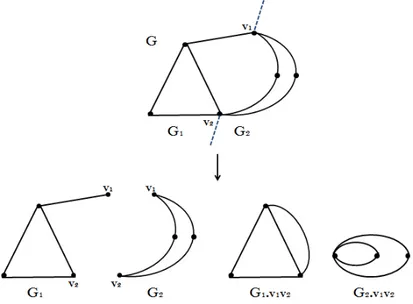
2.2.3.3 Les graphes planaire de type G = G1|G2 . . . 49
2.2.3.4 Les graphes planaire de type G = G1‡G2 . . . 51
2.2.4 Approche de dualit´e . . . 53
2.2.4.1 Le graphe dual . . . 53
2.2.4.2 Les arbres couvrants d’un graphe dual . . . 54
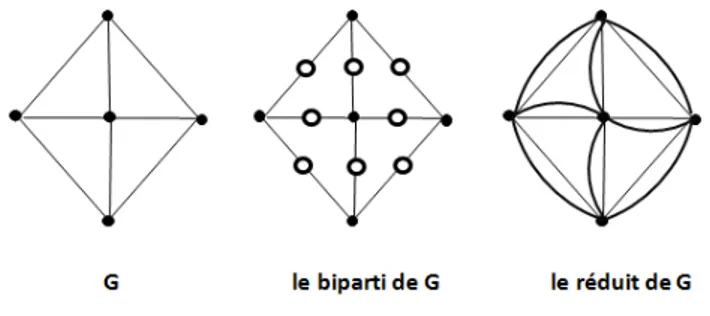
2.2.5 Approche de bipartition . . . 55
2.2.5.1 Le graphe biparti . . . 56
2.2.5.2 Les arbres couvrants du graphe biparti . . . 56
2.2.6 Approche de r´eduction . . . 57
2.2.6.1 Le graphe r´eduit . . . 57
2.2.6.2 Les arbres couvrants du graphe r´eduit . . . 57
2.3 Le nombre d’arbres couvrants de certaines familles des graphes planaires . 58 2.3.1 Le cas du graphe Fan . . . 58
2.3.2 Le cas du graphe wheel . . . 63
2.3.3 Le cas du graphe grille . . . 63
2.3.3.1 Les arbres couvrants de la grille `a deux lignes . . . 65
2.3.3.2 Les arbres couvrants de la grille circulaire . . . 68
2.4 Conclusion . . . 69
Chapitre 3 : Le calcul du nombres d’arbres couvrants des r´eseaux pla-naires . . . 71
3.1 L’´enum´eration des arbres couvrants du r´eseau ´electrique ext´erieur Light . 73
3.1.1 Introduction . . . 73
3.1.2 Le graphe planaire ext´erieur light . . . 73
3.1.3 Principaux r´esultats . . . 76
3.1.3.1 La complexit´e du graphe Xn. . . 76
3.1.3.2 La complexit´e du graphe Gn . . . 77
3.1.3.3 La complexit´e du graphe Hn. . . 78
3.1.3.4 La complexit´e du graphe An . . . 80
3.1.3.5 La complexit´e du light graphe Ln . . . 81
3.2 Etude de la robustesse des r´´ eseaux sociaux ferm´e en utilisant l’approche des arbres couvrants . . . 83
3.2.1 Introduction . . . 83 3.2.2 La complexit´e de Gn,k . . . 86 3.2.2.1 La complexit´e de Wk0 . . . 87 3.2.3 La complexit´e de Fn,k . . . 88 3.2.4 La complexit´e de Hn,k . . . 88 3.2.5 La complexit´e du graphe Mn,k . . . 90
3.2.6 Comparaison des diff´erents graphes . . . 91
3.3 Conclusion . . . 92
Chapitre 4 : Les graphes planaires maximaux . . . 93
4.1 Introduction . . . 93
4.1.1 Caract´erisation des sommets complets d’un graphe planaire maximal 94 4.2 Le graphe planaire maximal avec deux sommets complets . . . 96
4.2.1 Formule pour le nombre d’arbres couvrants du graphe ζn . . . 101
4.3 Le graphe planaire maximal sans aucun sommet complet . . . 103 4.3.1 Formule pour le nombre d’arbres couvrants du graphe Lantern Ln . 103
4.3.1.1 Les arbres couvrants du graphe biparti du maximal lantern 104 4.3.1.2 Les arbres couvrants du graphe r´eduit du maximal lantern 104
xi
4.4 Conclusion . . . 105
Chapitre 5 : L’´evaluation du nombre d’arbres couvrants des r´eseaux pla-naires non-simple `a multiple connections . . . 107
5.1 Les arbres couvrants des graphes avec multiple arˆetes . . . 108
5.2 La complexit´e du graphe Fan avec multiple arˆetes . . . 109
5.2.1 Le graphe Fan r´egulier `a k-multi-arˆetes . . . 109
5.2.2 Le graphe Fan `a (k0, k)-multi-arˆetes . . . 112
5.3 La complexit´e du graphe Wheel avec multiple arˆetes . . . 113
5.4 La complexit´e du graphe Fan avec multiple sommets . . . 114
5.5 La complexit´e du graphe Wheel W v(n,m) avec multiple sommets . . . 116
5.6 Conclusion . . . 116
Conclusion et perspectives 119 Bibliographie . . . 121
T
ABLE DES FIGURES1.1 Les ponts de Konigsberg et le graphe associ´e . . . 10
1.2 Le graphe G( V = v1, v2, v3, E = e1, e2, e3, e4, e5) . . . 12
1.3 Un graphe isomorphe `a celui de la figure 1.2. . . 13
1.4 Exemple des degr´es des sommets . . . 14
1.5 Les graphes complets . . . 15
1.6 Exemples de sous-graphes. . . 17
1.7 Les graphes cycle Ci. . . 18
1.8 Graphe chain´es. . . 18
1.9 Graphes connexe et non connexe . . . 19
1.10 Une repr´esentation plane d’un graphe. . . 20
1.11 les graphes complets K5 et K3,3 . . . 22
1.12 Graphes planaires maximal. . . 24
1.13 Graphe planaire ext´erieur . . . 25
1.14 Arbre couvrant d’un graphe planaire . . . 30
1.15 Les arbres couvrants du graphe carr´e . . . 32
1.16 Diffusion d’un message M dans une topologie . . . 34
1.17 Diffusion d’un messgae M selon un arbre couvrant d’une topologie . . . 35
2.1 le graphe F2 est sa complexit´e qui a 8 arbres couvrants . . . 38
2.2 Exemple de graphe dont on souhaite appliquer la m´ethode de kirchhoff. . . 41
2.3 Les 16 diff´erents arbres couvrants de K4 . . . 44
2.5 le graphe ´etoile et le graphe chaine . . . 47
2.6 le graphe G = G1:G2 . . . 47
2.7 Exemple des graphes G = G1:G2, G1, G2, G1.v1v2 et G2.v1v2 . . . 48
2.8 Cas des graphes particulier . . . 49
2.9 le graphe G = G1|G2 . . . 49
2.10 la complexit´e de G = G1|G2 . . . 50
2.11 le graphe G = G1‡G2 . . . 51
2.12 La construction du dual d’un graphe . . . 54
2.13 Un graphe G, son graphe biparti et son graphe r´eduit. . . 56
2.14 Le graphe Fn et le graphe Wn . . . 58
2.15 application du th´eor`eme 2.2.7 sur le graphe fan . . . 59
2.16 Repr´esentation des complexit´es des m´ethodes utilis´ees . . . 62
2.17 Le graphe planaire grille G4×5 . . . 65
2.18 La grille G2×n . . . 66
2.19 Les extensions ´etiquet´ees de E1 `a E8 . . . 66
2.20 La grille circulaire C2×6. . . 68
3.1 Graphe planaire ext´erieur . . . 74
3.2 Les graphes planaires ext´erieurs Gn . . . 74
3.3 Le graphe planaire ext´erieurs Ln . . . 75
3.4 Le graphe Xn . . . 76
3.5 calcul de τ (Xn) suivant le th´eor`eme 2.2.7 . . . 77
3.6 calcul de τ (Gn) suivant le th´eor`eme 2.2.7 . . . 78
3.7 a : Le graphe Hn, b : Le graphe Jn et c : Le graphe In. . . 79
3.8 calcul de τ (Hn) suivant le th´eor`eme 2.2.7 . . . 79
3.9 a : le graphe An, b : le graphe On et c : le graphe Nn. . . 80
3.10 calcul de τ (An) suivant le th´eor`eme 2.2.7 . . . 81
3.11 a : Light graph Ln et b : le graphe Mn . . . 81
xv
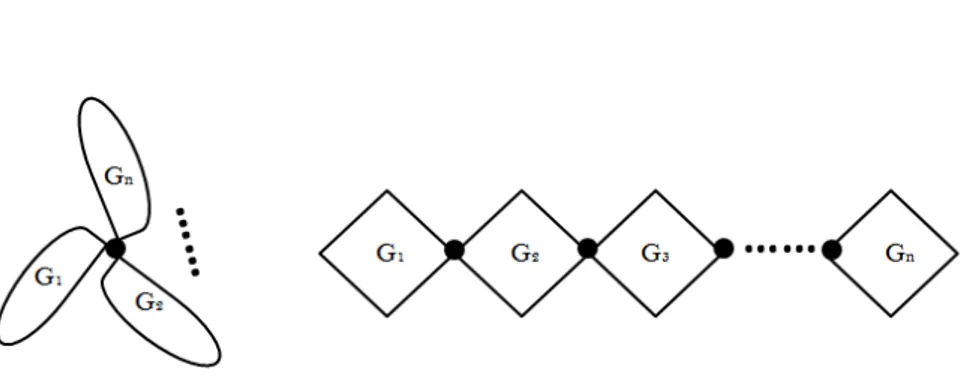
3.13 chaˆıne ferm´e de graphes planaires. . . 85
3.14 application de l’´equation du th´eor`eme 3.2.1 sur Gn,k . . . 87
3.15 Fk.uv et son dual Fk∗.uv . . . 87
3.16 la complexit´e de Wk0 en se basant sur la suppression-contraction d’une arˆete 88 3.17 application du th´eor`eme 2.2.5 `a Fn,k . . . 89
3.18 L’application d’´equation du th´eor`eme 3.2.1 sur Hn,k . . . 89
3.19 d´ecomposition de Mn,k bas´ee sur l’´equation du th´eor`eme 3.2.1 . . . 90
3.20 Les graphes G.uv, Fk, Nk+1 et son isomorphe. . . 91
4.1 Un graphe planaire maximal G1 avec 3 sommets complets. . . 95
4.2 Suppression de l’arˆete rouge du graphe G1. . . 95
4.3 Suppression des arˆetes verte et bleue. . . 96
4.4 Suppression des sommets de degr´e 3. . . 96
4.5 Le graphe K3,3 . . . 96
4.6 le graphe planaire maximal ζn . . . 97
4.7 le graphe planaire maximal ζ4 donne lieu `a 16 arbres couvrants . . . 102
4.8 le graphe planaire maximal lantern . . . 103
4.9 Ln et son graphe dual L∗n . . . 104
4.10 a : Ln b : Bip(Ln) and c : Red(Ln) . . . 104
5.1 Les graphes Fan et Wheel `a k multiple arˆetes . . . 108
5.2 Les graphes G, G − ek et G.uv. . . 109
5.3 La famille des graphes Fan avec k-multi-arˆetes : F0, F1,k, F2,k, F3,k, . . . ,Fn,k. . 110
5.4 Le graphe Fan `a (k0, k)-multi-arˆetes Fn,k0,k. . . 112
5.5 La complexit´e de F4,k+1,k. . . 113
5.6 La complexit´e de A4,k.. . . 114
5.7 Le Fan et le Wheel `a m-multi-sommets . . . 115
5.8 La construction du dual de Wheel W v(n,m) `a multi-sommets . . . 116
L
ISTE DES TABLEAUX2.1 Quelques valeurs de τ (Fn). . . 62
2.2 Quelques valeurs de τ (Wn). . . 63
3.1 Quelques valeurs des complexit´es des graphes Gn et Ln. . . 83
3.2 Quelques valeurs des complexit´es des r´eseaux ferm´es τ (G4,k), τ (F4,k), τ (H4,k)
et τ (M4,k). . . 91
4.1 Quelques valeurs de τ (ζn). . . 102
I
NTRODUCTION G´
EN´
ERALEContexte g ´en ´erale
La th´eorie des graphes est un domaine class´e comme une sous discipline de l’informa-tique th´eorique en raison de l’importance des algorithmes, et parfois comme sous-discipline des Math´ematiques en raison de sa proximit´e avec la Combinatoire. Il n’est null besoin aujourd’hui de souligner l’importance et l’utilit´e de la th´eorie des graphes. Science jeune, elle s’est essentiellement d´evelopp´ee au cours du XXe si`ecle, et s’est vite impos´ee par ses
liens avec d’autres branches des sciences et par l’´etendue de ses applications. La th´eorie des graphes nourrit en effet des liens ´etroits avec les math´ematiques, pures et appliqu´ees, l’informatique, en particulier avec l’algorithmique et la r´ecente th´eorie de la complexit´e, l’optimisation combinatoire et plus g´en´eralement ce qu’on appelle les math´ematiques de la d´ecision. On trouve aussi des applications plus ´eloign´ees, comme en sociologie. Il s’agit plutˆot d’une repr´esentation de la notion abstraite, comme un ensemble de points et de lignes reliant certains de ses points. On comprend que, par sa simplicit´e mˆeme, cette no-tion peut repr´esenter, ”mod´eliser”, des situations concr`etes tr`es vari´ees.
Les graphes sont actuellement l’outil privil´egi´e pour mod´eliser des ensembles struc-tur´es complexes. Ils sont indispensables si on veut repr´esenter et ´etudier des relations entre des objets. Leurs applications sont tr`es nombreuses : mod´elisation de l’´evolution d’un syst`eme dans le temps (en ´economie, en automatique), r´eseaux divers (´electriques, routiers, sociaux, de communications, ou d’adduction de l’eau), d´ecompositions en tˆaches d’un projet (en informatique, dans le bˆatiment et les travaux publics), liens entre
infor-mations dans les bases de donn´ees, etc.
Un premier exemple s’impose `a l’esprit : la repr´esentation d’un r´eseau de communica-tion, les points repr´esentant les centres o`u les nœuds du r´eseau et les lignes repr´esentant les liaisons. A partir de ce ”mod`ele” du r´eseau, on peut poser beaucoup de questions, par exemple : ce r´eseau permet-il une communication entre tous les centres, soit d’une mani`ere directe, soit en passant par des centres interm´ediaires ? Ou encore : ´etant donn´e deux centres, trouver les chemins qui les relient. En particulier trouver ”un plus court chemin” plus court du point de vue nombre de liaisons interm´ediaires, on parle ici d’un ”graphe non valu´e”. A propos de cette derni`ere question, la probl´ematique peut s’´elargir pour l’envoie d’une information d’un hˆote vers tous les autres, on souhaite donc minimiser le nombre de messages envoy´es et ´eviter la redondance. La structure de communication r´epondant `a ces crit`eres est l’arbre couvrant. Il n’y a plus qu’un message qui circule par arˆete, donc la diffusion d’informations par arbre couvrant est plus performante et moins redondante que par graphe. Plus le graphe a plusieurs arbres couvrants plus il est fiable et robuste en cas de faille ou de panne.
Un premier probl`eme que l’on peut se poser en parlant des arbres couvrant est le d´enombrement des diff´erents arbres couvrants d’un graphe (r´eseau). Ce nombre est un invariant important conduisant `a des r´esultats et des applications int´eressantes. Il repr´ e-sente une mesure importante de la fiabilit´e d’un r´eseau.
Si un graphe n’a aucun arbre couvrant, c’est qu’il n’est pas connexe, et s’il n’en a qu’un seul, on dit que c’est un arbre. On note le nombre d’arbres couvrants d’un graphe G par τ (G), nomm´e aussi la complexit´e de G.
La recherche du nombre d’arbres couvrants dans un graphe a une longue histoire qui remonte `a 1847, avec le th´eor`eme de Kirchhoff (connu en anglais sous le nom ”Matrix Tree Theorem”) qui exprime sous forme de d´eterminant du Laplacien le nombre d’arbres couvrants d’un graphe (Kirchhoff, 1847). Cela nous donne un moyen d’obtenir le nombre d’arbres couvrants de tout les graphes. Sauf que, pour les graphes larges, le calcul du
3
d´eterminant devient une tˆache difficile voir impossible, et la r´esolution de ce probl`eme revient alors `a d´evelopper une technique qui permet ce calcul sans passer par le d´ etermi-nant. Ainsi, Cayley (1889) a d´emontr´e une formule r´ecursive pour le graphe complet Kn
qui compte nn−2 arbres couvrants (Cayley, 1889). ´Egalement, nous trouvons la m´ethode combinatoire de Feussner (1902) qui se base sur la suppression et la contraction d’une arˆete simple pour calculer la complexit´e d’un graphe (Feussner, 1902). Cette m´ethode a ´
et´e g´en´eralis´ee pour traiter le cas des graphes contenant des chemins simples (Modabish et El Marraki, 2011).
La plupart des recherches qui se sont pench´ees sur le calcul du nombre d’arbres cou-vrants, se sont consacr´ees `a la d´etermination exacte des formules pour le nombre d’arbres couvrants dans de nombreux types de graphes sp´eciaux. Prenons l’exemple de Myers, Bog-danowicz and Haghighi qui ont d´eriv´es des formules exacte pour calculer τ (Fn) et τ (Wn) ;
le nombre d’arbres couvrants des graphes Fan et Wheel (Myers, 1971; Bogdonowicz, 2008; Haghighi et Bibak, 2009).
L’´enum´eration des arbres couvrants d’un graphe a fait l’objet de plusieurs ´etudes dans l’histoire des math´ematiques. Cependant, ce domaine est encore un domaine de recherche tr`es actif, car le nombre d’arbres couvrants est un invariant tr`es important du fait de l’int´erˆet qu’il porte pour de diff´erentes disciplines, tels que la fiabilit´e des r´eseaux de communication (Atajan et Inaba, 2004; Aggarwal et Rai, 1981; Li et Huang, 1999), la robustesse des r´eseaux sociaux (Lemmouchi et al., 2013), la capacit´e de synchronisation (Takashi et Motter, 2006) et l’´etude des marches al´eatoires (Marchal, 2000).
Contributions et organisation
La pr´esente th`ese se positionne dans le domaine de l’´etude des graphes planaires. Elle s’int´eresse principalement `a l’´etude du nombre d’arbres couvrants des r´eseaux complexes qui repr´esente une mesure importante de la fiabilit´e, en se basant sur des techniques com-binatoires.
Cette th`ese est organis´ee comme suit :
chapitre 1 : Les concepts de base de la th´eorie des graphes. Dans ce chapitre, nous don-nerons, apr`es une introduction sur l’origine de la notion de graphe, quelques d´efinitions et terminologies du vocabulaire de base des graphes qui va ˆetre utilis´e tout au long du rapport. Nous aborderons diff´erents types de graphes entre autres : les graphes planaires, les arbres et les arbres couvrants, avec leurs propri´et´es et des exemples ainsi que leurs re-pr´esentations non graphique. En pr´ecisant l’int´erˆet des arbres couvrants dans le domaine pratique, et qui a fait de leur ´etude un invariant tr`es important.
chapitre 2 : M´ethodes d’´enum´eration des arbres couvrants d’un graphe planaire. Dans ce deuxi`eme chapitre, nous pr´esentons les diff´erentes techniques de calcul du nombre d’arbres couvrants d’un graphe planaire : la m´ethode de Kirchhoff, la formule de Cayley, la m´ethode de suppression et de contraction ainsi que sa g´en´eralisation, les m´ethodes de d´ecompositions et enfin les m´ethodes de dualit´e, de bipartition et de r´eduction. Toutes ces diff´erentes m´ethodes jouent un rˆole tr`es important dans la d´etermination du nombre d’arbres couvrants des graphes planaires. Cependant, nous pr´eciserons les limites de cha-cune d’elles.
chapitre 3 : Le calcul du nombre d’arbres couvrants des r´eseaux planaires complexes. Ce chapitre traite en premi`ere partie l’´enum´eration des arbres couvrants d’un r´eseau ´ elec-trique complexe nomm´e light (Sahbani et El Marraki, 2014c). Et en deuxi`eme partie il se base sur l’approche des arbres couvrants pour pr´esenter une ´etude de robustesse des r´eseaux sociaux `a chaˆıne ferm´ees (Sahbani et El Marraki, 2015), (Sahbani et El Marraki, 2016c), (Sahbani et El Marraki, 2016a).
chapitre 4 : Les graphes planaires maximaux. Ce chapitre traite une cat´egorie de graphes bien sp´ecifique ; celle des graphes maximales. Nous avons prouv´e dans un premier lieu qu’un graphe maximal ne peut contenir plus que deux sommets complets. Ensuite, nous nous sommes int´eress´es `a l’´etude des formules exactes calculant le nombre d’arbres cou-vrants dans un graphe maximal (Sahbani et El Marraki, 2014a).
chapitre 5 : L’´evaluation du nombre d’arbres couvrants des r´eseaux planaires non-simple `
a multiple connections. Les travaux de recherche sur les techniques facilitant le d´ enom-brement des arbres couvrants traitent le cas des graphes simples, bien que de nombreux
5
probl`emes `a int´erˆet pratique ne peuvent ˆetre repr´esent´es que par des graphes avec connec-tions multiples. Ce dernier chapitre pr´esente notre derni`ere contribution ou nous propo-sons une g´en´eralisation de la formule de Feussner pour traiter les graphes larges avec de multiples connections entre ses composants (Sahbani et El Marraki, 2016b).
L
ISTE DES PUBLICATIONSRevues internationales
Hajar Sahbani et Mohamed El Marraki (2016). On the number of spanning trees in graphs with multiple edges. Journal of Applied Mathematics and Computing, pages 1-11. Springer.
Hajar Sahbani et Mohamed El Marraki (2014). Ennumeration of the number of spanning trees in the lantern maximal planar graph. Applied Mathematical Sciences, 8(74), pages 3661-3666. Hikari.
Hajar Sahbani et Mohamed El Marraki (2014). Formula for the number of spanning trees in light graph. Applied Mathematical Sciences, 8(18), pages 865-874. Hikari.
Conf ´erences internationales
Hajar Sahbani et Mohamed El Marraki (2016). Robustness study in closed social networks using spanning tree approach. In International Colloquium on Information Sience and Technology (CIST). Tanger, Morocco. IEEE.
Hajar Sahbani et Mohamed El Marraki (2016). Complexity of closed networks based on spanning tree approach. In International Conference on Multimedia Computing and Systems (ICMCS). Marrakech, Morocco. IEEE.
Hajar Sahbani et Mohamed El Marraki (2015). Reliability of the closed-chain-fan social network. In 3rd International Conference In Future Internet of Things and Cloud (FiCloud), pages 722-725. Rome, Italie. IEEE.
Conf ´erences nationales
Hajar Sahbani et Mohamed El Marraki (2015). ´Etude de la fiabilit´e d’un r´eseau planaire par le nombre d’arbres couvrants. Les journ´ees URAC du LRIT. l’Institut Scientifique - Rabat.
Hajar Sahbani et Mohamed El Marraki (2014). Enumeration of spanning trees in the fan planar network. In International Workshop on WIreless Networks and mobile COMmunications (WinCom). Faculty of Science - Rabat.
Hajar Sahbani et Mohamed El Marraki (2014). Several methods to calculate the number of spanning trees in the n-fan planar graphe. Journ´ees Doctorales en Tech-nologies de l’Information et de la Communications (JDTIC). ENSIAS - Rabat. Hajar Sahbani et Mohamed El Marraki (2014). Enumeration of the number of
span-ning trees of planar graphs. Les journ´ees Doctoriales de la FSR (JDFSR). Faculty of Science - Rabat.
Chapitre
1
L
ES CONCEPTS DE BASE DE LA TH´
EORIE DES GRAPHESL
bl`es graphes repr´emes combinatoires, qui seraient, sans cela, difficilement abordables par des tech-esentent un instrument puissant pour mod´eliser de nombreux pro-niques classiques comme l’analyse math´ematique. En plus de son existence en tant qu’objet math´ematique, le graphe est aussi une structure de donn´ees puissante pour l’in-formatique. Ce premier chapitre pr´esente apr`es une introduction sur l’origine de la notion de graphe, le vocabulaire de base des graphes qui va ˆetre utilis´e tout au long du rapport. Comprendre et utiliser les graphes n’est pas difficile, `a condition d’en connaitre le langage. Ce langage peut sembler rebutant au premier abord, car il contient de nombreux termes sp´ecialis´es. Comme les graphes sont utilis´es dans de nombreux domaines, en particulier en informatique, les d´efinitions et parfois aussi la terminologie sont assez variables dans la litt´erature aussi bien francophone qu’anglophone. Les choix faits ici pour les d´efinitions et la terminologie nous paraissent les plus raisonnables et les plus conformes `a la tradition de la th´eorie, et les concepts restent de toutes fa¸cons les mˆemes.1.1 Origine de la notion de graphe
Les graphes constituent une m´ethode de pens´ee qui permet de mod´eliser une grande vari´et´e de probl`emes concrets en se ramenant `a l’´etude de sommets et d’arcs. C’est mˆeme `
a partir de certains d’entre eux que la ”Th´eorie des Graphes” est n´ee et s’est d´evelopp´ee. On cite souvent un probl`eme qui date du XV IIIe si`ecle et que le math´ematicien Euler a r´esolu, le bien connu ”probl`eme des ponts de Konigsberg”. Dans cette ville, aujourd’hui enclave russe dans les pays baltes et appel´ee Kaliningrad, il y a sept ponts dispos´es sur le fleuve comme le montre la figure 1.1. A l’´epoque les habitants se demandaient s’il ´
etait possible de traverser tous ces ponts, chacun une fois lors d’une mˆeme promenade avec retour au point de d´epart. Le math´ematicien Euler s’est int´eress´e au probl`eme et a explicit´e la condition qui faisait que ce n’´etait pas possible ; d’o`u le qualificatif d’eul´erien aujourd’hui utilis´e.
La mod´elisation du probl`eme en un graphe se fait de la mani`ere suivante : On associe `a
Figure 1.1 – Les ponts de Konigsberg et le graphe associ´e
chaque quartier de la ville un sommet et `a chaque pont une arˆete reliant les deux sommets associ´es aux quartiers reli´es par ce pont. Mais historiquement le probl`eme qui a ´et´e le principal moteur de la conceptualisation de la notion de graphe et de son d´eveloppement th´eorique a ´et´e le fameux ”probl`eme des quatre couleurs”. Il date du milieu du XIXe si`ecle lorsqu’un ´etudiant anglais, du nom de Guthrie, remarqua qu’il ´etait possible de colorier une carte de son pays avec seulement quatre couleurs, en respectant la condition que deux r´egions voisines, c’est-`a-dire ayant une fronti`ere commune, re¸coivent des couleurs diff´erentes. Il se demanda si la propri´et´e ´etait g´en´erale, `a savoir si toute carte g´eographique dessin´ee sur le plan pouvait ˆetre colori´ee en au plus quatre couleurs de telle sorte que deux r´egions voisines aient des couleurs diff´erentes. On se rend compte que quatre couleurs peuvent ˆetre effectivement n´ecessaire.
1.2. D ´EFINITION DES GRAPHES 11
La fa¸con d’associer un graphe `a ce probl`eme est simple : un point dans chaque r´egion et une ligne reliant deux de ces points lorsque les r´egions correspondantes sont voisines, lignes traversant une fois la ligne fronti`ere. D’abord le graphe ainsi d´efini est ”planaire” c’est-` a-dire peut ˆetre dessin´e sur le plan sans croisement de lignes en dehors des points qu’elles relient. Ensuite ce probl`eme du coloriage de la carte revient `a attribuer des couleurs aux points du graphe de telle sorte que deux points reli´es par une ligne aient des couleurs diff´erentes. D’abord le graphe ainsi d´efini est ”planaire” c’est-`a-dire peut ˆetre dessin´e sur le plan sans croisement de lignes en dehors des points qu’elles relient. Ce th´eor`eme des quatre couleurs exprime que tout graphe planaire peut ˆetre ainsi colori´e ses sommets en utilisant au plus quatre couleurs.
Nous allons maintenant formaliser cette notion de graphe, les points vont s’appeler les ”sommets” et les lignes les ”arˆetes”.
1.2 D ´efinition des graphes
Un graphe non orient´e G est d´efini par deux ensembles finis : un ensemble V , non vide, d’´el´ement appel´es sommets, un ensemble E (qui peut ˆetre vide) d’´el´ements appel´es arˆetes, avec, associ´es `a chaque arˆete e, deux sommets x et y distincts ou non, appel´es les extr´emit´es de e.
1.2.1 Notations
On ´ecrit G = (V, E). La donn´ee d’un ensemble V des sommets est not´e V (G) et l’ensemble des arˆetes E ((x, y)∈E⇔(y, x)∈E) not´e E(G). On note habituellement par n le cardinal de V , |VG| = n qui est le nombre de sommets du graphe, et par m le cardinal
de E, |EG| = m , c’est-`a-dire le nombre d’arˆetes du graphe.
Graphiquement, on dessine les graphes sur un plan, les sommets sont repr´esent´es par des points et les arˆetes par des lignes reliant les extr´emit´es comme le montre la figure 1.2. On notera que la disposition des points et la longueur ou la forme (rectiligne ou incurv´ee) des lignes n’a aucune importance. Seule l’incidence des diff´erentes arˆetes et sommets compte.
Figure 1.2 – Le graphe G( V = v1, v2, v3, E = e1, e2, e3, e4, e5)
En observant le graphe de la figure 1.2, on peut extraire quelques caract´eristiques, notamment, Le nombre de sommets |VG| = 3, et celui des arˆetes |EG| = 5. A l’arˆete e2
sont associ´es les sommets extr´emit´es v1 et v2, `a e3 sont associ´es v1 et v3, `a e5 sont associ´es
v2 et v3, `a e5 sont ´egalement associ´es v2 et v3, `a l’arˆete e1 enfin est associ´e deux fois le
sommet v1 (cas d’une boucle).
Il y a ´evidement plusieurs de telle repr´esentations possibles d’un mˆeme graphe donn´e, due au diff´erentes fa¸cons de placer les sommets et de tracer les arˆetes dans le plan.
1.2.2 Terminologie
En pr´esence d’une arˆete e = (x, y) qui peut ˆetre not´ee simplement xy, on dit que x et y sont les extr´emit´es de e, que e est incidente en x et en y, et que y est un successeur ou voisin de x (et vice versa). On peut avoir x = y, dans ce cas l’arˆete e est une boucle, on dit qu’un graphe est sans boucle si E ne contient pas d’arˆete de la forme (x, x), c’est-`a-dire joignant un sommet `a lui-mˆeme. Deux arˆetes e et e0, ou plus, peuvent avoir les mˆemes ex-tr´emit´es x et y, on dit alors qu’elles sont parall`eles ou qu’on a une arˆetes multiple (double, triple, etc., suivant le nombre d’arˆetes) entre x et y. Le nombre de sommets est appel´e ordre du graphe.
Un graphe ne poss´edant pas de boucle ni d’arˆetes parall`eles (deux arˆetes distinctes joi-gnant la mˆeme paire de sommets) est appel´e graphe simple ou 1-graphe. En revanche un p-graphe est un graphe pour lequel il existe p arˆetes de la forme (x, y) (trait´e dans le dernier chapitre ).
1.2. D ´EFINITION DES GRAPHES 13
1.2.3 Isomorphismes et graphes
On d´efinit de fa¸con naturelle un isomorphisme de deux graphes non orient´es Gi =
(Vi, Ei), i = 1, 2, par une bijection f : V1 → V2 qui est tel que
(x, y) ∈ E1 ⇔ (f (x), f (y)) ∈ E2
(resp. tel que (x, y) ∈ E1 ⇔ f (x), f (y) ∈ E2). Cette d´efinition s’adapte au cas de multi-graphes orient´es. Deux multi-graphes Gi = (V i, Ei), i = 1, 2, sont isomorphes s’il existe
une bijection f : V1 → V2 tel que (x, y) est un arc de multiplicit´e k de G1 si et seulement
si (f (x), f (y)) est un arc de multiplicit´e k de G2 (Balakrishnan, 1997). Bien ´evidemment,
une telle application f est qualifi´ee d’isomorphisme de graphes. Bien sur, si f est un isomorphisme, il en va de mˆeme pour f−1 (voir un exemple `a la figure 1.3).
Figure 1.3 – Un graphe isomorphe `a celui de la figure 1.2.
Deux graphes isomorphes sont en fait identiques quant `a leurs structures de graphe, ils ont exactement les mˆemes propri´et´es et ne se distinguent que par leurs ensembles d’´el´ e-ments, sommets et arˆetes, concr`etement par les noms donn´es `a ces ´el´ements. La figure 1.3 illustre un graphe isomorphe `a celui de la figure 1.2, Des bijections qui d´efinissent un iso-morphisme entre ces deux graphes se devinent ais´ement : le sommet s1 est n´ecessairement
associ´e au sommet v1 du graphe pr´ec´edent, `a cause de la boucle a1 associe `a e1 du graphe
pr´ec´edent, la paire de sommets s2, s3 doit ˆetre associ´ee `a la paire v2, v3, par exemple s2 `a
1.2.4 Degr ´es
On appelle degr´e (ou valence) d’un sommet x d’un graphe, et on note deg(x), le nombre d’arˆetes incidentes `a ce sommet, c’est-`a-dire ayant x comme extr´emit´e. Une boucle sur un sommet compte double.
Dans un graphe simple, on peut aussi d´efinir le degr´e d’un sommet comme ´etant le nombre de ses voisins (la taille de son voisinage).
Un sommet est dit isol´e si son degr´e est nul (Fournier, 2011).
Dans le multigraphe ci-contre (figure 1.4), nous avons les degr´es : deg(a) = 2, deg(b) = 3, deg(c) = 4, deg(d) = 0 et deg(e) = 3.
Figure 1.4 – Exemple des degr´es des sommets
En se basant sur le nombre des degr´es des sommets d’un graphe, nous pouvons calculer le nombre de ses arˆetes, la formule permettant ceci est consid´er´ee comme ´etant la premi`ere proposition de la th´eorie des graphes. Chaque arˆete est incidente `a deux sommets ; alors :
Proposition 1.2.1. Si G est un graphe ou multi-graphe, alors la somme des degr´es des sommets de G est ´egale `a deux fois le nombre d’arˆetes.
X
v∈VG
deg(v) = 2|EG|
Dans le graphe de la Figure 1.4 nous avons le nombre d’arˆetes est 6, et la somme des degr´es des sommets de ce graphe est 12.
Le degr´e maximal d’un graphe, not´e ∆(G), et le degr´e minimal de ce graphe, not´e δ(G), sont respectivement le maximum et le minimum des degr´es de ses sommets. Dans le graphe de la Figure 1.4, le degr´e maximal est 4 et le degr´e minimal est 0.
1.2. D ´EFINITION DES GRAPHES 15
Remarque 1.2.1. Il r´esulte de la proposition 1.2.1 les in´egalit´es suivantes :
nδ(G) ≤ 2m ≤ ∆(G)
Dans un graphe r´egulier, tous les sommets ont le mˆeme degr´e, et on peut donc parler du degr´e du graphe.
1.2.5 Graphes r ´eguliers
Un graphe G est dit r´egulier lorsque les degr´es de ses sommets sont tous ´egaux. On peut pr´eciser le degr´e commun k des sommets en disant k-r´egulier (Fournier, 2011). Les graphes 3-r´eguliers sont dits cubiques.
Remarque 1.2.2. On a pour un graphe G k-r´egulier la relation suivante entre k et les nombres de sommets n et d’arˆetes m :
nk = 2m
C’est une relation tr`es utile, qui se d´eduit imm´ediatement de la proposition 1.2.1
1.2.6 Graphes complets
Les graphes complets sont les graphes simples tels que deux sommets distinct quel-conques sont reli´es par une arˆete. Comme graphe non orient´e, un graphe complet est simplement d´etermin´e par son nombre n de sommets (Fournier, 2011), il est g´en´eralement not´e Kn (voir figure 1.5 pour le cas n = 1, 2, 3, 4, 5).
Figure 1.5 – Les graphes complets
Notons que le nombre d’arˆetes m de Kn est ´egale au coefficient binomial
n 2 ,
c’est-`
a-dire : m = n(n−1)2 du fait que Knest un graphe r´egulier de degr´e n − 1 et donc il contient
n(n − 1)/2 arˆetes.
1.3 Sous-graphes
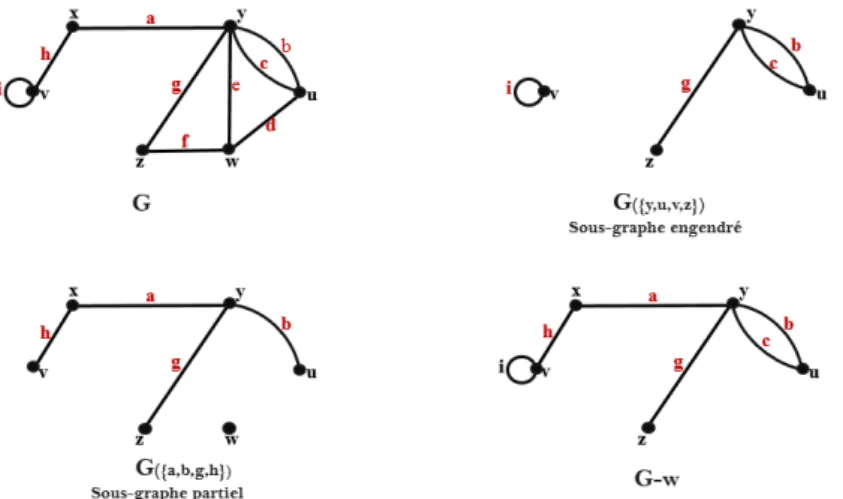
Soit G = (V, E) un graphe. Un sous-graphe de G est un graphe de la forme H = (X, Y ) o`u X ⊂ V et Y ⊂ E sont tels que toute arˆete de Y a ses extr´emit´es dans X. Notons que le fait qu’un sous-graphe est un graphe implique cette propri´et´e que toute arˆete de Y a ses extr´emit´es dans X.
Un sous-graphe H de G est dit engendr´e (ou induit), et on peut le pr´eciser par un ensemble de sommets X ∈ V , s’il est de la forme H = (X, Y ) o`u Y est l’ensemble des arˆetes de E qui ont leurs extr´emit´es dans X. On note ce sous-graphe GX.
Un sous-graphe H de G est dit couvrant, si X = V . On dit aussi dans ce cas que H est un graphe partiel de G. On peut pr´eciser que le graphe partiel engendr´e par Y , c’est le graphe (V, Y ) et on le note G(Y ) (Fournier, 2011).
La figure 1.6 donne des exemples de sous-graphes.
1.3.1 Notations courantes
G − X o`u X ⊂ V : sous-graphe de G engendr´e par V/X (sous-graphe obtenu en enlevant de G les sommets de X, avec leurs arˆetes incidentes).
G − Y o`u Y ⊂ E : graphe partiel de G engendr´e par E/Y (graphe partiel de G obtenu en enlevant les arˆetes de Y ).
On ´ecrira en particulier : G − x `a la la place de G − v pour v ∈ V et G − y `a la la place de G − e pour e ∈ E.
Par extension de ce dernier cas, on note parfois G + e le graphe obtenu en ajoutant `a G une nouvelle arˆete e (en pr´ecisant bien sˆur ses extr´emit´es dans G).
1.4. LA CONNEXIT ´E 17
Figure 1.6 – Exemples de sous-graphes.
1.4 La Connexit ´e
1.4.1 Chaˆınes et cycles, ´el ´ementaires et simples
Une chaˆıne est une s´equence finie et altern´ee de sommets et d’arˆetes, d´ebutant et finissant par des sommets, tel que chaque arˆete est incidente avec les sommets qui l’en-cadre dans la s´equence. Une arˆete ne doit pas intervenir plusieurs fois dans la s´equence contrairement `a un sommet.
Le premier et le dernier sommet sont appel´es (sommets) extr´emit´es de la chaˆıne. La longueur de la chaˆıne est ´egale au nombre d’arˆetes qui la compose.
Si aucun des sommets composant la s´equence n’apparait plus d’une fois, la chaˆıne est dite chaˆıne ´el´ementaire.
Si aucune des arˆetes composant la s´equence n’apparait plus d’une fois, la chaˆıne est dite chaˆıne simple.
Un cycle est une chaˆıne dont les extr´emit´es co¨ıncident (voir Figure 1.7).
Un cycle ´el´ementaire (tel que l’on ne rencontre pas deux fois le mˆeme sommet en le par-courant) est un cycle minimal pour l’inclusion, c’est-`a-dire ne contenant strictement aucun autre cycle (Diestel, 1997),(Fournier, 2011).
Figure 1.7 – Les graphes cycle Ci.
1.4.2 Chemins et circuits, ´el ´ementaires et simples
Un chemin est une s´equence finie et altern´ee de sommets et d’arcs, d´ebutant et finissant par des sommets, tel que chaque arc est sortant d’un sommet et incident au sommet suivant (voir Figure 1.8).
Si aucun des sommets composant la s´equence n’apparait plus d’une fois, le chemin est dit chemin ´el´ementaire.
Si aucune des arˆetes composant la s´equence n’apparait plus d’une fois, le chemin est dit chemin simple.
Un circuit est un chemin dont les extr´emit´es co¨ıncident.
En parcourant un circuit ´el´ementaire, on ne rencontre pas deux fois le mˆeme sommet.
Figure 1.8 – Graphe chain´es.
1.4.3 Graphes connexes
De mani`ere intuitive, la notion de connexit´e est triviale. Un graphe est connexe si l’on peut atteindre n’importe quel sommet `a partir d’un sommet quelconque en parcourant diff´erentes arˆetes. De mani`ere plus formelle, nous avons :
Un graphe G est connexe s’il existe au moins une chaˆıne entre une paire quelconque de sommets de G (Tutte, 1966),(Lando et Zvonkin, 2004), (Fournier, 2011). La v´erification de la connexit´e d’un graphe est l’un des premiers probl`emes de la th´eorie des graphes.
1.5. GRAPHES PLANAIRES 19
Figure 1.9 – Graphes connexe et non connexe
1.5 Graphes Planaires
La fa¸con de repr´esenter les graphes sur le plan a ´et´e tr`es ´etudi´ee, particuli`erement pour les applications : repr´esentation des graphes sur un ´ecran d’ordinateur par exemple, ou encore conception de circuits imprim´es. Un cas particulier remarquable de graphe est celui o`u on peut imposer `a une repr´esentation plane du graphe la condition que deux lignes arˆetes ne se coupent pas, en dehors d’extr´emit´es communes, qui sont les graphes planaires, qui ont jou´e un rˆole important dans la th´eorie du fait de leurs propri´et´es remarquables (Aldous et Robin, 2000).
Il faut distinguer un graphe G, notion abstraite, et une repr´esentation de celui-ci sur le plan, comme on vient de la d´efinir , appel´ee repr´esentation plane de G. Un graphe planaire est donc un graphe qui admet une repr´esentation plane. Une repr´esentation planaire du graphe G est la donn´ee, dans le plan, d’un ensemble de points de mˆeme cardinal que V , reli´es deux `a deux par des courbes continues du plan lorsque les sommets correspondant du graphe sont reli´es, et tels que ces courbes ne se croisent pas (Lando et Zvonkin, 2004). Il y a en g´en´eral beaucoup de repr´esentations planes possibles d’un graphe donn´e (ne serait-ce que par ”d´eformations” continues dans le plan des lignes repr´esentant les arˆetes) (Nishizeki et Rahman, 2004).
On appelle faces d’une repr´esentation plane les parties connexes, au sens de la topologie du plan, d´ecoup´ees dans le plan par cette repr´esentation. L’une des faces est non born´ee, appel´ee la face ext´erieure.
Exemple 1.5.1. Si l’on consid`ere le cube comme un graphe(Figure 5.9), une repr´ esenta-tion de perspective classique (`a gauche) ne sera pas planaire. Ceci pourrait nous inciter `
a penser que le graphe correspondant ne l’est pas non plus. Il n’en est rien, comme le montre la repr´esentation de droite du mˆeme graphe, planaire cette fois.
Figure 1.10 – Une repr´esentation plane d’un graphe.
Pour un graphe planaire G, une face F de G est une r´egion maximale du plan d´elimit´ee par un ensemble d’arˆetes de G, et qui n’en contient aucune. Le degr´e de F , not´e deg(F ), est le nombre d’arˆetes de G qui bordent F (Nishizeki et Rahman, 2004).
Dans la repr´esentation planaire pr´ec´edente du graphe du cube, nous avons exactement 6 faces, num´erot´ees de 1 `a 6. Toutes sont bord´ees par 4 arˆetes du graphe exactement, c’est-`a-dire qu’elles sont toutes de degr´e 4.
Premi`ere propri´et´e de planarit´e
Proposition 1.5.1. Soit G un graphe planaire et m le nombre d’arˆetes de G. Alors
X
f f ace
deg(f ) = 2m
Cette propri´et´e est presque ´evidente : elle n’exprime ni plus ni moins que le fait qu’une arˆete donn´ee du graphe G borde exactement 2 faces. Elle contribue pour 1 au degr´e de chacune.
Lorsque l’on calcule la somme X
F f ace
deg(F ), on aura donc compt´e exactement deux fois chaque arˆete du graphe.
Toujours dans le cas de notre repr´esentation planaire du graphe du cube, les 6 faces sont toutes de degr´e 4, soit un total de 6.4 = 24, et nous avons bien 24/2 = 12 arˆetes.
1.5.1 Relation d’Euler
Proposition 1.5.2. ´Etant donn´e une repr´esentation plane d’un graphe planaire connexe G, f le nombre de faces de cette repr´esentation, n le nombre de sommets et m le nombre d’arˆetes de G, on a :
1.5. GRAPHES PLANAIRES 21
n − m + f = 2
La relation suivante peut parfois ˆetre utilis´ee pour v´erifier qu’un graphe donn´e n’est pas planaire. En effet, c’est principalement grˆace `a ce r´esultat que nous montrerons que K5 n’est pas planaire. Cette relation est en fait connue depuis longtemps, bien avant les
graphes.
Exemple 1.5.2. Reprenons notre exemple du cube de la Figure 5.9 : il v´erifie n = 8, m = 12, et f = 6. Et l’on a bien 8 − 12 + 6 = 2.
1.5.2 Crit `eres de graphes planaires
Corollaire 1.5.1. Si G est un graphe simple connexe et planaire tel que n ≥ 3, alors on a (Diestel, 1997) :
m ≤ 3n − 6 Si de plus G est sans triangle, alors : m ≤ 2n − 4.
D´emonstration. Soit en effet G un graphe simple planaire connexe. G est simple, il n’y a pas de ”boucle” ni d’arˆete multiple, donc toute face est bord´ee par au moins 3 arˆetes.
C’est-`a-dire que pour toute face f, on a deg(f) ≥ 3. Si l’on somme cette in´egalit´e sur toutes les faces du graphe, on obtient X
f f ace
deg(f ) ≥ 3f . Mais d’apr`es la propri´et´e 1.5.1, on a X
f f ace
deg(f ) = 2m, et donc :
2m ≥ 3f
D’autre part, on tire de la formule d’Euler l’expression f = 2 + m − n. Rempla¸cant f par cette valeur, on obtient 2m ≥ 3(2 + m − n), soit :
m ≤ 3n − 6
La deuxi`eme partie du corollaire se d´emontre de fa¸con identique. Si le graphe est sans triangle, on a pour toute face f , deg(f ) ≥ 4. On obtient alors par sommation 2m ≥ 4f , puis grˆace `a la formule d’Euler :
m ≤ 2n − 4
Remarque 1.5.1. Dans ce ce travail, on s’int´eresse juste aux graphes planaires, pour plus de d´etail et explications sur les graphes planaires voir (Berge, 1973),(Biggs, 1993),(Bondy et Murty, 1976),(Diestel, 1997), (Harary, 1969),(Bollob´as, 1978),(West, 2001),(Wilson, 1985).
1.5.3 Caract ´erisation des graphes non planaires
Th´eor`eme 1.5.1. K5 et K3,3 ne sont pas planaires, voir Figure 1.11.
D´emonstration. Le graphe K5 est le graphe complet `a 5 sommets, c’est-`a-dire le
graphe qui relie par une arˆete tout couple de sommets pris parmi 5. Il poss`ede 5.42 = 10 arˆetes. C’est un graphe simple, connexe, donc il v´erifierait |E| ≤ 3|V |−6 s’il ´etait planaire. Or, manifestement, 10 > 3.5 − 6, et donc K5 n’est pas planaire.
K3,3 poss`ede, lui, 6 sommets et 3.3 = 9 arˆetes. Comme 9 < 3.6 − 6 = 6, le premier crit`ere
ne suffit plus `a montrer que ce graphe n’est pas planaire.
!
Figure 1.11 – les graphes complets K5 et K3,3
En fait, ce graphe est de plus sans triangle. En effet, le graphe relie chaque sommet de l’ensemble A, B, C `a chaque sommet de l’ensemble D, E, F . Un triangle comporterait n´ecessairement deux sommets (voir trois) du mˆeme groupe (par exemple,A, B et D). Mais alors, les deux sommets en question n’ont pas `a ˆetre reli´es par une arˆete de K3,3, qui est
donc sans triangle. Les cycles les plus courts sont de longueur 4, par exemple le cycle (A, D, B, E, A).
Appliquant la deuxi`eme partie de notre corollaire, on en d´eduit que, s’il ´etait planaire, le graphe K3,3 devrait v´erifier la formule |E| ≤ 2|V | − 4. Mais cette fois, on a 9 > 2.6 − 4,
1.5. GRAPHES PLANAIRES 23
Le probl`eme 2 n’a donc lui non plus aucune solution. En r´ealit´e, K5 et K3,3 sont les deux
exemples fondamentaux de graphes non planaires.
1.5.4 Caract ´erisation des graphes planaires
Plusieurs conditions n´ecessaires et suffisantes pour qu’un graphe soit planaire sont connues, la suivante est l’une des premi`eres donn´ees (d´es les ann´ees 30), et a une tr`es grande port´ee dans la th´eorie. C’est une condition dite par configuration exclues
Th´eor`eme 1.5.2. (Kuratowsky) Un graphe G est planaire si et seulement s’il ne contient pas, comme sous-graphe, une subdivision de K5 ou de K3,3 (Nishizeki et Rahman, 2004).
On appelle subdivision d’un graphe H tout graphe obtenu en rempla¸cant certaines arˆetes de G par des chaˆınes ´el´ementaires de longueurs ≥ 2, ces chaˆınes n’ayant pas de sommets interm´ediaires communs. Concr`etement, c’est comme si on ajoutait sur certaines arˆetes de H un ou plusieurs sommets de degr´e 2. Au vu de ce th´eor`eme, les graphes K5 et
K3,3jouent un rˆole particulier : ce sont, `a l’op´eration de subdivision pr`es, les configurations
dont la pr´esence fait qu’un graphe n’est pas planaire, et, r´eciproquement, la non-pr´esence fait que le graphe est planaire (Nishizeki et Rahman, 2004). Il est assez facile de montrer la condition n´ecessaire du th´eor`eme de Kuratowski, sachant que K5 et K3,3 ne sont pas
planaires. En effets, observons d’abord les point suivants, faciles `a v´erifier : si un graphe est planaire, tous ses sous-graphes sont planaires.
si un graphe n’est pas planaire, aucune de ses subdivisions n’est planaires.
D`es lors, si un graphe contient comme sous-graphe une subdivision de K5 ou de K3,3, il
ne peut pas ˆetre planaire puisqu’il contient un sous-graphe non planaire.
La condition suffisante du th´eor`eme de Kuratowski est beaucoup moins facile `a montrer et nous l’admettrons ici.
1.5.5 Graphe planaire maximal
Un graphe planaire maximal est un graphe planaire simple tel que si on ajoute une arˆete il devient non planaire. le nombre d’arˆetes d’un graphe planaire maximal est 3|V |−6.
De plus toutes les faces mˆeme l’ext´erieur sont des triangles (cycle de longueur trois)(Cahit, 2011),(Xu, 2012),(Helden, 2007),(Modabish et al., 2011).
D´efinition 1.5.1. Soit Ξn la famille des graphes planaires qui contient :
• n sommets, deux sommets complets de degr´e n − 1, deux sommets de degr´e 2 et n − 4 sommets de degr´e 4,
• 2(n − 2) faces de degr´e 3, • 3(n − 2) arˆetes,
Alors, la famille de ces graphes est appel´ee les graphes planaires maximal pour laquelle aucune nouvelle arˆete ne peut ˆetre ajout´e sans violer la plan´eit´e de ce graphe.
Figure 1.12 – Graphes planaires maximal.
La figure 1.12 pr´esente la famille des graphes planaires maximal εn, les graphes ε3 et
ε4 sont complets (tout les sommets sont complets).
1.5.6 Graphe planaire ext ´erieur
Un graphe non orient´e est planaire ext´erieur (outer-planar) s’il peut ˆetre dessiner dans le plan sans croisements, de telle fa¸con que tous les sommets appartiennent `a la face ext´erieure du trac´e, autrement dit qu’aucun sommet ne soit entour´e par des arˆetes. On d´emontre qu’un graphe G est planaire ext´erieur si et seulement si le graphe form´e en ajoutant `a G un nouveau sommet et toutes les arˆetes le reliant aux sommets de G est un graphe planaire.
Les graphes planaires ext´erieurs poss`edent des caract´erisations par graphes exclus analogues `a celles des graphes planaires : un graphe est planaire ext´erieur si et seulement si il ne contient pas de subdivision du graphe complet K4 ou du graphe biparti complet K3,3. De mˆeme, un graphe est planaire ext´erieur si et seulement si il ne contient ni K4, ni
1.6. REPR ´ESENTATION NON GRAPHIQUE 25
Figure 1.13 – Graphe planaire ext´erieur
K3,3 comme mineur, c’est-`a-dire comme graphe obtenu en contractant et en supprimant
des arˆetes.
Tout graphe planaire ext´erieur est ´evidemment planaire. Cependant, la r´eciproque est fausse : le graphe complet K4 est planaire, mais n’est pas planaire ext´erieur,de mˆeme
pour le graphe biparti complet K3,3.
1.6 Repr ´esentation non graphique
Comme nous l’avons mentionn´e pr´ec´edemment, l’essor de la th´eorie des graphes est essentiellement du `a l’av`enement de puissants calculateurs. Il est donc l´egitime de s’int´ e-resser `a la mani`ere de repr´esenter les graphes au sein d’un ordinateur. Plusieurs modes de repr´esentation peuvent ˆetre envisag´es selon la nature des traitements que l’on souhaite appliquer au graphe consid´er´e. Pour classer les diff´erentes possibilit´es de repr´esentations en machine des graphes, on peut distinguer les trois principes suivants(Clark et Holton, 1991) :
1.6.1 Matrice d’adjacence
Les outils classiques d’alg`ebre lin´eaire peuvent ´egalement ˆetre utilis´es pour coder les graphes. Donner la possibilit´e de d´eterminer que deux sommets donn´es sont voisins, c’est-`
a-dire reli´es par une arˆete dans le graphe. La fa¸con naturelle de r´ealiser ceci est la dite matrice d’adjacence d´efinie comme suit :
d’adjacence de G est ´egale `a la matrice U = (uij) carr´ee de dimension n ∗ n tel que
(uij) =
1 si (i, j)∈E c’est-`a-dire (i,j) est une arˆete) 0 sinon
Une telle matrice, ne contenant que des ”0” et des ”1” est appel´ee, de mani`ere g´en´erale, une matrice bool´eenne.
Un graphe orient´e quelconque a une matrice d’adjacence quelconque, alors qu’un graphe non orient´e poss`ede une matrice d’adjacence sym´etrique. L’absence de boucle se traduit par une diagonale nulle. La matrice d’adjacence du graphe de la Figure 1.2 est la suivante : A = 0 1 1 1 0 1 1 1 0
Ce mode de repr´esentation engendre des matrices tr`es creuses (i.e. comprenant beau-coup de z´eros). Cependant la recherche de chemins ou de chaˆınes s’effectue ais´ement avec une telle repr´esentation . De plus, la matrice d’adjacence poss`ede quelques propri´et´es qui peuvent ˆetre exploit´ees. Consid´erons un graphe G et sa matrice d’adjacence associ´ee U :
la somme des ´el´ements de la i-`eme ligne de U est ´egale au degr´e sortant de xi du
sommet xi de G.
la somme des ´el´ements de la j-`eme colonne de U est ´egale au degr´e entrant de xj du
sommet xj de G.
U est sym´etrique si, et seulement si, le graphe G est sym´etrique.
Une telle repr´esentation d’un graphe prend une place m´emoire de l’ordre de n2, o`u n le nombre de sommets du graphe. Compte tenu du fait qu’un traitement sur le graphe prend au moins le temps de la lecture de sa donn´ee, cela signifie que tout algorithme sur des graphes repr´esent´es par matrice d’adjacence demandera une complexit´e d’au moins O(n2).
1.6. REPR ´ESENTATION NON GRAPHIQUE 27
1.6.2 Matrice d’incidence
La seconde id´ee, permettant une repr´esentation matricielle d’un graphe, exploite la relation d’incidence entre arˆetes et sommets.
D´efinition 1.6.2. Consid´erons un graphe non orient´e sans boucle G = (X, A) comportant n sommets x1, ..., xnet m arˆetes a1, ..., am. On appelle matrice d’incidence de G la matrice
M = (mij) de dimension n × m tel que :
(mij) =
1 si xi est une extremit de aj
0 sinon
La matrice d’incidence du graphe de la Figure 1.2 s’´ecrit sous la forme suivante :
I = 1 1 0 0 1 0 1 1 0 1 1 1
1.6.3 Matrice des degr ´es
La matrice des degr´es est une matrice qui contient des informations sur le degr´e de chaque sommet d’un graphe. La matrice des degr´es est une matrice diagonale. Elle est utilis´ee en conjonction avec la matrice d’adjacence pour construire la matrice laplacienne d’un graphe.
D´efinition 1.6.3. ´Etant donn´e un graphe G = (V, E) contenant n sommets, la matrice des degr´es D de G est la matrice carr´ee n × n d´efinie par :
dij := deg(vi) si i = j 0 sinon
La matrice des degr´es du graphe de la Figure 1.2 est : D = 3 0 0 0 3 0 0 0 3 1.6.4 Matrice laplacienne
En th´eorie des graphes, une matrice laplacienne, ou matrice de Laplace, est une ma-trice repr´esentant un graphe, elle est utilis´ee par le th´eor`eme de Kirchhoff pour calculer le nombre d’arbres couvrants d’un graphe (Brouwer et Haemers, 2012).
D´efinition 1.6.4. Soit G un graphe simple non valu´e, orient´e o`u non. On d´efinit la matrice laplacienne (Laplacian matrix) L = D − A, o`u D est la matrice diagonale des degr´es, tel que di,i est ´egal au degr´e (nombre de liens adjacents) du sommet i, not´e δi,
donc : Lij = δi si i = j
−1 si i6=j, (i, j)∈E 0 sinon
La matrice laplacienne du graphe de la Figure 1.2 est :
L = 3 −1 −1 −1 3 −1 −1 −1 3
Ces principes de repr´esentations sont g´en´eraux et dans tel ou tel cas particulier on peut avoir besoin d’informations particuli`eres suppl´ementaires. En outre, au-del`a des des-criptions pr´ec´edentes, on d´efinit pour certaines applications des repr´esentations plus sp´ e-cifiques.
1.7 Arbres et forˆets
Les graphes permettent de repr´esenter de nombreuses situations. Il existe de nom-breuses applications (i.e. programmes) les utilisant. La complexit´e d’un algorithme consiste
1.7. ARBRES ET FOR ˆETS 29
essentiellement `a savoir, pour un probl`eme donn´e, combien de temps est n´ecessaire pour le r´esoudre et quel est l’espace machine que cela va utiliser. Certaines repr´esentations de graphes permettent d’obtenir de meilleures performances, c’est-`a-dire que le probl`eme est r´esolu plus rapidement ou en occupant moins d’espace. Dans certains cas, un probl`eme NP-complet (classe la plus ardue) sur une repr´esentation d’un graphe peut ˆetre r´esolu en temps polynomial (classe simple) avec une autre repr´esentation ; l’id´ee n’est pas qu’il suf-fit de regarder le graphe diff´eremment pour r´esoudre le probl`eme plus vite, mais que l’on ”paye” pour le transformer et que l’on ”´economise” alors pour r´esoudre le probl`eme. Une telle transformation est la d´ecomposition arborescente. Intuitivement, une d´ecomposition arborescente repr´esente le graphe d’origine par un arbre couvrant, o`u nous pr´eservons les mˆeme sommets du graphe d’origine et on supprime quelques arˆetes de fa¸con `a avoir un seul chemin entre un sommet et un autre. Nous d´efinissons et ´etudions dans cette section les arbres et les arbres couvrants, qui jouent un tr`es grand rˆole dans la th´eorie et les applications et qui constituent le type principal de graphes de notre th`ese.
1.7.1 Arbres
Les arbres sont des graphes particuliers, tr`es populaires en algorithmiques et en in-formatique.
D´efinition 1.7.1. Un arbre (tree) est un graphe simple connexe acyclique non orient´e : il n’est donc pas possible en partant d’un sommet de parcourir des liens pour revenir `a ce sommet.
On constate ´egalement que T = (V, E) est un arbre si et seulement s’il existe une chaˆıne et une seule entre deux sommets quelconques.
pour plus de d´etails et explications sur les arbres voir (West, 2001). Une feuille ou sommet pendant est un sommet de degr´e 1.
Ajouter un lien `a un arbre cr´ee n´ecessairement un cycle.
Th´eor`eme 1.7.1. Les affirmations suivantes sont ´equivalentes pour tout graphe T `a |V | sommets :
2. T est sans cycle et comporte |V | − 1 arˆetes, 3. T est connexe et comporte |V | − 1 arˆetes,
4. chaque paire u, v de sommets distincts est reli´ee par une seule chaˆıne simple (et le graphe est sans boucle).
Th´eor`eme 1.7.2. Pour un arbreX
v
deg(v) = 2(|V |−1) ; il y a donc au moins 2 sommets de degr´e strictement inf´erieur `a 2. Comme un arbre est connexe, ces deux sommets sont de degr´e 1.
Corollaire 1.7.1. Chaque arbre non trivial admet au moins deux sommets finaux. L’une des grandes utilisations des arbres est la recherche dans un graphe connexe de l’arbre recouvrant (spanning tree) c’est-`a-dire l’arbre (ou l’un des arbres) permettant d’inclure tous les sommets et une partie des liens du graphe ´etudi´e. On peut souhaiter chercher l’arbre couvrant comprenant un minimum de liens et on parle alors du graphe couvrant minimum (minimum spanning tree). L’arbre couvrant peut ´egalement servir pour repr´esenter de mani`ere simplifi´ee des graphes comprenant plusieurs milliers de sommets et de liens. Dans la figure 1.14, l’arbre de droite repr´esente l’un des arbres couvrants du graphe connexe de gauche. Si on examine uniquement l’arbre couvrant (`a droite), on retrouve bien tous les sommets du graphe de d´epart.
Figure 1.14 – Arbre couvrant d’un graphe planaire
1.7.2 Forˆets
Une forˆet (forest) est un graphe acyclique non orient´e et non connexe. La d´efinition d’une forˆet correspond donc bien au sens usuel d’un ensemble d’arbres, chacune de ses composantes connexes ´etant un arbre.
1.7. ARBRES ET FOR ˆETS 31
Proposition 1.7.1. Dans une forˆet G on a m ≤ n − 1, avec l’´egalit´e si et seulement si G est un arbre.
D´emonstration. Soient C1, C2, ..., Cp les composantes connexes de G, en appliquant
la proposition `a chacune de ces composantes , avec ni et mi respectivement le nombre de
sommets et d’arˆetes de Ci, donc pour i = 1, 2, ..., p : mi = ni− 1. la sommations de toutes
ces ´egalit´es, donne :
p X i=1 mi = p X i=1 ni− 1 = p X i=1 ni− p X i=1 1 D’o`u : m = n − p
Et comme p ≥ 1 (p est le nombre de composantes connexes de G) :
m ≤ n − 1
L’´egalit´e a lieu si et seulement si p = 1, c’est-`a-dire si et seulement si G est connexe, soit, comme G est d´ej`a par hypoth`ese acyclique, si et seulement si G est un arbre.
1.7.3 Arbres couvrants d’un graphe
On consid`ere un graphe G = (V, E), V est l’ensemble des sommets de G et E l’en-semble de ses arˆetes. On suppose que le graphe G est connexe, i.e. que toute paire s, t de sommets de V peut ˆetre reli´ee par un chemin d’arˆetes {s, r1},{r1, r2}, . . . ,{rp, t} de E.
D´efinition 1.7.2. On appelle graphe couvrant de G tout graphe dont l’ensemble des som-mets est V , dont l’ensemble des arˆetes est contenu dans E et qui est connexe.
Soit G un graphe connexe `a |V | sommets et |E| arˆetes. Un arbre couvrant T de G est un sous-graphe sans cycle et ayant |V | − 1 arˆetes. la Figure 1.15 donne un exemple des
arbres couvrants du graphe carr´e.
Figure 1.15 – Les arbres couvrants du graphe carr´e
Pour plus de d´etails les arbres couvrants, nous r´ef´erons le lecteur vers (West, 2001).
1.7.4 Int ´erˆet des arbres couvrants
Les arbres couvrants poss`edent de nombreuse applications pratiques ainsi que d’int´ e-ressantes propri´et´es th´eoriques. En particulier :
1. Ils sont utilis´es dans le cadre de r´eseaux maill´es o`u les hˆotes sont reli´es de proche en proche sans hi´erarchie centrale. On a alors besoin de pouvoir calculer un sous-r´eseau tel que les deux hˆotes puissent toujours ˆetre reli´es, et ce de mani`ere unique. Dans le cas contraire, la pr´esence de boucles est `a l’origine de tempˆetes de diffusions qui pa-ralysent le r´eseau. L’algorithme utilise pour g´en´erer les arbres couvrants n´ecessaires est le protocole STP (spanning tree protocol) d´efinit dans le standard IEEE 802.1D (Shirinivas et al., 2010).
Les nouveaux syst`emes distribu´es ´emergeants, comme les r´eseaux ad-hoc, les r´eseaux de capteurs ou encore pair-`a-pair, se focalisent sur l’efficacit´e des structures de com-munication distribu´ees et en particulier les arbres couvrants (Shirinivas et al., 2010). Par exemple, une des principales probl´ematiques dans les r´eseaux ad-hoc est le coˆut des communications. Si l’infrastructure de communication contient des nœuds de forts degr´es, des effets ind´esirables peuvent ˆetre observ´es. Parmi ces effets, on peut citer le ph´enom`ene de congestion, la perte de messages dˆue `a leurs collisions. Sans compter que les nœuds de fort degr´e sont des cibles privil´egi´ees lors d’attaques de s´ecurit´e visant un r´eseau. En effet, la paralysie des nœuds de fort degr´e perturbe, voir empˆeche, l’acheminement des informations dans un r´eseau. Dans les r´eseaux pair-`a-pair, les nœuds sont incit´es `a mentir sur les caract´eristiques r´eelles de leur