The complexity of sampling from a weak quantum
computer
by
Saeed Mehraban
MASSACHUSETTS INSTITUTE OF TECHNOLOGYOCT 0 3 2019
LIBRARIES
Submitted to the Department of Electrical Engineering and Computer
Science
in partial fulfillment of the requirements for the degree of
Doctor of Philosophy
at the
MASSACHUSETTS INSTITUTE OF TECHNOLOGY
September 2019
@
Massachusetts Institute of Technology 2019. All rights reserved.
Signature redacted
A u th o r
...
..
..
..
..
....
...
...
..
Department of Electrical Engineering and omputer Science
Certified
by ...
ignature redacted
August 30, 2019
Scott J. Aaronson
Professor of Computer Science, UT Austin
Certified by....
Signatureredacted
Thesis Supervisor
Aram W. Harrow
Associate Professor of Physics, MIT
Thesis Supervisor
Accepted by...
Signature redacted...
I
l'e A. Kolodziejski
Professor of Electrical Engineering and Computer Science
The complexity of sampling from a weak quantum computer
by
Saeed Mehraban
Submitted to the Department of Electrical Engineering and Computer Science
on August 30, 2019, in partial fulfillment of the
requirements for the degree of
Doctor of Philosophy
Abstract
Quantum computers have the promise of revolutionizing information technology, artificial
intelligence, cryptography, and industries such as drug design. Up until this point our main
understanding of quantum computing has been bound to theoretical speculations which
has successfully lead to the design of algorithms and communication protocols which would
dramatically change information technology but work well only assuming if we can
exper-imentally build a reliable and large quantum computer which at the moment seems to be
beyond the bounds of possibility. As of August 30, 2019, it appears that we are about to
enter a new era in quantum technology. Over the next few years, intermediate-scale
quan-tum computers with ~ 50-100 qubits are expected to become practical. These computers are
too small to do error correction and they may not even capture the full power of a universal
quantum computer. This is a significant step and inevitably we encounter the question "what
can we do with this new technology?".
A major theoretical challenge is to understand the capabilities and limitations of these
devices. In order to approach this challenge, quantum supremacy experiments have been
proposed as a near-term milestone. The objective of quantum supremacy is to find
com-putational problems that are feasible on a small-scale quantum computer but are hard to
simulate classically. Even though a quantum supremacy experiment may not have practical
applications, achieving it will demonstrate that quantum computers can significantly
outper-form classical ones on, at least, artificially designed computational problems. Among other
proposals, over the recent years, two sampling-based quantum supremacy experiments have
been proposed:
(1) The first proposal, known as Boson Sampling (Aaronson Arkhipov '10), is based on
lin-ear optical experiments. A baseline conjecture of Boson Sampling is that it is #P-hard
to approximate the permanent of a Gaussian matrix with zero mean and unit variance
with high probability. This is known as the permanent of Gaussians conjecture.
(2) The second one is based on sampling from the output of a random circuit applied to
task on a processor composed of a few
(~
50-100) superconducting qubits. In orderto argue that this sampling task is hard, building on previous works of Aaronson,
Arkhipov, and others, they conjectured that the output distribution of a low-depth
circuit, i.e., depth scaling asymptotically as the square root of the number of qubits, is
anti-concentrated meaning that it has nearly maximal entropy. This is known as the
"anti-concentration" conjecture.
The first part of this thesis makes progress towards the permanent of Gaussians conjecture
and shows that the permanent of Gaussian matrices can indeed be approximated in
quasi-polynomial time with high probability if instead of zero mean one considers a nonzero but
vanishing mean
(~
1/ poly log log in the size of the matrix). This result finds, to the best of
our knowledge, the first example of a natural counting problem that is #P-hard to compute
exactly on average and #P-hard to approximate in the worst case but becomes easy only
when approximation and average case are combined. This result is based on joint work with
Lior Eldar.
The second part of this thesis proves the anti-concentration conjecture for random
quan-tum circuits. The proof is an immediate consequence of our main result which settles a
conjecture of Brandio-Harrow-Horodecki '12 that short-depth random circuits are
pseudo-random. These pseudo-random quantum processes have many applications in algorithms,
communication, cryptography as well as theoretical physics e.g. the so-called black hole
in-formation problem. This result is based on joint work with Aram Harrow. We furthermore
study the speed of scrambling using random quantum circuits with different geometrical
connectivity of qubits. We show that this speed crucially depends on the way we define
scrambling and on the details of connectivity between qubits. In particular, we show that
entanglement and the so-called out of time-ordered correlators are inequivalent measures of
scrambling if the gates of the random circuit are applied between nearest-neighbor qubits on
a graph with a tight bottleneck, e.g., a binary tree. A major implication of this result is that
the scrambling speed of black holes may depend critically on the way one defines scrambling.
Previously, it was believed that black holes are the fastest scramblers of quantum
informa-tion. This result is based on joint work with Aram Harrow, Linghang Kong, Zi-Wen Liu,
and Peter Shor.
Thesis Supervisor: Scott J. Aaronson
Title: Professor of Computer Science, UT Austin
Thesis Supervisor: Aram W. Harrow
Acknowledgments
Let me start with a cliche which ends up being true most of the time: This thesis was a
synthesis of the help of multiple people and I was only one of them. I owe this process to
many. It is impossible to rank them according to priority or importance.
The MIT community was beyond what I could imagine.
I admire the spirit of the
community. During the six years I worked as a graduate student there, I was asked multiple
times whether I would suggest getting a Ph.D. from MIT. In response, I would tell them "I
don't know why I chose MIT but I will tell you why I will choose it again.". The answer
is: "MIT created a need in me to quest and diagnose real-world problems and at the same
time taught me I am wrong most of the time. MIT taught me thinking has paramount value
and thinking together has paramount power. MIT gave me the insight to discern central
questions and sufficient courage to tackle them. MIT taught me questions precede answers.
During these six years, I learned that wisdom has a power equal to power itself."
I admire the people in the community. My Ph.D. was not an easy one. If it wasn't for
three people I couldn't finish perhaps even the first semester: Leslie Kolodziejski, Martin
Schmidt and Janet Fischer. The story is long and secret, its consciousness is the content of
this Thesis.
I admire my advisors Scott Aaronson and Aram Harrow. Their wisdom, altruism,
sup-port, hospitality, teaching, and personality had been the main driving force that not only
lead to the material of this thesis but also grew me into someone I could not imagine I would
become. They taught me the significance of discerning central questions. They taught me
the courage to learn anything when I need them. I admire them for they made my
free-dom possible. They made it possible for me to think for long periods before coming with
conclusions. I don't recall them ever judging me with efficiency or lack of efficiency.
I admire my thesis committee Ryan Williams who beyond his academic support, like
many other Professors at TOC CSAIL, framed the means of friendship between the students
and the faculty.
Scott and Aram I leanred standards to choose central questions. From Greg Kuperberg I
learned precision and rigor. From Adam Bouland I learned effective presentation. From Lior
Eldar, I learned the courage to think big (sometimes crazy big). From Peter Shor, I learned
my need for critical thinking. From Mehdi Soleimanifar, Linghang Kong, and Zi-Wen Liu I
learned effective collaboration.
I admire my future teachers, John Preskill, Thomas Vidick, Fernando Brandao and
Umesh Vazirani for receiving me.
I admire Piotr Indyk, Ronitt Rubenfeld, Virginia Williams, Shafi Goldwasser, Silvio
Micali, Eric Demaine, Martin Demaine, Costis Daskalakis, Peter Shor, Pablo Parrilo, Yael
Kalai, David Karger, Nir Shavit, Ankur Moitra, Vinod Vaikuntanathan, Charles Leiserson,
Nancy Lynch, Ron Rivest, Aleksander Madry, and Mike Sipser (ordered at random) for their
friendship, support, and guidance. With of these people, I had the chance to meet and learn
something about science or humanity. I admire Mike Sipser, Isaac Chuang, Aram Harrow,
Scott Aaronson, Peter Hagelstein, Seth Lloyd and Seth Riskin who taught me teaching. I
admire Dirk Englund and Masoud Mohseni who helped me start my new chapter. I admire
Rafael Reif who taught me leadership. I admire Rebecca, Nancy, Debbie, Joanne and many
others for their assitance, presence and support.
I admire my friendships. USI admire my neverending friendship with Hamed who was
there at the times I needed friendship most. I admire my friendship with Anton and Tanya
who taught me style in friendship. I admire Hasan, and Behrooz who, beyond being my
friends, were the first role model I had the in high school. I admire Maryam Mirzakhani
and Asghar Farhadi who taught me the great value of a true work. I admire my frienship
with Ahmad and Hasti for their presence, conversation and support. I admire my friendship
with Neo (Mostafa) Mohsenvand who taught me brotherhood, who is literally the internet
of things, and who taught me innovation. I admire my close unbelievable friendship with
Francesca and Valerio whose friendship was the camomile of my heart. I admire my friendship
with Nicole who taught me simplicity. I admire my friendship with Mohammad whose
friendship taught me brotherhood. I admire my friendship with Maryam who taught me
thinking beautiful. I admire my friendship with Rasool who taught me friendships doesnAAt
recognize distance. I admire my friendship with Penny who taught me goodwill. I admire
my friendship with Paria who taught me the persistence of presence. I admire my friendship
with Thomas who taught me positivity. I admire my friendship with Ali who taught me the
need for listening. I admire my friendship with Giulio who taught me empathy. I admire my
fellow labmates, Daniel, Akshay, Luke, Lisa, Logan, Andrew, kai, Justin, Josh, Dylan, Greg,
Mina, Jerry, Gautham and many others who taught me respect and the sense of community.
I admire Mahboob for reminding me the value of being sociable. I admire my friendship
with Aviv who taught me thinking outside the box. I admire Ali, Soheil, Arman, Donna,
Azarakhsh and Omid who shaped the early elements of my personality when I entered MIT.
They taught me the need for support and empathy. I admire Soheil for a particular day
which saved my academic life and later taught me the need for attitude. I admire Maria
and Andzrej for inviting me to the new world. I admire my artist friends Nilin, Cameron,
Maria, Seth for welcoming me to their community. I admire Seth and Pavan who taught me
the meaning of vision. I admire Seth for reminding me of Holism in artistic style. I admire
Jeff for teaching me the American culture. I admire Lou who saved my soul by teaching me
the key to happiness is by taking a respite from needs and not to add more. I admire the
people of the united states who welcomed me. I admire many others who were in my life.
I admire the machine whose papers, agencies and credits supported me financially. I
admire the altruistic whose generosity supported me. I admire those who taught me not
behave in certain ways they did. I admire the officer who gave me a single entry visa which
separated me from my family for six years and helped me understand their value. I admire
the late president of the United States who motivated me to learn about cultures, societies
and philosophy. I admire those who ghosted away when there was no benefit. They taught
me the real meaning of friendship. I admire my false egos who taught me independence. I
admire the flawed who reminded me of my own flaws.
I admire my parents Fereshteh my angel and Alireza my strength for being the balancing
There is no doubt a big part of who I am is a projection of their loving parenthood. I admire
my sisters Sahar and Sara and family whose presence shaped my life.
I admire the two anonymous who taught me balance. I admire those who will come. And
Contents
1 Introduction
1.1
O utlook . . . .
1.2
Sununary of the results . . . .
1.2.1
The permanent-of-Gaussians conjecture and approximation algorithms
for the permanent and partition functions . . . .
1.2.2
The anti-concentration conjecture, pseudorandom quantum states, and
the black hole information problem . . . .
1.3
Future directions . . . .
1.3.1
Approximating the permanent and partition functions . . . .
1.3.2
Random quantum processes . . . .
1.3.3
Intermediate-scale quantum computing . . . .
1.3.4
Other future directions . . . .
2 Approximate and almost complexity of the Permanent
2.1
Introduction . . . .
2.1.1
Complexity of computing the permanent . . . . .
2.1.2
A complex function perspective . . . .
2.1.3
M ain results . . . .
2.1.4
Roots of random interpolating polynomials . . . .
2.1.5
Turning into an algorithm . . . .
2.1.6
Discussion and future work . . . .
17
17
23
25
27
29
29
31
32
32
35
. . . . .
36
. . . . .
36
. . . . .
38
. . . . .
40
. . . . .
41
. . . . .
42
. . . . .
44
2.2
Prelim inaries . . . .
2.2.1
N otation . . . .
2.3
Permanent-interpolating-polynomial as a random polynomial . . . .
2.3.1
Root-avoiding curves . . . .
2.4
Computational analytic continuation . . . .
2.5
Approximation of permanents of random matrices of vanishing mean
.
. . .
2.5.1
M ain theorem . . . .
2.5.2
Natural biased distributions . . . .
2.6
Inverse polynomial mean is as hard as zero mean
. . . .
2.7
Proof of Lem m a 13 . . . .
2.8
Average #P-hardness for the exact computation of the permanent of a random
Gaussian with vanishing mean . . . .
3 Pseudo-randomness and quantum computational supremacy through
shal-low random circuits
3.1 Introduction . . . .
3.1.1 Connections with quantum supremacy experiments 3.1.2 Our models . . . .
3.1.3
Our results . . . .
...
. . . .
3.1.4 Previous work . . . . 3.1.5 Open questions . . . . 3.2 Preliminaries . . . . 3.2.1 Basic definitions . . . .3.2.2 Operator definitions of the models . . . . 3.2.3 Elementary tools . . . ..
3.2.4 Various measures of convergence to the Haar measure . . . .
3.3 Approximate t-designs by random circuits with nearest-neighbor gates on
D-dim ensional lattices . . . .
3.3.1
B asic lem m as . . . .
4848
49
53
56
64
64
66
67
70
71
75
76
80
82
84
91
92
94
9496
99
101103
103
3.3.2
Gap bounds for the product of overlapping Haar projectors . . . .
105
3.3.3
Proof of Theorem 31; t-designs on two-dimensional lattices . . . .
106
3.3.4
Proof of Theorem 32; t-designs on D-dimensional lattices . . . 111
3.3.5
Proofs of the basic lemmas stated in Section 3.3.1 . . . .
118
3.3.6
Proofs of the projector overlap lemmas from section 3.3.2 . . . .
121
3.4
O(n in
2n)-size random circuits with long-range gates output anti-concentrated
distributions . . . .
138
3.4.1
Background: random circuits with long-range gates and Markov chains 138
3.4.2
Proof of Theorem 34: bound on the collision probability
. . . .
142
3.4.3
Proof of Theorem 81: relating collision probability to a Markov chain
143
3.4.4
Proof of Proposition 89: collision probability is non-increasing in time 147
3.4.5
Proof of Theorem 82: the Markov chain analysis . . . .
148
3.4.6
Towards exact constants . . . 176
3.5
Alternative proof for anti-concentration of the outputs of random circuits with
nearest-neighbor gates on D-dimensional lattices . . . .
179
3.5.1
The D = 2 case . . . .
179
3.5.2
Generalization to arbitrary D-dimensional case
. . . .
183
3.6
Scrambling and decoupling with random quantum circuits . . . .
185
3.7
Proofof Theoren126 ... .. .. . ...
. . . .. . .. . . . ...
189
3.8
Basic properties of the Krawtchouk polynomials . . . .
191
4 Separating measures of scrambling of quantum information and the black
hole information problem
195
4.1
From measures and architecture of quantum pseudo-randomness to the black
hole information problem . . . .
196
List of Figures
1-1
Summary of the results.
. . . .
24
1-2
Summary of future directions. . . . .
30
2-1 The curve
y
connects z = 0 and some value z#
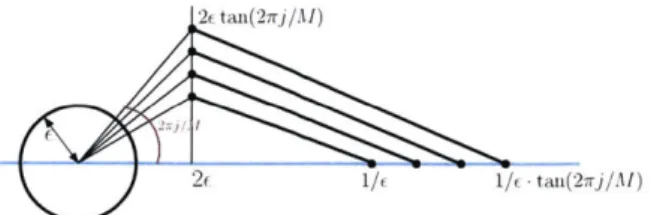
0 and is at distance at least R from any root of gA(z). Note that interpolation along the curve in small segments can reach a lot further than taking a single interpolation step which is bounded by blueshaded region -dictated by the location of the nearest root to the point z = 0. . . . . 45 2-2 The family of 2-piecewise linear curves interpolating from z = 0 to some point z on the realline. The curves branch out from the unit circle at an angle between r/4 and7r/4+ E. Each curve starts out at an angle of 2rj/M for some integer
j
and hits the imaginary axis atR(z)
= 2c. Hence the imaginary magnitude of the end-point of the first segment in the j-th curve is 2etan(27rj/M). After hitting the imaginary axis atR(z)
= 2f, they descend back to the real line in parallel, thus hitting the real line at different points. The bottom-most curve hits the real line at z = 1/e. Note that by this definition tubes of weightw
around each curve do not overlap outside the ball of radius e and in particular when they hit the imaginary axis at R(z) = 2e . . . . ..543-1
The architecture proposed by the quantum Al group at Google to demonstrate
quantum supremacy consists of a 2D lattice of superconducting qubits. This
figure depicts two illustrative timesteps in this proposal. At each timestep,
2-qubit gates(blue)
are applied across some pairs of neighboring qubits. . . 833-2
The random circuit model in definition 28. Each black circle is a qudit and
each blue link is a random SU(d
2) gate. The model does O(/P poly(t)) rounds
alternating between applying (1) and (2). Then for
O(Vn poly(t)) rounds
it alternates between (3) and then (4). This entire loop is then repeated
O (poly(t)) tim es. . . . .
85
4-1
(Figure borrowed from
[55])
An illustration of the binary tree model of depth
4. This graph is meant to model the cellular structure near the event horizon
of black holes specified in Figure 4-2. . . . .
199
4-2
(Figure borrowed from 841) The cell structure near the horizon of the black
hole. In this picture, each cell at each layer is connected to its nearest cells
and two cells below itself. The structure is roughly the same as the hyperbolic
geom etry. . . . .
199
List of Tables
2.1 The computational complexity of computing the permanent of a complex Gaussian matrix. We know that: Permanent is
#P-hard
to compute exactly in the worst case or average case. We also know that permanent is #P-hard to compute exactly on average. However, nothing is known about the ap-proximation of permanent in the average case. Our result demonstrates that the permanent can be approximated in quasi-polynomial time if the Gaussian ensemble has non-zero but vanishing mean. . . . . 38 2.2 The computational complexity of computing the permanent of a complexChapter 1
Introduction
1.1
Outlook
Every sentence in this thesis must have started with "in our opinion" or "to the best of our
knowledge", "our" meaning us and the community whom we referenced. In some sections
in particular Section 1.1 this section, in particular, they must have started with: "in my
opinion", or "to the best of my knowledge". I must assert that the values defined in this
thesis are in line only with the ones I encountered during my graduate work at MIT. There
is always enough room for skepticism.
Assuming a major goal is fast processing of resources, and that a major route towards
this goal is the process of information, and that the only venue to process information is by
means of the physical universe, quantum computing and in general physical computing and
understanding, their limitations is a major scientific goal. This Thesis makes an effort to
pursue this quest through a narrow but timely window. I first start off with a personal view
on the history of quantum computing.
Our whenabouts in the quantum quest
Over the past six years, during my Ph.D. work at MIT, I came to the following understanding
about the place we stand in the history of quantum computing. The presentation covers only
a tiny portion of what has actually happened.
Perhaps computation and information processing precedes us humans and date back to
the first form of life on earth, if not earlier. During the twentieth century, building on
mil-lennia of effort, through two different models, Alonzo Church and Alan Turing formulated
computation as a mathematical construct. Turing's model, now known as the Turing
ma-chine, was basically an abstraction of a mathematician writing down a proof on a piece of
paper. It was basically a new way of viewing what mathematicians, including Turing himself,
have been doing over the recent history. The Turing machine was shown to be equivalent
or preceding in power to a variety of exising computational models, ranging from Church's
A-calculus to grammars, circuits, etc. The twentieth century also enjoyed an enormous
am-bush of technological discoveries most of which stemmed mainly from a new scientific field,
electronics. Electronics would not have been discovered if we never managed to expand our
knowledge about the physical universe. In particular, quantum mechanics played a
signifi-cant role.
Turing's machine and its other equivalents, along with a new mathematical understanding
of information by Shannon's theory of communication, and electronic devices lead to the
digital revolution. The digital age defined symbols, which were indeed the main constituents
of our language, as the main carriers of information and provided means to transmit and
process them through physical devices which were called computers. Before that, a computer
was a person whose job was to do industrial computations using pen, pencil, erasers, and
paper.
The modern term computer is a physical device which executes an algorithm. An
algo-rithm is a series of commands designed to get executed through a physical realization later
on termed as hardware. The algorithm itself was termed as software. Hardware and
soft-ware may be wishfully regarded as the body and the soul of a computer. In a way, Turing's
machine is an algorithm designed for an abstract device inspired by classical physics. But
Turin's machine is closer to divine than earth since it has an infinite tape. One could view
a computer as an approximate implementation of Turing's machine with finite memory and
disturbed by noise. Now it was time to ask "what is the limit of the sky? How much can we
compute?". Church and Turing formulated a Thesis which stated that all that is computable
in the physical universe is computable on a Turing machine.
There were a few conceptual developments which hinted towards the need and possibility
of quantum computation. One was related to the hardware industry. Since their invention,
computers kept shrinking down in sizeand increasing in inefficiency. This was achieved by
computer and electrical engineering and industry. The speed at which the hardware shrank
in size followed a particular trend known as the Moore's law: "they shrank in half every
two years". Inevitably, the size of a single processor would get as small as a single atom,
below which classical laws of physics the way we know them do not hold and follow quantum
mechanics. That time is around now. In other words, the Turing machine which was designed
to work classically may not be the best we could achieve.
Another development was related to software. Softwares also kept getting more efficient.
Hence, once again, there was a question about the sky's limit: Are Turing machines as
efficient as the universe can get? Later, around 1990 Itamar Pitowsky, reformulated Church
and Turing's Thesis, this time in terms of efficiency: "all that is computable in the physical
universe efficiently is also computable on a Turing machine efficiently". It was speculated at
the time that this Thesis holds. We still don't know the answer.
Of course, along with the above two and other events, physics also played a significant
role. Quantum mechanics was discovered around the 1900s when a series of paradoxical
experimental observations were made. For example, certain double-slit experiments which
interfered beams of electrons like light suggested that matter behaves both like wave and
matter. Or, developments in thermodynamics suggested that light is composed of chunks
(quanta) which were called photons. The physics community came up with a mathematical
formulation about the small-scale universe, which, inspired by the term quantum, was called
quantum mechanics. Quantum mechanics was able to converge to classical laws at classical
space-time scales, and could simultaneously justify the existing counter-intuitive
experimen-tal observations. One aspect of this theory was that it was hard to predict its outcomes.
For example, predicting the properties of a molecule consisting of a few dozen atoms would
take at least decades using existing algorithms. In other words, classical computers were
un-able to simulate a molecule. Indeed, one would regard a molecule as a computer composed
of quantum elements if they knew what is about to come, and indeed the work of several
researchers such as Richard Feynman, Paul Benioff, and David Deutch accomplished this.
In 1981 Richard Feynman gave a magnificent keynote speech at a conference co-organized
by MIT and IBM [50]. There, he famously said "Nature isn't classical, dammit, and if you
want to make a simulation of nature, you'd better make it quantum mechanical, and by golly,
it's a wonderful problem because it doesn't look so easy.". Among his brilliant ideas was "The
rule of simulation that I would like to have is that the number of computer elements required
to simulate a large physical system is only to be proportional to the space-time volume of the
physical system." This exactly means each quantum system is a quantum computer whose
program is out of our control. A quantum computer is supposed to simulate that program.
Many regard Feynman's 1981 "quantum physics simulating quantum physics" as the birth
of quantum computing. Between 1981 and 1994 there was this strange era that quantum
computing was simultaneously in a superposition of being or not being a thing, and it would
take a true quantum computing believer to work religiously towards the development of the
field. Around the same time as Feynman, Paul Benniof discovered a reversible model of
quan-tum computation [21]. This was a response to several objections that quanquan-tum mechanics
which is reversible by nature cannot perform computations as computation dissipates energy.
Benioff's model which was built on the reversible model of Bennet [22] was purely quantum
mechanical and didn't dissipate energy. During the year 1985 David Deutsch formulated the
first physics-free task (namely, testing the balancedness of Boolean functions) which
quan-tum mechanical computation can solve
[44]
much faster than classical models. Right around
1994, the hope for performing quantum mechanical computations declined once again. The
objection was "sure they can do something but why can't they do something useful?". The
last of these seemingly useless attempts was by Simon who showed that quantum computers
can perform some tasks exponentially faster than classical ones [85]. Unfortunately, that
task was regarded useless and his paper was rejected multiple times. This was 1994.
Quantum computing's most glorious time, in my opinion, was 1994, when Peter Shor
discovered the Shor's algorithm which could factor astronomically large numbers in a fraction
of a second on a quantum computer. Shor was one of the few referees who admired Simon's
observation. He quickly realized that a generalization of Simon's idea would lead to an
exponentially fast algorithm for Factoring. Factoring was a problem that even Gauss had
thought about but couldn't manage to get any classical algorithms running faster than
exponential time. But he didn't know about the possibility of quantum computing. One
reason many regard factoring as a central problem is that it is involved at the core of a
widespread security protocol known as RSA. This result turned the field from a near sci-fi
quest to a research topic governments would support.
Shor's discovery had connected at least three main societal corporates: the governments,
the curious theoretical physicists, and curious theoretical computer scientists speculating the
physical Church Turing Thesis. Later on, more communities joined, and now the range of
interests in quantum computing and information hits the boundaries of knowledge about
quantum gravity and artificial intelligence.
Around 1994, after a series of objections to the quantum model of computation developed
around Shor's discovery, the field developed a theoretical design of a quantum computer
which would capture the full power of quantum mechanics in computation and was at the
same time fault-tolerant and robust. Three years later the complexity theory of the quantum
model of quantum computation also got birth [25]. Quantum computing also had found its
way to cryptography
[23].
Later it also introduced magical protocols such as teleportation
[241
which could harness quantum weirdness in the most unbelievable way. It was time to
build one. But, it turned out that controlling quantum bits were much harder than we
thought. To give an intuition, a number that is hard to factor on a classical computer should
have around 3000 digits, and the best fault-tolerance schemes demand to encode one bit of
quantum information into a thousand physical quantum bits. Hence, a million good quality
quantum bits is what we need in order to take advantage of the Shor's algorithm. The
number of qubits we had at the time was less than the number of fingers on one hand.
Once again, we asked about the limits of the sky, this time we knew its height but the
question was "how far can we climb?". This clear limitation raised a high degree of skepticism
among scientists, and for once again the governments were reluctant to invest. Around twenty
years later, around 2008, a number of theoretical computer scientists, including Aaronson,
Arkhipov, Bremner, Shephard, Jozsa, and others [4,
321,
came up with a beautiful line of
reasoning: "the first experimental application of quantum computing would be to disprove
the skeptic". They designed a paradigm, now known as the near-term intermediate-scale
quantum technology (NISQ) era
[79],
wherein we would build quantum computers that
use little error correction, are too small, and may not capture the full power of quantum
computing. Their main application would be to disprove the skeptic. History will tell.
As of August 30, 2019, at this point in the history, there are a number of experimental
groups within universities and renown companies such as Google and IBM that try to harness
the power of a NISQ computer. There are a variety of proposed applications, ranging from
machine learning, artificial intelligence, simulating physics, etc. Among these applications
is quantum supremacy which is basically: "design a computational task that one would
mathematically prove hardness of classical simulation for, and use a quantum computer that
is naturally designed for that task." The task is not very useful if we assume the purpose of
quantum computing is to manufacture immediate human needs such as video games. But it
is useful if it would bring awareness that quantum computing is real.
The work of Aaronson, Arkhipov, and many others suggested that a particular NISQ
model of quantum computing, based on sampling, what I call, golden numbers informant,
would outperform classical computers even using small (- 50-100) quantum bits, but onlyassuming certain deep and elegant mathematical conjectures. These golden mathematical
numbers merely evidence superiority of quantum over classical computing, if that is true.
This Thesis makes an effort to resolve these conjectures. We succeeded in proving one for
one model and find the boundaries of possibilities around another one for another model. We
also expand the context further to topics related to average-case complexity and theoretical
physics.
1.2
Summary of the results
This thesis is principally focused on the theoretical study of the capabilities and limitations
of small quantum computers that are predicted to become practical in the near future.
We are about to witness a new epoch in quantum computing, known as the NISQ
(noisy
intermediate-scale quantum) technology era [80]. In the NISQ era, small, noisy quantum
computers will be practical and accessible. One major milestone of the NISQ era is the
demonstration of quantum supremacy over classical computers. The primary theoretical
objective of quantum supremacy is to prove that these devices are hard to simulate classically,
and hence outperform the existing computational resources.
In order to approach these goals, we make two major contributions. These results also
make progress towards other areas in theoretical computer science, quantum computing, and
theoretical physics such as average-case complexity, efficient quantum pseudorandomness,
and black hole information problem.
Our first contribution [481 was to approach a conjecture of Aaronson and Arkhipov
[3].
They conjectured that it is hard to approximate the permanent of a Gaussian matrix that
has entries sampled independently from the zero mean-Gaussian with a unit variance for the
majority of inputs. We showed that this conjecture is false if instead of zero mean we choose
a non-zero but vanishing mean Gaussian matrices.
The second contribution
[53]
was to prove a conjecture by the Google Quantum Al
group [26]. Google is planning to build a small quantum computer, based on local random
circuits, with around one hundred qubits. They conjectured that the output distribution
sampled from their model would not be concentrated around a few outcomes. We proved
this conjecture. In so doing, we also found efficient ways to construct pseudorandom quantum
states. These pseudorandom states have central applications in quantum information and
computation. In a follow up work, in joint work with Aram Harrow, Linghang Kong,
Zi-Wen Liu and Peter Shor, we studied the speed of scrambling for quantum circuits acting
on geometries other than lattices. An application of this work was related to the black
hole information problem. In a joint work, we approached the so-called "fast scrambling
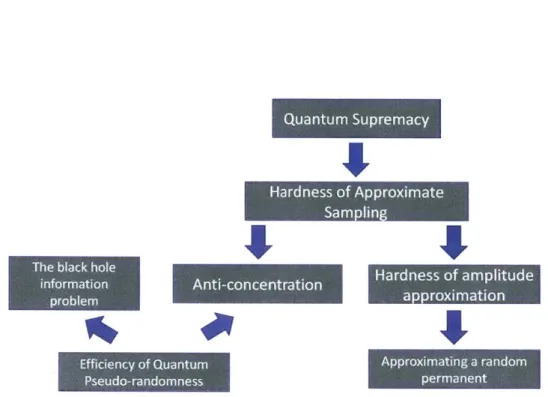
conjecture". Figure 1-1 gives a rough summary of the content of this thesis.
Quantum Supremacy
I
I
Anti- co ncentration Efficiency of Quantum Pseudo-randomness -Hardness of amplitude a ceroximationA...pprox rnating a- radomW_ permanent
Figure 1-1: Summary of the results.
In order to obtain these results, we utilize and develop tools from different disciplines,
including average-case complexity, approximate counting, stochastic processes, complex
anal-ysis, random matrix theory. These tools are likely to find applications in areas such as high
energy physics, condensed matter theory and machine learning.
In what follows (Sections 1.2.1 and 1.2.2) we explain in more details the main two parts
of this Thesis. Section 1.2.1 gives a summary of Chapter 3. Section 1.2.2 summarizes the
content of chapters 3 and 4. Section 1.3 the sketch of a future plan for the research presented
in this thesis.
1.2.1
The permanent-of-Gaussians conjecture and approximation
algorithms for the permanent and partition functions
In 2011, Aaronson and Arkhipov
[3]
conjectured that "it is hard to approximate the
perma-nent of a Gaussian matrix on average.". This conjecture is also known as "the permaperma-nent-
permanent-of-Gaussians conjecture". Along with another conjecture about the anti-concentration of the
Gaussian permanent, it implies that sampling within total variation distance from a
linear-optical experiment, known as BosonSampling, is hard for a classical computer. Our first
contribution
[48]
was to approach this conjecture.
Aaronson and Arkhipov
[3]
showed that exact computation of amplitudes of a linear
op-tical device is hard for the majority of inputs (that is, in the "average-case"). The hardness
of exact computation is, however, experimentally irrelevant due to the presence of
experi-mental noise. One way to achieve the hardness of approximate sampling is to show that
hardness holds in the average case, and approximately. The proof techniques
[31
used,
un-fortunately, fail at achieving thi. Recently, Bouland, Fefferman, Nirkhe, and Vazirani
[28]
extended the proof techniques of
[3]
and reconstructed the same result for the case of
Ran-dom Circuit Sampling. Unfortunately, their toolset also was unable to achieve the hardness
of approximation in the average case.
One may believe that hardness of average-case exact computation implies hardness of
average case and multiplicative approximation. One reason to believe so is that hardness
of exact sampling in the worst case, almost immediately, implies hardness of worst-case
multiplicative computation.
In a joint work with Lior Eldar
[48],
we showed the first counterexample for this intuition.
We found, to the best of our knowledge, the first natural counting problem that is hard to
compute in the average case exactly, and in the worst case approximately, but becomes
nearly-efficiently solvable (quasi-polynomial time) if approximation and average case are
combined. The computational problem is a very natural one: similar to BosonSampling, it
is the permanent of the Gaussian ensemble, where each entry has mean 1/polyloglog(n)
and unit variance. For mean value 1/ poly log(n) we found a sub-exponential time algorithm.
Prior to this work, it was widely believed approximating the permanent of a matrix with
many opposing signs must be hard due to the exponential amount of cancellation occurring
the permanent sum. Our result suggests that a proof of average-case approximation hardness
for a zero-mean matrix if the conjecture holds, must involve ideas beyond the ones used by
[3].
In order to prove this result, we designed an algorithm which finds a low-degree
(polylogarithmic-degree) polynomial that approximates the logarithm of the permanent function with mean
1/ poly log log n. In doing so, our strategy stemmed from a recent approach taken by
Barvi-nok [17] who used Taylor series approximation of the logarithm of a certain univariate
poly-nomial that interpolates the permanent from an easy-to-compute point to a hard instance.
Our work was the first average-case analysis of Barvinok's algorithm.
The interpolation technique [17] is relatively new and may find applications in different
areas of theoretical computer science and quantum computing. This algorithmic technique
has been proved to be a powerful approximation scheme for computational problems such as
the permanent and partition functions. However, this approach has not been studied in the
context of Hamiltonian complexity, for problems such as approximating the partition function
of quantum Hamiltonians. In an ongoing work with Aram Harrow, and Mehdi Soleimanifar
we use this technique to find approximation algorithms for the partition function of
Hamilto-nians at either high temperatures, certain instances of Ferromagnetic HamiltoHamilto-nians, or when
the system admits decay of correlation in the corresponding Gibbs state. In another work
with Fernando Brandao and Alex Buser we plan to study the application of this method to
adiabatic quantum computing.
1.2.2
The anti-concentration conjecture, pseudorandom quantum
states, and the black hole information problem
Our second contribution [53] was proving a conjecture [26] by the Google Quantum Al group.
Similar to Aaronson and Arkhipov
[3]
and Bremner, Montanaro and Shepherd
[33],
they
introduced two conjectures and showed that if both hold, sampling within total variation
distance from the device they are will be implementing in the next few years would be hard
for a classical randomized polynomial time computer. One of these conjectures is known as
"the anti-concentration conjecture", which says that the output of a random circuit is not
concentrated around a few outcomes. More specifically, the statement is: "for a constant
fraction of random circuits of depth
O(V/)
acting on a square lattice with n qubits, a fixed
amplitude is not too small". In joint work with Aram Harrow, we proved this conjecture.
We indeed proved a much stronger result: "Random quantum circuits with 0(t") . nl/D
depth acting on a D-dimensional lattice are approximate t-designs", a question which was
open since 2012 [30]. Prior to our work, the best construction was with a circuit with linear
depth for D = 1, even for t = 2 [30, 56]. Approximate t-designs are distributions over the
unitary group that agree, approximately, on the first t moments with the Haar measure. The
Haar measure has crucial applications in quantum algorithms, communication protocols,
cryptography, and, on the other hand, chaotic systems in statistical physics, condensed
matter theory and high energy physics (e.g. the quantum gravity and fast scrambling of black
holes [34, 821). The uniform measure is, however, very inefficient to prepare. Approximate
t-designs are both efficient and suitable for those applications.
We further showed that local quantum circuits of size O(log2 n) with random long-range
gates (like the model in
[56])
output anti-concentrated distributions. We were able to achieve
O(log n log log n) depth using a different random circuit model. We also showed that for any
circuit acting on n qubits Q(log n) depth is necessary to achieve anti-concentration. Our
result further improves on the previous bounds
[35]
for the depth sufficient for scrambling
'Along with a student, Matthew Khoury, at MIT, have indeed confirmed numerically that our bounds are tight up to logarithmic factors, and indeed the constant factors are not too large.
and decoupling with random quantum circuits with local interaction on a D-dimensional
lattice.
As an extension of this work, one of our contributions [55] was to provide a new insight
into the black hole information problem. While the exact dynamics of a black hole is not
known, we proved an intuition of Shor
[84]
that, under certain assumptions in quantum
gravity, strong measures of scrambling require a time proportional to the area of the black
hole. It is widely believed that a black hole scrambles quantum information in a time
proportional to the logarithm of its area. The entanglement measure is close to the one
considered in [93]. To show this we argue that the structure of space-time near the event
horizon of a black hole is such that the random circuit model will be constrained to act on
qubits located on a constant-degree tree. We then show that, even though a tree has a low
diameter, entanglement saturation is slow. Our result also suggests that, surprisingly, even
for weak measures of scrambling such as out-of-time-ordered correlators the diameter of the
interaction graph is not the right time-scale for scrambling. To prove these results we had
to significantly extend previous techniques introduced by [56, 30, 34], as well as introducing
more new ones. For detailed proof sketches, see our paper [53], Section 1.3.
In this line of work, one important question is to understand if quantum supremacy will
be maintained under noise. In an ongoing work with Fernando Brandao and Nick
Hunter-Jones we study this problem. It turns out if certain second moments of a random quantum
circuit match desired predictions random quantum circuits are relatively resilient to noise.
We seek out for new techniques in condensed matter theory which allow us to study these
moments.
Related previous work: New intermediate models of quantum
com-puting
In line with intermediate-scale models of quantum computing, a previous contribution
[6]
we made was to find two new intermediate models of quantum computing. The first model
was inspired by quantum field theory in one spatial dimension. We called this model the
ball-permuting model. The model is a very restricted one and belongs to a class of models
known as integrable. In physics, integrable models are very well-behaved, in the sense that
one can write down a solution explicitly. We showed that even with such simplicity the
model is computationally hard to simulate on a classical computer. To establish this result
we used techniques from representation theory that were not used before our work. During
the implementation of these techniques, we discovered another restricted model (which we
call TQP) that is hard to simulate. We furthermore, made interesting connections between
the two mentioned models and another restricted but hard to simulate model called the
one-clean-qubit model (a.k.a DQC1). We showed that the first model can be simulated by
DQC1, whereas the second model is intermediate in power between DQC1 and
BQP.
We also
defined a classical analog of this model and showed interesting connections between that
model and weaker classes such as LOGSPACE, AlmostLOGSPACE, and BPP.
1.3
Future directions
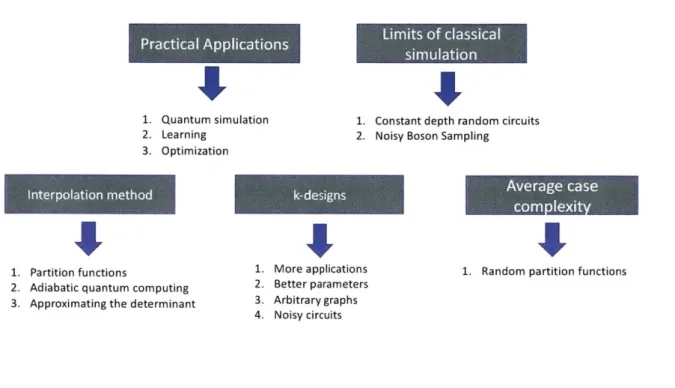
This section provides a sketch of possible future directions. A brief demonstration of these
directions is provided in Figure 1-2.
1.3.1
Approximating the permanent and partition functions
Very little about the full potentials of the interpolation technique is understood. This thesis,
along with other previous demonstrations such as
[17],
evidences that the technique can be
deployed for approximating interesting functions such as the determinant. One may expect
that this technique would enjoy an interplay with other techniques of approximation and
sampling such as the sum-of-squares hierarchy and the Markov chain Monte Carlo. There
are many problems these techniques can be applied to:
Practca Applications
1. Quantum simulation 2. Learning
3. Optimization
I
1. Constant depth random circuits 2. Noisy Boson Sampling
1. Partition functions
2. Adiabatic quantum computing 3. Approximating the determinant
I
1. More applications 2. Better parameters 3. Arbitrarygraphs 4. Noisy circuitsd t
1. Random partition functions
Figure 1-2: Summary of future directions.
the limits of classical simulation for computational problems related to noisy Boson-Sampling or low-depth or noisy random circuits.
(2) Even though these techniques are designed for finding algorithms, they can also be utilized to approach establishing hardness reductions for different problems such as the well-known permanent of zero-mean Gaussians
[3].
(3) In condensed matter physics or inference, they can be used to approximate the partition function for restricted models. For example, in the statistical mechanics literature [46] it is known that decay of correlation is the same as analyticity of the partition function. An important direction, which we are currently investigating in joint work with Aram