Digital computer study of the effects of manufactured errors on dynamic gear loads

JUN 27 1960

LIBRAR

DIGITAL COMPUTER STUDY OF THE EFFECTS OF MANUFACTURED

ERRORS ON DYNAMIC GEAR LOADS

by.

Michael G. Meacher

B. ENG. Nova Scotia Technical College

(1959)

SUBMITTED IN PARTIAL FULFILLMENT OF THE

REQUIREMENTS FOR THE DEGREE OF

MASTER OF SCIENCE

at the

MASSACHUSETTS INSTITUTE OF TECHNOLOGY

June, 1960

Signature of the

AuthorSignature

T

-Certified by

redacted

Thesis Supervisor

Accepted by

Signature redacted

Chairman, Department Committee on Graduate Studies

V -~ '-

iq~,k)

('* ~

~fi. A L) .<L A 6.1< *'~ Li iKO ;' :7

~iI

ItT> 'f

iI . A l ,

~B1IT

~3

T7 I'iIJ I~JU JILT VI T2 i U T DoA l 4U

~ .. \

i fij 10 0o1uls11IE

io~dv ~x~c*qn~2 ~ie~t~T

~ei1uI&~ ~~UJbL

d)

47L0 5~'IkLnATf~ ~C~L~8C ~ irc

11

N ,~ Al

- bo",li-is" --ya A -4

DIGITAL COMPUTER STUDY OF THE EFFECTS OF MANUFACTURED ERRORS ON DYNAMIC GEAR LOADS

by

Michael G. Meacher

Submitted to the Department of Mechanical Engineering on

May 24, 1960 in partial fulfillment of the requirements for the degree

of Master of Science.

ABSTRACT

A theoretical analysis was made to study the effect that the

disengagement of a tooth-pair has on dynamic loads of gear teeth. The

effect of friction was approximated by including an equivalent viscous

damping factor.

The gear teeth were assumed to have insignificant

manufactured errors compared to the deflections of the teeth under

load.

A digital computer program was written to study the effect a

manufactured error has on dynamic loads, stress and deflections of a

set of gear teeth. A concise method was used to determine the manner

in which engagement and disengagement of a tooth-pair occurs. The

non-linear variable elasticity of gear teeth was taken into account. A

damping term was included by considering an equivalent damping factor

proportional to the relative-displacement velocities of gear teeth.

Thesis Supervisor:

Title:

Herbert H. Richardson

Assistant Professor of

Mechanical Engineering

ACKNOWLEDGEMENT

The author wishes to sincerely thank those people, who

are not specifically mentioned here., for their assistance and cooperation in this investigation.

My sincere appreciation goes to Professor Herbert H. Richardson,

who acted as thesis supervisor,, for his encouragement, assistance and guidance throughout the preparation of this thesis.

The cooperation of the Hamilton Standard Division of United Aircraft Cooperation is gratefully acknowledged.

My appreciation goes to the competent staff of the M. I. T.

Computation Center for their advice and assistance.

Finally, a grateful acknowledgement is due Mr. Roy Breon for his competent help.

TABLE OF CONTENTS

Page

1. INTRODUCTION 1

1. 1. Problem Statement 1

1. 2. Summary 2

2. DYNAMIC LOADS IN HEAVILY-LOADED GEARS;

SINGLE DISENGAGEMENT 3

2. 1. Objective 3

2. 2. Assumptions 3

2. 3. General Analysis of the Dynamic Loads 3

2.4. Analysis of Dynamic Loads for Large p 10 2. 5. Analysis of Dynamic Loads for Small

p

11 2.6. Analysis of Loads Excluding Inertia Effects 15

2.7. Summary 19

3. DYNAMIC LOADING ! STRESS AND DEFLECTION CYCLES IN SPUR GEARS WITH A MANUFACTURED

ERROR 20

3.1. Objective 20

3. 2. Basic Equations Used in the Program 20 3. 3. Discussion of the Problem and Assumptions 23

3.4. Dynamic Load Equations 25

3.5. Symbol Table 31

3.6. Notes on the Program 33

3.7. Results 35

3.8. Summary 35

4. SUMMARY, CONCLUSIONS AND RECOMMENDATIONS 38

4. 1. Summary and Conclusions 38

4. 2. Recommendations 38 APPENDIX A 40 APPENDIX B 41 APPENDIX C 42 APPENDIX D 44 APPENDIX E 63 APPENDIX F 65 APPENDIX G 67

LIS T OF FIGURES

Figure No.

Page

1

Cam Model for Heavily Loaded Gears

4

2

Deflection Ratio Curves for Load Transfer

8

3

Dynamic Increment Load Versus

Fre-quency Ratio for Heavily Loaded Gears

13

4

Tooth-pair Separation Points. Inertia

Neglected During Load Transfer

17

5

_{Cam Model Including Manufactured Error}

₂₄

6a

Computation Flow Diagram

29

6b

Continuation of Fig. 6a

30

7

Sample Photograph of Computer Output

36

CHAPTER I INTRODUCTION

1. 1. Problem Statement

In recent years, much effort has been expended to improve the

methods of designing gears. This ha.- been brought about by the greater

demands of modern machinery for weight and volume economy, strength,

safety and reliability. Previously, design criteria depended upon

semi-empirical formulae which were not always accurate or reliable when

higher speeds and loads were required of gears. Hence, new methods

have been devised to analyze the "action" of gears in order to be able to

produce more consistant and accurate gear design information.

The design criteria of gears may be divided into the three distinct

effects of bending stress and wear in gear teeth and the temperature of

the lubricating fluid; any of which may be the limiting factor. However,

all of these criteria depend upon the loads carried by thegear teeth.

Therefore, an accurate design of gears depends upon a precise knowledge

of the loading of gear teeth when they are transmitting power.

A rigorous method for computing these loads has been devised by

1

H. H. Richardson in his doctoral thesis at M. I. T. A single-engagement

spring-mass and cam model of the dynamic gear action was presented to

study the effect of dynamic loads in a tooth-pair during single load transfer.

The oscillations of the mass caused by the load transfer were assumed to

die out before the next load transfer took place. This would be true at slow

speeds or in a critically damped system. In this analysis the damping effects

were assumed to be negligible during load transfer.

One object of this thesis is to study the effect of damping on the gear

system.

Gear action is damped mainly by the friction of the gear teeth

sliding on each other. In this analysis, an equivalent damping factor,

proportional to the relative velocity of the pitch circles was included.

The influence of manufactured errors was neglected in this analysis.

This corresponds to the case of heavily loaded gears as defined by J. B.

2

Reswick

.

_{The gears are considered to be heavily loaded when the deflections}

of the gear teeth under load are much greater than the manufactured errors

in the gears.

In order to study the over-all dynamic effects of gear

loads

in a tooth-pair, a computer must be used because of the complexity of the problem. A digital computer program was written by Wayne 0 'Neill3

to solve for the dynamic loads, stress and deflections of a perfect set of gear teeth (no manufactured errors). The non-linear variable elasticity of the gear teeth was included. The parameters for speed, damping and load were varied to study the effect of each.

The second object of this thesis is to extend O'Neills program

to include the effect of a simple manufactured error on the dynamic loads, stress and deflections of the gear teeth.

One tooth of the gear is considered to have a negative error, which is defined to be that error which decreases the load in the error tooth, below the load a perfect tooth would carry under the same conditions.

This error is constant along the profile of the tooth.

The heaviest stressing in this case is on the tooth following the error tooth since that tooth comes into contact early at its tip. In this position the tooth is under its largest bending moment since the bending arm is longest and the initial load is greater than usual. It is, therefore,

this tooth which is studied.

1. 2. Summary

The object of this thesis is to:

A. Analyze the effect of damping on the dynamic loads of a tooth-pair when single-load transfer takes place.

B. Study the effect a manufactured error has on the dynamic loads, stress and deflections of gear teeth.

CHAPTER 2. DYNAMIC LOADS IN HEAVILY LOADED GEARS; SINGLE DISENGAGEMENT

2. 1. Objective

In many cases, the maximum dynamic load on a tooth will occur soon after disengagement of the preceding tooth, and the effects of this disengagement will not depend on previous engagements or disengagements.

1

Richardson studied this case with no damping. In the following analysis damping has been included.

2.2. Assumptions.

The following assumptions are made in order to simplify the analysis.

1. In heavily loaded gears the manufactured errors are considered to be very small compared with elastic deflections and are neglected.

srt '. e (2. 1)

2. The viscous damping effects are proportional to sr. For two-tooth pair contact, the amount of damping is considered to be twice as large as for one tooth pair contact.

3. The tooth pair spring constants are considered to be constant during the load transfer process.

4. The velocity of the cam is the average velocity of the point of contact, along the line of action, of the two gears.

V=RB .0 (2.2)

2. 3. General Analysis of the Dynamic Loads.

Figure 1 shows the case when a tooth pair is disengaging. The load in the tooth pair on the flat of the cam is Ks r The load in the tooth pair disengaging is K(sr - u).

2b hr S sr

u

I.

S

-s

'

" K 0.V

////////11/77/7//7

Fig. 1. Cam Model for Heavily Loaded Gears

4I

w

The dynamic equation is

m' r + 2b 9r + 2Ksr = W + Ku

The cam shape can be approximated by a curve of the form:

u = cs2 (2.4)

where

s' = s - si#d

The distance from the pitch point to actual point of disengagement is s. The distance from the pitch point to the theoretical point of disengagement is s 0d. s*d is defined in Chapter 3.

The cam constant, for 200 involute gears, can be found in Ref. 1. It is obvious that

s= vt Therefore from Eq. (2. 4) and (2. 5)

u = cv t The following quantities are now defined.

W = Ks t r

W = total load being transferred. K = spring constant.

srt = relative displacement of a tooth pair (single tooth pair contact).

5

(2. 3)

(2.5)

(2.6)

mm ₂

m

== m +m

₁

₂

1 2 2 1 R2 Ji2

m

=

equivalent mass of the system at the pressure line.

RB = base circle radius.

b

a

,

T

b

b _m p = damping ratio.

b

=

proportional damping factor.

n =

a

b =I W = natural

na

W'i natural

frequency

frequency

V "'rb

of the system with two tooth pairs in contact.

of the system with one tooth pair in contact.

.(2.

₁₁₎

p

is proportional to the ratio of the natural period of the spring-mass system

to the time required to withdraw the cam if no oscillations take place.

Equation (2. 3) is now normalized using (2. 6), (2. 7), (2. 9), (2. 10) and

(2. 11). 1 5_r 2pa

Zst

Wi) r na na r s

t

r + r st 2 r 2

2

2

na

4

(2. 12)

6

(2. 9)

(2. 10)

At t = 0,

=

1,

=0

st 2 st

r

r

With these initial conditions Eq. (2. 12) is solved, assuming pa

'

1.

w

pt

-=

e

naa

4p

2

) cos V1

wPZ

t +

s rt

r3

3pa ~p

.

a 3 si

7

t2 + P I- )

2 2

4p

-

wp t+

-

+ -(2.

13)

2 [4 a 2 2 a na t+

Equation (2. 13) will hold until the disengaging tooth pair leaves

contact. At this point

u

2

2

2

(

- =

nb t1

(2.14)

Sr t Srt

st

The time at which contact is broken is defined as tl, shown in Fig. 2.

After this time only one tooth pair is in contact and a free vibration takes

place.

The equation for the dynamic effects of the single tooth pair contact

is now solved. The initial conditions from Eq. (2. 13) are:

sr

_r

_and

_(-sr

ti

_t

==.=..==.:..::.=:==.:..===:=.=:==:oo==l

===========================Jo=

:21

===r-==========

:=iiiii uin!!iiiiininlinlii!!iiiiiiiiii iiiiiiinni!!!!iiiii!!!~A4

... ... ... !..

====~~~~~~~~~0 -WO==========

========

====l====m===in========ul==:===========

====i~~~~~~~~-0

00====================

!=iii-00 i!!!= i!nm w n l!!iiii!iii!ii=!! LitiniRi

!!n==N E!!!!!!===nn!!!!!!!=5!nmuuunn=!====ni=!-map! inlniini iiiiiiiiiiiiiiiiiiiiiiinii~iininliiiniinninninliiiiiiiiiiMmiiil

===

==========================

iiii=i

iii!u!IiiiiiiinliN~idii= =!!iinli!!=i!!!ii==!iiiiiiiiOF

=== =========an======r-l==um=====00==

..

=================....=::=======1===

iiiiin

ineiinliinn~nliilin

ali!i""'inni!iiiiin!!ii!!iii;oi~

in!!o

%I-I u

nnnn!

r-- -1,-c Ad==M.. rc!

Huinsfim---H !HH

1 _r 2 Pb sr -s t "nb2 srt nb r Wd _{s r} Ksrt srt r r max s + r 1 srt r + (eP b( wnb(t-t))

I

2

+ ti

L

rS

+ Pb whb

2

s t n s t r r

whb

Pb

(2. 16)

ti Wd = W + W where

Wd = total dynamic load.

W = total static load (Eq. (2. 7)). W = dynamic increment load.

W dW -

-1+

--s. Ks rt Ks rt

9

(2.15)

[

/

S rl St r (2. 17) (2. 18)

2. 4. Analysis of Dynamic Loads for Large

p

-To simplify the above analysis further assumptions are made. In

this section a large

P

is assumed.

A large

P

implies that the period of one natural oscillation is

very large compared to the time of disengagement. In the limit, as

p

approaches infinity, the total load is instantaneously applied to the

mass-single tooth pair system.

For single tooth pair contact the equation for dynamic loading becomes:

msr +bsr +Ksr =W

(2. 19)

Using

obtained.

-

r

2 st

'nb

r

At t =

0,

the parameters defined in Sec.2.3, the following equation is

+ s

r

St:

r

5 + r=1

s t

_r

5

_r

₁

_s

- = - and = 0 5

_rt

₂

5

_rt

Let

nb n Pb =

I0

(2.20)

(2.21) W nd = [1

Using the initial conditions and Eq. (2'. 21), the solution to Eq. (2. 20)

becomes:

-pW t Pw -n

rcos

wndt +

In

sin wnt

(2.22)

The maximum values of Eq. (2. 22) are desired for the various values of p. It was found that the maximum values occurred when

ndt=r

or

(2.23)

n

1

= 1 + -e 2

(2.24)

The values of (sr/srt) max - 1 for various damping ratios, p,

are listed in Appendix A.

These are the maximum values of Wi/Ksrt, In Fig. 3,

for large values of P .

2. 5. Analysis of Dynamic Loads for Small p

A small P implies that the periods of the natural oscillations are

small compared to the time of disengagement.

For a very small

P

the dynamic effects and viscous damping in

Eq. (2. 12) may be neglected.

Equation (2. 12) becomes:

2 2 2

r

+

9

na1 t= 2 2

st 2 4 2 tnb, r

(2.25)

JI

st

r

1

-2

e

s

s

t

rmax.

.--

2

Disengagement occurs at time, t2 , as shown in Fig. 2.

point,

u

s _{rt t} r

(r~

2

Therefore

2 2 2

P

"nb

t

2 =

1

1

2

2

- + - W 0'b t2 2 2

Solve for

P2

and substitute the value in

sr i st 2

r

r

Eq. 2

(2.25)

1

+

- -t ) t2

t

2 (2.27) (2. 28)

Let

Pb

P

tt = t = t₂

Therefore the equation for single tooth pair contact becomes:

eq0 S

r

2 s t r 2p 8r S

-+

--n s t = 1 (2.29)

(2. 30)

srt

r

12

(2.26)

1

At this

mFT ======1=1=========-1=Vi===A

Ir

==============I== miniliiiiiiiiiii~~~~~~~~~~~~~~A 0-iiilnni!iiiiinn~iiisilsiiiiiiiiiin n =====or

EI

0====!=============

!!ii!!iiniiill iiiiiiiiiiiii!i~n!!!=!!!!!!!!!iiiiiiiin!!!!!!!inniinilOF

nil====!==!===========

!!==!!!!i!=! lin!!===5ui!Enisgun=i!!nin=i!!u!!n=.00'i

;ooiiiiiiii -A iiiiir nnaiiiinnnnn!iiiiiiiii I I Jiiinnii

=====nnn====Pi

.000

VM M V==========

=!uilinnini

iiiiiiiii~in~ijjisiininliiiiii!!!nilininin!=ii-00=

==muu===w====uuliana~~..00=============

========:==========================IF

iiilitiiiiii'OF i!!!in 2M nli!!

=

ii! i!! i

=

! I ITT

-11"Pl-

6 1 ni

u!=i===, y 1)'

731!=

Eii!uinnn!!!!!M !,==!!==!ui

ininininili!!i!!~ lii

~~~~

IfIn i!EilljnI!!= = !ii!ii= iiiin!

======-

-

==

- -

.---======= ======

========~~~~~~~

Af I=================

iiii!!iiiiiiiiiin l~~~~~~~~~~~~~~IFi= 2!!iiin!!!!iiiiiiiiiiiini!=iiiii!

=======

~xmm~i=========mu======='OF=

======

========================e=

At t' = 0,

0

s

r

r

1

and -

_

srt

srt

t

With the above initial conditions, the solution of Eq. (2. 30) becomes the

following, for p 4 1

=

1+e Pwnt

st

r

s

inf1

- p2

nt]

(2.31)

TI2

The maximum values of Eq. (2. 31) occur when

tann

p

The maximum values of Eq.

various values of p. These values

curves in Fig. 3, when

P

is small.

For critical damping (p

=

1),

becomes:

s

.=

1+

w C)t' e

St

n

r

(2. 31) are listed in Appendix B for

are used to find the initial slopes of

Eq. (2. 30) with its initial conditions

- ti

n

(2.32)

For overdamping (p ;P 1), Eq. (2. 30) with its initial conditions

becomes:

s t

r

n

p

/T-2

(2.33)

'A

s inh 172 _nt

s

S t)

_mrx

-pW t!

_1+ e

n

p

tanh /p I~ w1t '

=

_2 ~ P (2.35)

The values of Eq. (2. 34) are listed in Appendix B.

2. 6. Analysis of Loads Excluding Inertia Effects

When the inertia effects are neglected, Eq. (2. 12) becomes:

2 pa _{s r} ) s t

na

r

2 2 2

+

-

+

na

srt 2 4

r

(2.36)

Remembering Eqs. (2. 19), (2. 10) and the initial conditions for

Eq. (2. 12), the solution of Eq. (2. 36) becomes:

%bt

2 m

Sri1

2

2

- =- 4

_P2Pb

_e

s t

2

r

+ 8pb2 - 4Pbanbt + wnb t2

JF

(2.37)

Separation occurs at time, t₁, when

S(r ti rA W

u

sr wnb ~n Pb

P

'5

when

(2.34)

Let

Therefore

nt

1 = + e 2 + 4pwnt 8p2 8np (2.38)

p

2

The solutions of Eq. (2. 38) are plotted on Fig. 4. These are the points where the tooth pair separates. Notice that for large pn, Pn approaches 1/42 and for small pn' Pn approaches 1. 0.

For a very large cnt , and small pn' Pn approaches 1. 0 but

P

a 1/wn t [ and therefore

P

will be very small. In Sec. 2. 5,

P

was assumed very small. This is now justified because when

p

1. 0,

then separation will occur when sr/srt Q 1. 0.

In Sec. 2.4,

p

was assumed very large. This corresponds to a small w ti and consequently a large . Pn approaches 1//Z which corresponds to an initial displacement, s rt = 1/2.

However, it must be remembered that this curve can only be correctly used when mass or the inertia effects are small.

Now that the separation values are known, the free vibration of the single tooth pair is analyzed for a damping ratio of one; that is,

critical damping. It is desirable to know whether or not there is any over-shoot in this case.

Using the conditions in Eq. (2. 29) along with Eq. (2. 30), the general equation for critical damping (p = 1) becomes:

s _{-w t'}

r

n

(.9

-= 1 + (A + Bt') e (2.39)

s t

_r

The initial conditions for this equation are taken from Eq. (2. 37)

Therefore, at t' = 0, s

A -1 (2.40)

srt

I 1 1.

~~~~H

I I I IH MI i M I . L I I. U . Io

11HI I

i i II I I i1

H

0

H

1

I

M il 1 1 1 1. .oooo H I 1 -11 1 1 1 11 1 11 A l I 11 i 11 I .1 1 i 4 'D

OV

i-

01

OT *0

Iw

.

0

ITT 7116- I .~ I HI 7 1 mWM .M -M I I I

m

.. 1 .1 . 1 1 H il r I~~~~~ I II H 1 I. I Il d i I H il 11 .H 1 1111 .s m .M .111 IM..

a-

. 1~~

~ ~~~

i H i l I t s a em .. .m o = - 2

I1

=.

. rm1

=.

.

ti

8

sr

ti

If there is any overshoot then

sr/srt

=

0.

Therefore e-Wnt (B - wnA - B nt') = 0

n

n

This occurs when

B - w A - Bw t'= 0 n n

Let

-

A=

U s sV n (s t rt

Then

W t' = 1 + --..

_n

V

U

Using Eqs. (2. 40), (2. 41) and (2. 43) the value of V/U is calculated.

From Fig. 4, for small

P

p

_{and small wt}

₁

_,

_w

_Cnt,

and large w

tj, pw

nt approaches 1.

For large

approaches

1/2T.

When PCnt =

1

V1

U

4

When Pwnt

=

/J7

U

1

2

18

(2.41)

(2.42)

(2.43)

(2.44)

s B = r-E s r t

For all other values of wnt1 between 1 and 1/2 the values of V/U fall between 1/4 and 1/2. Within this range wnt' falls between - 0. 33

and -1 which can never be, since t' and u are always defined to be positive. Consequently for damping equal to or greater than one there will be no overshoot.

2. 7. Summary

In this chapter, the maximum dynamic load in a tooth pair was calculated for different damping ratios. The teeth were considered to be heavily loaded and one tooth pair was disengaging or moving out of

contact. For very large "P, the maximum incremental dynamic loads were plotted for various damping ratios.. Also for small P, the initial slopes of the curves, Fig. 3, were calculated. The curve for no damping was taken from Ref. 1 and the other curves were estimated, knowing the initial slope and maximum value for each damping ratio.

With inertia effects neglected, the parameters, pn and Pn were calculated at the point where separation of a tooth pair occurs. It was also shown that for critical or supercritical damping there is no over-shoot and therefore no dynamic incremental load on the gear teeth.

3. DYNAMIC LOADING, STRESS AND DEFLECTION CYCLES IN SPUR GEARS WITH A MANUFACTURED ERROR

3. 1. Objective

Wayne O'Neill, in his Master 's Thesis 3 wrote a program to be used on the IBM 704 Computer at M. I. T. This program was written

in order to find the dynamic loads, stress and deflections, in a perfect set of gears. The object of this chapter is to extend this program to include a manufactured error and to study the effect this error has on the dynamic loads, stress and deflections of spur gear teeth.

3. 2. Basic Equations Used in the Program

The following equations are essentially those derived by Richardson in Ref. 1 and are only changed in order to facilitate their use on the

Computer.

The equation for the normal pitch is:

P = .- rR cos

e

(3.1)

where

R = pitch circle radius

E

= pressure angle (200

i = number of teeth on the gear of radius R.

The normalized distance along the pressure line from the theoretical end of contact is:

P

n where

s = the distance measured from the pitch point, along the pressure line, to the actual point of contact of the tooth.

s = the distance measured from the pitch point, along the

pressure line, to the theoretical point of contact of the tooth

The normalized no-load separation along the pressure line is

,s cP n 2 (3.3)

P P n

where

c = the no-load separation constant or the cam constant.

The normalized theoretical distance to the initial or final point of contact is

s

Pn 2-rrcos

[

sin 2 e + 4cL

4a

_{- -}

i+

a

-

sinO

3

_(3.4)

where

i= the number of teeth ai gear 1.

aa = addendum distance of gear 1. (Ref. 1)

soe/Pn is the normalized theoretical distance to the point of en-gagement of gear 1. In order to calculate sld/Pn, the point of disengage-ment, i1 is changed to the number of teeth on the mating gear and aa is changed to the addendum distance of the mating gear.

The theoretical contact ratio is

n

Sf,

+

d

n

The compliance of a tooth-pair, at a certain sPn , is given by

+

= (

-n

)

8

+

A 7 )

+

A6

+

A

5 ( n nP n )' n) 4 3 2 + A4 s + A3s + A2s + A \ n 3 / s 1 I P

+ A

₀

(3.6)

(3.5)

This equation was formulated by O'Neill and Skinner 3.

The Taylor

Series coefficients, A

-

A

0

, were calculated by a program written by Skinner

and are presented in Appendix C for a gear and pinion of 27 and 18 teeth, respectively. Essentially this equation describes the curve of compliance in Richardson's thesis.

The bending stress in the root of the tooth being investigated is calculated from the Lewis equation which is normalized to the form below:

cb n

W

w

2

1

=-- cos

e

-W

_y

(3.7) where

a-b = the stress in the tooth being investigated.

W

=

the total load being transmitted.

W

=

the load in the tooth being investigated.

W

=

the total load per unit thickness.

1/y

=

the Lewis Form factor defined below.

3 cos

jCosd

\Cos

0/

J

i -

2CLd

-

..L.i

3cos cos

_Cos()

_J

i _i - 2d i) )2

_(inve

+

--i >38 teeth

i 438 teeth

where

*=

0

- 2ns/iPn - r/Zi

=

cos~

_{(cose /i-2ad/)}

22

1

Y

(3.8)

The manufactured error ratio is

E

E

p

T2

-- m mpe c (3. 10) Sr P 2 c

n

e

Unfamiliar parameters are defined further on in this chapter.

3. 3. Discussion of the Problem and Assumptions

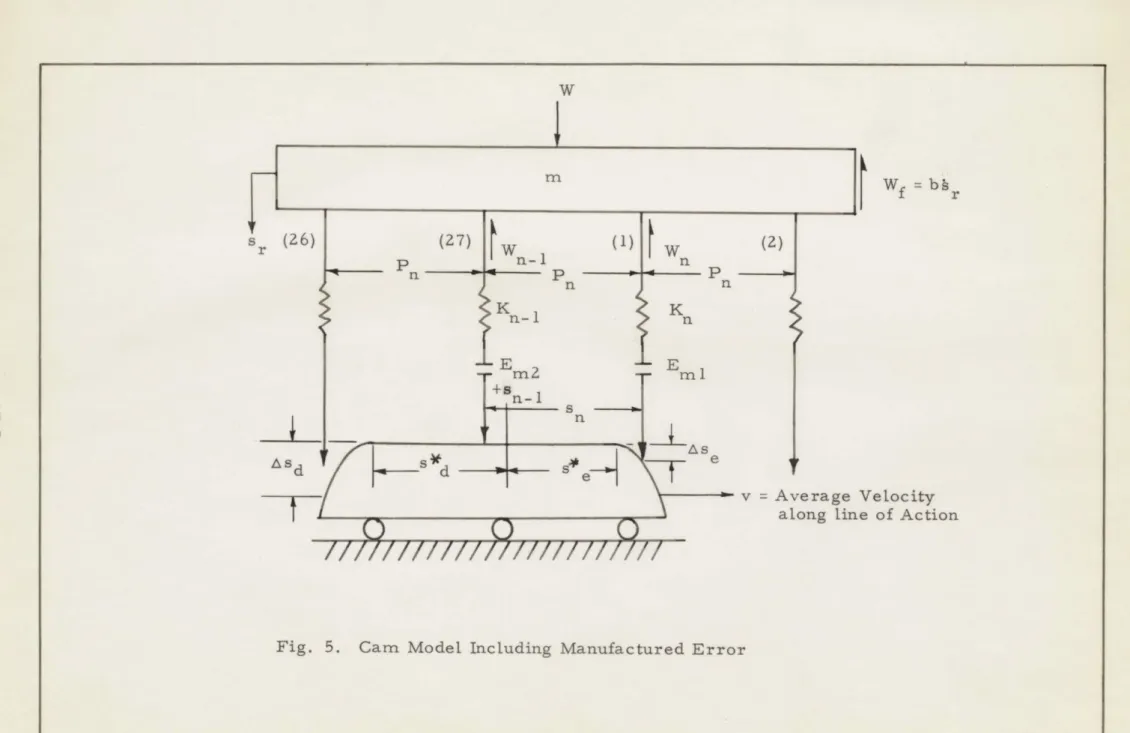
The spring-mass-cam system in Fig. 5 is a modification of the

1

Richardson Model . Tooth-pair (n) is always considered to be engaging

and tooth-pair (n-1) is always considered to be disengaging. A cycle

starts at the pitch point of tooth-pair (n-1) and ends at the pitch point of tooth-pair (n).

Since one tooth in the gear (27 teeth) has an error, a counting system is set up to include the error once in every 27 cycles. The

dynamic loads and stress are calculated for a tooth in the gear. Also the pinion is driving the gear.

Tooth-pair 1 is considered to have the error (-Em). When tooth-pair 1 is engaging, it coincides with tooth-tooth-pair (n). At this time Eml assumes the finite value, -Em. At the end of this cycle tooth-pair 1

coincides with tooth-pair (n-1). Therefore, EM2 assumes the finite value, -Em.

m

The initial conditions are not known for the solution of the differential equation, therefore, they are assumed initially and the differential equations are solved for one cycle, and another set of initial conditions are found.

This is repeated until a steady state is reached.

In order to save computer time, the program is set up to obtain two steady states, one with only perfect teeth and one after the error tooth has been through the mesh. If these two steady states are the same, then the

steady state obtained is the correct one. When the steady state is reached a plot and print-out of the load, stress and deflection ratio, of the tooth following the error tooth are produced.

m -. I

Wf

= bhr

r (26)

(27) w (1) (2) K Kn + n-1 n S sd

de04

S V= Ave alo

U

U

U

rage Velocity ng line of Action

Fig. 5. Cam Model Including Manufactured Error

71

S

//////,/////////

////

Perfect teeth are assumed except for tooth-pair 1 which has the negative manufactured error (-Em). This error remains constant

throughout the mesh. Viscous friction to ground is assumed. The maximum contact ratio is less than 2. 0.

3.4. Dynamic Load Equations

The general equation for the model (Fig. 5) is

mg + bt + W + W =W

The parameters are now defined.

the natural frequency of the gear system oscillating

on tooth-pair spring at tIrpitch point.

/K

mn~

b

p, =.

e

... ".

fre

hn rt tra

damping ratio

quency ratio for single load

nsfer

Pd

_v

d

Wa s t

n

s rt

.5s v

T

C

P

n

V

t=

W t

n

T 'w

_c

_nc

T

252

(3. 11)

(3. 12)

(3. 13)

(3. 14)

(3. 15)

(3. 16)

(3. 17)

(3.18)

(3.19)

S t n Srt t '

C

w

K 0

s

r du dt' ds

1

Ws

t

n r

r

dt

The superscripts are now dropped for the following equations.

Tooth-pair (n-1) is on the flat. No other teeth are in contact.

'd+ 2pti+ Ku u- E )2

T -r

Tooth-pair (n-i) is on the flat and tooth-pair (n) is engaging. u

+

2p

ii +

K 0

EM2

₎₊

Srt [1 K K4 where As -- c P s t e n r = e2 Tc n-i st r

(1

26

(3.20) (3.21) (3.22) (3.23) Case 1 Case 2 (3.24) As e s rt

)

= 1

Eml s rt (3.25)

Or2

e

n 2 (3.26) s *

- t

P

(3.27)

Tooth-pair (n-1) and tooth-pair (n) are both on the flat. \T+ ZpA+ K --IK, 0 Case 4 flat. E M2 m t+ srt K n K 0 Eml 8rt

Tooth-pair (n-1) is disengaging and tooth-pair (n) is on the

ft

9

+ Zpd +

K K 0 Asd srt r _ M2 s rt )

+

K

(

-n

E

=1

(3.29)

K srt o r - Pd t -s d] C Pn Case 5 flat.

Tooth-pair (n-1) is out of contact and tooth-pair (n) is on the

K I

UW+

2 pt + n

u-K

0 E m srt (3.31)

Combinations of the following conditions define when the above cases apply.

Conditioni: (u - As /srt - E 1 /srt) 4 0

This means that the force in tooth-pair (n) is negative, which is physically impossible with no-backlash. Therefore, tooth-pair (n) has not come into contact and this term must be held at zero, until it becomes positive, indicating engagement.

Condition 2: (t - Tc s )I Irt) 4 0.

This means that tooth-pair (n-1) is on the flat, therefore Asd/srt must be held at zero until this term becomes positive.

27

= 1 (3.28) Asd st (3.30) Case 3

Condition 3: T(I - s */P) - t] 6 0.

This means physically that tooth-pair (n) is on the flat, therefore

se/s rt must be set to zero.

Condition 4: [u - Asd/ rt - EM2 40.

This is similar to Condition 1. This term must be held at zero because tooth-pair (n-1) is no longer in contact.

Condition 5: t = Tc

This indicates the end of the cycle. The gears have advanced one normal pitch.

Condition 6: Counter R = 1

This indicates that toch-pair (n) has the manufactured error. Em2/sr t is zero and Emj/srt is set equal to -Em/s rt.

Condition 7: Counter R = 2.

This indicates that tooth-pair (n-1) has the manufactured error. EmlI/srt is set to zero and E m/srt is set equal to -Em/srt.

The following are the combinations of conditions which define when we have the previously defined cases.

Case 1: Conditions 1 and 2 hold. EM2/srt = 0 unless condition 7 holds.

Case2: Condition 2 holds. Condition 6 or 7 may hold. Condition 1 is violated.

Case 3: Conditions 2 and 3 hold. Condition 6 or 7 may hold. Condition 1 is violated.

Case 4: Condition 3 holds. Condition 6 or 7 may hold. Conditions 1, 2 and 4 are violated.

Case 5: Condition 3 and 4 hold. Condition 6 may hold. When condition 5 is reached the cycle is repeated.

P RINT 2 6&

cL

b STP

₄

Y ES NO YES 15a. i~a

STA RT LOAD I PRINT I _{YES PN}

13 /4NT yNo yNo

1

2

3

4

₁₆

0

I 1

3

1

5

l

17

Yes

246

TEWM A TERM I INo

27

26

25*

24 YE

23

2

1YS2

YE S

NO NO

TERMI

TERM I

TERM 2

24&

23& YES

NO

B

Fig. 6a. Computation Flow Diagram

/74

No

YE5

PRINT

26

29

30

YE

13

NO

O

NO

I

3

NO

Y

S

IS

IYE31

32

15CL

1 6C

lI

.

33

L

41

YES

40

39

YE

337YES

36 Y'Es 35

34

NO No PAINTr 6 PLOT NO

37

PLOT

Fig. 6b. Continuation of Fig. 6a

3. 5. Symbol Table

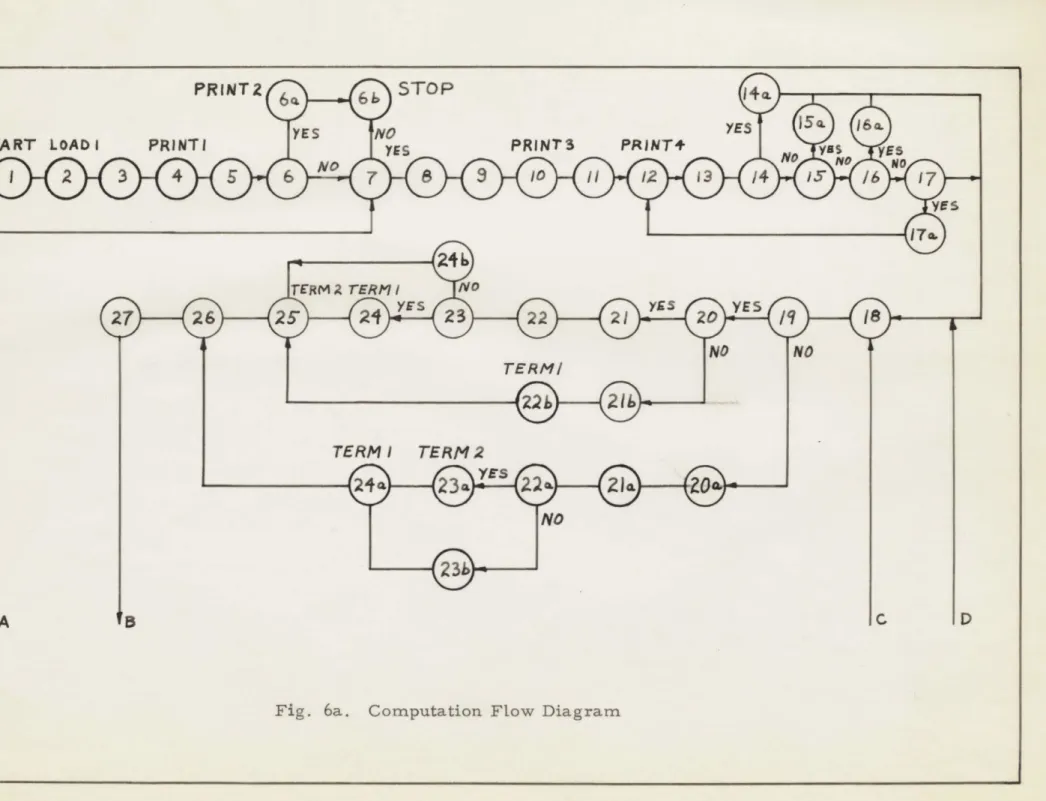
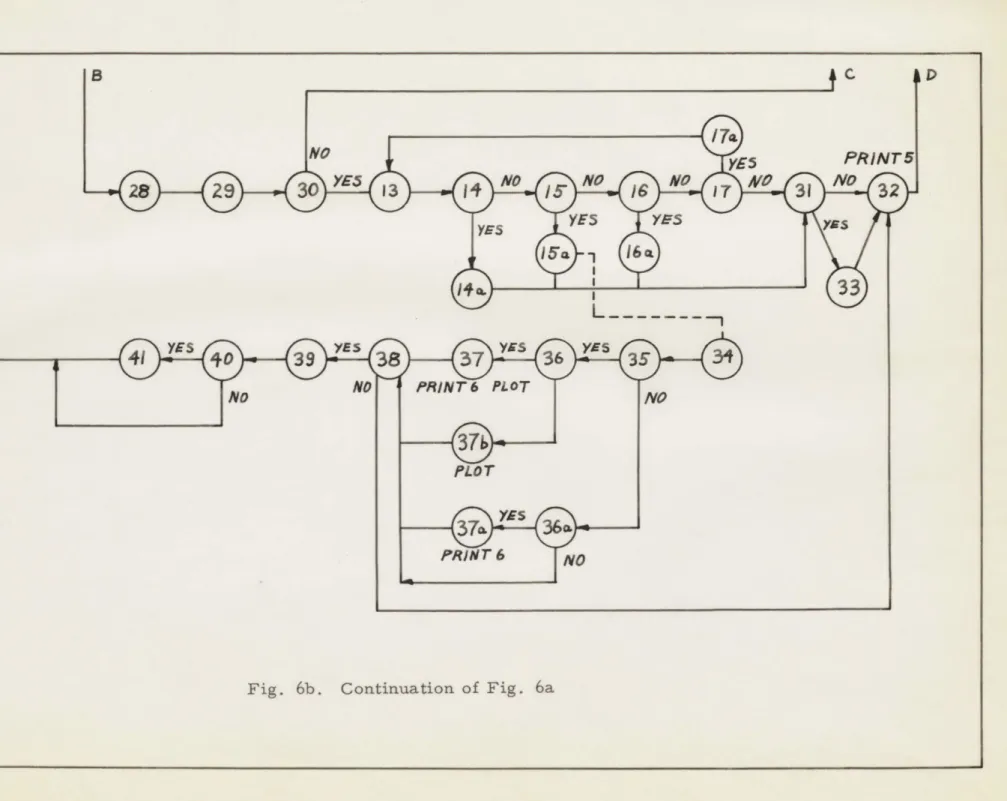
The following symbol table is to be used in conjunction with the Computation Flow Diagram, Fig. 6.

1. Start program.

2. Load 1 - Load data which may vary with each run but not with each pass. These constants are: e , aa, Cd, A9 - A0 (Taylor Series coefficients for the compliance or stiffness curve), max-imum permissible error ratio used in the integration sub-routine, independent variable spacing, u(t = 0), ti (t = 0), i and i , radius

gP

of the gear (R

),

no-load separation coefficient (ce) and profile error (-E).

3. Compute s *VPn, s '/Pn and theoretical contact ratio (T. C. R.). 4. Print 1 - Print out values of i , iP, T. C. R.

5. Compute Part 1 of the inverse Y factor constants. 6. Does i = 38?

g

6a. Yes, 1/Y not defined. Print 2 - Print out "Number of teeth = 38". 6b. Stop the computer.

7. Are there any more variables to be loaded for the next pass?

8. Load 2 - Load data which varies with each pass. These constants are

Pe'

Pd

Tc, 2Q, steady state determining reference (Ref. 3),

initial number to be placed in Counter R (the counter which determines which tooth-pair is in contact), case number for print out and alpha-numeric plot, format 1 and 2.

9. Initialize program.

10. Print 3 - Print out E, Sie/n, s *d/n' e #d, Tc, 2Q.

11. Compute Em/srt

12. Print 4 - Print out Em/srt

13. Increase Counter R by 1

14. Does Counter R = 1 ? Condition 6. 14a. Yes, set Emi/srt _{= Em/s rt'} 15. Does Counter R = 2 ? Condition 7.

15a. Yes, set Eml/srt = 0 and E m/srt = Em/srt'

16. Does Counter R equal an integer between 2 and 28? 16a. Yes, set E /srt = 0, Eml/srt = 0.

17. Does Counter R equal 28? 17a. Yes, set CounteT R = 0.

18. Compute K n-/K _{and Kn/K0 as functions of s/Pn.} 19. Is (t - T s* /Pn)

' O?

Condition 2.

20. Is (T (1 - s Ite'n) -' t) 1

o?

Condition 3. 20a. Compute Asd/srt.

21. Compute As e/srt.

2la. Compute (u - Asd/srt - Em2/srt) = term 2.

21b. Set Ase/srt = 0. Condition 3 satisfied. 22. Compute (u -

As/srt

- Emi/srt) = term 1.

22a. Is term 2 positive? Condition 4.

22b. Compute Kn/K, (u - Em1/srt) = term 1. 23. Is term 1 positive? Condition 1.

23a. Compute Kn-i/Ko

(u - Asd/s

rt

-

EmZ/rt)

= term 2.

23b. Set term 2 = 0. Condition 4 satisfied.

24. Compute Kn/Ko (u - Ase/srt - Emi/srt) = term 1. 24a. Compute Kn/K0 (u - E M/srt) = term 1.

24b. Set term 1 = 0. Condition 1 satisfied. 25. Compute K n-/Ko (u -

E m2/srt)

= term 2.

26. Calculate u = 1 - 2p u - n- 1

/K

0 F(u) - Kn/KoF(u).

27. Integrate ' to obtain u

-28. Integrate 11 to obtain u.

29. Enter up-date sub-routine. 30. Is t r T ? Condition 5.

31. Has the steady state condition been reached? Is I u(t = 0) - u(t= TC)1.4

Ref. 3?

32. Initialize for start of another cycle. Print 5 - Print out u(t=0 ), u(t=0), u(t= T c), u(t= T d

33. Has the error tooth been through the gear mesh? No,, proceed as indicated and calculate until another steady state is reached.

Yes, proceed as indicated for only one cycle. The dotted line from (1-%) to (34) shows the exit of this cycle. This initializes u and A for calculation of the load and stress in the tooth following the error tooth, tooth-pair 2.

34. Compute part 2 of the inverse Y factor and calculate the stress in the tooth following the error tooth.

35. Is sense switch 3 down for plotting on the scope? 36. Is sense switch 2 down for print 6?

36a. Is sense switch 2 down for print 6?

37. Plot (W/Wo)n+1 versus (s/Pndn+i on the scope and print 6. In this case (n+1) stands for tooth-pair 2.

37a. Print 6 - Print out error ratio, load, s/Pn, stress, time and

sr/srt. No plotting.

38. Is this the end of the first pass?

39. Print 7 - Print out actual contact ratio, maximum dynamic stress, maximum dynamic load, number of cycles calculated.

40. Is sense switch 3 down for plotting on scope?

41. Plot grid scales alpha-numeric information on scope for

(W/Wo)n+1 versus (s/Pn)n+1 and then plot the nominal dynamic stress versus (s/Pn)n+I with its grid and scales and alpha-numeric information.

3. 6. Notes on the Program

It has been suggested in Wayne O'Neill's thesis3 that the following values be used when operating the program.

1. The independent variable spacing should be divisable into

Tc from 150 to 250 tirnes. These are the number of corrector integrations which take place. 200 was found to be about optimum.

2. The integration error ratio should be between 0. 01 and 0. 0001.

0. 001 was found to be optimum.

3. Reference 3 for steady-state comparisons should be 0. 0005 but may be increased for low damping ratios in order to de-crease the amount of cycles required to reach steady state. However, a value of 0. 0025 was found to be quite satisfactory.

When Counter R reaches a value of 28, the error tooth is introduced

and Counter R is set to 0.

The initial input to Counter R is from an actual

number in the data deck. This number should be law enough to allow a

steady state condition to be reached on perfect teeth only. Once this

condition is reached, the error tooth is immediately introduced, and the

calculations proceed until the next steady state is reached.

In all calculations and in the analysis, Em/s rt is considered to be

the absolute value of the error ratio. However, a negative value of error

is placed in the data deck so that the print out will emphasize the negative

error.

3. 7. Results

The tabulated results of selected runs are listed in Appendix E.

In Fig. 7, photographs of the plotted results from the cathode-ray

tube are displayed. From top to bottom, plots are shown of Case 2, 3,

and 4 respectively.

The teeth are shown coming into contact in the region

of s/Pn

= -

0. 8.

The tooth comes into contact with the load on its tip and

leaves contact with the load on its base. These plots illustrate the

different effects on the tooth preceding the error tooth, the error tooth,

and the tooth following the error tooth respectively.

In Fig. 8, the effect of a large error ratio is shown.

The load on the

teeth is effectively low, therefore, the manufactured error is predominately

large compared to the deflection of the teeth. The tooth comes into contact

much earlier than it normally would. In effect a positive error may be

consid-ered to be on this tooth.

When contact is made an impact load is placed on the

tooth, which imports a large stress on the tooth.

When larger loads are placed on the teeth as in Case 4, the

manu-factured error ratio is reduced and the initial load is reduced considerably,

as shown in Fig. 7.

It is suggested that this program not be run for manufactured error

ratios less than 0. 500. It was found that below this amount the integration

routine would produce large errors.

3. 8. Summary

A program was written to include the effect of a manufactured error

on the dynamic loads, stress and deflections of gear teeth. The results

obtained compared favorably with the theory of gear teeth action.

65 -0-DYNAMI C 4-0-LOAD 3-20-0 OYNAMI C 1 5 -0!-MOM INA L: I

{

10 -RATIO 2-0 - - -(W/WO) 10--.-5 -1-0 0.0.

NORM- POS- A -L-O-A - * S/PN

DAMPING RATIOwO-10

TC=20- 0,BEI -0,SO I-0, IG 27, IP m18

M G MEACHER M11104 SPUR GEAR STUDY C

BENDING STRE 5-0- - -

-SS

0

.-L L

I-1.-S -1-0 0.0m

NORM- POS- A -L-O-A- 8/PNS

DAMPING RATI =0-10

TC=20 - 0, BEaI -0, BD I-0, IG m27, IP .18

M G MEACHER M 1104 SPUR GEAR STUDY C

--L

-6 - OT 5 - 04-DYNAMI C 4-0-LOAD 3-0-RATIO 2-0-(W/WO) I-0* - - -0-0. -1-5 '-1 -0 0.0

NORM- POS- A -L-O-A - * S/ PN

DAMPING RATI O0 10

TCu20- 0,BEI -0,BD 1 -0, IG s27, IP mIS

I G MEACHER M 1104 SPUR GEAR STUDY C

DYNAMI C LOAD 3-0-- -.-- - --RATIO 2-0- -(W/wO) 1-0- 0.--A -5 -1-0 0.0

NORM- POS- A -L-O-A - a S/PN

DAMPING RATIO.0-O 0

TCu20- 0,BEI -0,BD. I-0,IG =27, IP m1

M G MEACHER M 1104 SPUR GEAR STUDY C

20- 0 DYNAMI C NOMINA L 10-0-BENDING 5-0-STRESS -. 5

-I

F--1-0 0-0

NORM- POS- A -L-O-A- * S/PN

DAMPING RATIOw 0-10

TCw20 - 0, BEI -0, 0. I-0, IG m27, IP m18 M G MEACHER M11104 SPUR GEAR STUDY C

DYNAMI C 15 0 -NOMINAL BENDING 5-0- -STRESS 0 .0 Li- L I -1-5 -1-0 0-0

.NORM- POS- A -L-O-A- * S/PN

DAMPING RATI O.0-10

TC120- 0,BERI 10,B4 I -0,IGE7, IP= M G ME-ACHER M 1 04 SPUR GEAR STUDY C

Fig. 7

b *V

5

-0

DYNAMI

C

4 -A

LOAD

RATIO

2

00---

4-(W/WO)

-L5

-1-0

0.0

2-030

NORM-

POS-

A-L-0-A

-

S/PN

DAMPING RATI

O0-10

TC.20

-0,BE=2

-67BD

=240, IGu27o IPml

M

G

MEACHER

Ml

104

SPUR GEAR STUDY C

/.- V

DYNAMI C

mnMTMdIL

BEND

a

ING

-5 -

. .

STRESS

0 -

0-

---1-5

-l-o

0-0

2-03-0

NORM-

POS-

A-L-O-A

-

S/ PN

DAMPING RATI

O0- 10

TC.20

-

0,BE=2 -67,80 m2- 40, IGm27o IPaI

M

G

MEACHER M 1104 SPUR GEAR STUDY C

Fig. 8

15 O

-CHAPTER 4. SUMMARY, CONCLUSIONS AND RECOMMENDATIONS

4. 1. Summary and Conclusions

This thesis has been concerned mainly with the dynamic loads and stresses in gear teeth under various operating conditions.

An analysis of damping was made using a spring-mass and cam model of gear tooth action while single load transfer was taking place.

The maximum dynamic loads on a tooth-pair under idealized conditions for various damping factors were calculated and plotted against the frequency ratio p. The oscillations caused by previous load transfers were assumed to have died out. This was found to be a good assumption when the damping was critical or supercritical or the frequency ratio

P

was small.

A digital computer program was extended to include the effects

of a manufactured error on dynamic loads, stress and relative deflections of a set of gear teeth. Print outs and plots of these factors were made against the distance along the line of action of the tooth-pair as it moved through the gear mesh. Comparisons of the dynamic load and stress cycles for the tooth preceding and following the error tooth, and the error tooth, made with those of the static case (Ref. 1), proved to be quite satisfactory.

A large error ratio was investigated which showed how comparatively

-large stresses can be imposed on lightly loaded gears because of early contact.

4. 2. Recommendations

On the basis of this investigation, the following recommendations are made:

1. A short digital computer program should be written to solve

the cumbersome dynamic equation derived in Sec. 2. 2, which describes deflections of single load transfer of a single

tooth-pair for various damping and frequency ratios.

Z. A digital computer program should be written to include

more than one manufactured error. The errors could be programmed so as to vary as the tooth-pairs moves through the mesh. Positive errors and negative errors could be included in the same program.

APPENDIX A. LIST OF[(sr/srt) max

s

st

r

- 1 VERSUS p FOR LARGE

p

Wd Ksrt Wd =

W+ W

(Wj/Ksrt)

0

max

0.00004

0.00076

0.023 0.048 0.127 0.26

0.36

0.43

0.45

40

P

0.95

0.90

0.70

0.60

0.40 0.20 0.10

0.05

0.03

APPENDIX B. _{LIST OF (s/srt) VF} s

_wd

s t Kart r r

Wd

W+W

p

_(W/Ksr

max

0

1.00

0.05

0.926

0.10

0.862

0.20

0.756

0.40

0.602

0.60

0.498

0.70

0.460

0.90

0.394

0.95

0.381

1.00

0.367

1.10

0.351

2.00

0.336

10.00

0.050

4141

APPENDIX C, LISTING OF PROGRAM FORMAT, OPERATION CARDS AND A SAMPLE DATA DECK

RUN 111O4*d60 V.ACHE.I04 SAP M1104*680*GEAR STUDY LST OFF

SMT OFF PRG OFF

INSERT PROGRAM WRITTEN BY AUTHOR, APRIL,1960

LISTED IN APPENDIX D

INSERT THE FOLLOWING SUB-ROUTINES (REF 3) IN ORDER.

1 INTEGRATION ROUTINE WRITTEN BY WAYNE ONEILL-1959 (151 CARDS)

2 UPDATING SUB-ROUTINE WRITTEN BY WAYNE ONEILL-1959 (74 CARDS)

3 GRID PLOTTING ROUTINE FOR COVERING ARBITRARY PORTION OF SCOPE

WRITTEN BY WAYNE ONEILL-1959 (47 CARDS)

4 SCOPE CURVE (POINT) PLOTTING ROUTINE USING ALL OR ARBITRARY PORTION OF SCOPE (MUST BE USED WITH CR4 FOR ARBITRARY GRID) WRITTEN BY WAYNE ONEILL-1959 (102 CARDS)

5 NA.110 WRITL BCD CHARACTERS MODIFIED 8/18/58 BY ONEILL END START

SAMPLE DATA DECK CLR PAK RIP M'1104*880*(LAR*STUDY SWD 2,3 bGN M1104*880*GcAR*STUDY DEC 0.3490b69,l.0,l.157 YEC -5.0484973,-9 .9537395,9.5206339,10.0963819-5.8866139 DL.C 2.2752402,1.b532521,10.768726,0.3826269 17.924958 VEC 1.0#0.U. DEC 1.0 DLC 0.0 DEC 27.0,lb.0 DEC 4.50,0.5432,-O.001-DEL 2.670

,2.45,2e0o0o.2oo.ou

OCT 000021000000 BCD iSE UD BCL 1 05 BCD OTC=2O.0,ouE=2.u/7 ,DL=2.40, =27 , IP= BCD 40AMPINGi -(ATIu=o.10

INSER T UAFA CAR06 FOR S.CUN PAS6. KLFLk Tu rI.6

TRA 3,4

INSERT DATA UECK FOR %ECOND RUN. REFER TQ -IG.6 TEk M1104*880* ivEACHER*04

APPENDIX D. PROGRAM LISTING

PL.Vi r 1\ . I\-' I I \'.1 tM .A L . t I L L,.1' \4/~~ , I - I A l I r L.dQ .)9 i i

REM DEFLECTIONS OF GEAR TEETH WITH MANUFACTURED REM' ERikOR jNCLUVLL.

REM WkITTEN bY Mv*e MEACHLk APRIL i bU

REM PAK SYNONYM TAbLE APRIL 25,i900

CUMMON SYN /25

SQRT SYN /356 M SRT I

CQ1 SYN /42-3 UAS+Q1

6IN SYN /424 UAS+CI LOCK SYN /520 UABLCI

SET SYN /1342 iiIF TD T

OVER SYiN /137.: MIFTL)T

WOT SYN /1376 UASTHI

ARCO SYN /21 CLASCI

TAN SYN /2245 LLTANI

LOAD SYN /3534 UADBCL

FINISH SYN /4320 UADBCL

RTX SYN /4321 UATSM2 ORG FINISH TRA END ot<G uVER TRA INTEG-2 ORG /1070

REM LUADS DATA (CUNSTANTS FOR EACH RUN)

START TSX LQAD.4 PZE THETAOAO TRA *+2 TRA END TSX LOAD,4 PZE INTEG+149,0,INTEG+150 TRA *+2 TRA END TSX LOAD,4 PZE U,0,U TRA *+2 TRA END TSX LOAD,4 PZE U1,0,Ul TRA *+2 TRA END TSX LOAD,4 PZE IG,0,IP tRA *+2 TRA END TSX LOAD,4 PZE RG,0,.Eiv TRA *+2 TRA END ToV *+I TOO *+I CLA THETA TSX. COS,4 STO COSTH CLA THETA TSX SIN,4 STO SINTH CLA THETA TSX TAN,4

45

STO REF7 CLA Ul

STO REF8

REM CALCULATION OF S*E/PNS*0/iNANU THLURLTICAL CONTACT RATIO LXA COUN9,1 CLA IG STO I CLA 11 FA) AA FDP Ii FMP FUUR FL)P -II FiAP AA L TL - S I N H L~ SiNTH F PvF SINTH FAL) C U1MM1ivUN TSX SQRT,4 TSX iERROkt4 FSb SINTH STU C 0 UN+1 LLQ TWQ FMP P1 5 T C U!.:1,/ UN L)U CUS TH FMAP CcO~MN STO i:PICU CLA l Fw' 2PICQ FMP CQMMUN+1

STU

SL+2,1

TIX +,1 i TRA +4 CLA IP 6 TO Ii TRA START+42 CLA SE F ) 3Tu TCR TSX Fk4T4,4 P Z.E I j0 0qTcRl\

RkLv PAR\T 1 OF SiESS iVERSt:. Y FACTuw- CLUL.TiuNS L)Q TWQ eMP AL) FAU Iu fL) I ST(Q TEPA LO T ENiiP A FMP TEMPA STU COMiHN LDQ COLM-N FPP IG STU TEiMP6 CLA TEvlPA FiL' CL)STH

46

S TO LQ STL CLA FiP STh CLA FAi) CLA FRA . TA U CLAW

C A'S

T R

STO L L) STO TRA CLA FW-F T) P CL A T SX

~TQx

T .5

X

ST LX)

FSB

5Th

CLA

STO

STO

F MP LoU/A T SX LL)Q

5T L)A

F L ,5T L; TS X

Pz

TRA

TX

A TNA TRA

TSX

PZETRA TSX PZE Ti-iL.TA I iWVT

C

O M 1I N THEiv2 INVT TEP2

T EM PC

T

EM PC 1G REF 6+ L)NDEF T EPvj P C TEMPC TLM.A QdN L.

T

EMP H TAI~N .4 TNE

TEMPAH

TAN ' TEiPH

IN'.VX

T L

M

PC

TLIPC T E. iP C T Z rP C

L~A~S LAT/\

LCH VAKI

.

'4ITH

LACH

ASS

TEMPC L P F T +P2 LQLAL) p4 LUAD ,4 N* Ai + 5 LOAO .4 CaNAME50 ,CAOU+

47

TSX TRA TRA TSX P4. L T I A\ T.IN/A TuV TQU SWT TRA W TV CFF LX SXL LXA SXL) LXA SXL T CLA STO CLA 6T LLA 6 TO LLA .5T0 6- T sTO $TO T F S TOa L F P LD. F STU T6X PZEL. LD L STU CLA F0 V ST Lua AM~rL, PU NA

~ii+:)

*+ LND LUjAL) ,'4 * AD,4 *+.1 a 3 CQUNb6.1. CuUNu, 1 CoUUNC, I Co ,-J.4. 00UNO couUl. Co) U P L -LuUPO+i-7 TEMPE L )LPC+i 7 R L Fl NO H LOU -L u t-I LYOPD-4. L KW t PC 6LL b E

bE

0 F TF 4

suu

) IN F *ri 0 1 NV.%

~F

I co /,.>)

48

F L P FLA F rvi P F L) S T CLA FuP STQ T6X LMQ FP STO RE STZ STZ CLA STU TRA CLA ST L TSX PZE CLA STO CLA 5OK T X

TPL

STZ TA CLA S S TO

PLE

STU CLA ST TRAN CLA STNZ 10

IG

C

aL)

CL L6Lo( 9 U 9 L- , E Ivi S R

IC'JTIALIL TOOTH CUNT

EMSR 2 EIASR2 o A 6 L OLo P Y A ,A 6 N X/ F40T,4 I1)-NIILZ U t-A TH UN Ul EMS1 P L NM i3. T + 7 CuN TCL k i 0I TERMI EMSR2 *-+ 13

19