Bayesian Functional Linear Regression with Sparse Step Functions

Wavelet block thresholding for samples with random design: a minimax approach under the L p risk, Electronic Journal of Statistics, 1, 331-346..

Under the prior Π defined in Equations (14), the global l 2 rate of posterior contraction is optimal adaptive for the Gaussian white noise model, i.e.. Hence we obtain the

Despite the so-called ”curse of dimension“ coming from the bi-dimensionality of (1), we prove that our wavelet estimator attains the standard unidimensional rate of convergence un-

corresponds to the rate of convergence obtained in the estimation of f (m) in the 1-periodic white noise convolution model with an adapted hard thresholding wavelet estimator

Contributions In this paper, we design and study an adaptive wavelet esti- mator for f ν that relies on the hard thresholding rule in the wavelet domain.. It has the originality

The resulting estimator is shown to be adaptive and minimax optimal: we establish nonasymptotic risk bounds and compute rates of convergence under various assumptions on the decay

Aggregated hold-out (Agghoo) satisfies an oracle inequality (Theorem 3.2) in sparse linear regression with the Huber loss.. This oracle inequality is asymptot- ically optimal in

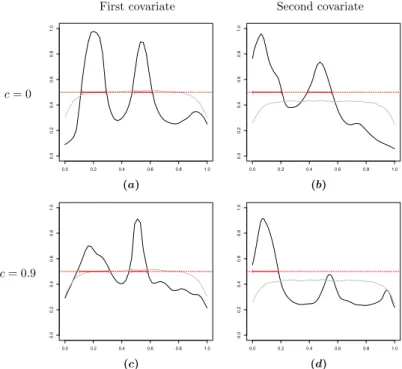
To this aim we propose a parsimonious and adaptive decomposition of the coefficient function as a step function, and a model including a prior distribution that we name