Anderson localization of thermal phonons : anomalous heat conduction in disordered superlattices

(1)

Anderson localization of thermal phonons:

Anomalous heat conduction in disordered

superlattices

by

Jonathan M. Mendoza

Submitted to the Department of Mechanical Engineering

in partial fulfillment of the requirements for the degree of

Doctor of Philosophy in Mechanical Engineering

at the

MASSACHUSETTS INSTITUTE OF TECHNOLOGY

June 2017

@

Jonathan M. Mendoza, MMXVII. All rights reserved.

The author hereby grants to MIT permission to reproduce and

distribute publicly paper and electronic copies of this thesis document

in whole or in pa

Signature redacted

A uthor...

Certified by..

Sigr

Department of Mechanical En ineering

May 5, 2017

-

.1....

Gang Chen

Carl Richard Soderberg Professor of Power Engineering

Thesis Supervisor

A ccepted by ...

Signature redacted

Rohan Ab aratne

Quentin

Berg Professor of Mechanics

Chairman, Department Committee on Graduate Students

The author hereby grants to MIT permission to

reproduce and to distribute publicly paper and

electronic copies of this thesis document in

whole or in part in any medium now known or

N Y

JUN 2

1 2017

LIBRARIES

Anderson localization of thermal phonons: Anomalous heat

conduction in disordered superlattices

by

Jonathan M. Mendoza

Submitted to the Department of Mechanical Engineering on May 5, 2017, in partial fulfillment of the

requirements for the degree of

Doctor of Philosophy in Mechanical Engineering

Abstract

In semiconductor devices, thermal energy is carried by phonons, the quantized exci-tation of atomic vibrations. These phonons scatter with impurities, electrons, grain boundaries, and other phonons. At a sufficiently large scale, phonon dynamics can be approximated as a Brownian random walk, leading to ordinary diffusion described

by the heat equation. However, such approximations fail at the scale of the phonon

mean free path. In this regime, a proper wave description encoding phonon scattering is required. For sufficiently short thermal systems, the thermal conductivity becomes extrinsic and exhibits linear scaling with system size. This scale is known as the ballistic transport regime. As the system size grows beyond this scale, the thermal conductivity asymptotes into the intrinsic, ordinary diffusive regime.

However, there are special circumstances where this transition does not occur. In this Thesis, we demonstrate the anomalous scaling of thermal conductivity. The source of this anomaly is the Anderson localization of thermal phonons. Anderson localization is the spatial trapping of waves due to extreme levels of elastic disorder. The hallmark of Anderson localization is an exponential decay law of conductance with increasing system size. Since thermal transport is a broadband process, this exponential suppression leads to a thermal conductivity maximum as a function of system size. Our numerical study of GaAs/AlAs superlattices with ErAs nanopar-ticles exhibits this thermal conductivity maximum, yielding quantitative agreement to experiments. We then generalize our elastic model to allow for the incorporation of finite-temperature effects. The inclusion of phonon-phonon scattering decoheres phonons, resulting in phonon delocalization. Counterintuitively, the additional inelas-tic scattering increases conductance for originally localized phonons. This localization to diffusive transition as a function of temperature is captured in our model at low temperatures (~20K).

(4)

(5)

Acknowledgments

I would like to thank my advisor, Professor Gang Chen, for the opportunity, guidance,

and resources to work in a wonderful research environment. I also dedicate this thesis

to my friends and family. Their love and support has helped me through my times at MIT.

(6)

(7)

List of Figures

1-1 Coarse-grained temperature profile and (zoomed) transient tempera-ture fluctuations at the nanoscale. . . . . 20

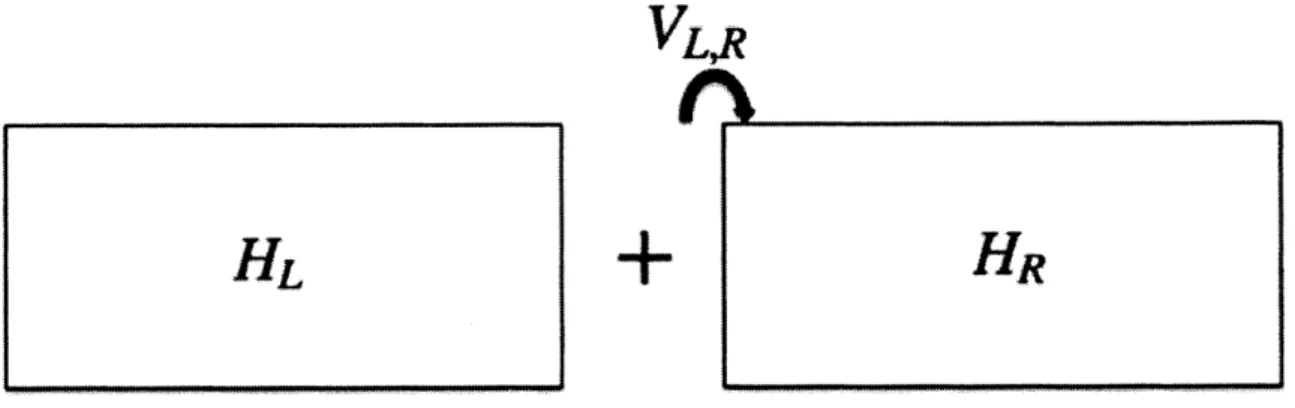
3-1 /3(g) for d = 1, 2, 3 dimensions. Taken from [1]. . . . . 46 4-1 The decomposition of the Hamiltonian, H, into intra-layer components

Hi and inter-layer components V,j . . . . 62

4-2 A system of N + 1 layers recursively constructed layer by layer. . . . 64 4-3 A decomposition of an N layer system into left and right subsystems. 65 5-1 Photon density of states. The shaded region corresponds to the

pseu-dogap of strongly localized photons (taken from [2]). . . . . 75 5-2 Propagation of waves A and B taking opposite paths through a set of

n scatterers (taken from [3]). . . . . 76 6-1 a. Depiction of the GaAs/AlAs superlattice with ErAs nanoparticles.

The GaAs and AlAs layers (half-periods) have equal thicknesses of 3

nm. The samples vary in their length and ErAs interfacial density. b.

TEM of the in-plane direction of a GaAs/AlAs superlattice without

ErAs. c. TEM of the ErAs nanoparticle (shaded-region). d.

In-plane TEM of the GaAs/AlAs superlattice with 8% ErAs interfacial

density. e. Plan-view TEM of the GaAs/AlAs superlattice with 8%

(12)

6-2 TDTR data for the 16 period superlattice with 25% ErAs nanoparticle interfacial density. Data sets a and b were taken at 40K. Data sets c

and d were taken at 296K. . . . . 83

6-3 Thermal conductivity as a function of ErAs concentration, length, and temperature. a. k(T) of the ordered superlattice. b. k(T) of the

superlattice with 8% ErAs interface concentration. c. k(T) of the

su-perlattice with 25% ErAs interface concentration. d. k(L) for the three

sets of superlattices measured at 30K and 200K. At 200K the thermal

conductivity linearly scales then asymptotes, indicating the standard

ballistic to diffusive transition. This transition is also observed for the

ordered superlattice at 30K. However, in the disordered superlattices

at 30K, the thermal conductivity reaches a maximum value at 16

pe-riods then reduces to its bulk value. e. Thermal conductivity of d

normalized by its asymptotic value at the length of 300 periods. The

normalization serves to emphasize the thermal conductivity maximum

at short length scales for the superlattices with ErAs. f. k(L) of the

superlattices with 25% ErAs concentration for various temperatures.

As the temperature is increased beyond 50K, the anomalous peak in

the thermal conductivity is lost. The measurements for temperatures

above lOOK again demonstrates the ballistic to diffusive transition. . 85

(13)

6-5 Frequency dependence of the phonon a, transmission function and b, transmittance for superlattices with only roughness and with both

roughness and ErAs nanoparticles. The transmission functions and

transmittances were averaged over the Brillouin zone. c,

Transmis-sion function as a function of superlattice length for superlattices with

perfect interfaces, interfacial roughness, and both interfacial roughness

and nanoparticles for normal incident 1.65 THz phonons. d,

Compari-son of the inelastic mean free paths of a perfect superlattice at 30K and

300K with the localization lengths of the superlattices with interfacial

roughness and nanoparticles. e, Thermal conductivity accumulation

for perfect superlattices, superlattices with interfacial roughness, and

superlattices with interfacial roughness and nanoparticles at 30K. f,

Normalized thermal conductivity as a function of superlattice length

for superlattices with and without nanoparticles at 30K. The inset

de-picts the unnormalized values of thermal conductivity . . . . . 93 7-1 Diagram of an ErAs disordered GaAs/AlAs superlattice connected to

semi-infinite GaAs leads. An infinitesimal temperature difference dT

establishes a net phonon flux across the disordered region. . . . . 99 7-2 Configuration averaged dimensionless conductance, (g), versus phonon

frequency, w, for GaAs/AlAs superlattices with 23.8% ErAs interfacial

coverage. The blue line corresponds to the dimensionless conductance

of a 560 nm ordered GaAs/AlAs superlattice. 20 configurations were

used for the averaging procedures for L > 140 nm while 40 configu-rations were used for L = 56 nm. Inset: Rescaled axes to show the

relative difference in dimensionless conductance between the ordered

(14)

7-3 The phonon mean free path (blue circles), localization length (red squares), and Thouless length (yellow crosses) versus frequency for

normal incident phonons (k1 = 0). 200 configurations were computed

to obtain the expected values (g) and (ln g) in order to fit lmfp and ,

respectively. . . . . 102

7-4 Thermal conductivity versus length of GaAs/AlAs superlattices with

2.38% and 23.8% interfacial coverage for T=1K. The linear scaling of

thermal conductivity with increasing L implies all phonon modes are

ballistic. . . . . 103

7-5 Normalized thermal conductivity versus length of GaAs/AlAs super-lattices with 2.38% and 23.8% ErAs interfacial coverage for T = 10K

and T = 100K. Each curve is normalized by its respective value at

560 nm. Anderson localization leads to the local thermal conductivity

maximum at L = 112 nm for the 23.8% interfacial disordered

configu-rations at 100K . . . . 105 7-6 Thermal conductivity versus temperature of GaAs/AlAs superlattices

with 23.8% ErAs interfacial coverage for various lengths. The crossing

of the curves of k(T) corresponds to the onset of appreciable localized

phonon transport with increasing T. . . . . 106 7-7 Histogram of the transmission eigenvalues for 345 GHz phonons at

nor-mal incidence. The dimensionless conductance g(w) 1 comes entirely

from the largest transmission eigenvalue of Tma = 1. The rest of the

transmission eigenvalues are zero. The bimodal distribution

corrobo-rates Imry and Pendry's description of open and closed transmission

(15)

7-8 Histogram (markers) and respective fits (lines) of -In g of 1.93 THz phonons with normal incidence. The mean of the log-normal

distribu-tion corresponds to (L). The histograms were generated from 3 x 104,

1.5 x 104, and 1 x 104 configurations of 50 period (blue circles), 100 period (red crosses), and 150 period (green diamonds) superlattices,

respectively. . . . . 109 7-9 Computed probability distribution of the dimensionless conductance

for three different disordered superlattices. Circle correspond to

su-perlattices with 0% ErAs, interfacial roughness, L = 935 nm, W = 1.93

THz, and N = 2.1 x 104 configurations. Crosses correspond to

super-lattices with 2.38% ErAs, interfacial roughness, L = 1120 nm, w = 1.52

THz, and N = 1.5 x 104 configurations. Diamonds correspond to

super-lattices with 4.76% ErAs, interfacial roughness, L = 577 nm, w = 1.52

THz, and N = 3.2 x 104 configurations. . . . . 110 8-1 Localization length of normal incidence phonons for various

nanopar-ticle masses me, embedded in a GaAs/AlAs superlattice. . . . . 114

8-2 Localization length of normal incidence phonons for various nanopar-ticle masses mn, embedded in bulk GaAs. . . . . 116 8-3 Localization length of normal incidence phonons for me, = 100a.m.u.

nanoparticles embedded in GaAs/AlAs (blue) and bulk GaAs (red). . 117

8-4 Localization length of normal incidence phonons for various

nanopar-ticle masses mn, embedded in bulk GaAs. . . . . 118 8-5 Resonant frequency as a function of nanoparticle mass for bulk GaAs

(blue/solid) and GaAs/AlAs superlattices (red/dashed). . . . . 119 8-6 Magnitude of jomrn) for w = 1.3 THz as a function of length along the

(16)

8-7 Logarithm of the magnitude of hra) for w = 4.5 THz as a function of length along the device region. The units of the wavefunction are

arbitrary. . . . . 122

8-8 Illustration of the inelastic scatterer (triangle) coupled to the ballis-tic wire (channels 1 and 2). The wire is connected to a reservoir at

chemical potential p via two leads (taken from [4]). . . . . 124

8-9 Dimensionless conductance of F-point phonons as a function of phonon frequency. The purely elastic model (blue) has a length-independent

conductance corresponding to ballistic transport. The perfect

super-lattices with anharmonicity at 30K exhibits power law decay. The

strength of the decay increases with increasing frequency. . . . . 133 8-10 Anharmonic mean free path as a function of temperature and phonon

frequency. . . . . 134

8-11 Elastic mean free path (blue), localization length (red), and inelastic

mean free path (yellow) of normal incident phonons at 30K. . . . . . 135 8-12 F-point conductance of a 140 nm disordered superlattice with (dashed)

and without (solid) inelastic scattering. . . . . 136 8-13 Temperature dependent conductance of F-point localized phonons in a

140 nm disordered superlattice. The calculations at OK are obtained

from the purely coherent model. . . . . 137

8-14 Accumulated thermal conductivity of a 84 nm disordered superlattice

obtained by the elastic (dashed) and inelastic (solid) models at

temper-atures up to 30K. For T < 20K, inelastic scattering increases thermal

conductivity due to the delocalization of thermal phonons. For T=30K, the diffusive transport of thermal phonons with w > 2 THz reduces the

(17)

Chapter 1 Introduction

1.1 Diffusion

Thermal transport is governed by the flow of energy carriers within a medium. In any

real system, these carriers interact with other carriers and imperfections, leading to

behavior that is approximated as a memoryless random walk. For a macroscopically

large number of carriers, the time evolution of an ensemble of Brownian carriers can be

represented by the density distribution, p(x, t). In one dimension, this distribution is

governed by the probability distribution, O(A), of a particle moving from x to x + A

from time t to t + r. Since a particle has an equal chance of moving left or right

(#(A) = q(-A)), the distribution obeys the continuity equation

- DV2p=O (1.1)

at

with diffusivity

D

= A2 (A)dA (1.2)

(18)

defined for sufficiently large At [5]. For a 1-d system of N particles located at the origin at t = 0, the distribution reads

N

2

p(x, t) = e 4Dt (1.3)

V4irDt yielding the mean-squared displacement

(x2₎₌_2Dt _(1.4)

The diffusivity connects the length and time scales of diffusive transport.

Since temperature is defined by the local energy near equilbibrium, which is

pro-portional to the local carrier density, the diffusion equation also describes the

macro-scopic evolution of heat via the substitution p(x, t) -* T(x, t). Similarly, the thermal

diffusivity is identified as D = k-, where k and C are the thermal conductivity and

heat capacity, respectively. At steady-state, Fourier's law

q = -kVT (1.5)

identifies the thermal conductivity as the relationship between the heat flux, q, and

the temperature gradient. Since the macroscopic thermal conductivity is an intrinsic

quantity, the flux can be computed from a 1-d temperature gradient, AT, established

over an arbitrary length scale, L. The 1-d steady state solution reads

L

T(x = 0) - T(x = L) = q- (1.6)

k

Since the temperature profile is linear, Ohm's law, R = -, can be identified through

(19)

conductivity, the thermal resistance

L

R = _{k A} (1.7)

grows linearly with L. If k were extrinsic, (1.5) would depend greatly on the scale over which the temperature gradient is established.

1.2 Microscopic breakdown of diffusion

The definition of diffusivity relies upon the assumption that the time scale, At, is large enough that the particle motion is uncorrelated between time t and t + At. For sufficiently small At, the carrier motion is correlated on distances on the order of the carrier's mean free path. As a result, the diffusivity cannot be properly defined for carrier transport shorter than the mean free path. At this scale, scattering processes are discrete events in space and time. This discreteness manifests as fluctuations in the carrier density and, hence, temperature. At the macroscale, these temperature fluctuations are small compared to the linear temperature profile. At the nanoscale, however, the temperature fluctuations emerge as a series of discrete jumps (Figure

1-1). The discrete jumps in temperature correspond to the points in space and time

where carriers scatter. These discrete events are coarse-grained over large distances and times to provide the continuum picture of macroscale heat transport.

1.3 Phonon transport regimes

In semiconductors and insulators, the primary energy carriers are phonons, the quanta of atomic vibrations. Since phonons are the solutions to the wave equation of a crystal lattice, the diffusion of heat derives from the multiple scattering of waves. The interaction of a phonon with other phonons, electrons, and structural imperfections

(20)

Lengthi

Figure 1-1: Coarse-grained temperature profile and (zoomed) transient temperature fluctuations at the nanoscale.

contributes to scattering and dictates the length scale of the phonon mean free path.

At scales smaller than the mean free path, phonons travel unobstructed, similarly

to classical ballistic particles; consequently, this scale corresponds to the ballistic

transport regime. Ballistic waves propagate perfectly, transmitting 100 percent of

their energy. Since a ballistic phonon transmits perfectly for L < 1"mfp, the thermal

resistance, -;, is independent of L, implying k oc L!. We no longer have an intrinsic

thermal conductivity (k(L) =, k). In the ballistic regime, the thermal conductivity

depends linearly on system size.

As the transport scale exceeds the phonon mean free path, the wave inevitably

scatters, randomizing its direction (elastic or inelastic scattering) and energy (inelastic

scattering). Unlike classical Brownian particles, the random motion of waves may

interfere. Interference may extend the length over which wave transport is correlated.

When scattering is inelastic or elastically weak, the randomness of the scattering

events is a sufficient condition to ignore interference. We can therefore assume that

(21)

diffusive phonon transport can be treated analogously to Brownian motion, which is

conventionally referred to as the phonon gas model.

The thermal conductivity of the phonon gas model is characterized by a phonon's

frequency, w, group velocity, vg, and scattering rate, r. Since the scattering rate is

frequency-dependent, thermal transport at a given length scale is usually a

combi-nation of ballistic and diffusive phonons. Because of their relatively higher group

velocities and weak scattering rates, low frequency phonons tend to be ballistic.

Un-fortunately, at room temperature, low frequency phonons do not significantly

con-tribute to thermal transport, due to their low energy density. To observe the k oc L

dependence of ballistic transport, measurements must be performed at short length

and/or temperature scales. In this limit, experimentalists have since demonstrated

the breakdown of diffusive thermal transport [6-8]. The linear behavior of thermal

conductivity was first demonstrated in graphite fibers [9] then corroborated by studies

of multi-walled carbon nanotubes [10].

1.4 Phonon scattering

In order to characterize thermal transport at the nanoscale, an accurate treatment

of interface and boundary scattering is necessary. Casimir initiated the study of

phonon boundary scattering by considering a thin cylinder without intrinsic scattering

processes. The boundaries were modeled as perfect blackbodies that emit phonons at

the locally defined equilibrium distribution. The phonon mean free path was found

to be equal to the diameter of the cylinder [11]. The same geometry was then studied

more generally by Ziman using the Boltzmann transport equation (BTE) [12]. Ziman

assumed diffuse boundaries, which corresponds to a phonon whose momentum, after

scattering off the boundary, is uniformly distributed and independent of the initial

(22)

yielded identical results to Casimir's model. The work was again generalized in the

BTE framework by allowing for partially specular and partially diffuse boundaries

[12].

The study of interfacial thermal resistance shares many similarities to boundary

scattering. Both theories require scattering that is partially specular and partially

diffuse. The specular model, known as the acoustic mismatch model (AMM), assumes

that reflection arises from the interfacial mismatch of the acoustic impedance, Z = pc,

where p and c are the density and speed of sound, respectively [13]. On the other

end of the spectrum, the diffuse mismatch model (DMM) assumes that a phonon

can elastically scatter into any momentum state. By allowing for the randomization

of the outgoing momentum, the DMM interfacial resistance is determined by the

density of states mismatch of the two materials [14]. Since the DMM allows for

the scattering into any channel of the same frequency, it represents the lower bound

for interfacial thermal resistance. Similarly, the constraint to purely forward and

backward scattering in the AMM constitutes an upper bound for interfacial thermal

resistance.

Unfortunately, the reality lies somewhere in between. If interfaces are perfect, the AMM would yield good agreement. If the interface has roughness whose power

spectrum is identical to white noise, the DMM is more applicable. The problem

is further compounded if the spacing between interfaces becomes on the order of

the phonon wavelength. For sufficiently specular interfaces with phonon wavelength

spacing, phonons can perfectly transmit (reflect) due to constructive (destructive)

interference. This interference effect is the thermal analogy of Bragg reflectance in

optics. In the regime where interference is important, the total interfacial resistance

is not proportional to the number of interfaces. A phonon gas model that treats each

interface to be independent of the others would overestimate the scattering rate of

(23)

phonons cause departures from the traditional treatment of phonons as point particles

[15].

1.5 Coherence

As we argued in the previous section, introducing features with sizes on the order

of the phonon wavelength can utilize the wave nature of heat. The characterization

of interference effects requires the introduction of the coherence length, the length

scale over which the phase of a wave is correlated. The coherence length needs to

be much larger than the distance required for a phonon wavepacket to interfere with

the nanostructures [16]. Since the phonon-phonon interaction is the dominant

in-elastic/dephasing mechanism, the coherence length is synonymous to the anharmonic

mean free path.

If the nanostructuring leads to a discrete translationally symmetric system, phonon

group velocities are heavily modified [17], leading to band gaps along high

symme-try directions [18]. These superperiodic systems, referred to as superlattices, have

exhibited the wave-like nature of thermal transport via thermal conductivity

mea-surements of superlattices with varying period lengths [19]. By holding the period

length constant, while varying the number of periods, the ballistic nature of phonon

transport was further corroborated in GaAs/AlAs superlattices [20].

The interference effects in phonon transport can be taken one step further by

introducing disorder to a material. In the long wavelength limit, phonon-impurity

scattering scales as w4, analogous to Rayleigh scattering of light off point-like

ob-jects [21]. As the wavelength decreases, the local structure can be probed by the

wave, leading to Mie resonance scattering for L oc A [22]. Introducing randomly

placed wavelength-sized nanostructures can dramatically reduce thermal

(24)

In a real system, a wave multiply scatters off impurities. Multiple scattering

effects are higher-order corrections to the elastic scattering rate [23]. In the dilute or

weakly disordered limit, the mutual interference of scatterers does not significantly

alter thermal conductivity predictions. For extremely large mass mismatch in the

non-dilute limit, multiple scattering must be included [24].

1.6 Localization

To see how multiple scattering can influence thermal transport, consider an extreme

example where all scatterers within a box of volume L3 are correlated by mutual interference. By increasing the size of the box to volume (L + 6L)3, the new scatterers

interfere with the original scatterers. The correlation of the new scatterers with the

original scatterers introduces a scattering rate, T(w, L), that is dependent on the size

of the box. Since k depends on the scattering rate, multiple scattering can produce a

size-dependent k(L) similarly to how ballistic thermal transport introduces k(L). The

anomalous k(L) behavior is the onset of Anderson localization, the spatial trapping

of a wave due to the presence of sufficiently strong disorder [25].

Anderson localization corresponds to an entirely new regime of transport. In this

regime, the resistance exponentially grows as

R oc eL/ (1.8)

where the localization length, , depends on the microscopic degrees of freedom, such as the disorder strength and phonon frequency. The localization length describes the

extent to which a wave is confined. At low levels of disorder, localization is weak or

nonexistent, allowing for the standard plane wave description, # oc eikx. As the level

of disorder grows, interference causes the wave to have an exponentially decaying

(25)

The observation of Anderson localization has been historically challenging. In

electronic systems, the electron-phonon interaction introduces a dephasing

mecha-nism that prevents localization. In photonic materials, an absorbing dielectric

in-troduces an additional form of exponential attenuation, which is indistinguishable

from Anderson localization in electromagnetic transmission measurements. In

ther-mal systems, heat transfer is a broadband process that depends on contributions from

ballistic, diffusive, and localized phonons. Isolating the influences of localized phonons

in thermal transport is extremely nontrivial. While low frequency acoustic phonons

have been observed to localize, their energy density is too low to contribute to thermal

transport. High frequency phonons, which generally have shorter localization lengths,

also contribute weakly to thermal transport, due to their large scattering rates. In

other words, the difference between the transport of a strongly scattering diffusive

wave and a localized wave is negligible. Intermediate frequency (~1-3 THz) thermal

phonons are thus the best candidates for observing localized phonon transport, due

to their preferable combination of sufficiently high energy density and sufficiently low

scattering rates.

1.7 Theoretical tools

The discussion, so far, has led us to a good set of qualitative heuristics for

observ-ing Anderson localization. However, in order to make predictions in real candidate

materials, we need to have a formalism and a set of computational tools that can

compute accurate phonon dispersions and scattering rates. Density functional

the-ory [26,27], an approximation of the many-body Schr6dinger equation, has provided

the most practical route for obtaining interatomic force constants that govern atomic

motion [28,29]. Perturbation theory can then be used to determine the anharmonic

(26)

mass mismatch [30] and second-order force constant mismatch [31].

Despite their accuracy, first principles methods cannot handle true disorder due

to their use of periodic boundary conditions. Effectively capturing the physics of

disordered transport remains a challenging numerical issue. Quantum mechanical

solvers are limited to domains on the order of 100 atoms, yielding - N100 possible

atomic configurations. In principle, each configuration must be calculated, weighted

by its Boltzmann factor, and averaged over. Significant approximations are necessary

to mitigate this exponential complexity. This combinatorial problem is alleviated via

mean field theories, which views disorder as a change to the average properties of a

material. The simplest of such methods takes the weighted average of the masses, mi, and force constants, 0j, of the disordered material. Given the occupation probability,

pi, of atom type i, the Virtual Crystal Approximation (VCA) [32] generates the mean

field

(M) = pimi (1.9a)

(0) = Pi (1.9b)

Elastic scattering rates are then obtained by considering the mass difference between

atom type i and the mass of the virtual crystal. This general procedure has

demon-strated great success in predicting the thermal conductivity of SiGei_2 alloys [33].

For sufficiently weak or dilute disorder, mean-field theories capture the essential

physics since multiple scattering effects are negligible. As the disorder strength grows, larger clusters of impurities must be considered for accurate evaluation of elastic

scattering rates. At the most extreme limit, where strong Anderson localization

occurs, the simulation box must be larger than the localization length. Real-space

Green's function methods [24] must be adopted to handle the spatial extent of multiple

(27)

expense of neglecting inelastic scattering. As long as the simulation box is smaller

than the anharmonic mean free path, purely elastic simulations are justified. In

this sub-micron regime, real-space methods have captured the ballistic to diffusive

transition in phonon transport [34]. The aim of this Thesis is to extend the

real-space method to larger, more disordered systems in order to quantify the effects of

phonon localization upon thermal transport.

1.8 Device applications

Semiconductor devices are exponentially decreasing in size due to the growing

preci-sion of fabrication methods. At the present time, 10 nm features can be fabricated.

This length scale is on the order of the wavelength of most thermal phonons [35].

Consequently, we are at technological tipping point where nanoscale transport

phe-nomena is leading to emerging thermal management problems and its corresponding

solutions. A description of thermal transport that supercedes ordinary diffusion is

required to engineer transistors to effectively transport heat away from the gates of

CMOS devices. Nanoscale fabrication may allow for selectively conducting regions,

potentially mitigating the hot spots that limit the capability of semiconductor devices.

While nanoscale fabrication can provide an avenue for thermally conducting

de-vices, thermal insulators can also be effectively engineered by understanding phonon

scattering and scaling phenomena. In materials that are thermally insulating and

electrically conductive, waste heat can be effectively recovered through the Seebeck

effect. More precisely, a temperature gradient within a thermoelectric material

gen-erates a proportional voltage gradient. The thermoelectric figure of merit

ZT

=

S2

T

(1.10)

k

(28)

Seebeck coefficient, electric conductivity, and temperature, respectively [36-39]. In the limit of ZT -+ 00, thermoelectric materials have efficiencies equivalent to the Carnot cycle. As previously mentioned, the thermal conductivity of a semiconductor is dominated by its lattice dynamics; consequently, introducing disorder that dis-rupts phonon transport may greatly reduce thermal conductivity while preserving electrical conductivity. A mature description of phonon-impurity scattering provides intuition for the optimization of thermoelectric material fabrication. Generally, the introduction of wavelength-sized impurities effectively scatters phonons. This concept was most effectively realized in disordered PbTe that incorporated dopants, nanos-tructures, and grain boundaries to suppress phonon transport over a wide range of frequencies [40].

Tailoring a material to have a specific thermal conductivity is the motivational foundation of thermal engineering. The introduction of disorder provides the choice of mass difference, nanoparticle size, and nanoparticle concentration to the engineer. In the macroscopic limit, these degrees of freedom adjust the thermal conductivity downward from its intrinsic value. If additional control is required, fabricating a device at the nanoscale introduces the k(L) dependence stemming from ballistic and localized phonon contributions. Specifying the size of the nanoscale device allows for an additional way in which to control the thermal conductivity of a desired material.

1.9 Organization of thesis

In this thesis, we investigate the impact of the Anderson localization of thermal phonons in nanoscale thermal transport. In Chapter 2, we introduce the standard formalism describing atomic motion. By including terms up to second-order, the phonon picture is exact. Perturbations due to third-order terms introduces finite-lifetimes to the phonon modes that are encoded by the relaxation time, T.

(29)

Incor-porating the phonon dynamics and relaxation times into the Boltzmann transport

equation (BTE), the thermal conductivity tensor, k,, can be computed and

com-pared to experiment.

Chapter 3 illustrates the historical paths that lead to Anderson localization. P.W.

Anderson's research concerned the study of random tight-binding models that yielded

insulating behavior for sufficiently strong disorder. Despite being first, his work

re-mained in obscurity for decades, due to its particularly rigorous mathematical

argu-ments. Landauer, on the other hand, discovered localization more intuitively

consid-ering the transport of waves subject to reflecting barriers. Landauer showed that the

resistance of this system exponentially increased with the number of reflecting

barri-ers. The theory was corrected by Anderson et. al to exhibit proper scaling laws in the

limit of low resistance (Ohm's law). P.A. Lee then unified the originally dissimilar

concepts of transmission and conductance, easing the computational study of

Ander-son localization in electronic systems. The formalism prescribed by P.A. Lee was then

generalized to allow for arbitrary boundary conditions, opening the avenue to

study-ing nanoscale phonon transport usstudy-ing Nonequilibrium Green's functions (NEGF) [41].

The length dependence of Anderson localized phonons is discussed, culminating in

the conclusion that a decreasing thermal conductivity with increasing length can only

be explained by localization.

Chapter 4 provides the implementation details of NEGF using force constants

obtained from density functional theory. The structure of the mixed-basis dynamical

matrix is presented to show how the sparse representation can speed up

computa-tion. The Green's function matrix elements are obtained recursively from repeated

inversions of small matrices. The full solution of the matrix elements responsible for

conductance and wavefunction computation are presented.

Chapter 5 presents the historical context for why localization should be significant

(30)

waves. This critical disorder was originally studied in electronics. S. John drew an

analogy between the electronic and phononic problem. He discovered a critical phonon

frequency, w, distinguishing high-frequency localized phonons from low-frequency

diffusive phonons. The band gap formation in superlattices is demonstrated to be

crucial to phonon localization, motivating our experimental investigation of disordered

superlattices.

Chapters 6 + 7 present the experimental and numerical study of Anderson

lo-calized thermal transport. At low temperatures and short lengths, the thermal

con-ductivity increases linearly with increasing L, signifying ballistic transport. At

in-termediate length scales, the thermal conductivity begins to decrease with increasing

L due to the exponential suppression of Anderson localized phonons. This effect

disappears at high temperatures due to the loss of coherence. NEGF simulations

cor-roborate the experimental findings and demonstrate the same thermal conductivity

maximum as a function of length. The localization length as a function of phonon

fre-quency is obtained, identifying significant localization of phonons beyond -1.5 THz.

Temperatures above -20K are required to significantly populate Anderson localized

phonons. Since conductance is configuration dependent, the probability distribution

of the conductance is computed. The form of the probability distribution

distin-guishes the ballistic, diffusive, and localized regimes. The universality of coherent

phonon transport is also observed in our numerical studies.

Chapter 8 extends the numerical investigation to different nanoparticle masses.

The localization length monotonically decreases for masses heavier than Ga. For

masses between values of Al and Ga in GaAs/AlAs superlattices, the localization

length is non-monotonic since the disorder is small for both m = mA, and m =

mGa-Using the Green's function matrix elements coupling the ends of the superlattice to

the intermediate regions, we are able to compute the wavefunction of the phonons

(31)

rapidly fluctuate with an overall power-law decay. In the localized regime, the

wave-function exponentially decays from the boundary, similarly to an evanescent wave.

Since the ballistic transport formalism is only valid when the inelastic mean free

path is larger than the system size, a method to perturbatively introduce anharmonic

scattering is implemented by attaching absorbers at every atom. By enforcing

zero-current flow into the absorbers, the conductance can be decomposed into coherent and

incoherent contributions. For sufficiently strong localization, anharmonic scattering

actually increases conductance since the phonon delocalizes via dephasing. Finally, the conclusion touches upon the future of Anderson localization thermal transport.

In low dimensional systems waves localize for any level of disorder. Consequently, the

adsorption of molecular degrees of freedom on truly 2-d materials can greatly alter

(32)

(33)

Chapter 2 Theory of thermal conductivity

A proper description of thermal transport in semiconductors requires an accurate

treatment of atomic motion. Starting from the interatomic force constants obtained

from quantum mechanical simulations, non-interacting phonon dynamics are

ob-tained. By combining the non-interacting phonon dispersion and the phonon lifetimes

stemming from interactions, the phonon contribution to thermal conductivity can be

calculated using the Boltzmann transport equation.

2.1 Phonon dynamics

The motion of atoms is governed by their interatomic potential, V. Denoting the

atomic displacement as xic = ric - ro,s, where ria and ro,ic, is ath component of the

atomic coordinate and equilibrium coordinate of atom i, respectively, the interatomic

potential can be expanded as [42],

=V 1 E 2+ 1 3V g xx8Xk-O(X4)

ia xia 2

iaoxiOa8

3! iko-y(xiaI9xjp,3Xk

(34)

For a stable atomic system, the first-order term

(9V

Xia = 0 (2.2)

implies that each atom sits in an approximate quadratic potential well. For notational

brevity, we introduce the second-order term,

Oap(ij) = (2.3)

49xiaaX

j

3

and third-order term,

93_V

$afy(i,

j,

k) = XiXjOXk(2.4)

The interatomic potential is simplified to,

V

= V + $(i, j)xiax, + a

Z

,y(i, j, k)XiaXj,3Xky + O(x') (2.5)

ijc43 ijkafy

The equations of motion can be obtained from Newton's first law,

F _ =9 -(z, 3 Xsp = mi ia (2.6)

Since the systems under consideration are symmetric under the transformation ri

-ri + R, where R corresponds to a lattice vector, it is convenient to replace the atomic

index i with the tuple (j, b), where

j

and b specify the position of the unit cell and basis atom, respectively. Invoking Bloch's theorem allows for the expansion of the

displacement in Fourier coefficients,

X (i, b) 1 Z Xa(k, b)ei(k-Ri-wt) (2.7)

Is t'a k

(35)

yields the dynamical matrix,

Da3 (b,

b';

k) = 1 a,(ib, jb')eik.Ri (2.8)

The equations of motion is written as the eigenvalue equation

w2

X,(k, b)

=

ED,, (b, b'; k)Xa(k, b')

(2.9)

b'I3

where w corresponds to the phonon frequency.

When the interatomic potential is limited to second-order, the dynamical matrix is Hermitian. Hermitian matrices have real eigenvalues, implying real phonon fre-quencies. Since phonon eigenfunctions have the time dependence of the form eiwt, a complex-valued eigenfrequency would correspond to a mode with a lifetime equal to the inverse of the imaginary part of the eigenvalue. The introduction of cubic force constants causes the phonon frequencies to become complex. The finite-lifetimes in-troduced by higher order terms come from the coupling between the eigenmodes of the second-order solution. The coupling of the eigenmodes is encoded in the three-body term V3, which is written in the Fourier space as

1 1

E JCG,k+k'+k"

E ),(kb, k'b', k"b"/)Xc(k, b)X,3(k', b')X,(k"9, b"/)

kb,k'b ,k"b" _aOy

(2.10) where

cay (kb, k'b',

k"

b")

=

3 '(Ob, jb',

kb")e(k'Ri+k"-Rk)

(2.11)

jk

Due to the 6

G,k+k'+k" term, the three modes that are coupled obey the conservation

of crystal momentum modulo G, the reciprocal lattice vector. When G = 0, the net

momentum of the outgoing state is equivalent to the net momentum of the incoming state. This scattering process is known as normal anharmonic scattering. While these

(36)

terms do not contribute to thermal resistance, i.e. momentum relaxation, they still influence the lifetime of a phonon mode, i.e. energy relaxation. When G

$

0, the

incoming and outgoing momentum are not preserved, resulting in momentum and

energy relaxation, which is conventionally known as Umklapp scattering [43].

2.2 Anharmonic scattering rates

The construction of a many-body wavefunction can be constructed from the tensor

product of single-particle states. For a bosonic system with k modes, the occupation

number basis is represented by,

|no7, nli,. . , nk) =

,O)no

D ₄,1)"n 9 ... 10k)nk (2.12)

where

(2.13)

10j) j := 100) (9 10 -),

The creation and annihilation operators, a and aj act on the occupation number

basis in the following manner,

aIno, nil... nj,..., n) = gnij+ 1|no, ni, ... nj

+

1, ..., nk) aj Ino, ni , ... nj,., nk) = ,~o i .y-1 .. nk)

(2.14)

(2.15)

For brevity, the subscript A encodes the wavevector k and polarization v with -A

corresponding to -k. The three-body potential is now

V3 = i

3

E 6G,k~k' k"Vf(A I A',I A/')(at~ - a-,) (at, - a-,\) (a,, - a-A,,) (2.16)

(37)

where

V(A, A',A") = h )2(kb, k'b', k"b") be/3b/ebl/ (2.17)

8NOwXWAW, Ombmy mbM

and eAb is the ath component of basis-atom b of eigenmode A. Using V3 as a

perturba-tion to the single-particle states obtained from the dynamical matrix, the transiperturba-tion

rate from state

Ii)

to

if)

is

27rI fV

Pi-f

=

V

33(f 1i)I26(Ef - E,) (2.18)

Due to the additional constraint of energy conservation imposed by Fermi's Golden Rule [44, 45], three-body terms of the forms aAa_yaa and atatalu have zero transition rate. Terms with non-zero transition rate are of the forms atat,a-Af and ataA'aA which couples the state InA, n.\, ny) to |nA + 1, n'

+

1, nAl - 1) and Inr +

1, nA' - 1, nr - 1), respectively.

2.3 Boltzmann transport equation

At equilibrium, the occupation number for a phonon mode A obeys the Bose-Einstein distribution

= (e - 1 (2.19)

The ath component of heat flux carried by phonons is

J = :nAhAVA' _(2.20)

where vA = is the phonon group velocity. At equilibrium, the integral of (2.20) is

zero, since the integrand is an odd function of k. More explicitly, nA and WA are even functions of k while VA is an odd function of k. Since the heat flux is related to the

(38)

temperature gradient through

=

OT

JT =(2.21)

/3'

where kafi corresponds to a component of the thermal conductivity tensor, the

sym-metry of the integrand is broken by a non-equilibrium distribution. In other words, a temperature gradient induces a nonzero value of nA

-The phonon distribution nA is governed by a conservation law that balances the

convection of the distribution with all possible phonon scattering processes,

On,\ On,\

vax - 17T- = -- (2.22)

V T at scattering

This conservation law is known as the phonon-Boltzmann transport equation (BTE).

In order to make the BTE tractable, two approximations are made. The first

approxi-mation assumes that the distribution is near equilibrium, allowing for the replacement

~, (2.23)

OT &T

The second approximation assumes that if a given nA is out of equilibrium, it is

interacting with in-equilibrium hy and hy, populations. This approximation, known

as the single-mode relaxation time approximation [12], allows for the scattering kernel

to be simplified to,

-- ₌

-(2.24)

at scattering TA

where

1I =

3

_A,)1_/\T(\2 _[2(At,\_- _f1)p)(WA ₊_WA'

- WA") + (1 + fA' + fiA")S(WA - WV- WA")]

TA _{A' A"}

(39)

The thermal conductivity tensor can then be expressed in closed form as,

(40)

(41)

Chapter 3 Disordered coherent transport

The cornerstone of Anderson localized transport is the exponential suppression of

con-ductance with increasing system size. The exponential scaling of transport in highly

disordered systems was approached from completely different places by Anderson and

Landauer. Landauer discovered the exponential scaling by investigating the resistance

of a system of randomly distributed reflecting walls. Anderson found similar

expo-nential laws in the tight-binding Schr6dinger equation governing the time-evolution of

electrons in a lattice of quantum wells with randomly varying well depths. Landauer's

scattering picture and Anderson's matrix models were unified through Green's

func-tion studies that connected the nofunc-tion of transmission and conductance. The Green's

function formalism was then modernized, allowing for compact notation that could

be applied to general wave transport.

3.1 Resistance of reflecting boundaries

By the 1950's, the relationship between diffusive transport and the Boltzmann

trans-port equation was widely accepted. Landauer, in an attempt to self-consistently

solve the Poisson-Boltzmann equation for electrons in the presence of diffuse and

(42)

con-ductivity [46]. Consider a current flowing perpendicular to a set of specular reflecting

walls with a reflection coefficient, r(O), where 6 is the angle between the incident

electron direction and the direction normal to the wall. The reflection coefficient is

related to the reflection probability, R, of a single interface as

Irn

2

= R. For a given

density of walls per unit length, R, Landauer finds the conductivity

e2

k

2 1 - r(9)

- = F

dQ

cos(0) (3.1)

87r3Rh I

r(9)

demonstrating resistivity proportional to R. The assumption that resistance linearly

scales with the number of scattering elements naively assumes that the resistance of

each individual scatterer is additive. This ultimately relies on interference between

subsequent scatterers to be negligible,

R Ir

+

r212 = ri l2 + 1r212 + rir* i12 + 1r₂ 2 (3.2)

In the presence of interference, the relationship between the reflection coefficient of

two individual obstacles with reflection coefficients r, and r2 obeys

1 1 + rir2 + 2(rir2)1/2 cos() (3.3)

1- r (1 - r1)(1 - r2)

r r1 + r2+ 2(rir2)1/2cos(O) (3.4)

1-r (1-r 1 )(1 - r2)

where 0 is the phase accumulated by the wave between the first and second obstacle

[47].

The argument generalizes by evaluating the total reflection coefficient of a random

obstacle placed after n - 1 obstacles all with identical reflection coefficients r. At each

step, the phase associated with the obstacle placement is averaged, corresponding to

(43)

relation 1 1 +rrn_ 1 ₊ (3.5) 1 -pr, (1 -r)(1 - r 1)(35 r. _{r + rn-1} (3.6) 1 - -n (1 - r')(1 - (3.6)

yielding the averaged resistance

P-(R )dsre 1+rn (3.7

p 1 - R 2 1 - r 2 3.

Landauer has ultimately demonstrated that the resistance exponentially grows with

the number of obstacles! In the limit of r << 1, the series expansion

I (I+r)" 1 1 + r2.. 1 1 .. 1)

S - r -

((I1+

r)(1 + r + r22 -(1+ 2r + . ."- nr

(3.8)

recovers classical Ohm's law.

3.2 Scaling theory of localization

A decade later, Anderson, Thouless, Abrahams, and Fisher found subtle

inconsisten-cies in Landauer's argument [48]. Consider the averaged conductance, (g), obtained

from combining two average resistances, (p1) and (P2). If one defines the total aver-aged resistance, (p), from the averaver-aged conductance as

1

(p) = = (PI) - (P2)1 (3.9)

the scaling law (additivity) for resistance cannot be recovered. This inconsistency

stems from the consequence of disorder averaging. If a given disordered system

(44)

distribution, then the corresponding support of the probability distribution for the

resistance spans orders of magnitudes. The expected value of the resistance is

dom-inated by the configurations with the shortest localization lengths. Oppositely, the

expected value of the conductance is dominated by the systems with the largest

lo-calization lengths; consequently, the mean resistance and mean conductance are no

longer inversely related. The four authors corrected the theory, yielding the additive

law

(ln(1 + p)) = (ln(1 + pi)) + (ln(1 + P2)) (3.10)

which reduces to Ohm's law for small dimensionless resistance. By identifying the

inverse localization length as the statistically definable object, the typical resistance

is inversely related to the typical conductance through

S(p)typ e " -'- ) = e

+ ) (3.11)

(g) typ

The additive properties of cxL implies the resistance scaling law

p aeL" - 1 (3.12)

and conductance scaling law

g g e (3.13)

where ga is the conductance at some arbitrary scale.

Equations (3.13) and (3.14) are prototypical examples of single parameter scaling

[1]. Single parameter scaling attempts to describe how conductance scales with system

size. Given a system of size L, increasing the size by 6L should obey the single

parameter scaling law

(45)

or its differential form a In g(L) = IL

(g(L))

(3.15)

Solving for the beta-function of (3.16) for (3.14),

0 In

g (L)

= ln(-) = O(g(L)) _(3.16)

alnL

ga

Since g < ga, the negative sign of the beta function corresponds to a system that

becomes more insulating as it grows in size. Conversely, a beta function with a positive

sign corresponds to a system that becomes more conducting as it scales to larger size.

Abrahams, Anderson, Licciardello, and Ramakrishnan used the asymptotic insulating

and conducting regimes of systems in d = 1, 2, 3 dimensions to qualitatively sketch

the beta-function. In the conducting limit, the conductance scales as

G(L) = uLd-2 (3.17)

yielding the beta-function

lim /3d(g) = d - 2 (3.18)

g-+oo

In d = 1, 2 dimensions, the beta-function is always negative; consequently,

Ander-son localization is present for any amount of disorder. In d = 3 dimensions, the

beta-function must change sign, implying a critical disorder separating the Anderson

localized phase from the metallic regime. The beta function for d = 1, 2, 3 and critical

conductance g, is visualized in Figure 3-1

3.3 Random matrix models

Until this point, the study of Anderson localization has been discussed abstractly in

(46)

P(g)

s In (g/g C)

d 3

9 d = 2 g

d = 1

Figure 3-1: 3(g) for d = 1, 2,3 dimensions. Taken from [1].

of randomly placed obstacles. P.W. Anderson, however, discovered localization in a

far less intuitive manner by studying the Schrddinger equation subject to a random

potential [25]. By expanding the wavefunction in terms of local orbitals 0" centered

at positions Ri

(r) = c() 0 (r - R,) (3.19)

n2 Z

the tight binding Hamiltonian takes the form

H

= n n

)j

(+V'#

n$)(

I+

h.c.

(3.20)

x n nm 1

Anderson originally considered a n = 1 orbital problem with constant nearest

neigh-bor coupling V on a cubic lattice. The disorder is encoded by a uniform distribution

on energy levels Ec between -W/2 and W/2. The solution of the Anderson model

Hamiltonian,

Anderson localization of thermal phonons : anomalous heat conduction in disordered superlattices

Anderson localization of thermal phonons:

Anomalous heat conduction in disordered

superlattices

by

Jonathan M. Mendoza

Submitted to the Department of Mechanical Engineering

in partial fulfillment of the requirements for the degree of

Doctor of Philosophy in Mechanical Engineering

at the

MASSACHUSETTS INSTITUTE OF TECHNOLOGY

June 2017

@

Jonathan M. Mendoza, MMXVII. All rights reserved.

The author hereby grants to MIT permission to reproduce and

distribute publicly paper and electronic copies of this thesis document

in whole or in pa

Signature redacted

A uthor...

Certified by..

Sigr

Department of Mechanical En ineering

May 5, 2017

.1....

Gang Chen

Carl Richard Soderberg Professor of Power Engineering

Thesis Supervisor

A ccepted by ...

Signature redacted

Rohan Ab aratne

Quentin

Berg Professor of Mechanics

Chairman, Department Committee on Graduate Students

The author hereby grants to MIT permission to

reproduce and to distribute publicly paper and

electronic copies of this thesis document in

whole or in part in any medium now known or

JUN 2

1

2017

LIBRARIES

ARCHIVES

Anderson localization of thermal phonons: Anomalous heat

conduction in disordered superlattices

by

Jonathan M. Mendoza

Abstract

Acknowledgments

Contents

List of Figures

Chapter 1

Introduction

1.1

Diffusion

D

N

L

1.2

Microscopic breakdown of diffusion

1.3

Phonon transport regimes

Lengthi

1.4

Phonon scattering

1.5

Coherence

1.6

Localization

1.7

Theoretical tools

1.8

Device applications

=

T

1.9

Organization of thesis

Chapter 2

Theory of thermal conductivity

2.1

Phonon dynamics