Relative periodic orbits in plane Poiseuille flow

O

pen

A

rchive

T

OULOUSE

A

rchive

O

uverte (

OATAO

)

OATAO is an open access repository that collects the work of Toulouse researchers and

makes it freely available over the web where possible.

This is an author-deposited version published in :

http://oatao.univ-toulouse.fr/

Eprints ID : 13922

To link to this article : DOI: 10.1016/j.crme.2014.05.008

URL :

http://dx.doi.org/10.1016/j.crme.2014.05.008

To cite this version : Rawat, Subhendu and Cossu, Carlo and Rincon,

François Relative periodic orbits in plane Poiseuille flow. (2014)

Comptes Rendus Mécanique, vol. 342 (n° 8). pp. 485-489. ISSN

1631-0721

Any correspondance concerning this service should be sent to the repository

administrator:

staff-oatao@listes-diff.inp-toulouse.fr

Relative

periodic

orbits

in

plane

Poiseuille

flow

Subhendu Rawat

a

,

Carlo Cossu

a,∗

,

François Rincon

b,c

a_{InstitutdemécaniquedesfluidesdeToulouse,CNRSandUniversitédeToulouse,alléeduProfesseur-Camille-Soula,31400Toulouse,France} b_{UniversitédeToulouse,UPS–OMP,IRAP,Toulouse,France}

c_{CNRS,IRAP,14,avenueÉdouard-Belin,31400Toulouse,France}

a b s t r a c t

Abranchofrelativeperiodic orbitsisfoundinplanePoiseuilleflowinaperiodicdomain at Reynolds numbers ranging from Re=3000 to Re=5000. These solutions consist in sinuousquasi-streamwisestreaksperiodicallyforcedbyquasi-streamwisevorticesina self-sustainedprocess. Thestreaks and thevorticesare located inthebulkofthe flow.Only theamplitude,butnottheshape,oftheaveragedvelocitycomponentsdoeschangeasthe Reynoldsnumberisincreasedfrom3000 to5000.Weconjecturethatthesesolutionscould thereforeberelatedtolarge- andverylarge-scalestructuresobserved inthebulkoffully developedturbulentchannelflows.

1. Introduction

Transitionto turbulence issubcritical in most canonical internal flows, such asthe pressure-driven plane channel and pipe flows, or the plane Couette flow. To gain insight into the transition process, a fruitful approach has been to apply thenonlineardynamicalsystemsmethodologytoanalyzethedynamicsoftheflowinsmallhorizontallyperiodic domains. Followingthisapproach,thesubcriticaltransitiontoturbulence,iscorrelatedwiththeappearanceofadditionalsolutionsof theNavier–Stokesequationsdisconnectedfromthelaminarsolution.Nonlineartravelingwaves(NTW),representingsaddles in phasespace, havebeen shown to appear atReynoldsnumbersmuch lower than thetransitional onesin plane Couette flow[24,3,29],planechannelflow[9,30],andpipeflow[10,31].Itwasinitiallybelievedthatturbulentsolutionsmayspend a significant time in the neighborhood of relevant NTW, but it was later shown that these visits last only 10–20%, on average, of the total time [19,26]. Attention hastherefore shiftedto unstable periodic (in time) solutions (periodic orbits orrelative periodic orbits),bothfortheir potentiallyvery importantrole inthetransitionprocess and becausetheymight providethe missingbuildingblocksto predictthestatisticsof thechaoticattractor orrepeller itself[1]. Periodicsolutions havebeen computedinplane Couette[4,18,28],plane channel[27]andpipeflows[7],aswellasintheasymptoticsuction boundary layer[22]. Theconfirmation that unstable periodicorbits and theirstableand unstable manifoldsare associated with transition to chaos in small spatially periodic domains has been recently given in plane Couette flow [23] and in magnetohydrodynamicKeplerianshearflows[25].

Nonlineartravelingwavesandperiodicsolutionsshowaninterplaybetweenquasi-streamwisestreaksandvorticesthatis alsocharacteristicoftheturbulentdynamics.Thisself-sustainedprocessisbelievedtoexplainthedynamicsinthenear-wall regionofturbulentflows[13,8],andself-sustainedprocessesatlargerscales[15,16],whichareimportantatlargeReynolds numbers(see,e.g.,[21,20,12]).

Inthisstudy,we considertheexistence ofperiodic solutionsin theplanechannel flow,which isless investigated than plane Couette andpipe flows, despiteitsintrinsicinterest anditsdynamicsimilarity withboundarylayerflows whichare of interestto industrialapplications. In thecaseof planePoiseuille flow atRe=3000 ina periodicdomain ofstreamwise and spanwisesize Lx=

π

h andLz=0.4πh,an NTWsolutionwas first found[17]usingabisectionprocedurethat started

with aninitial guess based ona turbulent solution.A laterstudy inthe samedomainatthe sameRe, but usingdifferent initial conditions in the bisection procedure, revealed the existence of a “periodic-like solution” [27], i.e. a solution that could beeitheragenuineperiodic solutionora heteroclinicconnection(asingleperiod ofthesolution wasaccessibledue to numerical precisionissues). Both solutionswere localized on asinglewall ofthechannel and are thereforethought to evolve to near-wall structures for increasing Reynolds numbers.In the current state of affairs, however, no solution that may becorrelated withthe large-scaledynamicsofdetached eddies inthebulk oftheflow is available.The scope ofthe present investigation isthereforeto findif periodic solutions related tolarge-scale structuresinfully developed turbulent flowsexist withamplitudesthatremainfiniteinthewholechannel.

After asummary oftheproblem formulationand of thetechniques used to isolate periodic solutionsinplane channel flow inSection 2,themainproperties oftherelative periodicorbits discoveredaredescribed inSection 3.The resultsare finallybrieflydiscussedinSection4.

2. Problemformulationandmethods

We consider thepressure-gradient-driven flow of anincompressible viscous fluid ofconstant density

ρ

and kinematic viscosity

ν

inaplanechannel ofheight2h.TheflowisruledbytheNavier–Stokesequations,whichindimensionlessform, read:

∇ ·

u

=

0 (1)

∂

u

∂

t

+

u

· ∇

u

= −∇

p

+

1 Re

∇

2_{u (2)}

where the Reynolds number Re=U₀h/

ν

is defined with respect to the maximum velocity U₀ of the usual laminar (parabolic)Poiseuillesolution.VelocitiesaremadedimensionlesswithrespecttoU₀,pressureswithrespectto

ρ

U2

0,lengths withrespecttoh and timeswithrespecttoh/U0.Wedenote byx thestreamwiseaxisalignedwiththepressure gradient, by y andz thewall-normaland spanwisecoordinatesandbyu,v and w thevelocitycomponentsalongx, y andz, respec-tively. The flow is solvedinside the domain [0,Lx]× [−1,1]× [0,Lz], with no-slip conditions on bothwalls and periodic

boundaryconditionsisthestreamwiseand spanwisedirections.

In order to find periodic solutions that do not migrate to the near wall-region for increasing Reynolds numbers, we found ituseful toenforce themid-plane reflection symmetry{u,v,w}(x,y,z)= {u,−v,w}(x,−y,z).Astandard bisection procedureontheinitialconditionswasusedtotracktheedgestatesolutionswithintheenforcedsymmetryclass.Theinitial conditionsconsideredconsistinthelaminarPoiseuillesolutionperturbedbyapairofstreamwiseuniformcounter-rotating vortices ofamplitude A₁ andasinuousperturbationofthespanwisevelocitywithamplitude A₂:

u0

=

©

Ulam

(

y

),

0,0ª +A1

½

0,

∂ψ

0

∂

z

, −

∂ψ

0

∂

y

¾

+

A2

{0,

0,wsin

}

(3) where

ψ

0

(

y

,

z

) =

¡

1

−

y2

¢

sin(

π

y

)

sin

µ

₂

_π

_z Lz

¶

;

w_sin

(

x

,

y

) =

¡

1

−

y2

¢

sin

µ

₂

_π

_x Lx

¶

(4) Thestreamfunctionψ0(y,z) isassociatedwithstreamwiseuniformvortices,while wsin providesthe(streamwise)sinuous perturbation.The initialvelocity fieldsu₀ aresolenoidalandhave thesamevolumeflux asthelaminarPoiseuillesolution

U_lam=1−y2.Thebisectionisoperatedon A₁ withtheratio A₂/A1=1/10 keptfixedtoarelativelysmall valueallowing thesubcriticaldevelopmentofthestreakinstability [5,6].

TheNavier–Stokesequationsareintegratedusingthechannelflowcode[11],whichisbasedonaFourier–Chebyshev– Fourier spatial pseudospectral discretization.Solutions are advancedin time usingasecond-order Crank–Nicolson Runge– Kuttatimestepping.Typically,resultswereobtainedwith16×41×16 pointsinthestreamwise,wall-normal,andspanwise directions, and enforcing a constant volume flux during the simulation. We verified that the characteristics of the peri-odic solutionsfound bybisectionon thecoarsegriddo notchangewhenthe numberofcollocationpointsis increasedto 32×65×32.Thenumericalresultswerefurthertestedbyrecomputingthesameperiodicsolutionswiththedifferentcode

diablo [2].Theconvergence oftheperiodic solutionswas validatedand improvedusingNewton-basediterativemethods and thentheirlinearstabilitywas analyzedusingthepeanutscode[14,25].

3. Results

Weconsider the domainofextension 2π×2×2.416,for which thenonlinear travelingwaves solutionsappear atthe lowest Reynolds number [30], and Reynolds numbers ranging from Re=3000 to 5000. For all these Reynolds numbers,

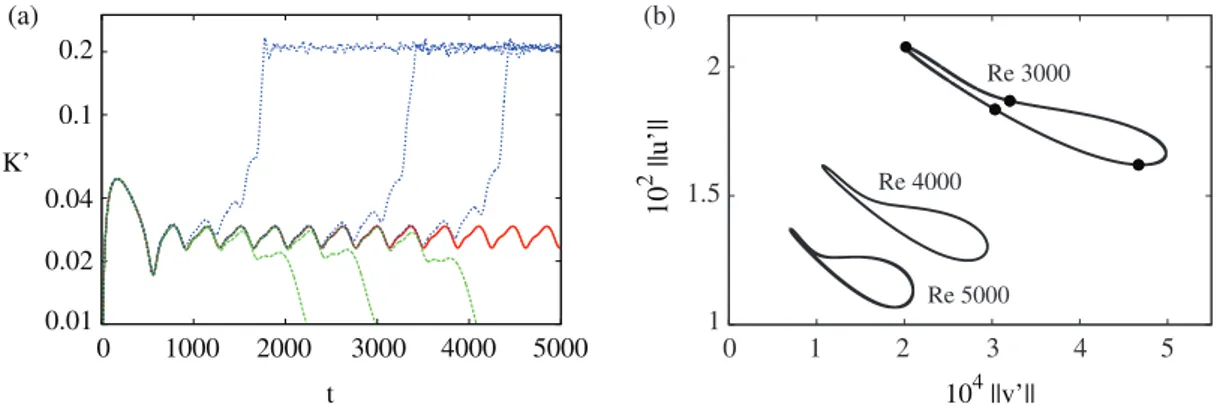
Fig. 1.(Coloronline.)Panel(a): TemporaldependenceoftheperturbationkineticenergyforselectediterationsofthebisectionprocessatRe=3000.The solutionontheedgerapidlyconvergestoaperiodicsolution.Panel(b): Convergedperiodicsolutionsrepresentedinthekv′_k–ku′_{kplaneforRe=3000,}

4000,and5000.

Fig. 2. (Color online.)Snapshotsof theconvergedperiodic solution obtainedat Re=3000.Foursnapshotsare takenin correspondence tothepoints

reportedonthecyclein Fig. 1bstarting fromthebottomleftpoint andthenrotatingcounterclockwise.Thesnapshotsaretakenatrespectively t=0 (panel (a)),t=120 (panel (b)),t=230 (panel (c))andt=310 (panel (d)).Onlythetophalfofthechannelisconsidered.Thefiguredisplaystheiso-levels oftheperturbationstreamwisevelocityfieldtakenat y=h/2 arereported.Ingreenisreportedthesurfacewherethestreamwisevelocityis75%ofits maximumvalueinthewholechannel.Inrespectivelyblueandredarereportedthesurfaceswherethestreamwisevorticityis±60%ofitsmaximumvalue inpanel (a)withthesamevalueinallpanels.Inparticular,novorticesarevisibleinpanel(c),becausetheyareofverylowamplitude.

the laminarPoiseuille solution islinearly stable,while perturbations with sufficiently largeamplitude lead to a turbulent state. Solutions livingon theboundary ofthe basinof attractionof thelaminar stateare found byapplying thebisection procedure described in Section 2. The bisection looks for the threshold A1 corresponding to the basin boundary. Values of A1 slightly above the threshold lead to turbulent solutions (dashed, blue lines in Fig. 1a), while values slightly below leadtothelaminarstate(dotted,greenlinesinFig. 1a).Forsufficientlylongtimesandforvaluesof A₁ thataresufficiently good approximations ofthe exactthreshold, thesolutions on thebasin boundary converge to arelative periodic orbit for all cases considered (see Fig. 1a for theRe=3000 convergence) with aperiod that increases with the Reynoldsnumber (T =739 for Re=3000, T=1090 for Re=4000 and T=1418 for Re=5000). The periodic solutions are found to travel in thestreamwisedirection withaphase speed Cx=0.98 forRe=3000 and 0.985 for thetwo other cases.Thisindicates that the active part of the process is located near the channel center. In Fig. 1b, the converged periodic solutions are shown in the kv′k–ku′k plane, where ku′k2= (1/V)R

V(u−Ulam)2dV and kv′k2= (1/V)

R

Vv2dV. The norm ku

′_{k ofthe}

streamwise perturbationvelocity isrepresentativeof the amplitudeof streamwisestreaks, while kv′_{k isrepresentativeof}

the amplitude of the quasi-streamwise vortices. The solutions rotate counter-clockwise in the cycles reported in Fig. 1b. Starting from a point on the bottom-right of thecycle, where the amplitude of thevortices is maximum, the amplitude of thevortices initiallydecays while that ofthestreaksincreases,due tothelift-up mechanism.The streaksthenreach a maximumamplitudewheretheyexperienceabreakdownduringwhichtheiramplitudedecaysfast,whileregeneratingthe vortices,whichclosestheloopoftheclassicalself-sustainedprocess[13].Thesolutiontravelsquitefastinthelowerpartof thecycle,ascanbeseenalsoinFig. 1a,whereitisseenthat thegrowth phase(lift-up)ofK′_{≈ ku}′_k2 _{ismuchslowerthan} the decay phase (breakdown). The evolution of theflow structures during thecycle can beseen in the snapshots ofthe flowfielddisplayedinFig. 2,takenincorrespondencetothefourpointsshowninFig. 1b.Theconvergedperiodicsolutions have theshift and reflect symmetry {u,v,w}(x,y,z)= {u,v,−w}(x+Lx/2,y,−z),which was not enforcedon the initial

Fig. 3.(Coloronline.)Rescaledrms amplitudesoftheperiodicvelocityperturbationsexpressedinwallunitsandaveragedoveroneperiod.Thestreamwise, wall-normalandspanwisecomponentsarereportedinpanels(a),(b)and(c),respectively.Thesolutionsarerescaledusingthevalueγ=0.8.

Table 1

Realpartsσj ofthe j-thFloquetexponentsoftheunstablemodesoftheperiodicorbitsolutions.

Re 103_σ

1 103σ2 103σ3 103σ4 103σ5

3000 3.99 3.34 3.32 2.99 2.73

4000 3.39 1.34 1.16 1.06 1.03

condition.Fromthesnapshotsitisseenhoweveryhalf-periodthelowspeedstreakandthequasi-streamwisevorticesshift byhalfspanwisewavelengthand thenrepeatthecycle exactlyinthesamewaydue totheshift andreflect thesymmetry ofthesolutions.Oneperiod thereforecorrespondstotwoloopsofthecyclesreportedinFig. 1b.

From Fig. 1bwe see that the amplitude of the relative periodic solutions decreases for increasing Reynoldsnumbers, which istypicalof‘lower branch’solutionsthat liveon theedgeofchaos(see, e.g.,[23]fortheasymptoticsuction bound-ary layer case). An examination of the root-mean-square velocity field perturbation, averaged over the horizontal planes and one temporalperiod,shows thatmost oftheperturbationrms kinetic energy resides inthestreamwisevelocity com-ponent (streaks) with amaximum amplitude locatednear y≈ ±1/2. The wall-normal and spanwise velocity rms profiles are consistent with center-channel quasi-streamwise vortices. These periodic solutions, therefore, unlike previously found periodic-likesolutions[27],arenotlocalizednearasinglewall,butinthebulkoftheflow.

When theReynolds numberis increased,the rms amplitudeof thevelocity field perturbationis seento decrease.The velocity rms profiles remain approximately self-similar, with amplitudes decreasing as Re−γ _{for the streamwise velocity} and Re−2γ _{for thewall-normal and thespanwisevelocity components, with}

_γ

_{≈0.8.Thefacts that thestreaksamplitude} is always larger than the vortices amplitude and that the ratio ofstreak to vortices amplitudesis almost proportional to the Reynolds number are additional indications that the non-normal amplification of streaks from the vortices plays an importantroleintheself-sustainmentoftheseperiodic solutions(Fig. 3).

These periodic solutions are unstable. A Floquet linear stability analysis was performed at Re=3000 and 4000, once the convergence of the periodic solution was improved to sufficient accuracy using Newton iterations. If no symmetry is enforced, five unstable exponents are found, but only one mode (the most unstable) has thesame symmetries of the periodic orbitsolution.All theunstableFloquetexponents arerealand theirrealpart,reportedinTable 1,decreaseswhen theReynoldsnumberisincreased.

4. Conclusions

Unstableperiodic solutions ofthe Navier–Stokes equations have been computed in aminimal box for plane Poiseuille flow atReynoldsnumbers rangingfrom Re=3000 to Re=5000. Thesesolutions have long periods that increase withRe

and that areoftheorderofa thousandconvectivetime units.The averagedvelocity fieldperturbations areapproximately self-similarinRe,withdifferentvelocitycomponentsscalingdifferentlywiththeReynoldsnumber.Theself-similarvelocity fields are associated with quasi-streamwise streaks and vortices located in the bulk of the flow. The streaky structures associated with the relative periodic orbits do not migrate to the near-wall region as the Reynoldsnumber is increased. Thesestructures,which remainsituatedinthebulkoftheflow forincreasingReynoldsnumbersandwhich areassociated withquitelowfrequencies ofoscillation,arethereforecompatible withlarge- andverylarge-scalestructureswhoseroleis crucialinturbulentflowsathighReynoldsnumbers.Tworecentinvestigationsindicateindeedthatself-sustainedprocesses exist atlarge- andverylarge-scaleinthebulkoftheflow [15]and inthelogarithmic layer[16]ofturbulentchannelflows and thattheseprocessesarenotforcedbythenear-wallcycle.Itisthereforetemptingtolinkthelargescaleself-sustained processesinthebulkoftheflow toa‘backbone’ofunderlyingperiodic solutions,followingthesamerationaleinvokedfor thenear-wallstructures.Currenteffortisaimedatprovidingevidencesupportingthisconjecture,namelybyquantifyingthe

phase speedsofthelarge-scalestructures,bycomputingtheircorrelationsto thefoundperiodic solutions,and,evenmost importantly,bycomputingadditionalperiodicsolutionsthatmightbeofinteresttothisapproach.

Acknowledgements

The use of the channelflow.org code [11] and financial support (grant no. 11050707) from PRES Université de ToulouseandRégionMidi-Pyrénéesarekindlyacknowledged.

References

[1]R.Artuso,E.Aurell,P.Cvitanovic,Recyclingofstrangesets: I.Cycleexpansions,Nonlinearity3(1990)325.

[2]T.R.Bewley,NumericalRenaissance:Simulation,OptimizationandControl,RenaissancePress,SanDiego,CA,USA,2008.

[3]R.M.Clever,F.H.Busse,Three-dimensionalconvectioninahorizontalfluidlayersubjectedtoaconstantshear,J.FluidMech.234(1992)511–527.

[4]R.M.Clever,F.H.Busse,TertiaryandquaternarysolutionsforplaneCouetteflow,J.FluidMech.344(1997)137–153.

[5]C.Cossu,M.Chevalier,D.S.Henningson,SecondaryoptimalgrowthandsubcriticaltransitionintheplanePoiseuilleflow,in:P.Schlatter,D.S. Henning-son(Eds.),SeventhIUTAMSymposiumonLaminar–TurbulentTransition,Springer,2010,pp. 129–134.

[6]C.Cossu,L.Brandt,S.Bagheri,D.S.Henningson,Secondarythresholdamplitudesforsinuousstreakbreakdown,Phys.Fluids23(2011)074103.

[7]Y.Duguet,C.C.T.Pringle,R.R.Kerswell,Relativeperiodicorbitsintransitionalpipeflow,Phys.Fluids20 (11)(2008)114102.

[8]T.Duriez,J.-L.Aider,J.E.Wesfreid,Self-sustainingprocessthroughstreakgenerationinaflat-plateboundarylayer,Phys.Rev.Lett.103(2009)144502.

[9]U.Ehrenstein,W.Koch,Three-dimensionalwavelikeequilibriumstatesinplanePoiseuilleflow,J.FluidMech.228(1991)111–148.

[10]H.Faisst,B.Eckhardt,Travellingwavesinpipeflow,Phys.Rev.Lett.91(2003)24502.

[11]J.F.Gibson,J.Halcrow,P.Cvitanovic,VisualizingthegeometryofstatespaceinplaneCouetteflow,J.FluidMech.611(2008)107–130.

[12]M.Guala,S.E.Hommema,R.J.Adrian,Large-scaleandvery-large-scalemotionsinturbulentpipeflow,J.FluidMech.554(2006)521–541.

[13]J.M.Hamilton,J.Kim,F.Waleffe,Regenerationmechanismsofnear-wallturbulencestructures,J.FluidMech.287(1995)317–348.

[14]J.Herault,F.Rincon,C.Cossu,G.Lesur,G.I.Ogilvie,P.-Y.Longaretti,Periodicmagnetorotationaldynamoactionasaprototypeofnonlinearmagnetic fieldgenerationinshearflows,Phys.Rev.E84(2011)036321.

[15]Y.Hwang,C.Cossu,Self-sustainedprocessatlargescalesinturbulentchannelflow,Phys.Rev.Lett.105 (4)(2010)044505.

[16]Y.Hwang,C.Cossu,Self-sustainedprocessesinthelogarithmiclayerofturbulentchannelflows,Phys.Fluids23(2011)061702.

[17]T.Itano,S.Toh,Thedynamicsofburstingprocessinwallturbulence,J.Phys.Soc.Jpn.70(2001)703–716.

[18]G.Kawahara,S.Kida,PeriodicmotionembeddedinplaneCouetteturbulence:regenerationcycleandburst,J.FluidMech.449(2001)291–300.

[19]R.R.Kerswell,O.R.Tutty,Recurrenceoftravelingwavesintransitionalpipeflow,J.FluidMech.584(2007)69–102.

[20]K.C.Kim,R.Adrian,Verylarge-scalemotionintheouterlayer,Phys.Fluids11 (2)(1999)417–422.

[21]L.S.G.Kovasznay,V.Kibens,R.F.Blackwelder,Large-scalemotionin theintermittentregionofa turbulentboundarylayer, J.FluidMech.41(1970) 283–325.

[22]T.Kreilos,B.Eckhardt,PeriodicorbitsnearonsetofchaosinplaneCouetteflow,Chaos22 (4)(2012)047505.

[23]T.Kreilos,G.Veble,T.M.Schneider,B.Eckhardt,Edgestatesfortheturbulencetransitionintheasymptoticsuctionboundarylayer,J.FluidMech.726 (2013)100–122.

[24]M.Nagata,Three-dimensionalfinite-amplitudesolutionsinplaneCouetteflow:bifurcationfrominfinity,J.FluidMech.217(1990)519–527.

[25]A.Riols,F.Rincon,C.Cossu, G.Lesur,P.-Y.Longaretti, G.I.Ogilvie,J.Herault,Globalbifurcations tosubcriticalmagnetorotationaldynamoactionin Keplerianshearflow,J.FluidMech.731(2013)1–45.

[26]T.M.Schneider,B.Eckhardt,J.Vollmer,Statisticalanalysisofcoherentstructuresintransitionalpipeflow,Phys.Rev.E75(2007)066313.

[27]S.Toh,T.Itano,Aperiodic-likesolutioninchannelflow,J.FluidMech.481(2003)67–76.

[28]D.Viswanath,Thedynamicsoftransitiontoturbulenceinplanecouetteflow,arXiv:physics/0701337,2007.

[29]F.Waleffe,Three-dimensionalcoherentstatesinplaneshearflows,Phys.Rev.Lett.81(1998)4140–4143.

[30]F.Waleffe,Homotopyofexactcoherentstructuresinplaneshearflows,Phys.Fluids15(2003)1517–1534.