Numerical and experimental investigations of a rigid cone striking the free surface of an incompressible fluid

HAL Id: hal-01008539

https://hal.archives-ouvertes.fr/hal-01008539

Submitted on 7 Dec 2018

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Numerical and experimental investigations of a rigid

cone striking the free surface of an incompressible fluid

Bundy Donguy, Bernard Peseux, Emmanuel Fontaine

To cite this version:

Bundy Donguy, Bernard Peseux, Emmanuel Fontaine. Numerical and experimental investigations of

a rigid cone striking the free surface of an incompressible fluid. ASME Pressure Vessel and Piping

Conference, 2001, Atlanta, United States. �hal-01008539�

NUMERICAL AND EXPERIMENTAL INVESTIGATIONS

OF A RIGID CONE STRIKING THE FREE SURFACE

OF AN INCOMPRESSIBLE FLUID

Bundl DONGUV

Laboratoire de Mecanique et Materiaux Division Mecanique des Structures Ecole Centrale de Nantes -1 , rue de La Noe

44321 Nantes Cedex 3, France bundi.donguy@ ec-nantes. fr

Bernard PESEUX

Laboratoire de Mecanique et Materiaux Division Mecanique des Structures Ecole Centrale de Nantes -1 , rue de La Noe

44321 Nantes Cedex 3, France bernard.oeseux@ ec-nantes. fr

Emmanuel FONTAINE Principia R&D Zone Portuaire de Bregaillon 83507, La Seyne sur Mer, France

Emmanuel. Fontaine@ ifp. fr

ABSTRACT

In the present paper, the hydrodynamic impact problem of a blunt and rigid body is considered. The three-dimensional asymptotic problem is solved numerically using variational formulation together with finite element method. The so-called wetting correction is obtained through an iterative procedure. The numerical method is successfully validated against analytical solutions for simple geometries such as wedges and cones.

The second part of the paper describes an experimental investigation, which consists in series of free fall drop - tests of cone shaped models with different deadrise angles. Pressures at different locations have been measured and are compared against the numerical simulations. Good agreement is generally reported.

1 INTRODUCTION

In severe sea conditions, ship hulls experience slamming loads due to their large amplitude motions. These impulsive loads associated with the impact may induce locally plastic deformations of the hull. In extreme cases, they may threaten the integrity of the overall ship structure due to a large increase of the global bending stresses. The ability to better predict local and global structural responses of the ship hull to these impulsive loads appears necessary. From a practical point of view local flexion are included among dimensioning criteria of the hull.

Generally, impact loads are commonly estimated within the

simplest to describe the violent motion of the free surface in the

·vicinity of a moving surface-piercing body. Despite these simplifications, the resulting problem remains strongly non-linear because of the free surface boundary conditions which do not only include quadratic terms but also are written on an a priori unknown boundary.

Impact loads are especially high when the tangents to free surface and the body are almost parallel near the contact point, i.e. for a blunt body striking an almost flat free surface. In this geometrical configuration, an asymptotic analysis of the problem can be performed using the ratio between the immersion and the wetted length as the perturbation parameter. The famous Wagner's

(1932)

intuitive analysis has since then been put into formal basis and extended using the framework of matched. asymptotic expansions (Cointe, 1989, 1991, Howison et al.,

1991).

In most studies planar flow in each cross section is assumed. Neglecting gravity effects, the free surface condition reduces, to the leading order, to a Dirichlet condition for the potential on the undisturbed position of the free surface. The flow is then similar to that around a flat plate placed perpendicularly into a uniform stream, for which an analytical solution can be derived.

These classical asymptotic two dimensional solutions have been validated against experiments for drop tests of planar wedges (Chuang,

1967,

Fontaine & Cointe,

1997),

cylinders (Cointe & Armand,

1987),

or more generally ship cross-section (Zhao et al,

reported although the comparisons require sometimes three­ dimensional side effects to be accounted for in a simplified way.

In the above mentioned studies, the body is assumed to be rigid. Structural deformations due to these two dimensional impact loads have been studied by Faltinsen

(1997)

and Korobkin

(1995)

assuming the deformations velocities to be small compared to the vertical impact velocity. Recently, Donguy, Peseux & Fontaine

(2000)

use the two-dimensional pressure distribution to compute the local deformations of the hull using FEM. For a realistic impact event, it is nevertheless shown that the local structural deformations exhibit a strongly three-dimensional character. If the two-dimensional cross flow assumption can be jus�ified for slender rigid bodies, three­ dimensional effects play a great importance when fully coupled fluid - structure interaction problem is considered.

One of the next improvements in the modeling of the hydrodynamic impact problem is therefore to take into account the three-dimensionality of the flow. Within the blunt body asymptotic analysis, the main difficulty for solving the simplified problem is the evaluation of the contact line between the body and the free surface. If analytic or quasi-analytic solutions can be obtained in the two­ dimensional case, a purely numerical approach has to be developed to treat the more general three-dimensional situation. The aim of this study is to develop a three dimensional simplified method which allows to evaluate impact loads on a rigid body.

In the present paper, the classical two-dimensional asymptotic approach is extended to the three dimensional case. First, the simplified modeling is described, focusing attention on the physical assumptions sustaining the analysis. The numerical method used to solve the asymptotic problem is then presented. The approach is based on a variational formulation of the asymptotic problem together with the use of Finite Element Method. As suggested by Korobkin

(1982),

the contact line is evaluated using the displacement potential while the geometrical non-linearity associated with the determination of the wetted surface is solved through an iterative procedure. Pressure is finally obtained by velocity potential formulation approach. Comparing numerical results to classical asymptotic solutions finally validates the method. The two dimensional solutions for a wedge or a parabola, and the three­ dimensional one for the axisymmetric case of a cone are successfully recovered. The accuracy of the numerical scheme is also tested, in particular near the contact line where the asymptotic solution is singular.

The second part of the paper describes a preliminary experimental investigation, which consists in series of free fall drop tests of rigid cone shaped models with different deadrise angles. The experimental parameters have been tchosen so that realistic impact situation is reproduced. As shown in earlier experiments, see e.g. Chuang

(1967),

performing accurate drop test experiments is difficult due to the complexity of the involved phenomena. Experimental results are very sensitive to small perturbations, such as small variation of the effective deadrise angle or air trapped phenomenon. In the present experiments, pressures at different locations have been measured and are successfully compared with the numerical simulations for the smallest deadrise angle. The practical domain of validity of the asymptotic solution is finally discussed in connection with the deadrise angle increase.

2 THREE-DIMENSIONAL PROBLEMS 2.1 Exact formulation

The flow generated during the impact of a body on a free surface is considered. The fluid is assumed to be perfect and incompressible, and the flow is irrotational. The velocity field can therefore be evaluated according to v = grad(/J , where l/J=t/J(x,y,z,t) is the velocity potential. The body shape is assumed to be given by its position

u$

=

u$(x,y,z,t)

and the notation z=h(x,y,t) is used for the unknown free surface elevation.

z

Figure

1.

Geometrical definitions

Under these assumptions, the velocity potential satisfies the following boundary value problem :

�l/J=O aq, .:.

-an =us.n

a4'

+

.l(griid(/J)2

+.E..+

gz =

0

ar

2

_p dh = aq, dt ar in

.q.

(1)

on the body

(2)

on the free surface

(3)

on the free surface

(4)

Equation

(2)

states the continuity of the normal velocity on the body. The kinematic and dynamic free surface conditions, eq.

(3)

and

(4)

respectively, express that the free surface is a material surface with constant pressure. In the far field, the fluid is assume to be at rest:

and the following initials conditions:

h(x,y,O)=O t/J(x,y,z,O)=O

are imposed in the case of a fluid initially at rest. Once the potential is known, the pressure on the body can be derived from Bemoulli's equation:

P aq,

1

_ 2

- = ----(grad4J) - gz

2.2 Asymptotic formulation

.

As mentioned earlier, numerous difficulties arise if one wish to solve directly the unsteady nonlinear boundary value problem. Indeed, the motion of the free surface is violent. Experimentally, jets

_developing along the body are observed (see e.g. Greenhow,

1987).

Classically, according to Wagner

(1932),

the problem is simplified into:

�l/>=0

dl/J :.

-an

= us.n

l/>=0

dh = dl/>

dt dZ

(6)

onrs

(7)

(8)

(9)

where r8 and rL are respectively the projections on the plane

z

= 0 of

the wetted body surface and the free surface. The contact line fTt),

defined as the intersection between Ts and TL , is a priori Unknown.

The simplified problem

(6)-(9)

requires gravity effect and

quadratic terms to remain small compare to the linear terms. The ·

displacements of both, the body and the free surface, must also remain small to justify the geometrical linearisation of the boundary conditions. These assumptions can be justified formally through an asymptotic analysis of the impact problem for a blunt and rigid body

(Cointe,

1989,

Wilson,

1989).

The small parameter used in the

asymptotic expansion is the ratio between the immersion and characteristic length scale of the body wetted area. The method of matched asymptotic expansions leads then to define three different zones in which three asymptotic expansions are performed and matched successively:

• the far field domain, where the flow is similar to the that

around a flat plate of unknown width in an unbounded fluid,

• the spray root domain near the contact line, where the flow overturns to create a jet,

• and the jet domain, along the body.

The perturbation procedure relies strongly on the blunt body

assumption. In the far field, the body boundary condition

(2)

can be

written on the undisturbed position of the free surface without

introducing significant error, therefore justifying eq.

(6).

To the

leading order, the quadratic terms in eq.

(3)

and (4) can be neglected

in the far field, but must be retained to describe the flow within the

jet. The exact dynamic condition, eq.

(3),

has been replaced by a

Dirichlet condition for the potential on the undisturbed position of the

free surface. Equation

(7)

is therefore applied on

z

= 0. Physically,

the acceleration in the fluid has been assumed to be large compared to gravity. For a body impacting the free surface with constant speed

V,

this assumption is justified until g. tiV < < 1. Finally, the simplified

kinematic free surface condition states that the vertical displacement of the free surface is equal to the fluid vertical motion, evaluated on the linearised position of the free surface.

Within this modelling, the solution is singular on the contact line since the slope of the free surface and the vertical velocity tend to infinity. This singularity is physically correlated with the existence of a jet located near the intersection between the free surface and the body surface. This singularity also appears in the pressure distribution given to the leading order by :

dfP

p=-p­

_dt

(10)

In the present modelling, the far field solution for the pressure is matched to the asymptotic splution describing the flow in the spray root domain. The resulting composite solution is therefore regular and can be integrated to evaluate the corresponding impact loads.

At this stage, it is important to note that the three dimensional character of the flow has been retained in the equations. In particular, Laplace's equation is not simplified into its two dimensional form as would be usually done using strip theory based on slender body

assumption (see e.g. Fontaine et at

1997).

3 NUMERICAL RESOLUTION 3.1 Variational formulation

The weighted residual method consists in searching for

functions

l/>

that cancel the integral quantity:

W

((/�)

=

i

q> •

R((/J) dD

_{(1 1)}

n/

for all weighting functions q>. For our problem, the residue R(

l/>)

is set

equal to

L1lf>.

After applying Green's identity and taking into account

the boundaries conditions, the integral eq.

(11)

gives:

(12)

The discretization of this equation is performed' using Gal er kin's

method. The potential

q,

and the weight functions q> are approximated

using the same shape functions according to

(13)

The functions N1 depend on the types of elements, and

{ l/>t

denotes

the nodal potential vector of the finite element (e). Using these

approximations into eq.

(12)

leads to linear matrix system for the

H{Q>} = {G,}

H� =foe N;,JNJ,;dD

{G� }e = fr• {N, }(�1.n)dS

B

3.2 Determination of the wetted surface

(14)

(15)

(16)

To evaluate the right hand side of eq. (16), it is necessary to

know the wetted portion of the body, or, equivalently, the position of

the contact line between the body and the fluid. Due to the

deformations of the free surface, the wetted surface is part of the

unknown of the problem. An additional equation is therefore needed

to close the problem. Physically, the contact line is determined by

·

imposing to the solution to satisfy volume of the fluid conservation

(Wilson, 1989, Fontaine

&

Cointe, 1992) or equivalently, by

imposing the existence of an intersection point between the elevation

of the free surface and the body as intuitively done by Wagner

(1932). Volume conservation should be automatically satisfied since

Laplace's equation is solved. Nevertheless, the problem is singular at

the initial time when the contact line reduced to a single point, thus

the need for an extra closure equation. As suggested by Korobkin

(1982), it is easier to introduce the displacement potential given by:

1f!(x,y,z;t)= f�tJ>(x,y,z;s)ds

(17)

instead of the velocity potential. The boundary value problem

satisfied by

1f1

is similar to the one satisfied by

_Q>

except for the body

boundary condition. The main advantage of introducing this

transformation is that the value of

1f1

on

z = 0

is by construction the

free surface elevation. Solving for

1f1

does not require the knowledge

of the temporal evolution of the free surface elevation. From a

numerical point of view, the same discretisation scheme is applied to

the displacement potential leading to:

H{lfl) =(G.,)

(18)

where the discretised body boundary condition writes:

(19)

The wetted surface is determined through an iterative procedure:

starting from an initial surface guess for (T8)0, the problem for

displacement potential problem is solved until that the free surface

elevation is equal to the position of the body at the boundary

fTt) :

(20)

Once convergence has been reached, the position of the contact line

is known. the linear system for the velocity potential is then solved. It

is worth noting that the matrix

H

which depends only from the

geometry has already been assembled and so doesn't have to be

computed once again to solve the velocity potential problem. From

one time step to the other, the boundary mesh doesn't move, and

therefore no substantive derivative has to be introduced. As a result, a

simple first order backward finite difference scheme give an accurate

estimation of the pressure even close to the singularity as will be

demonstrated in the next section.

4 VALIDATION OF THE NUMERICAL PROCEDURE 4.1 Two dimensional case

The example of a two dimensional parabolic hull defined by

z=a/,

penetrating with constant velocity V a free surface initially at

rest, is considered. The numerical method previously described has

been applied to this case. Comparisons between numerical and

analytical results are presented in fig. 2 and 3. Triangular and

quadrilateral elements were used for the numerical computation.

0.1 ,..---r---, 0.05

�

0 "' 0 0.1 analytical numerical 0.2 0.3 y(m) 0.4 0.5

Figure 2.

Comparison between numerical and analytical solutions for the free surface elevation around a parabolic hull.

4 ··· ··· ··· 35 . · analytical 3-numerical · error(%)

11

"i::"25 ..

�

..

�

2-�

�1.5 ... 1 .. ··· ···· ··· ·· ···2 0

ti::

)

.14 !12�. l

�:

.

i�o�

6

i4

•:

������-:.;

...

u��.

,..!JJ;J:

0 0.05 0.1 0.15 0.2 y(m)

Figure 3.

Comparison between numerical and analytical solutions for the outer pressure distribution on a parabolic hull. The errQr

The analytical expressions for the wetted width, the free surface elevation and the outer expansion of the pressure are classically given

by (Cointe,

1989):

·

d2(t)

= 2

Vt

a

h(y,t) = -Vt-

[

ra

y(al- 2Vt))'i- al

]

P0.,,(y,t) = P

1V2(a(2Vt- al)�

(21) (22)

(23) Although the solution is singular at the intersection, the numerical scheme gives a relatively good estimation of the pressure distribution in this region. Practically, the error increase near the singularity has no real implications since the numerical solution is matched to the nonlinear spray root solution.

4.2 Three dimensional axlsymmetric case

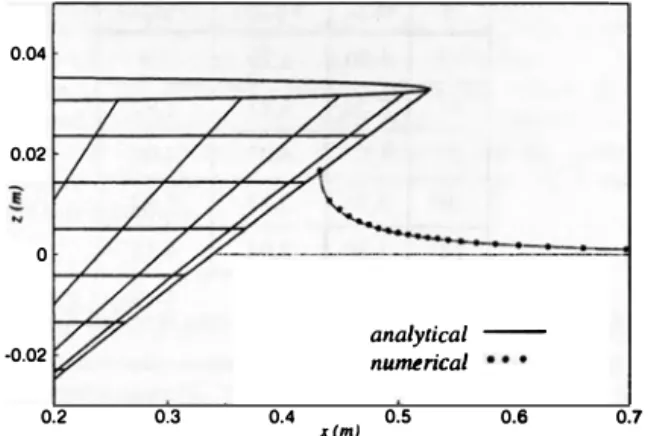
Comparisons for a cone shaped hull are presented in fig. 4 and

5.

Hexahedron types of elements were used in the numerical simulation. Good agreement between numerical and analytical results is obtained again. All parameters being comparable to the previous two­ dimensional computation, the relative error remains of the same order, despite the mesh is this time really three dimensional. In fig.

6,

the pressure distribution for a two-dimensional wedge and a cone having the same immersion are compared to estimate roughly three­ dimensional effects. The maximum error on the pressure distribution is around

30%.

The figure also shows that the two dimensional computations appears also to be conservative.

0.04 0.02 0 ..0.02 0.2 0.3 0.4 x(m) analytical -­ numuical 0.5 0.6 0.7

Figure 4. Comparison between numerical and analytical solutions for the free surface elevation around a cone shaped hull

To conclude this section, analytical and numerical results are very close to each others for both 20 and 30 cases. The evaluation of the free surface elevation remains nevertheless sensitive to the boundary between the structure and the fluid. To represent the singular behavior of the solution in the vicinity of this boundary, the finite elements mesh has to be refined in this zone. The regularity of the mesh is also an important parameter which controls the accuracy of the numerical resolution.

:r

anorync

�

l-

-=

----nn

�:

16�

numerical

16

14

�

error(%)

₁₁

₁₄

8

6

4

2 ·

12_

oo�wu�o�.1ww�o�2�Ld�WL��o

y(m}

Figure

5.

Comparison bet�en numerical and analytical solutions

for the outer pressure distribution on a cone shaped hull

%�

�0�.2��0.�4��0�.6--�0.�8��

_.v(m)

Figure

6.

Comparison between the pressure distributions along a

cone and a wedge penetrating the free surface with same velocity. At each time, the immersion is the same for the two bodies

5 EXPERIMENTS 5.1 Experimental set-up

Free fall drop test experiments have been carried out on the

impact tower of the Fluid Dynamics Laboratory. at the Ecole Centrale

of Nantes (see fig.

7).

The use of a relatively large experimental

facility ( 10 m height and

1

,4 m width) allows for a typical size of

0.32m for the tested models, therefore reducing the possible influence of surface tension effects.

Cable

(j)

-.r+--+-t---- pliers

®

n==;::�l�tj�--

Guided frame

Figure

7.

Impact tower: experimental set-up

Cones shaped models were rigidly attached to a cylindrical support

itself connected to the guided frame of the

impact tower. The models

were set free without initial velocity by means

of pliers �operated

by two

hydraulic jacks.

During the

drop, the cone was guided by a

system of cables <V

which

allows

to control the relative position

between the body and the free surface. After impact into water

surface, the cone was

stopped progressively by a metallic frame

covered with foam.

Three different cone shaped

models with deadrise angles of 6,

10, and 14 degrees have been successively tested (see fig. 8). The

effective thickness of the steel models

were sufficiently important,

reaching from

25

to

50

mm, so that the

rigid body assumption is

verified during impact. The aim

of this first set of experiments is to

test the accuracy and domain of validity of

the simplified numerical

method previously described, but also to prepare

more complex

experiments to study the influence of hydroelasticity effects. The impact velocity was chosen to rise realistic values from

3 to 6 m/s

approximately.

The drop height of the model was set up to 3.0 m.

Due to rubbing of the pulley-cables connections,

additional

weight were necessary to reach the desired impact

velocity.

Cone

I.

I

Sensor 2 Sensor 1

I

�A�--- .

_.·.__ ���·, �· ... ,� .... ' .---n.----40 e = 16

Figure

8.

Detailed views of the cone shaped models with different

deadrise angles

Drop velocity and pressure

measurements

were performed

during impact. Two quartz ICP

compensated pressures sensors were

set at 40

mm and

90 mm from the cone symmetry axis (fig. 8). These

sensors are well suited for impact measurements.

Their sampling

frequency is up to

400 kHz,

and the measurement range

is

0

to

69

bar. They also allow for the use of relatively long

wires

(20

m)

without altering the electric signal

so that the data processing system

does not need to be too close to the

water.

The drop velocity was measured by mean of a dynamo connected to

the guidance pulley of the cable.

Finally, pressure and velocity

signals are plotted

and recorded by a numerical memory oscilloscope.

The cones were dropped against

calm water. At least three drops were performed in

each test

condition to make sure of the repeatability of the measurements. Results presented below are representative' of these drop test series.

5.2 Comparisons between theorv and experiments

Table 1 reports the main parameters of

each experiment, i.e. the

drop height

(H)

and the falling velocity at the initial time

of impact

on sensor 1 and sensor

2.

The two maximum values of

the pressure at

the two locations, measured and calculated, for

the three deadrise

angles

(�) are presented in table

2.

Numerical and

experimental

results for the pressure levels are found to be in reasonable

agreement

although the pressure is always slightly over predicted, indicating

that

the numerical model is therefore conservative.

On the first sensor, and for the

s

m

allest deadrise angle, the

experimental value is by far over predicted.

Physically, it is believed

that air entrapment

occurs, leading to a decay of the pressure. This

phenomenon has also been observed by Chuang (1971)

on cones with

deadrise angles smaller than 1°, and

by Hagiwara, Yuhara

(1974)

for

wedges with deadrise angles lower than 3

degrees.

�

Hcml _{vl(m/s) v2(mls)}

60

1,80

3,79

3,9

60

2,70

5,87

5,9

2 IQO

1,80

4,03

4,08

IQO 2,70

5,87

5,92

14°

1,80

3,94

4,16

Table 1.

Measured velocities for different free fall drop heights

P1 (bar) P2 (bar)

�

Exp.

Nu m.

Exp.

Nu

m.

60

7,8

10,5

8,3

11

60

15

25,3

26,4

25,7

IQO

3,5

4,2

5,2

4,3

10°

7,8

9

10,6

9,1

14°

1,3

2

1,7

2,2

Table

2. Experimental-numerical pressures levels comparison for different heights of impacts

Examples of temporal evolution of the pressure on the two

probes are presented in fig. 9 (a) to (e) corresponding to the different

deadrise angles and impact velocities. Although experimental and

numerical distribution pressures don't fit exactly the same in details,

the experimental distribution is globally well represented by the

'numerical simulation. Both signals show a pressure peak travelling

along the body, followed by a plateau. The location of the peak is

clearly well described by the simplified theory. The wetted length

seems therefore to be correctly estimated. This local qJ.Iantity results

nevertheless from global volume conservation property as mentioned

previously. It is therefore not surprising that the modeling is able to

give a good estimate of this quantity. The pressure rise immediately

after impact is also well reproduced. The simplified model is indeed

asymptotically valid for small times. The level of the peak, i.e. the

maximum pressure, is reasonably estimated for the smallest deadrise

angle, but the error increase with an increase of the deadrise angle.

According to the asymptotic solution, the level of the pressure peak

should not vary along the body. The experiments clearly indicate that

the peak intensity increases between the two probes. This discrepancy

can be partially explained by the fact that the impact velocity of the

cone is also increasing due to gravity acceleration. This phenomenon

is not reproduced in the numerical simulation where the impact

velocity remains constant. A posteriori calculus confirms that the

velocity increases immediately after impact, the acceleration

decreasing but remaining downward. The plateau level is also slightly

over estimated, certainly as a result of using a simplified body

boundary condition. It is well know that the geometrical linearisation

of the boundary condition yields to an overestimation of the pressure

coefficient (see e.g. Faltinsen, 1997, Fontaine

&

Cointe, 1997).

Secondly, we observe two zones where oscillations are

generated. In the first zone we couldn't give definitely an explanation

for this oscillations. In the second zone, the oscillations correspond

not only at the moment when the cylindrical support come into the

water but also to the flat circumference. Then, this is the body

geometry which generates the second zone oscillation.

Even if the different experimental results outline above are

rather good, examination of the angle impact, who doesn't fit exactly

with the real one, prevent us to validate wholly the experimental

investigation. We are now setting a new scheme which allows to

control this parameter.

6 CONCLUSION

In the present paper, the three-dimensional Wagner problem is

solved numerically using a variational formulation together with a

finite element method. The so-called wetting correction is obtained

through an iterative procedure. The numerical resolution is validated

computing simple problems, such as the water impact problem of a

wedge with small deadrise in the two dimensional case, or a cone for

the three-dimensional case. Good agreement is obtained between

numerical and analytical solution. This paper also describes a first

series of drop-test experiments. These drop-tests consist in the

impacts of rigid cones on a free surface initially at the rest.

Experimental histories are well predicted by numerical pressure

simulations, although differences are reported. In particular, it has

been found a dissimilarity between peak pressure values (the first

peak being weaker than the second), resulting from an increase in the

velocity. The retardation effect, resulting from impact loads, appears

latter on in the experiments.

We are now leading new drops-tests investigation for which

measurement of the velocity is made by incremental coder. It allows

us a more accurate analysis of results.

7 ACKNOWLEDGMENTS

The authors gratefully acknowledge the financial support of

French Direction Scientific of the Delegation Generale de

l'Armement.

8 REFERENCES

Cointe, R., Armand, J.L., 1987, "Hydrodynamic impact analysis of a

cylinder"

J. Offshore Mechanics and artic Engineering,

vol. 9, pp.

237-243

Cointe, R., 1989, ''Two dimtnsional water solid impact"

Journal of

Offshore Mechanics and Arctic Engineering,

vol.l l 1, pp.1 09-114

Chuang, S.L., 1967, "Experiments on slamming of wedge- shaped

bodies"

Journal of Ship Research,

pp. 190-198

Chuang, S.L., Milne, D.T., 1971, "Drops test of cones to investigate

the three-dimensional effects of slamming"

Navy Naval Ship

Research and Development Center, Report 3543

Donguy,

B.,

Peseux, B., Fontaine, E., 2000, "On the ship structural

response due to slamming loads "

Proc. of European Congress on Computational Methods in Applied Sciences and Engineering,

Barcelona

Faltinsen,

0.,

Zhao, R. 1997, "Water entry of �hip sections and

axisymetric bodies"

High Speed Body Motion in Water,

Kiev

Faltinsen,

0.,

1997, 'The effects of hydroelasticity on ship

slamming"

Phi/. Trans. R. Soc. Lond.,

vol. 355, pp. 575-591

Fontaine, E., Cointe, 1997, "Asymtotic theory of water entry",

High

Speed Body Motion in Water,

Kiev, NATO conference.

Greenhow, M., 1987, "Wedge entry into initially calm water"

Applied Ocean Research,

vol. 9, pp. 214-223

Hagiwara, K., Yuhara T.,1974, "Fundamental study of wave impact

loads on ship bow"

Journal of the Society of Naval Architect

vol. 135

Howison, S.D., Ockendon, J.R., Wilson S.K., 1991, "Incompressible

water entry problems at small deadrise angles"

Journal of Fluid Mec

ha

nics

,vo1

.

222,pp. 215-230

Korobkin, A.A., 1982, "Formulation of penetration problem as a

variational inequality"

Din. Sploshnoi Sredy,

vol. 58, pp. 73-79

Magee, A, Fontaine, E, 1_998, "A cou

p

led approach for the. evaluati.on

of slamming loads on shtps"

Proc. 7t lnt. Symp. on Practzcal Deszgn

of Ships and Mobil Units,

The Hague Netherlands

Korobkin, A.A., 1995, "Wave impact on the bow end of a catamaran

wetdeck"

Journal of Ship Research,

vol. 39, pp. 321-327

Wagner, H., 1932, "Uber Stoss und Gleitvorgange an der Oberflache

von Fltissigkeiten"

Z. Ang. Math. Mech.,

vol. 12, pp. 193-215

Wilson, S.K., 1989, 'The mathematics of ship slamming"

Ph.D. thesis, University of Oxford

Zhao, R., Faltinsen, O.M., Aarsnes, J.V., 1996, "Water entry of

arbitrary two-dimensional sections with and without flow separation"

& �. -.---�---.---,---�--�

(b)

I

5 f- ---·---1--..,..----+----l----1 12,---�---�---.---,

(c)

r 10 r---- ___ . ---l--1---+---l pressure on sensor pl pressure on sensor p2 numerical simulation .---.---·-�---·---·-·

101---ll---t 81---(d) (e) 24�-�---�-�----�----�

!

20 1---�i----___....__j_

___________ i --··----· -. I I

f

�----��---�·---· -

-'---.1

t

1----&---iM--+---

---r---

_,

Figure 7. Pressure histories (a) cone 14°- (b)-(c) cone 10°- (d)-(e) cone 6° (I) velocity during all the drop test