Trou spectral pour un système désordonné de gaz coloré

UNIVERSITÉ BADJI MOKHTAR

DE ANNABA

-

-Faculté des Sciences

Département de Mathématiques

Thèse

Présentée en vue de l’obtention du diplôme de Doctorat

Par

ZEGHDOUDI Halim

Intitulé :

Trou spectral pour un système désordonné de gaz coloré

Option

Probabilités

Année : 2010

Directeur de thèse :

BOUTABIA Hacène

Prof U.B.M. ANNABA

Membres du Jury

PRÉSIDENT :

REMITA Med Riad

MC U.B.M.

ANNABA

EXAMINATEUR :

MOHDEB Zaher

Prof U.M.CONSTANTINE

EXAMINATEUR :

BOUSSEBOUA

Moussedek

MC U.M.CONSTANTINE

Je tiens tout particulièrement à remercier Professeur

Boutabia

Hacène

d avoir accepté de me diriger pendant ces années de thèse

et d avoir consacré beaucoup de temps à me « former ».

Je remercie

REMITA.Med.Riad

qui a accepté d'être le président

de ce jury.

Je remercie vivement Professeur

MOHDEB Zaher

et Docteur

BOSSEBOUA Moussedek

de l université Mentouri, Constantine

ainsi que Docteur

DJELLAB Natalia

pour l honneur d avoir

accepter de faire partie du jury.

Je m'estime très honorer par l'intérêt qu'ils ont bien voulu

accorder a mon travail et leur suis gré de leurs remarques, qui

ont aidé à voir les ponts qui pouvaient exister entre mon travail

et d'autres perspectives mathématiques.

Je remercie l ensemble des mes collègues du département de

mathématiques pour les moments d amitiées partagés. J exprime

également ma gratitude Professeur

Mourragui Moustapha

de

université de Rouen pour son accueil lorsque je suis arrivé dans

l'équipe du laboratoire de mathématiques Raphael Salem.

Je remercie également Monsieur

Touati Ali Bey

et Professeur

Benchettah .A

pour les discussions et les corrections de la

rédaction de ma thèse.

.

]

13

. [

Table des matières

Table des …gures 3

1 Généralités sur les processus et semigroupes 11

1.1 Martingales . . . 11

1.2 Processus de Markov, générateurs et semi-groupes . . . 12

1.3 Réversibilité . . . 19

1.4 Processus d’exclusion simple . . . 21

1.5 Equation hydrodynamique . . . 22

1.5.1 Echelles spatio-temporelles . . . 22

2 Mesures de Gibbs et inégalité de Poincaré d’un système désordonné coloré 26 2.1 Description du modèle . . . 26

2.1.1 Dynamique sur le volume . . . 27

2.1.2 Générateur de Markov . . . 28

2.1.3 Mesures de Gibbs et mesures canoniques . . . 29

2.1.4 Trou spectrale et Inégalité de Poincaré . . . 30

2.2 Construction des mesures de Gibbs pour un système désordonné coloré 32 2.3 Inégalité de Poincaré pour un système désordoné . . . 34

2.3.1 Stratégie générale . . . 34

2.3.2 Réduction au processus unidimensionnel . . . 38

2.4 Estimation du trou spectral de gaz coloré . . . 41

2.5 Schéma du preuve du théorème(SGP) . . . 42

2.5.1 Estimation de la combinaison a¢ ne de la mesure canonique . 43 2.5.2 Réprésentation de (f2_{) et (f} Pf) . . . 44

2.5.3 Expression de . . . 44

2.5.4 Lemme clé . . . 45

3 Trou Spectral pour un système désordonné de gaz coloré 47 3.1 Mesures canoniques des con…gurations . . . 48

3.2 Calcul du trou spectral . . . 52 3.3 Simulation pour les valeurs propres du matrice X . . . 57

4 ANNEXE 60

4.1 Démonstration du Theorem 2.2 . . . 60

Table des …gures

1.1 Échelle macroscopique et microscopique . . . 23 2.1 Si le site y est occupé, le saut est supprimé, sinon il est e¤ectué avec

BIBLIOGRAPHIE PERSONNELLE

Article publié

Écrit en collaboration avec Pr. BOUTABIA Hacène. Computation for the canonical measures of a colored disordered lattice gas and spectral gap. JOURNAL OF MA-THEMATICAL PHYSICS 50, 103302 (2009) :

Articles en préparation

Gibbs’s Measures of a Multi-Colored Disordered Lattice Gas.

Abstract

In this work we deal with spectral gap and canonical measures related to a model called colored disordered lattice gas. We consider the approach used in the work of Dermoune and Heinrich (cf: [9]). We suggest a new computation for the canonical measures. Also, we propose the explicit form of the spectral gap for colored disorde-red lattice gas of exclusion processes which plays an important role in the study of hydrodynamic limit.

Résumé

Nous nous proposons, dans cette thèse, de donner la forme explicite des mesures canoniques et du trou spectral d’un processus d’exclusion simple pour un système désordonné de gaz coloré qui joue un rôle important dans l’étude limite hydrodyna-mique. L’approche que nous avons utilisé est similaire à celle considèrée par Dermoune et Heinrich (cf: [9]).

Introduction

Les systèmes de particules ont été introduits dans les années 70 à la suite des travaux de F . Spitzer aux Etats-Unis ([31] ; [32] ; [33]) et de R. L. Dobrushin en U.R.S.S. ([14] ; [15]) :

En dehors des motivations probabilistes, ce nouveau domaine s’est développé a…n de résoudre des problèmes inspirés de la mécanique statistique. En e¤et, un système de particules est un processus de Markov décrivant l’évolution sur un réseau d’un nombre …ni ou in…ni de particules interagissantes et qui permet de modéliser et d’analyser la dynamique microscopique d’un ‡uide. A…n de caractériser ses états d’équilibre déterminés par la recherche des mesures invariantes. Les principaux résultats en ce domaine ont été réunis dans le livre de T. M. Liggett [24] :

En suite, le domaine d’application de ces systèmes s’est développé rapidement. Ces systèmes ont d’autres champs d’application, avec la biologie, les sciences sociales,... En général aux phénomènes impliquant un grand nombre de composants identiques. Dans ce travail, qui s’inspire sur le travail de F aggionato et M artinelli [13] ; nous nous intéressons au mouvement d’électrons libres dans un cristal en présence d’impuretés. Contrairement au cas de non présence d’impuretés où le cristal crée un champ électromagnétique périodique qui in‡ue sur le transport d’électrons, ici une des modélisations d’impuretés, consiste à considère le champ un caractère aléatoire et les électrons comme des particules évoluant sur un réseau constitué de sites, soumises à un principe d’exclusion où les promenades aléatoires décrivant les sauts entre les sites,

dépendent localement du champ potentiel chimique aléatoire (le désordre), et pour la décomplexi…cation du modèle nous négligeons les interactions entre les électrons.

Plus précisément, ce phénomène peut être décrit comme suit : une particule se trouvant sur un site x d’un réseau du treillis Zd attend un temps exponentiel et puis tente de sauter vers un site y. Si le site y est occupé alors le saut est supprimé, autrement il est réalisé avec un taux c_xy dépendant seulement des valeurs ( x; y)

représentant le désordre des sites x et y. Pour simpli…er, on suppose que le champ de désordre f xg_x2Zd est une collection de variables aléatoires i.i.d. et bornées. Ainsi

l’Hamiltonien du système est donné par H( ) = P_x( x+ ) x, où x est le nombre

de particules sur le site x; et est le potentiel chimique externe.

Plusieurs travaux ont été destinées pour avoir une information sur la vitesse de la convergence de _x vers l’état d’équilibre de la dynamique stochastique noté . A cet e¤et, il est nécessaire d’avoir d’estimation sur le trou spectral (_{j j) du générateur} de Markov ou de le calculer si possible.

Des résultats ont été établis par Lu et Y au [27] et par Cancrini et M artinelli [3] à l’aide des évaluations di¤usives utilisées pour la dynamique de Kawasaki en présence d’une haute température:

Ensuite, Boudou et autres [2] ont développé une technique générale basée sur une identité de type-Bochner pour estimer l’ensemble spectral du générateur de Markov, que Caputo [4] utilisé pour prouver aussi bien l’inégalité de Poincaré pour un système désordonné de gaz monocoloré dans l’espace produit avec un ou plusieurs lois de

conservation, que pour un processus d’exclusion simple et un processus de Ginzburg-Landau.

Dans la suite Dermoune et Heinrich [9] développé l’idée précédente pour l’étude de la limite hydrodynamique d’un processus d’exclusion simple d’un système désor-donné de gaz coloré semblable au modèle originel de F aggionnato et M artinelli [13]. Ici, notre travail porte sur l’étude de l’estimation du trou spectral "spectral gap" que l’on rencontre dans de nombreux domaines, notamment en probabilités [1; 12], en statistiques [19; 30], en géométrie [6; 7; 8; 28], en analyse d’image [20; 22], en statistique bayésienne [18], en physique mathématiques [25; 29] .... Par exemple dans - Les méthodes de Monte Carlo par une chaînes de Markov (méthodes M CM C). - Les transitions de phase en physique statistique (modèle d’Ising).

Dans cette thèse, nous avons réussi à expliciter les mesures canoniques pour un système désordonné de gaz coloré, qui nous a permis à la suite de calculer le trou spectral.

Ainsi, dans le premier chapitre nous rappelons certaines dé…nitions et certains résultats qui nous utilisons par la suite à savoir les notions de processus et chaînes de Markov, semi-groupes, mesures invariantes ....

Dans le chapitre 2, nous faisons une synthèse des travaux de Dermoune et Heinrich [9; 11] et de Caputo [4] sur les mesures de Gibbs qui rendent la dynamique réver-sible en temps, ce qui leur permet de prouver l’inégalité de Poincaré d’un système désordonné de gaz (monocoloré- coloré).

En…n, le dernier chapitre contient l’essentiel des travaux où nous avons réussi d’abord à expliciter les mesures canoniques d’un système désordonné de gaz coloré (Th 3:1), et ensuite, à trouver la valeur exacte du trou spectral (Th 3:3) et nous montrons qu’elle correspond bien à la plus petite valeur propre de la matrice déter-ministe, qui dépend uniquement du nombre de sites du réseau en question.

Ces 2 résultats ont fait l’objet d’une publication dans le journal of mathematicl physics, sous le titre "Computation for the canonical measures of a colored disordered lattice gas and spectral gap".

Chapitre 1

Généralités sur les processus et

semigroupes

Dans ce chapitre on donne quelques rappels sur les processus, les chaînes de Mar-kov, les semi-groupes et leurs générateurs in…nitésimaux.

1.1

Martingales

Soient ( ; F; P; (Ft)t 0) un espace probabilisé …ltré satisfaisant les hypothèses

habituelles (i.e. la …ltration (Ft)t 0 est continue à droite au sens que pour tout

t_{2 [0; +1[, F}t = \

u>tFuet complète). Sur l’espace ( ; F; P; (Ft)t 0);un processus

sto-chastique à valeurs réelles est appelé martingale (resp. surmartingale, sousmartingale) si les conditions suivantes sont satisfaites :

2. (Xt)est (Ft)-adapté.

3. Pour tout 0 s t,

E(Xt j Fs) = Xs p:s:(resp:E(Xtj Fs) Xs; E(Xtj Fs) X p:s:):

Un résultat incontournable sur les martingales est le théorème de décomposition de Doob-Meyer. On noteM2 l’ensemble des martingales réelles de carré intégrable, conti-nues à droite et pourvues de limites à gauche (càdlàg). Pour tout (Mt) 2 M2, il

existe un unique processus A = (At)t 0 prévisible intégrable, nul en zéro et tel que

(M_t2 At)t 0soit une (Ft) martingale. Le processus A est le compensateur prévisible

de M et on le note (< M >t)t 0=< M > :

1.2

Processus de Markov, générateurs et semi-groupes

Soit E un espace métrique, complet et séparable muni de sa tribu borélienne. Soit D([0; +1); E) l’ensemble des fonctions de [0; +1) dans E càdlàg. D([0; +1); E) peut être vu comme l’espace canonique pour un processus de Markov ( s) d’espace d’état

E :( s) étant le processus des coordonnées dé…ni par s( ) = s, F la plus petite

-algèbre rendant mesurable les s et Ft= f s; 0 s tg.

Dé…nition 1.1 _{Une famille fP ; 2 Eg de mesure de probabilités sur D([0; +1); E)} est un processus de Markov sur E si elle véri…e les conditions suivantes :

(a) Pour tout _{2 E, on a P ( : 2 D([0; +1); E) :} 0 = ) = 1;

(c) P ( s+:2 A j Fs) = P (A)p:s: pour tout 2 E et A 2 F.

On notera par E l’espérance par rapport a P E Z =

Z

D[0;+1)ZdP :

Soient C(E) l’ensemble des fonctions continues sur E et Cb(E) l’ensemble des

fonc-tions continues bornées sur E. Cb(E) est un espace de Banach muni de la norme

jjfjj1 = sup 2Ejf( )j.

Pour f 2 Cb(E), on note S(t)f ( ) = E f( t). Le caractère mesurable de

l’ap-plication f ! S(t)f découle de la condition (b) (Dé…nition 1.1), d’autre part on a

jjS(t)fjj1 jjfjj1 (1.1)

d’où S(t) est un opérateur borné sur Cb(E). Par linéarité de l’intégrale on a

pour des scalaires , et des fonctions f et g. Ceci entraîne que S(t) est linéaire. Finalement par la propriété de Markov on a

S(s + t)f ( ) = E (f (Xs+t)) = E [E (f (Xs+t)j Fs)] = E EXs_{(f (X} t)) = E (S (t) f (Xs)) = S (s) S (t) f ( ) :

Ainsi la famille fS(t); t 0_{g forme un semi-groupe, i.e. S(0) = I et S(t + s) =} S(s)S(t):De l’inégalité 1.1 on déduit que S(t) est une contraction.

Dé…nition 1.2 _{1)Un processus de Markov fP ; 2 Eg est un processus de Feller si} S(t)f _{2 C}b(E); pour tout t 0 et f 2 Cb(E).

2)On dit que fS(t)g est un semi-groupe fortement continu si jjS(t)f f_{jj1 ! 0} lorsque t ! 0, pour tout f 2 Cb(E).

Dé…nition 1.3 _{Le générateur in…nitisimal L d’un semi-groupe fS(t)g est un} opéra-teur non borné, dé…ni par

Lf = lim

t!0

S(t)f f t ; et par son domaine D(L) = f _{2 C}b(E); lim

t!0

S(t)f f

t existe .

Lemme 1.4 (Ligget) _{Supposons que fS(t)g est un semi-groupe fortement continu} de générateur L. Alors on a :

a) Pour tout f 2 Cb(E) et t > 0; Z t 0 S(t)f ds_{2 D(L);} et S(t)f f = L Z t 0 S(t)f ds b) Pour tout t 0, f _{2 D(L) et S(t)f 2 D(L) on a} d dtS(t)f = LS(t)f = S(t)Lf c) Pour tout f 2 D(L) et t 0, S(t)f f = Z t 0 LS(t)f ds = Z t 0 S(t)Lf ds

A chaque processus Markovien, on peut associer une famille de martingales qui le caractérise. Supposons que (Xt) est un processus de Feller et que S(t)f (x) =

E [f(Xt)j X0 = x]soit un semi-groupe fortement continu sur Cb(E);de générateur L.

Si f 2 D(L) , alors

Mt= f (Xt) f (X0)

Z t 0

est une (Ft) martingale, continue à droite de moyenne nulle. En e¤et, remarquons (en posant Ex_{[f (X} t)] = S(t)f (x)) que Z t 0 Ex(Lf (Xs))ds = Z t 0 S(s)Lf (x)ds = Z t 0 (S(s)L)f (x)ds = Z t 0 d dsS(s)f (x) = S(t)f (x) S(0)f (x) = Ex[f (Xt)] Ex[f (X0)] :

Et en utilisant la propriété de Markov et la remarque précédente, on en déduit que si 0 s t on a Ex(Mt j Fs) = Ex(f (Xt)j Fs) f (X0) Z s 0 Lf (Xu)du Z t s 0 Ex(Lf (Xu+s)j Fs)du = Ms+ EXs(f (Xt s)) EXs(f (X0)) Z t s 0 EXs_{(Lf (X} u))du = Ms:

On termine cette section par donner la dé…nition du "core". Soit L un générateur in…nitésimal, un sous espace C de D(L) est un "core" pour L si L est la fermeture de sa réstriction à C (i.e. L = L=C). Soit P l’ensemble de toutes les mesures de probabilités sur E, muni de la topologie de la convergence faible au sens que _{n ! dans P si} et seulement si R f d _{n !} R f d _{, pour toutes fonctions f 2 C}b(E). Si 2 P et

fP ; 2 Eg est un processus de Markov, alors le processus markovien correspondant de distribution initiale est un processus stochastique dont la distribution est donnée

par P = Z EP (d ) : Il en résulte que E (f ( t)) = Z E S (t) f d : Soit _{2 P et S(t) 2 P. Alors} Z f d [ S (t)] = Z S (t) f d ;

pour tout f 2 Cb(E). La mesure de probabilité S(t) est interprétée comme la

dis-tribution du processus à l’instant t quand la disdis-tribution initiale est .

Dé…nition 1.5 Une mesure _{2 P est dite invariante si S (t) =} pour tout t 0. La classe de toutes les mesures invariantes sera notée .

La proposition suivante donne une caractérisation des mesures invariantes. Proposition 1.6 Soit L le générateur in…nitésimal d’un processus markovien dont le semi-groupe est fS(t); t 0_{g, alors}

=_{f 2 P ;} Z

Lf d = 0 _{8f 2 Cg:}

Dé…nition 1.7 _{Le processus de Markov de semi-groupe fS(t); t} 0_{g est dit ergodique} si

a) =_{f g est un singleton,} b) lim

La théorie de Hille-Yosida des semigroupes des opérateurs linéaires est naturelle-ment placée dans le contexte d’un espace général de Banach. Nous nous bornerons dans cette partie au cas de l’espace de Banach C(E) et aux semi-groupes qui corres-pondent aux processus de Feller sur E.

Théorème 1.8 (Hille-Yosida) Il y a une correspondance linéaire sur C(E) entre les générateurs de Markov et les semi-groupes de Markov. Cette correspondance est donnée par a) D (L) = f _{2 C (E) ; lim} t!0 S (t) f f t existe ; et Lf = lim t!0 S (t) f f t , pour tout f 2 D (L) ; b) S (t) f = lim n!1 I t nL n f_{, pour f 2 C (E) et t} 0 de plus, c) Si f 2 D (L), alors S (t) f _{2 D (L) et (}d dt)S (t) f = LS (t) f = S (t) Lf et en…n

d) Pour g 2 C (E) et 0 la solution de f Lf = g est donnée par f =

1

Z

0

L s’appelle le générateur de S(t), et S(t) est le semi-groupe produit par L: Des preuves du théorème de Hille-Yosida peuvent être trouvées dans le chapitre 1 Dynkin [16], le chapitre 2 Gihman et Skorohod [21], le chapitre IX de Yosida [40], et le chapitre 1 Ethier et Kurtz [17].

1.3

Réversibilité

La réversibilité est l’analogue probabiliste de la symétrie pour les opérateurs. Dans cette partie, on présente la réversibilité dans le contexte important d’un processus de Feller sur un espace d’état compact. Pour cela le contexte des chaînes de Markov sur un ensemble dénombrable est intéressant à étudier.

Pour commencer, supposons que E est un espace métrique compact et que fS(t); t 0_{g est un semigroupe de Markov sur C(E).}

Dé…nition 1.9 Une mesure de probabilité _{2 P est dite réversible pour un processus} de semigroupe S(t) si

Z

f S(t)gd = Z

gS(t)f d

pour tout f; g 2 C(E). L’ensemble de toutes les mesures réversibles pour un processus serait dénoté par R:

On a la proposition immédiate suivante : Proposition 1.10 _{(cf. [21]) R} :

Rappelons que est nécessairement non vide ( voir la proposition 1:8(f ) du chapitreI (cf .[21]), comme il est facile de voir à travers des exemples de chaînes de Markov, que R peut être vide. En fait dans un certain sens, R est habituellement vide. Néanmoins, pour plusieurs processus intéressants R n’est pas vide.

Le résultat suivant explique le terme réversible, et donne un critère pour la réver-sibilité en termes du générateur L de S(t).

Proposition 1.11 _{Soient fS (t) ; t} 0_{g un semi-groupe de Markov sur C(E) de} générateur L, et _{2 . Alors les conditions suivantes sont équivalentes :}

(a) _{2 R;} (b) Z f S(t)gd = Z gS(t)f d _{pour tout f; g 2 D (L) ;} (c) Z f S(t)gd = Z

gS(t)f d _{pour tout f; g 2core de L ;}

(d) _{f t}; _{1 < t < 1g et t}; _{1 < t < 1 ont la même distribution où t} est le processus stationnaire de distribution initiale et de semi-groupe S(t).

Notons que dans le cas où le processus est une chaîne de Markov de matrice de probabilité de transition (q ( ; )) sur un espace d’état …ni de générateur

Lf ( ) =Xq ( ; ) [f ( ) f ( )] ; les conditions (b) et (c) ci-dessus peuvent être récrites comme

( ) q ( ; ) = ( ) q ( ; ) pour tout ; _{2 E:} Démonstration. Voir [24] p:92 94:

1.4

Processus d’exclusion simple

Exemple 1.12 Ce processus décrit l’évolution d’une in…nité de particules indistin-guables sur l’ensemble des sites S = Z: Il y a au plus une particule par site, autrement dit une con…guration _{de particules est un élément de X = f0; 1g}S; avec (x) = 1 s’il y a au plus une particule au site x et (x) = 0 sinon. Chaque site est muni d’une horloge exponentielle de paramètre 1, et toutes les horloges sont mutuellement indé-pendantes. Lorsque l’horloge située en x sonne et que de plus (x) = 1; la particule présente en x saute en x + 1 avec probabilité p si (x + 1) = 0; ou en x 1 avec pro-babilité q si (x 1) = 0; (p + q = 1); sinon, il ne se passe rien. Ainsi le déplacement des particules est une marche aléatoire sur Z: L’interaction consiste donc à interdire l’occupation multiple d’une site, d’où le nom d’exclusion.Formellement, le processus d’exclusion simple est un processus de Markov( t) sur X; de semi-groupe (St) et de

générateur in…nitésimal dé…ni sur les fonctions cylindriques (i.e. ne dépendant que d’un nombre …ni de coordonnées) par

Lf ( ) = X x2S (x) (1 (x + 1)) p f x;x+1 f ( ) +X x2S (x) (1 (x 1)) q f x;x 1 f ( ) où x;y_{(z) =} 8 > > > > > > < > > > > > > : (y) si z = x (x) si z = y (z) sinon

Remarque 1.13 Le processus d’exclusion simple est dit symétrique si la probabilité de transition est symétrique. Tous les autres cas sont dits asymétriques.

Exemple 1.14 Pour une chaîne de Markov sur un espace d’état dénombrable dans Zd_{, le processus d’exclusion le générateur est un opérateur non borné donné par}

Lf ( ) =X

x;y

p (x; y) (x) (1 (y)) [f ( x;y) f ( )] et son domaine est un sous-espace de C(X) dé…ni par

lim

t!0sup_2X

S (t) f ( ) f ( )

t Lf ( ) = 0 le domaine D(L) contient les fonctions cylindriques.

1.5

Equation hydrodynamique

1.5.1

Echelles spatio-temporelles

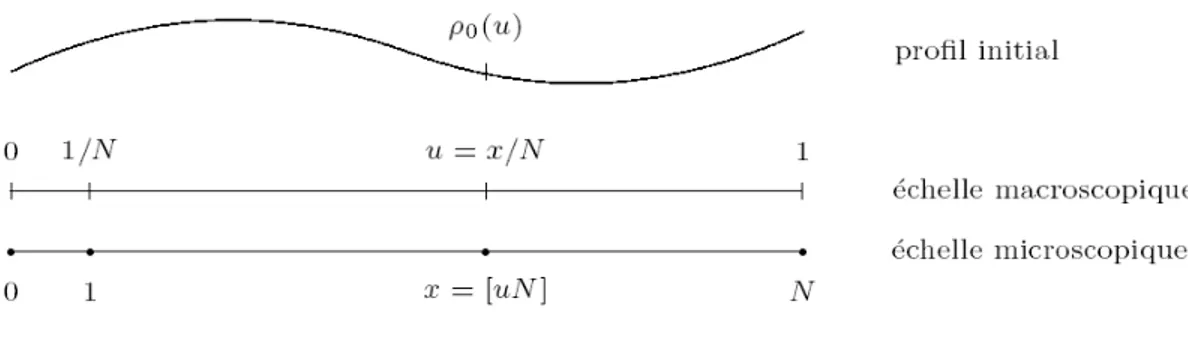
On s’intèresse, dans cette partie, à l’étude du comportement hydrodynamique du processus d’exclusion simple symétrique à plus proches voisins, le but étant d’illustrer, à travers un exemple simple, une méthode standard permettant de déduire l’évolution d’un système de particules à partir de ses caractéristiques microscopiques. Initialement positionnée sur le tore TdN = (Z=NZ)

d

, chaque particule tente, avec un taux de saut exponentiel et une probabilité uniforme 1=2d, d’atteindre l’un de ses sites adjacents ; si le site visé est inoccupé le saut a e¤ectivement lieu, sinon, en vertu de la règle

Fig. 1.1: Échelle macroscopique et microscopique

d’exclusion, le saut est annulé. En particulier, on peut montrer que la con…guration

tdu système a l’instant t 0est un processus de Markov de générateur in…nitésimal

LNf ( ) = X jx yj=1 1 2d (x) (1 (y))(f ( xy_{) f ( ))}

et de mesure invariante la mesure produit de Bernoulli N _{de paramètre . Dans}

la formule précédente, xy _{désigne la con…guration déduite de après échange des}

particules présentes aux sites x et y.

Considérons maintenant, en vue d’étudier le comportement hydrodynamique du processus, la mesure empirique N

t associée au système N t = 1 Nd X x2Td N tN2(x) _x=N

Dans cette dernière expression, l’entier N , destiné a tendre vers l’in…ni, représente l’inverse de la distance macroscopique entre les particules. Par ailleurs, la probabilité pétant symétrique, chaque particule, à t = N , se situe, en vertu du théorème central limite, à une distance d’ordre pN de sa position initiale (comportement di¤usif).

L’observation d’un mouvement à l’échelle macroscopique nécessite par conséquent une accélération quadratique du temps t 7 ! N2 _{(changement d’échelle parabolique).}

Soit _{0 : T}d

! [0; 1] un pro…l initial de particules dé…ni sur T = [0; 1]d_{. La mesure} N _{étant indexée par la densité de particules, il est naturel de considérer la mesure}

produit N

0(:) associée au pro…l 0 dé…nie par

N

0(:)f ; (x) = 1g = 0(x=N ) pour tout x 2 TN

L’étude du comportement hydrodynamique du système consiste alors à montrer que la suite de mesures PN _{associée au processus} N

t issu de N₀(:) converge, dans l’espace

D([0; T ];_M+_{), vers la loi déterministe}

(t;u)du où la fonction (t; u) est la solution

faible d’une EDP appelée équation hydrodynamique du système. Donc (t; u) est solution faible de l’équation de la chaleur

@t =

1 2

Théorème 1.15 (Caractérisation de la limite hydrodynamique) Soient 0 : [0; 1]d

! [0; 1] un pro…l initial de densité et N

0(:) la mesure produit de Bernoulli associée à

0

N

0(:)f : (x) = 1g = 0(x=N ) pour tout x2 T

d N

Alors, pour tout t 0, la suite

N t = 1 Nd X x2Td N tN2(x) _x=N

converge en loi vers la mesure t dont la densité (t; u) par rapport a la mesure de

Lebesgue est la solution de l’équation de la chaleur 8 > > < > > : @t = 1₂ (0; :) = ₀(:) où =Pd_i=1@2 ui désigne le laplacien de . Démonstration. Voir [23] :

Chapitre 2

Mesures de Gibbs et inégalité de

Poincaré d’un système désordonné

coloré

Le but de ce chapitre est la construction des mesures de Gibbs rendant la dyna-mique réversible en temps et d’établir l’inégalité de Poincaré d’un système désordonné de gaz coloré.

2.1

Description du modèle

Considérons un sous-ensemble …ni _{du réseau d-dimensionnel Z}d_{. À chaque site}

de particules on sous entend une application = _{f x}; x_{2 g 2 f 1; 0; +1g telle} que : x = 8 > > > > > > < > > > > > > :

+1 si le site x est occupé par une particule bleue, 0 si le site x est vide;

1 si le site x est occupé par une particule blanche.

Semblable à [13], on suppose que les xsont i.i.d, et bornnés par une certaine constante

B. La mesure produit correspondante (resp.espérance) sur D = [ B; B] sera notée

par P (resp.E). Pour la simplicité, on considère les con…gurations de f0; 1g :

+ x = 1f x=1g; x = 1f x= 1g (2.1a) de sorte que x = + x x et j xj = + x + x +

x; x sont alors des variables de Bernoulli véri…ant +x x = 0:

2.1.1

Dynamique sur le volume

Pour la con…guration (particules) f x; x2 g simplement notée par , si fx; yg est

une paire de sites, on notera par x;y _{la con…guration dérivée de par la permutation} x avec y, ce qui signi…e que x;yx = y, x;yy = x et le reste est inchangé. La

dynamique des particules est donnée par un processus de Markov f (t); t 2 R+

g, qu’on peut décrire comme suit : une particule se trouvant en x attend un temps exponentiel et essaye de sauter à un site voisin y. Si ce site est occupé alors le saut

Fig. 2.1: Si le site y est occupé, le saut est supprimé, sinon il est e¤ectué avec le taux c_xy

est supprimé, autrement elle le réalise avec un taux de probabilité

c_x;y( ) = fe( x;j xj ; y; y ) (2.2a)

où fe une fonction bornée sur (R f0; 1g)2 satisfaisant les conditions suivantes :

1.fe(a; s; a0; s0) = fe(a0; s0; a; s) ( condition de symétrie ),

2.ss0 _{6= 0 =) f}

e(a; s; a0; s0) = 0 ( condition d’exclusion),

3.ss0 _{= 0 =) f}

e(a; s; a0; s0) > 0 ( condition uniforme),

4.fe(a; s; a0; s0) = fe(a; s0; a0; s) exp( (s0 s)(a0 a) ( condition de balance).

2.1.2

Générateur de Markov

Les conditions précédentes nous permettent de dé…nir un générateur de Markov désordonné L, au sens que L dépend de = _f x; x2 g. Le générateur mentionné

L:= L _{est donné pour une fonction bornée f sur f 1; 0; 1g par :} Lf ( ) = X

x;y2

c_x;y( ) [f ( x;y) f ( )] (2.3a) Remarque 2.1 _{Le processus de Markov f (t); t 2 R}+_{g d’espace d’état f 1; 0; 1g} et de générateur L , induit un procesus de markov, fj (t)j ; t 2 R+

g d’espace d’état f0; 1g , qui a été étudié par Fagginato [13].

2.1.3

Mesures de Gibbs et mesures canoniques

Soient +; deux nombres réels. On pose = ln(e + + e ) et on considére la mesure produit = ; +;

dé…nie sur f 1; 0; 1g par : ( "

x) =

exp( x+ ")

1 + exp( x+ )

( x₂ et _{2 f ; +g)} (2.4a) Ainsi pour tous _{2 f 1; 0; 1g ; on a :}

(_{f g) = Z} 1exp( H( ))

où Z est une constante de normalisation et H est l’Hamiltonien dé…ni par : H ( ) = X

x2

xj xj + + +

x + x

La mesure de probabilité s’appelle la mesure de Gibbs sur de désordre et de potentiel chimique le couple ( +; ). En outre, pour compter les particules bleues et blanches dans , on introduit pour _{2 f ; +g le nombre de} particules qui est :

N ( ) =X

x2 x

Considérons les variables aléatoires m+= N

+

j j et m = N

j j (j j désigne le cardinal de l’ensemble ), qui sont respectivement les densités des particules bleues et blanches. Soit (m+_{; m )}

2 f0; 1= j j ; 2= j j ; :::::; 1g2 tel que m = m+ _{+ m 1. Il est bien}

connu d’après [9] qu’il existe un unique réel = ( ; m), appelé potentiel chimique. La mesure de probabilité de Gibbs ; _{sur f0; 1g satisfait la relation (cf.[13])}

;

(m++ m ) = m: La relation entre et ; est alors :

(f _{j:j) =} ; (f ) ; _{pour toute fonction bornée f sur f0; 1g} on a également la mesure canonique correspondante :

(:) = (:_{jS ); où S = N}+ = N+; N = N

Notons que ne dépend pas de ( +; )(cf. [13]): Un résultat important établit dans [9]stipule que pour un tel couple (m+_{; m )et pour tout , il existe un unique couple}

( +; ) dépendant de ( ; m+_{; m ; ) tel que}

(N ) = N ; ( _{8 2 f ; +g)} (2.5a)

2.1.4

Trou spectrale et Inégalité de Poincaré

Soit la forme de Dirichlet dé…nie par D(f ) = 1

j j X

x;y2

et soit Pf = 1 j j X y2 (f _{j y}); _{pour tout f 2 L}2( )

Notons que cet opérateur linéaire P préserve la positivité sur L2_{( ), de norme}

infé-rieure ou égale à un, et satisfait PI = I. Ces propriétés assurent que P I est un générateur de Markov. De plus, _{est réversible pour P} I, plus précisèment on a :

(f (_P I)g) = (g(_P I)f ) _{pour tout f , g 2 L}2:_{( )}

et

D(f ) = (f (I _P)f) Le trou spectral = (_{j j) est dé…ni comme suit}

(_{j j) =} inf f 2L2_{( ); (f )=0} D(f ) (f2₎ (TS) où (f ) = Z f d Pour une constante c > 0, l’inégalité

(f ; f ) cD(f )

pour f 2 L2:_{( ), s’appelle inégalité de Poincaré de constante c, où (f ; f ) désigne la}

2.2

Construction des mesures de Gibbs pour un

système désordonné coloré

Cette section constitue une première étape pour étendre les résultats de Faggionato et Martinelli [13] au cas des particules multicolorées. On considère un modéle de la dynamique de gaz coloré dans Zd _{en présence de désordre noté , dé…ni comme}

auparavant. L’interaction entre les particules dans un volume _Zd _{a lieu suivant}

le générateur L (1). Dans le Théorème 2.2, on caractérise les mesures produits de Gibbs pour lesquelles L est réversible. Ce paragraphe se termine par l’extension au cas des particules multicolorées des paramètres de potentiel chimique empirique et de compressibilité statique qui …gurent dans Faggionato et Martinelli [13]:

Théorème 2.2 Soit une mesure désordonnée de probabilité sur tels que, pour presque tout ; sous les variables aléatoires _7! x, x 2 sont

indépen-dantes. Alors, pour presque tout ; (3), (4) sont satisfaites et si seulement s’il existe ( +; )_{2 R}2 tel que : (a) e + + e = e (b) ( + x) = e x+ + =(1+e x+ +_+e x+ _{), (} x) = e x+ =(1+e x+ + +e x+ _)(x2 ):

Démonstration. Voir l’annexe.

Proposition 2.3 Soit ₂ D …xé, et soit (m+; m ) 2 [0; 1]2 tel que m++ m 1

et m = m+_{+ m : Alors on a :}

(i) Le système de variables inconnues ( +; )

exp( +) + exp( ) = exp( ( ; m))

a une unique solution unique ( +( ; m+_{; m ); ( ; m}+_{; m )), appelée le potentiel}

chimique empirique coloré.

(ii) Le système de variables inconnues ( +; ) Eh ; +; ( +₀)i _{= E} exp( (0) + + ) 1 + exp( (0) + ) = m +_; E h ; +_; ( ₀) i = E h exp( (0)+ ) 1+exp( (0)+ ) i = m ; exp( +) + exp( ) = exp( 0(m))

a une solution unique ( +₀( ; m+_{; m );}

0( ; m+; m )), appelée le potentiel chimique

recuit(annealed ) coloré .

(iii) Posons pour la simplicité = ; +0( ;m+;m ); 0( ;m+;m ):Soit la matrice colorée

de la compressibilité statique

(m+_{; m ) = E[ (} +₀; ₀); ( +₀; ₀)

où ( +₀; ₀); ( +₀; ₀) est la matrice de covariance du vecteur aléatoire ( +₀; ₀) sous la mesure :

nombre …ni des variables aléloires x; x), nous avons @ @ + ; +; (f ) = ; +; f ; N+ ; @ @ ; +; (f ) = ; +; f ; N ; nous obtenons une matrice identitée

@ @m 0 ; m+; m : ; 0 _{2 f+; g} = @ @ ; +; (m ) : ; 0 _{2 f+; g} 1 @ @m 0 0 ; m +_{; m : ;} 0 _{2 f+; g = (m}+_{; m )} 1_:

2.3

Inégalité de Poincaré pour un système

désor-doné

Dans cette section nous allons prouvé l’inégalité de Poincaré pour un système désordonné de gaz monocoloré dans l’espace produit avec un ou plusieurs lois de consevation. La méthode a montré le rendement des résultats bien connus, tels que les limites di¤usives du trou spectral d’un processus d’exclusion simple.

2.3.1

Stratégie générale

Considérons un espace probabilisé générique (X; F; ) : Dans les applications dis-cutés ci-dessous, on prend X = N, Z ou R selon le modèle utilisé. Soient N = XN

et N = N la mesure produit associée. La loi de conservation est exprimée en

paramètre _{2 R qui jouera le rôle d’une densité, nous considèrons la con…guration} =_{f kg}N_{k=1 2} N telle que N X k=1 ( _k) = N:

Si nous dé…nissons = ;nous considèrons l’ensemble mesurable :

N; := ( 2 N : N X k=1 ( _k) = 0 ) (2.1) et la mesure canonique de probabilité conditionnée par l’événement N; :

N; = N(:j N; ) (2.2)

La dynamique de graphe complet sera décrite par la forme de Dirichlet du type DN; (f ) = 1 N N X k=1 N X l=1 N; h f k;l f ( ) 2 i avec k;l _{est la con…guration où}

k et l ont été échangés. Notons par V arN; (f )la

variance usuelle de f 2 L2₍

N; N; ) par rapport à N; . La constante de Poincaré,

pour N et …xés, est dé…nie par :

(N; ) = sup

f

V arN; (f )

DN; (f )

Soit Fk le algèbre engendrée par les variables k; k = 1; :::; N, et soit l’opérateur

stochastique non négatif P : L2₍

N; )! L2( N; ) dé…ni par Pf = _N1 N X k=1 N; (f j Fk) (2.5)

Notons que 1 _{P peut être interprété comme un générateur de Markov avec la mesure} réversible N; . Par symétrie, Nous pouvons écrire que

N; ( k)j j = j := +

j

si k 6= j; de sorte que

N; ( k)j j =

1

N 1 j

où nous allons utilsé la notation f _{j j} pour désigner la probabilité conditionnelle (f _{j F}j) ( )par rapport à une mesure de probabilité donnée . Il s’en suit que toute

fonction de la forme f ( ) = N X k=1 k ( k) ; 2 R N

satisfait les relations :

Pf = 1

N 1f , (1 P)f =

N 2 N 1f

L’inégalité du trou spectral se formule comme suit : nous disons que la propriété (SGP) _{est véri…ée, s’il existe C < 1,} > 0 pour chaque N 3, _{2 R et f 2} L2₍ N; ) avec N; (f ) = 0on a : N; (f (1 P)f) N 2 N 1 1 CN 1 N; f2 (SGP) Dé…nissons la constante (N ) = sup (N; ) (2.7) Proposition 2.4 (Caputo) Supposons que (N ) < _{1 pour tout N 2 N. Si SGP} est véri…ée, alors on a l’inéqualité uniforme de Poincaré

sup

N

Démonstration. Il su¢ t de prouver que (SGP) implique l’inégalité suivante : (N ) 1 + CN 1 (N 1) (2.8) avec > 0 _{et C < 1 indépendantes de} et N:

Prenons une fonction arbitraire f 2 L2( N; ) avec N; (f ) = 0. L’espérance

conditionnelle N; (f j k)est identi…ée à la moyenne N 1;

k (f ) ;où k est donnée

dans (2:6) : Pour chaque k nous obtenons alors la décomposition

N; f2 = N; h V arN 1; k(f ) i + N; N; (f j k) 2 et par suite N; f2 = 1 N N X k=1 N; h V arN 1; k(f ) i + N; [fPf] (2.9)

avec l’opérateur P dé…nit dans (2:5) et les constantes dans (2:7) V arN 1; k(f ) (N 1)DN 1; k (f ) = (N 1) N 1 X j6=k X l6=k N; (vj;lf )2 j Fk (2.10)

Des inégalités (2:9) et (2:10) et de l’identité 1 N N X k=1 N; h DN 1; k(f ) i = N 2 N 1DN; (f ) nous obtenons l’estimation

N; (f (1 P)f)

N 2

N 1 (N 1)DN; (f ) (2.11) (2:8) découle alors de (2:11) et de l’hypothèse (SGP).

2.3.2

Réduction au processus unidimensionnel

Semblable à [5] le spectre de P peut être étudié en termes de spectre d’un opérateur unidimensionnel K (voir (2:12)). Nous prouvons à cet e¤et que l’estimation (SGP) se déduit d’une estimation spectrale appropriée sur K, voir (SGK) ci-dessous.

Soit k la projection canonique de N sur X donné par k = k. Soit 1N;

la première marginale de N; ;i.e. 1N; = N; 11, la distribution de 1sous la

probabilité N; :Par symétrie de permutation toutes les marginales coïncident. Soit

H l’espace de Hilbert L2 X; 1_{N; avec h:; :i le produit scalaire correspondant. Notons} hgi la moyenne d’une fonction g 2 H par rapport à 1

N; et par H0 le sous-espace des

fonctions g 2 H telles que hgi = 0, on dé…nit l’opérateur stochastique auto-adjoint K : H ! H par la forme bilinéaire :

hg; Khi = N; [(g 1) (h 2)] ; g; h 2 H (2.12)

L’identité (2:6’) montre que

K = 1

N 1 (2.13)

pour chaque : Ainsi le spectre de K contient toujours les valeurs propres _N1 ₁ et 1: _{On dira que la propriété (SGK) est vérifée si le reste du spectre de K est con…né} autour de zéro dans un voisinage de rayon O N 1 _{pour certain > 0 uniforme}

par rapport à N , _{au sens qu’il existe C < 1,} > 0 pour chaque N , _{et g 2 H}0

satisfaisant g; = 0 on a

Lemme 2.5 (Caputo) (SGK) implique (SGP) :

Démonstration. On dé…nit le sous-espace fermé de L2₍

N; ) constitué des

sommes de fonctions de moyennes nulles dépendant chacune d’une seule variable : = ( f _{2 L}2( N; ) : f = N X k=1 gk k; g1; :::; gN 2 H0 ) (2.14) Observons d’abord que Pf 2 pour chaque f 2 L2₍

N; ) telle que N; (f ) = 0:Par

conséquent Pf = 0 dès que f 2 ?telle que f a une moyenne nulle, en particulier on peut se restreindre à f 2 pour prouver (SGP).

Soient f = P_kgk k 2 ; et 'f =

P

kgk la fonction dans H0:Un calcul simple

montre que

N; f2 = 'f;K'f +

X

k

hgk; (1 K) gki (2.15)

et par le même calcul nous obtenons :

N; (f (1 P) f) = N 2 N 'f;K (1 K) 'f (2.16) +1 N X k hgk; (1 K) [(N 1) +K] gki :

Considérons maintenant le sous-espace S des fonctions symétriques : S = ( f _{2 L}2( N; ) : f = N X k=1 g k; g 2 H0 ) (2.17) Puisque S est invariant pour P, i.e. PS Salors nous pouvons considérer séparément les cas f 2 S et f 2 S? _{le complémentaire orthogonal dans : Lorsque f =}PN

k=1g k2 S on a 'f = N g et en réarrangeant les termes des égalités (2:15) et (2:16) nous

obtenons : N; f2 = N (N 1) g; K + 1 N 1 g (2.18) et N; (f (1 P) f) = (N 1)2 g; [1 K] K + 1 N 1 g (2.19) En voyant de (SGK) que K + 1

N 1 est non négatif sur le sous-espace H0 . D’autre

part, si f = 0, quand g est un multiple de , nous pouvons alors se restreindre au cas g; . Écrivant ~g = _{K +N}1₁

1 2 _g

et observons que h~gi = 0 et ~g; = 0; la supposition (SGK) entraîne alors que

N; (f (1 P) f) (N 1) 2 1 CN 1 _{h~g; ~gi} (2.20) N 2 N 1 1 CN 1 N; f2 ; f 2 S

Pour étudier le cas f 2 S?; observons d’abord que nous pouvons supposer, sans perdre la généralité, que f 2 est telle que '_f; = P_k gk; = 0: En e¤et si

c = N ; 1P_k gk; et ~gk = gk c ; on a P_k~gk k = P_kgk k dans

L2( N; ) ; puisque, la loi de conservation

P

k k = 0. Maintenant, pour chaque

u_{2 S; u =}P_ku0 k; avec u0 2 H0 on a

N; (uf ) = (N 1) 'f; K +

1 N 1 u0

Ainsi f 2 S? implique que K + N11 'f est constant dans H: Puisque 'f = 0 et

'_f; = 0;(SGK) implique alors que 'f = 0:En posant ^gk = (1 K)

1 2 _g

(2:15) et (2:16) impliquent que N; f2 = X k h^gk; ^gki (2.21) et N; (f (1 P) f) = 1 N X k h^gk; [K + (N 1)] ^gki (2.22)

Puisque h^gki = 0 pour tout k; et nous utilisons (SGK) pour avoir l’estimation

h^gk;K^gki 1 N 1h^gk; ^gki De (2:21) et (2:22) nous obtenons N; (f (1 P) f) N 2 N 1 N; f 2 _{; f} 2 S? (2.23) Les inégalités (2:20) et (2:23) signi…ent que (SGP) est satisfaite, ce qui achève la démonstration.

Pour chaque ! …xé on note !(N; ) la constante de Poincaré. Théorème 2.6 (Caputo) Pour tout _{2 (0;}1₂] il existe C <_{1 tel que}

sup N 2 sup !2[ ;1 ]N sup 2(0;1) !_{(N; ) C} Démonstration. Voir [4] :

2.4

Estimation du trou spectral de gaz coloré

L’objectif de ce paragraphe est d’estimer le trou spectral liée au modèle appelé système désordonné de gaz coloré. Le résultat principal est énoncé pour un générateur

auxiliaire de Markov via la stratégie générale developpée par Caputo [4], où il donne l’inégalité de Poincaré en ce qui concerne la dynamique originale du modèle.

Nous pouvons maintenant énoncer le résultat principal du A. Dermoune et P. Heinrich[11] (SGP). Pour cela, on introduit les hypothèses suivantes

(H1) m+ _m j j 1+ 1 pour 1 2 (0; 1) et m+ m = 0(lnj j) (H2) m2 j j 1+ 2 _pour 2 > 0 où m = m++ m

Théorème 2.7 (SGP) Supposons que (H1) ou (H2) sont satisfaites . Alors il existe c_{2 (0; 1) et 2 (0; 1=8) tels que pour f 2 L}2_{( ) avec (f ) = 0 et}

j j 3; (f (1 _P)f) j j 2

j j 1 1 cj j

1

(f2) (2.24)

2.5

Schéma du preuve du théorème(SGP)

Nous adopterons les notations et les conventions suivantes :

Notation 2.8 Dans la suite, on utilisera la notation suivante : A B s’il existe une constante positive C telle que A CB. Si A B et B Aalors on écrit A B.

0 = 8 > > < > > : 1 = 0 0 ₆₌ 0

2.5.1

Estimation de la combinaison a¢ ne de la mesure

cano-nique

Lemme 2.9 Pour tout (c1; c2; c3)2 R3et (x; y) 2 2 on a

c1 ( +x) + c2 ( x) + c3 c1 ( +y) + c2 ( y) + c3 (2.25)

Démonstration. Pour simpli…er nous détaillons seulement le cas particulier où c1 = 1 et c2 = c3 = 0: Supposons que x 6= y et présentons le sous-ensemble de

con…gurations suivant : EJ+_;J = 8 < : 2 f 1; 0; 1g : X z6=x;y + z = N + _J+_;X z6=x;y z = N J 9 = ;

avec J est le nombre d’ particules occupées par les sites x et y. Notons que J 2 f0; 1; 2g : Alors, par la dé…nition de et l’indépendance par rapport à , on a :

( + x) ( + y) = ( + x) (1 ( y ) (E1;0) + ( +y) (E2;0)+ ( y) (E1;1) ( + y) (1 (j xj) (E1;0) + ( +x) (E2;0)+ ( x) (E1;1)

et on conclu par le fait que

( _x) ( _y); 1 (_{j xj)} 1 ( _y )

car les variables aléatoires ( _x)_{(resp. (j xj)) et ( y})(resp. ( y )) sont i.i.d.

D’après le lemme précédent nous obtenons

c1 ( +x) + c2 ( x) + c3 c1m++ c2m + c3;

1 (_{j xj)} 1 m et ( x; x) m (1 m )

2.5.2

Réprésentation de

(f

2

) et (f

_Pf)

Pour plus de détails dans ce paragraphe consulter le chapitre 3. On trouve une matrice non négative Q et un vecteur g tels que

(f2) = gQgT; (f_{Pf) =} 1 j jgQ

2_gT

de sorte que, si nous posons

h = Q1=2g et = I Q alors (f2) = hhT (f2) = hhTet (f (I _{P)f) = h(}(j j 1)I j j + j j)h T _(2.26)

2.5.3

Expression de

Premièrement, notons que det (Cxx) = Cxx C ++ xx C + xx 2 = C_xx C_xx++h1 R+_xx 2i> 0

où la positivité résulte de l’inégalité de Cauchy-Schawrz. Pour les calculs plus loin, on sait que 1 R+_xx 2 = 1 ( + x) ( x) (1 ( + x)) (1 ( x)) 1 m+ _m (1 m+_{) (1 m )} 1 2

On déduire pour tout x, y 2 ++ xy = y x R++ xy R+xy R+yy R+xx Rxy++ R+xx Rxy R+yy q 1 _jR+ xx j 2q 1 R+ yy 2 ++ xy = R+_xy R+_xx R_xy q 1 _jR+ xx j 2 ++ xy = y x Rxy

En particulier, notons que _xy0 = 0 pour tout ; 0 _{2 f+; g :}

2.5.4

Lemme clé

Supposons que nous avons prouvé pour certains _{2 0;}1₈ et c ( ) > 0

c ( )_{j j} ; (2.27)

au sens matriciel. En suite, il est immédiat de voir que (2:26) et (2:27) implique (SGP). Semblable au travail de Caputo [4] ; (2:27) provient du lemme ci-après. Lemme 2.10 Supposons que (H1) ou (H2) sont satisfaites . Alors il existe c > 0 et

2 (0; 1=8) tels que pour tout !; ; et x 6= y;

0 xy 0 xylnj j j j cj j 1 ; (2.28)

avec xy0 est une matrice 2j j par 2j j non négative dépend de (!; ) et uniformément

bornée par c:

Montrons que le Lemme 2.10 implique (2:27) : En e¤et, il résulte de (2:28) que hv; vi =X x6=y 6=0 0 xyvxv 0 y c ( )j j hv; vi ;

pour certaine constante positive c ( ) dépend seulement de ; et c’est exactement (2:27) :

La preuve du Lemme 2.10 sous les hypothèses (H1) ou (H2) se trouve dans [11] :

Chapitre 3

Trou Spectral pour un système

désordonné de gaz coloré

Le but de ce chapitre est de calculer les mesures canoniques et de donner en-suite notre résultat principal à savoir que le trou spectral d’un processus d’exclusion simple désordonné de gaz coloré, qui joue un rôle important dans l’étude de la limite d’hydrodynamique, ne dépend pas du désordre et correspond bien à la plus petite valeur propre de la matrice déterministe, qui dépend uniquement du nombre de sites du réseau en question. Notre approche s’inspire de celle de Dermoune et Heinrich via la stratégie générale developpée par Caputo.

Dans la suite, nous supposons que les variables aléatoires _7! x; x 2 sont

f0; 1g , associée à , ce qui signi…e que

x( ) = 1f x6=0g, pour x 2 :

3.1

Mesures canoniques des con…gurations

Il résulte des dé…nitions de et ; et du fait que _xet _y0 sont indépendants sous , que pour tout ; 0 _{2 f ; +g ; on a :}

x 0 y = ( _x) ( _y0) (S) N + nfx;yg = N + + + 0; N _nfx;yg = N 0 ; (3.7) x y = ( _x) ( _y) (S) N + nfx;yg = N + ₂ +_{; N} nfx;yg = N 2 ; (3.8) et ( _x) = ( x) (S) N + nfxg = N + + ; N _nfxg = N ; (3.9) où 0 est le symbole de Kronecker .

Posons ;0 x;y = N+_nfx;yg = N+ + + 0; N _nfx;yg = N 0 ; ; x;y = N + nfx;yg = N + ₂ + ; N _nfx;yg = N 2 ; et x = N + nfxg = N + + ; N _nfxg = N :

Dans la suite, si P est une mesure de probabilité alors P (f; g) désignera la covariance P (fg) P (f) P (g) entre les variables aléatoire f;g sous P:

Le théorème suivant explicite les mesures canoniques des con…gurations : Théorème 3.1 Pour tous , 0 _{2 f ; +g et x, y 2 , on a pour j j 3}

1) x 0 y = N N 0 j j (j j 1)e x(1 x( ))+ y(1 y( )) 2) x y = N (N 1) j j (j j 1)e x(1 x( ))+ y(1 y( )) et 3) ( _x) = N j je x(1 x( ))

Remarque 3.2 _{Il est facile de voir que pour tout (x; y) 2} 2 _{et pour}

6= 0_{; on a} pour j j 3 1) x; 0 y = N N 0 j j2(_{j j} 1)e x(1 x( ))+ y(1 y( )) 2) x; y = (N )2 _{j j N} j j2(_{j j} 1) e x(1 x( ))+ y(1 y( )) 3) ( _x; _x) = N j j(1 N j j)e 2 x(1 x( ))_;

et 4) x; 0 x = N N 0 j j2 e 2 x(1 x( ))

Démonstration. Calcul de (S) ; _x;y;0; _x;y; ; et _x On a (S) = X V+_{[V [V}0₌ jV+ j=N+_; jV _j=N ;_jV0 j=j j N Y z2V+ + z Y z2V z Y z2V0 (1 (_{j zj)} La somme est prise sur fV+_{; V ; V}0

g tels que V+_{; V ; V}0 _{, où V}+ _{est l’ensemble}

des sites occupés par les particules bleues; V est l’ensemble des sites occupés par les particules blanches, V0 _{est l’ensemble des sites vides et N = N}+_{+ N : La formule}

(2:4:a) implique que : (S) = X V+_{[V [V}0₌ e +N++ N Y z2V+ e z (1 + e z+ ) Y z2V e z (1 + e z+ ) Y z2V0 1 (1 + e z+ ) = e +_N+_{+ N} Q z2 (1 + e z+ ₎ X V+_{[V [V}0₌ Y z2V+_[V e z

Notons que le nombre de triplet fV+_{; V ; V}0

g est égal au nombre de permutations avec répétition, d’où en posant

u = X z2V+_[V z = X z2 z z on a : (S) = e +_N+_{+ N} Q z2 (1 + e z+ ) j j! N+_{!N ! (j j N )!}e u (3.10)

En utilisant les notations précédentes, et en posant : ux;y = X z2 nfx;yg z z( ) et ux = X z2 nfxg z z( )

on obtient par un raisonnement similaire :

;0 x;y = e (N 1)+ 0(N 0 1) Q z2 nfx;yg (1 + e z+ ) (_{j j} 2)! (N 1)!(N 0 _{1)! (} j j N )!e ux;y_{; si} 6= 0 ; x;y = e (N 2)+ 0N 0 Q z2 nfx;yg (1 + e z+ ₎ (_{j j} 2)! (N 2)!(N 0)! (_{j j} N )!e ux;y_; et x = e (N 1)+ 0N 0 Q z2 nfxg (1 + e z+ ₎ (_{j j} 1)! (N 1)!N 0! (_{j j} N )!e ux

ce qui nous permet d’écrire ( _x) ( _y0) _x;y;0 = e N + 0N 0 Q z2 (1 + e z+ ) (_{j j} 2)!eux;y+ x+ y (N 1)!(N 0 _{1)! (} j j N )!; (3.11) ( _x) ( _y) _x;y; = e N + 0N 0 Q z2 (1 + e z+ ₎ (_{j j} 2)!eux;y+ x+ y (N 2)!(N 0)! (_{j j} N )! (3.12) et ( _x) _x = e N + 0N 0 Q z2 (1 + e z+ ) (_{j j} 1)!eux+ x (N 1)!N 0_{! (} j j N )!: (3.13) En substituant les égalités (3:10) ; (3:11) ; (3:12) et (3:13) respectivement dans (3:7) ; (3:8) et (3:9) ; on conclut que x 0 y = N N 0 j j (j j 1)e x(1 x( ))+ y(1 y( ))_; x y = N (N 1) j j (j j 1)e x(1 x( ))+ y(1 y( )) et ( _x) = N j je x(1 x( ))_;

ce qui achève la preuve.

3.2

Calcul du trou spectral

Soit X= 2 6 6 4 Y Z Z Y 3 7 7 5

la matrice carrée en blocs, symétrique, de taille 2j j et telle que Y = (yij)_{(i;j)2j j j j}

avec yii= 1 + 1 j j (j j 1); yij = 1 j j (j j 1);8i 6= j et Z = (zij)_{(i;j)2j j j j} avec zii= j j 1 j j ; zij = 0;8i 6= j:

On désigne par s1 = s1(j j) la plus petite valeur propre de la matrice X et on fait

l’hypothèse c_x;y( ) = 1:

Le théorème suivant est le résultat principal de cette thèse.

Théorème 3.3 _{On suppose quej j} 3: Alors le trou spectral égal à :

(_{j j) = s}1 (*)

Remarque 3.4 Il est remarquable de constater que le trou spectral ne dépend pas du désordre .

Démonstration. Remarquons que d’aprés Caputo [4],que (_{j j) = inf} (f (I P)f)

(f2₎

où la borne inférieure est prise sur toutes les variables aléatoires non nulles de la forme :

f =X

x2

f_{x x} + f_x+ + x;

où _x = _x ( _x)et les coe¢ cients f_{xsont des nombres réels pour x 2 ; = f ; +g.} Maintenant, on prend les représentations des matrices (f2)_{et (f Pf) utilisées dans} [11]_{. Soit pour x; y 2} et ; 0 _{2 f ; +g} (C_xy0) = ( _x; _y0); R_xy0 = C 0 xy q C 0 xxC 0 yy

C = (C_xy0) _{est de2 j j par 2 j j matrice de covariance et R = (Rxy}0) la matrice correspondante de corrélation . Soit (fx; x 2 ; = ; +) 2 R2j j, nous identi…erons

f =P_x2 f_{x x} + f+

x +x; par conséquent on peut écrire

(f2) = X

x;y

X

;

f_xf_y ( _{x y}) = f CfT (3.13’) En plus, notons que

(f_{Pf) =} 1 j j X z2A (f (f _{j z})) = 1 j j X z X x;y X ; f_xf_y ( _y ( _{x j z})) (3.14) Parceque +x; y sont des variables de Bernoulli satisfait +x y = 0; alors on peut

écrire

( _{x j y}) = a_xy+ +

a_xy+et axy étant des nombres réels. En multipliant (3:15) par +y ou y et en intègrant, on obtient : a + xy a_xy = 1 det(Cyy) C_yy C+ yy C+ yy Cyy++ C + xy C_xy (3.16) où Cyy = (Cyy); 2f ;+g. Notons que 8 y; det(Cyy) 6= 0 à moins que v( y ) = 1. En

inspectant (3:16), on s’apperçoit que la matrice A = axy satisfait l’égalité :

A = CD (3.17)

où D = D_xy0 _{est une matrice carré symétrique de taille 2 j j, dé…nie par :} D_xx0 = (2 0 1)C_xx0 det(Cxx) ; D_xy0 = 0 pour x_{6= y} (3.18) De (3:14), (3:15), (3:17) et (3:18) on obtient : (f_{Pf) =} 1 j j X x;y X ; f_xf_y " X z a_xz+v( + z y) + axzv( z y) # = 1 j j X x;y X ; f_xf_y(AC)_xy = 1 j j X x;y X ; f_xf_y(CDC)_xy = 1 j jf CDCf T _(3.19)

Changement de variables dans

(f2₎

_et

_(f

Pf)

Maintenant, on trouve une matrice non négative Q et un vecteur g tels que (f2) = gQgT; (f_{Pf) =} 1

j jgQ

2_gT _(3.20)

de sorte que, si on pose

alors (f2) = hhT et (f (I _{P)f) = h(}(j j 1)I j j + j j)h T _(3.21)

On cherche une matrice carré triangulaire supérieure U de taille 2 j j par 2 j j telle que D = UT_{U: On remarque de (3:18) que la matrice D se compose de quatre}

sous-matrices diagonales de sorte que la matrice U doit satisfaire les identités de " bloc "suivantes :

U + = 0; U++U++= D++; U+ U++= D+ U+ U+ + U U = D

ceci implique que U_xy = 0 _{si x 6= y et} U_xx++=pD++ xx ; U ++ xx = D+ xx p D++ xx ; U_xx = s D_xx jD + xx j 2 D++ xx (3.22) Il est facile de voir que la matrice U est bien dé…nie et inversible puisque D est diagonale. Posant g = f U 1 et Q = U CUT _{de sorte que de (3:130) et (3:19) on se} raméne à (3:20) et aussi à (3:21).

En utilisant le théorème 3.1, on trouve inf f 2L2_{( ); (f )=0} (f (I _P)f) (f2₎ = inf_h6=0 hXhT hhT (3.23)

Il existe une matrice orthogonale P telle que X = P 1_{SPoù S = Diag(s}

1; s2; :::; s2j j)

En faites P = (e1; e2; :::; e_{2j j}) est la matrice de passage, où les ei sont les vecteurs

propres de X. Alors X peut être écrite comme suit : X= 2j j X i=1 eieTi Si h 6= 0 on a h = 2j j X i=1 hiei;

on déduit alors que

hXhT hhT = P2j j i=1sih2i P2j j i=1h2i s1 P2j j i=1h2i P2j j i=1h2i = s1

Maintenant, si on choisit h = e1, on s’apperçoit que l’inférieure est réalisé, d’où

inf

h6=0

hXhT hhT = s1

3.3

Simulation pour les valeurs propres du matrice

X

Pour j j = 3;on a X = 2 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 4 7 6 1 6 1 6 2 3 0 0 1 6 7 6 1 6 0 2 3 0 1 6 1 6 7 6 0 0 2 3 2 3 0 0 7 6 1 6 1 6 0 2₃ 0 1₆ 7₆ 1₆ 0 0 2 3 1 6 1 6 7 6 3 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 5

qui admet comme valeurs propres : 13₆ ;5₆;1₃;5₃, d’où s1 = min 13₆ ;5₆;1₃;5₃ = 1₃:

Pour j j = 4;on a X = 2 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 4 13 12 1 12 1 12 1 12 3 4 0 0 0 1 12 13 12 1 12 1 12 0 3 4 0 0 1 12 1 12 13 12 1 12 0 0 3 4 0 1 12 1 12 1 12 13 12 0 0 0 3 4 3 4 0 0 0 13 12 1 12 1 12 1 12 0 3₄ 0 0 ₁₂1 13_{12 12}1 ₁₂1 0 0 3 4 0 1 12 1 12 13 12 1 12 0 0 0 3_{4 12}1 ₁₂1 ₁₂1 13₁₂ 3 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 5 qui admet comme valeurs propres : 25

12; 7 12; 1 4; 7 4, d’où s1 = min 25 12; 7 12; 1 4; 7 4 = 1 4:

Pour j j = 5;on a X = 2 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 4 21 20 1 20 1 20 1 20 1 20 4 5 0 0 0 0 1 20 21 20 1 20 1 20 1 20 0 4 5 0 0 0 1 20 1 20 21 20 1 20 1 20 0 0 4 5 0 0 1 20 1 20 1 20 21 20 1 20 0 0 0 4 5 0 1 20 1 20 1 20 1 20 21 20 0 0 0 0 4 5 4 5 0 0 0 0 21 20 1 20 1 20 1 20 1 20 0 4₅ 0 0 0 ₂₀1 21_{20 20}1 ₂₀1 ₂₀1 0 0 4₅ 0 0 ₂₀1 ₂₀1 21_{20 20}1 ₂₀1 0 0 0 4₅ 0 ₂₀1 ₂₀1 ₂₀1 21_{20 20}1 0 0 0 0 4_{5 20}1 ₂₀1 ₂₀1 ₂₀1 21₂₀ 3 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 5

qui admet comme valeurs propres : 41₂₀;₂₀9 ;1₅;9₅, d’où s1 = min 41₂₀;₂₀9;1₅;9₅ = 1₅:

Remarque 3.5 On remarque, d’après la simulation, que la plus petite valeur propre de la matrice X est manifestement égale à _{j j}1 _{lorsque j j est petit. Il serait intéressant} d’étudier le cas où j j est grand, via le calcul formel par exemple.

j j 3 4 5

Conclusion et Perspectives

Ainsi, nous avons réussi à expliciter les mesures canoniques d’un système désor-donné de gaz bicoloré, et ensuite, à trouver la valeur exacte du trou spectral et nous montrons qu’elle correspond bien à la plus petite valeur propre de la matrice déter-ministe, qui ne dépend pas du désordre.

Par la suite, il serait intéressant d’obtenir la limite hydrodynamique d’un système désordonné de gaz bicoloré. Aussi, nous pouvions dans nos recherches futures de considérer des cas plus généraux à savoir :

- Étude du cas où j j est grand.

- Calcul du trou spectral d’un processus d’exclusion généralisé pour un système désordonné multicoloré.

Chapitre 4

ANNEXE

4.1

Démonstration du Theorem 2.2

Posons m+(a) = e a+ + 1 + ea+ + _{+ e}a+ ; m (a) = e a+ 1 + ea+ + _{+ e}a+ ;

m(a) = m+(a) + m (a):

et supposos que les conditions (i) et (ii) de la Proposition 2.3 véri…ées. Soit x 2 et en intégrant la relation +x + x = j xj par rapport à , on a immédiatement

(2:3a)_{. Pour prouver (2:4a), nous posons s = j xj ; s}0 ₌

y ; a = x et a = y:Alors

(2:4a) peut être exprimée comme suit :

Si ss0 _{6= 0 , l’égalité (4:1) est évidente d’aprés la condition d’exclusion (2) sur f}e . Si

ss0 _{= 0; les conditions (3) et (4) réduisent (4:1) à :}

(_f x;y_{g) =} (_{f g) exp( (s}0 s)(a0 a)):

Supposons par exemple que x = 0 et y = 1: Alors, par indendence, on a :

(_{f g) = m}+(a0)(1 m(a)) ( _y); avec y; z 2 r fx; x + eg

(_f x;y_{g) = m}+(a)(1 m(a0)) ( _y) avec y; z 2 r fx; yg

où est la mesure marginale de sur _rfx;yg;Dans le cas où s = 0 et s0 = 1; la relation (4:1) est équivalente à

exp(a a) = m

+_(a0_{)(1 m(a))}

m+_{(a)(1 m(a}0₎₎;

et cette dernière égalité est facilement examinée en utilisant (2) et en notant que 1 m(a) = (1 + exp(a + )) 1 et de façon similaire on al’égalité correspondante à a0. Les autres cas sont semblables par symétrie.

Supposons maintenant que les conditions (2:3a) et (2:4a) véri…és. Considérons tel que x = 0 et y = 1. Et gardons les notations précédentes, en particulier a = x

et a0 ₌

y, on a

exp(a a) = m

+_{(a)(1 m(a))}

Donc, on peut écrire

exp( a0)(1 m(a0)) 1m+(a0) = exp( a)(1 m(a)) 1m+(a):

Puisque les variables aléatoires a et a0 _{sont indépendantes par rapport à P, on déduit}

qu’il existe une constante positive non aléatoire c+

tel que, P-prèsque sûrement, exp(a)(1 m(a))

m+_(a) = c +_:

Notons que c+_{ne dépend pas de x aussi puisque la loi de a =}

x ne dépend pas de x.

Il découle de l’égalité précédente et du fait que [1 m(a)] 1 = 1 + exp(a + )tel que P-prèsque sûrement, que

m+(a) = c+ exp( a) 1 + exp(a + ):

De même, il existe une constante positive non aléatoire c tel que P-prèsque sûrement m (a) = c exp( a)

1 + exp(a + ):

Bibliographie

[1] D. Aldous and M. Brown. Inequalities for rare events in time-reversible Markov chains. IMS Lecture Notes-Monograpg, Stochastic Inequalities, 22 :1-16, (1993). [2] Boudou.A.S, Caputo.P, Dai Pra. P, Posta. G. Spectral gap estimates for inter-acting particle systems via a Bochner-type identity. J. Funct. Anal. 232 : no. 1, 222–258 (2006).

[3] N. Cancrini, F.Martinelli. On the spectral gap of Kawasaki dynamics under a mixing condition revisited. Probabilistic techniques in equilibrium and nonequi-librium statistical physics. J. Math. Phys. 41 : no. 3, 1391–1423 (2000).

[4] P. Caputo . Spectral gap inequalities in product spaces with conservation laws. Stochastic analysis on large scale interacting systems, 53–88, Adv.Stud. Pure Math : 39, Math. Soc. Japan, Tokyo (2004).

[5] E. Carlen, M.C. Carvalho, M. Loss, Determination of the spectral gap in Kac’s master equation and related stochastic evolutions, preprint (2002).

[6] I. Chavel. Eigenvalues in Riemanian geometry. Academic Press, New York, (1984).

[7] M. F. Chen. Optimal Markovian couplings and applications. Acta Math. Sin. New Ser., 10(3) :260-275, (1994).

[8] Y. Colin de Verdière. Spectres de graphes. Cours de DEA, Universit e Joseph Fourier -ENS Lyon, (1994).

[9] A.Dermoune, P. Heinrich. A small step towards the hydrodynamic limit of a colored disordered lattice gas. C. R. Math. Acad. Sci. Paris 339 : no. 7, 507– 511(2004).

[10] A.Dermoune, P. Heinrich. Equivalence of ensembles for colored particles in a disordered lattice gas, Markov Processes Relat. Fields 11 : 405-424 (2005). [11] A. Dermoune, P. Heinrich. Spectral gap inequality for a colored disordered lattice

gas.Lecture Notes in Mathematics, Vol. 41. Seminaire de Probabilites XLI : 1-18 (2008).

[12] P. Diaconis and L. Salo -Coste. Comparison thechniques for random walk on nite groups. Ann. Appl. Probab., 21 :2131-2156, (1993).

[13] A.Faggionato, F. Martinelli . Hydrodynamic limit of a disordered lattice gas. Probab. Theory Related Fields 127 : no. 4, 535–608 (2003).

[14] Dobrushin, R. L.Markov processes with a large number of locally interacting components : existence of a limit process and its ergodicity. Problems Inform. Transmission, 1 : 149-164 (1971).

the reversible case and some generalizations. Problems Inform. Transmission, 7 : 235-241(1971).

[16] Dynkin, E. B. Markov Processes, I. Academic Press, New York(1965).

[17] Ethier, S. N. and Kurtz, T. G. Markov processes : characterization and conver-gence. Wiley, New York (1985).

[18] A. Gelman and D. B. Rubin. Inference from iterative simulation using multiple sequences (with discussion). Statistical Science, 7 :457-511, (1992).

[19] D. Geman and S. Geman. Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Ma-chine Intelligence, PAMI-6 :721-741, (1984).

[20] D. Geman. Random elds and inverse problems in imaging. Lect. Notes. Math., Ecole d’été de probabilités de Saint-Flour XVIII-1988 :113-193, (1990).

[21] Gihman, I. I. and Skorohod, A. V. The Theory of Stochastic Processes, II. Springer-Verlag, New York (1975).

[22] U. Grenander. Tutorial in pattern theory. Brown University, Providence, (1984). [23] C. Kipnis, C. Landim. Scaling limits of interacting particule systems.

Grundleh-ren dermathematischen Wissenschaften, Springer-Verlag, (1999).

[24] T. M. Liggett. Interacting particle systems, volume 276 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences].Springer-Verlag, New York, (1985).

[25] B. M. McCoy and T. T. Wu. The two-dimensional Ising model. Havard Univ. Press, Cambridge, Massachusetts, (1973).

[26] E. Saada. A limit theorem for the position of a tagged particle in a simple exclusion process. Ann. Probab., 15, 375-381 (1987).

[27] Lu. Sheng Lin,Yau. Horng-Tzer. Spectral gap and logarithmic Sobolev inequa-lity for Kawasaki and Glauber dynamics. Comm. Math. Phys. 156, no. 2, 399– 433(1993).

[28] R. Schoen and S. T. Yau. Di¤erential Geometry. Science Press, Beijing, China, (1988).

[29] R. Schonmann. Slow droplet-driven relaxation of stochastic Ising models in the vicinity of the phase coexistence region. Commun. Math. Phys., 161 :1-49, (1994).

[30] A.D. Sokal and L.E. Thomas. Absence of mass gap for a class of stochastic contour models. J. Statis. Phys., 51 5/6 :907-947, (1988).

[31] Spitzer, F. Random Processes De…ned Through the Interaction of an In…nite Particle System. Springer Lecture Notes in Mathematics, Vol. 89 : pp. 201-223(1969).

[32] F. Spitzer, Uniform motion with elastic collision of an in…nite particle system. J. Math. Mech, 18 : 973-989, 1969.

[34] J. Quastel, Di¤usion of color in the simple exclusion process, Comm. Pure Appl. Math. 45, 623–679, 1992.

[35] J. Quastel, Bulk di¤usion in a system with site disorder, Annals of Probability 34 : 1990-2036, 2006.

[36] G.H. Weiss. Aspects and Applications of the Random Walk. Random Materials and Processes. North-Holland, Amsterdam. 103, 104- 110 (1994).

[37] D. Wick. A dynamical phase transition in an in…nite particle system. J. Stat. Phys. 38 : 1015–1025 (1985).

[38] C.N. Yang and T.D. Lee. Statistical Theory of Equations of State and Phase Transitions. I. Theory of Condensation. Phys. Rev. 87(3) : 404–409 (1952). [39] H.T. Yau. Relative entropy and hydrodynamics of Ginzburg-Landau models.

Lett. Math. Phys. 22 : 63–80 (1991).