Estimation bayésienne dans un modèle de lindley généralisé

(1)

يملعلا ثحبلاو لياعلا ميلعتلا ةرازو

راـتخم يـجاب ةـعماج

ةـباـنع

Université Badji Mokhtar

Annaba

Badji Mokhtar University -

Annaba

Faculté des Sciences

Département de Mathématiques

Laboratoire de Probabilités et Statistique

THESE

Présentée en vue de l’obtention du diplôme de

Doctorat en Mathématiques

Option :

Modélisations Mathématiques

Estimation Bayésienne dans un modèle de Lindley

généralisé

Par:

Aouf Fairouz

Sous la direction de :

Pr. Chadli Assia

Devant le jury

PRESIDENTE :

EXAMINATRICE :

(

Sedd Seddik-Ameur Nacira

Messaci Fatiha

Nemouchi Nahima

Pr

U.B.M.Annaba

U.M.Constantine

(2)

Table des matières

Dédicace iii Remerciements iv Résumé v Abstract vi Introduction viii 1 Outils mathématiques 1

1.1 Durées de survie ou …abilité . . . 1

1.1.1 Fonction de survie S . . . 1

1.1.2 Fonction de répartition F . . . 1

1.1.3 Densité de probabilité f . . . 2

1.1.4 Risque instantané (ou taux de hasard) . . . 2

1.2 Quantités associées à la distribution de survie . . . 3

1.2.1 Moyenne et variance de la durée de survie . . . 3

1.2.2 Quantiles de la durée de survie . . . 3

1.3 Données censurées . . . 4

1.3.1 Censure à droite . . . 5

1.3.2 La censure de type I . . . 5

1.3.3 La censure de type II . . . 6

1.3.4 La censure de type III (ou censure aléatoire de type I) 6 1.3.5 La censure à gauche . . . 7

1.3.6 Censure par intervalle . . . 7

1.3.7 Censures progressives . . . 8

(3)

TABLE DES MATIÈRES

1.4.1 La loi Exponentielle . . . 10

1.4.2 Le modèle de Weibull . . . 10

1.4.3 Le modèle Gamma . . . 11

1.4.4 Distribution Log-Normale . . . 12

2 Les méthodes d’estimation 14 2.1 Dé…nition et propriétés d’un estimateur . . . 14

2.2 La méthode des moments . . . 16

2.3 Approche du Maximum de Vraisemblance . . . 16

2.4 L’estimation Bayésienne . . . 18

2.4.1 Coût et décision . . . 19

2.4.2 La loi a posteriori. . . 19

2.4.3 Le risque de Bayes . . . 20

2.4.4 Fonctions de perte . . . 21

2.4.5 Propriétés de l’estimateur de Bayes . . . 23

2.4.6 Modélisation de l’information a priori . . . 24

2.4.7 Intérêt de la démarche Bayésienne . . . 25

2.4.8 Di¢ culté de la démarche Bayésienne . . . 27

2.4.9 Les méthodes de Monte Carlo par chaînes de Markov . 27 2.5 Les Critéres de Comparaisons . . . 30

3 Modéles de Lindley et de Lindley généralisé 31 3.1 Modèle de Lindley (L) . . . 32

3.1.1 Dé…niton du modèle . . . 32

3.1.2 Estimation du paramétre et de la fonction de …abilité par maximum de vraisemblance . . . 34

3.1.3 Estimations à l’aide d’une approche Bayesienne . . . . 35

3.2 Le modèle de Lindley Généralisé . . . 38

3.2.1 Dé…nition du modèle . . . 38

3.2.2 Les moments . . . 40

3.2.3 Estimations par maximum de vraisemblance en pré-sence de données censurées de typeII . . . 42

3.2.4 Estimations par la méthode des Moments . . . 43

3.2.5 Estimation bayésienne sous di¤érentes fonctions de perte en présence de données censurées de typeII . . . 44

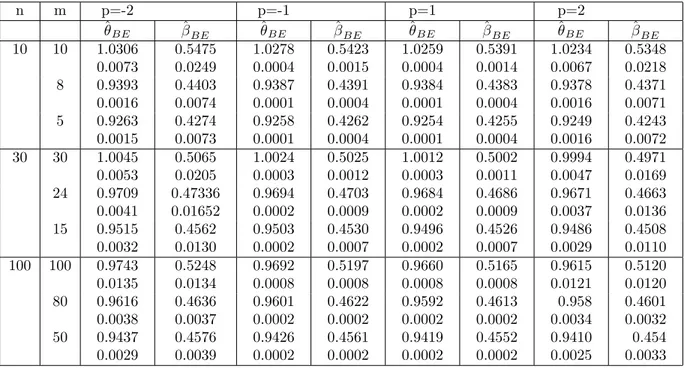
3.2.6 Estimations avec des données progressivement censurées 47 3.2.7 Simulations . . . 53

(4)

Dédicace

A ma maman et mon papa, A mes soeurs, mes cousines, A mes tantes, mes oncles, A mon …ancé,

(5)

Remerciements

Je suis très reconnaissante à ma directrice de thèse, Madame Chadli Assia Professeur à l’université Badji-Mokhtar d’Annaba et membre du la-boratoire LaPS, pour m’avoir fait con…ance en me proposant ce travail de thèse. Je la remercie sincèrement pour sa disponibilité, sa gentillesse, ses conseils avisés et son soutien continu. Qu’elle trouve ici mon admiration et mon profond respect.

Je tiens à exprimer toute ma gratitude à Madame Seddik-Ameur Pro-fesseur à l’université Badji-Mokhtar d’Annaba, d’avoir accepté de juger mon travail et de présider le jury de ma thèse.

Je suis très honorée par la présence au sein du jury de ma thèse, en tant qu’examinateurs, de :

- Madame Messaci Fatiha, Professeur à l’université de Constantine, - Madame Nemouchi Nahima, Professeur à l’université de Constan-tine,

- Monsieur Zeghdoudi Halim, Maître de conférences A à l’université B.M.Annaba.

Qu’ils trouvent, ici, l’expression de ma profonde gratitude.

En…n, je remercie du fond du cœur et avec grand amour mes chère parents (Sakina, Nour-eddine) qui n’ont jamais cessé de croire en moi pendant toutes mes années d’études. Merci pour les sacri…ces consentis à mon éducation, pour le soutien et surtout pour la patience. Merci aussi à ma sœur (Rayane et Zineb) qui m’ont toujours encouragé et a toutes ma familles et aussi à mon …ancé (Hamza), a mes cousines surtout (Sara), a mes amies sourtout Wafa Treidi et Khawla Boujerda.

(6)

Résumé

Dans cet travail, On s’est intéressé essentiellement à un modèle de sur-vie : le modèle de Lindley généralisé. L’étude des estimateurs de Bayes des paramètres, de la fonction de …abilité et de la fonction taux de panne sous di¤érentes fonctions de pertes et avec plusieurs type de données a été réalisé d’un point de vue théorique appuyée par une étude par simulations. Les lois a priori utilisées dans ce travail sont de deux types ( lois a priori conjuguées naturelles et lois a priori non informatives).

Deux approches ont été utilisées, l’approche classique du maximum de vraisemblance puis une approche Bayésienne dans le cas d’une distribution de Lindley généralisée. Les estimateurs Bayésiens et les risques a posteriori sont obtenues en utilisant des fonctions de pertes symétriques ( la fonction de perte quadratique et la fonction de perte entropie) puis des fonctions de perte asymétriques (la fonction de perte Linex). Dans le cas de l’approche classique, les estimateurs sont solutions d’un système non linéaire dont les solutions ne sont pas explicites analytiquement ; des méthodes numériques ont été adoptées. Dans l’approche Bayésienne, les estimateurs sont donnés sous forme d’un rapport d’intégrales, les méthodes de Monte-Carlo et en particulier Metropolis -Hastings pour procéder à des simulations et une à analyse de données ont été appliquées.

Finalement, Nous avons utilisé le critère de Pitman et le critère "integra-ted mean square error" (IMSE) pour comparer les estimateurs bayésiens et les estimateurs du maximum de vraisemblance.

Mots clés : Modèle de Lindley, estimateurs de Bayes, Les lois a priori, les méthodes de Monte Carlo, le critère de Pitman, IMSE

(7)

Abstract

In this work, we focused on a survival model : the generalized Lindley distribution. The study of bayesian estimators of the parameters, the reliabi-lity function and the failure rate function under di¤erent loss functions and several type data was realized supported by a simulation study. The prior laws used with this work are the natural conjugate and the non- informative ones.

Two approaches were used, the classical approach of maximum likelihood and the Bayesian approach in the case of the Lindley generalized distribution. Bayesian estimators and posterior risks are obtained using symmetric loss functions (The loss quadratic function and the loss entropie function) and asymmetric loss functions (the Linex function).

In the case of the classical approach, the estimators are solutions of a non- linear system from which the solutions cannot be given explicitly ; so, numerical methods were adopted.

In the bayesian approach, the estimation are given as report of integrals. Monte-Carlo methods, particularly, Metropolis-Hastings have been applied for simulations and data analysis.

Finally, we use the Pitman criteria and the « integrated mean square error » (IMSE) criteria to compared the Bayesian estimators and the maximum likelihood estimators.

Keywords : Lindley model, Bayes estimators, the prior laws, Monte-Carlo methods, Pitman criteria, IMSE criteria.

(8)

vii

:صخلم

يف

اذه

،لمعلا

انزكر

اساسأ

ىلع

جذومن

ءاقبلا

ىلع

ديق

ةايحلا

:

يف لثمتملا

جذومن

يلدنيل

ممعملا

.

تناكف

ةسارد

لا تاريدقتلا

زياب

ةي

لل

عم

م

لا

ت

و

ةلادلا

ةيقوثوملا

و

ةلاد كلذك

بطعلا ةبسن

تحت

ةراسخلا لاود فلتخم

ةدعو

عاونأ

نم

تانايبلا

تذفنو

نم

ةيحانلا

ةيرظنلا

ةموعدم

ب

ةسارد

ةاكاحملا

.

نا

وه لمعلا اذه يف لمعتسملا يهيدبلا نوناقلا

لا

.يعيبطلا جوازتملا يهيدبلا نوناق

انمدختساو

اضيأ

نيتقيرط

،

لا

ةقيرط

يديلقتلا

ة

لثمتملا

ة

يف

لإا

ةيناكم

لا

ىوصق

و

يف لثمتت ةيناثلا ةقيرطلا

ةيرظنلا

ةيزيابلا

.

مت

لوصحلا

ىلع

تاردقملا

ةيرظنلا

لا

ةيزياب

و

رطاخملا

ةيدعبلا

مادختساب

د

ءاطخلأا لاو

ةيرظانتلا

(

ةلاد

ءاطخلأا

نم

ةجردلا

ةيناثلا

ةلادو

ءاطخأ

Entropie

)

و

ريغ ءاطخأ ةلاد

ةيرظانت

(

ءاطخأ ةلاد

LINEX

.)

يف

ةلاح

لا

ةقيرط

يديلقتلا

ة

،

تاردقملا

يه

لولح

ماظنل

ريغ

و يطخ

يتلا

يه

لولح

تسيل

تارابع اهل

ةيليلحتلا

ةحيرص

دقو

مت

لاا

دامتع

ىلع

قرطلا

ةيددعلا

.

ىرخأ ةهج نم

لا

ةبراقم

ةيرظنلا

لا

,ةيزياب

متي

ءاطعإ

تاردقملا

ت بسن ةغيص ىلع

لاماك

ت

.

دقو

مت

قيبطت

قرط

تنوم

ولراك

ىلعو

هجو

صوصخلا

Metropolis -Hastings

ل

لإ

ءارج

ةاكاحملا

ليلحتو

تانايبلا

.

،اريخأ

انمدختسا

رايعم

نامتيب

رايعمو

(

IMSE

)

ةنراقمل

تاردقملا

ةيرظنلا

ا

ةيزيابل

.ةيكيسلاكلا و

:ةيحاتفملا تاملك

جذومن

يلدنيل

ممعملا

لا تاريدقتلا ,

زياب

,يهيدبلا نوناقلا ,ةي

قرط

تنوم

ولراك

,

رايعم

نامتيب

رايعمو

(

IMSE

)

(9)

Introduction

La …abilité est un vaste domaine contribuant à la compréhension, à la modélisation et à la prédiction des mécanismes de dégradation et de vieillis-sement susceptible de conduire le composant à la défaillance et le système à la panne. La connaissance des relations entre les limites physiques, les défauts intrinsèques, les imperfections technologiques et les contraintes environne-mentales et internes constitue la substance même de cette activité vaste et complexe. La conservation de la …abilité concerne la maintenabilité, un autre aspect important des performances du système. Elle s’occupe de ce qu’il faut faire pour qu’un produit soit ramené dans des conditions aussi proches que possible de celles prévues au début de son fonctionnement.

Le but de la …abilité et de la maintenabilité est de garantir un usage prévu du produit au coût total minimal pendant la période spéci…ée, dans des conditions d’entretien et de réparation précises.

D’une manière générale, l’analyse de la …abilité constitue une phase in-dispensable dans toute étude de sûreté de fonctionnement. L’analyse de la …abilité est appliquée pour évaluer la performance d’une structure (systèmes ou composants), ou pour optimiser la géométrie d’une structure en respectant un certain niveau de …abilité ou de coût espéré. De plus, la …abilité des struc-tures est un outil d’aide à la décision pour établir un plan de maintenance et d’inspection.

Les modèles classiques les plus utilisés en …abilité sont les modèles expo-nentiels et les modèles de Weibull, cependant, ces dernières années plusieurs nouveaux modèles applicables dans les problèmes de durée de survie ont été dé…nis ; on peut citer parmi les plus récents : Bertholon, Kumaraswamy, Lindley,. . .

Dans cette thèse, on s’est intéressé au modèle de Lindley généralisé (LG). Les propriétés mathématiques telles que la fonction génératrice, les di¤érents moments et les statistiques d’ordre ont été traités dans l’article de R.Shanker

(10)

et al (2016). Le problème de l’estimation des paramètres du modèle (LG) à l’aide d’une approche classique du maximum de vraisemblance a été traité par R.Shanker et al (2013).

On se propose d’étudier le problème de l’estimation des paramètres et de la fonction de …abilité à l’aide d’une approche Bayesienne, dans un plan d’expérience censuré à droite. Pour le choix de la loi a priori, on opte pour une loi conjuguée naturelle sur le paramètre de forme et une loi non informative sur le paramètre d’échelle. Les estimateurs Bayesiens dépendent du choix de la fonction de perte qui souvent est une fonction de perte quadratique de forme symétrique. On considère, dans cette thèse un panel de fonctions de perte symétriques (perte Quadratique et perte Entropie) et asymétrique (perte Linex).

L’expression des estimateurs de notre modèle n’a pas une forme ana-lytique simple, aussi bien par l’approche classique que par l’approche Baye-sienne (solutions d’un système non linéaire pour l’une et forme intégrale pour l’autre) ; c’est pourquoi on utilisera les méthodes MCMC qui permettent l’échantillonnage de variables aléatoires, le calcul d’intégrales et l’optimisa-tion de foncl’optimisa-tions.

Une comparaison entre les estimateurs du maximum de vraisemblance et les estimateurs Bayesiens a été étudiée à l’aide de deux critères de proxi-mité : le critère de Pitman et l’intregral-mean square error(IM SE) sur la base d’une étude par simulations et d’une analyse de données réelles.

Le manuscrit est organisé de la manière suivante :

Au chapitre 1, on donne quelques dé…nitions et propriétés des principaux outils mathématiques utilisés dans cette thèse. En particulier, la notion de …abilité et ses caractéristiques, avec un rappel des modèles usuels dans les durées de survie. Le chapitre deux est consacré aux méthodes d’estimations. Au chapitre trois, on étudie le modèle de Lindley généralisé, dont le modèle de Lindley découle. On donne les estimateurs de ses paramètres, de sa fonction de …abilité et de son taux de panne à l’aide d’une approche classique du maximum de vraisemblance, puis à l’aide d’une approche Bayesienne, dans un plan d’expérience censuré à droie. Dans cette dernière approche, on utilise di¤érentes fonctions de perte. D’autre part, les estimateurs des paramètres de la loi LG ont été traités dans le cadre d’un plan d’expérience progressivement censuré.

Une étude par simulations et une analyse de données réelles ont été réali-sées. On termine par une étude comparative des estimateurs obtenus à l’aide

(11)

CHAPITRE 0. INTRODUCTION

de deux critères de proximité : le critère de Pittman et le critère IMSSE. Le manuscrit s’achève par une bibliographie et des annexes contenant l’implé-mentation dans R des di¤érents algorithmes utilisés.

(12)

Chapitre 1

Outils mathématiques

1.1 Durées de survie ou …abilité

En analyse de survie, nous nous attachons à d´écrire la distribution des temps de survie, à comparer la survie de plusieurs groupes de sujets et á étudier l’impact de facteurs de risque sur le délai de survenue de l’événement d’intêrét. Cet événement peut être associé à un changement d’état au cours de la progression de la maladie. Dans le cas le plus simple, l’analyse de survie peut se voir comme l’étude du passage irréversible entre deux états …xés.

Supposons que la durée de survie X soit une variable positive ou nulle, et absolument continue, alors sa loi de probabilité peut être défnie par l’une des cinq fonctions équivalentes suivantes (chacune des fonctions ci-dessous peut être obtenue à partir de l’une des autres fonctions) :

1.1.1 Fonction de survie S

La fonction de survie S pour t …xé est la probabilité de survivre jusqu’à l’instant t, c’est -à -dire

S(t) = P (X > t); t 0 (1.1)

1.1.2 Fonction de répartition F

La fonction de répartition (ou c.d .f. pour "cumulative distribution func-tion") représente, pour t …xé, la probabilité de mourir avant l’instant t; c’est-à-dire :

(13)

CHAPITRE 1. OUTILS MATHÉMATIQUES

F (t) = P (X t) = 1 S(t) (1.2)

1.1.3 Densité de probabilité f

C’est la fonction f (t) 0telle que pour tout t 0 : F (t) =R₀tf (u) du Si la fonction de répartition F admet une dérivée au point t alors :

f (t) = lim

h !0

P (t X < t + h)

h = F

0_{(t) =} _S0_(t) _(1.3)

Pour t …xé, la densité de probabilité représente la probabilité de mourir dans un petit intervalle de temps après l’instant t.

1.1.4 Risque instantané

(ou taux de hasard)

Dé…nition 1.1.1 Le risque instantané (ou taux d’incidence), pour t …xé ca-ractérise la probabilité de mourir dans un petit intervalle de temps après t, conditionnellement au fait d’avoir survécu jusqu’au temps t (c’est-à-dire le risque de mort instantané pour ceux qui ont survécu) :

(t) = lim h!0 P (t X < t + h_jX t) h = f (t) S(t) = (ln S(t)) 0 _(1.4)

La fonction de risque est une mesure de propension au décès en fonction de l’age de l’individu. En d’autres termes, cette fonction donne un risque de décès par unité de temps tout au long du processus de vieillissement. Les épidémiologistes ont baptisé cette fonction taux de mortalité. La fonction de risque donne habituellement plus d’informations sur le mécanisme de décés que la fonction de survie. C’est pourquoi cette fonction est souvent employée pour résumer les données de survie.

Dé…nition 1.1.2 La fonction de risque cumulée (cas continue) est dé…nie par : (t) = t Z 0 (x)dx = ln[S(t)] (1.5)

(14)

1.2. QUANTITÉS ASSOCIÉES À LA DISTRIBUTION DE SURVIE

1.2 Quantités associées à la distribution de

survie

1.2.1 Moyenne et variance de la durée de survie

Le temps moyen de survie E(X) et la variance de la durée de survie V (X) sont défnis par les quantités suivantes :

E(X) = 1 Z 0 S(t)dt (1.6) V (X) = 2 1 Z 0 tS(t)dt (E(X))2

1.2.2 Quantiles de la durée de survie

La médiane de la durée de survie est le temps t pour lequel la probabilité de survie S(t) est égale à 0:5; c’est-à-dire, la valeur tm qui satisfait

S(tm) = 0; 5. Dans le cas où l’estimateur est une fonction en escalier, il se

peut qu’il y ait un interval le de temps vérifant S(tm) = 0:5. Il faut alors être

prudent dans l’interprétation, notamment si les deux événements encadrant le temps médian sont éloignés. Il est possible d ’obtenir un intervalle de con…ance du temps médian. Soit [Bi;Bs]un intervalle de con…ance de niveau

de S(tm); alors un intervalle de con…ance de niveau du temps médian tm est :

S 1(Bs); S 1(Bi)

- La fonction quantile de la durée de survie est dé…nie par :

q(p) = inf_{ft : F (t)} p; 0 < p < 1_g = inf_{ft : S(t)} 1 p_g

Lorsque la fonction de répartition F est strictement croissante et continue alors

q(p) = F 1(p); 0 < p < 1 (1.7) = S 1(1 p)

(15)

Le quantile q(p) est le temps où une proportion p de la population a disparu.

La représentation graphique de la survie, appelée courbe de survie, est une fonction monotone non croissante de la probabilité de survie en fonction du temps. Son taux de déclin varie selon le risque d’expérimenter l’événement au temps t. F ig 1:1 est un exemple de courbe de survie. Elle représente la survie d’hommes sou¤rant d’angine de poitrine (voir Aide en ligne de SAS (1999), procédure LIFETEST, exemple 37.2). Le temps de survie est mesuré en années depuis le diagnostic.

F ig:1:1 :Distribution de la survie aprés le diagnostic d’angine de poitrine. Le temps 0 correspond au diagnostic d’angine de poitrine.

1.3 Données censurées

Une des caractéristiques des données de survie est l’existence d’observa-tions incomplètes. En e¤et, les données sont souvent recueillies partiellement, notamment, à cause des processus de censure. Les données censurées pro-viennent du fait qu’on n’a pas accès à toute l’information : au lieu d’observer des réalisations indépendantes et identiquement distribuées (i.i.d.) de durée

(16)

1.3. DONNÉES CENSURÉES

de vie X, de loi P on observe la réalisation de la variable X soumise à di-verses perturbations, indépendantes ou non du phénomène étudié.Il est clair que dans le cas de données complètes (X1; :::; Xn) (en l’absence de censures)

la vraisemblance s’écrit : L (x_{j ) =} n Q i=1 f (xij ) (1.8)

Cette vraisemblance sera modi…ée selon le plan d’expérience dont on dis-pose ; on intègre alors les données censurées, qui peuvent être de plusieurs types. Nous donnerons l’expression de la vraisemblance, dans le cas des seuls cas des plans utilisés dans cette thèse ; à savoir, pour des données censurées de type II et pour des données progressivement censurées.

La censure est le phénomène le plus couramment rencontré lors du recueil de données de survie. Pour l’individu i, considérons

- son temps de survie Xi;

- son temps de censure Ci,

- la durée réellement observée Ti,

1.3.1 Censure à droite

La durée de vie est dite censurée à droite si l’individu n’a pas subi l’évé-nement à sa dernière observation. En présence de censure à droite, les durées de vie ne sont pas toutes observées ; pour certaines d’entre elles, on sait seulement qu’elles sont supérieures à une certaine valeur connue.

1.3.2 La censure de type I

Soit C une valeur …xée, au lieu d’observer les variables X1; ::::::; Xn qui

nous intéressent, on n’observe Xi uniquement l’orsque Xi C; sinon on sait

uniquement que Xi > C : On utilise la notation suivante :

Ti = Xi^ C = min(Xi; C):

Ce mécanisme de censure est fréquemment rencontré dans les applications industrielles. Par exemple, on peut tester la durée de vie de n objet identiques (ampoules) sur un intervalle d’observation …xé [0; u] : En biologie, on peut tester l’e¢ cacité d’une molécule sur un lot de souris (les souris vivantes au bout d’un temps u sont sacr…ées).

(17)

1.3.3 La censure de type II

Elle est présenté quand on décide d’observer les durées de survie des n patients jusqu’à ce que k d’entre eux soient décédés et d’arrêter l’étude à ce moment là. Soient X(i) et T(i) les statistiques d’ordre des variables Xi et Ti :

La date de censure est donc X(k) et on observe l es variables suivantes :

T(1) = X(1) . . T(k)= X(k) T(k+1) = X(k) . . T(n)= X(k)

La vraisemblance associée à un plan d’expérience cesuré à droite est alors donnée par : L (x_{j ) _} k Q i=1 f (xij ) [1 F (xk)] n k (1.9)

1.3.4 La censure de type III (ou censure aléatoire de

type I)

Soient C1; :::::; Cn des variables aléatoires i .i.d. On observe les variables

Ti = Xi^ Ci:

L’information disponible peut être résumée par : - la durée réellement observée Ti;

- un indicateur i = 1_fXi Cig

- i = 1 si l’événement est observé (d’où Ti = Xi). On observe les

vraies durées ou les durées complètes.

- i = 0si l’individu et censuré (d’où Ti = Ci). On observe des durées

incomplètes (censurées).

La censure aléatoire est la plus courante. Par exemple, lors d’un essai thérapeutique, elle peut être engendrée par :

La perte de vue : le patient quitte l’étude en cours et on ne le revoit plus (à cause d’un d’éménagement, le patient décide de se faire soigner ailleurs). Ce sont des patients perdus de vue .

(18)

1.3. DONNÉES CENSURÉES

L’arrêt ou le changement du traitement : les e¤ets secondaires ou l’ ine¢ cacité du traitement peuvent entraîner un changement ou un arrêt du traitement. Ces patients sont exclus de l’étude.

La …n de l’étude : l’étude se termine alors que certains patients sont toujours vivants (ils n’ont pas subi l’événement). Ce sont des patients vivants . Les perdus de vue (et les exclusions) et les exclus-vivants correspondent à des observations censurées mais les deux mé-canismes sont de nature di¤érente (la censure peut être informative chez les perdus de vue ).

1.3.5 La censure à gauche

La censure à gauche correspond au cas où l’individu a déjà subi l’événe-ment avant que l’individu soit observé. On sait uniquel’événe-ment que la date de l’événement est inférieure à une certaine date connue. Pour chaque individu, on peut associer un couple de variables aléatoires (T ; ) :

T = X _{_ C = max((X; C);} = 1_{fX Cg}

Comme pour la censure à droite, on suppose que la censure C’est indé-pendante X. Un des premiers exemples de censure à gauche rencontré dans la littérature considère le cas d’observateurs qui s’intéressent à l’horaire où les babouins descendent de leurs arbres pour aller manger (les babouins passent la nuit dans les arbres). Le temps d’événement (descente de l’arbre) est ob-servé si le babouin descend de l’arbre après l’arrivée des observateurs. Par contre, la donnée est censurée si le babouin est descendu avant l’arrivée des observateurs : dans ce cas on sait uniquement que l’horaire de descente est inférieur à l’heure d’arrivée des observateurs. On observe donc le maximum entre l’heure de descente des babouins et l’heure d’arrivée des observateurs (l’heure correspond à une durée).

1.3.6 Censure par intervalle

Une date est censurée par intervalle si au lieu d’observer avec certitude le temps de l’événement, la seule information disponible est qu’il a eu lieu entre deux dates connues. Par exemple, dans le cas d’un suivi de cohorte, les personnes sont souvent suivies par in- termittence (pas en continu), on sait alors uniquement que l’événement s’est produit entre ces deux temps d’observations. On peut noter que pour simplier l’analyse, on fait souvent

(19)

l’hypothèse que le temps d’événement correspond au temps de la visite pour se ramener à la censure à droite.

f ig:1:2 : di¤érents types d0obsravation

1.3.7 Censures progressives

Supposons qu’un échantillon de taille n soit soumis à un test de survie. Un système de censure progressive ~R = (R1; R2; ::::; Rm)est pré-…xé de sorte que,

après la première défaillance, R1 éléments parmi les (n 1)survivants soient

retirés du reste de l’échantillon ; après la deuxième défaillance, R2 éléments

sont retirés parmi les (n R1 2)éléments restants, et ainsi de suite.

Il est clair que

m

X

i=1

Ri+ m = n:

Remarque 1.3.1 a)

Si R1 = R2 = :::: = Rm = 0 , Alors le système de censure progressive est

réduit à un schéma d’échantillonnage complet.

b) Si R1 = R2 = :::: = Rm 1 = 0 et Rm = n m; Alors ce schéma se

réduit à un schéma classique de censure de type II.

c) Pour générer les données progressivement censurées d’une distribution connue, on utilise l’algorithme de Balakrishnan et Sandhu avec les cinq étapes suivantes :

1- générer m variables identiquement indépendantes distribuées (u1; u2; :::; um)

(20)

1.4. MODÈLES DE SURVIE USUELS

2- Soit zi = log(1 ui), zi sont identiquement indépendantes distribuées

de la distribution exponentielle standard.

3- En donnant les censures R (R1; R2; :::; Rm), soit y1 = z_m1, et pour

i = 1; :::; m

yi = yi 1+

zi

n Pi 1_j=1Rj i 1

Donc, (y1; y2; :::; ym)sont des données progressivement censurées d’un

échan-tillon U (0; 1).

4- Soit wi = 1 exp( yi).

5- Soit xi = F 1(wi)i.e wi = F (xi), donc, (x1; x2; :::; xm)sont des données

progressivement censurées de la distribution qu’on veut générer.

Dans le cas d’un plan d’expériece avec des données progressive-ment censurées, la vraisemblance s’écrit :

L( ; x1; :::; xn) = A m Y i=1 f (xi)(1 F (xi))Ri (1.10) R = (R1; R2; :::; Rm) A = n(n 1 R1)(n 2 R1 R2):::(n m X i=1 (Ri+ 1)):

1.4 Modèles de survie usuels

On ne reprend ci-après que les modèles les plus courants ; d’une manière générale, toutes les distributions utilisées pour modéliser des variables po-sitives (log-normale, Pareto, logistique, etc.) peuvent être utilisées dans des modèles de survie, la distribution de base des modèles paramétriques de durée est la distribution exponentielle.

Le choix du modèle détermine en particulier la forme de la fonction de hasard ; on distinguera notamment les modèles à fonction de hasard mono-tone des modèles permettant d’obtenir des fonctions de hasard en forme de baignoire ; ces derniers modèles sont peu usités en assurance, la situation de référence étant un taux de hasard croissant (au sens large) avec le temps, Les deux lois simples les plus utilisées : Loi Exponentielle, Loi de Weibull

(21)

1.4.1 La loi Exponentielle

La loi exponentielle est la plus utilisée dans les études de …abilité pour sa facilité d’emploi et son interprétation très simple. Elle représente la distribu-tion de la durée de vie moyenne T d’un système, dont le taux de défaillance

est constant avec le temps.

La spéci…cation la plus simple consiste à poser h(t) = , avec > 0 . On en déduit immédiatement que

S(t) = e t

Le modèle exponentiel est caractérisé par le fait que les fonctions de survie conditionnelles fSu(:) ; u > 0g sont exponentielles de même paramètre > 0

. Cela signi…e que le comportement de la variable aléatoire T après l’instant ude dépend pas de ce qui est survenu jusqu’en u. Il est également caractérisé par le fait que la fonction de survie est multiplicative, au sens où S(u + t) = S(u)S(t) Ces propriétés découlent aisément de l’expression de la fonction de survie conditionnelle présentée en ci-dessus.

On véri…e aisément par un calcul direct que : E(T ) = 1 et V (T ) = 12

L’estimation par maximisation de la vraisemblance du paramètre est classique, à partir de l’expression L( ) = nexp( Pi=n_i=1Ti) qui conduit

facilement à ^ = _P_i=nn i=1Ti = 1 T

1.4.2 Le modèle de Weibull

La forme générale de la fonction de …abilité est désignée par R(t) repré-sentant la probabilité de bon fonctionnement à l’instant t:

S(t) = e (t )

Avec les paramètres et signi…cation :

; ; dé…nissent la distribution de Weibull. On utilise trois paramètres :

- : paramètre de forme( > 0) - : paramètre d’échelle( > 0) - : paramètre de position( 2 R)

(22)

Sa fonction de répartition F (t) est la probabilité que le dispositif soit en panne à l’instant t.

Elle est exprimée par :

F (t) = 1 R(t) = 1 e (t )

Son taux instantané de défaillance (t) est un estimateur de …abilité. Il s’exprime par :

(t) = t

1

Sa densité de probabilité f (t) se calcule par l’expression suivante :

f (t) = R(t) (t) = t

1

e (t )

1.4.3 Le modèle Gamma

Le modèle Gamma est une autre généralisation naturelle du modèle ex-ponentiel : supposons que la durée Tr soit la durée d’attente de la réalisation

d’un service dans une …le d’attente et que la …le d’attente soit composée de r serveurs indépendants et identiques qui traitent chacun une partie du service (ils sont donc montés en série). On fait l’hypothèse que la durée de réalisation du traitement de chacun des serveurs est une loi exponentielle de paramètre > 0:

Alors la durée globale de service est la somme de r variables exponentielles de même paramètre ; on en déduit que la durée de service est distribuée selon une loi Gamma de paramètre (r; ) ;

Sr(t) = +1 Z t r ur 1 (r 1)!e u_du

On a l’expression suivante pour la fonction de hasard : h(t) = tr 1_e t

R+1

t xr 1e xdx : L’espérance et la variance d’une loi Gamma sont données par : E(T ) = r et V (T ) = r2

On déduit de ces expressions que le coe¢ cient de variation d’une distri-bution gamma est : cv = _{E(T )}(T ) = p1

(23)

On peut ainsi obtenir très simplement une estimation grossière du pa-ramètre de forme en calculant l’inverse du carré du coe¢ cient de variation. On peut également véri…er que la fonction de hasard hr; est croissante si

r > 1 et décroissante si r < 1 ; de plus lim_t!+1hr; (t) = ;ce qui signi…e

qu’asymptotiquement on retrouve le modèle exponentiel.

1.4.4 Distribution Log-Normale

La durée de vie T a une distribution log-normale si Y = log(T ) a une distribution normale.

Ainsi, si Y est une variable aléatoire gaussienne d’espérance Y et de

variance 2 Y et donc de densité (y) = 1 Y p 2 exp " 1 2 y _Y Y 2# ; _{1 < y < 1} alors T est une variable aléatoire de densité :

f (t) = 1 t _Yp2 exp " 1 2 log(t) _Y Y 2# ; t > 0:

où est le paramètre d’échelle et est le paramètre de forme. Contrai-rement à la loi normale, les paramètres ne donnent pas la moyenne et la variance de la loi.

La fonction de survie d’une variable suivant une loi log-normale est donnée par

S(t) = 1 log(t) Y

Y

Où (:) est la fonction de répartition d’une loi gaussienne centrée-réduite,

(x) = x Z 1 1 p 2 e _v2 dv

Le taux de panne est de la forme :

h(t) = 1 Y p 2 exp 1 2 y _Y Y 2 1 log(t) Y Y

(24)

Pour évaluer S(t) et donc aussi h(t) il est nécessaire d’évaluer numérique-ment.

Avec la distribution log-normale, la fonction de risque h(t) est croissante puis décroissante avec h(0) = 0 et lim

t!1h(t) = 0:

Comme la fonction de risque décroît pour de grandes valeurs de t, la distribution ne paraît pas plausible comme modèle de survie dans la plus part des situations. Malgré cela, ce modèle peut être intéressant lorsque de très grandes valeurs de t ne sont pas d’un intérêt particulier.

(25)

Chapitre 2

Les méthodes d’estimation

Soit (X1; X2; :::Xn)un n-échantillon d’une variable aléatoire X de loi P :

Les techniques de statistique descriptive, comme l’histogramme ou le graphe de probabilité, permettent de faire des hypothèses sur la nature de la loi de probabilité Xi. Des techniques statistiques plus sophistiquées, les tests

d’adéquation, permettent de valider ou pas ces hypothèses.

On supposera ici que ces techniques ont permis d’adopter une famille de loi de probabilité bien précise pour la loi des Xi.

On notera le paramètre inconnu, le problème traité est celui de l’estimation du paramètre . Comme on l’a déjà dit, il s’agit de donner, au vu des obser-vations x1; :::; xn, une approximation ou une évaluation de que l’on espère

la plus proche possible de la vraie valeur inconnue.

Il existe de nombreuse méthodes pour estimer un paramètre .

Par exemple, les estimations graphiques à partir des graphes de probabilité. Dans cette section, nous ne nous intéressons qu’aux trois méthodes d’estima-tion les plus usuelles, la méthodes des moments et la méthode de maximum de vraisemblance, estimation bayésienne.

Mais il faut d’abord dé…nir précisément ce que sont une estimation et surtout un estimateur.

2.1 Dé…nition et propriétés d’un estimateur

Dé…nition 2.1.1 Un estimateur d’une grandeur est une statistique Tn

fonction des variables Xi à valeurs dans l’ensemble des valeurs possibles de

(26)

2.1. DÉFINITION ET PROPRIÉTÉS D’UN ESTIMATEUR

Dé…nition 2.1.2

On appellera biais d’un estimateur Tn , la quantité :

bn(Tn) = E (Tn) : (2.1)

Dé…nition 2.1.3

On appellera erreur quadratique moyenne de Tn; la quantité :

EQM (Tn) = V ar(Tn) + b2n(Tn) (2.2)

EQM (Tn)= variance de l’estimateur + carré de son biais.

Dé…nition 2.1.4 On dira d’un estimateur qu’il est e¢ cace, si :

V ar(Tn) = 1 In(Tn) (2.3) Où In(Tn) = E @ 2_l

@ 2 : l( ) (appelée fonction log-vraisemblance)

Un estimateur Tnde sera un bon estimateur s’il est su¢ samment proche,

en un certain sens de . Il faut donc dé…nir une mesure de l’écart entre et Tn. On appelle cette mesure le risque de l’estimateur. On a intérêt à ce que

le risque de l’estimateur soit le plus petit possible.

Par exemple, les risques Tn , jTn j, (Tn )2 expriment bien l’écart entre

Tn et . Mais comme il est plus facile d’utiliser des quantités déterministes

que les quantités aléatoires, on s’intéresse en priorité aux espérances des quantités précédentes. En particulier :

Si Tn est un estimateur sans biais, EQM (Tn) = var(Tn). On a donc

in-térêt à ce qu’un estimateur soit sans biais et de faible variance. Par ailleurs, on en déduit immédiatement que de deux estimateurs, le meilleur est celui qui a la plus petite variance.

Il existe plusieurs méthodes de constructions ; nous allons dé…nir quelques unes, que nous utiliserons dans le cadre d’un modèle de Lindley généralisé.

(27)

CHAPITRE 2. LES MÉTHODES D’ESTIMATION

2.2 La méthode des moments

C’est la méthode la plus naturelle, que nous avons déjà utilisée sans la formaliser. L’idée de base est d’estimer une espérance mathématique par une moyenne empirique, une variance par une variance empirique, etc...

Si le paramètre à estimer est l’espérance de la loi de Xi, alors on peut l’estimer

par la moyenne empirique de l’échantillon. Autrement dit, si = E(X), alors l’estimateur de par la méthode des moments (EM M ) est :

b_n = 1 n n X i=1 xi: (2.4)

Plus généralement, pour ₂ , si E( ) = '( ), où ' est une fonction inversible, alors l’estimateur de par la méthode des moments est :

b_n= ' 1(Xn): (2.5)

De la même manière, on estime la variance de la loi des Xi par la variance

empirique de l’échantillon S2 n= 1 n Pn i=1X 2 i X 2

n:Plus généralement, si la loi

de deux paramètres 1 et 2 tels que (E(X); var(X)) = '( 1; 2), où ' est

une fonction inversible alors les estimateurs de 1 et 2 par la méthode des

moments sont :

(b1n; b2n) = ' 1(Xn; Sn2): (2.6)

Ce principe peut naturellement se généraliser aux moment de tous ordres, centrés ou non centrés : E((X E(X))k) et E(Xk); k 1.

2.3 Approche du Maximum de Vraisemblance

Les méthodes d’estimation du maximum de vraisemblance sont des es-timations ponctuelles puisqu’elles cherchent a trouver une valeur estimée ^ pour un paramétre à partir d’un ensemble d’échantillons donnés.

Elles sont attractives pour plusieurs raisons. D’abord, elles possédent de bonnes propriétes de convergence et d’é¢ cacite quand le nombre d’échan-tillons est trés grand. Les estimateurs du (M V ) ont asymptotiquement la variance la plus faible parmi tous les estimateurs sans biais. De plus, l’es-timation par maximum de vraisemblance est plus simple que les méthodes

(28)

2.3. APPROCHE DU MAXIMUM DE VRAISEMBLANCE

alternatives, telles que les méthodes bayésiennes. En e¤et, du point de vue complexité, les méthodes de maximum de vraisemblance ne nécessitent que des techniques de calculs di¤erentiels ou une recherche de gradient, tandis que les méthodes bayésiennes peuvent nécessiter des intégrations multidi-mensionnelles complexes.

Une caractéristique majeure indésirable de l’estimation par maximum de vraisemblance, est que ses propriétes avec des petits éhantillons peuvent être trés di¤érentes de ses propriétes asymptotiques.

Soit X une variable aléatoire de densité de probabilité f (x j ).

Soit x = fx1; x2; :::::xng un n-échantillon de X . Selon le plan d’expérience

dans lequel on se place, on note par L(x j ), la fonction de vraisemblance. La méthode du maximum de vraisemblance consiste a trouver les valeurs ^ de qui maximisent la vraisemblance L(x j ), en la considérant comme une fonction de :

^ = arg max

2

L(x_{j )} étant l’espace des paramètres. (2.7) Grace a la monotonie de la fonction Logarithme, ^ peut être trouvé en maxi-misant le logarithme de la fonction de vraisemblance l( ) (appelée fonction log-vraisemblance). Cela posséde l’avantage en calcul de remplacer un pro-duit par une somme.

dans le cas d’un plan complet

l( ) = log(L(x_{j ) =}

n

X

i=1

log(f (xij ) (2.8)

dans le cas de données censurées de typeII

l( ) = n! (n k)! " _k X i=1 log f (xi) + (n k) log(1 F (xm) # (2.9)

On peut écrire la solution sous la forme : ^M V = arg max 2

l( )

Si le paramétre est de dimension égal a p, alors le vecteur de p compo-santes de est : = ( 1; :::; p)t, et 5 est l’opérateur gradient.

5 = 2 6 6 4 @ @ 1 : : @ @ p 3 7 7 5 D’aprés l’équation (2:8) on a :

(29)

CHAPITRE 2. LES MÉTHODES D’ESTIMATION 5 l = n X i=1 5 log(f(xij )) (2.10)

La solution ^ doit satisfaire la condition : 5 l = 0

Il est noter qu’une solution ^ trouvée peut ne pas représenter un vrai maximum global. Elle peut représenter un maximum ou un minimum local ou encore un point d’in‡exion de la fonction l( ) . Une véri…cation de chaque solution trouvée est nécessaire pour s’assurer qu’il s’agit d’un vrai maximum, ou un calcul des dérivées secondes peut con…rmer la nature de l’optimum trouvé.

L’estimation de maximum de vraisemblance a l’avantage de simplicité et rapidité de son calcul si l’équation (2:10) est simple a résoudre comme par exemple dans le cas des familles exponentielles. Le principe du maximum de vraisemblance fournit une approche d’estimation bien connue dans le cas de distributions normales et plusieurs autres problémes. Toutefois, dans le cas de problémes complexes, un estimateur de maximum de vraisemblance peut devenir inapproprié ou peut méme ne pas exister. En e¤et, dans le cas ou l’équation (2:10) ne peut pas être analytiquement résolue, il faut avoir recours à des méthodes itératives comme la méthode de Newton Raphson, la méthode des scores ou encore l’algorithme Expectation-Maximization pour essayer de trouver un maximum de la fonction de vraisemblance, ce qui n’est pas toujours faisable.

2.4 L’estimation Bayésienne

L’analyse Bayésienne des problèmes statistiques propose d’introduire dans la démarche d’inférence, l’information dont dispose a priori le praticien. Dans le cadre de la statistique paramétrique, ceci se traduira par le choix d’une loi sur le paramètre d’intérêt. Dans l’approche classique, le modèle paramétrique est (X ; A; P ; 2 ).

Ayant un a priori sur le paramètre, modélisé par une densité de probabi-lité que nous noterons ( ), loi a priori sur ; on "réactualise" cet a priori au vu de l’observation en calculant la densité a posteriori ( _{jx), et c’est à} partir de cette loi que l’on mène l’inférence.

On peut alors, par exemple, de manière intuitive pour le moment retenir l’espérance mathématique ou encore le mode de cette densité a posteriori

(30)

2.4. L’ESTIMATION BAYÉSIENNE

comme l’estimateur de .

Le paramètre devient donc en quelque sorte une variable aléatoire, à la-quelle on associe une loi de probabilité dite loi a priori.

On sent bien d’emblée que les estimateurs bayésiens sont très dépendants du choix de la loi a priori.

Di¤érentes méthodes existent pour déterminer ces lois a priori. On peut se référer à des techniques bayésiennes empiriques, où l’on construit la loi a priori sur la base d’une expérience passée, usant de méthodes fréquentistes, pour obtenir formes et valeurs des paramètres pour cette loi. Nous verrons que l’on peut aussi modéliser l’absence d’information sur le paramètre au moyen des lois dites non informative (Voir Christian Robert).

2.4.1 Coût et décision

Le problème très général auquel on s’intéresse ici est celui d’un individu plongé dans un environnement donné (nature) et qui, sur la base d’observa-tions, est conduit à mener des actions et à prendre des décisions qui auront un coût.

Les espaces intervenant dans l’écriture d’un modèle de décision sont : X : l’espace des observations.

: l’espace des états de la nature (l’espace des paramètres dans le cas d’un problème statistique)

A : l’espace des actions ou décisions, dont les évènements sont des images de l’observation par une application appelée règle de décision (une statistique (i.e fonction des observations) dans le cas d’un problème statistique )

D : l’ensemble des règles de décisions , applications de X dans A (les esti-mateurs possibles). On note a une action. On a a = (x).

L’inférence consiste à choisir une règle de décision _{2 D concernant} ₂ sur la base d’une observation x 2 X , x et étant liés par la loi f (xj ).

2.4.2 La loi a posteriori.

C’est la loi conditionnelle de sachant x. Sa densité est notée ( jx). En vertu de la formule de Bayes, on a :

(31)

( _{jx) =} _Z f (xj ) ( ) f (x_{j ) ( ) d}

(2.11)

La loi du couple ( ; X) : Sa densité est

h( ; x) = f (x_{j ) ( )} (2.12) .

La loi marginale de X. Sa densité est :

m( ; x) = Z

f (x_{j ) ( ) d} (2.13)

L’estimateur bayésien de noté ^Bsous une fonction de perte quadratique

n’est autre que l’espérance de par rapport à la densité a posteriori. Formellement, on a : ^ B = E [ =x] = Z ( _{jx) d =} R f (x_{j ) ( ) d} Z f (x_{j ) ( ) d} (2.14)

Le calcul de cette intégrale de l’équation (2:14) peut être un probléme di¤cile a résoudre. Dans le cas ou ce calcul n’est pas faisable, on peut ap-procher l’intégrale par un seul point. L’estimation du maximum a posteriori (MAP) peut rendre le calcul plus facile en faisant l’hypothèse que ( _jx) présente un pic.^B = arg max 2 ( jx)

2.4.3 Le risque de Bayes

La recherche d’estimateurs de Bayes peut se faire dans le cadre de la théo-rie de la décision. La démarche consiste alors a …xer une régle de préférence entre estimateurs et a chercher un estimateur optimal au sens de cette règle de préférence. Rappelons qu’en statistique classique la régle de préférence repose (le plus souvent) sur le risque quadratique, notée R( ), est dé…nit comme suit :

(32)

2.4. L’ESTIMATION BAYÉSIENNE R(^B) = V ar(^B) + h biais(^B) i2 (2.15)

L’approche Bayésienne fait reposer la règle de préférence sur le risque de Bayes. La densité a priori ( ) etant …xée, le risque de Bayes de ^B est notée

r(^B). Il est dé…ni comme suit :

r(^B) = E[R(^)] =

Z

R(^B) ( =x) d (2.16)

On dira que ^1 est meilleur que ^2 au sens du risque de Bayes,

si r(^1) < r( ^2).

Remarque 2.4.1 : selon la fonction de perte choisie, l’estimateur de Bayes de est obtenu en minimisant le risque a posteriori.

On dé…nira çi-dessous, les di¤érentes fonctions de perte avec les risques a posteriori correspondants pour un paramètre :

2.4.4 Fonctions de perte

a-Fonction de perte quadratique

Proposée par Legendre (1805) et Gauss (1810), cette perte est sans au-cun doute le critère d’évaluation le plus commun : L( ; d) = ( d)2: Dans son article de 1810, Gauss a déjà reconnu le caractère aléatoire de la perte quadratique et le défendait pour des raisons de simplicité. De telles critiques restent valides aujourd’hui. Mais cette perte n’en demeure pas moins utili-sée car elle donne en général des solutions bayésiennes acceptables, i.e. celle fournies par une inférence non-décisionelle fondée sur la densité a posteriori.

Proposition 2.4.1 L’estimateur de Bayes associé à la distribution a priori et avec la perte quadratique, est donné par l’ésperance a posteriori

= E [ =x] = R

f (x= ) ( )d R

(33)

b-Fonction de perte erreur absolue

Une solution alternative à la perte quadratique est l’utilisation de la perte erreur absolue : L( ; d) = j d_j

considérée par Laplace (1773), ou plus généralement une fonction multi-linéaire :

Lk1;k2( ; d) =

k2( d) si > d

k1(d ) sin on

(2.18)

c- Fonction de perte Linex

Une fonction de perte asymétrique très pratique est la fonction de perte Linex ( Linear Exponential). Elle a été introduite par Varian (1975). Cette fonction croît presque exponentiellement d’un coté de zéro et est approxima-tivement linéaire de l’autre côté. Sous l’hépothèse que la perte minimale est obtenue pour ~ = ; la fonction de perte Linex pour soit ; s’exprime par

L( )_{/ e} 1; _{6= 0} (2.19) où = (~ ) et ~ est un estimateur de : Le signe et la norme de représentent respectivement la direction et le degré de symétrie ( > 0 : la sur-estimation est plus grave que la sous-estimation et vice-versa). Pour proche de zéro, la perte Linex est approximativement la fonction de perte quadratique devient :

E (L(~ ))_{/ e} ~E e (~ E ( )) 1 (2.20) où E (:) représente l’espérance a posteriori relative à la densité a poste-riori de : L’estimateur de Bayes ~L de ~ sous la fonction de perte Linex est

la valeur de ~ qui minimise (2:20). Pour trouver l’etimateur, nous dérivons l’équation (2:20) par rapport à ~ et nous obtenons :

d

d~ E L ~ = e

~

E e

En égalant cette expression à 0, nous obtenons

e ~E (e u) = d_{0ou e} ~ = E e En appliquant le logarithme, nous trouvons :

(34)

~ = ln(E e

Alors, l’estimateur de Bayes ~Lde sous la fonction de perte Linex est :

~

L =

1

ln(E e (2.21)

d- Fonction de perte Entropie

Cette fonction de perte découle de la fonction de perte Linex, et a été utilisée par Calabria et Pulcini (1994) ; elle est dé…nie par :

L( ; d) = d

p

p ln d 1_{) ^}E = E( p)

1

p _(2.22)

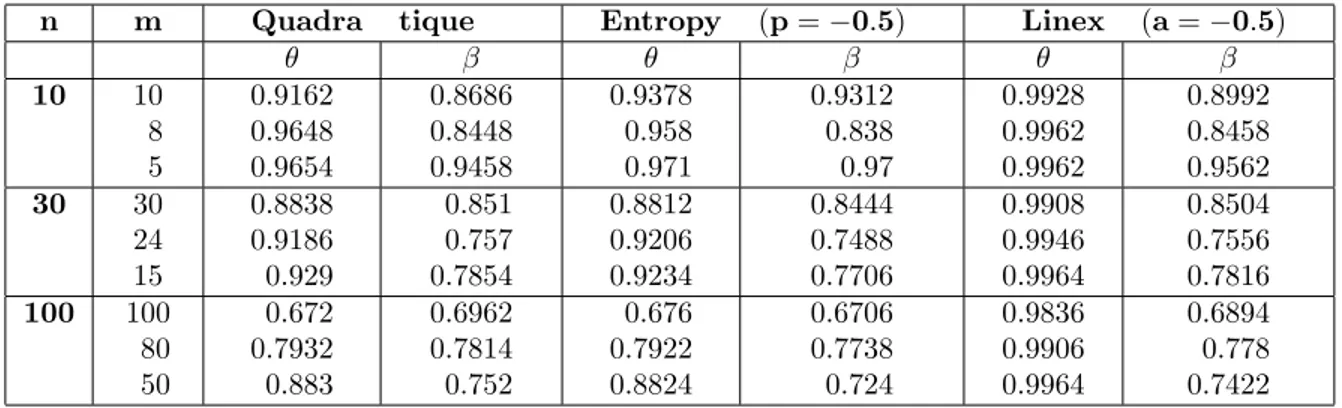
On résumera dans le tableau cidessous, les di¤érentes fonctions de perte utilisées, et pour chacune d’elles on donnera l’estimateur Bayesien (d) et le risque a posteriori correspondant pour un paramètre :

F P fonction de perte Estimateur Bayesien Risque a posteriori Quadratique ( d)2 d^Q = E ( ) E (( d^Q)2) Entropie d p p: ln d 1 d^E = [E ( ) p] 1 p _p h E (ln( ) ln d^E ) i Linex ea(d ) _{a (d} ₎ ₁ _d_^ L= _a1ln(E (e a )) a( ^dQ d^L)

Tab. 2.1 –Les di¤érentes fonctions de perte

2.4.5 Propriétés de l’estimateur de Bayes

- L’estimateur de Bayes est admissible. - L’estimateur de Bayes est biaisé.

- Sous certaines hypothèses de régularité le plus souvent satisfaites en pratique, on a les deux propriétés :

L’estimateur de Bayes est convergent en probabilité (quand la taille de l’ échantillon n ! +1).

La loi a posteriori peut être asymptotiquement (c.a.d. pour de grandes valeurs de n) approximée par une loi normale _{N(E[ jx] ; V ar[ jx]]):}

(35)

2.4.6 Modélisation de l’information a priori

Le choix des lois a priori est une étape fondamentale dans l’analyse bayé-sienne. Ce choix peut avoir di¤érentes motivations. Les stratégies sont di-verses. Elle peuvent se baser sur des expériences du passé ou sur un intui-tion, une idée que le particien a du phénomène aléatoire qu’il est en train de suivre. Elles peuvent être également motivées par des aspects calculabilité . En…n, ces stratégies peuvent également tenir compte du fait qu’on ne sait rien sur le truchement des lois non informatives

1- Lois a priori conjuguées naturelles

Une des di¢ cultés de l’approche bayésienne est le calcul de la loi a poste-riori. Ce calcul est facilité lorsque loi a priori et loi a posteriori ont la même forme. Dans ce cas, on parle de loi a priori conjuguée naturelle.

Remarque 2.4.2 :

Il est plus intéressant d’un point de vue calculatoire, d’utiliser des familles de densités a priori conjuguées naturelles telles que celles-ci aient la même forme fonctionnelle que la fonction de vraisemblance. Dans ce cas, le passage de la fonction de vraisemblance à la densité a posteriori se réduit à un chan-gement de paramètre et non à une modi…cation de la forme fonctionnelle de la famille correspondante .

Exemples de lois conjuguées naturelles

f (x_{j )} ( ) (x_{j )} E(x_{j )} N ( ; 2₎ _{N ( ;} 2₎ _N x 2 + 2; 1 2 + 1 2 1 _x 2 + 2 G(n; ) G( ; ) G( + n; + x) +n +x B(n; ) ea( ) _{a (} ₎ ₁ _{B( + n;} _{+ x)} +n +n+ +x

Tab. 2.2 –Exemples de lois conjuguees

Une loi conjuguée naturelle peut être déterminée en considérant la forme de la vraisemblance L(xj ) et en prenant une loi a priori de la même forme que cette dernière vue comme une fonction du paramètre. Les lois a priori conjuguées obtenues par ce procédé sont dites naturelles.

(36)

2- Lois a priori non informatives

Une loi non informative est une loi qui porte une information sur le pa-ramètre à estimer dont le poids dans l’inférence est réduit. Certains auteurs la dé…nissent également comme une loi a priori qui ne contient aucune infor-mation sur ou encore comme une loi qui ne donne pas davantage de poids à telle ou telle valeur du paramètre. Par exemple, supposons un ensemble …ni de taille q, une loi a priori non informative pourra être une loi de la forme : P ( i) = 1_q; i = 1; :::q

On a équiprobabilité, les valeurs possibles de se voientt attribuer le même poids.

La règle de Je¤reys :

Une méthode proposée par Je¤reys (1961) permet de fabriquer des lois a priori non informative. Cette méthode utilise l’information de Fischer : In( ). L’argument pourrait être le suivant. In( ) représente une mesure de

la quantité d’information sur contenue dans l’observation. Plus In( ) est

grande, plus l’observation apporte de l’information. Il semble alors naturel de favoriser (au sens rendre plus probable suivant ( )), les valeurs de pour lesquels In( ) est grande ; ce qui minimise l’in‡uence de la loi a priori au

pro…t de l’observation. Le choix de ce type de loi conduit ainsi souvent à des estimateurs classiques du type maximum de vraisemblance. La règle de Je¤reys consiste donc à considérer des lois a priori de la forme :

( ) = CpIn( ) ou In( ) = E

@2

@ 2 ln f (xj ) (2.23)

2.4.7 Intérêt de la démarche Bayésienne

Les principales di¤érences de l’approche bayésienne comparées à l’ap-proche classique ou fréquentielle qui font son intérêt et les raisons de son utilisation sont les suivantes :

La vision subjective des probabilités, à la base de l’approche Bayésienne, est plus cohérente que les théories fréquentistes qui interprètent la probabilité comme une portion limitée déterminée sur la base d’une séquence in…nie d’expériences.

L’interprétation bayésienne de la probabilité est associée à une notion de pari rationnel : la probabilité attribuée à un événement est dé…nie par les

(37)

conditions aux quelles un individu rationnel est prêt à parier sur la réalisation de tel événement. La rationalité de l’individu, est nécessaire pour éviter que la dé…nition de la probabilité soit arbitraire et est décrite par certaines règles de comportement, face à l’incertitude .

La formule de Bayes est l’instrument qui permet de combiner les infor-mations (ou la vision) subjective du modélisateur et l’évidence des résultats expérimentaux. Vu que dans la pratique, on est souvent confronté à des don-nées peu représentatives ou incohérentes mais en revanche on dispose de l’avis technique des experts qui, sur la base de leur expérience et savoir-faire, sont capables de donner des informations complémentaires de grande utilité, qu’il serait dommage de ne pas prendre en compte.

L’analyse bayésienne fournit des résultats d’interprétation plus directe que ceux de la démarche fréquentielle. Pour les bayésiens, l’estimateur de la probabilité a posteriori est un intervalle dit de crédibilité avec un taux de con…ance (1 ): On l’appelle intervalle de crédibilité car ses limites sont …xes et contiennent le paramètre avec une probabilité donnée. Par exemple l’intervalle de crédibilité a posteriori à 95% est typiquement celui délimité in-férieurement par le percentile d’ordre 2.5% et supérieurement par le percentile d’ordre 97.5%. Dans l’inférence classique, l’intervalle de con…ance fréquentiel a des bornes aléatoires.

Dans l’inférence classique cette assertion n’est plus vraie parce que le paramètre (inconnu) du modèle n’est pas une variable aléatoire mais une grandeur constante. L’interprétation correcte de l’intervalle de con…ance est que, si on imagine l’ensemble des échantillons aléatoires pouvant être obtenus à partir du modèle, paramétré par , 95% des intervalles de con…ance calculés (sur la base des di¤érents échantillons) contiennent la vraie valeur du para-mètre. L’interprétation bayésienne, décidément plus naturelle, est d’ailleurs celle de la plupart des praticiens qui font de l’inférence bayésienne sans le savoir .

Les résultats de l’inférence bayésienne sont plus riches que les estima-teurs fournis par les techniques classiques d’inférences . Les techniques bayé-siennes permettent d’obtenir la loi jointe des paramètres du modèle et donc de prendre en compte simultanément l’e¤et de l’incertitude globale sur l’en-semble des paramètres inconnus sur les prévisions futures du comportement du système étudié et sur les décisions suggérées par ce comportement.

(38)

2.4.8 Di¢ culté de la démarche Bayésienne

La démarche bayésienne a été formalisée et relancée au 20eme siècle dans les années 1930. Les di¢ cultés algorithmiques sont maintenant résolues grâce au développement du calcul intégral puis de logiciels dédiés et à l’emploi des ordinateurs. Mais les di¢ cultés majeures liées à la démarche bayésienne restent :

Le choix d’une distribution de probabilité a priori appropriée à l’état des connaissances initiales, est une démarche complexe, qui peut laisser place à une appréciation subjective dont il est di¢ cile de spéci…er une loi a priori précise pour les modéliser. Malgré latitude dans le choix de la loi a priori, on souhaite lui associer les propriétés suivantes :

Le calcul de la densité jointe a posteriori à partir du produit des distri-butions a priori et celle de l’échantillon d’observation doit être aussi simple que possible ;

La distribution a posteriori doit être de préférence du même type que la distribution a priori a…n de permettre un calcul d’actualisation itératif ;

La distribution a priori doit pouvoir représenter un grand nombre de situations ou de phénomènes physiques ;

Elle doit être paramétrable, et les paramètres doivent pouvoir être in-terprétés physiquement.

- L’informativité des connaissances a priori a un impact sur la densité a posteriori (résultat). La probabilité a posteriori est une moyenne pondérée entre l’information fournie a priori et les observations du retour d’expérience (la fonction de vraisemblance) : intuitivement elle sera attirée par la distribu-tion qui apportera le plus d’informadistribu-tions, donc celle qui sera la plus précise par rapport à sa valeur moyenne.

Ainsi, en fonction du type de distribution choisie pour modéliser l’infor-mation a priori qui peut être plus ou moins informative vis-à-vis des observa-tions, donc plus ou moins d’impact sur la densité de probabilité a postériori.

2.4.9 Les méthodes de Monte Carlo par chaînes de

Markov

Considérons un modèle paramétrique : on désigne par x le vecteur des paramètres de ce modèle et par y le vecteur des observations. Alors que les paramètres sont considérés comme …xes dans les méthodes statistiques fré-quentistes, ces derniers sont traités comme des quantités aléatoires dans les

(39)

approches bayésiennes (Parent et Bernier, 2007). Nous nous intéressons donc à la distribution de ces paramètres. L’estimation bayésienne consiste, tout d’abord, à traduire la connaissance que l’on a du phénomène étudié, et donc des paramètres x qui lui sont associés, par une loi de distribution sur les paramètres appelée loi a priori et notée (x). On se donne ensuite un mo-dèle statistique paramétré représentant le mécanisme aléatoire de génération des données y connaissant les paramètres x et la vraisemblance qui lui est associée f (yjx). L’information a priori (x) est alors actualisée au vu de l’in-formation contenue dans les observations, c’est-à-dire que l’on détermine la distribution des paramètres x connaissant les données y. Cette loi est appe-lée loi a posteriori sur les paramètres. Elle est obtenue en utilisant la version continue du théorème de Bayes :

(x_{jy) =} R f (yjx) (x)

f (y_{jx) (x)dx} (2.24) où désigne l’ensemble de dé…nition des paramètres. L’inférence statis-tique bayésienne consiste à déterminer les caractérisstatis-tiques (moyenne,médiane, mode, etc) de la distribution a posteriori des paramètres x. La moyenne a posteriori est choisie ici comme estimateur des paramètres x. Notons que la médiane ou le mode a posteriori auraient également peut être choisis comme estimateur. La moyenne a posteriori est l’espérance de x sous la loi a poste-riori (xjy) :

^

x = E [x_{jy ] =} Z

x (x_jy)dx (2.25) Pour les modèles les plus simples, la loi a priori (x) est conjuguée (Ro-bert, 1992), c’est-à dire que la loi a priori et la loi a posteriori appartiennent à la même famille paramétrique de lois. La moyenne a posteriori peut alors être calculée analytiquement. Pour les modèles plus complexes, notamment pour les modèles en grande dimension, la loi a priori a généralement une structure quelconque et les propriétés induites par les lois conjuguées ne peuvent pas être exploitées (Parent et Bernier, 2007). Des méthodes numériques comme les méthodes de Monte Carlo et les méthodes de Monte Carlo par chaînes de Markov (M CM C) sont alors utilisées pour approcher la moyenne a poste-riori.

Il existe di¤érentes méthodes M CM C. Une d’entre elle est présentée ci-dessous : l’algorithme de Metropolis Hastings:

(40)

- L’algorithme de Metropolis-Hastinsg

L’algorithme de Metropolis-Hastings est un algorithme MCMC. Cet algorithme développé par Hastings(1970) est une généralisation de l’algo-rithme de M etropolis(M etropolis et al:; 1953). L’algol’algo-rithme de Metropolis-Hastings peut être considéré comme une extension des algorithmes de si-mulation standard comme les méthodes d’acceptation-rejet qui sont toutes basées sur l’utilisation d’une loi de proposition. La loi de proposition de l’algo-rithme de Metropolis-Hastings a la particularité d’être markovienne (Marin et Robert, 2007). On la note q(x; y). L’algorithme de Metropolis-Hastings permettant de simuler des réalisations de la loi cible .

Algorithme de Metropolis-Hastings

Entrées : x(0) _{(valeur initiale de la chaîne de Markov), T (nombre}

d’ité-rations)

Sorties : x(1)_; _{.. . ,x}(T )

pour t allant de 1 à T faire

Connaissant x(t 1)_{, générer un candidat ~}_x _q(x(t 1)_{; x).}

r(x(t 1_{); ~}_x) ( minn (x(t(~x)=q(x1)_)=q(~(t_x;x1)(t;x)1)₎; 1 o GénérerU U[0;1] si U r(x(t 1)_{; ~}_x)_alors x(t) ( ~x sinon x(t) _{( x}(t 1) …ni …n pour retourner x(1); :::; x(T )

Pour mettre en oeuvre l’algorithme de Metropolis-Hastings, nous n’avons besoin de connaître la loi cible et la loi de proposition q qu’à une constante de proportionnalité près, puisque les deux constantes se compensent dans le calcul du ratio de Metropolis-Hastings r (dé…ni dans l’algotithme ). La convergence de l’algorithme de Metropolis-Hastings est théoriquement ga-rantie pour un large choix de lois de proposition q, à condition cependant que le support de la fonction q contienne le support de la loi cible . En pratique, le choix de la loi de proposition q in‡uence fortement la vitesse de convergence. En e¤et, si la loi de proposition q ne permet que de petits déplacements dans l’espace des paramètres, le taux d’acceptation est élevé et

(41)

la chaîne reste dans le voisinage de la valeur initiale. Au contraire, si la loi de proposition q autorise de grands sauts dans l’espace des paramètres, le taux d’acceptation est faible et la chaîne bouge di¢ cilement. La loi de proposition qchoisie doit permettre de bien explorer le support de la loi cible . Gelman et al. (1996) ont montré que la vitesse de convergence de l’algorithme de Metropolis-Hastings est optimale si la loi de proposition q choisie conduit à un taux d’acceptation compris entre 25% et 40%.

2.5 Les Critéres de Comparaisons

Plusieurs critères de proximité pour comparer des estimateurs entre eux, le plus utilisé est la comparaison à partir de leurs variances, ce pendant le calcul des variances théoriques est souvent sinon impossible. Nous propo-sons de comparer les meilleurs estimateurs bayésiens avec l’estimateur du maximum de vraisemblance. Pour cela, nous proposons d’utiliser les critères suivants : la proximité Pitman (Pitman, 1937, Fuller, 1982 et Jozani, 2012) et l’erreur quadratique intégrée (IMSE) dé…nie comme suit :

De…nition 1 : Un estimateur ^1 de paramétre domine dans le sens du

critère de proximité Pitman un autre estimateur ^2; si pour toute 2

P h ^1 < ^2

i

> 0:5 (2.26)

De…nition 2: L’erreur quadratique moyenne intégrée est dé…nie comme :

IM SE = PN

i=1 ^i 2

(42)

Chapitre 3

Modéles de Lindley et de

Lindley généralisé

Dans la théorie de la …abilité, on s’intéresse à la durée de vie d’un sys-tème ou d’un élément. On considère des systhèmes réparables justables à une distribution de durée de survie de Lindley généralisée, dont la distribu-tion de Lindley est un cas particuler. On traite le problème de l’estimadistribu-tion paramétrique des paramètres et de quelques caractéristique de …abilité.

Notez que la distribution de Lindley est un mélange des distributions exp( ) et Gamma (2; ) avec les proportions de mélange sont respectivement p = ₁₊ et (1 p) = ₁₊1 .

Cette distribution fournit un meilleur ajustement à l’ensemble empirique des données considérées que les distributions binomiale et Hermite négatifs. Récemment, une bonne partie de l’attention a été accordée à cette fonction de densité de probabilité (pdf) dans la littérature statistique. Par exemple, Ghitany et al. (2008) et Ghitany et Al-Mutairi (2009) ont étudié certaines propriétés de la distribution de Poisson-Lindley discrète proposée par San-karan (1970). Ce travail a été prolongé par Mahmoudi et Zakerzadeh (2010). Shanker et. Al. ont introduit une distribution Lindley à deux paramètres. Za-kerzadeh et al. ont proposé une nouvelle distribution de durée de vie à deux paramètres : modèle et propriétés. Ghitany et al. ont travaillé sur l’estimation de la …abilité d’un système de contraintes de la distribution de puissance de Lindley. Elbatal et al. ont proposé une nouvelle distribution généralisée de Lindley.