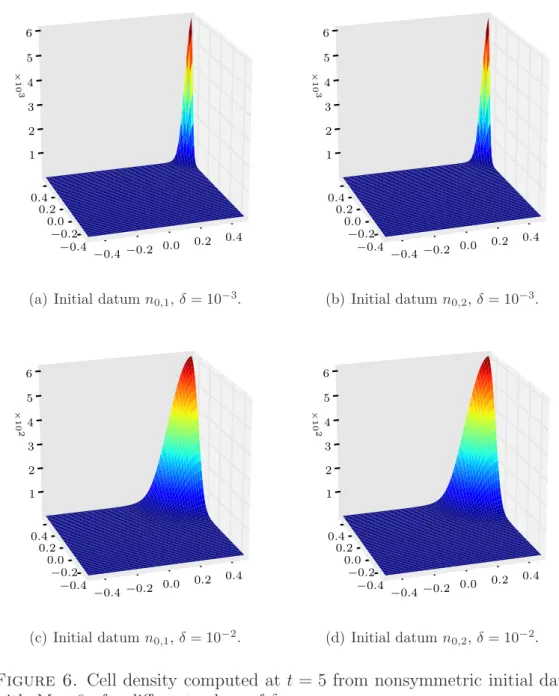
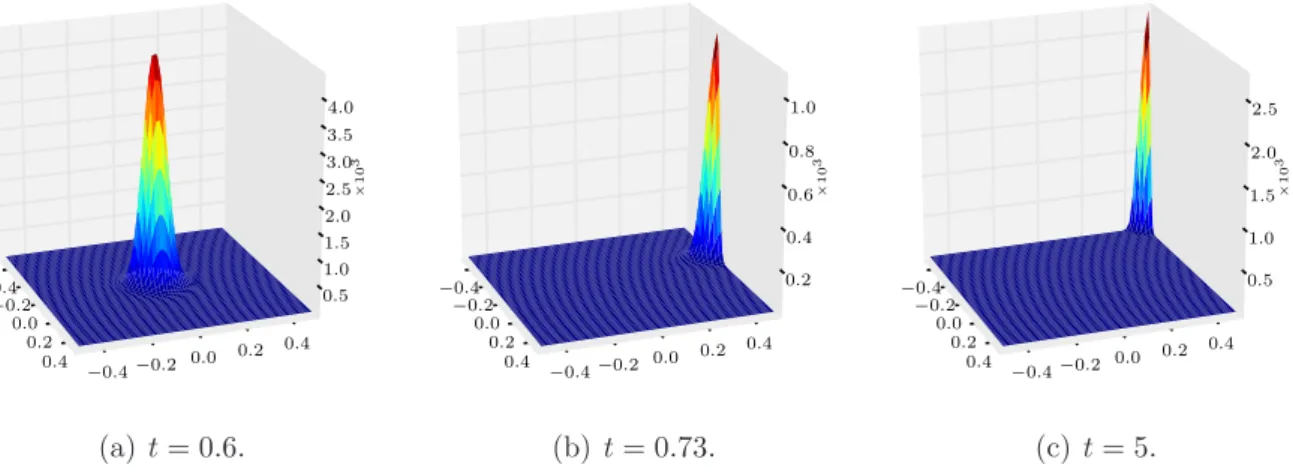
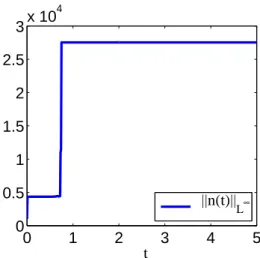
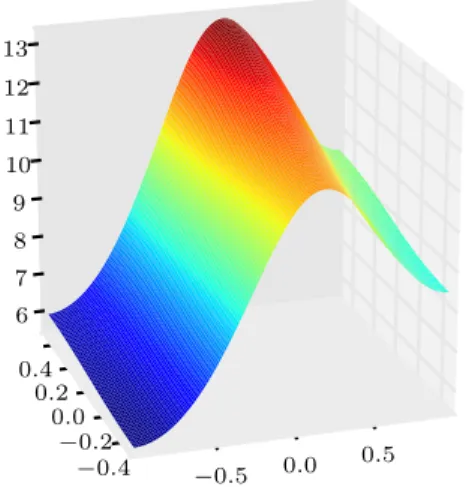
A finite volume scheme for a Keller-Segel model with additional cross-diffusion
Texte intégral
Figure

![Figure 2. Relative entropy E[n k | n ∗ ] versus time t k in semi-logarithmic scale for various values of δ and µ.](https://thumb-eu.123doks.com/thumbv2/123doknet/11481004.292376/21.892.131.754.294.560/figure-relative-entropy-versus-logarithmic-scale-various-values.webp)
![Figure 3. Relative entropy E[n k | n ∗ ] versus time t k in semi-logarithmic scale for various mesh and time step sizes.](https://thumb-eu.123doks.com/thumbv2/123doknet/11481004.292376/22.892.133.751.146.417/figure-relative-entropy-versus-logarithmic-scale-various-sizes.webp)
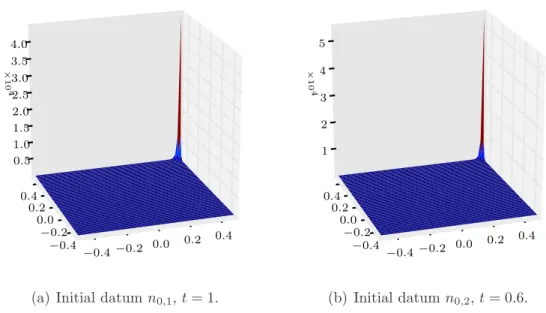
Documents relatifs
Wellknown discretization methods are finite differences, finite volumes and finite elements. The mathemat- ical study of convergence is quite wellknown in the case of
This relaxation scheme is straightforwardly obtained as an extension of the relaxation scheme designed in [16] for the isentropic Baer-Nunziato model and consequently inherits its
After proving well-posedness, stability, exponential return to equilibrium and convergence, we gave several test cases that confirm the satisfying long time behavior of the
The numerical results indicate that H is also a Lyapunov functional for system (1)-(4), even if the assumptions of [15] are not satisfied, and that scheme (16)-(20) preserves
We here propose a new semantics that is based on the logic of here-and-there: we add epistemic modal operators to its language and define epistemic here-and-there models.. We
Given a microarchitectural timing model and a program, the task of microarchitectural analysis is to determine bounds on the execution times of program fragments.. The main
Interestingly, because we also observed in the AS lines high glycolate and aspartate contents in the exudates associated with impaired sugar transport, one hypothesis is that
The proof of this convergence result is divided into Section 4 (basic a priori estimates and existence of a solution to the scheme), Section 5 (compactness for discrete solutions)