HAL Id: hal-01881281
https://hal.archives-ouvertes.fr/hal-01881281
Submitted on 26 Feb 2019
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of
sci-entific research documents, whether they are
pub-lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diffusion de documents
scientifiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
Gas microflows in the slip flow regime: A critical review
on convective heat transfer
Stéphane Colin
To cite this version:
Stéphane Colin. Gas microflows in the slip flow regime: A critical review on convective heat
trans-fer. Journal of Heat Transfer, American Society of Mechanical Engineers, 2012, 134 (2), pp.020908.
�10.1115/1.4005063�. �hal-01881281�
GAS MICROFLOWS IN THE SLIP FLOW REGIME: A CRITICAL REVIEW ON CONVECTIVE HEAT
TRANSFER
Stéphane Colin
Université de Toulouse; INSA, UPS, Mines Albi, ISAE; ICA (Institut Clément Ader) 135 avenue de Rangueil, F-31077 Toulouse, France
stephane.colin@insa-toulouse.fr
KEY WORDS
Slip flow, convection, heat transfer, microchannel, microtube, rarefied flow, Nusselt number, viscous dissipation, constant heat flux, constant wall temperature, Brinkman number, Peclet number
ABSTRACT
Accurate modeling of gas microvection is crucial for a lot of MEMS applications (micro-heat exchangers, pressure gauges, fluidic microactuators for active control of aerodynamic flows, mass flow and temperature micro-sensors, micropumps and microsystems for mixing or separation for local gas analysis, mass spectrometers, vacuum and dosing valves…). Gas flows in microsystems are often in the slip flow regime, characterized by a moderate rarefaction with a Knudsen number of the order of 102 - 101. In this regime,
velocity slip and temperature jump at the walls play a major role in heat transfer.
This paper presents a state of the art review on convective heat transfer in microchannels, focusing on rarefaction effects in the slip flow regime. Analytical and numerical models are compared for various microchannel geometries and heat transfer conditions (constant heat flux or constant wall temperature). The validity of simplifying assumptions is detailed and the role played by the kind of velocity slip and temperature jump boundary conditions is shown. The influence of specific effects, such as viscous dissipation, axial conduction and variable fluid properties is also discussed.
1. INTRODUCTION
Due to the trend of miniaturization of electromechanical systems, there is an increasing need for micro heat exchangers. The applications concern for example the cooling of electronic components, MEMS or MOEMS. More generally, heat transfer is involved in most of microfluidic systems, and especially in those that use gases. In addition to compressibility, rarefaction of the flow at small scale has a significant impact on heat transfer.
Shrinking down the dimensions of fluidic microsystems submitted to internal gas flows leads to an increase of the Knudsen number
h
Kn D
(1)
defined as the ratio of the mean free path
of the molecules over a characteristic length, for example the hydraulic diameter D of a h microchannel. The Knudsen number encountered in classic microsystems is frequently between 10 and 10, which is the typical range of the well-known slip flow regime [1]. In this moderate rarefied regime, velocity slip and temperature jump at the wall strongly influences heat transfer. In the past ten years, a number of theoretical and numerical studies have been aimed at modeling gas convective heat transfer in microchannels, taking into account rarefaction effects.Reviews on this topic are dating, do not focus on gases and do not take into account the last research contributions. Sobhan and Garimella [2] presented in 2001 a compilation and analysis of the results from investigations on fluid flow and heat transfer in micro- and mini-channels, with special emphasis to experimental studies. The case of both liquids and gases was treated, but without analysis of rarefaction effects on gas microconvection. In 2001, Rostami et al. [3] published a review devoted to gaseous flows in microchannels, but the analysis was essentially focused on hydrodynamics and not on heat transfer. More recently, in 2004, Morini [4] reviewed experimental studies on single-phase convective heat transfer in microchannels. Most of the papers listed in this review concerned heat transfer with liquids; only four studies were including data on Nusselt numbers for gases in microchannels. Moreover, the dimensions were such that rarefaction effects were negligible.
The objective of this paper is to present a detailed review of investigations on slip flow heat transfer in microchannels. The analysis is focused on the Nusselt number Nu defined with the hydraulic diameter D as a reference length, and its dependence vis-à-vis h
rarefaction (Knudsen number Kn), viscous dissipation (Brinkman number Br or Br) and axial conduction (Peclet number Pe)
NOMENCLATURE
a fraction of the surface covered by adsorbed atoms, Langmuir’s model b half-width of rectangular section or minimal half-width of trapezoidal section
Br Brinkman number, dimensionless
Br modified Brinkman number, dimensionless
p
c specific heat capacity at constant pressure, J kg1 K1
h
D hydraulic diameter, m
h half-depth of parallel plate channel or of rectangular section; depth of trapezoidal section
k thermal conductivity, W m1 K1
Kn Knudsen number, dimensionless
n normal coordinate, m
Nu Nusselt number, dimensionless
p pressure, Pa
Pe Peclet number, dimensionless
Re Reynolds number, dimensionless
Pr Prandtl number, dimensionless
0
r radius of circular section, m
R specific gas constant, J kg1 K1
s spanwise tangential coordinate, m
t streamwise tangential coordinate, m
T temperature, K
u streamwise velocity, m s1
v velocity component normal to the wall, m s1
Greek symbols
aspect ratio of trapezoidal section, dimensionless angle of trapezoidal section, rad ratio of specific heats, dimensionless mean free path, m
µ dynamic viscosity, Pa s density, kg m3
T
thermal accommodation coefficient, dimensionless
u
tangential momentum accommodation coefficient, dimensionless *
coefficient of slip, dimensionless *
temperature jump distance, dimensionless
Subscripts w at the wall
fully developed conditions Acronyms
AE analytical model - explicit formulation
AI analytical model - implicit formulation
C circular microtube CHF constant heat flux CWT constant wall temperature E experimental study
HFDF hydrodynamically fully developed flow N numerical simulation
PP parallel plate microchannel TFDF thermally fully developed flow TDF thermally developing flow TR trapezoidal microchannel UHW unsymmetrically heated walls
1IW one insulated wall 2IW two insulated walls
2. SCOPE OF THE REVIEW
In this review, we consider pressure driven flows of gases with heat transfer in straight microchannels with constant cross-section (see Fig. 1). Heat transfer in circular microchannels is analyzed in section 4, the case of parallel-plate microchannels is discussed in section 5, rectangular and trapezoidal or triangular sections are considered in sections 6 and 7 respectively, whereas other sections are treated in section 8.
The flow is laminar and the regime is the slip flow regime. Investigations on thermally fully developed and thermally developing flows (TFDF and TDF), with constant heat flux (CHF) or constant wall temperature (CWT) are reviewed. The different slip flow and temperature jump boundary conditions are presented in section 3.
3. SLIP FLOW AND TEMPERATURE JUMP BOUNDARY CONDITIONS
From a theoretical point of view, the slip flow regime is particularly interesting because it generally leads to analytical or semi-analytical models. In this regime, continuum Navier-Stokes equations are still valid, provided they are associated with velocity-slip and temperature-jump boundary conditions. Different forms of these boundary conditions can be found in the literature; the most frequently used and relevant for this review are listed below.
Velocity slip boundary conditions
First-order slip boundary conditions have been first written by Maxwell, and can be found on different simplified forms in the literature. The simplest one does not take into account thermal creep and assumes a totally diffuse reflection at the wall:
w u u u n . (2)
Although the tangential momentum accommodation coefficient u is generally found to be close to unity [5], lower values can be considered using the boundary condition
2 u w u u u u n (3)
2 3 4 u w u u R T u u n p t . (4)
In case of wall curvature, the previous equation should be extended as
2 3 4 u w u u v R T u u n t p t . (5)
since the first term of the RHS derives from the tangential shear stress at the wall which also depends on the derivative v t of the normal velocity [6, 7]. This additional derivative should also be taken into account in microchannels with significant roughness inducing two components of the velocity in the vicinity of the wall. In some papers [8-10], however, the term dv dt is written du dt , leading to 2 3 4 u w u u u R T u u n t p t . (6)
This form is not supported by any physical analysis and should be not be used, although [10] refers –erroneously– to the book of Hirschfelder et al. [11] as a reference for Eq. (6). The second term of the RHS is often neglected in theoretical analysis, as it is of
2Kn
, while the first term is of
Kn . The accuracy of the first term could be improved, adding a correcting coefficient –of the order of 1.1– calculated from the kinetic theory. Including the actual value of u, first-order slip boundary condition can be written in a more general form as:1 w u u u u n (7)
with u1 generally slightly higher than unity. Second-order boundary conditions have been proposed in the literature, in an attempt to increase the Knudsen range of applicability of the slip flow regime. In the specific case of a plane flow, they can be written on the general form [12]: 2 2 1 2 2 w u u u u u u n n (8)
with different values proposed in the literature for u2. Recent papers [13, 14] provide accurate values of u1 and u2 according to
the actual value of the accommodation coefficient u. Another kind of slip boundary condition is the one of Langmuir’s model, which takes into account adsorption/desorption of gas molecules at the wall and reads:
1
w n
where a is the fraction of the surface covered by adsorbed atoms.
In the same way, temperature jump boundary conditions are proposed in different first-order or second-order forms: 2 1 w T T T Pr n (10) 2 2 1 T w T T T T Pr n (11) 1 w T T T T n (12) 2 2 1 2 2 w T T T T T T n n (13)
1
w n TaT a T (14)Equations (10), (11), (12), (13) and (14) are generally used in parallel with eqs. (2), (3), (7), (8) and (9), respectively.
4. HEAT TRANSFER IN CIRCULAR MICROCHANNELS
Heat transfer in circular microtubes has been extensively studied, both analytically and numerically, for gas flows in the slip flow regime (see Table 1). We consider in this section a microchannel with constant circular cross section, the radius of which is r (see 0 Fig. 1b).
4.1. Fully developed flow and uniform wall heat flux
The problem of hydrodynamically and thermally fully developed flow (HFDF and TFDF, respectively) in a microtube with uniform and constant heat flux (CHF) at the wall has been analytically solved in the slip flow regime by Sparrow and Lin [15]. They used classic first-order boundary conditions (3)-(11) and obtained an exact expression for the Nusselt number, which can be written as:
1 2 C, ,CHF 2 * 11 64 * 96 * 2 48 1 4 * r r r r Nu . (15) In this equation, 0 2 * u r u r (16)0 2 2 1 * 1 T r T Pr r (17)
is the dimensionless temperature jump distance.
In the absence of rarefaction effects, both coefficients r* and r* are zero and the Nusselt number has the classic value 48 114.36. We can extend the validity of Eq. (15) to more general first-order boundary conditions such as (7) and (12), provided the definition of the coefficient of slip and the temperature jump distance are generalized as r* u1 r0 and r* T1 r0 , respectively. The Nusselt number can then be expressed as a function of the Knudsen number
0 2 Kn r (18) as:
1 2 2 1 1 1 C, ,CHF 2 1 11 128 384 48 1 8 u u T u Kn Kn Nu Kn Kn . (19)The same result has been demonstrated by Ameel et al. [16] in the case of full accommodation, with the boundary conditions (2) and (10), which correspond to
T12
1
Pr and u11. It is also possible to include thermal creep effects, replacing theboundary condition (3) with the boundary condition (4). Sparrow and Lin [15] showed that this leads to a correction of Eq. (15). Equation (15) points out that the velocity slip tends to increase the Nusselt number, while the temperature jump decreases it. In most practical cases, the later effect is predominant, and the Nusselt number is reduced, as rarefaction increases.
Li et al. [17] studied the same problem of fully developed flow with constant heat flux at the wall. They kept classic boundary conditions, i.e. no velocity slip and no temperature jump, but they assumed a wall-adjacent layer in which the viscosity and thermal conductivity differ from those in the bulk flow. The thickness of this layer is about 3 to 5 times the mean free path of the molecules and the modification of viscosity and thermal conductivity in this layer is calculated from a simplified kinetic theory assuming hard sphere molecules and full accommodation (u T 1) at the wall. This analysis leads to:
2 C, ,CHF 2 48 1 4.1075 11 1 10.4556 18.4057 Kn Nu Kn Kn . (20)In this equation, the Nusselt number does not depend on the Prandtl number, neither on the ratio
of the specific heats. Although Eq. (20) shows the same tendency as Eq. (19), it underestimates the decrease of the Nusselt number when rarefaction increases (see Fig. 2).Effects of viscous heating
Effects of viscous heating have been taken into account by Tunc and Bayazitoglu [18] in 2001 and later by Aydın and Avcı [19] and Jeong and Jeong [20], both in 2006, then by Hooman [21] in 2007. They introduced the modified Brinkman number
2 2 0 2 w h w u u Br D r , (21)
where u is the mean velocity and w the uniform heat flux at the wall transmitted to the fluid. In [18, 19, 21], boundary conditions (2)-(10)were considered, i.e. full accommodation was assumed, whereas in [20], more general boundary conditions (3)-(11) were considered. Tunc and Bayazitoglu [18] solved the problem by the integral transform technique and provided calculated data for
0.01
Br and Br 0.01. Aydın and Avcı [19] obtained an analytical solution of the Nusselt number:
C, ,CHF, 0 2 3 4 1 1 1 1 8 1 16 4 4 2 16 1 3 6 3 1 Br Nu Br Br Br Kn C C C C Pr
(22) where 1 1 8 C Kn. (23)Equation (22) generalises Eq. (19), taking into account viscous dissipation, in the case u11 and
T12
1
Pr. As forJeong and Jeong [20], they found the solution:
2 2 C, ,CHF, 0 2 2 2 2 2 2 2 2 3 2 2 48 6 4 1 48 8 2 3 1 Br C Nu C C C C C Br C C (24) with
2 1 8 2 u u C Kn (25) and
3 2 T 2 T 1 C
Kn
Pr
. (26)For a heated surface (Br 0), an increase of viscous heating leads to a decrease of the Nusselt number, whereas for a cooled surface (Br 0), the opposite is observed. The data provided by Tunc and Bayazitoglu are in rough agreement with Eqs. (22) and (24), although the effect of viscous dissipation they predicted is more pronounced for low Knudsen numbers, at least for Br 0.01 and
0.01
the equations reported in his paper, which does not allow a precise comparison with the previous studies. The plotted results for 0.01
Br , however, seems to be in close agreement with those calculated by Eqs. (22) and (24).
The same problem of fully developed slip flow heat transfer with CHF and viscous heating has been recently extended by Çetin and Bayer [32], considering second-order boundary conditions (8)-(13). The analytical solution should be tested with more appropriate values of the velocity slip and temperature jump coefficients
u1, u2, T1, T2
. Comments on the values recommended for thesecoefficients can be found in section 6.
Effects of radial fluid properties variation
Hooman and Ejlali [22] recently extended their model, taking into account, in addition to viscous dissipation, the radial variation of the viscosity µ and the thermal conductivity k with the temperature. Their study is based on a perturbation technique, assuming
1
w , (27)
1
w k kk , (28)were
and k are small parameters and
is the dimensionless temperature difference between the local temperature and the temperature in the fluid at the wall. The model is illustrated with data for k 0.2, Pr0.7, 1.4 and u T 1. TheNusselt number is increased, with a value close to 4.65 for the limit KnBr 0. It would be interesting to compare results from this model with numerical simulations performed by a CFD code.
A comparison of the fully developed Nusselt number NuC, ,CHF fct Kn( ) for CHF, calculated from the studies cited above, is shown
in Fig. 2, in the case of a gas with a Prandtl number Pr0.7 and a specific heat ratio 1.4, and for accommodation coefficients
1
u T
.
4.2. Fully developed flow and uniform wall temperature
Sparrow and Lin [15] studied the case of fully developed flow with uniform and constant wall temperature (CWT). The eingenval ue problem was numerically solved, and the derived Nusselt number is provided in Table 2 as a function of coefficients r* and r*. When r*0 and r*0, the Nusselt number tends to the classic value 3.66.
Barron et al. [24, 25] and Mikhailov and Cotta [26] studied the same problem, but they did not take into account temperature jump at the wall. As a consequence, they found that the Nusselt number increases with the Knudsen number, due to the slip of velocity (see
Fig. 3). As the temperature jump, however, plays the main role in practical cases, a decrease of Nusselt number is expected when rarefaction increases, as predicted by Sparrow and Lin.
Effects of viscous heating
The effect of viscous heating has been taken into account by Tunc and Bayatoziglu [18], Aydın and Avcı [19], Jeong and Jeong [20] and Hooman [21]. The intensity of viscous dissipation is quantified by the Brinkman number
2 0 w u Br k T T , (29)where T is the temperature of the fluid at the tube entrance and k its thermal conductivity. In the case of CHF, the fully developed 0 Nusselt number depends on the value of the modified Brinkman number. Conversely, in the CWT case, when viscous dissipation is taken into account, whatever the Brinkman number, the fully developed Nusselt number is only function of the Knudsen number [20, 21, 30]. According to the value of the Brinkmann number, however, the distance t from the entrance at which Nu reaches the fully developed value changes [30]. Moreover, when Br0, the fully developed Nusselt number can be explicitly obtained, while for
0
Br , the implicit solution requires a numerical calculation. Jeong and Jeong [20] obtained the analytical solution
C, ,CWT, 0 1 1 1 3 48 1 4 48 Br C Nu C C C . (30)
Hooman [21] found the same result in the case of full accommodation, for u T 1. For Kn0, the solution tends to 48 59.6.
Values obtained for Kn
0;0.04;0.08
are confirmed by Çetin et al. [30] (see Fig. 3). On the other hand, Tunc and Bayatoziglu [18] found a limit value of 6.42, lower than the expected one.A comparison of the values of fully developed Nusselt number NuC, ,CWT fct Kn( ) calculated from the studies cited above is shown
in Fig. 3, in the case of a gas with a Prandtl number Pr0.7 and a specific heat ratio 1.4, and for accommodation coefficients
1
u T
. The solution without viscous dissipation is given by Sparrow and Lin [15], taking into account both velocity slip and temperature jump at the wall. The solution obtained by Barron et al. [25] does not take into account the temperature jump at the wall, and consequently, erroneously predicts an increase of the Nusselt number with rarefaction, instead of a decrease, at least in the case of full accommodation at the wall. This solution is plotted, however, in Fig. 3, as it allows quantifying the conjugate and opposite effects of velocity and temperature jump. When viscous dissipation is taken into account, the data obtained by Jeong and Jeong [20], Hooman [21] and Çetin et al. [30] in the fully developed region are in close agreement. Although based on the same equations and the same definition (29) of the Brinkman number, the results calculated by the integral transform technique by Tunc and Bayatoziglu [18] are
most likely erroneous and are not reported in Fig. 3. Aydın and Avcı [19] analysed the effect of the viscous dissipation for the same problem using another definition of the Brinkman number: the temperature difference
T0Tw
in Eq. (29) was replaced with
TwTc
, where Tc is the temperature on the centerline of the tube. For this reason, they found that the Nusselt number depends bothon the Knudsen and on the Brinkman numbers, as in the case of CHF (see section 4.1).
Effects of radial fluid properties variation
As in the CHF case, Hooman et al. [23] took into account the radial variation of viscosity and thermal conductivity with the temperature, according to Eqs. (27) and (28). They obtained an explicit expression of the Nusselt number. For k 0.2, Pr0.7,
1.4
and u T 1, they observed that the effect of properties variation on the Nusselt number is negligible.
4.3. Developing flow: the extended Graetz problem
The problem of developing flow has been studied by several authors. It is an extension to the slip regime of the Graetz problem, which considers a hydrodynamically fully developed flow and a thermally developing flow (TDF), the gas experiencing heat transfer at the entrance of the microtube due to a constant heat flux or a constant temperature imposed at the wall. In the Graetz problem, the flow is assumed steady and incompressible, with constant fluid properties, no swirl component of velocity and negligible dissipation effects. Moreover, an implicit assumption is that of a high Peclet number Pe, which means that the axial conduction is negligible in comparison with the axial convection. Several authors have extended the analysis of Graetz, who initially assumed Kn0, Br0
and Pe, by taking into account rarefaction (Kn0) and in some cases including viscous dissipation (Br0) and axial conduction (finite Pe) effects.
Constant heat flux
Ameel et al. [16] calculated the velocity profile and the Nusselt number in the entrance region of a microtube for a thermally developing flow with a uniform temperature T at the entrance (0 z0) and a constant heat flux at the wall for z0. They obtained
an extension of Eq. (19) for total accommodation at the wall. The thermal entrance length z , defined as the heated length required for e
the Nusselt number to approach within 5 % the fully developed value, was found to increase with the Knudsen number. On a dimensionless form, ze ze
r Re Pr0
was fitted by a polynomial as:2 3
0.0828 0.5030 3.0804 8.6806
e
z Kn Kn Kn (31)
Xiao et al. [33] extended the analysis to the case of second-order slip flow and temperature jump boundary conditions, for hydrodynamically fully developed and thermally developing flow with CHF at the wall. They focused, however, on the specific boundary conditions early proposed by Deissler (Eqs. (47) and (48)), the coefficients of which are unfortunately not quantitatively correct (see a rapid discussion about these coefficients in section 6).
Effects of viscous dissipation and of axial conduction have been taken into account by Jeong and Jeong [20] and by Çetin et al. [29]. Coupled effects of Kn, Pe and Br on Nu are discussed in [29]. Data found in the fully developed region are in close agreement with those from [19, 20]. The thermal entrance length increases as Pe decreases, due to the increased effect of axial conduction. Increasing the Brinkman number leads to a decrease of the Nusselt number, and the influence of viscous dissipation is less pronounced as rarefaction increases, which confirms what is observed in the fully developed region.
Constant wall temperature
A first analysis of the Graetz problem with constant temperature at the wall can be found in [15], although the goal of the study from Sparrow and Lin was to determine the fully-developed Nusselt number value, obtained far from the entrance region. Data on Nusselt numbers in the entrance region were provided for the specific case Pr0.7, 1.4 and u T 1. The same problem was more
recently treated by Barron et al. [24, 25], who experienced numerical instabilities issues fixed later by Mikhailov and Cotta [26]. In these papers, however, the authors did not take into account the temperature jump at the wall although they cited the boundary condition (11). As a consequence, they neglected the main contribution of rarefaction effects on the heat transfer and found an increase in the Nusselt number as the Knudsen number was increased. This is illustrated in Fig. 3, which shows the fully-developed Nusselt number corresponding to TFDF calculated in [24, 25]. This issue was later fixed by Larrodé et al. [27], who used the first-order boundary conditions (7) and (12). Their results were presented in function of T1 u1 and they were in agreement with those from Barron et al. in the limit case where 0, when the temperature jump is neglected. For a gas with a Prandtl number Pr0.7
and a heat ratio 1.4 and full accommodation at the wall, however, 1.671 and heat transfer decreases as rarefaction increases.
The effects of viscous dissipation were treated by Tunc and Bayazitoglu [18]. Although the fully developed Nusselt number does not depend on the value of the Brinkman number Br, in the thermally developing region, an increase of Br leads to an increase of Nu. The values provided in [18] should be considered with precaution, however, as the values calculated in the fully developed region differ from those calculated in [21].
A more detailed analysis can be found in [30], in which axial conduction is also considered. Taking into account axial conduction complicates the problem due to the presence of the non self-adjoint eingenvalue problem, which makes the linearly independent eingenfunctions non-orthogonal. Çetin et al. [30] solved the energy equation numerically by using a finite difference scheme. They observed that for Br0 the local Nusselt number Nu increases with decreasing Pe, as it is the case for Nu. The thermal entrance
length also increases with decreasing Pe. For Br0, corresponding to a cooling of the fluid, Nu experiences a jump due to viscous dissipation, the location of which depends on both Pe and Br. The fully developed value Nu, however, is only function of Kn.
For negative values of the Brinkman number, corresponding to a heating of the fluid, there exists a singular point where Nu goes to the infinity, because the bulk mean temperature of the fluid becomes equal to the wall temperature. Beyond this location, the fluid heats the wall.
The Graetz problem with CWT has also recently been studied by Myong et al. [28], who employed Langmuir boundary conditions (9) and (14), and compared the results with those obtained from the classic Maxwell boundary conditions (3) and (11). They found very similar trends, but a slightly more pronounced reduction of the Nusselt number due to rarefaction was observed. As an example, for a Knudsen number Kn0.02 and a monatomic gas, the reduction for the fully-developed Nusselt number was 5.7% with Maxwell boundary conditions and 8.3 % with the Langmuir model. In addition, the authors investigated the influence of the axial heat conduction. For Pe10, a significant increase of the Nusselt number is observed in the entrance region, and this effect decreases with increasing rarefaction.
Aziz and Niedbalski [34] recently analyzed convective heat transfer with CWT conditions in a hydrodynamically fully developed and thermally developing flow in a microtube. They took into account viscous dissipation and axial conduction effects and compared Deissler second order (47) with Maxwell first order (3) slip boundary conditions, but only considering first order (10) temperature jump conditions.
In a recent paper, Satapathy [31] analyzed heat transfer for a thermally developing flow in a microtube with constant wall temperature, assuming uniform fluid velocity (slug flow) and taking into account axial conduction. The temperature boundary conditions were those of Eq. (11). There was no discussion, however, on how a slug flow of gas can be observed in a microtube, which limits the practical interest of this study.
4.4. Experimental data
There are very few experimental papers dealing with heat transfer with gases in circular microtubes, especially due to the difficulty to control thermal boundary conditions and to access local temperature measurements. Choi et al. [36] published experimental heat
transfer data for a flow of nitrogen in microtubes with diameter of 9.7, 53 and 81.2 µm. The gas was heated at a temperature in the order of 60°C before entering the microtube and cooling was due to the lower temperature –approximately 20°C– of the air around the microtube. Thermocouples were mounted at 6 locations along the microtube to determine the bulk temperature distribution. In the laminar regime, a correlation was proposed for the fully developed Nusselt number depending both on the Prandtl and the Reynolds numbers. As the cooling conditions were not precisely controlled, it is difficult to draw sound conclusions on heat transfer from these experiments. Moreover, the inlet pressure was high (between 5.7 and 10 MPa) leading to negligible rarefaction effects with Knudsen numbers lower than 10.
In a more recent study, Demsis et al. [35] provided first data on heat transfer with nitrogen in the slip flow regime. They investigated a range of the Knudsen number from 1.1 10 4 to 1.5 10 2, using low pressures instead of low hydraulic diameters. The tube was a stainless steel tube with an inner diameter of 25 mm. It was heated by an outer flow of hot water. It was observed that the mean Nusselt number, based on a log mean temperature difference, decreased as Kn increased, which was expected from physical considerations. Very low values down to 6.2 10 4, however, were measured in the slip flow regime. As commented in [37], one possible explanation of this very low value could be due to an erroneous estimation of the outlet bulk temperature linked to a default of insulation between the end of the heated section and the outlet side port.
5. HEAT TRANSFER IN PARALLEL PLATE MICROCHANNELS
A number of theoretical works have been devoted to heat transfer between parallel plates in the slip flow regime (see Table 3). In this section, the Knudsen number Kn, as well as the modified Brinkman number Br, are still based on the hydraulic diameter, which is
4
h
D h for parallel plates 2h away from each other (see Fig. 1c). Consequently, Eqs. (18) and (21) still hold, provided Dh 2r0 is
replaced with Dh 4h.
5.1. Fully developed flow and uniform wall heat flux
Inman [38] calculated the analytical solution of heat transfer for a HFDF and TFDF between parallel plates with one insulated wall (1IW) and one heated wall with uniform heat flux. The boundary conditions were first-order velocity slip (3)and temperature jump (11)conditions. He obtained the temperature profile and the Nusselt number:
1 2 PP, ,CHF-1WI 2 * 26 147 * 210 * 4 140 1 3 * h h h h Nu , (32)2 2 * u 4 u h u u Kn h (33)
is the dimensionless coefficient of slip and
2 2 1 2 8 1 * 1 1 T T h T T Kn Pr h Pr (34)
is the dimensionless temperature jump distance. For a symmetrically heated microchannel, the solution is
1 2 PP, ,CHF 2 * 17 84 * 105 * 4 140 1 3 * h h h h Nu , (35)with the no-slip limit solution 140 178.24. Zhu et al. [39] extended the solution to the case of two unsymmetrically heated walls (UHW) by combining the solutions of two sub-problems similar to the above problem.
Li et al. [17] studied the same problem of fully developed flow with constant heat flux at the wall, assuming a wall-adjacent layer in which the viscosity and thermal conductivity differ from those in the bulk flow. They found for u T 1:
2 PP, ,CHF-1WI 2 70 1 6.1614 13 1 14.3764 51.1024 Kn Nu Kn Kn . (36)for the case of one insulated wall, and
2 PP, ,CHF 2 140 1 6.1614 17 1 14.3764 52.104 Kn Nu Kn Kn . (37)for a symmetrically heated microchannel. Although Eqs. (36) and (37) show the same tendency as Eqs. (32) and (35), respectively, they underestimate the decrease of the Nusselt number when rarefaction increases (see Fig. 4).
Effects of viscous heating
Effects of viscous heating have been treated by Jeong and Jeong [40], who obtained the following analytical expression of the fully developed Nusselt number:
2 4 PP, ,CHF, 0 2 2 2 2 4 4 4 4 3 4 4 420 35 14 2 420 4 42 33 6 Br C Nu C C C C C Br C C (38) with
4 1 12 2 v v C Kn (39)The same result has been found by Sadeghi and Saidi [50], who extended the analysis to the case of unsymmetrically heated walls. As for Aydın and Avcı [41], they obtained in the case u11 and
T12
1
Pr:
PP, ,CHF, 0 2 3 4 5 5 5 5 6 1 84 66 12 1 1 12 2 5 35 35 35 1 Br Nu Br Br Br Kn C C C C Pr (40) where 5 1 12 C Kn. (41)Eq. (40) gives exactly the same result as Eq. (38), but it is restricted to the specific case u11 and
T12
1
Pr. For this reason, Eq. (38) should be preferred, as it allows using more realistic boundary conditions, i.e. more realistic values of u1 and T1, simply modifying the expression of coefficients C and 3 C . 4Nusselt numbers calculated from Eqs. (32), (35), (36), (37) and (38) are plotted in Fig. 4, for a gas with Pr0.7 and 1.4, and for
accommodation coefficients u T 1. Van Rij et al. [42] extended the solution to second-order boundary conditions.
Hooman and Ejlali [22] took into account, in addition, the radial variation of the viscosity µ and the thermal conductivity k with the temperature, through Eqs. (27) and (28). They drew similar conclusions as in the case of circular microtubes.
In the previously cited studies, the Nusselt number was deduced assuming that the heat flux at the wall
w T k n (42)
is fully transmitted by conduction in the fluid. Maslen [54] early suggested, however, that in case of slip flow, the heat transfer at the wall should be modified to include the shear work done by the slipping fluid and should read
w T u k µ u n n . (43)
Following Maslen, Sparrow and Lin [15] later suggested to extend their models for slip flow heat transfer in microtubes (Eq. (15) and Table 2) taking into account this new expression of the wall heat flux, but without quantifying its consequence on the Nusselt number. Discussions about the role played by the shear work in slip flow were also conducted by Lockerby and Reese [55] and Hadjiconstantinou [56]. A clear demonstration of the origin of the additional second term in Eq. (43) can be found in [57]. This condition has not been, however, often implemented in slip flow heat transfer analysis. Miyamoto et al. [51] analyzed the effect of viscous heating in CHF heat transfer between parallel plates in the slip flow regime using Eq. (43) and obtained an expression which is different from Eq. (38) calculated by Jeong and Jeong [40]:
1 2 2 1 1 2 1 1 1 1 2 2 PP, ,CHF, 0 1 1 1 9 3 84 560 17 336 1680 8 35 1 12 1 12 140 1 12 u u u u T T Br u u u Br Kn Kn Kn Kn Nu Kn Kn Kn Kn Kn (44)Eq. (44) gives exactly the same results as Eq. (38) in the case of no rarefaction (Kn0) and in the case of no viscous dissipation (Br 0), which was expected as shear work in the Knudsen layer scales with the Brinkman number [56]. On the other hand, when rarefaction and viscous heating are both taken into account, the influence of rarefaction is stronger when shear work is taken into account (Fig. 4).
5.2. Fully developed flow and uniform wall temperature
The case of fully developed flow with uniform wall temperature was analyzed by Hadjiconstantinou and Simek [43], who took into account axial heat conduction. The boundary conditions were initially Eqs. (7)-(12), but the accommodation coefficients and correcting coefficients were absorbed in Kn, finally leading to the use of Eqs. (2)-(10). They compared the results from their analytical model with molecular simulations by the DSMC method, and found a good agreement between continuum and molecular results. They concluded that slip flow models, neglecting viscous dissipation, expansion cooling and thermal creep were able to capture heat transfer. The effect of axial heat conduction was to increase the Nusselt number.
Effects of viscous heating
In the CWT case, when viscous dissipation is taken into account, whatever the Brinkman number, the fully developed Nusselt number is only function of the Knudsen number [40]:
PP, ,CWT, 0 4 4 4 3 140 1 7 140 Br C Nu C C C , (45)
with a limit at 17.5 when Kn0. Hooman et al. [23] extended this solution, taking into account variable properties according to equations (27) and (28).
5.3. Extended Graetz problem
The extended Graetz problem was numerically studied by Kavehpour et al. [44] for both CWT and CHF conditions, using a control volume finite difference. They took into account compressibility effects and considered a thermally and hydrodynamically developing flow. They found that the Nusselt number was reduced taking into account rarefaction. Yu and Ameel [45] considered a thermally developing flow with constant wall temperature, taking into account axial conduction. According to the value of the ratio
1 1
T u
value of 0.2 separates the region of heat transfer enhancement from the region of heat transfer reduction. The value 1.67, which correspond to a diffuse reflection (u 1) and a total thermal accommodation (T 1) for air ( 1.4; Pr0.7) is a representative
value, however, for many engineering applications. In this case, heat transfer is significantly reduced when the temperature jump is taken into account. Mikhailov and Cotta [46] analytically solved the same problem.
Jeong and Jeong [40] took in addition into account viscous dissipation and streamwise conduction, for both the CHF and CWT cases. Chen [53] numerically solved the same problem in the CWT case, but found different results. For example, in the fully developed region, the limit value of the Nusselt number calculated by Jeong and Jeong (Eq. (45)) is 17.5 and Chen found 16.03. The origin of this deviation is still to be clarified.
Unsteady convection with CHF due to a sudden heat flux change or due to a sudden inlet pressure change were numerically investigated by Sun and Jaluria [47], taking into account viscous dissipation and thermal creep effects.
Roughness effects
Roughness effects in the CWT case have been taken into account by Khadem et al. [8], with slip boundary conditions that should be adapted to curved surfaces, but unfortunately as mentioned in section 3, with an inappropriate velocity derivative term leading to Eq. (6) instead of the correct Eq. (5) . The authors also considered thermal creep in their numerical simulation. The wall roughness was modeled with periodically distributed triangular elements and random shaped micro peaks. It was found that roughness resulted in a decrease of Nusselt number and had more significant effect on higher Knudsen number flows with higher relative roughness. In another paper [9], Hossainpour and Khadem investigated the role played by the roughness shape (rectangular, triangular, trapezoidal or make of random peaks) and shown that the Nusselt number is more sensitive to the roughness density than to the roughness shape. As well as in [8], however, Eq. (6) was used instead of Eq. (5) and the consequence on the results should be further investigated. Ji et al. [48] considered the same problem with second-order boundary conditions and drew qualitative similar conclusions. Croce and d’Agaro [49] analyzed the competition between rarefaction and compressibility effects for high pressure drop flows in rough microchannels. They took into account viscous dissipation and covered a wide range of the Mach number. The slip boundary condition was similar to Eq. (5) but without the thermal creep term:
2 u w u u v u u n t . (46)
It was found that compressibility was the most dominant effect at high Mach number, yielding even inversion of heat flux, while roughness had strong effects when rarefaction was significant.
5.4. Experimental data
There are very few experimental data on convective slip flow heat transfer between parallel plates. The group of Miyamoto [58] measured the surface temperature distribution of a slip chocked flow of low-density air through a millimeter-size parallel plate channel with adiabatic walls. The same authors [51] later published data on the same problem with uniformly heating walls. In both studies, the parallel-plate channel was 1 mm in depth, 50.5 mm in width and 120 mm in length. The cross-section had an aspect ratio of 0.02, and in that case, 3D effects are not totally negligible but remain limited, typically of the order of 2% [59]; for this reason, the experimental data were compared to a parallel plate model which takes into account viscous dissipation and shear work at the wall (Eq. (43)).
In the configuration with uniform heat flux at the wall [51], the relative deviation between the measured and calculated wall temperature distribution was very small, of the order of 1 or 2% for the reported data, with an increased discrepancy for increasing Knudsen number. This very good agreement between model and experiment was later confirmed by Hong and Asako [52] with a numerical analysis based on the same hypothesis. In the experiments the Knudsen number, however, was limited to values lower than 5×104 at the inlet and 5×103 at the outlet for the reported data and in this range slip flow and temperature jump effects are not very
significant.
In the configuration with adiabatic walls [58], a few data were reported for higher Knudsen numbers, up to 6×103 at the inlet and
6×102 at the outlet, well in the slip flow regime. There is very good agreement with the simulated wall temperature distribution,
taking into account shear work at the wall. On the contrary, when this shear work is not taken into account, the wall temperature can be underestimated with a deviation of a few percents. This analysis confirms that Eq. (43) should be used instead of Eq. (42) and that most of the analytical and numerical models proposed in the literature for convective heat transfer in gas microflows should be corrected to take into account the shear work at the wall.
6. HEAT TRANSFER IN RECTANGULAR MICROCHANNELS
Microchannels with rectangular cross-sections are frequently encountered in fluidic microsystems such as micro heat exchangers. There are easily manufactured, for example, by deep reactive ion etching in silicon wafers. Hydrodynamics of gases in such microchannels in the slip flow regime were analytically modeled, both with first-order [60] and second-order [59] boundary conditions. These models have been validated by experiments for simple gases or binary mixtures of gases [5, 61, 62]. The problem of heat transfer in rectangular microchannels is rather complicated because it requires 2D and 3D analysis and involves complex thermal boundary conditions, the most frequent of which are classified as [63, 64]:
i) Constant temperature at the wall (CWT);
ii) Uniform wall temperature along perimeter at a specified cross-section, with a linear evolution in the streamwise direction (H1); iii) Constant wall heat flux (H2), with eight versions involving different combinations of heated and adiabatic walls: four heated sides (4), three heated sides and one adiabatic short side (3L), three heated sides and one adiabatic long side (3S), two heated long sides and two adiabatic short sides (2L), two heated short sides and two adiabatic long sides (2S), one short and one long heated sides (2C), one heated long side (1L) and one heated short side (1S).
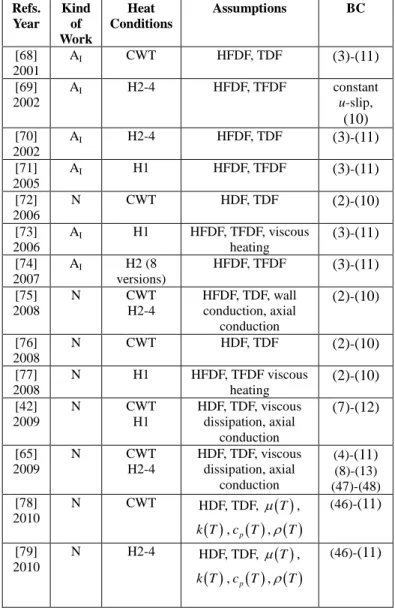
In addition, the aspect ratio h b of the cross section (see Fig. 1d) is another parameter to take into account. Table 4 gives a summary of recent investigations of heat transfer in rectangular microchannels in the slip flow regime.
Van Rij et al. [65] have analyzed the role played by various types of boundary conditions, of first order (4)-(11), of classic second order equations such as (8)-(13) and more elaborate second order equations such as the equations proposed by Deissler [66], which includes 3D effects that should be considered in rectangular sections:
2 2 2 2 2 2 2 2 9 2 16 u w u u u u u u u n n t s (47) and 2 2 2 2 2 2 2 2 2 9 177 145 2 1 256 1 T w T T T T T T T Pr n n t s (48)
It should be noted, however, that this form of second-order slip boundary conditions is not the best one. It takes into account 3D effects but the values of first and second order coefficients should be corrected, taking into account numerical data obtained from the Boltzmann equation. For example, for 2D flows, it has been demonstrated [13, 14] that the values of slip coefficients u11.11 and
2 0.24
u
should be considered for the second-order boundary condition (8) in case of diffuse reflexion for a simple gas, with a mean free path
RT 2 p. As the values of these coefficients directly depend on the definition of the mean path of the molecules, which can takes different forms, it is also possible to define the viscous and thermal slip coefficients using a unique definition of an equivalent mean free path; a discussion and accurate values of these coefficients can be found in [67]. Corrections of Deissler’s coefficients used in Eq. (47) have also been proposed in [5], showing a better agreement with both kinetic models and experimental data in isothermal slip flows through rectangular microchannels.Trapezoidal microchannels are also easily etched in silicon by chemical (for example with KOH) etching. The cross-section is defined by its depth h , its smallest width 2b , and its side angle (see Fig. 1e). The aspect ratio of the section is h
2b . Slip flow heat transfer in such channels has been investigated by Niazmand et al. [80] who considered a developing flow (HDF and TDF) with constant wall temperature. A control-volume based numerical method was employed, assuming first-order boundary conditions (2)-(10), Pr1 and 1.4. Different channel aspect ratios and side angles were investigated. Heat transfer is significantly reduced as Kn is increased in the entrance region. The following correlation was proposed for the fully developed Nusselt number: 0.26 0.21 1 2 TR , ,CWT 2.87 4.8 exp 3.9 2 2 Nu G G (49) with
0.64 1 1 1.75 1 0.72 tanh 2 G Kn
(50) and
2 1 0.075 1 exp 0.45 G Re Pr . (51)This correlation is in agreement within 10% with the numerical simulations for all considered aspect ratios (
0.25;0.5;1; 2
) andside angles ( n with n
2;3; 4;6
).Kuddusi and Çetegen [81] considered the case of a microchannel etched by KOH in a silicon wafer, for which the crystalline structure of the substrate leads to an angle 54.74. The H2-4 constant heat flux problem for thermally developing flow was numerically solved in a square computational domain obtained by transformation of the trapezoidal geometry. Numerical data on the Nusselt number were provided for different values of the aspect ratio. More recently, Kuddusi [82] analyzed the effect of viscous dissipation in fully developed flows in the same microchannel with H2-3S constant heat flux conditions. He observed that viscous dissipation effects could not be neglected when 3
5 10
Br .
Triangular microchannel is a specific case of trapezoidal microchannel, for which
. Slip flow heat transfer in isosceles triangular microchannels was investigated by Zhu et al. [83] who considered unsymmetrical heat conditions: one side insulated with two sides at constant temperature, or two sides insulated and one side at constant temperature. They finally proposed correlations for these two layouts in the case of an equilateral triangular section. Thermal creep effects have been taken into account in the numerical analysis of Shojaeian and Dibaji [10], who investigated fully developed slip flows in triangular microchannels with various aspectratios. Their slip flow boundary condition was given by Eq. (6) instead of Eq. (5) but as it was applied to a fully developed flow in a straight channel, the erroneous derivative u t, as well as the exact one v t , should be zero and should not modify the result.
8. HEAT TRANSFER IN MICROCHANNELS WITH OTHER SECTIONS
Microchannels with annular cross-sections
Slip-flow heat transfer with viscous dissipation in a micro-annulus, with uniform heat flux at one wall and adiabatic conditions at the other wall, was analytically studied by Avcı and Aydın [84]. The case of uniform heat flux with different values of the flux on the two walls has been analyzed by Sadeghi and Saidi [50], who took into account viscous dissipation.
The same geometry with constant wall temperature was numerically analyzed by Char and Tai [85], taking into account viscous dissipation.
Duan and Muzychka [86] published an explicit analytical solution for the fully developed Nusselt number in annular microchannels, considering either CHF at one wall and adiabatic conditions at the other wall, or CHF on both walls.
Microchannels with other kinds of cross-sections
A semi-analytical model of fully developed heat transfer with CHF in microchannels with semi-circular cross-section is proposed in [87].
Developments on slip flow heat transfer with CWT in microchannels with rhombus section can be found in [88], whereas considerations on the modeling of slip flow heat transfer in microchannels of arbitrary cross sections are presented in [89] and [90]. Developing slip flow CWT heat transfer in wavy or constricted microchannels is analyzed in [91] and [92], respectively. The boundary conditions (4)-(11) take into account the thermal creep and significant viscous dissipation effects are observed.
CONCLUSIONS AND RECOMMENDATIONS
The literature on slip flow heat transfer is now well stocked, with a series of available analytical solutions or numerical analysis for various heat conditions and microchannel geometries. The limits of the analytical solutions, based on simplifying assumptions, are not, however, always well documented. The influence of variations in gas properties has been analyzed in details [93], but there are few studies in the slip flow regime [78]. When viscous dissipation has to be taken into account, the effect of shear work at the wall is generally not considered, and most of the analytical solutions should be extended to include its non negligible effect. In addition, the most accurate slip flow and temperature jump conditions are often not used, particularly when 3D flow are analyzed and/or when higher-order boundary conditions are considered.
On the other hand, although the theory of gas hydrodynamics in the slip flow regime is now supported by smart experiments [5, 61, 94], there is a crucial lack of experimental data concerning heat transfer in this regime. Providing accurate experimental data on slip flow heat transfer is a challenge for the next years, which would allow a real discussion on the validity of velocity slip and temperature jump boundary conditions, as well as on the limits of applicability of slip flow theory, in terms of degree of rarefaction.
ACKNOWLEDGMENTS
The support of the European Community under grant PITN-GA-2008-215504, ‘Gas flows in Micro Electro Mechanical Systems’ is gratefully acknowledged.
REFERENCES
1. Colin, S., Rarefaction and compressibility effects on steady and transient gas flows in microchannels. Microfluidics and Nanofluidics, 2005. 1(3): p. 268-279.
2. Sobhan, C.B. and S.V. Garimella, A comparative analysis of studies on heat transfer and fluid flow in microchannels. Microscale Thermophysical Engineering, 2001. 5(4): p. 293-311.
3. Rostami, A.A., A.S. Mujumdar, and N. Saniei, Flow and heat transfer for gas flowing in microchannels: a review. Heat and Mass Transfer, 2002. 38(4-5): p. 359-367.
4. Morini, G.L., Single-phase convective heat transfer in microchannels: a review of experimental results. International Journal of Thermal Sciences, 2004. 43(7): p. 631-651.
5. Pitakarnnop, J., Varoutis, S., Valougeorgis, D., Geoffroy, S., Baldas, L., and S. Colin, A novel experimental setup for gas microflows. Microfluidics and Nanofluidics, 2010. 8(1): p. 57-72.
6. Lockerby, D.A., Reese, J. M., Emerson, D.R., and R.W. Barber, Velocity boundary condition at solid walls in rarefied gas calculations. Physical Review E, 2004. 70: p. 017303/1-4.
7. Barber, R.W., Sun, Y., Gu, X.-J., and D. R. Emerson, Isothermal slip flow over curved surfaces. Vacuum, 2004. 76: p. 73-81. 8. Khadem, M.H., M. Shams, and S. Hossainpour, Numerical simulation of roughness effects on flow and heat transfer in
9. Hossainpour, S. and M.H. Khadem, Investigation of Fluid Flow and Heat Transfer Characteristics of Gases in Microchannels with Consideration of Different Roughness Shapes at Slip Flow Regime. Nanoscale and Microscale
Thermophysical Engineering, 2010. 14(3): p. 137-151.
10. Shojaeian, M. and S.A.R. Dibaji, Three-dimensional numerical simulation of the slip flow through triangular microchannels. International Communications in Heat and Mass Transfer, 2010. 37(3): p. 324-329.
11. Hirschfelder, J.O., C.F. Curtiss, and R.B. Bird, Molecular theory of gases and liquids. 1964, New York: John Wiley and Sons, Inc.
12. Kandlikar, S.G., Garimella, S., Li, D., Colin, S., and M.R. King, Heat transfer and fluid flow in minichannels and microchannels. 2006, Oxford: Elsevier. 450.
13. Cercignani, C. and S. Lorenzani, Variational derivation of second-order slip coefficients on the basis of the Boltzmann equation for hard-sphere molecules. Physics of Fluids, 2010. 22(6): p. 062004-8.
14. Lorenzani, S., Higher order slip according to the linearized Boltzmann equation with general boundary conditions. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2011. 369(1944): p. 2228-2236.
15. Sparrow, E.M. and S.H. Lin, Laminar heat transfer in tubes under slip-flow conditions. J HEAT TRANS-T ASME, 1962. 84: p. 363-369.
16. Ameel, T.A., Wang, X., Barron, R.F., and R.O.J. Warrington, Laminar forced convection in a circular tube with constant heat flux and slip flow. Microscale Thermophysical Engineering, 1997. 1(4): p. 303-320.
17. Li, J.-M., B.-X. Wang, and X.-F. Peng, 'Wall-adjacent layer' analysis for developed-flow laminar heat transfer of gases in microchannels. International Journal of Heat and Mass Transfer, 2000. 43(5): p. 839-847.
18. Tunc, G. and Y. Bayazitoglu, Heat transfer in microtubes with viscous dissipation. International Journal of Heat and Mass Transfer, 2001. 44(13): p. 2395-2403.
19. Aydın, O. and M. Avcı, Heat and fluid flow characteristics of gases in micropipes. International Journal of Heat and Mass Transfer, 2006. 49(9-10): p. 1723-1730.
20. Jeong, H. and J. Jeong, Extended Graetz problem including axial conduction and viscous dissipation in microtube. Journal of Mechanical Science and Technology, 2006 20(1): p. 158-166.
21. Hooman, K., Entropy generation for microscale forced convection: Effects of different thermal boundary conditions, velocity slip, temperature jump, viscous dissipation, and duct geometry. International Communications in Heat and Mass Transfer,
2007. 34(8): p. 945-957.
22. Hooman, K. and A. Ejlali, Effects of viscous heating, fluid property variation, velocity slip, and temperature jump on convection through parallel plate and circular microchannels. International Communications in Heat and Mass Transfer,
2010. 37(1): p. 34-38.
23. Hooman, K., F. Hooman, and M. Famouri, Scaling effects for flow in micro-channels: Variable property, viscous heating, velocity slip, and temperature jump. International Communications in Heat and Mass Transfer, 2009. 36(2): p. 192-196.
24. Barron, R.F., Wang, X.M., Warrington, R.O., and T. Ameel, Evaluation of the eigenvalues for the Graetz problem in slip-flow. International Communications in Heat and Mass Transfer, 1996. 23(4): p. 563-574.
25. Barron, R.F., Wang, X.M., Ameel, T.A., and R.O. Warrington, The Graetz problem extended to slip-flow. International Journal of Heat and Mass Transfer, 1997. 40(8): p. 1817-1823.
26. Mikhailov, M.D. and R.M. Cotta, Eigenvalues for the Graetz problem in slip flow. International Communications in Heat and Mass Transfer, 1997. 24(3): p. 449-451.
27. Larrodé, F.E., C. Housiadas, and Y. Drossinos, Slip-flow heat transfer in circular tubes. International Journal of Heat and Mass Transfer, 2000. 43(15): p. 2669-2680.
28. Myong, R.S., D.A. Lockerby, and J.M. Reese, The effect of gaseous slip on microscale heat transfer: An extended Graetz problem. International Journal of Heat and Mass Transfer, 2006. 49(15-16): p. 2502-2513.
29. Çetin, B., A.G. Yazicioglu, and S. Kakaç, Slip-flow heat transfer in microtubes with axial conduction and viscous dissipation - An extended Graetz problem. International Journal of Thermal Sciences, 2009. 48(9): p. 1673-1678.
30. Çetin, B., A.G. Yazicioglu, and S. Kakaç, Fluid flow in microtubes with axial conduction including rarefaction and viscous dissipation. International Communications in Heat and Mass Transfer, 2008. 35(5): p. 535-544.
31. Satapathy, A.K., Slip flow heat transfer in an infinite microtube with axial conduction. International Journal of Thermal Sciences, 2010. 49(1): p. 153-160.
32. Çetin, B. and O. Bayer, Evaluation of Nusselt number for a flow in a microtube using second-order slip model. Thermal Science, 2011. 15(SI Suppl. 1): p. S103-S109.
33. Xiao, N., J. Elsnab, and T. Ameel, Microtube gas flows with second-order slip flow and temperature jump boundary conditions. International Journal of Thermal Sciences, 2009. 48(2): p. 243.