Équations aux dérivées partielles et systèmes dynamiques appliqués à des problèmes issus de la physique et de la biologie
Texte intégral
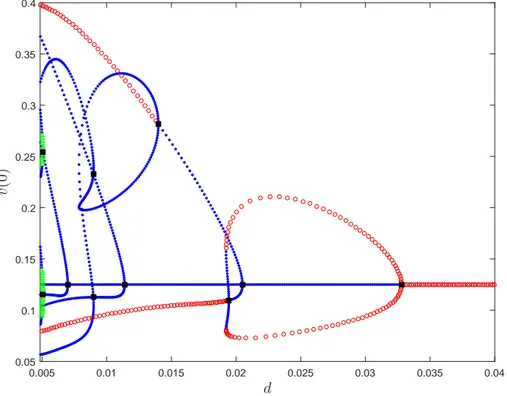
Figure



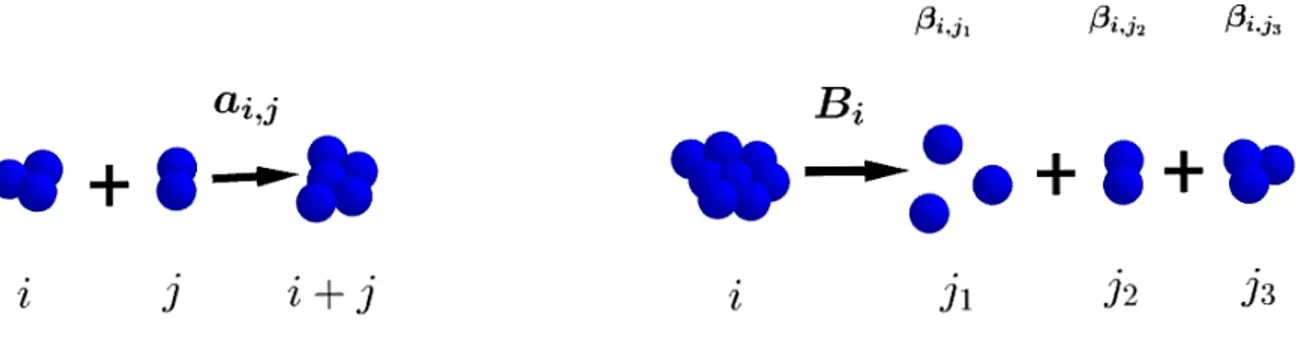
Outline
Documents relatifs
D'une équation linéaire on peut déduire deux nouvelles équations également linéaires à l'aide des transformations de Laplace qui sont les seules transformations de Bàcidund
admet une solution conlinne et une seule pour laquelle , - a des valeurs données sur le bord ; il peut v avoir seulemeni.exception pour certaines valeurs de A racines
Si l'on considère ensuite un arc de courbe MP rencontré au plus une fois par toute parallèle à l'axe des x et à l'axe desj, et q u e l'on se donne les valeurs de ^ et de- sur cet
Nous remarquerons, en outre, que dans A les intégrales communes ne peuvent avoir, comme singularités, que les lignes singulières fixes de F ou les caractéristiques de cette équation,
En nous plaçant, comme nous, l'avons toujours fait, au p o i n t de vue.. SUR LES ÉQUATIONS LINÉAIRES AUX DÉRIVÉES PARTIELLES, ETC. — Dans une région oà loules les racines
— Avec un calcul symbolique bilinéaire de type paradifférentiel, on démontre, pour une solution d'une équation aux dérivées partielles non linéaires strictement hyperbolique,
Elle est basée sur les propriétés (<î>i),. Nous la redonnons cependant intégralement, pour les raisons suivantes : le lemme 6 est le plus important point d'appui de la preuve
Ces identités conduisent directement aux solutions des équations aux dérivées partielles avec second membre sans qu'il soit nécessaire de faire appel à la méthode de variation