• Aucun résultat trouvé

The Tamed Unadjusted Langevin Algorithm

N/A
N/A
Info
Télécharger
Protected

Academic year: 2021

Partager "The Tamed Unadjusted Langevin Algorithm"

Copied!
36
0
0

Chargement.... (Voir le texte intégral maintenant)

Texte intégral

Loading

Figure

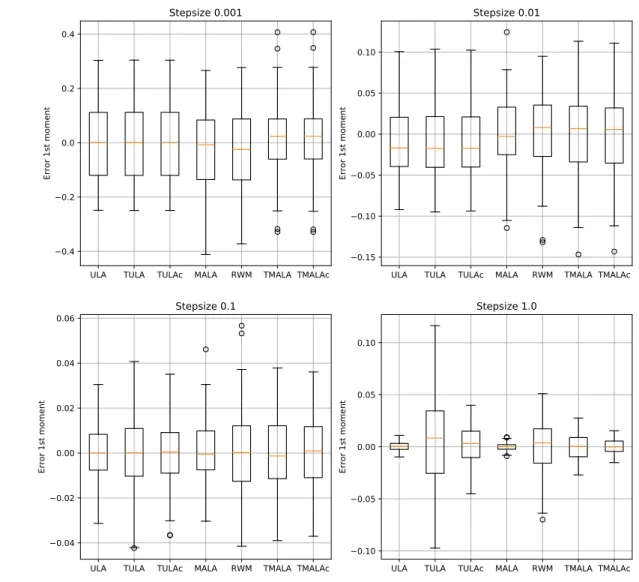
Figure 1: Boxplots of the first order error for the multivariate Gaussian (first coordinate) in dimension 1000 starting at 0 for different step sizes.
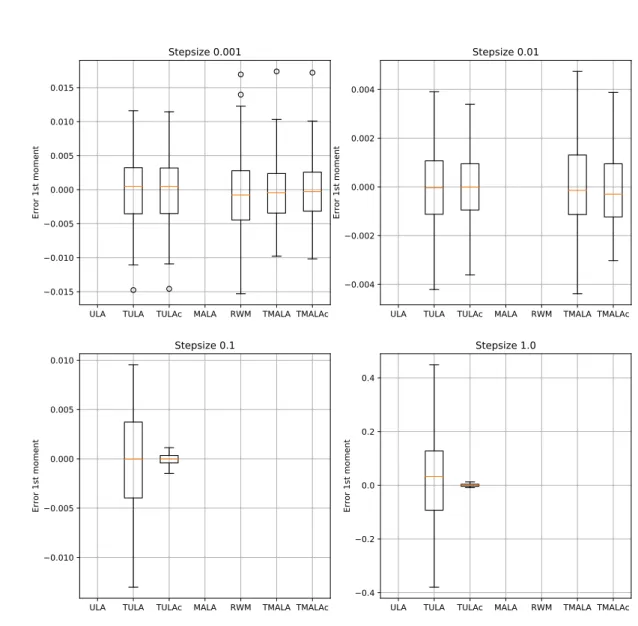
Figure 2: Boxplots of the first order error for the double well in dimension 100 starting at (100, 0 ⊗99 ) for different step sizes.
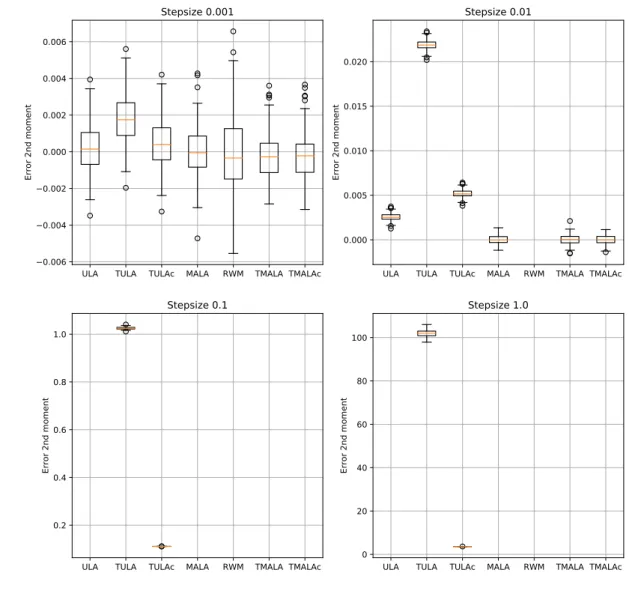
Figure 3: Boxplots of the second order error for the double well in dimension 100 starting at 0 for different step sizes.
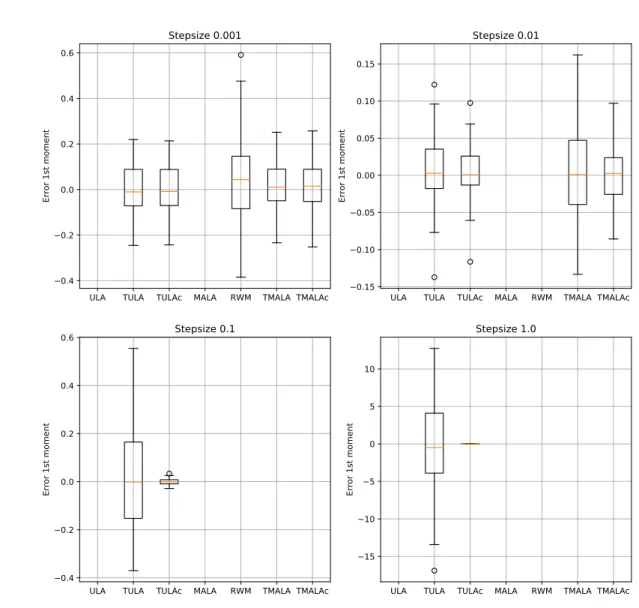
Figure 4: Boxplots of the first order error for the Ginzburg-Landau model in dimension 1000 starting at (100, 0 ⊗999 ) for different step sizes.
+2

Références

Télécharger maintenant ( PDF - 36 Page - 844.59 KB )

Documents relatifs

Classical and Quantum Part of the Environment for Quantum Langevin Equations

Among quantum Langevin equations describing the unitary time evolution of a quantum system in contact with a quantum bath, we completely characterize those equations which are

Approximation of the invariant distribution for a class of ergodic SDEs with one-sided Lipschitz continuous drift coefficient using an explicit tamed Euler scheme

We justify the efficiency of using the explicit tamed Euler scheme to approximate the invariant distribution, since the computational cost does not suffer from the at most

The promises and pitfalls of Stochastic Gradient Langevin Dynamics

This method is based on the Langevin Monte Carlo (LMC) algorithm proposed in [19, 20]. Standard versions of LMC require to compute the gradient of the log-posterior at the current

Supplement to "High-dimensional Bayesian inference via the Unadjusted Langevin Algorithm"

The dependency on the dimension and the precision is same compared to [1, Proposition 2] (up to logarithmic terms), but this result only holds if the initial distribution is a

The design of pressure-equalized rainscreen walls

L’accès à ce site Web et l’utilisation de son contenu sont assujettis aux conditions présentées dans le site LISEZ CES CONDITIONS ATTENTIVEMENT AVANT D’UTILISER CE SITE WEB.

Unajusted Langevin algorithm with multiplicative noise: Total variation and Wasserstein bounds

More precisely, the objective of this paper is to control the distance of the standard Euler scheme with decreasing step (usually called Unajusted Langevin Algorithm in the

Bacteria can form interconnected microcolonies when a self-excreted product reduces their surface motility: evidence from individual-based model simulations

However, the pattern of interconnected microcolonies cannot be obtained with these usual mechanisms: immotile bacteria form isolated microcolonies and constantly

Wasserstein Control of Mirror Langevin Monte Carlo

We establish for the first time a non-asymptotic upper-bound on the sampling error of the resulting Hessian Riemannian Langevin Monte Carlo algorithm.. This bound is measured