Evolution des corrélations quantiques et processus de décohérence en théorie quantique de l’information.

THÈSE DE DOCTORAT

Présentée par :

ESSABER Rim

Spécialité : Physique mathématique

Evolution des corrélations quantiques et processus de

décohérence en théorie quantique de l’information

Soutenue

le 16 Avril 2016

Devant le jury :

Président

:

Ahmed KASSOU-OU-ALI

Examinateurs

:

Malika

AIT BEN HADDOU

Bouzid MANAUT

Mohamed

DAOUD

El

Hassan SAIDI

Invités :

Rachid

AHL LAAMARA

Mohamed

El FALAKI

PES, Faculté des Sciences de Rabat.

PES, Faculté des Sciences de Meknès.

PH, Faculté Polydisciplinaire, Beni Mellal.

PES, Faculté des Sciences Ain Chock Casablanca.

PES, Faculté des Sciences de Rabat.

PA, CRMEF, Meknès.

PA, Faculté des Sciences d'El Jadida.

Faculté des sciences, 4 Avenue Ibn Battouta B.P. 1014 RP, Rabat-Maroc

Rabat

A ceux qui ont toujours dévoué et sacrifié pour moi : ceux qui m’ont aidé du

mieux qu’ils pouvaient pour réussir : ceux qui m’ont accompagné

tout au long de ce parcours : ce qui ont toujours été

là dans mes moments de détresse,

A mes très chers parents,

A mon mari

A mon cher frère et ma chère sœur

A mes respectueux professeurs

A mes très cher(e)s ami(e)s

A tous ma famille sans aucune exception

Et à tous ceux que ma réussite leur tient à cœur.

ESSABER Rim

Remerciements

Les travaux présentés dans cette thèse ont été réalisés au sein du Lab/UFR de Physique des Hautes Energies Modélisation et Simulation de la Faculté des Sciences de Rabat, sous les directions de Monsieur El Hassan SAIDI, Professeur de l’enseignement supérieur à la Faculté des Sciences de Rabat et Monsieur Mohamed DAOUD, Professeur de l’enseignement supérieur à la Faculté des Sciences Ain Chock Casablanca, en collaboration avec Monsieur

Rachid AHL LAAMARA, Professeur Assistant à la CRMEF à Meknés.

Je remercie tout d’abord mon directeur de thèse, Monsieur le Professeur El Hassan SAIDI, Professeur de l’enseignement supérieur à la Faculté des Sciences de Rabat de m’avoir accepté au sein de son laboratoire, ainsi d’avoir d’être parmi le jury.

Je remercie également mon encadrant Monsieur Mohamed DAOUD, Professeur de l’en-seignement supérieur à la Faculté des Sciences Ain Chock Casablanca, pour son encadrement scientifique et pour la confiance qu’il m’a accordée depuis mes premiers pas dans l’équipe du Lab/UFR de Physique des Hautes Energies Modélisation et Simulation à Rabat jusqu’à la rédac-tion de ce manuscrit. Il a su me laisser l’autonomie dont j’avais besoin, tout en étant présent dans les moments de doute. Toujours encourageant, jamais défaitiste, il a eu le don de trouver les mots qu’il fallait lorsque je m’interrogeais sur la pertinence de mon travail.

Je tiens à remercier mon co-encadrant Monsieur Rachid AHL LAAMARA, Professeur Assistant à la CRMEF à Meknés, pour m’avoir aidé durant cette thèse et le remercier sincère-ment pour sa disponibilité et pour m’avoir fait bénéficier de ses compétences. Et d’avoir partagé avec moi ces connaissances informatiques.

Je remercie vivement Monsieur Ahmed KASSOU-OU-ALI, Professeur de l’enseigne-ment supérieur à la Faculté des Sciences de Rabat, pour l’honneur qu’il m’a fait de présider

mon jury de thèse.

Je tiens également à remercier Madame Malika AIT BEN HADDOU, Professeur de l’enseignement supérieur à la Faculté des Sciences de Meknès, pour l’intérêt qu’elle a porté à mon travail, ainsi d’avoir d’être parmi le jury.

Je voudrais remercier le rapporteur de cette thèse Monsieur Bouzid MANAUT, Profes-seur Habilité à la Faculté Polydisciplinaire de Beni Mellal, pour avoir accepté de faire partie de mon jury de thèse et apporter des précisions en vue d’améliorer la qualité de ce document.

Je tiens aussi à remercier Monsieur Mohamed El FALAKI, Professeur Assistant à la Faculté des Sciences d’El Jadida, qui a bien voulu faire partie du jury et d’apporter ses vives contributions à l’enrichissement de ce travail.

Mes remerciements s’adressent également à toutes les autres personnes avec lesquelles j’ai eu le plaisir de collaborer au cours de cette thèse. En particulier, je voudrais remercier H.ELHADFI,

S.SEDDIK et W.KAYDI. Finalement, un grand Merci chaleureux et de tout mon coeur à

mes parents H.ESSABER et R.MAANINOU, sans qui je ne serais absolument pas où j’en suis aujourd’hui. Je les remercie sincèrement pour leur soutien inconditionnel et constant, pour m’avoir donné du courage et de l’espoir, pour être toujours présents même à distance. Je leur dois ce que je suis. Aussi un Merci de tout mon coeur à mon mari A.OTMANI mon cher frère Hatim et ma chère soeur Nihal et mes ami(e)s pour m’avoir donné l’occasion d’avoir mes véritables amis dans ma vie, pour leur gentillesses et leur encouragement à continuer mes études. Je vous remercie de tout mon coeur. Enfin, je remercie toutes les personnes, qui de loin ou de près ont contribué à l’aboutissement de cette étude.

Résumé

Dans le domaine de la physique de l’information quantique, les corrélations quantiques constituent un outil essentiel pour améliorer certains processus de traitement de l’information par rapport à leurs analogues classiques. Dans ce sens, la quantification, la caractérisation et l’identification des mesures adéquates de ces corrélations revêt une importance capitale. D’un autre coté, l’information codée dans un système quantique peut être facilement détruite au vue de l’intrication du système avec son environnement et qui induit la décohérence du système quantique.

Dans cette thèse intitulée "Evolution des corrélations quantiques et processus de décohé-rence en théorie quantique de l’information", nous étudions les mesures bipartites des corré-lations quantiques dans des systèmes multipartites. Ces mesures sont faites par le biais de la concurrence, l’entropie de formation, la discorde quantique et sa variante géométrique basée sur le concept de la distance de Hilbert-Schmidt. Afin de tenir compte des effets du couplage des états cohérents avec l’environnement, nous avons développé un modèle simple où les effets de décohérence sont modélisés par un diviseur de faisceau. La distribution des corrélations quan-tiques entre le système bipartite et l’environnement est étudié en détail. En effet, nous avons établit les conditions de violation de la relation de la monogamie de l’entropie de formation, la discorde quantique et la discorde géométrique. Un autre aspect de ce travail concerne la distri-bution des corrélations quantiques dans un état tripartite constituée par des systèmes préparés dans des états non-orthogonaux. Une relation de conservation entre les entropies de formation et les discordes quantiques bipartites est obtenue. De plus une étude détaillée de la relation de monogamie est présentée.

Mots clés :

Discorde quantique - Intrication quantique - Etats cohérents - Séparabilité - Systèmes quantiques ouverts Equation d’évolution Opérateurs de Krauss Canaux quanquantiques

to improve some of the information processing compared to their conventional analogues. In this sense, quantification, characterization and identification of appropriate measures of these correlations is crucial. On the other hand, the information encoded in a quantum system can be easily destroyed in view entanglement of the system with its environment and induces decoherence of the quantum system.

In this thesis entitled "Evolution of quantum correlations and process of decoherence in quantum information theory", we study the bipartite measurements of quantum correlations in multi-party systems. These measurements are made through competition, the entropy of formation, quantum discord and geometric variant based on the concept of distance Hilbert-Schmidt. To consider the effects of the coupling of coherent states with the environment, we have developed a simple model where the effects of decoherence are modeled by a beam splitter. The distribution of quantum correlations between the two-party system and the environment is studied in detail. Indeed, we have established the conditions for a breach of the relationship of monogamy entropy of formation, quantum discord and geometric discord. Another aspect of this work concerns the distribution of quantum correlations in a tripartite state consists of sys-tems prepared in states nonorthogonal. A conservation relationship between entropy training and quantum discord bipartite is obtained. More detailed study of monogamy relationship is presented.

Keywords :

Quantum discord - Quantum entanglement - Coherent states - Separability - Open quantum systems Master equation Kraus operators Quantum channels

Table des matières

Table des figures v

Introduction générale 1

1 Historique . . . 1

2 Vers une technologie quantique . . . 2

3 Structure de la thèse . . . 4

I Principes de la théorie classique et quantique de l’information 7 1 Introduction . . . 7

2 Théorie classique de l’information . . . 8

2.1 Définition de l’entropie de Shannon . . . 9

2.2 Entropie conjointe, conditionnelle et information mutuelle . . . 10

3 Théorie quantique de l’information . . . 12

3.1 Définition de l’entropie de von Neumann . . . 12

3.2 Espace de Hilbert . . . 13

3.3 Mesures quantiques et OMVP . . . 13

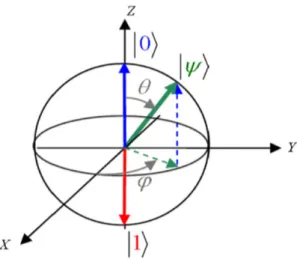
3.4 Qubit et sphère de Bloch . . . 14

3.5 Opérateur et matrice densité . . . 16

4 Conclusion . . . 17

II Les mesures des corrélations quantiques 19 1 Introduction . . . 19

3 Quantification et caractérisation de l’intrication . . . 20

4 Décomposition de Schmidt . . . 21

5 Les mesures des corrélations quantiques . . . 22

5.1 La négativité logarithmique . . . 22

5.2 La concurrence . . . 23

5.3 La discorde quantique . . . 24

5.4 La mesure géométrique de la discorde quantique . . . 28

6 Schéma unificateur pour les corrélations des états mixtes de systèmes bipartites 32 6.1 Quantificateurs des corrélations basés sur l’entropie relative . . . 32

6.2 Quantificateurs géométriques des corrélations . . . 33

6.3 Etat X à deux qubits . . . 34

6.3.1 Etat produit le plus proche d’un état X . . . . 34

6.3.2 L’état classique le plus proche et son état produit le plus proche 35 6.3.3 Quantificateurs des corrélations géométriques . . . 37

7 Conclusion . . . 38

III Modèles de décohérence et canaux quantiques 39 1 Introduction . . . 39

2 Dynamique des systèmes ouverts . . . 40

2.1 L’équation de Schrödinger (ou von Neumann) . . . 40

2.2 Equation d’évolution avec l’approximation de Born-Markov . . . 41

2.3 Equation d’évolution avec l’approximation de l’onde tournante . . . 44

2.4 Représentation de la dissipation . . . 45

3 Les opérateurs de Kraus . . . 46

3.1 Opérateurs d’évolutions des systèmes dynamiques : approche qualitative 46 3.2 Correspondance entre les opérateurs Lindblad et les opérateurs de Kraus 46 3.3 Les canaux quantiques et opérateur de Kraus . . . 48

3.3.1 Le canal de dépolarisation . . . 48

3.3.2 Le canal d’amortissement de la phase . . . 49

3.3.3 Le canal d’amortissement de l’amplitude . . . 49

4 Conclusion . . . 50

IV La monogamie des corrélations quantiques dans les systèmes multipartites 51 1 Introduction . . . 51

Table des matières

3 Mesures d’intrication bipartite . . . 56

3.1 Intrication des états purs bipartites . . . 56

3.2 Intrication des états mixtes bipartites . . . 57

4 Monogamie de l’intrication dans les systèmes à trois qubit . . . 59

4.1 La monogamie de l’intrication des états W et états GHZ . . . . 59

4.2 La monogamie de l’intrication pour des états mixtes de trois qubits et plus 62 5 Conclusion . . . 63

V La dynamique des corrélations quantiques des états chat de Bell 65 1 Introduction . . . 65

2 Etats de type Bell en termes des états de Glauber . . . 66

3 Mécanisme de perte de photon pour un état chat de Bell . . . 67

4 Intrication de formation . . . 70

4.1 Concurrence et intrication de formation . . . 71

4.2 La monogamie de la concurrence et l’intrication de formation . . . 73

5 Discorde quantique . . . 77

5.1 la discorde quantique et la relation de Koashi-Winter . . . 77

5.2 Calcul analytique de la discorde quantique . . . 77

5.3 La monogamie de la discorde quantique . . . 80

6 Mesure géométrique de la discorde quantique . . . 82

6.1 L’expression de la mesure géométrique . . . 82

6.2 La monogamie de la discorde géométrique . . . 85

7 Conclusion . . . 86

VI Corrélations quantiques globales dans des états tripartites non orthogonaux et les propriétés de la monogamie 87 1 Introduction . . . 87

2 Etats tripartites non orthogonaux . . . 89

2.1 Bipartitions purs d’un état tripartite . . . 89

2.2 Bipartitions mixtes d’un état tripartite . . . 91

3 La discorde quantique et l’intrication de formation dans des états tripartite non orthogonaux . . . 92

3.1 Mesures bipartites de l’intrication de formation et de la discorde quantique 92 3.2 La discorde quantique dans des états tripartites purs non orthogonaux . 94 4 La discorde quantique géométrique dans un état tripartite . . . 96

4.1 Mesure géométrique de la discorde quantique pour les états bipartites pures 96 4.2 Mesure géométrique de la discorde quantique pour les états bipartites

mixtes . . . 97

5 Illustration : Les états chat de Schrödinger à trois modes . . . 98

5.1 Corrélations quantiques globales et la relation de monogamie . . . 100

5.1.1 La concurrence . . . 100

5.1.2 L’intrication de formation et la discorde quantique . . . 101

5.1.3 La discorde quantique géométrique . . . 103

6 Conclusion . . . 106

Conclusion générale 107

Table des figures

I.1 Le système général de la communication de Shannon. . . 8

I.2 L’entropie H(p) en fonction de la probabilité p . . . 9

I.3 L’information mutuelle . . . 11

I.4 La sphère de Bloch . . . 15

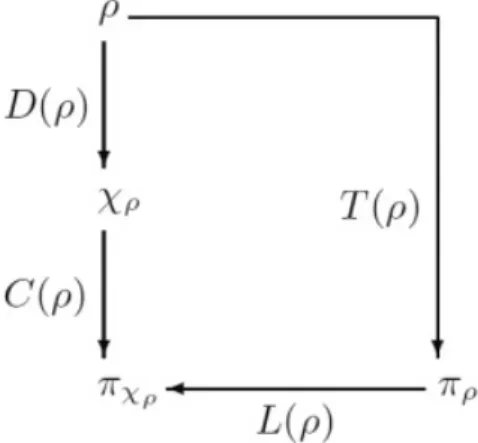
II.1 Schéma unificateur des corrélations (totale, quantique et classique). . . 33

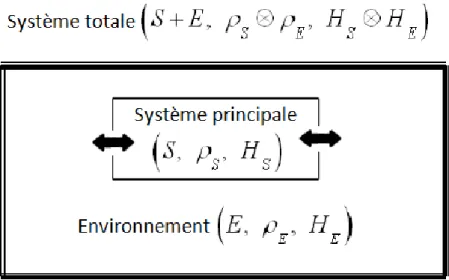
III.1 Le modèle du système combiné S + E. Le système principal(ouvert) interagit avec l’environnement. . . 42

IV.1 Etat singulet de deux qubit et la monogamie du système de 3 qubits : si les sous systèmes A et B sont dans l’état singulet, il ne peut y avoir de partage d’intrication entre A et C, ni entre B et C. . . . 54

IV.2 Caractérisation de l’intrication bipartite partagée dans les systèmes à trois qu-bits : l’inégalité Coffman, Kundu et Wootters. . . 62

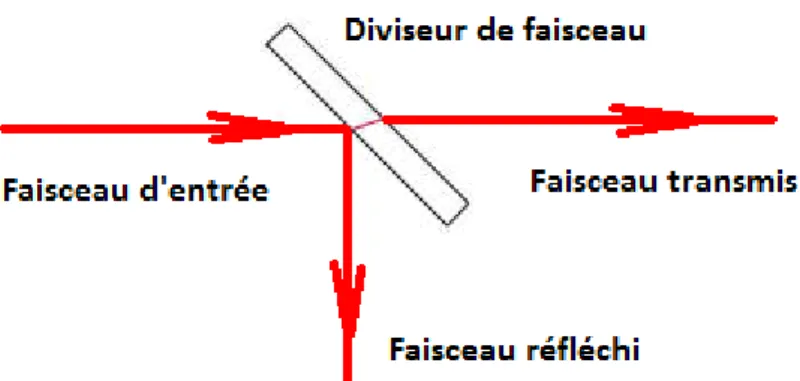
V.1 Schéma d’un diviseur de faisceau. . . 69

V.2 Variation τA,B,E en fonction du paramètre de recouvrement p et le coefficient t2 pour m = 0. . . . 74

V.3 Variation τA,B,E en fonction du paramètre de recouvrement p et le coefficient t2 pour m = 1. . . . 74

V.4 E = EA,B,E en fonction du p et t2 pour m = 0. . . . 75

V.6 E = EA,B,E en fonction du p et t2 pour m = 1. . . . 76

V.7 D = DA,B,E en fonction du paramètre de recouvrement p et le coefficient de

réflexion r2 _{pour m = 0. . . . 80}

V.8 D = DA,B,E en fonction du paramètre de recouvrement p pour t2 = 1₂ et m = 0. 81

V.9 D = DA,B,E en fonction du paramètre de recouvrement p et le coefficient de

réflexion r2 pour m = 1. . . . 81 V.10 D = DA,B,E en fonction du paramètre de recouvrement p pour t2 = 1₂ et m = 1. 82

V.11 Dg = Dg(A, B, E) en fonction du paramètre de recouvrement p pour t2 = 1₂ et

m = 0. . . . 85 VI.1 E = Ei|jk en fonction du paramétre de recouvrement p pour m = 0 et m = 1. . . 102

VI.2 Corrélations quantiques tripartites en fonction du paramétre de recouvrement p pour m = 0. . . . 104 VI.3 Corrélations quantiques tripartites en fonction du paramétre de recouvrement p

Introduction générale

"I think it is safe to say that no one understands quantum mechanics." Richard Feynman

1

Historique

La mécanique quantique est une branche de la physique élaborée par les physiciens de la première moitié du XXe _{siècle pour rendre compte des phénomènes mis en évidence par}

l’expérimentation à l’échelle des systèmes infiniment petit (atomes, électrons ou photons). Elle a radicalement changé notre compréhension du monde microscopique de la matière [1, 2]. Au niveau microscopique, les lois qui régissent les interactions physiques sont très différentes de ce qu’on observe à notre échelle. Richard Feynman [3–5] a été le premier à avoir l’intuition qu’on peut utiliser les phénomènes quantiques pour améliorer les capacités de calcul des ordinateurs dit "classiques". Deux concepts principaux sont à la base de la formulation de la mécanique quantique, celle de "observables" et celui de "l’état".

L’ensemble des états d’un système physique isolé est en correspondance avec l’espace projec-tif d’un espace de Hilbert H. En particulier, un état physique quelconque peut être représenté par un vecteur normalisé |ψi ∈ H. De plus, toute propriété physique d’un système qui peut être mesurée est une observable et toutes les observables sont représentés par des opérateurs linéaires (hermitiques) agissant sur l’espace des états H. Chaque valeur propre d’une observable correspond à une valeur physique possible de cet observable.

En 1935, le paradoxe Einstein, Podolsky et Rosen [6] a été avancé comme un argument selon lequel la mécanique quantique ne pouvait pas être une théorie complète, mais devrait être complétée, en postulant l’existence de variables dites cachées. Ces variables supplémentaires devraient reconstituer la causalité de la théorie et la localité [7]. De ce fait, Schrödinger a affirmé qu’au lieu de renoncer à la théorie de la mécanique quantique, il faut abandonner l’hypothèse de la localité [8]. Deux particules peuvent effectivement s’influencer non localement parce que leur état combiné est décrit par une seule fonction d’onde. Dans son expérience de pensée "chat de Schrödinger" (ou superpositions de deux états morts ou vivants), ces superpositions conduisent à des résultats particulièrement dérangeants lorsqu’on les transpose à l’échelle classique : un chat pourrait, par exemple, être mort et vivant en même temps [8].

Près de 30 ans plus tard, en 1964, John Bell propose ses fameuses inégalités [9], qui se sont révélées être le moyen de régler cette discussion une fois pour toute, et faire place à un immense champ de recherche nouveau. Il s’est ensuivi de nombreuses applications contre-intuitives de la non localité quantique et souvent technologiquement très prometteuses, en particulier dans le champ de l’information quantique.

2

Vers une technologie quantique

L’information quantique est un domaine de recherche assez jeune, qui utilise les principes de la physique quantique avec celles de la théorie de l’information. Sans aucun doute, il pourra conduire à des applications pour les communications quantiques et le calcul quantique en ex-ploitant des propriétés quantiques comme le principe de superposition et l’intrication.

L’intrication quantique est une ressource physique associée avec les corrélations non clas-siques qui sont possibles entre les systèmes quantiques séparés. C’est une propriété fondamentale des systèmes quantiques et aussi une ressource physique de base pour l’informatique quantique [10], la cryptographie quantique [11,12], la téléportation [13], le codage [14], et le calcul quan-tique [15]. D’autre part, il constitue également un ingrédient clé pour une variété de phénomènes observés en physique, par exemple la supraconductivité [16], transitions de phase quantiques [17, 18], ou l’effet Hall quantique fractionnaire [19]. L’intrication quantique peut être partagée entre deux ou plusieurs particules, atomes, et les photons, etc., même si elles sont éloignées et n’interagissent pas les unes avec les autres. Dans un système multi-partite, il est indispensable de se doter de mesures et critères pour distinguer les états quantiques intriqués et non intriqués. Par conséquent, la quantification et la caractérisation de l’intrication est nécessaire pour com-prendre et développer la théorie des mesures des corrélations quantiques. Plusieurs mesures de

Introduction générale

corrélations quantiques ont été proposées pour les systèmes à deux particules, et étendues en-suite au cas multi-partite [20]. L’intrication dans le cas bipartite est relativement bien comprise tandis que dans le cas multipartite l’évolution des corrélations requiert des calculs compliqués. Pour les systèmes bipartites, les problèmes liés à l’intrication ont été résolus à l’aide de la décomposition de Schmidt [21,22]. Par conséquent sa généralisation aux états multipartite peut résoudre des problèmes difficiles liés à l’intrication multipartite. Le système à trois qubits peut être intriqué de deux façons inéquivalentes : l’état Greenberger-Horne-Zeilinger (GHZ) [23] et l’état W [24].

Cependant, tous les systèmes quantiques interagissent inévitablement avec leurs environne-ments. Ces interactions provoquent la disparition rapide des états superposés. Cette disparition a été reconnue comme la décohérence. La décohérence est un phénomène quantique résultant du couplage d’un système quantique avec l’environnement. Ce sont ces interactions qui provoquent la disparition rapide du phénomène de la superposition et par conséquent des corrélations de nature purement quantique. Cependant, dans la plupart des cas, on ne s’intéresse pas à la dynamique globale du système mais à l’évolution du système quantique en tenant compte l’in-fluence de l’environnement. Depuis les débuts de la mécanique quantique, la compréhension de la transition quantique-classique restait une question ouverte. C’est dans les années 1980 que W.H.Zurek [25] y apportera un élément de réponse concret. En effet, il a proposé un méca-nisme simple permettant de comprendre pourquoi les propriétés quantiques ne se manifestent pas généralement à notre échelle : l’interaction avec un environnement. A partir d’un article de J.P.Paz et W.H Zurek [26], l’idée du modèle de la décohérence a été émise : pour chaque expérience il faut distinguer trois sous-systèmes, que sont : l’objet, l’appareil de mesure et l’en-vironnement. En raison du fait que n’importe quel système réaliste est soumis à un couplage avec un environnement incontrôlable qui influence l’évolution dans le temps du système. Par conséquent, la théorie des systèmes quantiques ouverts joue un rôle important dans tous les domaines de la mécanique quantique, où il n’est pas possible d’isoler les systèmes ou contrôler les degrés de libertés de l’environnement. Une autre raison plus fondamentale pour l’étude des systèmes quantiques ouverts, est que le processus de mesure pourrait être interprété comme une sorte de dynamique des systèmes ouverts.

La dynamique d’un système quantique ouvert est décrite en termes de l’opérateur de den-sité réduite, qui est obtenu à partir de l’opérateur de denden-sité de l’ensemble du système en effectuant une trace sur les degrés de liberté de l’environnement. Afin d’éliminer les degrés de liberté de l’environnement diverses approximations sont nécessaires et qui conduisent à une équation compacte pour décrire la dynamique de la matrice densité du système ouvert. Dans un système multipartite, l’intrication peut être transférée d’une partie à une autre à travers un

canal quantique [27]. Dans ce sens on dit que l’intrication est une ressource qui se partage entre les différentes parties. Alternativement une partie peut consommer l’intrication avec d’autres parties du système global. La distribution des corrélations quantiques au sein d’un système multipartite suit des restrictions assez sévères contrairement à la distribution des corrélations classiques. Ces restrictions ont conduit au concept de monogamie des corrélations quantiques.

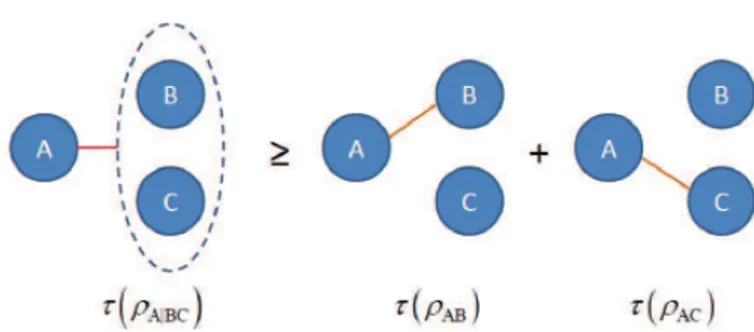
La monogamie de l’intrication a d’abord été proposée par Coffman, Kundu et Wootters [28] pour un système de trois qubits. C’est une caractéristique essentielle qui permet la sécurité dans la distribution de clés quantiques (cryptographie quantique) [29]. Dans la littérature, le concept de monogamie pour une mesure d’intrication E se traduit par l’inégalité suivante

EA/BC ≥ EA/B + EA/C, (1)

où A, B et C désignent les parties d’un système tripartite. Cette inégalité n’est pas satisfaite par la plupart des mesures des corrélations quantiques à l’exception de la concurrence [30].

3

Structure de la thèse

Ce travail de thèse porte sur l’étude de l’évolution des corrélations quantiques présentes dans quelques systèmes en contact avec l’environnement. En d’autre terme, il s’agit de com-prendre les effets induisant la décohérence dans ces systèmes quantiques. Nous envisageons de quantifier les mesures des corrélations pour quelques classes de superpositions particulières d’états cohérents. En particulier, nous dérivons les mesures de l’entropie d’intrication, la dis-corde quantique et sa variante géométrique. Ensuite, l’étude de l’évolution des corrélations quantiques dans des systèmes quantiques préparés dans des états cohérents pour mettre en relief l’effet de l’environnement. Il s’agit de modéliser l’interaction avec l’environnement pour comprendre les phénomènes de décohérence.

Le plan de ce manuscrit est développé en six chapitres organisés comme suit :

Dans le premier chapitre, nous allons rappeler les notions de base de la théorie classique de l’information. Nous allons revenir sur les fondements de cette théorie en se basant sur les travaux de Claude Shannon. Ensuite, nous nous intéressons à décrire les assises de base de la théorie quantique de l’information. La première partie sera consacrée à expliquer le concept de l’entropie de Shannon en utilisant l’exemple d’un schéma général d’un système de communica-tion quantique, qui consiste à transmettre de l’informacommunica-tion entre un émetteur vers un récepteur. Puis on définira l’entropie conjointe, conditionnelle et l’information mutuelle. Dans la deuxième partie, nous introduisons les notions essentielles à la compréhension de l’information quantique

Introduction générale

en présentant les outils mathématiques de base utilisés dans la description des états quantiques, les mesures quantiques, le formalisme de l’opérateur densité. Ensuite, on aborde l’essentiel de la théorie : l’entropie de von Neumann et ses propriétés.

Le deuxième chapitre, nous discutons l’intrication quantique pour les systèmes à va-riables continues, et comment quantifier et caractériser cette quantité. Ensuite, nous intro-duisons quelques mesures des corrélations quantiques pour les systèmes quantiques bipartites discrètes, par exemple la négativité logarithmique, la concurrence, l’intrication de formation, la discorde quantique et sa variante géométrique. Nous présenterons un schéma géométrique pour les corrélations (totale, quantique et classique) des états mixtes dans des systèmes bipartites. Nous donnons des expressions explicites pour la discorde quantique, sa variante géométrique, et un schéma unificateur pour une classe d’états bipartites, notamment, une famille appelée états X largement utilisés dans le domaine de l’information quantique.

Dans le troisième chapitre, nous donnerons brièvement un ensemble d’outils mathéma-tiques nécessaire dans l’étude de la dynamique des systèmes quanmathéma-tiques ouverts. Nous intro-duisons, dans la première section, la dynamique des systèmes ouverts ainsi que l’équation de Schrödinger (ou von Neumann). Dans la seconde section, nous dérivons l’équation d’évolution via plusieurs approximations (Born-Markov, l’onde tournante...), et nous allons discuter la re-présentation du dissipateur. Dans la troisième section, nous donnons la rere-présentation de Kraus pour différents canaux quantiques (le canal de dépolarisation, le canal d’amortissement de la phase, et le canal d’amortissement de l’amplitude) qui offre une façon alternative pour décrire les systèmes quantique ouverts.

Le quatrième chapitre, nous allons introduire le concept de monogamie. Nous discutons quelques mesures d’intrication des systèmes, purs et mixtes à deux qubits. Nous discutons également l’évolution analytique de ces mesures pour des systèmes en basses dimensions afin de disposer des outils pour discuter leurs monogamies dans des états de type W et GHZ. Nous allons nous limiter aux mesures basées sur la concurrence, l’entropie linéaire et la notion de tangle.

Dans la cinquième chapitre, nous introduirons les états chat de Bell en termes des états de Glauber. Ensuite, nous discutons leur évolution sous l’effet de l’amortissement de l’amplitude qui peut être modélisée par l’action d’un diviseur de faisceau. Nous exprimons les matrices densités réduites des différents sous-composants du système des états chat de Bell couplés à l’environnement. Nous allons aussi considérer la distribution des corrélations quantiques entre eux. Pour approcher cette question, nous utiliserons les mesures bipartites : intrication de formation, la discorde quantique et sa variante géométrique.

Le sixième chapitre est organisé comme suit. Afin de discuter les corrélations quantiques bipartites dans les états tripartites non orthogonaux, nous introduisons, dans la seconde section, deux différents schémas de bipartition. Dans la troisième section, nous donnerons les expressions analytiques de l’intrication de formation bipartite et de la discorde quantique. Nous discuterons la relation de conservation entre ces deux mesures entropiques qui implique que la mesure globale tripartite de la discorde quantique et l’intrication de formation sont identiques. Dans la quatrième section, nous dérivons la discorde quantique géométrique pour tous les sous-systèmes bipartites possibles. A titre d’illustration, nous considérerons dans la cinquième section, les états chat de Schrödinger à trois modes, basés sur les états cohérents de Glauber. En particulier, nous discutons la propriété de la monogamie de l’intrication mesurée par la concurrence, l’intrication de formation, de la discorde quantique et la discorde quantique géométrique.

Finalement, en guise de conclusion nous allons terminer cette thèse par rappeler l’essentiel des résultats de ce travail.

Chapitre I

Principes de la théorie classique et quantique de

l’information

1

Introduction

La théorie de l’information permet de répondre à deux problématiques. La première concerne les ressources nécessaires pour stocker un message constitué de symboles, tirés selon une certaine loi de probabilité. Puisque les symboles n’ont pas tous la même probabilité d’être choisis, certains sont moins probables que d’autres, et apportent ainsi plus d’information. L’entropie permet de quantifier cette notion, ainsi que les ressources nécessaires pour stocker une suite de symboles sans perte d’information à la limite asymptotique. La seconde problématique concerne les communications, qu’elles soient classiques ou quantiques.

Les outils mathématiques de la mécanique quantique et de la théorie de l’information clas-sique sont nécessaires pour aborder la théorie de l’information quantique. Ceci vient du fait que toute l’information codée sur un support quantique est décrite par l’entropie de von Neu-mann qui est un prolongement naturel de l’information classique en théorie de l’information quantique.

Ce chapitre portera sur l’étude formelle de l’information classique et quantique [31]. Dans la première partie nous décrirons les concepts de base de la théorie de l’information classique qui a été introduite par Claude Shannon en 1948 [32], comme utile pour étudier la quantité de l’information envoyée. Puis on définira l’entropie de Shannon, entropie conjointe, conditionnelle et l’information mutuelle [33]. Dans la deuxième partie, nous allons nous concentrer sur la

théorie de l’information quantique [34] en présentant les outils mathématiques de base utilisés dans la description des états quantiques, les mesures quantiques, et le formalisme de l’opérateur densité. Ensuite, on aborde l’essentiel de la théorie : l’entropie de von Neumann et ses propriétés.

2

Théorie classique de l’information

La théorie de l’information a été introduite par Claude Shannon dans les années 40 [32]. Elle s’agit d’une application de la théorie probabiliste permettant de quantifier le contenu moyen en information d’un ensemble de messages, en particulier dans le domaine des communications ou de transmissions de signaux à travers des canaux. La communication est d’abord perçue comme un transfert d’information de l’émetteur vers le récepteur. D’une manière simplifiée, le schéma général d’un système de communication peut être représenté comme suit

Figure I.1 – Le système général de la communication de Shannon.

Ce schéma est linéaire et on trouve deux pôles qui définissent une origine et une fin. La communication repose alors sur une chaîne qui est constituée d’une source, un émetteur, un canal, un récepteur, et un destinataire. Une personne (source de message) parle dans un appareil téléphonique (émetteur), qui convertit le son de la parole en un signal électrique. Ce signal électrique est alors transmis sur des lignes téléphoniques (canal) soumis à des interférences (bruit). Lorsque le signal atteint le récepteur téléphonique (récepteur) à l’autre extrémité de la ligne, il est reconverti en sons vocaux. Enfin, le destinataire (récepteur de message) entend le message d’origine.

La théorie de l’information classique est une représentation mathématique et physique. Elle est codée par des bits classiques qui peuvent prendre deux valeurs 0 ou 1. Un bit d’information est envoyé avec une certaine probabilité. Sa transmission peut échouer à cause des bruits exté-rieurs induisant une distorsion du signal ou l’interception du signal par une personne indésirable. La quantité d’information est quantifiée à l’aide de l’entropie de Shannon.

I.2 Théorie classique de l’information

2.1

Définition de l’entropie de Shannon

L’entropie de Shannon constitue un outil fondamental de la théorie de l’information classique [35]. Elle peut être définie pour des variables aléatoires discrètes ou continues. Dans le cas discret, où la variable ne prend qu’un nombre fini ou valeur dénombrable voir [36,37], l’entropie d’une variable aléatoire p est défini comme

H(p) =

k

X

i=1

−pilog2pi, (I.1)

où piest une distribution de probabilité. L’entropie peut également appelé l’incertitude moyenne

(la réduction moyenne de l’incertitude pour un récepteur). On note que la distribution de probabilité d’une variable aléatoire X par PX qui est décrit par H(X).

Pour k = 2 (l’entropie binaire), on a une distribution de probabilité (p, 1 − p) d’une variable aléatoire binaire. Elle est donnée par l’entropie de Shannon qui est une fonction de p

H(p) = −p log p − (1 − p) log(1 − p). (I.2) Pour p = 1₂ l’entropie est maximale, et pour p = 0, p = 1 l’incertitude de l’observateur est nulle voir figure (I.2).

Les propriétés de l’entropie de Shannon : – Elle est positive H(p) ≥ 0.

– H(p) est une fonction continue de p. – Elle est symétrique H(p).

– H(X) + H(Y ) ≥ H(X, Y ) si X et Y sont independants. – Elle est concave (pour une matrice densité ρ, on a H(ρ) ≥P

xpxH(ρx)).

– L’entropie d’un opérateur de densité est invariante sous les opérations unitaires

H(ρ) = H(U ρU†).

2.2

Entropie conjointe, conditionnelle et information mutuelle

Les entropies conjointe et conditionnelle sont des extensions simples qui mesurent l’incerti-tude dans la distribution conjointe d’une paire de variables, et l’incertil’incerti-tude dans la distribution conditionnelle d’une paire de variables aléatoires [33]. L’entropie conjointe H(X, Y ) représente la quantité d’informations nécessaires en moyenne pour spécifier la valeur de deux variables aléatoires discrètes, avec une distribution conjointe p(x, y). Elle est définie par

H(X, Y ) = −X

x,y

p(x, y) log p(x, y). (I.3) Cette grandeur quantifie l’incertitude totale sur la paire (X, Y ). Elle peut s’écrire sous la forme d’une somme

H(X, Y ) = H(X) + H(Y ), (I.4)

seulement si X et Y sont des événements indépendants.

L’entropie conditionnelle mesure l’entropie restante provenant de la variable aléatoire Y , si l’on connait parfaitement la seconde variable aléatoire X. C’est l’entropie de Y conditionnée par X. L’entropie conditionnelle H(X/Y ), qui mesure l’information dans X sachant que Y est connue, est donnée par

H(X/Y ) = −X

x,y

p(x, y) log p(x/y). (I.5) Les entropies conditionnelle et conjointe sont reliées par :

H(X, Y ) = H(X) + H(Y /X)

I.2 Théorie classique de l’information

L’information mutuelle c’est la quantité d’information moyenne que la connaissance d’un mes-sage reçu apporte sur le mesmes-sage émis. L’information mutuelle I(X, Y ) mesure l’écart par rapport à l’indépendance entre X et Y . En d’autres termes c’est la quantité d’information que l’une des deux variables du couple (X, Y ) apporte sur l’autre. L’information mutuelle entre les deux variables aléatoires discrètes X et Y , dont la distribution commune est définie par p(x, y), est donnée par la relation suivante

I(X, Y ) = X x,y P (x, y) log P (x, y) P (x)P (y) = X x,y P (x, y) logP (x/y) P (x) = X x,y P (x, y) log P (x/y) −X x,y P (x, y) log P (x) = −(−X x,y P (x, y) log P (x/y) +X x,y P (x, y) log P (x)) = −H(x/y) + H(x) = H(x) − H(x/y) = H(x) + H(y) − H(x, y). Il s’en suit que l’information mutuelle s’écrit

I(X, Y ) = H(x) + H(y) − H(x, y). (I.6)

L’information mutuelle satisfait les propriétés suivantes :

– I(X, Y ) = 0 si et seulement si X et Y sont des variables aléatoires indépendantes. – Elle est positive I(X, Y ) ≥ 0.

– Elle est symétrique I(X, Y ) = I(Y, X).

3

Théorie quantique de l’information

L’informatique quantique est une théorie récente. Elle date des années 80 [34]. C’est une théorie qui se base sur l’information classique et utilise le concepts de la mécanique quantique. Elle constitue un espoir pour le calcul, la communication, le stockage, et le cryptage etc..., en utilisant les propriétés quantiques de la matière. En effet, le calcul quantique exploite certaines propriétés quantiques fondamentales, tel que le principe de superposition des états, afin de résoudre certaines taches plus rapidement qu’avec un ordinateur classique. Il y a aussi les communications quantiques, pour transférer un état quantique d’un endroit à l’autre. Comme par exemple la téléportation quantique et la sécurisation de l’échange de clés secrètes de codage (cryptographie quantique)[38].

3.1

Définition de l’entropie de von Neumann

L’entropie de von Neumann est définie par John von Neumann en 1932 [39] comme le prolongement du concept classiques de l’entropie. En mécanique quantique, un système physique est décrit dans un espace de Hilbert, les observables correspondent aux opérateurs auto-adjoints et les opérateurs statistiques sont associés avec les états. L’entropie de Shannon est remplacée par l’entropie de von Neumann. Autrement dit les valeurs propres de la matrice densité d’un système ρ forment une distribution de probabilité. Puis la densité des opérateurs peut être considérée comme une généralisation pour les distributions des probabilités. L’entropie de von Neumann est définie par la relation suivante

S(ρ) = −T r(ρ log ρ) = −X

i

λilog λi, (I.7)

où λi : sont les valeurs propre de la matrice densité ρ.

L’entropie de von Neumann satisfait les propriétés suivantes :

– L’entropie est définie positive et nulle si et seulement si ρ est un état pur, S(ρ) ≥ 0. – L’entropie est additive pour des systèmes indépendants, S(ρA⊗ ρB) = S(ρA) + S(ρB).

I.3 Théorie quantique de l’information

– L’entropie est sous-additive, S(ρAB) ≤ S(ρA) + S(ρB).

– L’entropie est fortement sous-additive pour toutes les trois systèmes A, B et C,

S(ρABC) + S(ρC)+ ≤ S(ρA) + S(ρB).

3.2

Espace de Hilbert

A tout système quantique S est associé un espace de Hilbert complexe H tel que tout vecteur de norme 1 de l’espace H définit un état possible du système S. Un espace de Hilbert est un espace vectoriel complexe linéaire menu d’un produit scalaire, et complet pour la norme kxk =q_{hx, xi. Soit H un espace vectoriel complexe. Une fonctionnelle hx, yi : H × H → C de} deux variables est appelée produit interne si

– Le produit scalaire hx, yi = hy, xi∗

– L’additivité hx + y, zi = hx, zi + hy, zi (x, y, z ∈ H).

– Une application linéaire conjuguée hλx, yi = λ hx, yi , (λ ∈ C, x, y ∈ H). – La propriété symétrique-hermitienne hx, yi =hy, xi(x, y ∈ H).

– La norme positive hx, xi ≥ 0 pour x ∈ H et nulle hx, xi = 0 seulement pour x = 0.

3.3

Mesures quantiques et OMVP

Les mesures quantiques sont décrites par une collection d’opérateurs de mesure {Mm}, qui

vérifient la condition suivante

X

m

M_m†Mm = I, (I.8)

où I est l’opérateur identité.

Lorsque le résultat d’une mesure sur l’état |ψi est m, l’état du système après la mesure est

|ψ0i = M√m|ψi

pm

, (I.9)

où la probabilité d’obtenir le résultat m correspondant à l’opérateur Mm est

pm = hψ| Mm†Mm|ψi (I.10)

Les mesures quantiques satisfaisant les propriétés suivantes : – P

mMm†Mm = I.

– Mm = Mm†.

Les OMVP (Opérateurs de mesure à valeur positive) c’est la formulation la plus générale d’une mesure dans la théorie de la physique quantique. Ils s’agissent d’opérateurs hermitiques {Em}

non négatives (à valeurs propres positives ou nulles) sur un espace de Hilbert qui satisfont la condition de normalisation suivante :

X m Em = X m M_m†Mm = I. (I.11)

La probabilité d’obtenir l’élément Em du OMVP est

pm = T r(ρEm), (I.12)

et l’état du système après la mesure n’est pas simplement exprimé en fonction des Em.

3.4

Qubit et sphère de Bloch

La mécanique quantique nous dit que le système quantique le plus simple est un système à deux états c’est le qubit (ou le bit quantique). Il est l’unité de base de l’informatique quantique. Il s’agit d’un système quantique à deux niveaux (une superposition d’états), c’est à dire évoluant dans un espace de Hilbert à deux dimensions H = C2_{. En général, l’état d’un bit quantique}

(qubit) est décrit par

|ψi = α |0i + β |1i , (I.13)

où α et β sont des nombres complexes qui doivent satisfaire la condition de normalisation |α|2+ |β|2 = 1 et les états |0i et |1i doivent être orthogonaux. Si les qubits |ψi et |φi sont des états α |0i + β |1i et γ |0i + δ |1i respectivement, l’état d’un système à deux qubits composée de ces deux qubits est donné par leur produit tensoriel

|ψi ⊗ |φi = αγ |00i + αδ |01i + βγ |10i + βδ |11i . (I.14) Cette construction se formalisme à des systèmes à plusieurs niveaux et à des systèmes compre-nant plus de deux sous-systèmes. Pour un système à d niveaux (états) (d > 2), le dit quantique ou qudit peut prendre toutes les valeurs qui sont des superpositions de d différents états dans l’espace de Hilbert H = Cd_.

I.3 Théorie quantique de l’information

La sphère de Bloch fournit une représentation géométrique interessante de l’état d’un sys-tème de spin +1/2. Nous considérons un état fondamental |−1/2i et un état excité |+1/2i. Tout état de superposition peut être exprimé comme suit :

|ψi = cosθ

2|0i + e

iφ

sinθ

2|1i , (I.15)

où θ et φ sont réels. Le paramètre θ exprime l’amplitude relative des états de base, tandis que

φ exprime leur phase relative Voir (figI.4).

Figure I.4 –La sphère de Bloch

La matrice densité du système d’états purs correspondante à |ψi peut être exprimée à travers les matrices de Pauli et le vecteur de Bloch, tel que :

ρ = |ψi hψ| =   cos2 θ 2 e −iφ_sinθ 2cos θ 2

eiφsin₂θcosθ₂ sin2 θ₂

  = 1 2  

1 + cosθ sinθ(cosφ − isinφ) sinθ(cosφ + isinφ) 1 − cosθ

  = 1 2(I + n1σx+ n2σy + n3σz) = 1 2(I + − →_{n −}→_{σ ).}

et σx, σy, σz sont les matrices de Pauli usuelles. σx =   0 1 1 0  , σ_y =   0 −i i 0  , σ_z =   1 0 0 −1  . (I.16)

3.5

Opérateur et matrice densité

Le formalisme de la matrice densité permet de décrire tout l’ensemble possible des états quantiques d’un système physique donné à un instant donné, mariant ainsi la mécanique quan-tique et la physique statisquan-tique. La matrice densité ρ d’un état |ψi est l’opérateur défini comme le produit extérieur

ρ = |ψi hψ| , (I.17)

qui est un état pur. Si toutefois un état n’est pas complètement connu, mais seules les proba-bilités {pi}, avec lequel l’un de plusieurs états |ψii est connu, il est appelé un système d’états

mixtes. La matrice densité prend la forme

ρ =X

i

pi|ψii hψi| . (I.18)

Pour qu’un opérateur soit une matrice densité, il doit satisfaire les propriétés suivantes – Sa Trace doit être égale à 1 : T r(ρ) = 1.

– La matrice densité est hermitienne : ρ = ρ†. – La matrice densité est positive : ρ > 0.

Une matrice densité ρ est pure si est seulement si T r(ρ2_{) = 1 et ρ}2 _{= ρ, alors que pour}

une matrice densité mixte T r(ρ2_{) < 1. La trace partielle a des applications dans des calcules}

de quantités physiques dans le domaine de l’information quantique et l’étude des processus induisant la décohérence. Soit l’opérateur densité ρAB décrivant un état du système composite

agissent dans l’espace de Hilbert H = HA⊗ HB. On définit la trace partielle de l’opérateur

densité par ρA = T rB(ρAB) = d−1 X j=0 hj| ρAB|ji , ρB = T rA(ρAB) = d−1 X i=0

hi| ρAB|ii , (I.19)

I.4 Conclusion

4

Conclusion

La théorie quantique de l’information est une extension de la théorie classique de l’infor-mation et qui prend en compte les spécificités des systèmes quantiques. John von Neumann a défini la théorie de l’information sur des définitions de bases différentes de celles de Shannon mais dont les propriétés sont similaires.

Dans ce chapitre, nous avons définit les notions importantes de base de la théorie de formation classique, à savoir l’entropie de Shannon, entropie conjointe, conditionnelle et l’in-formation mutuelle. Nous avons introduit également les notions essentielles de l’inl’in-formation quantique, qui sont : l’entropie de von Neumann, les mesures quantiques et les opérateurs OMVP, le qubit, et opérateur et matrice densité.

Chapitre II

Les mesures des corrélations quantiques

1

Introduction

Le traitement de l’information quantique dépend essentiellement de divers phénomènes de la mécanique quantique, parmi lesquels l’intrication a été considérée comme l’un des éléments les plus cruciales. L’intrication quantique joue un rôle important dans plusieurs domaines de l’information quantique tels que la téléportation quantique [13,40], la cryptographie quantique [12, 41], le codage [14, 42, 43] et le calcul quantique [44–46], etc... L’intrication quantique est une forme de corrélation entre deux ou plusieurs particules (qui peuvent ou ne peuvent pas être séparés). Le but principal dans les études de l’intrication est de trouver une manière générale pour quantifier et caractériser la quantité d’intrication d’un état quantique donné. Il s’agit là de questions centrales en théorie quantique de l’information. Beaucoup d’efforts ont été consa-crés à ce domaine de recherche et plusieurs mesures de l’intrication ont été proposées pour les systèmes quantiques bipartites et multipartites.

Dans ce chapitre, nous allons définir l’intrication quantique pour les systèmes à variables conti-nues, et comment quantifier et caractériser cette quantité. Ensuite, nous introduirons quelques mesures des corrélations quantiques pour les systèmes quantiques bipartites, par exemple la négativité logarithmique [47], la concurrence [48], l’intrication de formation, la discorde quan-tique [49] et sa variante géométrique [50]. Enfin, nous présenterons un schéma unificateur pour les corrélations (totale, quantique et classique) des états mixtes dans des systèmes bipartites.

2

Intrication quantique pour les systèmes à variables

continues

Le phénomène de l’intrication(entanglement) joue un rôle essentiel en théorie quantique de l’information et en calcul quantique [51]. C’est une propriété spécifique de la physique quantique qui n’existe pas en mécanique classique. Elle se manifeste, en général, par le fait que lorsque plusieurs particules ont été préparées ensemble, et ont interagies pendant un certain intervalle de temps, qui peut être très court, elles restent fortement corrélées même si elles sont séparées par une très grande distance. L’intrication apparait presque dans tous les protocoles de la communication et les algorithmes quantiques (la téléportation, le codage superdense, etc...). Un système bipartite est composé de deux sous-systèmes dont les espaces de Hilbert sont HA

et HB, tels que l’espace de Hilbert total H est formé par le produit tensoriel H = HA⊗ HB,

par définition, les sous systèmes A et B sont définis dans un état intriqué. Si

|ψi_AB 6= |ψi_A⊗ |ψi_B, (II.1)

où |ψi_A et |ψi_B sont des états définis dans les espaces de Hilbert HA et HB respectivement.

3

Quantification et caractérisation de l’intrication

L’un des objectifs de la théorie d’intrication est d’obtenir un critère de séparabilité pour distinguer les états séparables où les états non séparables (intriqués).

Etats séparables :

– Dans le cas d’un état pur bipartite ρAB, c’est à dire ρAB = |ψiABhψ| est séparable si et

seulement si |ψi_AB = |ψi_A⊗ |ψi_B. Ainsi, un état pur est séparable si l’un des opérateurs densités réduites, ρA ou ρB est dans un état pur.

– Un état mixte est dit séparable s’il peut être représenté comme un mélange statistique des états purs séparables

ρAB = X i piρAi ⊗ ρBi = X i pi|ψiiAhψi| ⊗ |ψiiBhψi| , (II.2)

avec |ψii_A et |ψii_B sont des vecteurs d’états sur les espaces HA et HB respectivement, et

II.4 Décomposition de Schmidt

Etats non séparables(intriqués) :

– Un état pur est intriqué si et seulement si l’opérateur densité ρAB ne peut pas être écrit

comme un opérateur de produit, c’est à dire

ρAB 6= ρA⊗ ρB, (II.3)

comme par exemple l’état |φ+_{i = √}1

2(|00i + |11i).

– Un état mixte est intriqué si et seulement si l’état est corrélé et non séparable

ρAB 6=

X

i

piρA⊗ ρB. (II.4)

Nous faisons remarquer que les deux systèmes en interaction deviennent en général non séparables. La détermination de la séparabilité d’un état est un problème qui n’est pas aisé de façon générale. Il y a une autre façon de déterminer la séparabilité des états purs et mixtes. Cette méthode est basée sur la décomposition de Schmidt.

4

Décomposition de Schmidt

La décomposition de Schmidt, permet d’écrire n’importe quel état pur d’un système bipartite comme une combinaison linéaire d’états produits orthogonaux [52]. Pour un état pur |ψABi d’un

systéme AB, il existe des états orthonormés |αiiA et |βiiB c’est à dire

|ψABi = d

X

i=1

λi|αiiA⊗ |βiiB, (II.5)

où les λi sont des coefficients Schmidt, avec λi ≥ 0 et Piλi = 1. L’état |ψABi est séparable si

et seulement si le nombre de coefficients est supérieur à 1. Un état quantique mixte ρAB est

séprable si et seulement si peut être écrit comme

ρAB = d2 X i=1 λiρiA⊗ ρ i B, (II.6) où λi ≥ 0 , Piλi = 1 et ρAi ∈ HA, ρiB ∈ HB.

5

Les mesures des corrélations quantiques

Parmi les mesures des corrélations quantiques qui ont été proposées pour les systèmes com-posites, on cite la négativité logarithmique [47], la concurrence [48], l’intrication de formation, la discorde quantique [49] et sa variante géométrique [50].

5.1

La négativité logarithmique

En mécanique quantique, la négativité est une mesure de l’intrication quantique qui est facile à calculer [47]. C’est une mesure qui utilise le critère PPT comme critère de séparabilité appelé aussi (Critère Peres-Horodecki)1_{. Pour un opérateur A, nous définissons la norme trace}

par la somme des valeurs singulières de l’opérateur A par kAk = tr |A| = tr√A†_A.

La négativité est définie par

N (ρ) = ρ ΓA ₁− 1 2 , (II.7)

où ρΓA _{: est la transposition partielle de ρ par rapport au sous-système A. La négativité}

loga-rithmique est une quantité qui est facilement calculable, elle est définie comme

EN(ρ) = log2 ρ ΓA ₁, (II.8)

avec ΓA : est l’opérateur de transposition partielle.

Elle est reliée à la négativité par la formule

EN(ρ) = log2(2N (ρ) + 1). (II.9)

La négativité logarithmique satisfait les propriétés suivantes :

– Elle peut être nulle, même si l’état est intriqué (si l’état est PPT intriqué). – EN(ρ ⊗ σ) = EN(ρ) + EN(σ)(additif sur les produits tensoriels)

– Elle ne se réduit pas à l’entropie d’intrication sur l’état pur comme la plupart des autres mesures d’intrication.

1_{est une condition nécessaire, pour la matrice densité conjointe de deux systèmes quantiques A et B, pour}

II.5 Les mesures des corrélations quantiques

5.2

La concurrence

Parmi les outils de la quantification des corrélations quantiques, la concurrence fournit un moyen d’accéder à la séparabilité d’un système à deux qubits [48,53]. On considère un état pur |ψi de deux qubits. La concurrence C(|ψi) de cet état est définie comme

C(|ψi) = hψ   ψe E  , (II.10)

où le tilde représente l’opérateur "spin-flip"  ψe

E

= (σy ⊗ σy) |ψ∗i, avec σy est la matrice de

pauli suivant la direction y et |ψ∗i est le conjugué complexe de |ψi dans la base standard {|00i , |01i , |10i , |11i}. Un état pur à deux qubits prend la forme

|ψi = α00|00i + α01|01i + α10|10i + α11|11i . (II.11)

où α00, α01, α10et α11sont des nombres complexes qui remplissent la condition de normalisation

suivante

|α00|2+ |α01|2+ |α10|2+ |α11|2 = 1. (II.12)

On peut montrer que |ψi est séparable si α00α11 = α01α10. De sorte que l’on peut prendre la

différence entre α00α11et α01α10en tant que mesure de l’intrication et on définit la concurrence

par

C(ψ) = 2 |α00α11− α01α10| . (II.13)

La concurrence est égal à 0 pour un état séparable et à 1 pour un état est maximalement intriqué.

L’intrication de formation d’un état pur |ψi est exprimée en terme de la concurrence C(|ψi) par la relation

E(|ψi) = ξ(C(|ψi)), (II.14)

où la fonction ξ est définie comme

ξ(C) = H(1 + q

1 + |C|2

2 ), (II.15)

avec H(x) = −x log₂x − (1 − x) log₂(1 − x) est l’entropie binaire.

La concurrence pour un état mixte de deux qubits est définie comme suit

C(ρ) = inf X

i

où C(|ψii) est la concurrence de l’état |ψii qui est donnée par l’équation (II.13). Wootters et

Hill ont obtenu une formule explicite de la concurrence [54]. Elle est donnée par

C(ρ) = max{0, λ1− λ2− λ3− λ4}, (II.17)

avec λ1 ≥ λ2 ≥ λ3 ≥ λ4 sont les racines carrés des valeurs propres de la matrice ρ(σy ⊗

σy)ρ∗(σy ⊗ σy) (ρ∗ le complexe conjugé de ρ). L’intrication de formation d’un état mixte de

deux qubits est définie par

E(ρ) = ξ(C(ρ)). (II.18)

5.3

La discorde quantique

Un état quantique bipartite contient à la fois des corrélations classiques et quantiques [49]. Elles sont quantifiées conjointement par leur "information mutuelle quantique" qui est une mesure de l’information de la corrélation totale dans l’état quantique bipartite. Elle est donnée par

I(A, B) = S(ρA) + S(ρB) − S(ρAB), (II.19)

où ρAB est l’état d’un système quantique bipartite composé de la particule A et B, ρA(B) =

T rB(A)(ρAB) est l’état réduit de A(B), et S(ρ) est l’entropie de von Neumann de l’état ρ (voir

[55]). Considérons les opérateurs de projections {Mk} pour décrire une mesure de von Neumann

pour le système A. Nous rappelons que l’opérateur de mesure à valeur positive généralisé n’est pas nécessaire. Alors l’état aprés mesure de la particule B qui correspond au résultat k est

ρAB → ρBk =

(MkNI)ρAB(MkNI)

pB k

, (II.20)

où la mesure de von Neumann pour le sous-système A est écrite comme

Mk = U πkU†: k = 0, 1, (II.21)

avec πk = |ki hk| est le projecteur pour le sous-système A dans la base |ki, U ∈ SU (2) est

l’opérateur unitaire de déterminant unité et la probabilité pB_k est égale

pB_k = T r[(Mk⊗ I)ρAB(Mk⊗ I)]. (II.22)

En utilisant tous les éléments de l’ensemble η des OMVP, les états après mesure de la particule

II.5 Les mesures des corrélations quantiques

après mesure. L’information sur la particule B que acquiert la partie A, en faisant usage d’un ensemble des OMVP spécifique, est donnée par

S(ρB) −

X

k

pB_kS(ρB_k). (II.23)

La dépendance de la procedure de la mesure peut être eliminée par une procedure de maximi-nisation sur tout les ensembles η possibles. Donc, la mesure des corrélations classiques résultante est donnée par

J (ρAB) = max M [S(ρB) − X k pB_kS(ρB_k)] (II.24) = S(ρB) −Se_min, (II.25)

oùSe_min désigne la valeur minimale de l’entropie conditionnelle. Nous avons e

Smin =

X

k

pB_kS(ρB_k) (II.26)

La discorde quantique est une mesure de la corrélation quantique qui est développées par Ollivier et Zurek en 2001 [56]. C’est la différence entre l’information mutuelle (une quantité qui mesure la corrélation totale) entre deux sous-systèmes (classique et quantique) et la corrélation classique. Il s’en suit le résultat suivant

D(ρAB) = I(ρAB) − J (ρAB) = S(ρB) +Se_min− S(ρ_AB). (II.27)

Il n’y a aucun algorithme direct pour calculer la discorde quantique pour des états mixtes. Des résultats partiels uniquement ont été obtenus pour certaines formes spéciales qu’on appelle les états X [57–60].

La discorde quantique satisfait les propriétés suivantes : – La discorde quantique est toujours positive D(ρAB) ≥ 0.

– D(ρAB) = 0 si et seulement si l’état ρAB est la diagonale de Bloch dans sa propre base

est

ρAB =

X

j

pjρABpj,

où ρAB=Pjτjpj, avec {τ } c’est une distribution de probabilité.

– La valeur de la discorde quantique est supérieure ou égale à l’entropie de von Neumann du sous système mesuré, c’est-à-dire D(ρAB) ≤ S(ρA).

Illustrons maintenant le concept de la discorde quantique par un exemple simple d’état de type X. la matrice densité d’un état de ce système de deux qubits AB dans la base standard {|00i , |01i , |10i , |11i} est donnée par

ρAB =         ρ00 0 0 ρ03 0 ρ11 ρ12 0 0 ρ21 ρ22 0 ρ30 0 0 ρ33         , (II.28)

qui s’écrit dans la base {|00i , |11i , |01i , |10i} sous la forme suivante

ρAB =         ρ00 ρ03 0 0 ρ30 ρ33 0 0 0 0 ρ11 ρ12 0 0 ρ21 ρ22         . (II.29)

Autrement, cette matrice densité ρAB s’écrit

ρAB = (ρAB)1+ (ρAB)2 (II.30) avec (ρAB)1 =   ρ00 ρ03 ρ30 ρ33   (ρ_AB)₂ =   ρ11 ρ12 ρ21 ρ22  . (II.31)

Les valeurs propres de la matrice densité ρAB de deux qubits sont données par

λ±₁ = 1 2tr(ρAB)1± s (1 2tr(ρAB)1) 2_{− det(ρ} AB)1, (II.32) ou λ±₂ = 1 2tr(ρAB)2± s (1 2tr(ρAB)2) 2_{− det(ρ} AB)2. (II.33)

Donc pour que ρAB soit de rang 2, il suffit de considérer

det(ρAB)1 = 0, det(ρAB)2 = 0. (II.34)

Dans ce cas, les valeurs propres de la matrice densité ρAB de rang 2 de deux qubits sont données

par

II.5 Les mesures des corrélations quantiques

λ+₂ = tr(ρAB)2 = ρ11+ ρ22. (II.35)

On fait remarquer que

λ+₁ + λ+₂ = 1, (II.36)

c’est à dire que

tr(ρAB)1 6= 0, tr(ρAB)2 6= 0. (II.37)

L’entropie conjointe de l’état ρAB est

S(ρAB) = −λ+1 log2λ + 1 − λ + 2 log2λ + 2. (II.38)

où ρA et ρB sont les états marginaux de ρAB avec

   S(ρA) = −λA1 log2λ1A− λA2 log2λA2, S(ρB) = −λB1 log2λ1B− λB2 log2λB2, (II.39)

où les valeurs propres de ρA et ρB sont

   λA 1 = ρ00+ ρ11, λA2 = ρ22+ ρ33, λB 1 = ρ00+ ρ22, λB2 = ρ11+ ρ33. (II.40)

Il en résulte que l’information mutuelle, définie par (I.6), prend la forme

I(ρAB) = H(λA1) + H(λB1) − H(λ+1). (II.41)

Pour calculer la forme explicite de la corrélation classique J (ρAB), nous utilisons la

décompo-sition sepectrale de la matrice densité ρAB

ρAB = λ+₁|ψ1ihψ1| + λ+2|ψ2ihψ2|, (II.42)

où les valeurs propres λ+₁ et λ+₂ sont données par (II.35) et les états propres |ψ1i et |ψ2i sont

|ψ1i =

1

q

|ρ03|2+ |ρ33|2

[ρ03|00i + ρ33|11i], (II.43)

|ψ2i =

1

q

|ρ12|2+ |ρ22|2

En attachant un qubit C au système bipartite AB, nous écrivons la purification de ρAB

comme

|ψi =qλ+₁|ψ1i ⊗ |0i +

q

λ+₂|ψ2i ⊗ |1i, (II.45)

de telle sorte que l’ensemble du système ABC est décrit par l’état pur de densité ρABC = |ψihψ|

pour que ρAB = TrCρABC et ρBC = TrAρABC. D’après la relation de Koashi-Winter [65], la

valeur minimale de l’entropie conditionnelle coïncide avec l’intrication de formation de ρBC

e

Smin = E(ρBC), (II.46)

qui est donnée par

e Smin = E(ρBC) = H( 1 2 + 1 2 q 1 − |C(ρBC)|2), (II.47)

où le concurrence de la matrice densité ρ23 est

|C(ρBC)|2 =

4(ρ00+ ρ33)(ρ11+ ρ22)(|ρ03||ρ12| − |ρ22||ρ33|)2

(|ρ03|2+ |ρ33|2)(|ρ12|2+ |ρ22|2)

. (II.48)

Il en résulte que la discorde quantique est donnée par

D(ρAB) = S(ρA) − S(ρAB) + E(ρBC), (II.49)

Finalement en utilisant les équations (II.38), (II.39) et (II.47), l’expression explicite de la dis-corde quantique s’écrit

D(ρAB) = H(ρ00+ ρ11) − H(ρ00+ ρ33) + H(1 2+ 1 2 v u u t1 − 4(ρ00+ ρ33)(ρ11+ ρ22)(|ρ03||ρ12| − |ρ22||ρ33|)2 (|ρ03|2+ |ρ33|2)(|ρ12|2+ |ρ22|2) )

Pour obtenir la discorde quantique, il faut faire des efforts considérables pour réduire au mini-mum l’entropie conditionnelle Se_min de toutes les mesures possibles sur les particules A. Dans

la prochaine partie, nous présentons une méthode géométrique sur le concept de la discorde quantique.

5.4

La mesure géométrique de la discorde quantique

La mesure géométrique de la discorde quantique (MGDQ), a été introduite par Dakic et al [50]. Elle quantifie la corrélation quantique à l’aide de la distance de Hilbert-Schmidt entre