يملعلا ثحبلاو يلاعلا ميلعتلا ةرازو
راـتخم يـجاب ةـعماج
ةـباـنع
Université Badji Mokhtar
Annaba
Badji Mokhtar University -
Annaba
Faculté des Sciences
Département de Mathématiques
Laboratoire LaPS
THESE
Présentée en vue de l’obtention du diplôme de
Doctorat en Mathématiques
Option : Modélisation Mathématiques-Actuariat
Méthodes statistiques pour l’assurance non-vie et la
finance
Par:
Lazri Nouara
DIRECTEUR DE THESE : ZEGHDOUDI Halim M.C.A U.B.M. Annaba
CO-DIRECTEUR DE THESE: REMITA Med Riad
Prof.
U.B.M. Annaba
Devant le jury
PRESIDENT :
Chadli Assia
Prof.
U.B.M. Annaba
EXAMINATEUR :
Hadji
Mohamed Lakhder
M.C.A
U.B.M. Annaba
EXAMINATEUR :
Benchaabane Abbes
M.C.A
U. Guelma
Remerciement
Nous tenons à remercier
Tout puissant ALLAH le clément qui manifeste sa clémence, Le
prophète MOHAMED que la bénédiction et salut de Dieu soient sur lui.
Notre encadreur, monsieur Dr. Zeghdoudi Halim, pour nous avoir
encadré, dirigé et conseillé, et pour avoir mis à notre disposition tous les
moyens nécessaires à l’accomplissement de ce travail.
Mon co-encadreur le Prof Remita Mohamed Riad qui part sa bonne
gestion, directifs et conseils à contribuer au déroulement à bon terme de
ma thèse.
Un très grand merci à Le Professeure Mme Chadli Assia qui m’a fait
l’honneur de présider mon jury de thèse.
Je remercie vivement Dr. Hadji Mohamed Lakhder ainsi que Dr.
Benchaabane Abbes de l’université de Guelma, pour l’honneur de
d’avoir accepté de faire partie de jury.
Je remercie chaleureusement Le Dr.
Bhati
Deepesh
de l’université
centrale du Rajasthan, Kishangarh, Inde, pour
ses efforts dans les
expériences numériques.
Enfin nous remercions nos parents, nos familles et nos amis, ainsi
que tous ceux qui ont contribué de prés ou de loin à l’achèvement de ce
travail.
Je clos enfin ces remerciements en dédiant cette thèse de doctorat à
mes parents et mes frères.
Table des matières
1 Généralités sur les variables aléatoires continues 9
1.1 Fonction W de Lambert . . . 9
1.2 Fonction génératrice des moments . . . 11
1.3 Les valeurs extrêmes . . . 11
1.3.1 Loi des extrêmes généralisée, approche block maxima . . . 12
1.4 Entropie . . . 15 1.4.1 Entropie Shannon . . . 15 1.4.2 Entropie de Rényi . . . 16 1.5 Lois de probabilité . . . 16 1.5.1 Distribution de Lindley . . . 16 1.5.2 Distribution de Pareto . . . 18 1.5.3 Distribution de Gamma . . . 20
2 Méthodes combinés et Transformé-Transformer 23 2.1 Modèles combinés . . . 24
2.1.1 Générer des valeurs aléatoires à partir de la fonction de densité combiné . . . 27
2.1.2 Inférence statistique . . . 27
2.2 Méthode de Transformé-Transformer (T X) . . . 30
3 Distributions Gamma(2; )-Pareto combiné et Lindley-Pareto 34 3.1 Gamma(2; )-Pareto combiné . . . 34
3.1.1 Générer des valeurs aléatoires à partir de la distribution Gamma(2; )-Pareto combinée . . . 37
3.1.2 Estimation des paramètres . . . 37
3.2 Distribution Lindley-Pareto . . . 39
3.2.1 Propriétés de la distribution Lindley Pareto . . . 40
3.2.2 Moments et fonction génératrice des moments . . . 43
3.2.3 Variance . . . 44
3.2.5 Statistiques de command extrêmes . . . 49
3.2.6 Entropie . . . 50
3.2.7 Estimations du maximum de vraisemblance (MV) . . . 51
4 Application et simulation 53 4.1 Simulations et des exemples illustrés . . . 53
4.1.1 Premier exemple . . . 54
4.1.2 Deuxième exemple . . . 55
4.2 Applications et simulations . . . 57
4.2.1 Simulations . . . 57
4.2.2 Application aux ensembles de données réelles . . . 59
5 Annexes 66
Résumé
Nous nous proposons, dans cette thèse, d’introduire quelques nouvelles distribu-tions continues nommées respectivement les distribudistribu-tions Lindley Pareto et Gamma(2; ) Pareto combiné , qui ajoutera une certaine valeur à la littérature existant sur la mo-délisation des données à vie, des sciences biologiques et des sciences actuarielles.
Abstract
In this thesis, we give a treatment of the mathematical properties for new dis-tributions named respectively Lindley Pareto (L-PD) and composite Gamma(2; ) Pareto. The properties studied include : the quantile function, maximum likelihood estimation. Simulations studies and data driven applications are also reported.
صخلم
حرتقن
يف
هذه
ةديدج ةرمتسم تاعيزوت ةحورطلأا
و
مادختساب اهديلوتب انمق يتلا
.اهصاوخ ةسارد و قرط ةدع
تاعيزوت يه و
وتيراب
يلدنيل
)
(
Lindley Pareto
اماغو
(
2
؛
λ
)
وتيراب
(
Gamma(2;λ) Pareto
)
،
يتلاو
فوس
ةميق فيضت
ىلإ
تاباتكلا
ةدوجوملا
ةايحلا تانايب ىلع
،
مولع
ايجولويبلا
و
لا
مولع
.ةيراوتكلاا
Introduction
Les statistiques jouent un rôle crucial dans les applications de la vie réelle. Sou-vent en utilisant l’analyse statistique qui dépend fortement du modèle de probabilité supposé ou des distributions. Les chercheurs récemment ont proposé de nombreuses distributions, les plus populaires étant les généralisations des distributions exponen-tielles, gamma, Weibull, Pareto et Lindley. Ghitany et al. (2008) ont étudié de la majorité de propriétés statistiques de la distribution de Lindley et plusieur cher-cheurs, à savoir Dolati (2009), Zamani et Ismail (2010), Nadarajah (2011), Elbatal et al. (2013), Hassan (2014), Bhati (2015), Zeghdoudi and Nedjar (2016) ont proposé de nouvelles classes de distribution en modi…ant la distribution de Lindley et ont discuté de diverses propriétés de leurs généralisations proposées. L’idée principale est toujours dirigée en intégrant les anciennes distributions à des structures plus ‡exibles avec des générateurs di¤érents, les générateurs les plus utilisé : famille Beta-G par Eugene et al. [35], famille transformée-transformer (T X) par Alzaatreh et al. [1], famille exponentielle T X par Alzaghal et al. [2] et modèles combinés par Cooray et Ananda [26].
Dans certaines situations, les statisticiens rencontrent des données qui proviennent évidemment de deux modèles di¤érents C’est souvent le cas avec par exemple : Les données sur les paiements d’assurance, lorsque les actuaires doivent traiter des don-nées plus petites avec des fréquences élevées et des dondon-nées plus grandes occasion-nelles avec des fréquences plus basses. La distribution correspondante peut alors être
modélisée sous la forme d’une combinaison de deux distributions, consistant en une distribution moins lourde (queue "légere") jusqu’à une certaine valeur de seuil et une répartition à queue grossie (queue "lourde") à partir de ce seuil.
Cooray et Ananda [26] ont suggéré le modèle combiné et introduit un modèle Lognormal-Pareto combiné avec la densité Lognormal jusqu’à une certaine valeur de seuil et la loi de Pareto à partir de ce seuil. Sur la base des mêmes distributions, Scollnik [9], a proposé deux modèles combinés di¤érents, plus généraux que celui étudié par Cooray et Ananda [26]. De la même manière, Teodorescu et Vernic [42] ont suggéré des modèles Exponential-Pareto combiné. De plus, Preda et Ciumara [5] ont réalisé une étude comparative entre les distributions combinés Weibull-Pareto et Lognormal-Pareto. Le choix de la distribution de Pareto est dû au fait d’être une distribution classique à queue lourde.
Dans cette thèse, nous introduisons des nouvelles distributions à savoir :
-la distribution de Lindley Pareto en utilisant le modèle transformé-transformer (T X) qui introduit par Alzaatreh, et al.(2013) [1] ,
-la distribution Gamma (2, ) -Pareto combinée en utilisant le modèle combinés, inspiré par les travaux de Teodorescu et Vernic (2009) [42], Cooray et Ananda (2005) [26], Preda et Ciumara (2006) [42]. Plus précisément, nous étudions le modèle Gamma (2, ) -Pareto combiné, nous choisissons la densité Gamma (2, ) pour f1 où f1 est
généralement considérée comme une distribution à queue légère, et une densité de Pareto pour f2, où f2 est une distribution à queue lourd.
Notre projet de recherche est organisé comme suit :
le premier chapitre est consacré aux rappels de certaines dé…nitions et certains résultats qui nous utilisés par la suite à savoir :
- fonction W de Lambert ; - statistiques d’ordre extrême ; - entropie ;
-quelques distributions de probabilités.
Chapitre II donne une synthèse sur les modèles de mélange transformé-transformer (T X) (Alzaatreh, et al.(2013) [1]) et le modèle combinés (Cooray et Ananda (2005) [26]).
Le chapitre III s’articule autour des nouvelles distributions (Gamma (2, )-Pareto combiné , Lindley-Pareto) dont nous donnons quelques propriétés probabilistes à sa-voir : la fonction quantile, entropies, méthode des moments, estimation du maximum de vraisemblance et la distribution de limitation des statistiques d’ordre extrême.
En…n, le dernier chapitre contient l’essentiel des travaux regroupés dans les articles [20; 21; 22] en nous inspirant des travaux originaux de Lindley (1958)[10], et Teodo-rescu et Vernic (2009) [42] en adaptant certains résultats. Par ailleurs, une simulation de biais et l’erreur quadratique moyenne des estimateurs obtenus par la méthode du maximum de vraisemblance sera e¤ectué. De plus, une étude comparative entre plusieurs distributions a été donnée.
Chapitre 1
Généralités sur les variables
aléatoires continues
Dans ce chapitre nous faisons un rappel sur quelques propriétés statistiques et lois de probabilité qui nous utilisons par la suite.
1.1
Fonction W de Lambert
La fonction W Lambert est dé…nie comme la fonction inverse de
y exp y = z (1.1)
la solution étant donnée par y = W (z), ou bientôt W (x) exp W (x) = z.
Depuis le z ! z exp z = z le mappage n’est pas injectif, il n’existe pas d’inverse unique de la fonction z exp z = z. Comme on peut le voir sur la Figure 1.1, la fonction
W Lambert comporte deux branches réelles avec un point de rami…cation situé à ( e 1; 1). La branche inférieure, W
1(z), est dé…nie dans l’intervalle x 2 [ e 1; 0]
et a une singularité négative pour x ! 0 . La branche supérieure est dé…nie pour x2 [ e 1;1].
FIG. 1.1 : Les deux branches de la fonction W Lambert, W 1 (z)en bleu et W0(x)en rouge. Le
point de rami…cation ( e 1; 1) est dsign par un
tiret vert
La première mention du problème de l’équation (1.1) est attribué à Euler. Cepen-dant, Euler lui-même a crédité Lambert pour son travail antérieur sur ce sujet. La fonction W (z) a commencé à s’appeler Lambert seulement récemment, au cours des 10dernières années environ. La lettre W a été choisie par la première implémentation de la fonction W (z) dans le logiciel informatique Maple.
1.2
Fonction génératrice des moments
Le calcul des moments d’ordre k d’une variable aléatoire est une tâche qui peut rapidement devenir laborieuse. Il existe cependant une manière permettant de les obtenir tous à partir d’une unique fonction, appelée fonction génératrice des moments G (t), donnée par :
G (t) = E etx = Z +1
1
etxf (x) dx
pourvu que E [etx]existe, c’est-à-dire que l’intégrale correspondante soit convergente.
En dérivant k fois cette expression par rapport à t, on obtient : dkG (t)
dkt =
Z +1 1
xketxf (x) dx
et l’évaluation de cette dérivée au point t = 0 donne donc : dkG (t)
dkt t=0
= E Xk
L’intérêt principal de la fonction génératrice des moments est d’obtenir par un procédé simple et systématique les moments d’ordre quelconque de la variable aléa-toire sans avoir recours au calcul intégral ; il est en e¤et aisé d’obtenir les dérivées successives d’une expression.
1.3
Les valeurs extrêmes
Il s’agit dans l’étude des valeurs extrêmes d’analyser l’épaisseur des queues de distributions, ou encore d’étudier les plus grandes observations d’un échantillon pour
caractériser sa loi initiale. Ainsi, la théorie des extrêmes vient en complément de la théorie statistique classique où il est plus commun d’étudier le comportement d’une distribution autour de sa moyenne plutôt que dans le domaine des observations ex-trêmes souvent appelées événements rares. Nous allons voir que toute la théorie des extrêmes est fondée sur un équivalent au théorème central limite mais pour les queues de distribution.
On s’intéresse au comportement du maximum d’un échantillon, variable aléatoire dé…nie par
Mn = max (X1; :::; Xn) ;
où X1; :::; Xn est un échantillon de n variables aléatoires indépendantes et de même
loi F .
La distribution de Mn peut s’écrire de la façon suivante :
P (Mn x) = P (X1 < x; :::; Xn < x)
= P (X1 < x) ::: P (Xn< x)
= Fn(x)
1.3.1
Loi des extrêmes généralisée, approche block maxima
G (x) = 8 > > < > > :
exp [1 + x] 1 , pour tout x tel que 1 + x 0; 6= 0 exp ( exp ( x)), pour tout x 2 R; si = 0
Théorème de Fisher et Tippett
Ce théorème a été énoncé pour la première fois par Fisher et Tippett en 1928, puis démontré par Gnedenko en 1943.
Théorème 1.2.1. S’il existe des suites de réels an > 0 et bn 2 R telles que :
lim n!1P Mn bn an = G (x) où encore, lim n!1F n(a nx + bn) = G (x)
pour tout x 2 R et G non dégénérée, alors G (x) appartient à la famille de loi GEV (Generalized Extrême Value).
Fn est la fonction de répartition de M
n tandis que G (x) est la fonction de
répartition limite de Mn correctement renormalisée par an et bn. On dira que Fn
est dans le domaine d’attraction D .
Les lois limites possibles
Le comportement de la queue de distribution d’une suite de variables aléatoires sera complètement caractérisé par le paramètre appelé indice des valeurs extrêmes.
Une partie sera consacrée aux méthodes d’estimation de ce paramètre. Le signe de a une forte in‡uence sur la distribution des extrêmes, et on distingue trois cas :
Domaine d’attraction de Gumbel : lorsque = 0, la distribution G0 est
appelée distribution de Gumbel. Le support de cette loi est R et dans ce cas les queues de distribution sont légères et décroissent de manière exponentielle. G0 sera
parfois notée .
Domaine d’attraction de Fréchet :lorsque > 0, on a : (x) = exp x 1= 1x>0.
De telles distributions possèdent des queues lourdes et la convergence de Fn vers la
loi limite se fait très lentement.
Domaine d’attraction de Weibull : lorsque < 0, on pose = 1 > 0 et on note (x) = exp ( ( x) ) si x est négatif, et 1 sinon. Dans ce cas la queue de la distribution sera très mince.
Théorème 2.2.2. (Lois extrêmes du minimum)
S’il existe des suites de normalisation an et bn2 R et une distribution limite non
dégénérée G telles que :
lim
n!1P
Mn bn
an
x = lim (1 F (anx + bn))n = G (x) ;
alors G est dite loi des valeurs extrêmes du minimum.
En utilisant la relation : min (Xi) = max ( Xi)il vient que 8x 2 R; 1 i n
P [min (Xi) > x] = p [max ( Xi) x] = Fn( x) = 1 (1 F (x))n
sont :
– (x) = 1 exp ( exp (x)) ; avec x 2 R (distribution de Gumbel) – (x) = 1 exp x 1= ;(distribution de Fréchet)
– (x) = exp ( ( x) ) ; (distribution de Weibull)
1.4
Entropie
L’entropie est la mesure du désordre dans les systèmes physiques, ou une quantité d’information qui peut être acquise par les observations des systèmes désordonnés. Claude Shannon [8] dé…nit une mesure formelle de l’entropie, appelée entropie de Shannon
1.4.1
Entropie Shannon
L’entropie de Shannon est une fonction décroissante d’une dispersion de variable aléatoire, et est maximale lorsque tous les résultats sont également probables.
L’entropie de Shannon est comme :
1.4.2
Entropie de Rényi
Alfred Renyi [5] est proposé d’entropie généralisée qui pour s = 1, se réduise à l’entropie de Shannon. L’entropie de Renyi est dé…nie comme :
IR(s) = 1 1 s ln Z 1 1 gs(x) dx s > 0; s6= 1
Il a des propriétés similaires à celles de l’entropie de Shannon : - elle est additive
- il a maximum = ln (n) pour pi = n1
Mais elle contient un paramètre supplémentaire s qui peut être utilisé pour le rendre plus ou moins sensible à la forme des distributions de probabilité.
1.5
Lois de probabilité
On va présenter dans cette section quelques lois des probabilités qui doivent être utilisées dans la suite de cette thèse.
1.5.1
Distribution de Lindley
La distribution de Lindley a été introduite par Lindley avec un paramètre de forme (nombre réel positif) [10] pour analyser les données de temps d’échec, en particulier dans les applications de modélisation de la …abilité de la résistance au stress. La moti-vation de la distribution de Lindley découle de sa capacité à modéliser les données de temps d’échec avec des taux de risque croissants, décroissants, unimodaux et en forme
de baignoire. La distribution de Lindley appartient à une famille exponentielle et elle peut être écrite comme un mélange de distributions Exponentielles ( ) et Gamma (2; ) avec leurs proportions de mélange sont ((1+ )1 ) et ((1+ ) ) respectivement. La distribution représente une bonne alternative aux répartitions de temps de défaillance exponentielle qui ne présentent pas de taux de défaillance unimodaux et en forme de baignoire [18]. Ghitany et al. [29; 31] déclarent qu’il est particulièrement utile pour la modélisation dans les études de mortalité et étudient leurs propriétés et la procédure inférentielle pour la distribution de Lindley.
Cette distribution a des queues minces parce que la distribution diminue exponen-tiellement pour de grandes valeurs-x. Le terme « Distribution Lindley-Exponentielle» est souvent utilisé pour désigner la forme généralisée de la distribution. Il est dé-montré que la distribution de Lindley est meilleure que la distribution exponentielle lorsque le taux de risque est unimodal ou en forme de baignoire. Mazucheli et Achcar [25] ont également proposé la distribution de Lindley comme une alternative possible aux distributions Exponentielles et Weibull.
Dé…nition 1.5.1. Une varible aléatoire. continue X suit une loi de Lindley de paramètres 2 R+, si elle admet pour densité de probabilité la fonction :
f (x) = 8 > > < > > : 2 1+ (1 + x) e x , x > 0, > 0 0 sinon ceci est noté X L ( ).
de survie S (x) de X sont données par : F (x) = 8 > > < > > : 1 e x(1+ + x)1+ , x > 0, > 0: 0 sinon et S (x) = 8 > > < > > : e x(1+ + x) 1+ , x > 0, > 0 0 sinon
Propriété 1.5.2.Si X L ( )alors la moyenne théorique et la variance théorique de X sont données respectivement par :
E (X) = + 2 ( + 1) ; V (X) = 2 + 6 + 2 2(1 + )2 :
Propriété 1.5.3.Si X L ( )alors le coe¢ cient d’asymétrie théorique (skewness) et le coe¢ cient d’aplatissement théorique (kurtosis) de X sont donnés respectivement par : 1 = 2 3+ 6 2+ 6 + 2 2+ 4 + 2 32 et 2 = 3 3 4+ 24 3+ 44 2 + 32 + 8 2+ 4 + 2 2
1.5.2
Distribution de Pareto
L’économiste italien Vilfredo Frédérico Damaso surnommé par ses étudiants Mar-quis de Pareto est le premier à mettre en évidence l’application d’une loi puissance à un phénomène économique. En 1906 il étudie la répartition des revenus des habitants de divers pays industrialisés et constate que 80% des richesses appartiennent à 20% de la population et ce, quel que soit le pays observé.
En e¤et, par projection, ce principe se véri…e dans de nombreux domaines. La majorité des résultats ou des impacts, sont dûs à une minorité des causes. 20% des
bugs sont responsables de 80% des plantages de logiciels, 20% des articles en stock représentent 80% du coût de stockage, etc. D’où la seconde appellation : la loi des 20=80 (ou 80=20).
- En gestion des stocks, sous sa forme de loi ABC de Joseph Juran qui énonce que les ressources représentant 70 à 80% du CA sont rassemblés dans la classe A, les ressources contribuant entre 10 à 15% au CA sont dans la classe C et la classe B rassemble les ressources intermédiaires. Juran déclare que : le principe de Pareto permet seulement de séparer les choses en deux parts. En réalité, il existe 3 parties. La troisième est un « résidu » qui prend place entre les composantes prioritaires et les composantes secondaires. Ce « résidu » peut être dénommé « zone à risques » (awkward-zone). Chaque élément de cette zone à risques n’est pas assez important pour justi…er un lourd investissement dans l’analyse, mais leur regroupement dépasse les capacités d’analyse.
Dé…nition 1.5.2. Une variable aléatoire. continue X suit une loi de Pareto de paramètres , k 2 R+, si elle admet pour densité de probabilité la fonction :
f (x) = 8 > > < > > : k x k+1 si x 0 si x < Ceci est noté X P a ( ; k).
fonction de survie S (x) de X sont données par : F (x) = 8 > > < > > : 1 x k si x 0 si x < et S (x) = 8 > > < > > : x k si x 0 si x <
Propriété 1.5.5. Si X P a ( ; k) alors la moyenne théorique et la variance théorique de X sont données respectivement par :
E (X) = k
1 (n’existe que si k > 1) ; V (X) = k
2
( 1)2( 2) (n’existe que si k > 2) :
Propriété 1.5.6. Si X P a ( ; k) alors le coe¢ cient d’asymétrie théorique (skewness) et le coe¢ cient d’aplatissement théorique (kurtosis) de X sont donnés respectivement par : 1 = 2 (k + 1) k 3 r k 2 k si k > 3 et 2 = 9k3 15k2 12 k3 7k2+ 12k si k > 4
1.5.3
Distribution de Gamma
En théorie des probabilités et en statistiques, une distribution Gamma ou loi Gamma est un type de loi de probabilité de variables aléatoires réelles positives.
La loi de distribution gamma repose sur une fonction portant le même nom. Cette fonction est une intégrale n’admettant pas de primitive sous la forme d’une fonction élémentaire. Elle s´écrit
( ) =
1
Z
0
Cette intégrale converge seulement si > 0 et on peut véri…er que
( + 1) = ( ) ; > 0 et (n + 1) = n!; 8 n 2 N
Dé…nition 1.5.3. Une variable aléatoire continue X suit une loi Gamma de paramètres et (strictement positifs), sa fonction de densité de probabilité s’écrit
f (x) =
x 1exp x
( ) ; x > 0:
Ceci est noté X Ga ( ; ).
Propriété 1.5.7. Si X Ga ( ; ) alors la fonction de répartition F (x) et la fonction de survie S (x) de X sont données par :
F (x) =
;x
( ) et S (x) = 1
;x ( )
Propriété 1.5.8. Si X Ga ( ; ) alors la moyenne théorique et la variance théorique de X sont données respectivement par :
E (X) = ;
V (X) = 2:
Propriété 1.5.9. Si X Ga ( ; ) alors le coe¢ cient d’asymétrie théorique (skewness) et le coe¢ cient d’aplatissement théorique (kurtosis) de X sont donnés respectivement par : 1 = 2 p et = 2 = 3 ( + 2) .
La loi Gamma est un bon modèle de probabilité pour prévoir la durée de vie des appareils qui subissent une usure (ex. véhicules, appareils ménagers, ordinateurs). Cette loi est parfois utile en météorologie (nombre de pluie durant un interval de temps T) est peut utiliser en biostatistique.
Chapitre 2
Méthodes combinés et
Transformé-Transformer
Les distributions statistiques sont couramment utilisées pour décrire les phéno-mènes du monde réel. En raison de l’utilité des distributions statistiques, leur théorie est largement étudiée et de nouvelles distributions sont développées. L’intérêt pour le développement de distributions statistiques plus souples reste important dans la profession statistique. De nombreuses classes de distributions généralisées ont été dé-veloppées et appliquées pour décrire divers phénomènes. Une caractéristique commune de ces distributions généralisées est qu’elles ont plus de paramètres.
2.1
Modèles combinés
Les modèles combinés sont dé…nis en matière de deux fonctions de densité de probabilité, des poids de mélange et de la limite de porter du domaine. qui est suggéré par Cooray et Ananda [26]. Ils ont construit un modèle combiné ayant la fonction de densité de probabilité f (x) = 8 > > < > > : cf1(x) 1 < x cf2(x) x <1 (2.1)
où f1 et f2 sont des fonctions de densité de probabilité, tandis que c est une constante
de normalisation qui résulte en imposant des conditions de continuité et de di¤éren-tiabilité, (2.1) est appelé un modèle épissé à deux composantes des petites pertes. Par conséquent, le rôle du seuil (0 < < limite supérieure du contrat) est très important, étant le point où sur la base de l’analyse des données.
D’aprés Cooray et Ananda [26], f1 est pris comme étant la densité Lognormal,
alors que f2 est la densité de Pareto. Sur la base des mêmes distributions, Scollnik
[9] a proposé deux modèles combinés di¤érents, plus généraux que ceux étudiés par Cooray et Ananda [26]. De la même manière, Teodorescu et Vernic [39] ont proposé des modèles Exponentiel-Pareto combinés. De plus, Preda et Ciumara [43] ont réalisé une étude comparative entre les distributions Weibull-Pareto et Lognormal-Pareto.
Construction et caractéristiques du modèle combiné
Suivant Cooray et Ananda (2005) [26], une densité combiné est dérivée de
f (x) = 8 > > < > > : cf1(x) 1 < x cf2(x) x <1
a…n d’obtenir une fonction de densité combiné lisse, on imposants des conditions de continuité et de di¤érentiabilité au seuil , c’est-à-dire R01f (x)dx = 1; f1( ) = f2( )
et dxdf1( ) = dxdf2( ):
Scollnik [7] a remarqué que la fonction de densité du modèle combiné (2.1) pourrait également être écrite comme
f (x) = 8 > > < > > : rf1 (x) 1 < x (1 r) f2 (x) x <1 (2.2)
où 0 r 1, tandis que f1 (x)et f2 (x)sont des troncatures adéquates des fonctions de densité f1 et f2. Plus précisément, si Fi désigne la distribution de répartition de
fi, nous avons f1 (x) = f1(x) F1(x) ; 1 < x (2.3) f2 (x) = f2(x) 1 F2(x) ; x <1
Il est facile de voir que la fonction de densité (2.2) peut être interprétée comme un modèle de mélange à deux composants avec des poids de mélange r et 1 r (c’est-à-dire une combinaison convexe de deux fonctions de densité).
Dans [39], Teodorescu et Vernic ont déduit certaines propriétés du modèle (2.2) concernant sa fonction de répartition, les moments initiaux et la fonction caractéris-tique. Ces propriétés sont présentées ci-dessous. Si X est une variable aléatoire avec fonction de densité f , on note son moment initial de la nieme entrée par
En(f ) = E (Xn)
et sa fonction caractéristique par
'f(t) = 'X(t) = E eitX :
Proposition 2.1.1.
a) Soit F la fonction de répartition complète de la fonction de densité donnée dans (2.2). alors F (x) = 8 > > < > > : rF1(x) F1( ) 1 < x r + (1 r)F2(x) F2( ) 1 F2( ) x <1 (2.5)
b) En supposant que toutes les quantités impliquées existent, le niemeordre moment
initial de la fonction de densité (2.2) est
En(f ) = rEn(f1) + (1 r) En(f2) ;
alors que sa fonction caractéristique est
'f(t) = r'f
2.1.1
Générer des valeurs aléatoires à partir de la fonction
de densité combiné
A…n de générer de telles valeurs aléatoires, on suggérait d’utiliser la méthode d’in-version, en supposant que F1 et F2 admettent des fonctions inverses. Par conséquent,
si u est une valeur générée à partir de la distribution uniforme U (0; 1), nous obtenons une valeur x générée à partir de (2.2) comme
-Si u F ( ) = r puis résolvez u = rF1(x)
F1( ) Pour x, c’est-à-dire, x = F1 1 u rF1( ) ; -si u > r résout u = r + (1 r)F2(x) F2( ) F2( ) Pour x, c’est-à-dire, x = F2 1 u r + (1 u) F2( ) 1 r :
2.1.2
Inférence statistique
Dans Teodorescu et Vernic [39], l’algorithme suivant basé sur la méthode du maxi-mum de vraisemblance (MV) a été suggéré. Supposons que la fonction de densité (2.2) dépend des paramètres réels 1; :::; l, , où l 2 N, et considérer l’échantillon de
données aléatoires (x1; ::::; xn). Sans perte de généralité, nous supposons qu’il s’agit
d’un échantillon ordonné, c’est-à-dire x1 ::: xn. Pour appliquer la méthode
du maximum de vraisemblance, nous devons connaître la valeur entière m telle que le paramètre inconnu est entre les observations mieme et (m + 1)eme
xm xm+1. En supposant que, d’une certaine manière, nous connaissons ce m,
la fonction de vraisemblance est
L (x1; :::; xn; 1; :::; l; ) = m Y i=1 rf1(xi) n Y i=m+1 (1 r) f2(xi) = rm(1 r)n m m Y i=1 f1(xi) n Y i=m+1 f2(xi):
Malheureusement, en général, nous ne connaissons pas la valeur exacte de m ; notez également que si m change, l’estimation du maximum de vraisemblance change également. Par conséquent, nous proposons l’algorithme d’estimation suivant qui tient compte de toutes les valeurs possibles de m telles que xm xm+1 :
Etape 1. Pour chaque m = 1; 2; :::; n 1, do
evaluer ^1; :::; ^l; ^en tant que solutions du système du maximum de vraisemblance
8 > > < > > : @ ln L @ i = 0; i = 1; :::; l @ ln L @ = 0: (2.6)
Si xm xm+1 alors les estimations de maximum de vraisemblance sont
^M V
1 = ^i; i = 1; :::; l; ^ M V
= :
Etape 2. Si l’étape 1 ne donne aucune solution pour , alors nous sommes dans une des deux situations : m = n ou m = 0, donc nous recommandons d’utiliser uniquement f1 et, respectivement, f2 pour la fonction de vraisemblance.
Remarque 2.1.Avec cet algorithme, il faut véri…er les intervalles n 1, de sorte que le temps de calcul dépend fortement de l’amplitude de n.
2.2
Méthode de Transformé-Transformer (T
X)
Eugene et al. (2002) [35] a introduit la famille de distributions bêta-généralisée avec fonction de répartition
G (x) =
Z F (x)
a
b (t) dt; (2.7)
où b (t) est la fonction de densité de probabilité du variable aléatoire bêta et F (x) est la fonction de répartition pour un autre variable aléatoire. La fonction de densité de probabilité correspondant à (2.7) est donné par
g (x) = 1
B ( ; )f (x) F
1(x) (1 F (x)) 1
:
La variable aléatoire bêta se situe entre 0 et 1, de même que la fonction de réparti-tion F (x) d’un autre variable aléatoire. La limitaréparti-tion de l’utilisaréparti-tion d’un générateur avec un support compris entre 0 et 1 soulève une question intéressante : « Peut-on utiliser d’autres distributions avec un support di¤érent en tant que
gé-nérateur pour dériver di¤érentes classes de distributions ?» Cette section abordera cette question et introduira une nouvelle technique pour dériver des familles de distributions en utilisant n’importe quelle fonction de densité de probabilité en tant que générateur.
Alzaatreh et al. (2013) [1] a étendu la famille bêta généralisée et a dé…ni la famille T X(W ). La fonction de distribution cumulative de la distribution T X(W )est
G (x) =
Z W (F (x))
a
où r(t) la densité de probabilité d’une variable aléatoire T 2 [a; b], pour 1 a < b 1. Soit W (F (x)) une fonction de la fonction de répartition F (x) de toute variable aléatoire X pour que W (F (x)) satisfait aux conditions suivantes :
8 > > > > > > < > > > > > > : W (F (x))2 [a; b]
W (F (x))est di¤érentiable et monotoniquement non décroissante si x ! 1; W (F (x)) ! a et si x ! 1; W (F (x)) ! b:
(2.8)
La méthode pour générer des nouvelles familles de distribution est présentée à la suivante dé…nition.
Dé…nition 2.2.1 Soit X une variable aléatoire avec fonction de densité de proba-bilité f (x) et fonction de répartition cumulative F (x). Soit T une variable aléatoire continue avec fonction de densité de probabilité r(t) dé…nie sur [a; b]. La fonction de distribution cumulative d’une nouvelle famille de distributions est dé…nie comme
G (x) =
Z W (F (x))
a
r (t) dt (2.9)
où W (F (x)) satisfait aux conditions de (2.8). La fonction de distribution cumulative G(x) dans (2.9) peut être écrit comme G(x) = R fW (F (x))g, où R(t) est le La fonction de distribution cumulative de la variable aléatoire T . La fonction de densité de probabilité associée à (2.9) est
g (x) = d
dxW (F (x)) rfW (F (x))g (2.10) Notez que :
La fonction de distribution cumulative dans (2.9) est une fonction composite de (R:W:F )(x).
La fonction de densité de probabilité r(t) dans (2.9) est "transformé" en un nouveau fonction de distribution cumulative G(x) à travers la fonction W (F (x)) qui agit comme un « transformateur» . Par conséquent, nous nous référerons à la distri-bution g(x) dans (2.10) transformée à partir de la variable aléatoire T par la variable aléatoire du transformateur X et l’appeler "Transformé-Transforme" ou distribution T X.
La variable aléatoire X peut être discrète et dans ce cas G(x) est le fonction de distribution cumulative d’une famille de distributions discrètes.
Des di¤érentes W (F (x)) donneront une nouvelle famille de distributions. La dé-…nition de W (F (x)) dépend du support de la variable aléatoire T . Voici quelques exemples de W (:).
1. Lorsque le support de T est borné : Sans perte de généralité, on suppose que le support de T est [0; 1]. Les distributions pour ce type de T incluent des distri-butions uniformes (0; 1), bêta, Kumaraswamy et d’autres types de distribution bêta généralisée. W (F (x)) peut être dé…ni comme F (x) ou F (x). Il s’agit de la famille de distributions générées par le bêta qui ont été bien étudiées au cours de la dernière décennie.
2. Si le support de T est [a; 1), a 0 : Sans perte de généralité, on suppose que a = 0. W (F (x)) peut être dé…ni comme log (1 F (x)), 1 F (x)F (x) , log (1 F (x))
et 1 F (x)F (x) .
3. Lorsque le support de T est ( 1; 1) : W (F (x)) peut être dé…ni comme log [ log (1 F (x))], logh1 F (x)F (x) i, log [ log (1 F (x))] et logh1 F (x)F (x) i.
Tableau 2:1
Fonctions de densité de certaines familles T X basées sur di¤érentes fonctions W (:) T W (F (x)) g(x) [0;1) 1 F (x)F (x) (1 F (x))f (x) 2r h F (x) 1 F (x) i [0;1) log (1 F (x)) 1 F (x)f (x) r [ log (1 F (x))] [0;1) 1 F (x)F (x) f (x)F 1(x) (1 F (x))2 r h F (x) 1 F (x) i [0;1) log (1 F (x)) f (x)F1 F (x)1(x)r [ log (1 F (x))] ( 1; +1) logh1 F (x)F (x) i F (x)(1 F (x))f (x) rhlog 1 F (x)F (x) i
( 1; +1) log [ log (1 F (x))] (F (x) 1) log(1 F (x))f (x) r [log ( log (1 F (x)))] ( 1; +1) logh1 F (x)F (x) i F (x)(1 F (x))f (x) rhlog 1 F (x)F (x) i
Chapitre 3
Distributions Gamma(2; )-Pareto
combiné et Lindley-Pareto
Dans ce chapitre, nous avons représenté deux nouvelles distributions qui sont générées par la distribution de Pareto.
3.1
Gamma(2; )-Pareto combiné
Pour générer cette distribution, nous avons utilisé la formule (2:1) de modèles combiné comme décrit à la section 2.1.
Soit X la variable aléatoire avec densité
f (x) = 8 > > < > > : cf1(x) 0 < x cf2(x) x <1
où f1 est une densité de Gamma(2; ), f2 une densité de Pareto à deux paramètres
et c la constante de normalisation. Par conséquent,
f1(x) = 2x exp( x); x > 0; (3.1)
f2(x) =
x +1; x > ; (3.2)
où > 0, > 0 , > 0 sont des paramètres inconnus.
A…n d’obtenir une fonction de densité lisse combiné, nous imposons des conditions de continuité et de di¤érentiabilité au point de seuil , c’est-à-dire
8 > > < > > : f1( ) = f2( ) d dxf1( ) = d dxf2( ) (3.3)
ces deux restrictions donnent 8 > > < > > : 2 exp( ) = 2 ( 1) exp( ) = ( +1)2 (3.4)
et après un certain calcul, nous obtenons 8 > > < > > : = 2:511 8 = 0:511 8
et pour trouver la constante de normalisation, nous imposons la condition
1 Z 0 f (x)dx = 1; ce qui donne c = 1 2 e e = 0:583 05:
Ainsi, f (x) peut être réécrit comme suit : f (x) = 8 > > < > > : 3: 678 5x2 exp 2: 511 8 x 0 < x 0:298 4 x1: 511 8 0:511 8 x < 1 (3.5)
Proposition 3.1.1.La fonction de distribution cumulative de ce modèle combiné est
F (x) = 8 > > > < > > > : 0:583 04 1 0:4(2: 5 + 6: 279 5x) e( 2: 511 8x) 0 < x 1 0:583 04 x 0:511 8! x <1 (3.6)
Proposition 3.1.2.Le mode unique de la distribution Gamma(2; )-Pareto combinée est
xmod e = 0:398 12
où 0 < x
3.1.1
Générer des valeurs aléatoires à partir de la
distribu-tion Gamma(2; )-Pareto combinée
Pour générer de telles valeurs aléatoires, nous suggérons d’utiliser la méthode d’inversion, dans ce cas la fonction de distribution cumulative F peut être inversée. Si u est une valeur générée à partir de la distribution uniforme U (0; 1), on obtient une valeur x générée à partir de (1) comme
-si u F ( ) = p alors, x = 0:398 12 (LambertW ( 1; e 1(1:715 1u 1)) + 1) ; -si u > p alors, x = 0:583 041 u
1 0:511 8.
3.1.2
Estimation des paramètres
Dans cette sous-section, nous présenterons deux algorithmes pour l’estimation du paramètre inconnu .
Premier algorithme : Une procédure ad hoc basée sur des percentiles
La procédure ad hoc suivante fournit une forme fermée pour le paramètre , es-timée à l’aide de percentiles. Sur la base des percentiles, le paramètre peut être estimé, en tant que pieme percentile, où p = F ( ) :
De Klugman et al. (1998) [41], nous avons une estimation empirique lisse du pieme
percentile donné par
avec 8 > > < > > : m = [(n + 1)p] h = (n + 1)p m
ici [a] indique le plus grand entier plus petit ou égal avec a.
Notez que si ^ est plus proche de x1 ou xn, alors Pareto ou Gamma(2; ) sera
respectivement un modèle supérieur à celui du composite.
Deuxième algorithme : Estimation du maximum de vraisemblance (MV)
La fonction de vraisemblance est donnée par L(x1; :::; xn; ) = n Y i=1 f (xi) = m Y i=1 f (xi) n Y i=m+1 f (xi) = k 0:5118n 2:5118me( 2: 511 8 1Pmi=1xi) avec k = (0:2984)n m(3:678)m m Q i=1 xi n Q i=m+1 x1:5118 i Etape 1.
La dérivée ln L par rapport à donne d ln L d = 0:5118n 2:5118m +2: 511 8 Pm i=1xi 2 ;
par conséquent, la solution de l’équation de vraisemblance d ln Ld = 0 est ^ = 2: 511 8mx(m) 2:5118m 0:5118n; où x(m) = Pm i=1xi m
si xm ^ xm+1 alors les estimations de MV sont
Etape 2.Si l’étape 1 ne donne aucune solution pour , nous sommes en situation : Pour chaque m (m = 1; 2; :::; n 1), évaluer de (4).
Véri…ez si ^m est entre xm ^ xm+1 Si oui, puis
^M V = ^m,
si non, passez à la prochaine m.
3.2
Distribution Lindley-Pareto
La fonction de répartition de la famille de distributions T X dé…nie par Alzaa-treh, et al. [1] est donné par
G (x) =
Z F (x) 1 F (x)
0
r (t) dt (3.7)
est une autre idée pour obtenir une nouvelle distribution.
Dans ce travail, nous introduisons une nouvelle famille de distribution générée par une variable aléatoire T qui suit la distribution Lindley avec un paramètre > 0.
Soit T variable aléatoire suit la loi de lindley, T 2 [0; 1) et r (t) la densité de probabilité de cette loi.
La dé…nition (3.7) conduit à la famille Lindley-X avec la densité de probabilité g(x) = 2 1 + f (x) (1 F (x))2 1 + F (x) 1 F (x) exp F (x) 1 F (x) : (3.8) Et soit X une variable aléatoire suit la loi de Pareto, alors (3.2) se réduit à
g(x) = k
2
e ( + 1) 2kx
La fonction de répartition cumulative de la nouvelle distribution est donnée par G (x) = 1 1 ( + 1) k k+ xk exp x k k 1 : (3.10)
Nous renvoyons la variable aléatoire avec la fonction de distribution cumulative (3.10) comme distribution de Lindley Pareto (LP) avec les paramètres , et k que nous désignons par LP( ; ; k).
3.2.1
Propriétés de la distribution Lindley Pareto
La dérivée de l’équation (3.9) par rapport à x est donnée par :
g0(x) = ke + 1 2 3kx 2k 2e xkk k 2k k+ kxk ; (3.11) -pour k 1
2 La fonction de densité de probabilité de la distribution LP diminue.
-pour k 21 et 0 < < 2, x0 = k1 (2k 1)
1
k est le point critique unique dont
la distribution LP est maximale. Le mode x0 est la solution de l’équation u(x) = 0,
où
u(x) = k 2k k+ kxk ;
le mode de distribution LP est donné par
mode(X) = 8 > > < > > : 1 k (2k 1) 1 k si k > 1 2 et 0 < < 2 si non
FIG. 3.2 : Plot de fonction de densité pour di¤érentes valeurs de et k
FIG. 3.3 : Plot de fonction de densité pour di¤érentes valeurs de et k
Fonction de hasard
La fonction de hasard de la distribution LP est
h (x) = g(x) 1 G(x) = k 2 k x2k 1 ( xk+ k); x > ; (3.12)
les comportements limitants de la fonction de densité et la fonction de hasart de X sont donnés dans le théorème 3.2.1.
Théorème 3.2.1.
La limite de la fonction de densité de X si x ! 1 est 0. Lim
x! +g(x) = Limx! +h(x) =
2
k
( + 1): (3.13) Les limites de la fonction de hasard de X si x ! 1 sont données par :
Lim x!+1h(x) = 8 > > > > > > < > > > > > > : 0 ; k < 1 k k ; k = 1 +1 ; k > 1 (3.14)
Preuve. La plupart des résultats de ce type peuvent être facilement illustrés par les équations (3.9) et (3.10). Il su¢ t d’obtenir le résultat (3.12). Pour ce faire, on peut voir à partir de la fonction hasard dans (3.6) que
Lim x!+1h(x) = k 2 k x!+1Lim 1 x2k 1 x2k
cela implique le résultat dans (3.14).
Proposition 3.2.1. Soit h(x) la fonction de taux de risque de X. Alors h(x) augmente pour k > 1.
Preuve. La fonction (x) = g0(x)=g(x) pour la distribution LP est donnée par (x) =
k 2k k+ kxk
et
0(x) = k (k 1) xk k(1 2k)
x2 ;
-si 0(x) < 0;pour 0 < k < 12, il s’ensuit que, à partir du théorème (b) de Glaser [38], le taux d’échec diminue.
-lorsque 12 < k < 1 et > k(k 1)1 2k , il découle du théorème (b) de Glaser [38] que le taux d’échec diminue et pour < k(k 1)1 2k , en outre, nous notons que le taux d’échec peut être une baignoire à récurrence.
-si k > 1, alors 0(x) > 0. Il résulte du théorème (b) de Glaser [38] que le taux d’échec augmente.
3.2.2
Moments et fonction génératrice des moments
Fonction génératrice de moments
La fonction génératrice de moments de la distribution LP est donné par
MX (t) = Z 1 etxg (x) dx = Z 1 X1 i=0 tixi i! g (x) ! dx = 1 X i=0 ti i!E X i = e ( + 1) 1 X i=0 ti i i! ki i k + 2; : (3.15) Moments
Le n ième moment sur l’origine de la distribution LP est :
E (Xn) =
ne
( + 1) nk
n
les deux premiers moments de X peuvent être écrits comme E (X) = e ( + 1) 1k 1 k + 2; ; E X2 = 2e ( + 1) 2k 2 k + 2; :
3.2.3
Variance
La variance de la distribution LP est donnée par
var (X) = 2e ( + 1)2 k2 ( + 1) 2 k + 2; + e 2 1 k + 2; : (3.17) Les coe¢ cients de variation , skewness et kurtosis de la distribution LP ont été obtenus comme = e 2 q ( + 1) 2k + 2; + e 2 1 k+ 2; 1 k + 2; ; skewness = 1 e12 ( + 1)32 3 k + 2; ( + 1) k2 + 2; + e 2 1 k + 2; 3 2 ; kurtosis = 1 e ( + 1) 3 4k + 2; ( + 1) 2k+ 2; + e 2 1 k + 2; 2:
Remarque 3.2.1. Toutes ces expressions sont indépendantes du paramètre et dépendent des paramètres et k.
Tableau 3:1
Mean, Median, Mode, Var, , skewness, kurtosis pour certaines valeurs de et k avec = 0:5
k Mode(x0) Mean Median variance skewness kurtosis
0:5 1:5 0:961 50 1: 276 6 1: 186 1 3: 539 2 1: 473 7 0:403 66 0:512 11 2 0:866 03 0:994 51 0:955 73 2: 072 4 1: 447 5 0:351 63 0:383 22 3 0:746 9 0:782 67 0:770 10 1: 250 9 1: 429 0 0:316 14 0:305 11 5 0:646 00 0:650 99 0:647 91 0:853 94 1: 419 5 0:298 47 0:269 13 7 0:603 09 0:602 79 0:601 67 0:729 49 1: 416 9 0:293 66 0:259 67 10 0:571 41 0:569 45 0:569 17 0:649 77 1: 415 5 0:291 11 0:254 71 20 0:535 21 0:533 35 0:533 47 0:569 19 1: 414 5 0:289 28 0:251 17 1 1:5 0:605 71 0:896 53 0:831 92 1: 699 7 1: 454 2 0:319 11 0:429 78 2 0:612 37 0:767 1 0:732 49 1: 213 4 1: 436 0:286 69 0:339 57 3 0:592 82 0:660 78 0:644 95 0:884 89 1: 423 6 0:265 46 0:286 04 5 0:562 37 0:589 22 0:582 51 0:697 61 1: 417 5 0:255 35 0:262 15 7 0:546 23 0:561 69 0:557 64 0:632 48 1: 415 9 0:252 69 0:256 05 10 0:533 15 0:542 16 0:539 68 0:588 55 1: 415 0:251 3 0:252 92 20 0:516 98 0:520 5 0:519 46 0:542 1: 414 4 0:250 32 0:250 72
3.2.4
Fonction de quantile
GX est continue et strictement croissante, la fonction de quantile de X est QX( ) =
GX1( ), 0 < < 1: Dans le théorème suivant, nous donnons une expression explicite pour QX en termes de fonction W de Lambert. Pour plus de détails sur la fonction
W de Lambert, nous renvoyons le lecteur à Jodrà [36]. Théorème 3.2.2.
La fonction de quantile de la distribution X de LP est
x = 1 1LambertW ( 1; ( 1) ( + 1) exp ( ( + 1)))
1 k
; 0 < < 1, (3.18)
où ; ; k > 0 et LambertW désignent la branche négative de la fonction W de Lam-bert (W (z) exp (W (z)) = z, où z est un nombre complexe).
Preuve : Pour tout , ; k > 0 et …xes, soit 2 (0; 1). Nous devons résoudre l’équation GX(x) = par rapport à x, pour x > .
1 1 ( + 1) k k+ xk exp xk k 1 = kx k+ 1 exp xk k 1 = ( 1) ( + 1) ; (3.19)
en multipliant par e ( +1) les deux côtés de l’équation (3.19), nous obtenons :
kx
k
+ 1 exp kxk+ 1 = ( 1) ( + 1) e ( +1);
nous voyons que 1 + xkk est la fonction W de Lambert de l’argument réel
( 1) ( + 1) e ( +1).
Ainsi, nous avons
LambertW ( 1) ( + 1) e ( +1) =
kx
k+ 1 ; (3.20)
pour tout ; ; k > 0 et x > il est immédiat que 1 + kxk > 1 et on peut
également véri…er que kx
k+ 1 e ( kxk+1) = ( 1) ( + 1) e ( +1) 2 1
e ; 0
puisque 2 (0; 1). Pour cela, en tenant compte des propriétés de la branche négative de la fonction W de Lambert, l’équation (3.20) devient
LambertW 1; ( 1) ( + 1) e ( +1) = kxk+ 1 ;
donc on obtient, la solution pour x
x = 1 1LambertW 1; ( 1) ( + 1) e ( +1)
1 k
Réglage = 0:25; 0:50 et 0:75 dans (3.18), les trois quartiles de la distribution peuvent être obtenus
'1 = G 1(0:25) = 1 1LambertW 1; 1 4 1 ( + 1) exp ( ( + 1)) 1 k ; Median = '2 = G 1(0:5) = 1 1LambertW 1; 1 2 1 ( + 1) exp ( ( + 1)) 1 k ; '3 = G 1(0:75) = 1 1LambertW 1; 3 4 1 ( + 1) exp ( ( + 1)) 1 k :
Les tableaux 2 et 3 montrent certains quantiles de la distribution de Lindley Pareto, qui ont été calculés à partir de l’expression de forme fermée pour QX donnée
Tableau 3:2 : = 1 = 0:01; k = 0:75 = 0:1; k = 0:75 = 0:5; k = 1 = 1:5; k = 2:5 0:01 36: 644 2: 216 6 1: 059 2 1: 004 4 0:05 116: 91 5: 783 2 1: 282 7 1: 022 2 0:1 200: 06 9: 595 8 1: 544 1: 044 3 0:15 279: 38 13: 256 1: 795 4 1: 066 6 0:2 358: 86 16: 933 2: 043 1: 089 '1 = 0:25 440: 42 20: 71 2: 291 4 1: 111 8 0:3 525: 42 24: 65 2: 543 6 1: 134 9 0:35 615: 1 28: 81 2: 802 6 1: 158 6 0:4 710: 72 33: 246 3: 071 8 1: 183 0:45 813: 72 38: 024 3: 354 2 1: 208 3 '2 = 0:5 925: 84 43: 226 3: 653 6 1: 234 8 0:55 1049: 3 48: 956 3: 975 1: 262 6 0:6 1187: 1 55: 352 4: 324 1: 292 2 0:65 1343: 3 62: 604 4: 709 4 1: 324 1 0:7 1524: 1 70: 996 5: 143 1: 359 1 '3 = 0:75 1738: 8 80: 962 5: 643 1: 398 1 0:8 2003: 2 93: 24 6: 239 6 1:4430 0:85 2347: 4 109: 22 6: 989 1: 496 9 0:9 2839: 4 132: 06 8: 016 4 1: 567 0:95 3699: 8 172:0 9: 716 2 1: 674 5 0:99 5791:0 269: 08 13: 494 1: 883 8
Tableau 3:4 : = 2 = 0:01; k = 0:75 = 0:1; k = 0:75 = 0:5; k = 1 = 1:5; k = 2:5 0:01 73: 288 4: 433 2 2: 118 4 2: 008 8 0:05 233: 82 11: 566 2: 565 4 2: 044 4 0:1 400: 12 19: 192 3: 088 2: 088 6 0:15 558: 76 26: 512 3: 590 8 2: 133 2 0:2 717: 72 33: 866 4: 086 2: 178 '1 = 0:25 880: 84 41: 42 4: 582 8 2: 223 6 0:3 1050: 8 49: 3 5: 087 2 2: 269 8 0:35 1230: 2 57: 62 5: 605 2 2: 317 2 0:4 1421: 4 66: 492 6: 143 6 2: 366 0:45 1627: 4 76: 048 6: 708 4 2: 416 6 '2 = 0:5 1851: 7 86: 452 7: 307 2 2: 469 6 0:55 2098: 6 97: 912 7: 95 2: 525 2 0:6 2374: 2 110: 7 8: 648 2: 584 4 0:65 2686: 6 125: 21 9: 418 8 2: 648 2 0:7 3048: 2 141: 99 10: 286 2: 718 2 '3 = 0:75 3477: 6 161: 92 11: 286 2: 796 2 0:8 4006: 4 186: 48 12: 479 2: 886 0:85 4694: 8 218: 44 13: 978 2: 993 8 0:9 5678: 8 264: 12 16: 033 3: 134 0:95 7399: 6 344:0 19: 432 3: 349 0:99 11582 538: 16 26: 988 3: 767 6
3.2.5
Statistiques de command extrêmes
On peut dériver la distribution asymptotique de l’échantillon minimum X1:n en
utilisant le théorème 8:3:6 d’Arnold et. Al. [6], il s’ensuit que la distribution asymp-totique de X1:n est du type Weibull avec le paramètre de forme > 0 si
lim t!0 G (tx) G (t) = x 2k ; et lim t!1 1 G (t + x) 1 G (t) = exp x k :
Ainsi, si cela découle du théorème 1:6:2 dans Leadbetter et al.[33] qu’il doit y avoir des constantes de normalisation an> 0; bn; cn> 0 et dn tel que
Pr (an(Mn bn) x) ! exp exp
x k
et
Pr (an(mn bn) x) ! 1 exp x2k
Comme n ! 1. En suivant Corollaire 1:6:3 dans Leadbetter et al. (1983) [33] , nous pouvons déterminer la forme des constantes de normalisation. à titre d’illustra-tion, on peut voir que an = 2k et bn= G 1(1 1=n), où G 1(:)Désigne la fonction
inverse de G (:).
3.2.6
Entropie
L’entropie Rényi (1961) [5] pour la variable aléatoire X avec la fonction de densité g (x) est dé…nie comme
IR(s) =
1 1 s ln
Z 1
gs(x) dx s > 0; s6= 1; dans notre cas
Z 1 gs(x) dx = Z 1 ks 2ses ( + 1)s 2skx s(2k 1)exp s x k dx = k s 2ses ( + 1)s s Z 1 x s(2k 1) exp s x k dx;
= k s 2ses ( + 1)s s Z 1 1 ys(2k 1)exp syk dy = k s 2ses ( + 1)s s 1 2ks s+1 k ; s k ( s)2ksks+1 Z 1 gs(x) dx = k s 1 2ses 1 s k s2ksks+1 ( + 1)s s 1 2ks s + 1 k ; s IR(s) = 1 1 sln ks 2ses 1 s k s 2ks s+1 k ( + 1)s s 1 2ks s+1 k ; s k ! s > 0; s6= 1: (3.21) En outre, l’entropie de Shannon est dé…nie par E f ln (g (X))g c’est un cas spécial dérivé de lim
s!1IR(s).
3.2.7
Estimations du maximum de vraisemblance (MV)
Soit Xi LP ( ; k; ); i = 1; n;variable aléatoire. La fonction de log vraisemblance
ln l(x; ; ; k) est : L ( ) = ln l(x; ; ; k) = n ln k+2n ln +n 2kn ln n ln ( + 1)+(2k 1) n X i=1 ln xi n X i=1 xk k : (3.22) Les dérivés de L ( )) par rapport à ; k et sont :
dL ( ) d = 2n + n n ( + 1) n X i=1 xki k ; (3.23) dL ( ) dk = n k 2n ln + 2 n X i=1 ln xi n X i=1 lnxi x k i k ; (3.24) dL ( ) d = 2kn + k n X i=1 xki k+1 : (3.25)
Les trois équations (3.23), (3.24) et (3.25) ne peuvent pas être résolues directement, nous devons utiliser la méthode de …sher scoring. Nous avons
2 6 6 6 6 6 6 4 @2L( ) @ 2 @2L( ) @ @k @2L( ) @ @ @2L( ) @k@ @2L( ) @k2 @2L( ) @k@ @2L( ) @ @ @2L( ) @ @k @2L( ) @ 2 3 7 7 7 7 7 7 5 ^= 0 ^ k=k0 ^= 0 2 6 6 6 6 6 6 4 ^ 0 ^ k k0 ^ 0 3 7 7 7 7 7 7 5 = 2 6 6 6 6 6 6 4 dL( ) d dL( ) dk dL( ) d 3 7 7 7 7 7 7 5 ^= 0 ^ k=k0 ^= 0 ; (3.26) où @2L( ) @ 2 = 2n 2 + n ( +1)2; @2L( ) @k2 = n k2 Pn i=1 xk i k ln 2 xi; @2L( ) @ 2 = 2kn 2 (k + 1) k Pn i=1 xk i k+2 ; d2L( ) dkd = 2n+ Pn i=1 xk i k+1 k ln xi + 1 ; @2L( ) @ @ = k k+1 Pn i=1xki; @2L( ) @ @k = Pn i=1 ln xi xki k :
L’équation (3.26) peut être résolue itérativement où 0; k0; 0 sont les valeurs
Chapitre 4
Application et simulation
Dans ce chapitre, nous menons une étude de simulation complète pour évaluer la performance des estimateurs de vraisemblance proposés de l’estimateur de la distri-bution Gamma( ; 2) Pareto.
4.1
Simulations et des exemples illustrés
Permettez-nous maintenant d’illustrer la procédure d’estimation décrite dans le chapitre 2, sous-section 1.1, nous considérerons deux échantillons de données générés à partir du modèle Gamma (2, ) -Pareto. L’algorithme de génération utilisé est basé sur l’inversion du fonction de répartition (la méthode d’inversion présentée dans le chapitre 2, sous-section 1.2).
4.1.1
Premier exemple
Le premier ensemble de données composé de 100 valeurs a été échantillonné à partir d’une population Gamma (2, ) -Pareto avec le paramètre = 5 (voir tableau 4.1).
Tableau 4.1. 100 Valeurs de Gamma (2, ) -Pareto pour = 5
0:06222 7 0:08360 1 0:09989 3 0:118 93 0:120 32 0:231 5 0:372 07 0:393 59 0:557 29 0:718 96 0:965 91 1: 033 3 1: 043 2 1: 488 4 1: 673 1: 701 3 1: 952 9 2: 036 5 2: 175 9 2: 325 6 2: 429 5 2: 525 6 2: 620 9 2: 927 3: 049 5 3: 324 5 3: 434 3 3: 569 6 3: 697 2 3: 841 0 4: 118 4 4: 224 4 4: 885 9 4: 889 1 4: 934 8 4: 967 8 4: 984 5 5: 068 3 5: 225 8 5: 603 6 6: 024 2 6: 371 8 6: 494 4 6: 750 6 7: 311 1 7: 649 9 7: 978 9 8: 116 5 8: 293 7 8: 665 9 8: 712 3 8: 822 0 9: 273 6 9: 446 6 9: 715 2 9: 948 1 9: 995 7 10: 440 10: 543 11: 080 12: 525 12: 833 13: 705 14: 018 16: 975 17: 790 17: 845 18: 315 19: 836 22: 665 25: 354 26: 153 36: 598 39: 859 40: 844 49: 691 50: 788 55: 562 63: 398 71: 889 83: 511 93: 847 179: 06 197: 63 202: 50 242: 33 374: 76 363: 58 439: 32 503: 91 607: 06 807: 75 986: 43 1409:1 1647:0 1783: 8 3157: 8 6380: 8 8319: 4 8439: 3
Les valeurs estimées du paramètre sont :
- par l’algorithme 1 : pour m = 42; ^1 = 6: 386 1;
- par algorithme 2 MV étape 1 : ^2 = 5: 173 4;
- par algorithme 2 MV étape 2 : ^3 = 5: 027 6.
Nous avons également appliqué le test 2 pour véri…er le raccord de distribution
Tableau 4.2. Données groupées et test 2
(Les colonnes 2 et 3 résultent de l’échantillon de données, tandis que la colonne 4 est calculée à l’aide de la fonction de distribution Gamma(2; )-Pareto)
Classes F requences ni F req relafi F re theo pi n(fi pi)2
pi (cGP ) n(fi pi)2 pi (cEP ) [0; 2) 17 0:17 0:153 89 0:168 65 0:1086 [2; 6) 23 0:23 0:313 52 2: 224 9 1:5468 [6; 14) 23 0:23 0:187 39 0:968 89 3:5688 [14; 100) 19 0:19 0:219 0:384 02 0:2134 [100; 1000) 11 0:11 0:087 36 0:586 73 5:9002 [1000; 8440) 7 0:07 0:113 16 3: 948 0:1243 P 100 1 2 distance : 7: 694 5 10:125 Les distances 2 calculées pour les trois valeurs estimées des paramètres sont
d2 ^1 = 12:013;
d2 ^2 = 5:962 0;
d2 ^3 = 7:694 5:
Le test 2 accepte le modèle Gamma(2; )-Pareto pour les trois valeurs du para-mètre comme prévu. L’intéressant est que, contrairement à ce qui est attendu, d2 ^
2
est minimum.
4.1.2
Deuxième exemple
Le deuxième échantillon de données, de n = 500, a été prélevé sur le modèle Gamma(2; )-Pareto avec = 10.
Pour ces données, les valeurs estimées du paramètre sont : - par l’algorithme 1 : pour m = 208, ^1 = 11: 046
- par l’algorithme 2 MV étape 2 : ^3 = 9: 913 8.
Nous avons également appliqué le test 2pour véri…er le raccord de distribution
et les résultats pour ^3 sont donnés dans le tableau 4.3.
Tableau 4.3. Données groupées et test 2
(La signi…cation des colonnes est identique à celle du tableau 4.2)
Classes F requences ni F req rela fi F req theo pi n(fi pi)2
pi (cGP ) n(fi pi)2 pi (cEP ) [0; 5) 101 0:202 0:210 70 0:179 62 0:179 62 [5; 9) 77 0:154 0:176 77 1: 466 5 1: 466 5 [9; 14) 71 0:142 0:123 89 1: 323 6 1: 323 6 [14; 40) 91 0:182 0:203 12 1: 098 1: 098 [40; 100) 60 0:12 0:106 88 0:805 27 2:057 [100; 400) 43 0:086 0:090 77 0:125 33 0:125 [400; 1000) 21 0:042 0:032 89 1: 261 7 1:261 [1000; 2500) 15 0:03 0:020 58 2: 155 9 8:555 [2500; 10000) 11 0:022 0:017 48 0:584 39 4:84 [10000; 30000) 6 0:012 0:007 28 1: 530 1 3:31 [30000; 100000) 4 0:008 0:004 43 1: 438 5 2:85 P 500 1 2 distance : 11: 969 21:243 Les distances de 2 calculées pour les trois valeurs estimées des paramètres sont
d2 ^1 = 10:524;
d2 ^2 = 11:772;
d2 ^3 = 11:969:
Le test 2 accepte le modèle Gamma(2; )-Pareto pour les trois valeurs du
para-mètre comme prévu. La chose intéressante est que, contrairement à ce qui est attendu, d2 ^
4.2
Applications et simulations
4.2.1
Simulations
Dans cette sous-section, nous étudions le comportement des estimateurs MV pour une taille d’échantillon n. Une étude de simulation consistant en les étapes suivantes est e¤ectuée pour chaque quatuor ( , ,k; n ), où = 0:5; 0:75; 1:::; = 0:3; 0:5; 0:8:::, k = 0:5; 0:9; 1:25::: et n = 30; 50; 100.
- Choisir les valeurs initiales de 0; 0; k0 pour les éléments correspondants du
vecteur de paramètre = ( ; ; k) pour spéci…er la distribution LP( , ,k ), - choisir la taille de l’échantillon n,
- générer N échantillons indépendants de taille n de LP( , ,k ), - calculer l’estimation MV ^n de 0 pour chacun des N échantillons,
- calculer la moyenne des estimateurs obtenus sur tous les échantillons N ,
biais moyen ( ) = 1 N N P i=1 ^i 0 ;
et l’erreur quadratique moyenne
M SE ( ) = 1 N N P i=1 ^ i 0 2 :
Tableau 4.4. biais moyen des estimations simulées
=0:5; =0:3;k=0:9 =0:75; =0:3;k=1:5 =1:25; =0:3;k=2
biais( ) biais( ) biais(k) biais( ) biais( ) biais(k) biais( ) biais( ) biais(k)
n=30 0:3240 0:0668 0:0991 0:2034 0:0192 0:0768 0:3261 0:0071 0:0210
n=50 0:1088 0:0394 0:00431 0:0788 0:0087 0:02108 0:1460 0:0040 0:0589
n=100 0:0520 0:0186 0:0046 0:0653 0:0058 0:0066 0:0894 0:0022 0:0117
=1; =0:8;k=0:5 =1; =1:25;k=1:5 =1; =2;k=5
biais( ) biais( ) biais(k) bais( ) bais( ) bais(k) biais( ) biais( ) biais(k)
n=30 0:1971 0:0896 0:0151 0:5084 0:0494 0:1130 0:2532 0:0238 0:0237
n=50 0:1445 0:0680 0:0057 0:1784 0:0269 0:0220 0:1130 0:0165 0:0132
n=100 0:0521 0:0376 0:0091 0:1048 0:0167 0:0326 0:0993 0:0066 0:0567
=0:75; =0:5;k=1:25 =1:5; =1;k=1:25 =2; =3;k=1:25
biais( ) biais( ) biais(k) biais( ) biais( ) biais(k) biais( ) biais( ) biais(k)
n=30 0:155 0:0355 0:0150 0:5046 0:0239 0:1046 0:4865 0:0454 0:1284
n=50 0:1595 0:0258 0:0374 0:3976 0:0117 0:0826 0:1797 0:0396 0:0790
n=100 0:0827 0:0128 0:0172 0:2004 0:0073 0:0095 0:2808 0:0193 0:0444
=3; =1:5;k=2 =4; =3;k=3 =1:5; =5;k=7
biais( ) biais( ) biais(k) biais( ) biais( ) biais(k) biais( ) biais( ) biais(k)
n=30 1:5423 0:0097 0:1401 1:4481 0:0094 0:5102 0:4280 0:0251 0:3361
n=50 0:9111 0:0066 0:0729 0:7441 0:0071 0:5010 0:2127 0:0136 0:0616
Tableau 4.5. M SE moyen des estimations simulées
=0:5; =0:3;k=0:9 =0:75; =0:3;k=1:5 =1:25; =0:3;k=2
M SE( ) M SE( ) M SE(k) M SE( ) M SE( ) M SE(k) M SE( ) M SE( ) M SE(k)
n=30 0:1050 4:4654 10 3 9:8114 10 5 0:0414 3:6786 10 4 5:9026 10 3 0:1063 5:0350 10 5 4:4275 10 4
n=50 0:0118 1:5552 10 3 1:8561 10 5 6:2155 10 3 7:4996 10 5 4:4426 10 4 2:1316 10 2 1:5794 10 5 3:3969 10 3
n=100 0:0027 3:4546 10 4 2:1128 10 5 4:2580 10 3 3:3405 10 5 4:3903 10 5 7:9979 10 5 5:0401 10 6 1:3671 10 4
=1; =0:8;k=0:5 =1; =1:25;k=1:5 =1; =2;k=5
M SE( ) M SE( ) M SE(k) M SE( ) M SE( ) M SE(k) M SE( ) M SE( ) M SE(k)
n=30 0:0388 8:0237 10 3 2:2877 10 4 0:2584 2:4364 10 3 1:2763 10 2 6:4092 10 2 5:6487 10 4 5:6327 10 4
n=50 0:0209 4:6262 10 3 3:3000 10 5 0:0318 7:2359 10 4 4:8501 10 4 1:2762 10 2 2:7312 10 4 1:7385 10 4
n=100 0:0027 1:4167 10 3 8:3529 10 5 0:0110 2:7785 10 4 1:065110 3 9:8506 10 3 4:3718 10 5 3:2146 10 3
=0:75; =0:5;k=1:25 =1:25; =2;k=1:25 =2; =3;k=1:25
M SE( ) M SE( ) M SE(k) M SE( ) M SE( ) M SE(k) M SE( ) M SE( ) M SE(k)
n=30 0:0240 1:2623 10 3 2:2451 10 4 0:2546 5:7258 10 4 1:093510 2 0:2366 2:05867 10 3 1:6487 10 2
n=50 0:0254 6:6638 10 4 1:4017 10 3 0:1581 1:3610 10 4 6:8303 10 3 0:0323 1:5698 10 3 6:2404 10 3
n=100 0:0069 1:6307 10 4 2:9504 10 4 0:0401 5:3779 10 5 9:0554 10 5 0:0789 3:7259 10 5 1:9747 10 3
=3; =1:5;k=2 =4; =3;k=3 =1:5; =5;k=7
M SE( ) M SE( ) M SE(k) M SE( ) M SE( ) M SE(k) M SE( ) M SE( ) M SE(k)
n=30 2:3788 9:3359 10 5 0:01964 2:0969 8:8911 10 5 0:2603 0:1832 6:3244 10 4 0:1130
n=50 0:8301 4:3801 10 5 5:3191 10 3 0:5537 5:0155 10 5 0:2510 4:5248 10 2 1:8568 10 4 3:7919 10 3
n=100 0:2535 1:0024 10 5 5:9578 10 4 0:3670 1:1140 10 5 2:0932 10 2 2:4916 10 3 4:7630 10 5 5:3214 10 2
4.2.2
Application aux ensembles de données réelles
Dans cette sous-section, nous illustrons l’applicabilité de la distribution LP en considérant les di¤érents ensembles de données utilisées par di¤érents chercheurs (don-nés à vie). Dans chaque cas, les paramètres sont estimés par la méthode de maximum de vraisemblance comme décrit à la sous-section 3.2.7.
Comme x > , le MV de est la statistique de premier ordre x(1) c-à-d
= minfxig
dL ( ) d = 2n + n n ( + 1) 1 k n X i=1 xki dL ( ) dk = n k 2n ln + 2 n X i=1 ln xi k n X i=1 xki ln xi+ ln k n X i=1 xki
et en utilisant la commander Maxlik (https ://CRAN.R-project.org/package=maxLik) dans R.
Nous adaptons également les distributions LP, L-E, PL, L-W, E-P, L, GaL, P. A…n de comparer les modèles de distribution d’arbres, nous considérons des cri-tères comme 2LL, AIC (critère d’information d’Akaike), AICC (critère d’infor-mation Akaike corrigé) et BIC (critère d’inford’infor-mation bayésien) pour l’ensemble de données.
La sélection du modèle est e¤ectuée à l’aide des statistiques suivantes :
AIC = 2LL + 2p; CAIC = 2LL + 2pn n p 1
BIC = 2LL + p log (n).
Illustration 1 : Application à temps d’attente dans une …le d’attente
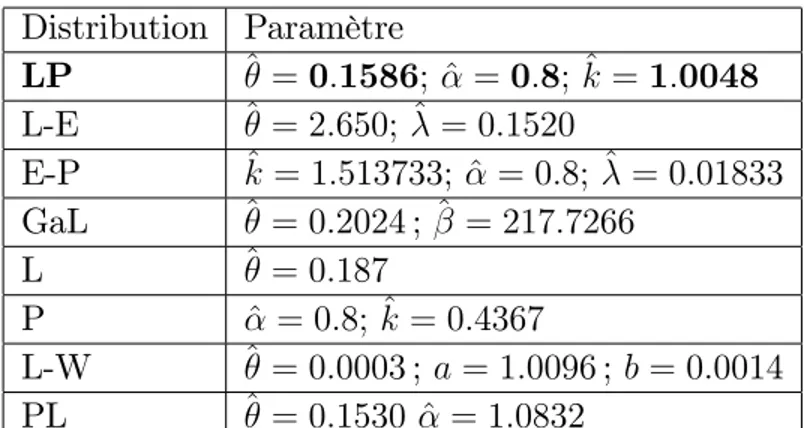
Nous considérons 100 observations sur le temps d’attente comme un exemple ré-current qui se produit pour le client a reçu un service dans une banque. Les ensembles de données et leur résultat sont représentés au tableau 5:1, tableau 4:7 respectivement.
Distribution Paramètre LP ^ = 0:1586; ^ = 0:8; ^k = 1:0048 L-E ^ = 2:650; ^ = 0:1520 E-P ^k = 1:513733; ^ = 0:8; ^ = 0:01833 GaL ^ = 0:2024 ; ^ = 217:7266 L ^ = 0:187 P ^ = 0:8; ^k = 0:4367 L-W ^ = 0:0003 ; a = 1:0096 ; b = 0:0014 PL ^ = 0:1530 ^ = 1:0832
Tableau 4.7. Les -LL, AIC, CAIC, BIC pour 100 clients bancaires Distribution -LL AIC CAIC BIC
LP 308:9731 621:9462 622:0874 627:6346 L-E 317:005 638:01 638:1337 643:2203 E-P 312:1154 628:2308 628:372 633:9192 GaL 317:3066 638:6132 638:7369 643:8235 L 319:00 640:00 640:0408 642:6052 P 381:7586 765:5172 765:5637 767:9945 L-W 317:3267 640:6534 640:9034 648:4689 PL 318:3186 640:6372 641:9156 645:8475
FIG. 4.1 : Densits estimes des modles pour l’ensemble de donnes 1.
Illustration 2 : Application aux patients atteints de cancer de la vessie
Nous considérons un ensemble de données non censurées correspondant au temps de rémission (en mois) d’un échantillon aléatoire de 128 patients atteints de cancer de la vessie. Cancer de la vessie est une maladie dans laquelle les cellules anormales se multiplient sans contrôle dans la vessie. Le type le plus commun de cancer de la vessie l’histologie normale récapitule de l’urothélium et est connue comme le carcinome à cellules transitionnelles. Ces données ont déjà été étudiées par Lemonte (2012) [3], Zea et al. (2012) [26], Lee et Wang (2003) [13] et Lemonte et Cordeiro (2013) [4]. Le
tableau 5.2 indique les temps de rémission du cancer de la vessie (présenté à l’annexe B). Dans le tableau 4.9, les résultats de ces données sont présentés.
Tableau 4.8. Estimation des paramètres pour les données sur le cancer de la vessie Distribution Paramètre LP ^ = 0:1229; ^ = 0:08; ^k = 0:6243 L-E ^ = 1:229; ^ = 0:0962 E-P ^k = 0:9379; ^ = 0:0128; ^ = 0:08 GaL ^ = 0:1167; ^ = 0:1045 L ^ = 0:196 P ^ = 0:08; ^k = 0:2458 W-L ^ = 0:0027 ; a = 0:6316 ; b = 0:0002 PL ^ = 0:3855 ; ^ = 0:7443
Table 4.9. Les -LL, AIC, CAIC, BIC pour les données sur le cancer de la vessie Distribution -LL AIC CAIC BIC
LP 398:0184 800: 0368 800:1336 805:7252 L-E 401:78 807:564 807: 656 813:2641 E-P 400:3128 804:6256 804:7224 810:314 GaL 402:9596 809:9192 810:0152 815:6233 L 419:52 841:040 841:0717 843:892 P 501:1292 1004:258 1004:29 1007:103 L-W 401:196 808:392 808:5855 816:9481 PL 402:2373 808:4746 808:5706 814:1787
FIG. 4.2 : Densits estimes des modles pour l’ensemble de donnes 2.
Discussion
Après une lecture visuelle de …gure 4, …gure 5, table 9 et table 12 on remarque les valeurs du crétaire sont plus petites pour la distribution Lindley Pareto par rapport aux valeurs des autres modèles. La nouvelle distribution semble être un modèle très compétitif pour ces données.
Conclusion et Perspectives
Ainsi, nous avons réussi à introduire des nouvelles distributions, ensuite, à étudier quelques propriétés à savoir : la fonction quantile, l’estimation par la méthode des moments, l’estimation du maximum de vraisemblance, la limitation de la distribution des statistiques extrêmes sont établies et une étude de simulation est réalisée pour examiner les estimateurs de distribution de Lindley Pareto. En…n on va faire une application sur un ensemble de données. En e¤ectuant une comparaison entre la distribution L-P avec d’autres modèles populaires, on peut conclure que la distribution LP est plus performante.
Par la suite, il serait intéressant d’utiliser des données censurées. Aussi, nous pourrons dans nos recherches futures proposer d’autres distributions à savoir :