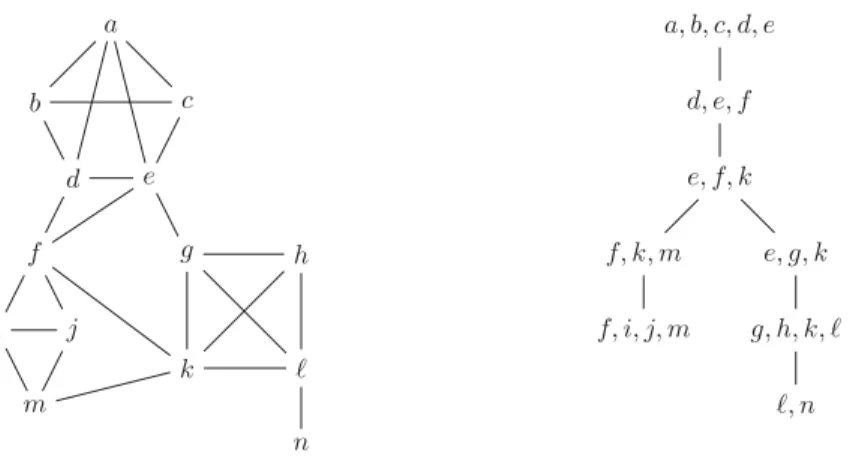Binary Constraint Satisfaction Problems Defined by Excluded Topological Minors

Any correspondence concerning this service should be sent

to the repository administrator:

tech-oatao@listes-diff.inp-toulouse.fr

This is an author’s version published in:

http://oatao.univ-toulouse.fr/24716

To cite this version: Cohen, David and Cooper, Martin and

Jeavons, Peter and Zivny, Stanislav Binary Constraint Satisfaction

Problems Defined by Excluded Topological Minors. (2019)

Information and Computation, 264. 12-31. ISSN 0890-5401

Official URL

DOI :

https://doi.org/10.1016/j.ic.2018.09.013

Open Archive Toulouse Archive Ouverte

OATAO is an open access repository that collects the work of Toulouse

researchers and makes it freely available over the web where possible

Binary

constraint

satisfaction

problems

defined

by

excluded

topological

minors

✩

David

A. Cohen

a

_,

_Martin

_{C. Cooper}

b

_,

_Peter

_{G. Jeavons}

c

_,

_{Stanislav Živný}

c

,

∗

a_{RoyalHolloway,UniversityofLondon,UK} b_{IRIT,UniversityofToulouse,France} c_{UniversityofOxford,Oxford,UK}

a

b

s

t

r

a

c

t

Keywords: Constraintsatisfaction Forbiddensubstructures Forbiddenpatterns Topologicalminors

The binary Constraint Satisfaction Problem (CSP) is to decide whether there exists an assignment to a set ofvariables which satisfies specified constraints between pairs of variables.AbinaryCSPinstancecanbepresentedas alabelled graphencodingboththe formsoftheconstraintsandwhere theyareimposed.Weconsider subproblemsdefined byrestrictingtheallowedformofthisgraph.Onetypeofrestrictionistoforbidcertain specifiedsubstructures(patterns).ThiscapturessometractableclassesoftheCSP,butdoes notcaptureclassesdefinedbylanguagerestrictions,orthewell-knownstructuralproperty ofacyclicity.

We extend thenotion ofpattern and introduce the notion ofa topologicalminor ofa binaryCSP instance.By forbidding afinite setofpatterns from occurringas topological minorsweobtainacompactmechanismforexpressingnoveltractablesubproblemsofthe CSP,includingnewgeneralisationsoftheclassofacyclicinstances.

2018ElsevierInc.Allrightsreserved.

1. Introduction

TheConstraintSatisfactionProblem(CSP)istodecidewhetheritispossibletofindanassignmenttoasetofvariables whichsatisfiesconstraintsbetweencertainsubsetsofthevariables.Thisparadigmhasbeenappliedindiverseapplication areassuchasArtificialIntelligence,BioinformaticsandOperationsResearch [40,30].

AstheCSPisknowntobe NP-complete,muchtheoreticalworkhasbeendevotedtotheidentificationoftractable sub-problems.Importanttractablecaseshavebeenidentifiedbyrestrictingthehypergraphstructure oftheconstrainedsubsets ofvariables [26,17].Othertractablecaseshavebeenidentifiedbyrestrictingtheformsofconstraints(sometimescalledthe constraintlanguage) [32,24].Workonboth oftheseareasisnow essentiallycomplete:full complexityclassifications have

beenestablishedforallstructuralrestrictions [28,37] andalllanguagerestrictions [4,43].

✩ _{Anextendedabstractofpartofthiswork appearedinthe}

Proceedingsofthe24thInternationalJointConferenceonArtificialIntelligence (IJCAI’15) [9]. TheauthorsweresupportedbyEPSRCgrantEP/L021226/1.StanislavŽivnýwassupportedbyaRoyalSocietyUniversityResearchFellowship.Thisproject hasreceivedfundingfromtheEuropeanResearchCouncil(ERC)undertheEuropeanUnion’sHorizon2020researchandinnovationprogramme(grant agreementNo. 714532).Thepaperreflectsonlytheauthors’viewsandnottheviewsoftheERCortheEuropeanCommission.TheEuropeanUnionisnot liableforanyusethatmaybemadeoftheinformationcontainedtherein.

*

Correspondingauthor.

E-mailaddresses:dave@cs.rhul.ac.uk(D.A. Cohen),cooper@irit.fr(M.C. Cooper),peter.jeavons@cs.ox.ac.uk(P.G. Jeavons),standa.zivny@cs.ox.ac.uk

(S. Živný).

However,identifyingthesubproblemsoftheCSPthatcanbeobtainedbyrestrictingeitherthestructureorthelanguage alone is not a sufficiently rich framework in which to investigate the full complexity landscape. For example, we may wish to identifyall the instances solvedby a particular algorithm,such asenforcing arc-consistency [18,40]. Ithas been shown [24,10] that this class ofinstances includes all instancesdefined by a certain structuralrestriction, together with all instances definedbya certain language restriction,aswell asfurtherinstances thatare not definedby eitherkindof restriction alone. Hence we needa more flexible mechanismfordescribing subproblems that will allow usto unifyand generalisesuchdescriptions.

Herewedevelopanewmechanismofthiskindthatusescertaintoolsfromgraphtheorytodefinerestrictedclassesof labelledgraphsthatrepresentbinaryCSPinstances.Ourmechanismallowsustoimposesimultaneousrestrictionsonboth thestructureandthelanguageofaninstance,andhenceobtainamorerefinedcollectionofsubproblems,allowingamore detailed complexityanalysis. Subproblems ofthe CSP ofthiskind aresometimes referred to ashybrid subproblems and, currently,verylittleisknownaboutthecomplexityofsuchsubproblems [15].

Thetoolsthatweusetoobtainrestrictedclassesoflabelledgraphsbuildonawell-establishedlineofresearchingraph theory,byconsideringlocal“obstructions”or“forbiddenpatterns”.Theideaofusingforbiddenpatternshaspreviouslybeen applied to the binary CSP andresulted in the discovery of a number ofnew tractable classes [7,8,12,23];related ideas alsoappeared in [36,34].Inmoredetail,[7] characterised allso-callednegativepatterns thatgive risetotractable classes of binary CSPs(thisresultis summarisedinTheorem 3.12below). Moreover,[12] characterised allpatterns consistingof atmosttwo constraintsthat give riseto tractable classesofbinary CSPs. Finally,[8] investigatedthenotion offorbidden patternsinthecontextofvariableandvalueeliminationinCSPs.

However,theexistingtheoryofforbiddenpatternsisnotsufficienttocaptureallknowntractablestructuralrestrictions, orlanguagerestrictions,asweshowbelow.Inparticular,weshowthateventhesimplesttractablestructuralclass,theclass oftree-structuresCSPinstances,cannot becapturedbyforbiddinganyfinitesetofpatterns(Corollary4.4).Todescribeall therelevantstructural,language andhybridrestrictionsthat canensuretractabilitythereforerequiresamoreflexible way todefinerestrictedclassesofinstances.

Ingraphtheoryitprovedusefultogobeyondtheideaofforbiddensubgraphsandintroducethemoreflexibleconceptof forbiddenminors.Awell-knownresultofRobertsonandSeymourstatesthatanysetofgraphsclosedundertheoperation oftakingminorsisspecifiedby afinitesetofforbiddenminors.Ratherthanadaptingthefullmachineryofgraphminors totheCSP framework,weconsiderheretheslightlysimplernotionofatopologicalminor [20].Weshow thatbyadapting thenotionoftopologicalminortotheCSPframeworkweareabletoprovideaunifieddescriptionofalltractablestructural classes,all tractable language classes,andsome newhybridtractable classesthat cannot becaptured aseitherstructural classesorlanguageclasses.Moreover,weareabletoshowthattheclassoftree-structuredCSPinstanceshasaverysimple descriptioninthisframework,andthereexisttractableclassesofthebinaryCSPthatproperlyextendthisclassandyetstill haveaverysimpledescription.

Anextendedabstractofpartofthisworkappearedin [9].

Thestructure ofthepaperisasfollows:inSection2we definetheCSPandthenotionofapattern, andshowhowto associateeach CSPinstancewithacorrespondingpattern. InSection 3wedefine whatitmeansforapatterntooccur in anotherpattern, eitherasasub-pattern orasatopologicalminor,andusethesenotions todefine restrictedclassesofCSP instanceswherespecifiedpatternsareforbiddenfromoccurringinoneorotheroftheseways.

InSection4weshowthatall tractablestructuralclassesoftheCSPcanbecharacterisedbyforbiddingcertain patterns from occurring as topological minors. We extend this idea in Section 5 to obtain novel hybrid tractable classes of CSP instances,includingclassesthatproperlyextendtheclassofacyclicinstances.

InSection6weconsiderthecomplexityofdeterminingwhetheragivenpatternoccursasatopologicalminorinaCSP instance,andinSection7weshowthatincludingadditionalstructureinpatternsallowsustocharacterisemoreclassesof CSPinstances,includingalltractablelanguageclasses.Finally,inSection8,weconcludewithadiscussionofourresultsand presentsomeopenquestions.

2. Preliminaries

2.1. TheCSP

Constraintsatisfactionisaparadigmfordescribing computationalproblems.Eachprobleminstanceisrepresentedasa constraintnetwork:a collectionofvariables thattake theirvalue fromsomegivendomain.Somesubsetsofthevariables have a further restriction on their allowed simultaneous assignments, called a constraint. A solution to such a network assignsavaluetoeachvariablesuchthateveryconstraintissatisfied.

In thispaper we consider onlybinary constraint networks, whereevery constraint limitsthe possibleassignments of precisely two variables. Ithas beenshown that anyconstraintnetwork can be reducedto an equivalentbinary network overadifferentdomainofvalues [19,41].

Definition2.1.Aninstanceofthebinaryconstraintsatisfactionproblem(CSP)isatriple

(V

,

D,C)whereV isafinitesetof variables,foreach v

∈

V ,D

(v)

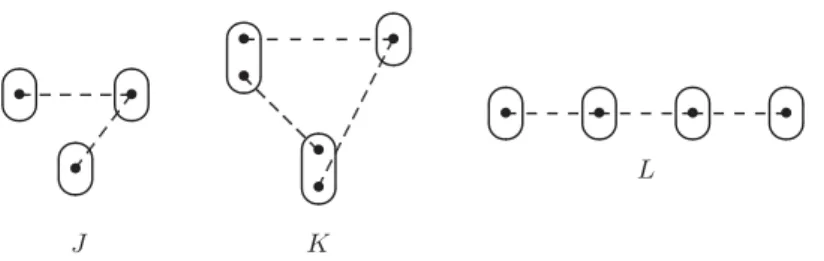
isafinitedomainofvaluesforv,andC isasetofconstraints,containingaconstraintRuv

Fig. 1. Some example patterns. Points are shown as filled circles, parts as ovals, positive edges as solid lines and negative edges as dashed lines.

foreachpairofvariables

(u,

v).Theconstraint Ruv

⊆

D(u)

×

D(v)isthesetofcompatibleassignmentstothevariables u andv.

Asolution toabinaryCSPinstanceisanassignment s

:

V

→

D ofvaluestovariablessuchthat,foreachconstraint Ruv,

(s(u),

s(v))

∈

Ruv.

We will assume that there is exactlyone binary constraint betweenany two variables. That is, if we define R′ uv as

{(b,

a)

| (a,

b)

∈

Ruv

}

,thenRvu

=

Ruv′ .Thisisjustanotationalconveniencesincewecanpre-processeachinstance,replacing

Ruv with Ruv

∩

R′vu. A constraintwill be calledtrivial if it is equal to the Cartesian product of the domains ofits two variables.

ThesizeofaCSPinstancewillbe takento bethesumofthesizesoftheconstraintrelations.Givenafixed boundon thesizeofthedomainforanyvariableandthearityoftheconstraints,thisispolynomial inthenumberofvariables.We willsaythataclassofCSPinstancesistractable ifthereisapolynomial-timealgorithmtodecidewhetheranyinstancein

theclasshasasolution.

Notethat Definition 2.1describesastandard formof mathematicalspecificationfora CSPinstance that isconvenient fortheoretical analysis. In thenext subsection we will introduce an alternative representation interms of patterns (see Construction2.5).Oftenmoreconciserepresentationsareused,andtrivialconstraintsareusuallynotrepresented [40].

Arc-consistency(AC)isafundamentalconceptforthebinaryCSP [18,40].

Definition2.2.Apairofvariables

(u,

v)issaidtobearc-consistentifforeachvaluea

∈

D(u)inthedomainofu,thereisa valueb

∈

D(v)inthedomainofv suchthat

(a,

b)

∈

Ruv.

AbinaryCSPinstanceisarc-consistent ifeverypairofvariablesisarc-consistent.

GivenanarbitraryCSPinstance I thereisaunique minimalsetofdomain valueswhichcanbe removedto makethe instancearc-consistent.Furthermorethediscovery ofthisunique minimal setofdomainvalues andtheir removal, called establishing arc-consistency, can be done in polynomial time [11]. For a given instance I we will denote by AC

(I)

the instanceobtainedafterestablishingarc-consistency.

2.2.Patterns

Wenowintroducethecentralnotionofapattern,whichcanbethoughtofasalabelledgraph,withthreedistinctkinds ofedges.

Definition2.3.Apattern isastructure

(X

,

E∼

,

E+

,

E−

)

,where

•

X isasetofpoints;

•

E∼isabinaryequivalencerelationover X whoseequivalenceclassesarecalledparts;

•

E+_{isasymmetricbinaryrelationover X whosetuplesarecalledpositiveedges;}

•

E−_{isasymmetricbinaryrelationover X whosetuplesarecallednegativeedges.} Thesets E∼andE+aredisjoint,andthesetsE∼andE−aredisjoint.

Inageneralpatternthere maybepairs ofpoints x and y in distinct partssuch that

(x,

y)isneither apositive nora negativeedge,andtheremaybepairsofpoints x and y indistinctpartssuchthat

(x,

y)isboth apositiveandanegative edge.A patternis calledcomplete if every pairof points x and y in distinct parts are connectedby either apositive or negativeedge(butnotboth),andhence E∼

∪

E+

∪

E−

=

X2.

Example2.4.SomeexamplesofpatternsareillustratedinastandardwayinFig.1. ThepatternshowninFig.1(a)iscomplete,buttheothersarenot.

✷

Itwilloftenbeconvenienttobuild specialpatternstorepresentbinary CSPinstances,sowenow definethefollowing construction.

Fig. 2. The pattern Patt(C3)constructed from the cycle graph C3by Construction2.7.

Fig. 3. The pattern Patt(K1,5)constructed from the star graph K1,5by Construction2.7.

Construction2.5.ForanybinaryCSPinstanceI

= (V

,

D,C),whereC

= {R

uv

|

u,v

∈

V

,

u

6=

v},wedefineacorrespondingcomplete

patternPatt

(I)

= (X

,

E∼

_,

_E+

_,

_E−

₎

_where

•

X

= {x

v,a

|

v

∈

V

,

a

∈

D(v)};

•

E∼

_{= {(x}

u,a

,

xv,b

)

∈

X

×

X

|

u

=

v};

•

E+

_{= {(x}

u,a

,

xv,b

)

∈

X

×

X

|

u

6=

v,

(a,

b)

∈

Ruv

};

•

E−

= {(x

u,a

,

xv,b

)

∈

X

×

X

|

u

6=

v,

(a,

b)

∈

/

Ruv

}.

We remarkthatforanyinstance I the points ofPatt

(I)

arethe possibleassignments foreachindividual variable,and thepartsofPatt

(I)

correspondtosetsofpossibleassignmentsforaparticularvariable.PositiveedgesinPatt

(I)

correspond to allowed pairs of assignments andare thereforeclosely related to the edges of the microstructure representationof I

definedin [33];negativeedges correspondtodisallowed pairsofassignments andarecloselyrelatedto theedges ofthe

microstructurecomplement discussedin [6].

Example2.6.Fig.1(a)showsthepatternPatt

(I)

forarathertrivialinstance I withthreevariables,eachofwhichhasonly one possiblevalue. Notethat I has no solution because the only possibleassignments fortwo pairs ofvariables are in negativeedgesandhencedisallowedbytheconstraints.

✷

A patternwith no positive edges will be called a negativepattern. It will sometimes be convenient to build negative patternsfromgraphs,sowenowdefinethefollowingconstruction.

Construction2.7.ForanygraphG

= (V

,

E

),

wedefineacorrespondingnegativepatternPatt

(G)

= (X,

E∼

_,

_∅,

_E−

₎

_where

•

X

= {x

e,v

|

e

∈

E,v

∈

e};

•

E∼

_{= {(x}

e,u

,

xf,v

)

∈

X

×

X

|

u

=

v};

•

E−

= {(x

e,u

,

xf,v

)

∈

X

×

X

|

e

=

f

,

u

6=

v}.

Example2.8.LetC3 be the 3-cycle, that is, thegraph withthree vertices, v1

,

v2

,

v3,and3 edges e1

,

e2

,

e3, where e1

=

{v

1

,

v2

},

e2

= {v

2

,

v3

}

ande3

= {v

3

,

v1

}

.TheassociatednegativepatternPatt

(C

3

)

definedbyConstruction2.7isthepattern with6points,3parts,and3negativeedges,showninFig.2.

LetK1,kbeastargraphwithk leaves;thatis,thegraphwithvertices

{u,

v1

,

. . . ,

vk

}

andedges

{u,

vi

}

for1

≤

i

≤

k.The patternPatt

(K

1,k

)

has2k points,k

+

1 parts,andk negativeedges.Thecaseofk

=

5 isshowninFig.3.

✷

In graphtheory,a subdivision operation ona graphreplaces an edge

(u,

v) witha path oflength two byintroducing a newvertex zuv,andconnectingu to zuv andzuv to v [20].A graphG is said tobe a topologicalminorofa graph H if some sequence ofsubdivision operationson G yields a subgraphof H [20]. We now define an operation on patterns thatisanalogoustothesubdivisionoperationongraphs,buttakesintoaccountthethreedifferenttypesofedgesthatare presentinapattern.Thissubdivisionoperationforpatternsiscrucialtotheideaofdefiningtopologicalminorsinpatterns, asdescribedinSection3.

Foranytwo distinctparts U

,

V of P ,we define E+_{U V}

=

E+

_{∩ (U}

_×

_V

₎

_{, E}−

U V

=

E−

∩ (U

×

V

)

,and ZU V

= {z

xy

| (x,

y)

∈

E+_{U V}

}

∪ {z

′

xy

,

z′′xy

| (x,

y)

∈

EU V−

}

.Thesubdivision ofP at U,V isdefinedtobethepatternPd

= (X

d

,

E_d∼

,

E_d+

,

E_d−

)

where

•

Xd

=

X

∪

ZU V;

•

E∼ d

=

E∼

∪ (

ZU V

×

ZU V

)

;

•

E+_d

= (E

+

\{(x,

y), (y,x) | (x,y) ∈E+_{U V}

})

∪ {(x,

zxy

), (z

xy

,

x), (zxy

,

y), (y,zxy

) | (x,

y) ∈E+U V

};

•

E−_d

= (E

−

\{(x,

y), (y,x) | (x,y) ∈E−_{U V}

})

∪ {(x,

z′_xy

), (z

′_xy

,

x), (z′′_xy

,

y), (y,z′′_xy

) | (x,

y) ∈E−_{U V}

}.

Pattern P′ _{is called a subdivision of P if it can be obtained from P by some (possibly empty) sequence of subdivision} operations.

Example2.10.ThepatternshowninFig.1(d)canbeobtainedbyperformingasinglesubdivisionoperationonthepattern showninFig.1(c).

✷

WeremarkthatpositiveandnegativeedgesaretreateddifferentlyinDefinition2.9:asingleextrapoint, zxy,isadded foreach positiveedge

(x,

y),andtwo extrapoints, z′

xy and z′′xy,areaddedforeachnegativeedge(see Example2.10).This difference reflects a semantic difference between positive and negative edges in a CSP instance, which we illustrate as follows.Supposethattheassignmentofvaluea tovariableu andvalue b tovariable v extendstoasolution.Inthiscase, foranyother variable w, thepoints

(u,

a) and

(v,

b)must both becompatible withsome commonpoint

(w,

c). Onthe otherhand,theassignmentofa tovariableu andb tovariable v mayfailtoextendtoasolutioniftherearepoints

(w,

c)

and

(w,

d)where

(u,

a)isincompatiblewith

(w,

c),

(v,

b)isincompatiblewith

(w,

d)andtherestoftheinstanceforces w

totakeeithervaluec orvalued.

3. Forbiddingpatterns

IntheremainderofthispaperweconsiderclassesofbinaryCSPinstancesthataredefinedbyforbidding aspecifiedset ofpatternsfromoccurringincertainways,whichwenowdefine.

3.1. Occurrencesofonepatterninanother

Definition3.1.ApatternP1

= (X

1

,

E∼

1

,

E+1

,

E−1

)

issaidtohaveahomomorphism toapatternP2

= (

X2

,

E∼

2

,

E+2

,

E−2

)

,ifthere isamappingh

:

X1

→

X2suchthat

•

if

(x,

y)

∈

E∼

1 then

(h(x),

h(y))

∈

E∼2,and

•

if

(x,

y)

∈

E+₁ then

(h(x),

h(y))

∈

E+₂,and

•

if

(x,

y)

∈

E−₁ then

(h(x),

h(y))

∈

E−₂.

Ahomomorphismh froma pattern P1

= (X

1

,

E∼

1

,

E+1

,

E−1

)

toa pattern P2

= (X

2

,

E∼

2

,

E+2

,

E−2

)

willbe said topreserve

parts ifitsatisfiestheadditionalpropertythatforall

(x,

y)

∈

X2₁,if

(x,

y)

∈

/

E∼₁,then

(h(x),

h(y))

∈

/

E∼₂.

Definition3.2.ApatternP1 issaidtooccurasasub-pattern inapattern P2,denotedP1

→

S P P2,ifthereisahomomorphism fromP1to P2thatpreservesparts.

Earlierpapers [7,12] havedefinedthenotionsofpatternandthenotionofoccurringasasub-patterninslightlydifferent ways,buttheseareallessentiallyequivalenttoDefinition3.2.

Example3.3.ThepatternshowninFig.1(d)hasahomomorphismtothepatternshowninFig.1(c),butdoesnotoccurasa sub-patterninthispattern.ThepatternshowninFig.1(d)doesoccurasasub-patterninthepatternshowninFig.1(b).

✷

Nowwe introducea newformofoccurrencethatwillbe ourfocusinthispaper,andwillallow ustodefine awider rangeofrestrictedsubproblemsoftheCSP.

Definition3.4.Apattern P1 issaidtooccurasatopologicalminor inapatternP2,denoted P1T M

→

P2,ifsomesubdivisionof

Example3.5.The patternshown inFig. 1(c)occurs asa topological minorin the patternshown inFig. 1(d) andin the patternshowninFig.1(b).

✷

Lemma3.6.ForanypatternsP

,

P′_andP′′_{thefollowingpropertieshold:}

(a) P

→

S P P andPT M

→

P ;

(b) IfP

→

S P P′,thenPT M

→

P′;

(c) IfP

→

S P P′_andP′

_→

S P _P′′_,thenP

_→

S P _P′′_; (d) IfPT M

→

P′andP′

→

T MP′′,thenPT M

→

P′′.

Proof. Part (a)is obtainedby takingthe identity function asa homomorphism,andan empty sequence ofsubdivisions. Part (b) isobtained by takingan empty sequence ofsubdivisions. Part (c)is obtainedby composing the two homomor-phisms.

Part (d)followsfromthefollowingobservation:assumethath isahomomorphismfromP1 to P2that preservesparts, and that P3 is the patternobtained by performing a subdivision operation on P2 atparts U and V .Now consider the

pattern Q obtainedbyperforming asubdivisionoperation on P1 atthe partsthat aremappedby h toU and V .Byour definitionofsubdivision,itfollowsthath canbeextendedtoahomomorphismh′_{from Q toP}

3thatpreservesparts. Henceinanysequenceofsubdivisionoperationsandhomomorphismsthatpreservepartswecanre-ordertheoperations toperformallsubdivisionsatthestart,andthencomposeallthehomomorphisms.

✷

Recallthatestablishingarc-consistencyinaninstanceI involvesremovingdomainvaluesfromI andyieldsthe(unique)

instanceAC(I),henceitcannotintroduceanoccurrenceofapatternasasub-patternorasatopologicalminorifitdidnot alreadyoccur.Thisgivesthefollowingresult.

Lemma3.7.ForanypatternsP andI ,whereI representsaninstance,thefollowingpropertieshold:

(a) IfP

→

S PPatt

(

AC

(I)),

thenP

→

S PPatt

(I);

(b) IfPT M

→

Patt

(

AC

(I)),

thenPT M

→

Patt

(I).

Establishing arc-consistencycan bedone inpolynomialtime,so formanyofourresultswewillonlyneedto consider arc-consistentCSPinstances.

3.2. Restrictedclassesofinstances

We can useDefinition 3.2to define restrictedclasses ofbinary CSP instances by forbiddingthe occurrenceofcertain patternsassub-patternsinthoseinstances.

Definition3.8.Let

S

beasetofpatterns.

WedenotebyCSP_SP

(S)

thesetofallbinaryCSPinstancesI suchthatforall P

∈ S

itisnotthecasethat P

→

S PPatt

(I)

. Definition3.9.WewillsaythatapatternP issub-patterntractable ifCSP_SP

({P

})

istractable;wewillsaythatapatternP is sub-patternNP-complete ifCSP_SP

({P

})

isNP-complete.

Forsimplicity,wewriteCSP_SP

(P

)

forCSP_SP

({P

})

.

ThecomplexityoftheclassCSP_SP

(S)

hasbeendeterminedforawiderangeofpatterns [13,7,12].Infact,forallnegative

patterns P thecomplexityofCSP_SP

(P

)

hasbeen completelycharacterised [7]. Todefine thischaracterisation,we need to

introducetheideaofstarpatterns.

A connected graph G iscalleda star if it is acyclic,andhas exactly one vertexof degree greater than 2.The vertex of degree greater than 2 ina stargraph will be calledthe central vertex. A pattern P will be calleda starpattern if it

can be obtainedfromthe patternPatt

(G)

forsome star graphG by merging zeroormore points inthe partof Patt

(G)

correspondingtothecentralvertexofG.

Example3.10.Sincetheempty graphisa stargraph,thesimpleststarpatternistheemptypattern,whichhasnopoints. SomeotherexamplesofstarpatternsareshowninFig.4.

✷

Definition3.11([7]).Foranyk

≥

1,thestarpatternwith3branches,eachoflengthk,whereexactlytwopointsaremerged inthecentralpart,asshowninFig.5,iscalledPivot(k).

Fig. 4. Examples of star patterns.

Fig. 5. The pattern Pivot(k).

Theorem3.12([7]).Foranyk

≥

1,thenegativepatternPivot(k)showninFig.5issub-patterntractable,asareallnegativepatterns P suchthatP

→

S P P i vot(k);allothernegativepatternsaresub-patternNP-complete.

Example3.13.ByTheorem3.12allthenegativepatternsshowninFigs.2,3and4aresub-patternNP-complete.

✷

Togobeyondtheearlierresultsforforbiddensub-patterns [7,8,12,23],anddefineawiderrangeofrestrictedclasses,we useDefinition 3.4todefine restricted classesofbinary CSP instancesby forbiddingthe occurrenceofcertain patternsas topologicalminorsinthoseinstances.

Definition3.14.Let

S

beasetofpatterns.

WedenotebyCSP_TM

(S)

thesetofallbinaryCSPinstancesI suchthatforall P

∈ S

itisnotthecasethat PT M

→

Patt

(I)

. Definition3.15.We will say that a pattern P istopological-minortractable if CSP_TM

({P

})

is tractable; we will say that a

patternP istopological-minorNP-complete ifCSP_TM

({P

})

isNP-complete. Forsimplicity,wewriteCSP_TM

(P

)

forCSP_TM

({P

})

.

ByLemma3.6(b),ifP occursasasub-patternofsomepatternQ ,thenitalsooccursasatopologicalminorof Q .Hence foranypatternP wehavethatCSP_TM

(P

)

⊆

CSP_SP

(P

)

.Thefollowingisanimmediateconsequence.

Lemma3.16.IfapatternP issub-patterntractablethenP isalsotopological-minortractable.

Example3.17.By theresults ofearlier work, thetwo patterns shownin Fig.1(a) and1(b) are knownto be sub-pattern tractable:thetractability ofthepatternshowninFig. 1(a)followsfromthetractability ofa moregeneralpattern(called JWP)definedin [14];thetractabilityofthepatternshowninFig.1(b)followsfrom [23,Lemma 46] (whereitcorresponds topatternU′

30).

Hencebothpatternsarealsotopological-minortractable,byLemma3.16.

✷

ByLemma3.6(d),if P occursasatopologicalminorin Q thenCSP_TM

(P

)

⊆

CSP_TM

(Q

)

.The followingisanimmediate

consequence.

Lemma3.18.IfpatternPT M

→

Q ,andQ istopological-minortractable,thenP isalsotopological-minortractable.

Example3.19.We can deduce from Lemma 3.18 that Fig. 1(d) is topological-minor tractable, since Fig. 1(d) occurs as a sub-pattern (and hence also as a topological minor) in Fig. 1(b), andit was shown in Example 3.17 that Fig. 1(b) is topological-minortractable.

✷

The converse ofLemma 3.16does not hold: there exist patternsthat are topological-minor tractable but sub-pattern NP-complete,asthefollowingexampledemonstrates.MoresignificantexampleswillbediscussedinSection5.

Example3.20.Fig. 1(c) is sub-pattern NP-complete, since it cannot occur as a sub-pattern of any instance, so for this pattern P, CSP_SP

(P

)

contains all possibleCSP instances. However, by Lemma3.18,Fig. 1(c)istopological-minor tractable, since it occursasa topological minorin Fig.1(d), andit was shownin Example3.19that Fig. 1(d) istopological-minor tractable.

✷

Forsome patternsP ,thesetsCSP_SP

(P

)

andCSP_TM

(P

)

areidentical,asournextresultshows.Apattern P willbecalled star-like ifremovingthepositiveedgesfromP givesanegativepatternP′suchthat P′

→

S P P′′ forsomestarpatternP′′.

Example3.21.AllofthepatternsshowninFigs.1,3and4arestar-like,butthepatternshowninFig.2isnotstar-like.

✷

Proposition3.22.IfP isastar-likenegativepattern,thenCSP_TM

(P

)

=

CSP_SP

(P

).

Proof. ByLemma3.6(b),foranypatternP wehavethatCSP_TM

(P

)

⊆

CSP_SP

(P

)

.

Toobtainthereverseinclusion,let P beastar-likenegativepattern,andlet Q be astarpatternsuch that P

→

S P Q .By the definitionofstar pattern, foranysubdivision Q′ of Q , we havethat Q

→

S P Q′.Hence, by Lemma3.6(c) P

→

S P Q′, so

CSP_SP

(P

)

⊆

CSP_SP

(Q

′

₎

_{.Butthisimplies,byDefinition3.4,thatCSP}

SP

(P

)

⊆

CSPTM

(P

)

.

✷

Example3.23.ByTheorem3.12,anypatternPivot(k)issub-patterntractable,andbyProposition3.22weknowthat forbid-dingPivot(k)asatopologicalminordefinesthesamesetofinstancesasforbiddingPivot(k)asasub-pattern.Therefore,for anyk

≥

1,thepatternPivot(k)isalsotopological-minortractable.

Similarly,byTheorem3.12,eachstarpatternP showninFig.4issub-patternNP-complete.ByProposition3.22,foreach

ofthesepatternsCSP_TM

(P

)

=

CSP_SP

(P

)

.Consequently,thesepatternsarealsotopological-minorNP-complete.

✷

Wenowgive apartialconverseofProposition3.22,byshowingthatforallpatterns P thatarenotstar-like,CSP_TM

(P

)

cannot beexpressedby forbiddinganyfinitesetofsub-patterns.Thismeans thatthenotionofforbiddingtheoccurrence ofapatternasatopologicalminorprovidesmoreexpressivepowerthanforbiddingarbitrary(finite)setsofpatternsfrom occurringassub-patterns.

Proposition3.24.IfP isapatternthatisnotstar-like,thenCSP_TM

(P

)

6=

CSP_SP

(S)

forallfinitesetsofpatterns

S

.

Proof. Let P beapatternthatisnot star-like,andlet P′_{be thenegativepatternobtainedbyremovingall positiveedges} of P .Notethat P′

_→

S P _{P .}

Inanypattern,saythatapartU isdistinguished iftwonegativeedgesshareasinglepointinU oriftherearenegative edgesfromU tomorethantwootherparts.

Since P isnotstar-like,thenegativepattern P′mustcontainsa cycleofpartsconnectedbynegativeedges, oratleast

twodistinguishedparts.

Hence,foranyfixedk,byasufficientlylongsequenceofsubdivisionoperations,wecanconstructasubdivision P′′ _ofP′ whicheitherhasacycleofpartsoflengthgreaterthank ortwodistinguishedpartsseparatedbyasequenceofconnected partsoflengthgreaterthank.Byaddingpositiveedges,wecanthenconvertP′′ intoacompletepatternoftheformPatt

(I)

forsomeCSPinstanceI .

Nowforanyfixedfinitesetofpatterns

S

therewillbeaboundk onthenumberofpartsofanypatternin

S

.Itfollows thatCSP_TM

(P

)

cannotbedefinedbyforbiddingthesub-patternsin

S

,since I

∈

/

CSP_TM

(P

)

butnopatternin

S

canoccuras asub-patterninPatt

(I)

.

✷

4. Structuralrestrictions

ForanyCSPinstanceI

= (V

,

D,C),theconstraintgraph of I isdefinedtobethegraph

(V

,

E),whereE isthesetofpairs

{x,

y}forwhichtheassociatedconstraintRxyisnon-trivial.AnumberoftractablesubproblemsoftheCSPhavebeendefined byspecifyingrestrictionsontheconstraintgraph;suchrestrictedclassesofinstancesareknownasstructuralclasses [28,37]. ItisknownthatastructuralclassofbinaryCSPinstancesdefinedinthiswayistractableifandonlyifeveryinstancehas a constraintgraphofboundedtreewidth [28,Theorem 5.1] (subjecttothe standardcomplexity-theoreticassumptionthat FPT

6=

W

[

1

]

,whichwewillassumethroughoutthissection;wereferthereadertothetextbooks [22,25] formoredetails).

Weshowinthissectionthatstructuralclassesofthiskindcannotbedefinedbyforbiddingtheoccurrenceofafinitesetof sub-patterns.However,theycan bedefinedbyforbiddingtheoccurrenceofoneormorepatternsastopologicalminors.

Wewillalsousethischaracterisation oftractablestructuralclassestoshow thata largeclass ofnegativepatternsare topologicalminortractable.

Firstweextendthenotionofaconstraintgraphtoarbitrarypatterns.

Definition4.1.Foranypattern P ,theconstraintgraph of P ,denotedGP,isdefinedtobethegraph

(V

,

E),where V isthe setofallpartsof P ,and E isthesetofpairsofparts

{U

,

W

}

suchthatthereisanegativeedge

(x,

y)

∈

P with x

∈

U and y

∈

W .

Foranybinary CSPinstanceI ,theconstraintgraphofI definedaboveisequaltoGPatt(I).Forsimplicity,thisgraphwill usuallybedenotedbyGI.

Nowwenotethecloselinkbetweenournotionofapatternoccurringasatopologicalminorofanotherpatternandthe standardnotionofatopologicalminorinagraph [20].

Lemma4.2.ForanygraphG andanypatternP ,Patt

(G)

T M

→

P ifandonlyifG isatopologicalminorofthegraphGP.

ThesimpleststructuralclassofCSP instancesofboundedtreewidth istheclassofinstanceswhoseconstraintgraphis

acyclic (thatis,hastreewidth1). Thisclassisknownastheclassofacyclicbinary CSPinstances andwas one ofthefirst

sub-problemsoftheCSPtobe showntobetractable [26].Wenow showthatthisclasscan becharacterisedverysimply byexcludingthesinglepatternPatt

(C

3

)

showninFig.2fromoccurringasatopologicalminor.

Proposition4.3.TheclassofacyclicbinaryCSPinstancesequalsCSP_TM

(

Patt

(C

3

)).

Proof. Theclass ofacyclic graphs maybe characterisedas graphs whichdo not contain C3 asa topological minor [20]. Hence,byLemma4.2andDefinition4.1,abinary CSPinstanceI hasanacyclicconstraintgraphifandonlyifitisnotthe

casethatPatt

(C

3

)

T M

→

Patt

(I)

.

✷

SincethepatternPatt

(C

3

)

isnotstar-like(see Example3.21),itfollowsimmediatelyfromProposition3.24thatacyclic CSPinstancescannotbedefinedbyanyfinitesetofforbiddensub-patterns.

Corollary4.4.TheclassofacyclicbinaryCSPinstancesisnotequaltoCSP_SP

(S)

foranyfinitesetofpatterns

S

.

Proposition 4.3 can easily be extended to any of the tractable structural classes of binary CSP instances defined by imposinganyfixedboundonthetreewidthoftheconstraintgraph [27],althoughinthiscasethesetof forbiddenpatterns isexplicitlyknownonlyfork

≤

3 [1].

Theorem4.5.Foranyfixedk

≥

1,theclassofbinaryCSPinstanceswhoseconstraintgraphhastreewidthatmostk equalsCSP_TM

(S

k

),

forsomefinitesetofpatterns

S

_k.

Proof. The graphminor theorem [39] implies that forany fixed k

≥

1 there is a finite set Ok of graphs such that the classofgraphsoftreewidthatmostk isprecisely theclassofgraphsexcludingall graphsfromtheset Ok astopological minors [20].(Moreprecisely,thegraphminortheoremgivesafinitesetofminorsasobstructionsbutthissetcanbeturned intoafinitesetoftopologicalminorsasobstructionsinastandardway,see [20,Exercise34,Chapter12].)Consequently,by Lemma4.2,foranyk

≥

1 theclassofbinaryCSPinstanceswithconstraintgraphsoftreewidthatmostk canbedefinedas CSP_TM

(S

k

)

forthefinitesetofnegativepatterns

S

kgivenby

S

k

= {

Patt

(G)

|

G

∈

Ok

}

.

✷

Infact,weareabletoshowthatmanyotherpatternsaretopological-minortractableusingother standardresultsfrom graphtheory.Thefollowingtheoremcharacterisesthetopological-minortractabilityofpatternsoftheformPatt

(G)

,forall

graphsG ofmaximumdegreethree.

Theorem4.6.LetG beanarbitrarygraphofmaximumdegreethree.Then,Patt

(G)

istopological-minortractableifandonlyifG is planar (assumingFPT

6=

W

[

1

]

).

Proof. Oneofthewell-knownresultsofRobertson andSeymourshowsthat theclassofgraphs obtainedby excluding G

asaminor hasboundedtreewidth ifandonlyif G isplanar [38] (see also [20,Theorem 12.4.3]). It isknown that fora

graphG ofmaximumdegreethreeandanygraphG′_{, G isaminorofG}′_{ifandonlyifG isa topologicalminorofG}′_[20, Proposition 1.7.4 (ii)]. Thus, for a graph G of maximum degree three, the class of graphs obtainedby excluding G as a topologicalminor hasboundedtreewidth if andonlyif G isplanar. The theorem then followsfromLemma 4.2andthe

factthat,assuming FPT

6=

W

[

1

]

,astructuralclassofbinary CSPinstancesistractable ifandonlyiftheassociatedclassof

Fig. 6. Three patterns which are topological-minor tractable.

Unfortunatelythisresultdoesnotextendtographsofhigherdegree,asthefollowingexampleshows. Example4.7.ConsiderastargraphG wherethecentralvertexhasdegree4.Notethat G isplanar.

In all subdivisions of G,the central vertexstill has degree 4,so it cannot occur as a topologicalminor inanygraph ofmaximumdegree three.Hence,by Lemma4.2,Patt

(G)

cannot occurasatopological minorinanyCSP instancewhose constraintgraphisahexagonalgrid.Sincethetreewidthoftheclassofhexagonalgridsisunbounded [20],thisstructural classofCSPinstancesisintractable,assumingFPT

6=

W

[

1

]

,bytheresultsof [28].

✷

5. Tractableclassesthatgeneraliseacyclicity

In thissection we willgive severalmore examples ofpatterns that are topological-minor tractable. We concludethe section withTheorem 5.4where we define several newtractable classes whichproperly extend theclass of acyclicCSP instancesdiscussedinSection4.

Consider thepatterns shown inFig. 6. ByTheorem 3.12, J issub-pattern tractable and hencealso topological-minor tractable,byLemma3.16.However,theremainingpatterns,K and L aremoreinteresting.

Theorem5.1.ThepatternK ,showninFig.6,issub-patternNP-completebuttopological-minortractable.

Proof. ByTheorem3.12, K issub-patternNP-complete.

To show that K is topological-minor tractable, consider an instance I in which the pattern K does not occur as a topologicalminor.Ifthepattern J fromFig.6doesnotoccur asasub-patterninPatt

(I)

thenwe aredonesince,asnoted above,CSP_SP

(

J)istractableandthusI canbesolvedinpolynomialtime.

Ontheotherhand,if J doesoccurasasub-patterninPatt

(I)

,thenwewillbuildaspecialtreedecompositionT ofthe constraintgraphof I ,whereeachnodeofT isasubsetoftheverticesoftheconstraintgraphof I ,andall non-leafnodes

ofT havesize1.

Inmore detail,let GI betheconstraintgraphof I .Supposethe pattern J , showninFig.6,occursasa sub-patternin Patt

(I)

onthethreepartscorrespondingtothetripleofvariables

(x,

y,z)inI ,with y beingthevariableatwhichthetwo negativeedgesmeet.Since K doesnotoccurasatopologicalminorinI ,itfollowsthatthereisnopathfromx toz in GI thatdoesnotpassthrough y.Hence y isanarticulationpointofGI.

LetC1

,

. . . ,

Ckbe thecomponentsofGI

\ {y}

,anddenoteby ICi thesub-instanceof I onthevariablesofCi

∪ {y}

.We

formatreedecompositionofGI asfollows:therootofT isthesubsetcontainingjustthevariable y andhask children.If thepattern J doesnotoccurasasub-patterninCi

∪ {y}

,thenthei-thchildoftherootisaleafnodecorrespondingtothe sub-instance ICi.Otherwise,ifthepattern J doesoccurasasub-patterninCi

∪ {y}

,thenweproceedinthesamefashion

anddecompose Ci intoasub-treerootedatthei-thchild.

Since CSP_SP

(

J

)

istractable,anysub-instance correspondingto aleafofthistreedecompositioncan besolved in

poly-nomial time for each possible assignment to its unique articulation variable which joins it to its parent node in the tree-decomposition.Henceinpolynomialtimewecansolvethissub-instance,eliminatethecorrespondingleaf,andpossibly eliminatesomevaluesinthedomainofthisarticulationvariable.Aftereliminatingallnon-trivialleafnodesinthisway,the remainingsub-instanceofGI istreestructuredandhencecanbesolvedinpolynomialtime.

✷

WewillshowinTheorem5.3belowthatthepatternL showninFig.6isalsotopological-minortractable.Inordertodo so,wewillextendtheprooftechniqueusedinTheorem5.1toagenericscheme forprovingtopological-minortractabilityof patterns.

Todevelopourgenericschemeweneedsomestandardresultsfromgraphtheory.If S isasetofverticesofagraphG,

wewriteG[S]fortheinducedgraphon S.

Atreedecomposition ofagraphG

= (V

,

E

)

isatreeT ,togetherwithasubsetVt oftheverticesofG foreachnodet

∈

T , such that

S

_t∈TVt

=

V ,eachedge e

∈

E iscontainedin Vt forsomet

∈

T ,andforanyvertexv

∈

V theset

{t

|

v

∈

Vt

}

is aconnectedsub-treeofT .Thetorsos ofatreedecomposition

(T

,

(V

t

)

t∈T

)

ofagraphG arethegraphs Ht,t

∈

T ,obtained fromG[Vt

]

byaddingalltheedges

{x,

y}suchthatx,y

∈

Vt

∩

Vt′ wheret′isanyneighbouroft inT .

Fig. 7. A graph and its Tutte decomposition.

A Tuttedecomposition of a graph G is a tree decomposition

(T

,

(V

t

)

t∈T

)

of G, where

|V

t

∩

Vt′

|

≤

2 for every pairof neighbourst andt′in T ,andthetorsoofeach nodeiseitherthree-connected,oracycle, orhasatmost2vertices.Itis knownthatevery finitegraphhasaTuttedecompositionofthiskind [42],andthatsuchadecompositioncanbefoundin lineartime [31].

Example5.2.Fig.7showsagraphandapossibleTuttedecomposition.

✷

Todemonstratetopological-minor tractability forapattern P weproceed asfollows.Let I bean instanceinwhich P

doesnotoccurasatopologicalminorandletGI beitsconstraintgraph.Wedenotebyn thenumberofvariablesinI and byd themaximumdomainsizeofanyvariablein I .

BuildaTuttedecompositionofGI,andconsideranyleafnodes inthisdecomposition.Thesubsetofvariablesassociated withnode s will bedenoted S,andthe variables associatedwiththe remainder ofthe nodesofthe treedecomposition afterremovingtheleafs willbedenotedbyT .Notethat S andT shareatmost2variables.LetI[S]bethesub-instanceof

I onS and I[T

]

bethesub-instanceof I onT .Supposethatthefollowingtwoassumptionshold:

(A1) I

[S]

can be solved and its solutions projected onto the variables shared with T in polynomial time; the resulting reducedinstanceonT willbedenotedby I′

_[T

_]

_.

(A2) P doesnotoccurasatopologicalminorinPatt

(I

′

[T

])

.

Thenit followsthata recursivealgorithm,whichateach stepchooses someleaf s ofthe decomposition,andthen solves theassociatedsub-problemI[S]toobtainthereducedinstanceI′

[T

]

,willsolvetheoriginalinstanceusingapolynomial(in n andd)numberofcallstothepolynomial-timealgorithmfrom(A1).

IntheproofsbelowwewillomitthesimplecaseswhereS andT shareonly1variable,orS containsatmost3vertices, orthetorsoofS isacycle(andhencehastreewidth2andissolvableinpolynomialtime).Hencewewillassumethatthe torsoof S containsmorethanthreeverticesandisthree-connected.

Finally,notethatifS andT sharethevariables

{u,

v},thenwehavethefollowing:

•

AnypathinGI fromavertexinS toavertexinT mustpassthroughu orv;

•

Theremustexistsomepathfromu tov inGI

[T

]

,whichwewilldenote pathT

(u,

v). WenowusethisgenericschemetoprovethetractabilityofpatternL fromFig.6.

Theorem5.3.ThepatternL,showninFig.6,issub-patternNP-completebuttopological-minortractable.

Proof. ByTheorem3.12,L issub-patternNP-complete.

Toestablishtopological-minortractabilityusingthegenericschemedescribedaboveweonly needtoestablishthetwo assumptions.

(A1) Let J be the pattern consisting of two intersecting negative edges, shown in Fig. 6. Suppose that J occurs in Patt

(I[S])

asa sub-pattern ontwo disjoint triples ofvariables

(x,

y,z) and

(x

′

_,

_y′

_,

_z′

₎

_{in I[S]. Asexplained above forthe} genericscheme,wecanassumethatthetorsoofS is3-connected.ItfollowsbyMenger’stheorem [21] thattherearethree

disjointpathsfromx tox′_{inthetorsoof S.Theremustbeoneofthesepaths,}

_π

_{,whichdoesnotpassthrough y ory}′_.We claimthattheremustbeasubpath

σ

of

π

whichbeginsatx orz andendsatx′_orz′_{andwhichdoesnotpassthroughany} othervariablesin

{x,

y,z,x′

_,

_y′

_,

_z′

_}

_{.Toprovetheclaimfirstnotethat if}

π

_{doesnotpassthrough z andz}′ _then

π

_satisfies

Fig. 8. Topological-minor tractable patterns derived from sub-pattern tractable patterns.

theclaim.Ifz appearson

π

butz′_{doesnotappearon}

π

_{thenthesubpath}

σ

_of

π

_{fromz tox}′_{satisfiestheclaim.Asimilar} argumentworksforthecasewhenz′appearson

π

butz doesnot.Ifbothz and z′ appearon

π

thenwehaveasubpath

of

_π

fromz toz′_{.Withoutlossofgenerality,supposethat}

_σ

_{joinsx tox}′_{.Butthen L occursasatopologicalminoronthe} extendedpath

σ

+ _givenbyz

_→

_y

_→

_x,

σ

_,

_x′

_→

_y′

_→

_z′_.

Butthisimpliesthat L occursasatopologicalminorinPatt

(I)

,sinceif

σ

+passesbytheedge

{u,

v}inthetorsoof S,

thisedgecan bereplacedby pathT

(u,

v

)

whichisapathfromu to v in T ,whoseexistence wasnotedinthediscussion above.Sincethiscontradictsourinitialassumption,wecandeducethat J doesnotoccurinPatt

(I[S])

asasub-patternon twodisjoint triples.

Wecanthereforededucethatall pairsoftriples ofvariables

(x,

y,z),

(x

′

,

y′

,

z′

)

forwhich J occursasasub-patternin

Patt

(I[

S])intersect,i.e.,

{x,

y,z}

∩ {x

′

_,

_y′

_,

_z′

_}

_{6= ∅}

_{.Now,consideranarbitrarytripleofvariables}

_(x,

_{y,z)onwhich J occursas} a sub-pattern.It followsthat theinstancewhichresultsafteranyinstantiation(and removal)ofthethree variablesx,y,z

containsnooccurrenceof J asasub-pattern,sinceforeachtripleofvariables

(x

′

,

y′

,

z′

)

onwhich J occursinI[S],atleast

oneofitsvariableshasbeeneliminatedbyinstantiation.

Thus, afterinstantiation ofatmostthree variables,Patt

(I[

S]) doesnot contain J asa sub-pattern.Thisalso holdsfor any version of I[S] obtainedby instantiating the variables u,v.As noted above, CSP_SP

(

J) is tractable. We can therefore determineinpolynomialtimewhichinstantiationsofu,v canbeextendedtoasolutionofI[S].Weremovethepair

(p,

q)

fromRuv inI whenevertheassignmentofp tou andq tov cannotbeextendedtoasolutiontoI[S].Finally,wedeleteall variablesinS from I apartfromu andv.ProceedinginthiswayweconstructI′

_[T

_]

_{inpolynomialtimeasrequired.}

(A2) Suppose, for a contradiction, that we introduce some occurrence of the pattern L as a topological minor in

Patt

(I

′

_[T

_])

_{whenreducing I to I}′

_[T

_]

_{.ThisoccurrenceofL mustuseanewly-introducededgeinI}′

_[T

_]

_{.Duringthereduction} from I to I′

_[T

_]

_{,we can introduce negative (butnot positive) edges in Patt}

_(I

′

_[T

_])

_{betweenthe parts corresponding to u} and v.Supposethatanegativeedge

(p,

q)isintroducedbythereductionfromI toI′

_[T

_]

_{.Thiscanonlybethecaseifthere} wasapath

_π

= (u,

w1

,

. . . ,

wt

,

v

)

intheconstraintgraphGI

[S]

andhenceasequenceofnegativeedgesbetweenthe corre-spondingpartsinPatt

(I[S])

linkingp toq.Thismeansthatwecanreplacethenewly-introducededgeintheoccurrenceof

L inPatt

(I

′

_[T

_])

_{byasequenceofnegativeedgessothatL occursasatopologicalminorinPatt}

_(I)

_{fortheoriginalinstance I.} ThiscontradictionshowsthatwecannotintroduceL asatopologicalminorinPatt

(I

′

[T

])

whenreducing I to I′

[T

]

.

Hence wehaveestablishedbothassumptions,sotheresultfollowsbyourgenericproofscheme.Notethatthenumber ofinstancesofCSP_SP

(

J)thatneedtobesolvedis O

(nd

5

)

.

✷

Asourfinalresultinthissectionweshowhowthewell-knowntractableclassofacyclicinstancescanbegeneralisedto obtainlargertractableclassesdefinedbyforbiddingtheoccurrenceofcertainpatternsastopologicalminors.Themaintool weusewillagainbethegenericschemebasedonTuttedecompositionsdescribedabove.

Theorem5.4.Let P0 beanysub-patterntractablepatternwiththreeparts,U1

,

U2

,

U3wherethereisatmostonenegativeedge betweenU1andU2,andbetweenU2andU3,andnoedgesbetweenU1andU3.

Let P bea patternwith fourparts U1

,

U2

,

U3

,

U4 obtainedbyextending P0 as follows.Thepattern P hassix newpoints

p1

,

p2

∈

U1,q1

,

q2

∈

U4,andr1

,

r2

∈

U3,togetherwiththreenewnegativeedges

{p

1

,

r1

},

{p

2

,

q1

},

{q

2

,

r2

}

(seeFig.8).Anysuch P istopological-minortractable.

Proof. Theproofusesthegenericschemedescribedinthissection,soweonlyneedtoestablishthetwoassumptions. (A1)Suppose firstthat P0 occursasa sub-patterninPatt

(I[

S]) onthe tripleofvariables

(x,

y,z).Asexplained above, when usingthegeneric schemewewillassume that thetorsoof S is three-connected.Then,by Menger’stheorem there are threedisjointpaths

π

1

,

π

2

,

π

3 fromx to z inthetorso ofS.Hencetheremustbe twoofthesepaths,say

π

1 and

π

2,

whichdonotpassthrough y.ButthisimpliesthatP occursasatopologicalminorinPatt

(I)

,sinceifeither

_π

1 or

π

2 passes throughtheedge

{u,

v}inthetorsoof S,thisedgecanbereplaced by pathT

(u,

v)whichisa pathfromu to v inGI

[T

]

, whoseexistence was showninthe discussionofthe generic schemeabove.Since thiscontradicts ourinitial assumption, wecanassumethat P0 doesnot occurasasub-patterninPatt

(I[S])

.Thisalsoholdsforanysub-problemofI[S]obtained

by instantiatingthevariables u,v. Therefore,by thesub-pattern tractabilityof P0,we candetermine inpolynomial time whichinstantiationsofu,v can beextendedtoasolutionofI[S].Weremove thepair

(p,

q)from Ruv in I wheneverthe assignmentofp tou andq tov cannotbeextendedtoasolutiontoI[S].Finally,wedeleteallvariablesinS fromI except

foru andv.ProceedinginthiswayweconstructI′

_[T

_]

_{inpolynomialtime,asrequired.}

(A2)Suppose,foracontradiction, thatweintroducethepattern P asatopologicalminorofPatt

(I

′

_[T

_])

_whenreducing

I to I′

[T

]

. This occurrence of P must use a newly-introduced negative edge. Observe that, by definition, P containsat

mostonenegativeedgebetweenanytwo parts.Supposethat a negativeedge

(p,

q)isintroduced by thereductionfrom

I toI′

_[T

_]

_{.Thiscanonlybethecaseiftherewas apath}

π

_{= (u,}

_w

1

,

. . . ,

wt

,

v) intheconstraintgraphGI

[S]

andhencea sequenceofnegativeedgesbetweenthecorrespondingpartsinPatt

(I[S])

linking p toq.Furthermore,inI′

[T

]

,ifthereisa positiveedge

(p

′

_,

_q′

₎

_{betweenthepartscorrespondingtou andv thenthereisnecessarilyasolutionto I[S] includingthe} assignments p′ _{tou andq}′_{to v (andhenceasolutiononthesubinstance I[}

_π

_]

_{of I[S]onthepath}

π

_{= (u,}

_w

1

,

. . . ,

wt

,

v) inI[S]).Thismeansthatwecanreplacetheedge

(p,

q)intheoccurrenceofP in I′

[T

]

byasequenceofnegativeedgesso thatP occursasatopologicalminorinPatt

(I)

fortheoriginalinstanceI .Thiscontradictionshowsthatwecannotintroduce

anoccurrenceofP asatopologicalminorinPatt

(I

′

_[T

_])

_{whenreducingI to I}′

_[T

_]

_.

Hencewehaveestablishedbothassumptions,sotheresultfollowsbyourgeneric proofscheme.Notethatthenumber ofinstancesofCSP_SP

(P

0

)

thatneedtobesolvedisO

(nd

2

)

.

✷

By [12, Theorem 1],all sub-pattern tractable patterns P0 satisfying the conditionsofTheorem 5.4 can be reducedto sub-patternsofone offivespecificpatterns.Extendingeachofthesetoapattern P asdescribedinTheorem5.4givesthe fivetopological-minortractable patternsshowninFig.8.Foreach ofthesepatterns P ,thepatternshowninFig.2occurs

asasub-patternandhenceasatopologicalminorof P .Thus,bythetransitivityofoccurrenceasatopologicalminor,each tractableclassCSP_TM

(P

)

necessarilycontainsallacyclicbinaryCSPinstances.

6. Detectionoftopologicalminors

ForeveryfixedundirectedgraphH ,thereisan O

(n

3

)

timealgorithmthattests,givenagraphG withn vertices,ifH is

atopologicalminorofG [29].

However,fordetectingtopologicalminorsinpatterns thesituationisdifferent.Characterisingallpatterns P forwhichit ispossibletodecide inpolynomialtime whether P occurs asa topologicalminorinagivenpattern P′ _{remains an open} problem.However,wehavethefollowingpartialresults.

ByLemma4.2,decidingwhetheranegativepatternoftheformPatt

(G)

forsomegraphG occursasatopologicalminor ina pattern P′ _{amounts todetecting whether G is a topological minorofthe constraintgraphof P}′_{,and hencecan be} achievedinpolynomialtime [29].ByProposition3.22,decidingwhetherastar-likenegativepatternoccursasatopological minorinaninstancecanalsobeachievedinpolynomialtimebecausethisisequivalenttodecidingwhetheritoccursasa sub-pattern,whichisachievableinpolynomialtimebyexhaustivesearch.

Proposition6.1.Foreachofthepatterns J ,K orL showninFig.6,decidingwhetherthatpatternoccursasatopologicalminorina giveninstanceI canbedoneinpolynomialtime.

Proof. Thepattern J shownin Fig. 6 isstar-like, andhence the resultfollows fromthe observation justmade. Forthe patternK showninFig.6itissufficienttodiscoverbyexhaustivesearchalloccurrencesof J asasub-patternofPatt

(I)

on thethreepartscorresponding tothetripleofvariables

(x,

y,z)in I ,with y beingthevariableatwhichthetwo negative

edgesmeet,andthencheckforeachonewhetherx andz areconnectedinGI

\

y.

ForthepatternL showninFig.6itissufficienttoconsiderallpairsofoccurrencesof J asasub-patternofPatt

(I)

on partscorrespondingto

(x,

y,z)and

(x

′

,

y′

,

z′

)

(wherethenegativeedgesmeetinparts y and y′).Wecanthen checkthat

either

(y,

z)and

(x

′

_,

_y′

₎

_{coincide,orz and x}′_{coincide,orz andx}′_{areconnectedbyapathinG}

I thatdoesnotpassthrough anyofthepartsx,y,y′

_,

_z′_.

_✷

ForeachofthepatternsshowninFig.8thecomplexityofdecidingwhetheritoccursasatopologicalminorinagiven instanceI iscurrentlyunknown.However,inpolynomialtimewecanbuildaTuttedecompositionforI anddecidewhether eachofthesub-problems associatedwithitsnodesaremembers ofCSP_SP

(P

0

)

fortheappropriate pattern P0,andthisis theonlyconditionrequiredtosolve I inpolynomialtimeusingthealgorithmdescribedintheproofofTheorem5.4.

Ournext resultshowsthat forsome patterns (suchasthe 4-partpattern M shownin Fig.9), it iscoNP-complete to determinewhetherthepatternoccursasatopologicalminorinanarbitrarygivenpattern.

Fig. 9. A pattern that is coNP-complete to detect as a topological minor.

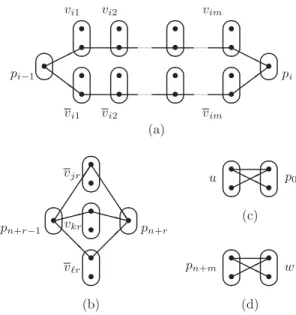
Fig. 10. The building blocks for the CSP instance I constructed in the proof of Theorem6.2.

Proof. TheproblemisclearlyincoNP,soit sufficestogiveareduction from3-SAT tothecomplementoftheproblemof deciding I

∈

CSP_TM

(M)

.

Let IS AT bean instanceof3-SATwithvariables x1

,

. . . ,

xn andclauses C1

,

. . . ,

Cm.Wewillcreateabinary CSPinstance

I withvariables

{u,

w}

∪ {p

i

|

i

=

0

. . .n

+

m}

∪ {v

ir

,

vir

|

i

=

1

. . .n,

r

=

1

. . .

m},suchthatdeterminingwhetherM T M

→

Patt

(I)

isequivalenttodecidingwhether IS AT hasasolution.Theinstance I thatwe createwill beBooleaninthesense thatall variables willhavedomain sizeatmosttwo.(In factall thevariables pi,exceptfor p0 and pn+m,willhavesingle-valued domains.)

ConsiderthepatternsshowninFig.10,whereeachpartislabelledwithavariableofI .Usingthesepatternswebuilda completepatterncorrespondingtotheinstanceI ,asfollows:

•

ForeachvariablexiinIS AT weincludeapatternPxi oftheformshowninFig.10(a).

•

ForeachclauseCr inIS AT weincludeapattern PCr oftheformshowninFig.10(b),wherethechoiceofvariablesfor

thethree centralpartsdependsonthe literalsintheclause Cr in thefollowingway:variable vir corresponds to

¬x

i occurringinclauseCrandvariablevir correspondstoxioccurringinclauseCr.Thatis,theexampleshowninFig.10(b) wouldcorrespondtotheclausexj

∨ ¬x

k

∨

xℓ.

•

WealsoincludethepatternshowninFig.10(c)andthepatternshowninFig.10(d).

•

Finally, we complete the resultingpattern to obtain Patt

(I)

by adding negativeedges between all pairs ofpoints in distinctpartsthatarenotalreadydirectlyconnectedbyapositiveornegativeedge.

TheonlypairsofpartsinPatt

(I)

thatareconnectedbymorethanonepositiveedgeare

{u,

p0

}

and

{p

n+m

,

w}.So,ifM occursasa topologicalminorinPatt

(I)

,thenthepointsof M mustmap injectivelytothesetwopairsofparts.Therefore, decidingwhetherM occursasatopologicalminorinPatt

(I)

isequivalenttodecidingwhetherthereisapath

π

ofpositive edgesfromp0 to pn+minPatt

(I)

whichpassesthrougheachpartatmostonce.

Any such path

π

must passthrough thepoints p0

,

p1

,

. . . ,

pn+m inthisorder, becausethe positive edges in Pxi (1

≤

i

≤

n)usedifferentpoints ineachpart(shownasthebottomofthetwo pointsinFig.10)fromthepositiveedgesin PCr

(1

≤

r

≤

m)(whichusethetoppoints),sotherearenoshort-cuts.

Ifsuchapath

π

exists,thenforeachvariablexi ofIS AT,thepath

π

mustselectin Pxi eithertheupperpaththrough

variables vir (r

=

1

,

. . . ,

m) orthe lower path through variables vir (r

=

1

,

. . . ,

m).Thus

π

selects a truth value foreach variablexi:TRUEif

π

followstheupperofthesetwopaths,FALSEotherwise.