HAL Id: hal-01404426
https://hal.archives-ouvertes.fr/hal-01404426
Submitted on 28 Nov 2016HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
Optimisation des codes LDPC irréguliers et algorithmes
de décodage des codes LDPC q-aires
Jean-Pierre Cances
To cite this version:
Jean-Pierre Cances. Optimisation des codes LDPC irréguliers et algorithmes de décodage des codes LDPC q-aires. [Rapport de recherche] Xlim UMR 7252. 2013. �hal-01404426�
Optimisation des codes LDPC irréguliers et algorithmes de décodage des codes LDPC q-aires
JP CANCES, Xlim, UMR CNRS 7252
Cette note technique est une synthèse basée sur les articles suivants :
-1 S.Y. Chung, T.J. Richardson and R.L. Urbanke,“ Analysis of Sum-Product Decoding of Low-Density Parity-Check Codes using a Gaussian approximation”, IEEE Trans On Inform Theory, February 2001, pp. 657-670.
-2 D Declercq, M Fossorier, “Decoding Algorithms for Nonbinary LDPC codes Over GF(q)”, IEEE Trans. Inform. Theory, April 2007, pp. 633-643
1) Calcul des profils optimaux de codes LDPC : principes de l’évolution de densité
Décodage des codes LDPC :
On utilise classiquement le décodage par propagation de croyance. Dans le graphe équivalent du code les nœuds de variables sont numérotés de 1 à n et les nœuds de parité sont numérotés de 1 à
nk. Le degré du nœud de variable i est appelé iet le degré du nœud de parité j sera noté j. On appelle
,1, ,2,..., ,
i
b b b i i i
e e e l’ensemble des nœuds de parité connectés au nœud de variable i et
,1, ,2,..., , i
c c c i i i
e e e l’ensemble des nœuds de variable connectés au nœud de parité i. Ce qui veut
dire que e représente le ki kb, ième lien connecté au nœud de variable i et que e représente le ki kc, ième
lien connecté au nœud de parité i. Un indice noté bcreprésente des quantités transmises depuis des nœuds de variable vers des nœuds de parité et vice versa. Par exemple, Lbpc(ei jb, ) désigne l’information extrinsèque en termes de LLR (Log Likelihood Ratio) qui est transmise lors de l’itération p depuis un nœud de variable vers un nœud de parité le long du lien entre le nœud de parité j et le nœud de variable i. L’algorithme d’échange des messages ou de propagation de croyance peut alors se résumer ainsi :
- Mise à jour des nœuds de variables :
Pour chacun des nœuds de variables i1, 2,...,n et pour chaque lien connecté à un nœud de variable depuis un nœud de parité, on calcule l’information extrinsèque envoyée depuis le nœud de variable étudié vers le nœud de parité correspondant par la formule :
1 , , 1, ( ) ( ) ( ) i p b p b b c i j ch i b c i k k k j L e L b L e
(1)Dans cette équation, la quantité Lch( )b désigne le rapport de vraisemblance logarithmique i
représentant l’information à priori du bit bi après propagation dans le canal assimilé à un canal de
Rayleigh non sélectif en fréquence avec un coefficient : h . On a de façon évidente : i
0 ( 1 ) 4. . ( ) log[ ] ( 1 ) i i i i ch i i i p x y h y L b p x y N (2)
- Mise à jour des nœuds de parité :
Pour chacun des nœuds de parités i1, 2,...,n k et pour chaque lien connecté au nœud de parité étudié, on calcule l’information extrinsèque envoyée depuis le nœud de parité étudié vers le nœud de variable correspondant par la formule :
1 , , 1, ( ) 2.tanh [ tanh( ( ) / 2)] i p c p c b c i j b c i k k k j L e L e
(3) - Prise de décisions: On calcule alors , 1 ( ) ( ) i P P b i b c i k k L b L e
et on prend la décision : ˆbi sign(L bP( ))i . On forme alors le produit : H b pour voir s’il existe encore des erreurs. .ˆ- Calcul du profil optimal du codeur, évaluation de la p.d.f des messages aux nœuds du codeur :
Dans tout ce qui suit nous allons supposer que la p.d.f des messages échangés aux différents nœuds est toujours un mélange de lois Gaussiennes. Nous allons voir que dans ce cas il est très simple d’obtenir les p.d.f’s des informations extrinsèques aux différents nœuds sans avoir recours à des produits de convolution compliqués. On appellera dans tout ce qui suit : ( )x la fonction définie par :( )x E[tanh( / 2)]u où la variable u suit une loi Gaussienne de moyenne x et de variance 2.x. On a par définition :
2 2 ( ) 4. 1 ( ) [tanh( / 2)] . tanh( / 2). . 4. . u x x x E u u e du x
(4)On peut par exemple écrire : ( ) 1x ( )x avec : 2 ( ) / 4. 1 1 . tanh( ). . if 0 2 ( ) 4. . 1 if 0 u x x u e du x x x x
(5)Et on peut utiliser les approximations numériques suivantes: 0.86 (0.4527. 0.0218) / 4 for [0,10] ( ) 20 . .(1 ) for 10 7. x x e x x e x x x (6)
Si on regarde alors ce qui se passe à un nœud de variable de degré i, on a les relations :
1 , , 1, 1 , , ( ) ( ) ( ) ( ) ( ) ( 1). ( ) i p b p b b c i j ch i b c i k k k j p b p b b c i j ch i i b c i k E L e E L b E L e E L e E L b E L e
(7)Ainsi, en appellant m( )v,li la moyenne des informations extrinsèques d’un nœud de variable de degré
i
à l’itération numéro l, on a la relation : 0 ( ) ( 1) v,i ( i 1). l l u u m m m (8) Où
0 ( ) u ch im E L b et u est un mélange de lois Gaussiennes. La variance de la densité en sortie du
nœud de variable de degré i est égale à : ( ) v,
2.
i
l
m . Ainsi, à l’itération l, un message v arrivant à un
nœud de parité aura une densité de probabilité qui se présentera sous la forme d’une mixture de Gaussiennes : ( ) ( ) ( ) v v, v, 2 . ( , 2. ) l i i d l l l i i f m m
N (9) Où v,( ) i lm est la moyennedes messages en sortie d’un nœud de variables de degré i. En prenant la moyenne de (9), on arrive alors à :
( ) v, 2 tanh(v / 2) 1 . ( ) l d l l i i i E m
(10)Si on regarde alors ce qui se passe à un nœud de parité j de degré j, on suppose que l’information extrinsèque LLR de sortie de ce nœud de parité est Gaussienne avec une moyenne p ,
b c j
m et en
prenant les valeurs moyennes de l’équation (3) on arrive à :
, , 1, 1 , tanh( ( ) / 2) [ tanh( ( ) / 2)] [ tanh( ( ) / 2) ] j p c p c b c i r b c i k k k r p c j b c i k E L e E L e E L e
(11) On obtient alors: 1 ( ) 1 ( ) , v, 2 (1 1 . ( ) ) j l j j d l l u i i m m
(12)En combinant ces valeurs moyennes pour des nœuds de parité de degrés 2,…, d ayant des poids r
, 2
j j dr
, on obtient l’équation suivante :
0 1 ( ) 1 ( 1) 2 2 ( 1) 1 1 ( . ) j l r j i j i i d d l l u u u m m m
(13)On définit alors pour 0 s et 0 t les fonctions ( , )
j f s t et f s t( , ): 0 1 1 2 ( 1) ( , ) 1 1 ( . ) j l j i i i d u f s t m t
(14) 2 ( , ) ( , ) r j j j d f s t f s t
(15)En utilisant ces fonctions, l’équation (13) se résume à:
1 ( , ) l l t f s t (16) Avec: 0 u sm et tl mu( )l .
tend vers l’infini avec l qui tend vers l’infini. Puisque ( )x est monotone décroissante pour
0 x , nous pouvons conclure que f s t( , ) est monotone croissante pour 0 s et
0 t . On en en déduit aisément que pour toute valeur de :ss*, *
( ) ( ) l l
t s t s et t s l( ) converge vers l’infini.
Lemme : ( ) l
t s converge vers l’infini si et seulement si: ( , )
t f s t (17) Pour tout t positif.
Preuve : si l’on suppose : t f s t( , ), t , puisque tl1 tl, t converge vers l t [0, [. Cependant la valeur tne peut être finie car cela entraînerait t f s t( , ).
Maintenant nous supposons t' f s t( , ') pour t', on a t'0 car f s( , 0)0. Puisque f est continue, il existe t0 0tel que t f s t( , ) pour t [0, ]t0 . Maintenant nous choisissons la plus petite valeur t'telle que t' f s t( , ') et t f s t( , ) for t [0, ']t . Puisque l’on a :
0 f s( , 0) f s t( , ')t' et f s t( , ) f s t( , ')t' pour t [0, ']t , on peut conclure que tl t' pour
0 l .
On peut également trouver une expression alternative à (16); pour 0 s et 0 r 1 on définit ( , ) i h s r et h s r( , ) sous la forme : 1 1 2 2 ( , ) ( 1) (1 (1 ) ) ( , ) ( , ) r j i j j l i i i d i d h s r s r h s r h s r
(18)L’équation (12) est alors équivalente à:
1 ( , ) l l r h s r (19) Avec
0 ( ) u ch iet seulement si rl 0. Ainsi la condition de convergence ( )r sl 0 est satisfaîte si et seulement si: ( , ) [0, ( )]
l
r h s r r s (20)
Cette expression est très utile pour optimiser ( )x car l’expression (18) est linéaire en
i
.
Le programme Matlab ci-après donne un exemple de calcul de seuil avec les distributions :
2 5 6 19 7 8 ( ) 0.23403 0.21242 0.14690 0.10284 0.30381 ( ) 0.71875 0.28125 x x x x x x x x x
Un calcul par évolution de densité donne un seuil de 0.9669 tandis que l’approximation Gaussienne utilisée ici donne une valeur de 0.9473.
function [r,seuil] = density_irregular_codes rr1=0; m1=0; [x,y,z,d] = mean_densitybis; %format double; Nb_iter=150; dr=9; dl=20;
%distribution aux noeuds de parité
ro=[0 0 0 0 0 0 0 0.71875 0.28125];
%distribution aux noeuds de variables
landa=[0 0.23403 0.21242 0 0 0.1469 0.10284 0 0 0 0 0 0 0 0 0 0 0 0 0.30381]; for ii=1:length(ro) rr1=rr1+ro(ii)/ii; end rr1; for jj=1:length(ro) m1=m1+landa(jj)/jj; end rendement=1-rr1/m1; mu0=2.419; [valeur,index]=min(abs(mu0-x)); r(1)=y(index); for ii=2:Nb_iter AA=0; for mm=2:dl bb=0; for kk=2:dr aa=double(1-(1-r(ii-1))^(kk-1)); [valeur,index]=min(abs(aa-z)); bb=double(bb+d(index)*ro(1,kk)); end [valeur,index]=min(abs(((mm-1)*bb+mu0)-x)); cc=y(index); AA=double(AA+landa(1,mm)*cc); end r(ii)=double(AA); end seuil=double(10*log10(mu0/(4*rendement))); return
2) Algorithmes simplifié de décodage des codes LDPC sur un corps à q éléments
Avant d’aborder l’algorithme de décodage, il est nécessaire de faire quelques rappels sur les corps de Galois.
1. Corps De galois : Définition
Un corps de Galois à q2m éléments noté GF(q) = GF(2m), où m est un entier positif est défini comme une extension polynomiale du corps GF(2) constitué simplement des éléments 0 et 1. Le polynôme g(x) à utiliser pour construire le corps GF(q) doit être irréductible c’est-à-dire non factorisable dans GF(2), de degré m et à coefficients dans GF(2). Les éléments du corps de Galois GF(q) sont définis modulo g(x) et ainsi, chaque élément du corps peut être représenté par un polynôme de degré au plus égal à (m – 1) et à coefficients dans GF(2). Exemple :
Considérons un polynôme irréductible dans le corps GF(2) de degré m = 2 : 1
)
(x x2 x
g (1)
Ce polynôme permet de construire un corps de Galois à 4 éléments. Les éléments de ce corps sont de la forme :
b
a où a,bGF(2) (2) soit :
GF(4) :
0,1,,1
(3)On peut remarquer que si on élève l’élément aux puissances successives 0,1 et 2, on obtient tous les éléments du corps GF(4) à l’exception de l’élément 0. En effet, le carré de est encore égal à (+1) modulo 2 1. L’élément est appelé élément primitif du corps
GF(4).
1.1 Elément primitif d’un corps de Galois
On appelle élément primitif d’un corps de Galois GF(q), un élément de ce corps qui, lorsqu’il est élevé aux puissances successives 0, 1, 2,…, (q - 2) ; q2m permet de retrouver tous les éléments du corps sauf l’élément 0. Tout corps de Galois possède au moins un élément primitif. Si est un élément primitif du corps GF(q) alors les éléments de ce corps sont :
Propriétés :
- Un élément primitif d’un corps de Galois GF(q) est racine de l’équation xn 10 si
1 q
n . En effet, si on tient compte du fait que q1 0 et que nq1 alors 0
1
n
(rappelons que –1 = 1 dans le corps GF(2) ainsi que dans un corps GF(2m)).
- Si l’élément est racine de xn 1 alors jest aussi racine de xn 1. En effet, nous avons 1
n
et ainsi nous pouvons écrire :
1 ) 1 ( ) (n j j En permutant les exposants n et j, nous obtenons :
0 1 ) ( 1 ) (j n j n
Ces deux propriétés peuvent être utilisées pour factoriser le polynôme xn 1 (n = q – 1) dans un corps de Galois à q2m éléments. En effet, si est un élément primitif du corps GF(2m) alors ,2,...,n sont aussi des racines de xn 1 et ainsi nous pouvons écrire :
n j j n x x 1 ) ( 1 (5) Exemple :
Factorisons le polynôme x31 sur le corps GF(4) construit à partir du polynôme 1
)
(x x2 x
g . Nous avons vu que est un élément primitif du corps GF(4) et ainsi, les 4 éléments de ce corps sont :
GF(4) :
0,1,,2
(6) Nous pouvons écrire :) ).( ).( ( ) ( 1 3 2 3 1 3 x x x x x j j (7)
En développant cette expression, on obtient :
1 1 ) 1 .( ) 1 .( 1 3 2 2 2 3 3 x x x x x (8)
En tenant compte du fait que les opérations dans GF(4) sont faîtes modulo 2 1, le deuxième terme de l’égalité (8) est bien égal à x3 1.
1.2 Polynôme minimal associé à un élément d’un corps de Galois 1.2.1 Cas des polynômes à coefficients dans GF(2)
Le polynôme minimal m(x) à coefficients dans GF(2) associé à un élément quelconque d’un corps de Galois GF(2m
), est un polynôme de degré au plus égal à m, ayant comme racine. Ce polynôme est unique et irréductible dans GF(2) mais deux éléments du corps de
Galois peuvent avoir le même polynôme minimal. Si est un élément primitif du corps de Galois GF(2m) alors le polynôme m(x)est exactement de degré m.
Avant de calculer le polynôme minimal associé à un élément rappelons qu’un polynôme à coefficients dans GF(2) vérifie la propriété suivante :
f(x)
2 f(x2)
f(x)
2p f(x2p) (9)Ainsi si est racine du polynôme f(x) alors 2,4,...sont aussi des racines de ce polynôme. Si le polynôme f(x) est de plus irréductible dans GF(2) et de degré m, alors si est racine de ce polynôme, les autres racines de ce polynôme sont simplement : 2,4,...,2m1.
Cette propriété des polynômes à coefficients dans GF(2), nous permet d’écrire le polynôme minimal associé à sous la forme :
).... ).( ).( ( ) ( 2 4 x x x x m (10) ou encore : ) )....( ).( ).( ( ) (x x x 2 x 4 x 2m1 m (11)
si est un élément primitif du corps GF(2m). Exemple :
Calculons le polynôme minimal associé à l’élément primitif du corps de Galois GF(4).
GF(4) :
0,1,,2
Le polynôme minimal associé à l’élément a donc pour racine et 2 (m = 2) et il a pour expression : 3 2 2 2 ) .( ) ).( ( ) ( x x x x x m (12)
En tenant compte du fait que 3 1 et que 2 1dans le corps GF(4), le polynôme )
(x
m est encore égal à :
1 )
(x x2x
m (13)
Pour clore ce paragraphe sur la notion de polynôme minimal, on peut rajouter la propriété suivante :
Soient 1,...,i,...,N les éléments d’un corps de Galois GF(2m) et soient ) ( ),..., ( ),..., ( 1 x m x m x m N i
éléments. Alors le polynôme g(x), de plus bas degré, à coefficients dans GF(2) ayant
N
i
1,..., ,..., comme racines est égal à :
)) ( ),..., ( ),..., ( P.P.C.M( ) ( 1 x m x m x m x g N i (14)
où P.P.C.M est l’abréviation de Plus Petit Commun Multiple. Si les polynômes minimaux sont distincts, (ce qui n’est pas toujours le cas puisque deux éléments d’un corps GF(2m
) peuvent avoir le même polynôme minimal) alors le polynôme g(x) est simplement égal à :
N i x m x g i 1 ) ( ) ( (15) 1.2.2 Cas des polynômes à coefficients dans GF(q)
Le polynôme minimal m(x), à coefficients dans le corps de Galois GF(q) associé à un élément j ( élément primitif du corps GF(q)) de ce corps, est le polynôme de plus bas degré ayant comme racine. En utilisant une généralisation de la relation (9) au cas des polynômes à coefficients dans GF(q), nous pouvons écrire :
f(x)
q f(xq)
f(x)
qp f(xqp) (16)Ainsi, si est racine du polynôme f(x) alors q,q2,...sont aussi des racines de ce polynôme.
En tenant compte du fait que dans le corps GF(q) q1 1, alors qp ( j)qp j et ainsi, le polynôme minimal m(x)est simplement égal à :
x x
m ( ) (17) 1.3 Polynôme primitif
Un polynôme à coefficients dans GF(2) est primitif si il est le polynôme minimal associé à un élément primitif d’un corps de Galois. Dans l’exemple présenté dans le paragraphe 1.2, le polynôme m(x) était un polynôme primitif.
Un polynôme primitif est donc irréductible dans GF(2) et peut par conséquent être utilisé pour engendrer un corps de Galois. Lorqu’un polynôme primitif est utilisé pour engendrer un corps de Galois, tous les éléments du corps sont obtenus en élevant l’élément primitif, racine du polynôme primitif à des puissances successivement croissantes. Les principaux polynômes primitifs étant repertoriés dans la littérature, la construction d’un corps de Galois à m
q 2
Exemples de polynômes primitifs
Degré du polynôme Polynômes primitifs
2 2 1 x x 3 3 1 x x 4 4 1 x x 5 5 2 1 x x 6 6 1 x x 7 7 31 x x 8 8 4 3 2 1 x x x x 9 9 4 1 x x 10 10 31 x x
Pour terminer cette partie introductive aux corps de Galois, nous donnons un exemple de corps de Galois à q16 (m = 4) éléments construit à partir du polynôme primitif x4 x1. Les éléments de ce corps sont :
2 3 14
,..., , , , 1 , 0 : ) 16 ( GF (18)A ces 16 éléments on peut associer une représentation polynomiale ainsi qu’une représentation binaire. La représentation polynomiale d’un élément de ce corps est de la forme :
d c b
a.3 .2 . (19)
où a, b, c d sont des coefficients binaires appartenant à GF(2). Le corps de Galois GF(16) étant constitué de 16 éléments, la représentation binaire d’un élément de ce corps est faîte à l’aide de 4 symboles binaires appartenant à GF(2). Ces 4 symboles sont respectivement égaux aux valeurs prises par les coefficients a, b, c et d.
Eléments du corps GF(16) Représentation polynomiale Représentation binaire
0 0 0000
1 1 0001
0010
2
3 3 1000 4 1 0011 5 2 0110 6 3 2 1100 7 31 1011 8 2 1 0101 9 3 1010 10 2 1 0111 11 32 1110 12 32 1 1111 13 3 2 1 1101 14 31 1001
Eléments du corps de Galois GF(16)
Dans un corps la somme de deux éléments du corps est un élément du corps. Nous pouvons vérifier cette propriété pour le corps de Galois GF(16). Faisons par exemple la somme des éléments 5 et 8. En utilisant les représentations polynomiales de ces deux éléments, nous avons à faire la somme de (2 ) et de (2 1) ce qui donne (1)4puisque
0 .
22 . Pour faire la somme de 5 et 8on peut aussi utiliser leur représentation binaire. Dans ce cas on doit faire la somme bit à bit de 0110 et de 0101 ce qui donne 0011 soit encore
4 .
2. Décodage des codes LDPC sur GF(q) 2.1 Représentation tensorielle des messages :
On suppose l’utilisation d’une matrice d’encodage G sur GF(q) avec conversion binaire des messages et passage en MDP-2 NRZ pour la transmission sur le canal de propagation que l’on supposera de type AWGN.
Pour l’algorithme de décodage et afin de se référer le plus possible aux algorithmes de décodage existant sur GF(2), il est utile d’utiliser une représentation tensorielle des messages transmis. Pour un code LDPC C défini sur GF(q) avec H q2m, la matrice de contrôle de parité du code H de taille M N qui définit le noyau du code est une matrice creuse telle que :
0
c Hc H ) . N q GF C ( (20)Le graphe factoriel du code consiste en un ensemble de nœuds de variables appartenant à
GF(q), connectés à un ensemble de nœuds de parité. Les arêtes qui connectent les deux types
de nœud transportent des messages qui représentent les densités de probabilité (pdf’s) des mots de code. Puisque ces mots de code sont des variables aléatoires sur le corps GF(q), les
messages sont des densités de probabilité discrètes de taille q. Lorsque le corps de Galois est une extension de GF(2), avec typiquement q2m, les messages peuvent être convenablement représentés par des tenseurs de taille 2 et de dimension m.
En effet, sur le corps GF(2m), les éléments du corps, comme on l’a montré dans le précédent paragraphe, peuvent être représentés à l’aide d’un polynôme
m l l l x i x i 1 1 . ) ( de degré p-1 avec
des coefficients binaires. Ainsi n’importe quel ensemble de m valeurs binaires
il l1,...,mdétermine un unique élément i(x). En utilisant cette représentation, un message )(x
i sur une arête connectée à un nœud de variable est un tenseur
m i i m i i U 1 ,..., 1 ] ,..., [ indexé parles coefficients binaires de i(x). Par exemple, U[0,1,1] correspond à la probabilité )
) (
(i x x x2
p dans GF(8).
2.2 Algorithme de décodage par propagation de croyance sur GF(2m) :
Pour un code sur GF(q), un nœud de parité est associé à l’équation de parité suivante :
c d k k k x m x i x h 1 ) ( mod 0 ) ( ). ( (21)
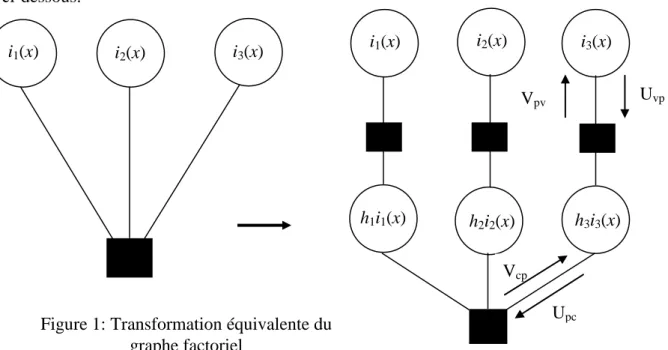
Où m(x) est un polynôme primitif de degré m-1 sur GF(q). L’équation (21) exprime que les nœuds de variables nécessaires au déroulement de l’algorithme de propagation de croyance pour un nœud de parité ne sont pas constitués uniquement des mots du code d’origine mais des mots du code multipliés par les valeurs non nulles de la matrice de parité H. La transformation correspondante sur le graphe est réalisée en additionnant des nœuds de variables correspondant à la multiplication des mots de code ik(x) par les valeurs correspondantes non nulles de H. La transformation correspondante est illustrée sur la figure 1 ci-dessous.
i2(x)
i1(x) i3(x) i1(x)
i2(x) i3(x)
h1i1(x) h2i2(x) h3i3(x)
Figure 1: Transformation équivalente du graphe factoriel
Upc
Vcp
La fonction de nœud qui connecte les deux nœuds de variables ik(x) et hk(x).ik(x) réalise une permutation des valeurs des messages. La permutation qui est utilisée pour mettre à jour les messages correspond à la multiplication des indices du tenseur par hk(x) pour passer du nœud ik(x) au nœud hk(x).ik(x) et à la division des indices par hk(x) dans l’autre sens. En utilisant cette transformation du graphe factoriel, la mise à jour aux nœuds de parité est une convolution de tous les messages entrants, exactement comme dans le cas binaire.
On utilise les notations suivantes : on note
v ,..., 1 v v d pV l’ensemble des messages entrant sur
un nœud de variable de degré d et v
v
,..., 1 v vp d
U l’ensemble des messages de sortie de ce
nœud. L’indice pv indique que le message arrive d’un nœud de permutation et se dirige vers un nœud de variables. De la même façon, l’indice vp indique l’autre sens de propagation. De la même façon on définit les messages
c ,..., 1 d c pc U (respectivement
c ,..., 1 d c pc V ) à l’entrée(respectivement à la sortie) d’un nœud de degré dc.
L’initialisation du décodeur est réalisée avec le calcul des rapports de vraisemblance du canal notéL[i1,...,ip]. Dans le cas où le canal a des données binaires et un bruit additif Gaussien le calcul des rapports de vraisemblance prend la forme :
p n n p l i i i L 1 1,..., ] ( ) [ (22)
avec l(in)Proba(yn bn in)exp((yn bn)2/2.2) et où b est le nn
ième
bit du symbol correspondant sur GF(q) et yn est la sortie bruitée du canal de propagation.
Les trois étapes d’une itération dans le décodage s’écrivent alors de la manière suivante : E1 : Mise à jour des nœuds de variables
Pour la mise à jour d’un nœud de variables de degré d : v
v t v , 1 v v v ,..., 1 .V . d p tp L t d U (23) soit encore :
v 1 1 v , 1 v v 1 1 ,..., 1 , 1 , 0 ) ,..., ( ] ,..., [ V ] ,..., [ ] ,..., [ v d t i i i i i i L i i U p p p d t p p p tp (24)où . est défini comme le produit terme à terme de tenseurs et L désigne le tenseur des rapports de vraisemblance issus du canal (voir équation (22)). De plus, comme les messages représentent des densités de probabilité, on doit normaliser les messages obtenus après l’étape (24) de telle sorte que : [ ,..., ] 1
,..., 1 1 p i i tp p i i U .
E2 : Etape de permutation, depuis les noeuds de variables vers les nœuds de parité On a : ) ( vec . ) ( vecUpc Ph(x) Uvp (25) ou encore :
p p p p p pc i i U j j i i U [1,..., ] v [ 1,..., ] (1,..., ) 0,1 avec i(x)h(x).j(x) (26)où Ph( x) est une matrice de permutation (q q) correspondant à h(x) et vec(U) rassemble dans un vecteur colonne toutes les valeurs du tenseur U. On peut remarquer que, puisque les corps de Galois sont des corps cycliques, la matrice de permutation Ph( x) représente un décalage cyclique des valeurs du message transmis. Dans l’autre direction, à savoir depuis les nœuds de parité vers les nœuds de variables, on utilisera bien sûr la matrice inverse 1
) ( x h P .
E3 : mise à jour des noeuds de parité
En utilisant les noeuds secondaires h(x).i(x), tous les nœuds de parité suivent les mêmes
règles et ne dépendent plus des entrées non nulles de H. L’algorithme de propagation de croyance pour un nœud de parité de degré d correspond à un produit de convolution des c
densités de probabilité sur GF(2m).
c pc d t c c tp c U t 1,...,d V 1, (27) ou encore : i x i x c d t c c pc c c t t tp i i U i i t d c t c c c p p] [ ,..., ] 1I 1,..., ,..., [ V dc 1 c 1 1 0 ) ( ) ( 1, (28)
Où la fonction 1 désigne une fonction indicatrice égale à 1 si et seulement si la condition S IS est remplie. On peut aussi exprimer la somme (28) sans l’aide d’une fonction indicatrice en utilisant un ensemble de configurations. On définit l’ensemble suivant :
c t d c c t c c x i i x i x 1 ) ( ( ) : ( ) 0 Conf (29)En utilisant (29), l’étape E3 peut se réécrire sous la forme :
Etape somme-produit : mise à jour d’un nœud de parité pour un nœud de degré dc.
( ) 1 1 Conf ) ( 1, ] ,..., [ ] ,..., [ V x t i c c p p x i d t c c pc c c t t tp i i U i i (30)
2.3 Simplification de l’algorithme par utilisation de FFT :
La complexité de l’étape E3 dans l’algorithme présenté précédemment peut devenir
rapidement prohibitive. En effet, le nombre d’opérations élémentaires nécessaires au calcul de
tp
V croît exponentiellement avec la taille du corps q et le degré des équations de parité dc.
Pour simplifier de façon importante cette étape, plusieurs auteurs ont proposé de réaliser l’étape E3 dans le domaine fréquentiel afin de transformer la convolution en produit simple.
La transformation des densités des variables représentées par des tenseurs dans le corps
GF(2m) depuis le domaine temporel vers le domaine fréquentiel est très simple puisqu’il s’agit
de transformée de Fourier d’ordre 2.
Proposition : appelons p i i
U ,...,
1 un tenseur d’ordre 2 et de dimension m et qui représente une
densité de probabilité de la variable aléatoire i(x)GF(2m), alors la transformée de Fourier de
p i i
U ,...,
1 est donnée par :
F F F p U U W ( ) 1 2 ... (31)
Où ×k représente le produit tensoriel sur la kième dimension du tenseur et F est la matrice de la
transformée de Fourier rapide donnée par :
1 1 1 1 . 2 1 F (32)
Avec ces définitions, le produit tensoriel ZUk F est défini par : (pour(i1,...,ik1,ik1,...,ip)
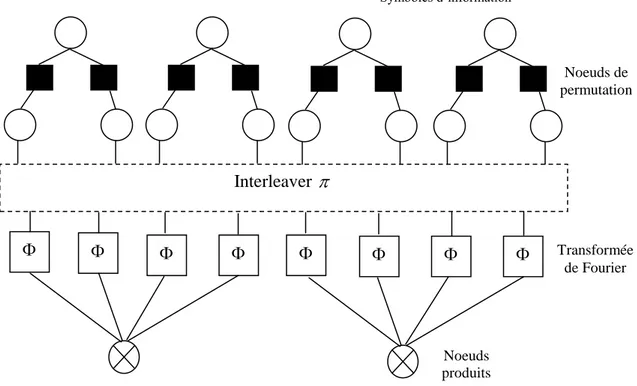
0,1 p1) ) ] ,..., , 1 , ,..., [ ] ,..., , 0 , ,..., [ .( 2 1 ] ,..., , 0 , ,..., [i1 ik 1 ik 1 ip U i1 ik 1 ik 1 ip U i1 ik 1 ik 1 ip Z (33) ) ] ,..., , 1 , ,..., [ ] ,..., , 0 , ,..., [ .( 2 1 ] ,..., , 1 , ,..., [i1 ik 1 ik 1 ip U i1 ik 1 ik 1 ip U i1 ik 1 ik 1 ip Z (34)En utilisant la transformée de Fourier (31), on change les nœuds de parité en nœuds produits dans le graphe factoriel du code sur GF(2m). La figure 2 illustre ces transformations dans le cas d’un code LDPC régulier avec (dv,dc)(2,4).
Avec le passage dans le domaine fréquentiel, l’étape E3 est modifiée de la façon suivante :
E’3 : mise à jour des noeuds de parité en utilisant une FFT La mise à jour dans le domaine fréquentiel s’écrit :
c d t c c pc tp U t d c ,..., 1 ) ( . V , 1 (35)
Ainsi, la complexité de l’étape E3 est réduite en (dc.m.q) with q2m. De plus, on peut
remarquer que la forme particulière de la FFT dans GF(2m) fait que l’on ne traite plus que des additions, il n’y a plus de multiplication.
Figure 2 : Graphe factoriel équivalent dans le domaine fréquentiel
2.4 Algorithme EMS dans le domaine logarithmique :
Nous présentons dans ce paragraphe un algorithme qui opère, comme pour le Max-log-MAP des turbo-codes dans le domaine logarithmique à l’aide de rapports de vraisemblance
logarithmiques. Le rapport de vraisemblance logarithmique s’exprime sous la
forme : ) 1 ( oba Pr ) 0 ( oba Pr log ) ( u u u
LLR dans le cas q = 2. Dans le cas q = 2m, le message est composé de q composantes dont q – 1 qui sont non nulles. On utilise alors la définition suivante pour les rapports de vraisemblance logarithmiques de n’importe quel message tensoriel U :
p p p p i i U i i U i i U ( ,..., ) 0,1 ] 0 ,..., 0 [ ] ,..., [ log ] ,..., [1 1 1 (36) Ainsi, on a forcément : U[0,...,0]0.Le but de l’algorithme EMS est de simplifier encore l’étape E’3 obtenue en travaillant dans le
domaine fréquentiel avec une FFT. Pour cela, la première idée est de sélectionner (on suppose un corps avec un nombre élevé d’éléments typiquement m est au moins égal à 6) dans chaque message arrivant Upc un nombre limité de valeurs à savoir les nm valeurs les plus élevées.
Toute la difficulté est bien sûr de bien choisir nm. Les auteurs de l’article original évoquent
une possibilité de changer sa valeur d’un message à l’autre en tenant compte d’une Interleaver Symboles d’information Noeuds de permutation Transformée de Fourier Noeuds produits Fourier
dynamique maximale. Cependant, pour des raisons de simplicité, on se contentera ici de prendre une valeur nm fixe. On note up c(kc), kc 1,...,nm les nm valeurs les plus élevées de Upc.
L’élément associé à une contrainte de parité dans le corps de Galois GF(2m) est noté:
] ... [ ) 0 ) ( ). ( ( oba P r )) ( ) ( ). ( ( oba P r log ) ( ) ( ) ( ) ( 1 c p c c c k c k c pc c c k c c c k pc U x i x h x x i x h u (37)
A partir ce cet ensemble de nm valeurs, on construit l’ensemble suivant des configurations :
1
1 1 ) ( 1 ) ( 1 ( ),..., ( )] : [ ,..., ] 1,..., [ ) ( Conf 1 1 c c c d c d m T d T k d k m x x k k n n k k (38)Chaque vecteur de taille dc 1 dans le corps GF(2m) est appelé une configuration.
L’ensemble Conf(nm) correspond à l’ensemble des configurations construites à partir des nm
valeurs de probabilité les plus grandes dans chaque message entrant. Ainsi, son cardinal est :
1 ) ( Conf dc m m n n (39) ) 1 (
Conf contient seulement une configuration qui sera appelée la configuration d’ordre zéro. Pour certains cas, lorsque les valeurs de d et c n sont importantes, le nombre de m
configurations dans Conf(nm) est trop important. Pour le réduire, on considère le sous-ensemble suivant de Conf(nm) pour nc dc 1 :
) ( ) 1 ( ) 0 ( ) ( Conf ... ) ( Conf ) ( Conf ) , ( Conf nc m m m c m n n n n n (40)
Où Conf(nm)(l) désigne le sous-ensemble de configurations qui diffèrent de la configuration d’ordre zéro pour exactement l entrées. L’ensemble Conf(nm,nc) est donc le sous-ensemble des configurations appartenant à Conf(nm) qui diffèrent par au moins nc entrées de la
configuration d’ordre zéro. Le nombre d’éléments dans Conf(nm,nc) est égal à:
c c c c c n m n d k m n k k d c m n C n C n n , ) ( 1) . ( Conf 1 0 1 (41)
L’idée d’utiliser Conf(nm,nc) à la place de Conf(nm) est, une fois de plus, de simplifier la complexité car la cardinalité de Conf(nm,nc) est généralement bien inférieure à celle de
) (
Conf nm . On a de plus : Conf(nm)Conf(nm,dc 1).
Un degré de confiance est attribué à chaque configuration, cette confiance est calculée par la formule : 1,..., 1 ) ( ) ( c c d c k c u L αk (42)
A partir des degrés de confiance L(αk) des configurations Conf(nm,nc), on est alors capable de definer un algorithme simplifié de propagation de croyance très efficace que les auteurs de l’article ont appelé algorithme EMS (Extended Min-Sum). Pour détailler cet algorithme on note Confi (x)(nm,nc)
c
d le sous-ensemble de Conf(nm,nc)défini par les contraintes aux
nœuds de parité : 1 -1 ) ( ) ( ( , ) Conf( , ): ( ). ( ) ( ) 0 Conf c c c c c d d c k c d d c c m x i n n αk nm n h x i x x (43)
Un problème peut se poser lorsque l’ensemble Conf(nm,nc) est vide. Si l’ensemble )
, (
Conf nm nc est vide pour certaines valeurs de i (x)
c
d , cela peut poser un problème de
convergence pour l’algorithme EMS. On peut cependant contourner ce problème en utilisant les sous-ensembles Conf (x)(q,1)
c d
i qui ne sont jamais vides pour n’importe quelle valeur
) ( ) (x GF q i c d . Algorithme EMS :
En utilisant les notations précédentes, on arrive alors à l’algorithme suivant : E1 : Mise à jour des nœuds de variables
Pour la mise à jour d’un nœud de variables de degré d : v
v v , 1 v v ,..., 1 V v d t L U d t p tp (44) Ou encore :
p p p d t p p p tp i i L i i i i i i U [ ,..., ] [ ,..., ] V [1,..., ] (1,..., ) 0,1 v , 1 v v 1 1 v (45)E2 : Etape de permutation, depuis les noeuds de variables vers les nœuds de parité On a : ) ( vec . ) ( vecUpc Ph(x) Uvp (46) ou encore :
p p p p p pc i i U j j i i U [1,..., ] v [ 1,..., ] (1,..., ) 0,1 avec i(x)h(x).j(x) (47)L’étape de permutation depuis les nœuds de parité vers les nouds de variables est réalisée avec la matrice Ph(1x).
E3 : mise à jour des noeuds de parité
A partir des dc1messages arrivant U , construire les ensembles : pc
) , ( Conf ) 1 , ( Conf ) ( i (x) i (x) m c i x q n n S c d c d c d ; On obtient alors :