La construction du concept de nombre chez un enfant ayant reçu un diagnostic d'autisme

(1)

LA CONSTRUCTION DU CONCEPT DE NOMBRE CHEZ

UN ENFANT AYANT REÇU UN DIAGNOSTIC D’AUTISME

Mémoire

Isabelle Malouin

Maîtrise en psychopédagogie – adaptation scolaire

Maître ès arts (M.A.)

Québec, Canada

(2)

(3)

(4)

(5)

iii

RÉSUMÉ

Le présent projet de recherche vise à décrire les progrès réalisés, par un élève autiste, dans l‟apprentissage du concept de nombre en travaillant dans une pédagogie développementale basée sur le jeu. On cherche à vérifier s‟il est possible de soutenir la construction du concept de nombre chez les enfants ayant reçu un diagnostic d‟autisme sans utiliser les méthodes béhavioristes habituelles, comme A.B.A. et T.E.A.C.C.H., mais plutôt en mettant en place un projet d‟intervention pédagogique basé sur la littératie et le jeu.

Pour ce faire, une expérimentation a été réalisée auprès d‟un enfant autiste de 10 ans, à raison de 3 heures par jour, pendant deux années scolaires, pour travailler, entre autres, la construction du concept de nombre. La cueillette de données consiste en quatre entrevues semi-dirigées portant sur des tâches mathématiques liées à la construction du nombre, entrevues réalisées sur ces deux années pour vérifier l‟évolution de la compréhension de l‟aspect ordinal et de l‟aspect cardinal du nombre chez l‟enfant. Les résultats indiquent, au terme de ces deux années d‟intervention, que l‟enfant a progressé au niveau de sa représentation du nombre.

(6)

(7)

v

TABLE DES MATIÈRES

RÉSUMÉ ... iii

TABLE DES MATIÈRES ... v

LISTE DES TABLEAUX ... ix

LISTE DES FIGURES ... xi

AVANT-PROPOS ... xiii

INTRODUCTION ... 1

1. Problématique ... 3

1.1. L‟autisme ... 3

1.2. La scolarisation des enfants autistes... 4

1.2.1.La méthode A.B.A. ... 5

1.2.2.La méthode T.E.A.C.C.H. ... 6

1.3. Les contextes d‟intervention privilégiés pour travailler le nombre ... 8

2. Cadre théorique ... 9 2.1. L‟abstraction ... 11 2.1.1.Le nombre ... 13 2.1.1.1 Aspect ordinal ... 16 2.1.1.2 Aspect cardinal ... 17 2.1.1.3 Opérations à construire ... 18

2.1.1.3.1 La correspondance terme à terme ... 18

2.1.1.3.2 La conservation ... 20

2.1.1.3.3 Le comptage ... 26

2.1.1.4 Autre procédure possible et difficultés reconnues... 30

2.2. Question générale ... 34

3. Approche d‟intervention pédagogique ... 37

3.1. Idées maîtresses d‟une approche développementale ... 37

3.1.1. La complexité de la tâche ... 37

3.1.2. Le sens des erreurs ... 38

3.1.3. La zone proximale de développement ... 38

3.2. Projet pédagogique d‟ensemble ... 39

3.3. Contextes mathématiques aux fins du mémoire ... 40

(8)

vi

3.3.2. Les jeux de règles ... 43

3.3.2.1 Jeu de Cher Ours polaire … ... 44

3.3.2.2 Autres jeux pour favoriser la construction du concept de nombre ... 45

4. Méthodologie... 49

4.1. But et objectifs de la recherche ... 49

4.2. Type d‟étude ... 49

4.3. Sujet ... 50

4.4. Modalités et temps d‟intervention ... 51

4.5. Collecte de données ... 51

4.6. Protocole d‟entrevue semi-dirigée ... 52

4.6.1. Description des items du protocole d‟entrevue ... 53

4.6.1.1 Items portant sur l‟aspect ordinal du nombre ... 53

4.6.1.1.1 Item 1 : Sériation d‟objets de tailles différentes ... 53

4.6.1.1.2 Item 2 : Sériation d‟objets faisant une course ... 54

4.6.1.2 Items portant sur l‟aspect cardinal du nombre ... 54

4.6.1.2.1 Item 1 : Comparaison de collections d‟objets identiques (correspondance terme à terme) ... 54

4.6.1.2.2 Item 2 : Comparaison de collections d‟objets différents (correspondance terme à terme) ... 56

4.6.1.2.3 Item 3 : Conservation de quantités continues ... 57

4.6.1.2.4 Item 4 : Conservation de quantités discontinues... 60

4.6.1.2.5 Item 5 : Comptage ... 61

4.6.1.2.6 Item 6 : Cardinalité ... 61

4.7. Plan d‟analyse des données ... 63

5. Analyses des résultats ... 65

5.1. Évaluation 1 : Octobre 2011 ... 65

5.1.1. Items vérifiant la compréhension de l‟aspect ordinal du nombre ... 65

5.1.1.1 Item 1 : Sériation d‟objets de tailles différentes ... 65

5.1.1.2 Item 2 : Sériation d‟objets faisant une course ... 67

5.1.2. Items vérifiant la compréhension de l‟aspect cardinal du nombre ... 69

5.1.2.1 Item 1 : Comparaison de collections (correspondance terme à terme) ... 69

5.1.2.2 Item 2 : Conservation de quantités continues ... 72

5.1.2.3 Item 3 : Conservation de quantités discontinues ... 75

(9)

vii

5.1.2.5 Item 5 : Cardinalité ... 84

5.1.3. Synthèse de la compréhension de l‟enfant en octobre 2011 ... 88

5.2. Évaluation 2 : Mai 2012 ... 89

5.2.2. Items vérifiant la compréhension de l‟aspect cardinal... 94

5.2.2.1 Item 1 : Comparaison de collections d‟objets identiques (correspondance terme à terme)... 94

5.2.2.4 Item 4 : Comptage ... 106

5.2.3. Synthèse de la compréhension de l‟enfant en mai 2012 ... 114

5.3. Évaluation 3 : Février 2013 ... 115

5.3.2. Items vérifiant la compréhension de l‟aspect cardinal du nombre ... 120

5.3.2.1 Item 1 : Comparaison de collections d‟objets identiques (correspondance terme à terme)... 120

5.3.2.2 Item 2 : Comparaison de collections d‟objets différents (correspondance terme à terme)... 124

5.3.2.5 Item 5 : Comptage ... 132

5.3.3. Synthèse de la compréhension de l‟enfant en février 2013 ... 140

5.4. Évaluation 4 : Juillet 2013 ... 141

(10)

viii

5.4.2.1 Item 1 : Comparaison de collections d‟objets identiques (correspondance

terme à terme) ... 148

5.4.2.2 Item 2 : Comparaison de collections d‟objets différents (correspondance terme à terme) ... 153

5.4.2.5 Item 5 : Comptage ... 161

5.4.3. Synthèse de la compréhension de l‟enfant en juillet 2013 ... 171

6. Discussion ... 173

6.1. Synthèse des résultats ... 173

6.1.1. Sériation ... 178

6.1.2. Correspondance terme à terme... 179

6.1.3. Conservation ... 180

6.1.4. Comptage ... 182

6.1.5. Cardinalité ... 183

6.2. Les implications pédagogiques ... 185

6.3. Les limites de l‟étude ... 186

6.4. Avenues prospectives ... 187

CONCLUSION ... 189

RÉFÉRENCES ... 191

(11)

ix

LISTE DES TABLEAUX

Tableau 1 Organisation de la collection ……… 31

Tableau 2 Limite de la reconnaissance visuelle ………..……… 32

Tableau 3 Problème lors de regroupements ………... 33

Tableau 4 Exemple de matériel utilisé pour faire un calendrier ………... 41

Tableau 5 Utilisation de divers jeux de règles commerciaux ………. 46

Tableau 6 Données collectées ………... 52

(12)

(13)

xi

LISTE DES FIGURES

Figure 1 Schéma conceptuel de l‟émergence de la construction du nombre …………. 9

Figure 2 Relation inclusive des nombres jusqu‟à 4 ………... 15

Figure 3 Collections de jetons éparpillés ………... 19

Figure 4 Utilisation de la correspondance terme à terme pour comparer deux collections ……… 19

Figure 5 Item de conservation des quantités continues ………..………... 23

Figure 6 Collection initiale de jetons ………... 24

Figure 7 Collection de jetons modifiée une première fois ………. 24

Figure 8 Collection de jetons modifiée une deuxième fois ………... 25

Figure 9 Présentation des jetons par l‟expérimentateur ………. 31

Figure 10 Échec à la reproduction d‟une rangée-modèle ……… 34

Figure 11 Plateau du jeu Cher Ours polaire … ……….. 44

Figure 12 Sériation de cinq pailles réalisée en octobre 2011..………... 66

Figure 13 Droites de projection imaginée ajoutées sur la sériation de cinq pailles…... 66

Figure 14 Ordre des voitures faisant la course ……… 67

Figure 15 Comparaison de collections inégales de jetons ………... 70

Figure 16 Comparaison de collections inégales de jetons après déplacement en octobre 2011 ………. 71

Figure 17 Première transformation effectuée avec la pâte à modeler …………... 72

Figure 18 Deuxième transformation effectuée avec la pâte à modeler ………... 73

Figure 19 Troisième transformation effectuée avec la pâte à modeler ……… 74

Figure 20 Rangée d'images présentée à l'enfant lors de l'item 3 ………. 76

Figure 21 Construction d'une rangée équivalente en octobre 2011 ………. 76

Figure 22 Disposition des rangées pour la comparaison de collections et pour la conservation des quantités discontinues en octobre 2011 ………... 79

Figure 23 Première disposition de jetons à dénombrer ………... 84

Figure 24 Seconde disposition de jetons à dénombrer ……… 85

(14)

xii

Figure 26 Sériation de pailles réalisée en mai 2012 ……… 90

Figure 27 Déplacement des collections inégales en mai 2012 ……… 94

Figure 28 Construction d'une rangée équivalente en mai 2012 ………... 102

Figure 29 Disposition des rangées pour la comparaison de collections et pour la conservation des quantités discontinues en mai 2012 ………. 104

Figure 30 Seconde disposition de jetons à dénombrer en mai 2012 ……… 111

Figure 31 Sériation de cartons réalisée en février 2013 ………...………... 116

Figure 32 Alignement des coureurs en février 2013 ………... 117

Figure 33 Comparaison de collections inégales d'objets identiques présentées à l'enfant en février 2013 ……….. 120

Figure 34 Comparaison de collections égales d'objets identiques présentées à l'enfant en février 2013 ……… 122

Figure 35 Comparaison de collections égales réduites d'objets identiques présentées à l'enfant en février 2013 ……… 123

Figure 36 Comparaison de collections d'objets différents en février 2013 ………. 125

Figure 37 Rangée d'images présentée à l'enfant en février 2013 ………. 129

Figure 38 Construction d'une rangée équivalente en février 2013 ……….. 129

Figure 39 Modification des rangées en conservation des quantités discontinues en février 2013 ………. 131

Figure 40 Présentation d'une rangée de bâtonnets à l'enfant ……….…... 135

Figure 41 Modification de la rangée de bâtonnets ………... 136

Figure 42 Cinq dames à habiller ……….. 138

Figure 43 Sériation de cartons réalisée en juillet 2013 ………... 142

Figure 44 Alignement des coureurs en juillet 2013 ………... 145

Figure 45 Comparaison de collections inégales d'objets identiques présentées à l'enfant en juillet 2013 ………... 149

Figure 46 Comparaison de collections égales d'objets identiques présentées à l'enfant en juillet 2013 ………. 151

Figure 47 Comparaison de collections d'objets différents en juillet 2013 ………... 154

Figure 48 Rangée d'images présentée à l'enfant en juillet 2013 ……….. 159

(15)

xiii

AVANT-PROPOS

Tout d‟abord, je voudrais remercier ma petite Marianne et sa famille d‟être passées dans ma vie. Merci à vous, chers parents, de m‟avoir confiée ce que vous aviez de plus précieux. Je voudrais exprimer ma profonde gratitude envers ma directrice de recherche, madame Hélène Makdissi, pour la confiance qu‟elle a su me témoigner et pour m‟avoir confié un projet de recherche si gratifiant! Merci Hélène de m‟avoir permis de réfléchir tout haut avec toi, pour tes clins d‟œil, pour nos discussions ô combien formatrices, pour ton implication et ton soutien sans borne, pour ton temps et pour la qualité de tes commentaires et de tes conseils. Même si parfois j‟étais découragée devant leur ampleur, ils m‟ont aidée à progresser et à devenir une meilleure intervenante. Je tiens à remercier ma codirectrice, madame Izabella Oliveira. Muito obrigado! Vous avez réussi à convertir une linguiste et m‟avez redonné le goût des mathématiques, ce n‟est pas rien! Merci également à madame Andrée Boisclair d‟avoir bien voulu réfléchir avec nous et d‟avoir accepté de corriger ce mémoire.

À mes amies et collègues de bureau, Alice, Camille, Claudia et Marie-Pierre, merci pour les dîners divertissants et pour vos conseils. Un merci particulier à Marie-Pierre et Claudia de m‟avoir soutenue et rassurée, soit pendant l‟année d‟intervention ou pendant celle de rédaction. Merci à mon amie, linguiste et future orthophoniste, Marie-Hélène, pour les périodes de détente et de loisir qui étaient nécessaires pour survivre à ce processus si intense que nous vivions, chacune dans notre pavillon.

Je n‟aurais pu mener ce projet à terme sans le soutien de mes parents, Céline et Marc, et de mon frère, Sébastien. Je sais que l‟aboutissement de mon projet vous tenait profondément à cœur et vous m‟avez toujours démontré que vous croyiez en moi, même quand je ne le faisais plus. À ma famille, merci d‟avoir compris la distance et le temps nécessaire à l‟atteinte de mes rêves. Finalement, à celui qui partage ma vie, David, je veux te remercier pour tes encouragements, ton objectivité, ta compréhension, ton soutien et ton amour lors de ce long processus.

(16)

(17)

1

INTRODUCTION

Au Québec, les méthodes favorisées dans les écoles pour travailler avec les élèves autistes sont les méthodes A.B.A. ( Applied Behavioral Analysis ) et T.E.A.C.C.H. ( Treatment and

Education of Autistic and related Communication handicapped CHildren ) (Lovaas, 1987;

Lovaas, Freitas, Nelson & Whalen, 1974; Rogers, 1998; Schopler, Brehm, Kinsbourne et Reichler, 1971; Schopler, Reichler & Lansing, 1988). Ces deux méthodes sont très inspirées du courant béhavioriste de la psychologie qui est basé sur un système de récompenses et de punitions. Toutefois, plusieurs apprentissages scolaires, comme celui du concept de nombre, ne peuvent se réduire à de telles associations de réponses attendues par autrui. En effet, la construction du nombre et les opérations qui y sont inhérentes prennent beaucoup de temps et d‟effort. Il faut plusieurs années pour que les élèves puissent bien comprendre le système numérique et faire des opérations sur les nombres qui le composent (ministère de l‟Éducation du Québec, 2001).

Le présent projet de recherche consiste en une étude de cas menée avec une enfant autiste de 10 ans qui a été suivie en intervention individuelle, trois heures par jour, sur une période de deux années scolaires. L‟objectif général de la présente étude est de décrire les progrès réalisés, par un élève autiste, dans l‟apprentissage du concept de nombre en travaillant les notions mathématiques par une pédagogie développementale basée sur le jeu. Le mémoire comprend un premier chapitre qui dresse la problématique à laquelle ces enfants sont exposés lors de leur scolarisation. Le deuxième chapitre, le cadre théorique, permet de comprendre les concepts clés impliqués dans l‟émergence et dans la construction du concept de nombre chez un enfant. Dans le troisième chapitre, l‟approche d‟intervention pédagogique mise en place pendant ces deux années sera explicitée. Le quatrième chapitre abordera la méthodologie qui a été utilisée dans le cadre de cette recherche. Le cinquième chapitre présentera les analyses des résultats à partir des données recueillies lors de cette étude. Et, finalement, le sixième chapitre comportera une discussion générale sur l‟ensemble des résultats observés, au regard d‟autres études sur la construction du nombre présentes dans la littérature.

(18)

(19)

3

1. Problématique

Ce chapitre tentera d‟expliciter ce qu‟est l‟autisme, de décrire les principales modalités d‟intervention reconnues pour la scolarisation des enfants autistes (qui se basent principalement sur les méthodes A.B.A. et T.E.A.C.C.H.) en les mettant en tension par rapport aux contextes d‟interventions qui sont privilégiés pour travailler le nombre avec les enfants.

1.1. L’autisme

Vers la fin des années 1930, Leo Kanner, pédopsychiatre de formation, s‟intéressa à 11 enfants qui présentaient des caractéristiques communes, en souffrant toutefois de troubles non répertoriés. En 1943, au terme de 8 années de recherche auprès de ces enfants, il dressa le tableau clinique de « l‟autisme infantile précoce ». À l‟époque, l‟autisme tel que défini par Kanner était considéré comme une psychose, au même titre que la schizophrénie (Ferrari, 1999). Les enfants observés par Kanner avaient principalement deux choses en commun : l‟isolement de l‟enfant (appelé aloneness) et son désir d‟immuabilité, son intolérance aux changements (ou sameness) (Kanner, 1943; Lenoir, Malvy & Bodier-Rethore, 2007).

Depuis ce temps, un manuel diagnostique et statistique des troubles mentaux a été créé par l‟American Psychiatric Association comme ouvrage de référence afin de classifier et de catégoriser les critères diagnostiques des troubles mentaux spécifiques. À travers les diverses éditions du Diagnostic and Statistical Manuel of Mental Disorders (DSM), l‟autisme, tel que décrit par Kanner, a été catégorisé de plusieurs façons. Dans les deux premières versions (DSM-I et DSM-II) parues respectivement en 1952 et 1968, l‟autisme était considéré comme une réaction schizophrénique de type infantile (Chamak, 2010; Habimana, Éthier, Petot & Tousignant, 1999). Par contre, dès la troisième édition, l‟appellation de « troubles envahissants du développement » est utilisée au lieu de psychose

(20)

4

(American Psychiatric Association, 1989, 2003). En effet, lors des années 1980, on réalise qu‟il ne s‟agit pas d‟un trouble infantile, mais bien d‟un dérèglement du développement, d‟où la raison pour laquelle ce trouble est décelé pendant l‟enfance (Frith, 1996).

En général, les enfants atteints d‟un trouble envahissant du développement dans la lignée de l‟autisme présentent des déficits dans trois domaines en particulier : une altération qualitative des interactions sociales, une altération qualitative de la communication et un caractère restreint, répétitif et stéréotypé des comportements, des intérêts et des activités (American Psychiatric Association, 2003; Habimana, Éthier, Petot & Tousignant, 1999). Comme le développement de ces enfants peut sembler différent de celui des enfants tout-venant en ce qu‟il présente un écart par rapport à une norme établie, certaines mesures d‟intervention ont été conçues dans une optique behavioriste pour favoriser leur acquisition d‟autonomie1. À cet effet, plusieurs thérapies et méthodes de prise en charge des enfants autistes ont été élaborées, dont les méthodes A.B.A. (Applied Behavioral Analysis) et T.E.A.C.C.H. (Treatment and Education of Autistic and related Communication

handicapped CHildren) (Ferrari, 1999; Lenoir, Malvy & Bodier-Rethore, 2007; Rogers,

1998).

1.2. La scolarisation des enfants autistes

Au Québec, au tournant des années „90, le ministère de l‟Éducation a changé sa vision de la scolarité que doivent recevoir les enfants ayant un trouble autistique (Maertens, 2004; MELS, 2007; MEQ, 1999; Saint-Laurent, 2008). Si auparavant ces enfants devaient être placés dans des classes spécialisées ou même dans des écoles particulières, on prône depuis de plus en plus l‟inclusion scolaire pour la majorité des élèves dits à risque (c‟est-à-dire

1_{Le développement des enfants atteints d‟un trouble autistique est considéré comme différent par les}

spécialistes qui mettent en place des méthodes béhavioristes d‟intervention. Ces dernières seront explicitées plus loin. Par contre, comme il sera possible de le constater à la lecture de ce mémoire, la posture ici adoptée se distingue de ce postulat. Dans une perspective développementale, il semble plutôt fécond, sous l‟angle pédagogique, d‟envisager plutôt un retard ou un décalage dans le développement de ces enfants que de le considérer comme atypique. C‟est justement pour pallier ce décalage que les hypothèses et les pratiques d‟intervention ont été élaborées.

(21)

5

ceux ayant de grandes difficultés d‟apprentissage ou de comportement ou une déficience intellectuelle légère) et pour la majorité des élèves handicapés (soit, ceux ayant une déficience intellectuelle plus prononcée, une déficience au niveau sensoriel ou moteur ou présentant un trouble envahissant du développement, etc.). Selon leurs besoins, ils bénéficient de mesures particulières, soit un accompagnement en tout temps par un professionnel (un technicien en éducation spécialisée par exemple) ou d‟un accompagnement régulier (l‟enfant peut recevoir pendant quelques heures durant la semaine un soutien fréquent d‟une personne qualifiée) (MELS, 2007).

En ce qui concerne les enfants ayant un trouble autistique, ils peuvent être accompagnés en tout temps d‟un spécialiste dans une classe régulière ou être scolarisés dans une classe spécialisée pour enfants ayant des troubles similaires, selon la décision de la commission scolaire où est scolarisé l‟enfant (MELS, 2007). Dans ces classes spécialisées, diverses méthodes sont utilisées pour travailler avec les enfants autistes, dont principalement les méthodes A.B.A. et T.E.A.C.C.H., ces méthodes seront donc explicitées.

1.2.1. La méthode A.B.A.

La méthode A.B.A. (Applied Behavioral Analysis) a été initiée par O. Ivar Lovaas dans les années „60. Ce chercheur norvégien s‟intéressait aux comportements sociaux et langagiers des enfants autistes. Dans ses recherches, il développe une méthode d‟intervention béhavioriste ayant pour but de contrôler les comportements de ces enfants pour favoriser leur communication (même si la plupart des enfants observés par son équipe n‟avaient pas développé de langage formel autre que l‟écholalie) et leur autonomie dans les aptitudes sociales (Lovaas, 1987; Lovaas, Freitas, Nelson & Whalen, 1974; Rogers, 1998).

Pour que les enfants modifient leurs comportements, ils doivent suivre un programme intensif pendant plus de 30 heures par semaine. Pendant ce temps d‟intervention, les thérapeutes veulent « enseigner » aux enfants explicitement les comportements qui sont

(22)

6

acceptables en recourant à l‟imitation2. Les comportements travaillés sont ceux pour lesquels l‟enfant présente des « déficits ». L‟adulte effectue le comportement correctement et il attend de l‟enfant que ce dernier le réalise de la même façon. Pour ce faire, le thérapeute doit entraîner l‟enfant; chaque fois que ce dernier reproduit le comportement cible qui se rapproche de celui de l‟adulte (c‟est-à-dire du comportement attendu), l‟enfant reçoit une récompense, comme une bouchée de sa nourriture préférée (Lovaas & al, 1974). Par cette brève description, il est possible de constater que cette méthode est avant tout comportementale. Lovaas et ses collaborateurs cherchaient à rendre l‟enfant autiste le plus autonome possible pour favoriser sa communication et ses habiletés sociales. Pour ce faire, l‟adulte doit, d‟une part, servir d‟exemple pour que l‟enfant manifeste les comportements qui sont attendus de lui et, d‟autre part, récompenser l‟enfant aussitôt qu‟il les réalise.

1.2.2. La méthode T.E.A.C.C.H.

Parallèlement à la méthode A.B.A. et dans la même optique béhavioriste, la méthode d‟intervention comportementaliste T.E.A.C.C.H. (pour Treatment and Education of Autistic

and related Communication handicapped CHildren) a été mise sur pieds par Eric Schopler

lors des années „60. Elle est basée sur le conditionnement opérant, tel que décrit dans la psychologie béhavioriste (Chamak, 2010; Rogers, 1998; Schopler, Brehm, Kinsbourne & Reichler, 1971; Schopler, Reichler & Lansing, 1988). Les thérapeutes qui utilisent cette méthode ont comme ligne de conduite le principe que, si on travaille pendant une période de temps suffisante, tout comportement indésirable peut être changé si des méthodes de renforcement sont appliquées (Schopler, Reichler & Lansing, 1988). Ces renforcements peuvent prendre la forme de récompenses : recevoir des bonbons lorsqu‟un exercice est bien réalisé selon les attentes du thérapeute, pouvoir accumuler des minutes pour jouer avec un jouet préféré ou pour écouter la télévision, etc. Elles servent principalement à motiver

2_{La définition sous-entendue ici pour l‟imitation est celle utilisée dans la psychologie béhavioriste qui se}

limite à une association directe et non différée d‟un comportement attendu. Il ne s‟agit pas de l‟imitation au sens piagétien.

(23)

7

l‟enfant dans son travail et à favoriser sa socialisation, car cette méthode vise l‟acquisition d‟un maximum d‟autonomie pour les personnes étant atteintes d‟un trouble du spectre autistique, tout au long de leur vie (Chamak, 2010).

Pour que l‟enfant réussisse les tâches qui lui sont problématiques, l‟adulte peut la décomposer en sous-étapes qui seront illustrées par des pictogrammes. De cette manière, lorsque l‟enfant vit de petites réussites (chaque sous-étape bien réalisée), il sera alors récompensé. Tout le matériel nécessaire à la réalisation d‟une tâche doit se trouver dans un même endroit (par exemple dans un panier) pour conserver l‟attention de l‟enfant sur des éléments jugés pertinents à la tâche par l‟adulte. Tout le matériel non nécessaire est rangé dans d‟autres paniers. Pour que cette méthode soit efficace, elle doit être utilisée autant à l‟école qu‟à la maison, avec le même système de pictogrammes, de paniers et de récompenses. Dans une étude menée en 1971, Schopler, Brehm, Kinsbourne et Reichler montraient que les enfants autistes réagissaient beaucoup mieux (c‟est-à-dire avaient de meilleurs comportements) lorsque les tâches étaient structurées et menées par le thérapeute que lorsqu‟elles étaient non structurées et décidées en cours de réalisation par l‟enfant (Schopler, Brehm, Kinsbourne & Reichler, 1971). Le fait de fournir à l‟enfant une structure qui peut être réutilisée à la maison permet de fournir à l‟enfant autiste des repères stables entre ces deux milieux (pour répondre à son besoin de sameness, présenté précédemment). Cette brève présentation permet de comprendre la posture épistémologique derrière cette méthode : pour rendre la personne autiste autonome, il suffit de lui offrir un contrôle externe sur son comportement par des récompenses alimentaires ou autres, en suivant un horaire structuré constant. Pour y arriver, les tâches qui normalement posent problème à la personne autiste sont décomposées en étapes par le thérapeute. Ces différentes étapes sont souvent présentées par des activités isolées (des exerciseurs visant l‟automatisation) et rangées dans des paniers qui contiennent tout le matériel nécessaire à leur réalisation.

(24)

8

1.3. Les contextes d’intervention privilégiés pour travailler le nombre

Comme démontré précédemment, on sait que les méthodes utilisées dans les écoles québécoises pour accompagner les enfants autistes sont principalement A.B.A. et T.E.A.C.C.H. Ces méthodes, bien qu‟elles soient considérées comme éducatives, servent principalement à contrôler le comportement plutôt qu‟à réaliser des apprentissages scolaires. Malgré cela, elles sont tout de même utilisées par les pédagogues pour soutenir des apprentissages complexes, comme la langue et le nombre par exemple.

A contrario, pour les enfants tout-venant, les apprentissages scolaires sont plutôt basés sur

un programme par compétences3, qui doivent être construites par les enfants avec le soutien des enseignants :

[Le Programme de formation de l‟école québécoise] propose une organisation des savoirs sous forme de compétences de manière à leur donner sens et ouverture et, d‟autre part, il retient un cadre conceptuel qui définit l‟apprentissage comme un processus actif et continu de construction des savoirs (p.4, MEQ, 2001).

En ce sens, le ministère adopte une position socioconstructiviste des savoirs pour les enfants tout-venant et dans les classes régulières dans lesquelles les enfants autistes peuvent être intégrés, alors qu‟une position béhavioriste est préconisée en classes spéciales.

Le nombre et le système de numération positionnelle est un construit social ayant subi plusieurs transformations et complexifications à travers l‟histoire (Gingras, Keatin & Limoges, 1999; Mainzer, 1999; Ross & Charbonneau, 2002; Sultan, 2008). Ils constituent des objets de savoir complexes exigeant de multiples abstractions. Or, le nombre n‟ajuste pas ses exigences aux enfants autistes. Il pose les mêmes exigences de conceptualisation et d‟abstraction, ce qui ne peut être produit par des imitations béhavioristes ou par de simples associations. La prochaine section vise précisément à étayer les fondements de la construction du nombre.

3_{Pour le MEQ (2001), une compétence est vue comme : « un savoir-agir fondé sur la mobilisation et}

(25)

9

2. Cadre théorique

Le présent cadre théorique permet d‟examiner les notions-clés à partir desquelles des interventions pédagogiques peuvent être construites pour travailler le concept du nombre avec tout enfant autiste, sans recourir aux méthodes habituelles, comme A.B.A. et T.E.A.C.C.H. La figure 1 tente de schématiser l‟émergence de la construction du concept de nombre chez l‟enfant.

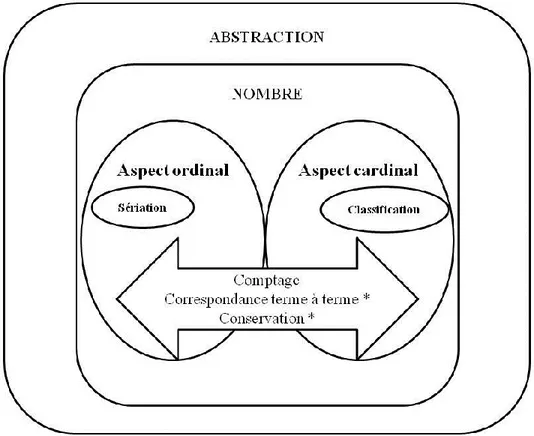
Figure 1 : Schéma conceptuel de l‟émergence de la construction du nombre4

4_{Comme on s‟intéresse à la construction du concept du nombre chez un enfant, le schéma conceptuel du}

nombre ne représente pas le nombre comme il sera une fois acquis (à ce moment, les aspects ordinal et cardinal seraient alors fusionnés), mais bien son émergence et les concepts qui y contribuent.

(26)

10

Cette figure met en relief la relation inclusive qui existe entre l‟abstraction et le nombre. En ce sens, pour que les nombres puissent être utilisés, le sujet doit faire preuve d‟abstraction. De plus, l‟abstraction ne se réduit pas seulement au nombre, elle est notamment présente lors de la construction et de l‟utilisation du langage. Le nombre en soi peut être décomposé en deux aspects : ordinal et cardinal. Lorsque le nombre est réellement construit, ces deux aspects convergent et s‟imbriquent pour devenir indissociables. Comme on s‟intéresse à la construction du concept du nombre chez un enfant, ce schéma conceptuel du nombre ne représente pas le nombre comme il sera une fois acquis (à ce moment, les aspects ordinal et cardinal seraient alors fusionnés), mais bien son émergence et les concepts qui y contribuent. Le schéma ici se penche sur l‟émergence du concept de nombre et de sa construction progressive vers une représentation mature. Si dans une compréhension mature, on peut envisager que les aspects ordinal et cardinal convergent et se combinent dans une vision unifiée du nombre, il n‟en demeure pas moins que cette fusion provient d‟un long travail de construction chez le jeune enfant. C‟est pourquoi le schéma présente ces deux aspects du nombre en sous-ensembles distincts qui devront progressivement être unifiés par l‟enfant notamment par trois opérations majeures à construire : le comptage, la correspondance terme à terme et la conservation. Ces deux dernières opérations peuvent émerger dans des contextes hors de ceux sollicitant directement le nombre, comme lors de comparaison (pour la correspondance terme à terme) et avec des quantités continues comme de la pâte à modeler (pour la conservation), voire en français dans la correspondance graphème-phonème du système alphabétique (correspondance terme à terme) et la conservation d‟une même chaîne de lettres pour représenter un même mot. Afin d‟étayer plus en profondeur ce schéma conceptuel de l‟émergence de la construction du nombre, l‟abstraction sera d‟abord explicitée, car elle demeure l‟assise fondamentale à la construction du nombre. Ensuite, le concept même de nombre sera défini, ainsi que les deux aspects qui permettent de le construire, soit l‟aspect ordinal et l‟aspect cardinal. Puis,

(27)

11

différentes opérations5 que l‟enfant doit construire pour identifier et travailler avec le nombre, soit la correspondance terme à terme, la conservation et le comptage.

2.1. L’abstraction

Pour pouvoir déterminer le cardinal d‟une collection ou établir un ordre entre les éléments la composant, l‟enfant doit être en mesure de faire abstraction des différences qui pourraient être présentes entre les éléments pour les considérer comme un ensemble possédant une caractéristique commune abstraite de chacun des objets de l‟ensemble, que ce dernier soit plus ou moins homogène ou plus ou moins hétérogène. Dans ses nombreux ouvrages, Piaget établit deux catégories principales d‟abstraction : l‟abstraction empirique (ou abstraction simple) et l‟abstraction réfléchissante (Piaget, 1977; Piaget & Szeminska, 1964).

Tout objet possède des propriétés physiques qui peuvent être observables par le sujet, comme sa couleur, sa forme, sa texture, etc. Pour pouvoir considérer ces propriétés, le sujet doit faire preuve d‟abstraction empirique (Kamii, 1980; Kamii & DeVries, 1981; Piaget, 1977). Pour ce type d‟abstraction, l‟attention de l‟enfant est centrée sur une propriété de l‟objet, habituellement physique (comme la couleur, la forme ou le type d‟objet) plutôt que sur l‟ensemble de ses caractéristiques (Kamii, 1980). À titre d‟exemple, lorsqu‟une assiette remplie de raisins lui est présentée lors de la collation, l‟enfant peut ignorer leur couleur pour énoncer le nombre total de raisins, plutôt que de distinguer les 8 raisins verts des 12 raisins rouges. L‟abstraction repose précisément sur l‟ignorance de critères spécifiques au profit de la construction d‟un critère générique, ici raisin.

5_{La section sur les opérations à construire qui sera présentée en 2.1.1.3 ne se trouve pas être une subdivision}

du nombre comme le sont l‟aspect ordinal et l‟aspect cardinal du nombre. Cette section devrait plutôt être subordonnée, à la fois, à l‟aspect ordinal et à l‟aspect cardinal du nombre, car la fusion de ces deux aspects du nombre provient de multiples actions de sériation et de classification faites par l‟enfant et de la construction progressive de régularités qui mèneront l‟enfant à envisager le comptage, la correspondance terme à terme et la conservation comme une opération. C‟est alors que la fusion des deux aspects sera possible et c‟est pourquoi ces trois opérations sont représentées, dans la figure 1, par des flèches d‟actions potentielles pouvant agir sur les aspects ordinal et cardinal du nombre.

(28)

12

Le nombre, quant à lui, en raison de sa conception hiérarchique et inclusive (en ce sens que 4 inclut 3, qui inclut 2, qui inclut 1), exige que l‟abstraction qui lui est portée soit tout autre et qu‟elle concerne davantage les relations qui existent entre les éléments comparés, dans ce cas-ci, les nombres eux-mêmes et les opérations qui y sont effectuées, peu importe les objets physiques qu‟ils représentent et leurs caractéristiques. C‟est l‟abstraction réfléchissante qui permet au sujet de réagir à la suite des opérations ou des actions qui ont été apportées en créant et en établissant des relations entre divers éléments (Kamii & DeVries, 1981). Les relations ainsi établies sont basées sur la coordination des actions qui peuvent être effectuées de façon inconsciente et pourront, dans le futur, créer des prises de conscience et de conceptualisations chez l‟enfant (Piaget, 1977). Ces relations sont d‟ordre logico-mathématique et elles se construisent sur des construits antérieurs de l‟enfant, notamment sur la base de multiples abstractions empiriques. Ce type d‟abstraction n‟est pas tiré des objets en tant que tels, comme le serait une seule abstraction empirique, mais bien des actions que l‟on peut effectuer, comme réunir des objets en une classe plus générale, ordonner, mettre en correspondance, etc. (Piaget, 1968). Il convient d‟illustrer cette notion par deux exemples.

D‟abord, lorsque l‟on tente de comparer la hauteur de la tour de Pise et la hauteur de la tour Eiffel, cette relation n‟existe pas ni dans la tour Eiffel même ni dans la tour de Pise, par contre, l‟enfant est capable de visualiser ces deux tours en connaissant leur hauteur6 : « la tour Eiffel est plus haute que la tour de Pise » peut être énoncée en tentant d‟établir une relation de correspondance entre leurs hauteurs respectives. Pour ce faire, l‟abstraction doit être réfléchissante, car elle ne concerne pas les caractéristiques des tours en soi, mais bien la relation qui existe entre leurs hauteurs respectives, soit 324 mètres est plus grand que 56 mètres.

Dans un même ordre d‟idées, on peut dresser une collection de 6 objets devant un enfant. Ce dernier arrive à les compter en utilisant une abstraction empirique. Il peut, en plus, faire preuve d‟abstraction réfléchissante lorsqu‟il énonce que la quantité ne changera pas, même

(29)

13

si l‟ordre et la disposition des éléments sont modifiés; il coordonne alors la cardinalité et l‟identité de la collection (DeBlois, 1993). C‟est ce type d‟abstraction qui permet de mettre les nombres en relation, comme lorsque l‟enfant est questionné sur quel nombre est le plus grand ou s‟il y a égalité.

2.1.1. Le nombre

Plusieurs auteurs abordent la définition du nombre (Baruk, 1995, 2003; Gelman & Gallistel, 1986; Piaget, 1967; Piaget & Szeminska, 1964; Van Nieuwenhoven, 1999). Parmi eux, Baruk (1995) établit deux sens très différents à la notion de nombre. Selon son sens mathématique premier, un nombre peut être défini comme : « un élément d‟un ensemble de nombres » (p.762), les ensembles de nombres étant, selon Baruk (1995, 2003) et Van Nieuwenhoven (1999), les nombres entiers naturels ( ), les nombres entiers relatifs ( ), les nombres rationnels ( ), les nombres réels ( ) et les nombres complexes ( ). Ces ensembles de nombres sont inclusifs, en ce sens que les nombres entiers naturels font partie de la classe des entiers relatifs, qui font partie de la classe des rationnels, etc. Pour travailler les nombres de cette façon, le sujet doit faire preuve d‟abstraction réfléchissante pour comprendre les relations qui existent entre ces classes de nombres, qui semblent pourtant assez différentes. Le deuxième sens, qui relève davantage du sens commun, évoque l‟idée de quantité liée au nombre, que Baruk (1995, 2003) nomme le « nombre-de ». À cet effet, dans un ouvrage paru en 2003, cette auteure écrit :

Certains caractères d‟une quantité peuvent s‟exprimer grâce aux nombres, mais doivent en être distingués : pour cela, il suffit que des nombres suivis de ce qu‟ils comptent, évaluent ou mesurent soient appelés des nombres-de (p.32).

De plus, il n‟y a rien dans l‟appellation du nombre en soi (dans le mot nombre) qui exprime ou représente une quantité, en ce sens que cela demeure arbitraire. La combinaison des phonèmes /d/, /i/ et /s/ qui forment le mot « dix » n‟a aucune valeur en soi, car le signifiant (le mot « dix ») et le signifié (ce qu‟est 10, le concept même, la représentation mentale que l‟on s‟en fait) sont unis arbitrairement. Piaget (1968) souligne, en exposant les conceptions de Saussure, que le signifiant n‟a rien dans ses caractéristiques phonétiques qui peuvent informer le lecteur ou l‟auditeur sur le contenu du signifié. Cela ne s‟applique pas

(30)

14

seulement aux mots nombres, mais bien à tous les mots du langage. Par contre, il est possible d‟affirmer que le nombre, s‟il est accompagné d‟un substantif nominal qui explicite ce qui est représenté, peut être utilisé dans le but de représenter une quantité. À titre d‟exemple, si on énonce « 6 » ou « 6 bonbons », le sens du nombre utilisé dans ces deux énoncés n‟est pas le même; dans le deuxième cas, il s‟agit nécessairement d‟un « nombre-de » au sens de Baruk. L‟enfant aura plus de facilité à conceptualiser « 6 bonbons », car il lui est possible de recourir à la visualisation de ces bonbons qui pourront être alors dénombrés, chose qui lui est beaucoup plus difficile à faire avec le nombre, comme objet mathématique, « 6 ». Si l‟on s‟intéresse à la construction du nombre et à son émergence chez le jeune enfant, la distinction de « nombre-de » qu‟apporte Baruk au nombre est plus pertinente dans le cadre de ce mémoire que la définition proprement mathématique.

Quant à eux, Piaget et Szeminska (1964) présentent deux aspects au nombre7 : l‟aspect ordinal et l‟aspect cardinal. En effet, au sein d‟une série d‟objets ordonnés, il est possible d‟utiliser des nombres pour représenter la position des éléments (aspect ordinal) et pour représenter la totalité des éléments (aspect cardinal). À titre d‟exemple, lors d‟une fête d‟Halloween, les enfants veulent amasser le plus de bonbons et organisent un concours. Celui qui aura obtenu le plus grand nombre de bonbons est celui qui possède la collection qui a le plus grand cardinal. Il sera le grand gagnant et donc terminera le concours premier. Il s‟agit de deux aspects du nombre en partie paradoxaux : en ce qui concerne l‟aspect cardinal, en général, il est préférable d‟obtenir le plus grand résultat (nombre de bonbons amassés, nombre de billes, nombre de buts lors d‟une partie de hockey, etc.) alors qu‟en ce qui concerne l‟aspect ordinal, il vaut mieux obtenir un petit nombre (il est préférable d‟être le premier plutôt que le trentième, bien que trente soit plus grand qu‟un).

La maîtrise des aspects du nombre doit permettre au sujet de comprendre que celui qui est né en 2005 est plus âgé que celui né en 2010 bien que, dans son aspect cardinal, à l‟inverse,

(31)

15

2005 est plus petit que 2010. D‟ailleurs, Piaget et Szeminska (1964) décrivent ce paradoxe comme suit :

[…] une série dont les termes, tout en se succédant selon les relations d‟ordre que leur assignent leurs rangs respectifs, sont également des unités équivalentes les unes aux autres et par conséquent susceptibles d‟être réunies cardinalement (p.204).

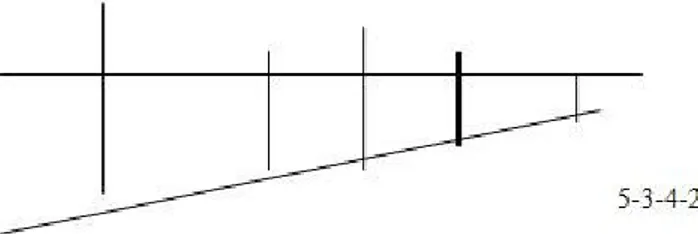
Dans cette optique, chez les piagétiens, la maîtrise du nombre est acquise lorsque l‟enfant est en mesure d‟établir ces deux types de relations entre les nombres : l‟ordre (aspect ordinal) et l‟inclusion hiérarchique (aspect cardinal). Ces deux relations sont interreliées; lorsque des éléments sont mis en ordre au sein d‟une même collection, ils sont forcément inclus dans un ensemble plus grand (la collection elle-même) qui est régi par une certaine hiérarchie (comme le 4e élément qui englobe à la fois le 3e, le 2e et le 1er). En effet, comme le souligne Fayol (1990), à l‟instar de Piaget, « l‟apprentissage “par cœur” de la chaîne numérique verbale […] ne permettrait pas de dénombrer n‟importe quelle collection au cardinal jusqu‟alors ignoré » (p.38). À cet effet, il est nécessaire de comprendre ce que représente le nombre et l‟inclusion qui existe dans la chaîne numérique (Figure 2).

Figure 2 : Relation inclusive des nombres jusqu‟à 4.

Comme ce mémoire s‟intéresse aux assises premières de la construction du concept de nombre par la maîtrise de ses aspects ordinal et cardinal, la définition de Piaget et Szeminska (1964) sera privilégiée, car elle concerne, à la fois, les aspects ordinal et cardinal du nombre, plutôt que celles de Baruk qui n‟abordent que le nombre proprement mathématique et la cardinalité. Étant donné leur importance dans la constitution et dans la compréhension du nombre, il convient d‟approfondir dans un premier temps les aspects ordinal et cardinal du nombre. Ces assises permettront d‟ouvrir ensuite sur le comptage.

(32)

16

2.1.1.1 Aspect ordinal

Dans une perspective piagétienne, pour bien saisir la relation d‟ordre entre les nombres, il est nécessaire de définir ce qu‟est l‟aspect ordinal du nombre. L‟aspect ordinal permet d‟identifier une position au sein d‟un ensemble ordonné préalablement établi. À titre d‟exemple, parmi un ensemble de sept voitures faisant une course, le nombre 5 désigne la voiture qui est à la cinquième position dans la course.

Van Nieuwenhoven (1999) ajoute que les nombres ordinaux « sont utilisés pour désigner un élément individuel par sa position à l‟intérieur d‟un ensemble plutôt que pour quantifier un ensemble comme un tout » (p.106). L‟aspect du nombre qui permettrait de quantifier l‟ensemble comme un tout serait l‟aspect cardinal du nombre. Ce dernier sera défini sous peu. Un exemple d‟aspect ordinal du nombre peut être observé au sein du calendrier. Dans le cas du calendrier grégorien, il débute toujours par le mois de janvier (1er mois) et il se termine par le mois de décembre (12e mois), ce qui fait référence à une collection quantifiable prédéterminée au sein de laquelle un ordre est établi. Il y a douze mois dans une année et chaque mois conserve toujours la même position.

L‟aspect ordinal du nombre se développe de façon progressive chez l‟enfant, ce dernier passant par trois stades lors de cette acquisition (Piaget & Szeminska, 1964). À titre d‟exemple, voyons comment se différencient les actions et les raisonnements d‟un enfant dans le contexte d‟une tâche de sériation pour chacun de ces trois stades. Au premier stade, l‟enfant ne parvient pas à dresser les éléments selon leur taille, il échoue la sériation. S‟il lui est demandé de sérier des pailles de différentes longueurs, l‟enfant prendra n‟importe quelle paille au hasard pour les placer l‟une à côté de l‟autre. Il peut également réussir à constituer de petites séries juxtaposées ou tenter de « créer un effet d‟escalier » en ne considérant que la partie supérieure de la paille (et donc, en ne plaçant pas les pailles sur une ligne horizontale). À ce stade, il fait preuve d‟un jugement pré-sérial. Au deuxième stade, l‟enfant parvient à sérier les pailles en effectuant plusieurs tâtonnements. Il arrive à construire la série correctement, au bout de plusieurs tentatives, mais il n‟est pas en mesure d‟établir des relations entre les éléments qui la composent. Son raisonnement est encore principalement basé sur les intuitions et sur sa perception. Finalement, au troisième stade,

(33)

17

l‟enfant comprend la sériation, en ce sens qu‟il considère qu‟une même paille peut être, à la fois, plus petite et plus grande qu‟une autre. Sa sériation n‟est plus basée sur sa perception et sur des intuitions, elle est opératoire due à une coordination des relations qui deviennent alors réversibles.

2.1.1.2 Aspect cardinal

Pour pouvoir comptabiliser les éléments d‟une collection une seule fois, il est nécessaire d‟utiliser une certaine organisation, d‟où l‟utilité de sérier les éléments avant d‟en faire le décompte pour déterminer leur nombre. En ce sens, Piaget et sa collaboratrice Szeminska définissent le nombre cardinal comme étant : « une classe dont les éléments sont conçus comme des unités équivalentes les unes aux autres et cependant comme distinctes, leurs différences consistant alors seulement en ceci que l‟on peut les sérier, donc les ordonner » (1964, p.204).

Si l‟on reprend l‟exemple précédent des voitures qui font la course, sur l‟ensemble des sept voitures, le nombre 5 désigne une quantité de voitures faisant la course : si l‟enfant en possède 5 sur un total de 7, il est celui qui en a le plus. Dans le même sens, pour connaître le nombre de fruits qui sont dans le panier, l‟enfant entreprend le comptage des éléments qui s‟y trouvent. Il compte 3 bananes, 2 oranges et 4 pommes. Il lui est nécessaire de sérier les bananes, les oranges et les pommes pour ne pas recompter un même fruit à plusieurs reprises. La banane qui est comptée en premier doit conserver sa première position pour que le dénombrement soit exact. De plus, pour connaître le nombre total de fruits, il doit considérer cet ensemble hétérogène comme un tout, d‟où l‟importance de la notion d‟inclusion hiérarchique : il doit regrouper les 3 bananes, les 2 oranges et les 4 pommes pour énoncer qu‟il y a 9 fruits. Il y a donc nécessité d‟abstraction réfléchissante permettant de réunir en une seule collection selon un critère commun ses éléments hétérogènes et distincts.

(34)

18

2.1.1.3 Opérations à construire

Pour pouvoir affirmer que le concept de nombre est construit, il est important de vérifier si l‟enfant a précédemment construit plusieurs opérations qui lui seront nécessaires, comme la correspondance terme à terme, la conservation et le comptage.

2.1.1.3.1 La correspondance terme à terme

Dans une perspective piagétienne, si l‟on souhaite que le comptage et la chaîne numérique ne prennent pas le sens d‟une simple comptine, il faut privilégier, chez le jeune enfant, l‟action concrète répétée et la réflexion sur elle pour favoriser les mises en relation. Pour ce faire, la procédure de correspondance terme à terme peut être réalisée de deux façons : 1) en faisant correspondre des éléments de deux collections distinctes ensemble, ce qui ne nécessite aucun comptage; ou 2) en énonçant un mot nombre par élément dénombré lors d‟un comptage.

Lors de la comparaison de collections, la correspondance terme à terme entre leurs éléments permet à l‟enfant d‟établir l‟égalité ou la non-égalité entre des collections distinctes qui lui seraient présentées. Par contre, pour pouvoir se prononcer sur la différence qu‟il soulève entre les collections, il devra recourir au comptage ou du moins à certaines notions qui le supposent : à cet effet, il devra faire correspondre un mot nombre pour chaque élément dénombré. À titre d‟exemple, après avoir fait des correspondances entre les éléments de deux collections de différentes tailles (12 éléments contre 15), l‟enfant énonce que la deuxième en contient plus parce qu‟il en reste 3 et qu‟il n‟y en a plus de l‟autre côté. À cette fin, il opère sur le nombre, il compare et il parvient à identifier quelle collection comporte le plus d‟éléments et laquelle en a le moins. L‟enfant se dote ainsi d‟un outil pour expliquer sa réponse, et ce, même si sa chaîne numérique ne se rend pas à 15. C‟est en partie en ce sens que l‟opération pour Piaget précède et constitue le nombre et le comptage,

(35)

19

contrairement à ce que postule Gelman et Gallistel (1986) et Van Nieuwenhoven (1996, 1999).

La correspondance terme à terme peut même devenir une opération8 en ce sens que si l‟on déplace les éléments devant l‟enfant, ce dernier pourrait utiliser des arguments de réversibilité, de non-ajout et de non-retrait pour maintenir sa réponse, et ce, même si le nombre d‟objets en jeu dépasse la chaîne numérique maîtrisée par l‟enfant. Viser à ce que l‟enfant procède par correspondance terme à terme et à ce qu‟il conceptualise cette action comme une opération devient donc un objectif essentiel dans la construction même du nombre, beaucoup plus que de simplement étendre la chaîne des nombres.

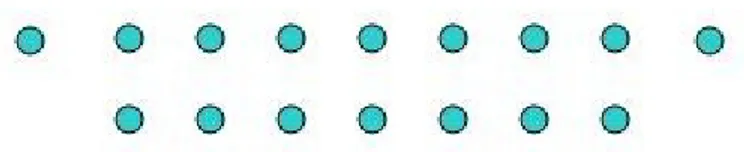
À titre d‟exemple, à la figure 3, deux collections de jetons sont éparpillées sur la table et sont présentées à l‟enfant. On lui demande si les deux collections comportent le même nombre de jetons ou si l‟une des deux est plus nombreuse. Ensuite, on demande à l‟enfant d‟expliquer comment il peut le savoir. Pour ce faire, il peut utiliser cette correspondance terme à terme comme démontré à la figure 4.

Figure 3 : Collections de jetons éparpillés

Figure 4 : Utilisation de la correspondance terme à terme pour comparer deux collections

8_{Ici, pour le terme « opération », c‟est la définition piagétienne tirée de Legendre-Bergeron (1980) qui est}

préconisée. Une opération est « une action intériorisée, c‟est-à-dire effectuée symboliquement ou en pensée et réversible » (p.139). Plus précisément, on s‟intéresse aux opérations logico-arithmétiques, car ces dernières portent sur « des éléments discrets réunis en classe, sériés ou dénombrés et sont indépendants de l‟espace et du temps » (p.140).

(36)

20

Lorsque la correspondance terme à terme dans la comparaison de collections est bien utilisée (en organisant les jetons de manière à pouvoir comparer les deux collections visuellement, c‟est-à-dire sans avoir besoin de compter), l‟enfant est capable de vérifier rapidement si les collections qui lui sont présentées sont équivalentes ou non. Même lorsque les jetons de la deuxième rangée sont déplacés, de sorte que les jetons dépassent à droite et à gauche, l‟enfant confirme que c‟est toujours pareil, car il énonce qu‟il est possible de les remettre comme ils étaient avant. Cela témoigne qu‟il comprend la réversibilité mise en jeu. La correspondance terme à terme devient dès lors une opération logico-arithmétique au sens piagétien, car elle porte sur des éléments discrets sériés dans des collections, indépendant de l‟espace occupé (Legendre-Bergeron, 1980). Elle est intériorisée symboliquement puisque l‟enfant établit ici l‟équivalence avant même l‟action pratique en anticipant que s‟il fait de nouveau une correspondance (lorsqu‟il veut remettre les éléments à leur état initial), il obtiendra ce qu‟il avait au départ. De cette façon, l‟enfant est en mesure de comparer des collections, et ce même s‟il ne parvient pas toujours à en déterminer le cardinal. Pour y arriver, il devra recourir à un nouvel outil : le comptage utilisé en correspondance terme à terme (un mot nombre par élément dénombré).

2.1.1.3.2 La conservation

Si l‟on conçoit l‟importance de l‟opération de la correspondance terme à terme dans la construction du nombre, il convient dès lors de la mettre en relation avec la capacité d‟établir la conservation. En effet, lors de la construction des deux aspects du nombre (l‟aspect ordinal et l‟aspect cardinal), il est important de vérifier si l‟enfant est capable de maintenir un jugement rationnel sur des quantités lorsque leur apparence est modifiée par une tierce personne, donc faire preuve de conservation.

Pour ce faire, l‟enfant doit faire preuve d‟abstraction réfléchissante, telle que définie précédemment et faire preuve de conservation. À l‟instar de Piaget, Legendre-Bergeron (1980) explique la conservation comme étant « la capacité de dégager les aspects invariants de l‟objet au travers des transformations qu‟il subit » (p.60). Vilette (1996) établit que l‟enfant a compris la notion de conservation lorsqu‟il est en mesure de comprendre la réversibilité (retour à l‟état antérieur) et les différences perçues entre les modifications. Les

(37)

21

tâches mathématiques proposées aux jeunes enfants visant la conservation ont été développées à l‟origine par Jean Piaget. Dans celle-ci, l‟enfant ne constate pas seulement les différences entre les collections qui lui sont présentées, mais il considère également les modifications qui y ont été apportées sous ses yeux. Malgré la différence qui subsiste visuellement entre les deux quantités à comparer, l‟enfant est capable de faire preuve d‟abstraction réfléchissante et d‟imaginer un possible retour à l‟état précédent sans avoir besoin de manipuler les collections elles-mêmes. Lorsque la conservation est acquise, Piaget et Inhelder (1967) décrivent que :

[…] les états sont dorénavant subordonnés aux transformations et celles-ci, étant décentrées de l‟action propre pour devenir réversibles, rendent compte à la fois des modifications en leurs variations compensées et de l‟invariant impliqué par la réversibilité (p.77).

La conservation peut être observée, entre autres, sur des quantités continues (comme des longueurs, du volume, ou du poids) et sur des quantités discontinues.

2.1.1.3.2.1 Quantités continues

La conservation de quantités continues peut être définie par la capacité de l‟enfant à faire abstraction de la forme pour déterminer la grandeur d‟une quantité comparativement à celle d‟une autre. Elle s‟acquiert en trois stades, qui sont assez similaires pour la conservation des quantités discontinues : 1) l‟absence de conservation; 2) les réponses intermédiaires; et 3) la conservation nécessaire (Piaget & Szeminska, 1964). Ce type de conservation est généralement évalué, chez les jeunes enfants, à l‟aide de boules de pâte à modeler. Lorsque les sujets sont plus âgés, la conservation de quantités continues peut être vérifiée à l‟aide de variation de longueurs, de volume et de poids, mais les stades sont les mêmes pour tous ces items. Si un adulte présente deux boules de pâte à modeler de même taille, l‟enfant doit établir l‟égalité entre ces deux parts de pâte. Lorsque l‟égalité a été établie, l‟adulte prend une des deux boules et la transforme sous les yeux de l‟enfant en trois temps : en galette, en rouleau et en miettes. Entre chaque transformation, il y a un retour à l‟état initial, c‟est-à-dire la formation de boule de même grosseur que celle de référence.

Au premier stade (absence de conservation), le fait que la part de pâte n‟ait plus la même apparence laisse croire à l‟enfant qu‟il s‟agit d‟une nouvelle quantité. Piaget et Szeminska

(38)

22

(1964) parlent de ce stade en l‟appelant « le stade de la quantité brute », en ce sens que l‟enfant utilise principalement sa perception pour déterminer la grosseur de la collection au lieu de recourir à une procédure plus efficace, telles que la quantification et l‟établissement de relations entre les éléments mis à sa disposition. L‟absence de conservation des quantités continues peut être observée lorsque l‟enfant pense que la modification de la forme (comme une boule de pâte à modeler qui est transformée en galette) entraine une modification dans la quantité. Si l‟apparence d‟une de ces deux boules est modifiée (en faisant un rouleau, une galette ou des miettes par exemple), l‟enfant énoncera qu‟une des deux parts contient plus de pâte que l‟autre (soit la boule initiale qui n‟a pas été modifiée ou la boule transformée), même si aucun ajout ou retrait de pâte n‟a été effectué. À ce moment, l‟enfant utilise seulement sa perception pour déterminer la ressemblance ou la différence de quantité des deux parts de pâte qui lui sont présentées. Pour un enfant « non conservant », il est inconcevable qu‟une quantité de matière « puisse demeurer invariante au travers des changements de forme » (Piaget & Szeminska, 1964, p.22). Cette absence de conservation est présente jusqu‟à 4 ou 5 ans.

Au deuxième stade (réponses intermédiaires), l‟enfant fournit des réponses qui montrent qu‟il a compris l‟idée de conservation quand les différences entre les quantités ne sont pas très importantes, mais lorsque les changements sont importants, il a tendance à douter de lui et il redevient « non conservant ». À ce stade, la quantification devient de plus en plus importante dans les réflexions de l‟enfant. En effet, l‟enfant tente de considérer, à la fois, l‟aspect perceptif et les relations opératoires effectuées sur les quantités pour fournir une réponse, mais il n‟y parvient pas toujours. Vers 6 ans, l‟enfant commence à comprendre que la quantité n‟est pas modifiée, mais ce n‟est pas stable encore dans son esprit. Lorsque la transformation est plutôt simple (comme lorsque l‟on écrase la boule pour en faire une galette), l‟enfant peut affirmer qu‟il s‟agit toujours de la même pâte que l‟on avait initialement. Par contre, lors de la transformation en rouleau ou en miettes, comme l‟apparence n‟est plus la même et que la pâte n‟occupe plus le même espace, un doute peut survenir chez lui; il fournit alors des réponses qui montrent que, pour lui, les quantités continues ne sont pas conservées à la suite de transformations. Lors de la transformation de la boule en miettes (Figure 5), l‟enfant doit prendre en considération l‟espace occupé par les miettes bleues, mais aussi leur grosseur : malgré le fait qu‟elles soient plus nombreuses

(39)

23

que la boule jaune, elles sont beaucoup plus petites. Les enfants du deuxième stade ont de la difficulté à intégrer toutes ces informations lors de leurs réflexions.

Figure 5: Item de conservation des quantités continues

Au troisième stade (conservation nécessaire), il n‟y a plus de doute dans l‟esprit de l‟enfant : peu importe les modifications qui sont apportées, il affirme qu‟il s‟agit toujours de la même quantité. L‟enfant n‟utilise plus seulement sa perception pour déterminer si les quantités sont égales ou non. Il est capable d‟analyser les changements qui ont été apportés et de comprendre que, même si la forme est différente, il s‟agit toujours de la même pièce de pâte à modeler. Ce stade est atteint vers l‟âge de 7 ans selon Piaget et Szeminska (1964) et vers 9 ans selon Meljac et Lemmel (2007).

2.1.1.3.2.2 Quantités discontinues

La conservation de quantités discontinues peut être définie par la capacité de l‟enfant de faire abstraction de la disposition des objets pour déterminer et maintenir le cardinal d‟une collection. Cette abstraction est réfléchissante, telle que définie précédemment. L‟enfant doit évaluer les relations entre les quantités qui lui sont présentées pour pouvoir les comparer. Son acquisition est caractérisée par trois grandes étapes de développement : 1) l‟absence de conservation; 2) le début de constitution d‟un ensemble; et 3) la conservation et la coordination (Piaget & Szeminska, 1964).

Au premier stade (absence de conservation), l‟enfant croit que les modifications qui sont faites par une autre personne sous son observation affectent la quantité des éléments qui avaient été préalablement dénombrés. Il ressent alors le besoin de dénombrer chaque fois qu‟une modification est faite à la collection par l‟expérimentateur, même si aucun ajout ni retrait n‟est fait. À ce moment, il ne se fie qu‟à sa perception, en ne considérant pas les modifications en tant que telles, mais seulement le résultat final, ce qui le laisse croire à un

(40)

24

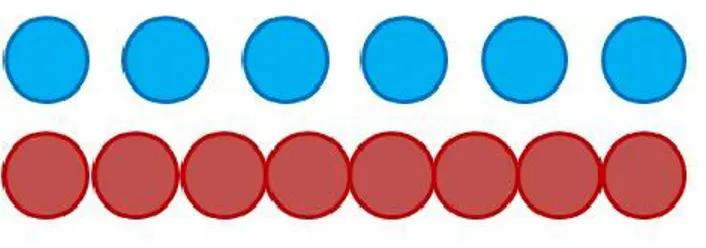
changement de la quantité d‟éléments qu‟il a toujours sous les yeux. Selon Piaget et Szeminska (1964), « les quantités sont d‟abord évaluées simplement en fonction des rapports perceptifs non coordonnés entre eux […] et c‟est cette incohérence initiale qui explique à la fois les continuelles contradictions entre les jugements successifs de l‟enfant et l‟absence de tout critère de conservation » (p.45). À titre d‟exemple, dans un premier temps, une rangée de six jetons comme suit est présentée à un enfant :

Figure 6 : Collection initiale de jetons

L‟enfant dénombrera la collection correctement et indiquera qu‟il y a six jetons. L‟expérimentateur prendra les mêmes six jetons et les déplacera légèrement de manière à ce que les jetons soient plus distancés, commeillustré à la figure 7 :

Figure 7 : Collection de jetons modifiée une première fois

À ce moment, l‟enfant qui n‟a pas compris l‟idée de conservation dénombrera à nouveau les jetons, même si aucun ajout ni retrait n‟a été apporté par l‟expérimentateur. Selon Piaget et Szeminska (1964), la non-conservation du nombre peut être présente jusqu‟à l‟âge de 5 ans.

Au deuxième stade (début de constitution d‟un ensemble), les réflexions de l‟enfant se situent entre la perception (les quantités brutes) et la quantification. L‟enfant hésite, car il sait qu‟aucun élément n‟a été ajouté ou retiré de l‟ensemble dénombré, mais l‟apparence n‟est plus la même; cela le pousse à les dénombrer de nouveau, ce qui est caractéristique d‟une non-conservation. À ce stade, la conservation du nombre commence à apparaître dans le raisonnement de l‟enfant (alors âgé de 5 ou 6 ans, selon les travaux de Piaget), même s‟il est possible de voir que ce n‟est pas toujours stable. Si, toujours à partir de la même rangée de départ (Figure 6), l‟expérimentateur prend les jetons et les regroupe de manière à faire un tas, comme démontré à la figure 8, l‟enfant pourrait revenir avec des