Le théorème de Perrine

UNIVERSITÉ DU QUÉBEC À MONTRÉAL

LE THÉORÈME DE PERRINE

MÉMOIRE PRÉSE TTÉ

COMME EXIGENCE PARTIELLE DE LA MAÎTRISE EN MATHÉ tiATIQUES

PAR

FATIHA DJERMA E

UNIVERSITÉ DU QUÉBEC À MONTRÉAL Service des bibliothèques

Avertissement

La diffusion de ce mémoire se fait dans le respect des droits de son auteur, qui a signé le formulaire Autorisation de reproduire et de diffuser un travail de recherche de cycles supérieurs (SDU-522 - Rév.1 0-2015). Cette autorisation stipule que «conformément à l'article 11 du Règlement no 8 des études de cycles supérieurs, [l'auteur] concède à l'Université du Québec à Montréal une licence non exclusive d'utilisation et de publication de la totalité ou d'une partie importante de [son] travail de recherche pour des fins pédagogiques et non commerciales. Plus précisément, [l'auteur] autorise l'Université du Québec à Montréal à reproduire, diffuser, prêter, distribuer ou vendre des copies de [son] travail de recherche à des fins non commerciales sur quelque support que ce soit, y compris l'Internet. Cette licence et cette autorisation n'entraînent pas une renonciation de [la] part [de l'auteur] à [ses] droits moraux ni à [ses] droits de propriété intellectuelle. Sauf entente contraire, [l'auteur] conserve la liberté de diffuser et de commercialiser ou non ce travail dont [il] possède un exemplaire.,

LISTE DES FIGURES RÉSUMÉ . INTRODUCTION CHAPITRE I LE GROUPE SL₂₍'Z,) 1.1 Générateurs de SL2('Z,) 1.2 Identités de Fricke CHAPITRE II

TABLE DES MATIÈRES

LE SOUS-GROUPE DES COM tl TATEURS SL2('Z,)' 2.1 Générateurs de SL2('Z,)'

2.2 SL2(Z)' est un groupe libre CHAPITRE III BASES ET AUTOMORPHISMES DE F2 3.1 Bases de F(a, b) . .. . . . 3.2 Endomorphismes de F(a,b) et de {a,b}* 3.3 Le groupe Aut(F(a, b)) : . . . . . CHAPITRE IV

L'ARBRE DES TRIPLETS DE MARKOFF 4.1 Triplets de Markoff .

4.2 L'arbre de Markoff CHAPITRE V

L'ARBRE DES PAIRES DE CHRISTOFFEL 5.1 L'arbre des paires de Christoffel .

5.2 Les mots de Christoffel . . . . 5.3 Les mots de Christoffel-suite CHAPITRE VI THÉORÈME DE PERRINE . . . v VIl 1 3 3 7 11 11 14 19 19 26 27 31 31 36 39 39 43 53 57

IV

6.1 Preuve du théorème de Perrine 6.2 Preuve du théorème de Cohn RÉFÉRENCES . . . . .. .. . .

57 59 61

- -- - -

-LISTE DES FIGURES

Figure

2.1 Régions associées aux transformations linéaires Tx ,Ty ,T x-I ,Ty-J . 2.2 2.3 2.4 4.1 (RTxfx (RTyfx (R _.yl'-1 )Tx

La règle pour construire 1 'arbre des triplets de Markoff 4.2 L'arbre des triplets de Markoff

5.1 La règle de construction de l'arbre des paires de Christoffel 5.2 L'arbre des paires de Christoffel . . .

5.3 Chemin qui discrétise par en-dessous 5.4 Mot d'intersection associé . . . 5.5 Le mot d'intersection est un palindrome 5.6 Reflet d'un mot de Christoffel . . . . 5.7 Pavage du plan par des parallélogrammes 5.8 Factorisation standard

5.9 Factorisation standard

5.10 w

=

uv est un mot de Christoffel 5.11 u est un préfixe de v . . . . . . . Page 16 16 17 18 36 37 39 40 44 44 45 45 47 49 49 50 52

RÉSU tlÉ

Le groupe SL2(Z) est l'ensemble des matrices de déterminant tmité dont les coefficients sont entiers. On définit SL2(Z)' comme le sous-groupe engendré par l'ensemble des commutateurs de SL2(Z). On prouvera que SL2(Z)' est un groupe libre de rang deux. On prouvera également le critère de Nielsen, qui dit qu'un automorphisme du groupe libre de rang 2 envoie aba-1_b-1 _{sur un conjugué de lui-même ou de on inverse.}

De plu , on introduira les triplets de Markoff, qui sont les solutions entières et positives de l'équation diophantienne x2+y2+z2 = 3xyz. On parlera aus ide mots de Christoffel inférieur ·, définis comme les mots dans {a, b} * qui codent les chemins qui discrétisent par en-dessous la diagonale qui va de (0, 0) à (p, q), où p, q E IN et p, q premiers entre eux.

Dans le dernier chapitre, on prouvera le théorème de Perrine qui affirme que tout triplet de Markoff ·'obtient en spécialisant une base du groupe libre sur deux générateurs a, b, en utilisant principalement le critère de lielsen et les identité de Fricke ainsi que la bijection entre les mots de Christoffel et les triplets de Markoff. De manière précise, cette pécialisation consiste à prendre les traces des deux éléments de la base, ainsi que de leur produit, et à diviser ces trois nombres par trois; on obtient ainsi un triplet de Markoff; tous les triplets de Markoff sont ainsi obtenus.

Mots clés : S L2 (Z) ; S L2 (Z)' ; cri t-re de Nielsen; triplet de Markoff; paire de Christoffel ; théorème de Perrine.

INTRODUCTIO 1

La théorie des nombres de Markoff fut développée vers 1880 par le célèbre théoricien des nombres Andrei Markoff. Les nombres de Markoff sont constitués des solutions entières à l'équation diophantienne

qu'on appelle équation de Markoff. Un triplet de Markoff est une solution de cette équ a-tion. Ce n'est que plus tard (1955 et après) qu'Harvey Colm mît en évidence les liens très étroits qu'entretient la théorie des nombres de Markoff avec le groupe SL2(Z). Il démon-tra entre autres que tout triplet de Markoff est de la forme

a

Tr(A), ~ Tr(B), ~ Tr(AB)}, où {A, B} est une base du sous-groupe dérivé de SL2(Z), qu'on note SL2(Z)l D'ailleurs, Serge Perrine, dan son livre intitulé "La théorie de Markoff et ses développements" (Pe r-rine, 2002), démontre la réciproque, c'est-à-dire que pour toute base {A, B} de S L2 (Z)', HTr(A), ~TT(B), ~Tr(AB)} est un triplet de Markoff. Dan ce mémoire, on fera une preuve complète des théorèmes de Perrine et de Colm et de tous les tenants et abouti s-sants.

Pour ce fair , on montrera dans le premier chapitre que SL2(Z) est engendré par les matcices

G

:)

et (:

~)

.

Ensuite on pmuvem la cêlêbce identité de Fl-icke ' Si X, Y E SL2(Z), alors

Tr(X)2 + Tr(Y)2 + Tr(XY)2 = Tr(X) Tt(Y) Tr(XY) + Tr(XY

x

-

1 _{y-J) + 2.}

2

et ( : :) . Pou< ce fai,·e, on sui vm la p<eu ve géomét<ique de A ignee (A ignee, 2013).

Le but du troisième chapitre est de démontrer la réciproque du critère de ielsen qui affirme qu'un endomorphi me du groupe libre F(a, b) est un automorphisme si et seul e-ment s'il envoie aba-1 b-1 _{sur son conjugué ou un conjugué de son inverse. On ne prouvera} que la réciproque du critère. Pour ce faire, on s'appuiera sur l'article de Nielsen (Nielsen, 1918) afin de montrer que le groupe des automorphismes de F(a, b) est engendré par les trois automorphismes (a-1_{, b), (b, a) et (a, ab) (on note ( u, v) l'automorphisme dans} F(a, b) qui envoie a sur u et b sur v).

Au chapitre quatre, on construira l'arbre des triplets de Markoff tel qu'il fut introduit par Colm en uivant les transformations élémentaires des triplets de Markoff.

Par la suite, on introduira l'arbre des paires de Christoffel et on montrera que l'arbre des triplets de Markoff est une spécialisation de l'arbre des paires de Christoffel (Bers tel et de Luca. 1997). On va également montrer que toute paire de Christoffel forme une base du groupe libre F(a, b). On utilisera clone ce deux ré ·ultat au dernier chapitre pour montrer la r· iproque du théorème de Perrine, qui nous vient de Cohn mais qui n'apparait pas chez Perrine.

Pour finir, on prouvera à la manière de Reutenauer le théorème de Perrin , en utilisant les deux générateurs de SL2(Z)' dont on a parlé, la réciproque de Niel en et l'identité de Fricke.

CHAPITRE I

LE GROUPE SL2(Z)

Dans ce chapitce, on va montm que SL,(Z) est engend;ê pm· les d ux mat;ices

C

:)

et (:

~)

.

De plus, on dêmont;e<·a les identités de Fricke qui nous sewnt utiles pa; la suite.

1.1 Générateurs de SL2(Z)

Définition 1.1.1. Le groupe spécial linéaire, noté S L2 (Z), e t le groupe de matrices d'ordre deux à coefficients dans 71, dont le déterminant est 1.

Remarque 1.1.2. SL2(Z) est un sou -groupe de GL2(Z).

Proposi lion L L3. (Ka" el et aL, 2008) Soient A

~

C

:)

et B

~

(:

~)

dans

SL2(Z). Alor·s A et B engendrent SL2(Z) Lemme 1.1.4.

4

De même pour En. •

Démonstration de la proposition 1. 1. 3. Soit M _{(: :) E SL2(Z). Mont>OŒ que} M E (A,B}.

Posons T

=

AB-1 _{A, alors :}

Donc,

( - 1 Be ou M

=

c

0)

=

(-I)B-c - 1 Or, - I E (A, B), car - I = (AB-1 A)2 tel que calculé ci-dessus. Donc, M E (A, B). Si b =/= 0, on pose M1

= A

n1l\lf. Alors : On peut choisir n1 E Z tel que 5

Si h

=

0, alors M1 E (A, B) par ce qu'on vient de voir, et donc ME (A, B). Si b1 =/= 0, on multiplie lV

h

à gauche parT :

6

On pose par la , ui te lVh = A n2 T fvh, alors :

On choisit n2 E Z tel que :

Ainsi, on a:

Si b2 = 0, on conclut que lVI E (A, B). Sinon, on continue ainsi jusqu'à obtenir :

Comme l\lfk est de cette forme, on est réduit au premier cas, c'est-à-dire Mk = Be~.-, ou

lVh

=

(

- I)B-q

Ainsi, M

=

A-n1_T-1 · _{· -A-n"-}1_T-1_{A-nkMk E (A,B).} De plus, A, B E SL2(Z), donc (A, B)ç SL2(Z) .

7

1.2 Identités de Fricke

Proposition 1.2.1 (Identité de Fricke). (Fricke, 1896) Soit X, Y E SL2(Z), on a

alors que :

(i) Tr(X2Y) = Tr(X) Tr(XY) - Tr(Y),

(ii) Tr(XY2) = Tr(XY) Tr(Y) - Tr(X),

(iii) Tr(X)2 + Tr(Y)2 + Tr(XY)2 = Tl·( X) Tl·(Y) Tr(XY) + Tr(XY x -I y-I) + 2.

Démonstration. Soit A une matrice d'ordre n, nous noterons PA(x) son polynôme ca -ractéristique. Par le théorème de Cayley-Hamilton, on a :

PA(A)

=

A2 - TI·(A)A

+

det(A)I

=

0, (1.1)

=:> A-1(A2- Tr(A)A + det(A)I) = A - TI·(A)I + det(A)A-1 = O.

Donc, si det(A) = 1,

A-1 = Tr(A)I - A. (1.2)

On en déduit aussi, puisque Tl·(!) = 2, Tl·(A-1

) = 2 Tl·( A)-Tl·( A) = Tl·( A).

(i) Comme X E SL2(Z), alors det(X) = 1. Ainsi, par 11, on a:

X2 - Tr(X)X + I = 0, ==:> X2 = Tr(X)X - !, ==:> X2Y = Tr(X)XY - Y,

==:> Tr(X2Y) = Tl·(X) Tr(XY) - Tr(Y).

(ii) De la même manière, on montre que Tr(XY2

8 (iii)On a par 1.2 : XY

x-

1 _{y -I = XY('lf(X)I - X)('lf(Y)I - Y)} = (Tr(X)XY - XY X) (Tr(Y)I - Y) = Tr(X) Tr(Y)XY - Tr(X)XY2 - Tr(Y)XY X

+

XY XY. Or, on a par 1.1 : De plus,

XY XY = 'lf(XY)XY - I (car XY E SL2(Z), donc det(XY) = 1), 'lf(XY XY) = Tr(XY)2

- 2, car 11'(1) = 2.

XYX = (XYXY)Y-1

= (Tr(XY)XY - I)Y-1

= Tr(XY)X- y -l,

===? Tr(XY X) = Tr(XY) 'If( X) - 1f(Y), car Tr(Y-1

) = TI:(Y).

Ainsi, on a:

Tr(X) TI·(Y) TI·(XY) - Tr(X) 1f(XY2 )

- 1f(Y) TI·(XY X) + TI:(XY XY)

1f(X) TI·(Y) TI·(XY) - Tr(X)('lf(XY) 'Il-(Y)- Tr(X))

- TI·(Y)(TI·(XY) 1f(X)- 1f(Y)) + Tr(XY)2 - 2 Tr(XY)(TI·(X) TI·(Y)- 1f(X) Tr(Y)- Tr(X) TI·(Y))

+

1\·(X)2

₊

_1\·(Y)2

₊

_Tr(XY)2 - 2

9

Donc,

Tr(X)2

+

Tr(Y)2

+

Tr(XY)2 = Tr(X) Tr(Y) Tr(XY)

+

Tr(XY

x

-

1 y -I)

+

2 .

•

CHAPITRE Il

LE SOUS-GROUPE DES COMMUTATEURS SL2(7J.,)'

Dans la première section, on va montrer que le sous-groupe des commutateurs SL2(7J.,)'

e't engend>·é pa< le> deux matnœ'

C

~

)

et

G :)

Don' la deuxième 'edion, on

va utiliser la preuve géométrique de Aigner (Aigner, 2013) pour montrer que SL2(7J.,)' est w1 groupe libre. Pour la suite, on notera H :::;J G pour dire que H est un sous-groupe

normal dans G.

2.1 Générateurs de SL2(7J.,)'

Définition 2.1.1. Soit G tm groupe et g, h E G. Le commutateur de g et h, noté

[g, h], est le produit ghg-1_h-1_{. On note G' le sous-groupe de G engendré par tous les}

commutateurs de G et on l'appelle le sous-groupe des commutateurs.

Il est clair que G' e t un sous-groupe normal de G, car le conjugué d'un commutateur est un commutateur. En effet, k [g, h] k-1 _{= [kgk-}1_{, khk-}1_].

Remarque 2.1.2. SL2(7J.,)' = ({[g,h]l g,h E SL2(7J.,)}). ( 1 1)

(

2

1) Pour ce chapitre, po ons X

=

1 2 et Y

=

1 1 .

12

Démonstration. Soit 1r : G ---1 GjN la projection canonique. Son noyau est N. Si a, bE G, alors

7r(a)7r(b)1r(a)-11r(b)-1 (car 1r est un homomorphisme) 1r(a)7r(a)-1_7r(b)1r(b)-1 _{(car GjNest commutatif)} 1.

Donc, aba-lb-1 E I< er(1r) = N. Ainsi, G' = ({[a, b]l a, bEG}) Ç N.

Lemme 2.1.4. (X, Y) est normal dans SL2(Z).

•

Démonstration. Il suffit de montrer que les générateurs X, Y de (X, Y) conjugués par le géné>atems

G

:)

et (:

~)

de SL,(Z) sont des génémtems de (X, Y)

13

1) et 2) montœnt que l'autommphisme 9 -+ 090-', oU a

~

G :).

envoie (X, Y) ur lui-même, car (X, Y)= (Y, Y

x

-

1 _{). Donc, a(X , Y)a-}1 _{= (X, Y).}

3) et 4) montcent que l'autommphisme 9-+ bgb-', oU b

~

( :

~

)

,

envoie

(X, Y) sm lui-même, car (X, Y) = (XY-1, X). Donc, b(X, Y)b-1 _{= (X, Y).}

Ainsi, pour tout g E SL2(Z), g(X, Y)g-1 = (X, Y). Donc, (X, Y) est normal dans

•

Lemme 2.1.5. SL2(Z)/(X, Y) est commutatif.

Démonstration. Il suffit de montrer que ab= ba mod(X, Y), c'est-à-dire que aba-1_b-1 _E

(X, Y). On a :

(

1 1

_{0 1 1 1 0}

) (1

0

) (

1

-

₁

1)

(

_-

1 0

_{1 1}

) (

2

₁

1

₁

) (

_-

2

_{1 1}

-

1

)

G

:

)(:

~r

~

Y

r'

E

(

X

,

Y

)

•

14

Corollaire 2.1.6. SL2('1l,)' Ç (X, Y).

Démonstration. On a montré au lemme 2.1.4 que (X, Y) :::;1 SL2('1l,) et au lemme 2.1.5

que SL2(7i,)j(X, Y) est commutatif. Ainsi, par le lemme 2.1.3, SL2('1l,)' Ç (X, Y). •

Proposition 2.1. 7. (X, Y) Ç S L2 (71,)'.

Démonstration. Il suffit de montrer que X, Y E SL2(71,)'- On a :

(1

_{0 1}

1

) (

_-

1

_{1 1}

0

) (

1

_{0 1 1 1}

-

1

) (

1 0

)

(

_-

0

₁

₁

1)

(

0

₁

-

₁

1)

c

~

)

~

x

Donc, X = [a,b-1_{) E SL2('1l,)'.}

De plus, on a vu que bYb-1 _{= X. Ainsi}

. Y = b-1_Xb

et pui que SL2(7i,)' :::;1 SL2(71,),

Y E SL2('1l,)'- •

Conclusion • On a ainsi montcé que (

C

~

)

,

G

:

)

)

~

SL,(Z)'. 2.2 SL2(71,)' est un groupe libre

Définition2.2.1. SoitunensemblenonvideX = {x1,··· ,xm}etX-1 = {x;-\··· ,.x;:;-t1} l'ensemble des inverses formels de X. On suppose que Xnx -1 _{= 0 et on note (Xux -}1 _)*

avec aiE X U

x

-

1. La longueur de w, notée

lwl

,

est n. On dit que west réduit si Vi, 1 ~ i ~ n - 1, ai =/= a;-_;₁.

15

X engendre librement un groupe G si X est l'ensemble des générateurs de G et si aucun mot non-vide et réduit sur (X U

x

-

1 _{)* ne représente l'identité de G. On dit que G est} un groupe libre de rang

l

X

I.

Théorème 2.2.2. SL2(Z)' est librement engendré par X et Y , et c'est donc un groupe

libre de rang 2.

Démonstration. (Aigner, 2013, p.117)

ilontrons que tout mot réduit sur {X, Y, x-1_{, y-l}, non-vide, ne peut être égal à I, la} matrice identité.

On fait agir

x

,

Y,

x

-

1, y -l comme des transformations linéaires TM : lR2 ----+ lR2' où vTM =vM. otons-les respectivement Tx,Ty,Tx-t,Ty-1. On a alors :

(a, bfx (a+b,a+2b),

(a, bf~' (2a + b, a+ b), (a, bfx-I (2a- b,-a+b),

(a, bfv-I (a - b, -a+ 2b).

Supposons que w = O'JÜ'2" 'Ü'l, l ?: 1, est un mot réduit sur {Tx ,Ty,Tx-t,Ty-t} . Montrons alors que w =!= id. Considérons d'abord les 4 régions ouvertes du plan associée

aux transformations linéaires :

16

(0.1)

R (-1.0)

Tx->

Figure 2.1 Régions associées aux transformations linéaires Tx ,Ty ,Tx-t ,Ty->.

1 / ( l.:!) / '

.

1 / 1 j / , ' , (0.1) -''.--(1.1) , / ,' ei:!.:q / Figure 2.2 (Rrx )Tx On a: (1, 1fx = (2, 3) E Rrx, (0, 1fx = (1, 2) E Rrx.

Comme on peut le voir dans la figure 2.2, le cône engendré par (2, 3) et (1, 2) est

De même: (0.1) 1 ' • 1 1.1 Figure 2.3 (Rry )Tx (1, O)Tx = (1, 1) E Rrx, (1, 1)Tx = (2, 3) E Rrx. 17

Comme on peut le voir à la figure 2.3, le cône engendré par (2, 3) et (1, 1) est strictement inclus dan.· celui engendré par (1, 1) et (0, 1). Donc, (Rry fx Ç Rrx.

Aussi:

(-1,1)Tx = (0,1) E Rrx,

(0,1)Tx

=

(1,2) E Rrx·

À la figure 2.4 ci-dessous, on peut voir que le cône engendré par (0, 1) et (1, 2) est strictement inclus dans celui engendré par (0, 1) et (1, 1). Donc, (RrY_1 fx Ç Rrx.

De la même manière, on démontre en général que pour a, (3 E {Tx, Ty, Tx-J, Ty-J}, on

a:

18

(0 1)

Figure 2.4 (Rry-J fx

CHAPITRE III

BASES ET AUTOMORPHISMES DE F2

Dans ce chapitre, on commencera tout d'abord par expliquer la con truction du groupe

libr F(a, b) et ju tifier quelques terminologies qu'on utilisera tout au long du chapitre. On prouvera également un théorème de Niel n sur le bases de F(a, b). Par la suite, on va démontrer que le groupe Aut(F(a, b)) est engendré par trois automorphismes de

F(a, b), puis on pourra conclure par la preuve du Critère de Nielsen, qui s'énonce comme suit.

Théorème 3.0.1. (Nielsen, 1918, p.393)

Un endomorphisme du groupe libre F(a, b) envoie aba-1b-1 sur un conjugué de aba-lb-1

ou de on inver e bab-1_a-1 _{si et seulement s'il est un automorphisme de F(a,b).}

Remarque. On ne prouvera que la réciproque.

3.1 Bases de F(a, b)

On construit F(a, b) en quotientant {a, b, a-1_{, b-}1 _{}* par :::::, où}

=

_{e t la congruence e} n-gendrée par les relations aa-1

=

₁

=

_a-1_{a, bb-}1

=

₁

=

_b-1 _{b. Chaque élément de F(a, b)} est représenté par des mots dans le monoïde libre {a,b,a-1,b-1}*. Ce dernier possède

un anti-automorphisme involutif, apJ elé inversion et qui échange les éléments dans

{a, b, a-1_{, b-}1_{} avec leurs inverses. Ainsi, pouru, v E {a, b, a-}1_{, b-}1 _{}*, ( uv)-}1

= v-1_u-1_. De plus, un élément de F( a, b) possède un unique représentant dans {a, b, a-1, b-1} *, qui est réduit. On définit la longueur d'un élément du groupe libre comme la longueur de son

20

représentant réduit dans le monoïde. On notera par exemple

l

u

i

la longueur d'un mot u. Pour éviter des confusions, il sera précisé dans ce chapitre si on considère un élément

"dans F(a, b)" ou "dans {a, b, a-I, b-1_{} *". Si on dit west réduit dans F(a, b), on veut dire}

que w est le représentant réduit dans le monoïde. Soit w = a1 · ··at E {a, b, a-1, b-1}

*

,

on dit que w est cycliquement réduit si w et w2 _{sont tous deux réduits dans le mono'ide,}

c'est-à-dire si w est réduit et si a1 =1- a{1.

Si u, v sont deux éléments réduits et que leur produit uv est également réduit dan le

monoïde, on dit que leur produit est réduit, ou sans simplification. On définit la longueur d'une paire d'éléments { u, v} comme la somme de leurs longueurs.

Lemme 3.1.1. Tout w E F(a,b) réduit possède dans {a,b,a-1_,b-1_{}* ·une ·un·ique ex} -pression réduite w = xyx-1 _{telle que x est réduit, y est cycliquement réduit et xy, yx-}1 sont sans simplification. Par suite, pour tout k =1- 0, xykx-1 est réduit.

Démonstmtion. Si w = 1, alors on prend x = y = 1. Sinon, prenons x E {a, b, a-1, b-1} *,

un préfixe de w de longueur maximale tel que x-1 _{soit un suffixe de w. Comme x est}

maximal, y e t cycliquement réduit et pour k =1- 0, yk aussi. De plus, xy et yx-1 sont sans simplification puisque w est réduit. Ainsi, :r;yk.T-1 est réduit.

•

Si 91 · · · 9n est un produit d'éléments réduits de F2, on dit que 9i (1 ~ i ~ n.) e t absorbé par ses voisins si on a les produits réduits 9i-l = xu-1, 9i

v-1y (on convient que go, 9n+1 = 1).

uV,9i+J

=

Lemme 3.1.2. Soit 91, · · · , 9n, n ? 2, des éléments réduits de F2 tels que 91 · · · 9n

= 1

. Alors, pour uni, 1 ~ i ~ (n - 1), 9i est absorbé par ses deux voisins.

Démonstmtion. On va écarter le cas évident où pour tout i, 9

= 1

et on prouvera par récurrence sur la longueur totale le cas non-trivial. Dans ce cas, il existe j, 1 ~

.

i

~ (n - 1) et c E {a,b,a-1,b-1} tels que 9.i = hjc et 9.i+l =

c

1hj+l sont des produits réduits.

Alors, h 1 · · · hn

=

1 et tous les hi sont réduits.

Par hypothèse de récurrence, :li, 1 ( i ( (n - 1) tel que hi-I

hi+l

=

v-1_{y, où les produits sont réduits.}

Montron alors que gi est absorbé par ses deux voisins. On a plusieurs cas :

1) Si i < j - 1, alors, i -1, i, i

+

1 < j. Donc :

gi- 1 = hi-1 = xu-1, gi = hi = uv, gi+l = hi+l = v-I y,

et tous ces produits sont réduits.

2) Si i = j - 1, alors, i - 1, i < j. Donc :

gi-I = hi-I = xu-1,

gi = hi= uv,

et tous ces produits sont réduits.

3) Si i = j, alors :

-]h - 1, -1 - 1 .9i+l = .9]+1 = c j+l = c 1i+l = c v y, et tous ces produits sont réduits.

Les ca i = j

+

1, i = j

+

2 et i > j

+

2 sont similaires.

Lemme 3.1.3. Le groupe libre F( a, b) ne peut être engendré par un élément.

21

uv et

22

Démonstration. Soit w

=

ah1_{bk1 • • • ahnbkn E F(a, b). Soit l'homomorphisme de groupes} surjectif 1r : F( a, b) ----1 71} défini par

1r(w) = (h, k) E Z2

où h

=

h1

+

·

· ·

+

hn et k

=

k1

+

·

·

·

+

kn. Cette fonction est appelée abélianisation. Comme Z2 ne peut être engendré par un élément, F(a, b) également.

•

Définition 3.1.4. Deux éléments u et v sont con_jugués dans {a, b, a-1, b-1 }* s'il existe x,y E {a,b,a-I,b-1}* tels que u = xy et v= yx. On dit également de deux paires

{ps,ps'} et {sp, s'p} qu'elles sont conjugués dans le monoïde libre.

Théorème 3.1.5. (Nielsen, 1918, p. 387-389) Soit u, v des éléments réduits quz e n-gendrent F(a,b). Alors :

(i) La paire {u,v} est conjuguée dans F(a,b) à une paire telle que les deux éléments de la paire sont cycliquement réduits et dont la longueur e t plus petite que celle de { u, v}. (ii) Si { u, v} sont cycliquement réduits, alors soit { u, v} e t une des paires {x, y}, x = a,a-1 _{et y = b,b-}1 _{ou {u,v} est conjuguée dans F(a,b) à une paire de même longueur} et telle qu'un de ses élément ou son inverse est, comme élément de {a,b,a-1,b-1}*, un préfixe ou un suffixe de l'autre.

Démonstration. Nous donnons la preuve originelle de Nielsen.

Étant donné que u,v engendrent F(a,b), on peut écrire a,b comme produit:

où ni, Pi "1- 0, sauf peut-être n1 ou Pk·

(i) Supposons que u n'est pas cycliquement réduit, alors on a le produit réduit u

- 1 E { b - l b-l }*

cwc , avec c a, , a , .

23

F(a, b), ce qui e t impossible par le lemme 3.1.3.

Si un des deux produits contient seulement u, alors le produit ne peut être égal à a ou b.

En effet, par le lemme 3.1.1, on peut écrire u d'une manière unique dans {a, b, a-1, b-1} *

comme un produit réduit u = xyx-1. Comme u n'est pas cycliquement réduit, x -j. 1

dans {a,b,a-1_,b-1_{}*. De plus, par le lemme, ui}

= xyix-1 _{est w1 produit réduit, donc}

ui = 1 ou

luil

;?: 3, or a et b sont de longueur 1, d'où la conclusion.

Ainsi, au moins un des deux produits contient u et v simultanément.

Comme v est réduit, par le lemme 3.1.1, on peut écrire v comme produit réduit x'y'x'-1 et pour i'

'1-

0, on a que vi' = x'y'i' x'-1 _{est également réduit et}

_lvi'

₁

_{;?: 1.}

Comme a ou b s'écrivent comme un produit de puissances de u et v et que

lu il+

lvi

'

1

;?: 4,

il doit y avoir certaines simplifications. Donc, soit v= cv' ou v= v'c-1.

Ainsi, on a que {u,v} est conjuguée dans F(a,b) aux paires {w,v'c} ou {w, c1v'} dont la longueur est plus petite. Ainsi, par récurrence sur la longueur de la paire, on a { w, v' c}

ou { w, c 1_{v'} sont conjuguées à une paire plus petite dont les éléments sont cycliquement}

réduits, ce qui nous donne (i).

(ii) Supposons que u et v sont cycliquement réduits. Les deux produits (*) peuvent

s'écrire dans {a b a-1 b-1 }* sous la forme hak et h'bk' où h = k = h' = k' = 1 dans

' ' ' '

F(a, b).

• Supposons que h -j. 1 dans {a,b,a-1_,b-1_{}* (le cas h' -j. 1 est similaire). Si n}

1 -j. 0 dans (

* ),

alors un1 _{est préfixe de h. En effet, si h est préfixe de un}1_{, alors h -j. 1 dans}

F(a, b) puisque u est cycliquement réduit. De même, si n1 = 0, alors vP1 est préfixe de

h. Considérons le cas n1

'1-

0 (l'autre cas est similaire). Alors, on a pour ry

=

±1 :

h = _{' - v - - '} uTI · · ·uTiv±1 · · ·p _, où pest préfixe de u±1 ₎ v±1 ₎

24

ou

h = u"~ · · · u'7 _{p, où p est préfixe de v±}1. '---v--"

n1 fois

Par le lemme 3.1.2, il existe un facteur qui est absorbé par ses deux voisins et ça ne

peut être p par la condition (n- 1) du lemme. D'ailleurs, si le facteur est absorbé par la droite par p, il l'est en conséquence par le mot dont p est le préfixe, c'est-à-dire u±l ou v±1_{. De plus, étant donné que u et v sont cycliquement réduits, ( u±l )}2 _{et ( v±}1

)2 ne

sont pas simplifiables. Ainsi, soit u ou u- 1 est absorbé par la droite ou par la gauche

par v ou par v-1_{, et vice-versa. Donc, u ou u-}1 _{est préfixe ou suffixe de v ou de v-}1_{, et}

vice-versa, ce qui prouve (ii). Sinon, on a les produits suivants :

v±1

=

xm-1,

ou les trois égalités en échangeant u et v dans les précédente Nous ne traiterons pas ce tout dernier cas, qui est similaire.

Lemme 3.1.6. Si u est absorbé par ses voisins dans le produit v±1_uv±1_{, alors u-}1 _est absorbé par ses voisins dans le produit v±1u-1v±1.

Démonstration. Pour 'TJ, v = ±1, on a : v'7 _{= xm-}1_{, u = rnp,} donc : - // - ] v = mx , tel que voulu.

•

On peut ainsi supposer que l'exposant de u est 1 (le cas - 1 est similaire, par le lemme 3.1.6). Donc, on a pour 'TJ, v = ±1 v'7 _{= xm-}1_{, u = mp,}

25

Si 'Tl

=

- 1 et v

=

1, alors :

u= mp,

Ainsi, v = mx-1 = p-1y, donc la première lettre de m est égale à la première lettre de p-1, donc à l'inverse de la dernière lettre de p. Ce qui n'est pas possible puisque u est

cycliquement réduit par hypothèse. De même pour 'Tl= 1 et v = - 1.

Donc 'Tl = v = ±l. Supposons qu'ils sont égaux à 1 (l'autre ca est similaire), alors :

v = xm-1_,

u = mp,

Donc, on a xm-1 _{= p-}1_{y dans {a,b,a-}1_,b-1_{}*. Ainsi, soit x est préfixe de p-}1 _ou

vice-versa. Dans F(a,b), {u,v} = {mp,xm-1_{} est conjuguée à la paire {u',v'} =}

{pm, m-1x }. Étant donné que u est cycliquement réduit, la dernière (respectivement la première) lettre de m n'est pas égale à l'inverse de la première (respectivement la der-nière) lettre de p, ainsi u' = pm est aussi cycliquement réduit. Le même raisonnement tient pour v' = m-1_{x. Donc, les deux paires ont la même longueur.}

Si u et v ont la même longueur, alors m et y aussi. Donc, x

=

p-1 et on a alors

u = mp = mx-1 = v-1 Ce qui est impossible puisque ça impliquerait que F(a, b) est engendré par un élément.

Si u est moins long que v, alors p est moins long que x, donc p-1 _{est préfixe de x. Alors}

u'-1

₌

_m-lp-1 _{est préfixe de m-}1_{x =v'.}

Si u est plus long que v, alors pest plus long que x, donc x est préfixe de p-1_{, donc x-}1 suffixe de p. Ceci implique que v'-1

=

x-1m est suffixe de pm= u'. Ce qui prouve (ii).

• Supposons que k

f=

1. Si Pk

f=

0 dans ( *), alors vPk est suffixe de k. En effet, si k est préfixe de vPk, alors k

f=

1 dans F(a, b) puisque v est cycliquement réduit. De même, si

26

Pk = 0, alors unk est suffixe de h. Considérons le cas Pk =1- 0 (J'autre cas est similaire). Alors, on a pour TJ

=

± 1 :

ou

k

=

p · · · u±1 v.,.,· ·· v.,., où p est suffixe de u±1 v±1

'-v---"' ' ' Pk fois

k

=

pv.,., ···v.,.,, où p est suffixe de u±1. '-v---"

Pk fois

En prenant l'énoncé symétrique du lemme 3.1.2, c'est-à-dire pour g1,· · · ,gn,n ~ 2, des éléments réduits de F2 tels que g1 · · · gn.

=

1, alors pour un i, 2 ~ i ~ n, gi est absorbé

par ses deux voisins. Le reste du raisonnement est similaire au cas h =1- 1. Le cas k' =1- 1 est aussi similaire.

• Si h,h',k,k' = 1 dans {a,b,a-1_,b-1_{}*, alors les deux produits(*) sont de longueur 1} dans {a, b, a-1

, b-1 }*, donc a et b sont égaux à u, u-1, v ou v-1 Ainsi { u, v} e t l'une

•

3.2 Endomorphismes de F(a,b) et de {a,b}*

Propriété universelle de F( a, b) : Pour tout groupe G et toute f nction cp : {a, b} --t G, il existe un unique morphisme de groupe~ de F(a, b) dans G qui prolonge cp et tel que ~(al··· an) = cp( al) ··· cp( an)·

Soit cp E End( {a, b} *), alors cp induit par restriction une fonction {a, b} --t {a, b} * '---+ F(a, b), où a f---t cp( a), b f---t cp(b) . Donc, par la propriété univer elle de F(a, b), il existe

un unique morphisme de groupe de F(a, b) vers F(a, b) qui prolonge cp. Ainsi, chaque endomorphisme elu monoïde libre {a, b }* s'étend uniquement en un endomorphisme <I> elu groupe libre F(a, b) qu'on notera (u, v), où u et v sont respectivement l'image de a et b par <I>.

27

3.3 Le groupe Aut(F(a, b)) :

Un automorphisme <I> est dit intérieur s'il existe

f

E G tel que \fg E G, <I>(g) = Jgf-1_.

On notera Int(G) l'ensemble des automorphismes intérieurs de G. Considérons les a

u-tomorphismes suivants de F(a, b) :

E = (b, a) et S = (a-I, b),

Les automorphisme élémentaires sont les huit automorphismes de la forme

(3.1)

et les huit autres automorphismes :

G =(a, ab), ê = (a, ba), D = (ab, b), D = (ba, b),

c-

1

₌

_(a,a-1_{b),ê -}1

₌

_(a,ba-1_),D-1

₌

_(b-1_a,b),D-1

₌

_(ab-1_{,b). (3.2)}

alors on a le corollaire suivant :

Corollaire 3.3.1. Le groupe Aut(F(a, b)) est engendré par les trois automorphismes

G,E,S.

Démonstration. Posons :

On a T, 1 E ( G, E, S). A lor on a :

D

=

EGE, ê

=

IGI, ÎJ

=

EêE,

28 De plus, et (a, a-1b)(a, ba) (a, a-1_ba) (b-1_{a, b)(ab, b)} (b-1_{ab, b).}

Ainsi, le groupe des automorphismes intérieurs Int(F(a,b)) est généré par

c

-

1

ê

et

n

-

1 _fJ.

Aussi, (E, S) est i omm·phe au groupe hyperoctaédral B2. En effet, on a que E2 = S2 = (a, b) et (ES)4 _{= (a-}1

, b-1

f

= (a, b). Donc, les morphismes du groupe (E, S) coïncident

avec les huit morphismes élémentaires dans eq. (3.1).

Il nous reste donc à montrer que les automorphismes élémentaires et les automorphismes intérieur· génèrent F( a, b). Pour cela, il suffit de montrer que pour ( u, v) E F( a, b), une base ordonnée, il existe un produit d'automorphismes élémentaires et intérieurs qui envoient (a, b) sur ( u, v). On va le montrer par récurrence sur la longueur totale, n, de (u,v). Si n = 2, alors (u,v) est l'image de (a,b) par l'un des huit automorphismes de eq. (3.1). Sin > 2, on va considérer deux cas :

Si u et v sont ycliquement réduits, alors par le théorème 3.1.5 (ii), (u, v) est l'une des paires (x, xy), (x, yx), (x, x-1_{y), (x, yx-}1

), (yx, y), (xy, y), (y-1x, y), (y-1 x, y) où x, y sont réduits et les produits sont sans simplifications. Dans chaque cas, (x, y) est une base, de longueur plus petite. Ainsi. par hypothèse de récurrence, il existe un produit d'automorphismes élémentaires et intérieurs f tel que f(a,b) = (x,y). Ainsi, il existe <P, un des automorphismes élémentaires clans l'équation (2) tel que cjJ(J(a, b)) = (u, v).

29

conjuguée à une paire plus petite, c'est-à-dire, ( u, v) est 1 'image par un automorphisme intérieur 'lj; d'une base (u', v') plus petite. Ainsi, par hypothèse de récurrence, il existe un produit d'automorphismes élémentaires et intérieurs f tel que f (a, b) = (u', v'). Donc,

(u, v) = 'lj;(f(a, b)). Ce qui finit notre récurrence.

On a donc montré que (G, E, S) engendre Aut(F(a, b)).

•

On peut alors en déduire le théorème 3.0.1 énoncé au début du chapitre :

(Critère de Nielsen) Un automorphisme du groupe libre F(a, b) envoie aba-1_b-1 _sur

un conjugué de aba-lb-1 _{ou de son inverse bab-la-}1_.

Preuve du théorème 3.0.1. Si

cp

E Aut(F(a,b)), alors par le corollaire précédent,

cp=

cp1

·

·

·

cpn

,

où

cp;

E {G,E,s,G-

1

,E-

1

,S-

1}

.

Montrons que

cp

envoie aba-

1

b-

1

sur un

conjugué de lui-même ou de son inverse. On va le montrer par récurrence sur n.

Si n = 1, al or : G(a)G(b )G(a)-1 _{G(b) - l} a( ab )a -1 _{(ab )-}1 a(aba-1b-1_)a-1_{, qui est un conjugué de aba-}1_b-1_, bab-1_a-1 -1( b -lb-1)-1 a a a a. C'est également vrai pour leurs inver e . En effet, si un morphi me

f

envoie x sur

w1 conjugué de x±1, alors

f

envoie x-1 sur un conjugué de :r'~'1. Cela découle de (ux±1_u-1 _{) -}1

_{= ux}

1_{u-1 .}

30 Si n? 2 , on a: ePI · · · cPn-l ( cPn ( aba -lb -l)). cPl · · · cPn-l (u(aba-lb-1 _)±lu-1_{) (o} ù u E F(a, b) ) cP1 · · · cPn-1 ( u) cP1 · · · cPn-1 ( aba - l b-1 )±1 cP1 · · · cPn-1 ( u) - l (car ePi automorphisme) ' - v - - " ' - v - - " :=u' :=u' u'v (aba- 1_b-1_)±1_v-1_·u'-1_{, où v}

E F(a, b) (par hypothèse de récurrence)

"-v-"

:=tu

CHAPITRE IV

L'ARBRE DES TRIPLETS DE MARKOFF

Dans ce chapitre, on introduira entre autres les définitions de triplet et équation de

Mar-koff. On con truira également l'arbre des triplets de Markoff et on conclura en montrant

que tout triplet de !VIarkoff propre apparait dans l'arbre.

4.1 Triplets de Markoff

Définition 4.1.1. On appelle équation de Markoff l'équation diophantienne

Un triplet d'entiers positifs (non ordonné) { a1, a2, a3} est dit triplet de Markoff s'il est

solution d'une équation d Markoff. On définit un triplet ordonné comme un triplet

(al, a2, a3); on dira que celui-ci est est associé à { _{a 1}, a2, a3}, ou qu'il le représente.

Si toutes les composantes du triplet sont distinctes, alors on dit que c'est un triplet de

Markoff propre, inon le triplet est impropre.

Exemple 4.1.2. {1,2,5} est un triplet de Markoffpropre. En effet, 12 +22 +52 = 30 =

1 * 2 * 5.

Proposition 4.1.3. Les seuls triplets de Markoff impropres sont {1, 1, 1} et {1, 1, 2}.

32

que x = y. Alors, on a :

===? xlz et :Je E ~+ tel que z = ex.

Ainsi, en remplaçant y et z dans l'équation de Markoff, on obtient :

===? (2 + e2) = (3ex), 2 ===? (e +-) = (3x), e ===? el2 puisque e, x E ~' ===? e

=

1 ou e

=

2, ===? x

=

y

=

1 dans les deux cas et z

=

1 ou z

=

2 (car z

=

ex).

•

Proposition 4.1.4. (Markoff, 1880, p.397) Soit {x,y,z} un triplet de Markoff propre, alors {3yz- x, y, z}, {x, 3xz-y, z} et {x, y, 3xy- z} sont aussi des triplets de Markoff De plus, si x < y < z, alors :

(i) 3xy - z < y ;

(ii) z < 3yz- x et z < 3xz - y.

Démonstration. Soit {x,y,z} un triplet de Markoff propre tel que x< y < z. On a. x est racine du polynôme :

L'autre racine est 3yz - x, en effet, on a :

p(3yz- x) (3yz -x) 2 - (3yz)(3yz - x)+ y2

+

z2

(3yz) 2- 6xyz + x2 - (3yzf

+

3xyz

+

y2

+ z

2

0 (car x 2

+

y2

+ z

2 = 3xyz),

donc {3yz - x, y, z} est aussi solution de l'équation de Markoff.

Étant donné que x, y, z E lN*, alors 3yz - x E Z. On a aussi :

3xyz = x2

+

y2

+ z

2, x2 + y2 + z2 3yz = , x y2

+ z

2 3yz - x

=

-'----x 33

Ainsi, 3yz-x > 0 et on a montré que {3yz- x, y, z} est un triplet de Markoff. Montrons maintenant que z < 3yz - x. On a y2 < yz < yz2 et 2z2 _{< 2yz}2 _{car 1 < y < z . Ainsi,} y2

+

2z2 < 3yz2 et on a :

< O.

Donc, puisque 3yz- x et x sont les deux zéros de p(a), x< z < 3yz - x, ce qui prouve (ii).

De plus, y est racine du polynôme :

34 L'autre racine est 3xz- y. On a 3xz-y E Z puisque x, y, z E lN*. On a aussi : 3xyz = x2 + y2 + z2, x2

+

y2

+

22 3xz= -y x2

+

z2 3xz - y= -y

Ainsi, 3xz- y > 0 et on a montré que {x, 3xz-y, z} est un triplet de Markoff. Montrons

maintenant que z < 3xz - y. On a x2 < xz < xz2 et 2z2 < 2xz2 car 1 ~ x < z . Ainsi,

x2

+

2z2 _{< 3xz}2 _{et on a :}

< O.

Donc, puisque 3xz-y et y sont les deux zéros de q(a), y < z < 3xz- y, ce qui prouve

(ii).

Pour finir, on a z est racine du polynôme :

L'autre racine est 3xy - z. On a 3xy- z E Z puisque x, y, z E lN* On a aussi : 3xyz = x2

+

y2

+

z2, x2

+

y2

+

22 3xy

=

,

z x2 + y2 3xy - z = ---=---z

Ainsi, 3xy- z > 0 et on a montré que {x, y, 3xy- z} est un triplet de Markoff. Montrons

Ainsi, x2

+

2y2 < 3xy2 et on a :

r(y) y2 - 3xy2

+

x2

+

y2

2y2

+

x2 - 3xy2

< O.

35

Donc, puisque 3xy- z et z sont les deux zéros de T(a), 3xy- z <y< z, ce qui prouve

(i).

•

Proposition 4.1.5. L'équation

a une solution entière positive ( a1, a2, a3) si et seulement si 3 divise a1 , a2, a3 et ( j , ~2 _{, ~)}

est un triplet de Markoff.

Démonstration. On va calculer modulo 3 : la congruence modulo 3 sera notée

=

·

Si ai est un multiple de 3, alors ai

=

0 et donc a;

=

O. Sinon, ai

=

1 ou ai

=

2, donc

a

;=

1. Supposons que tous les

a;

impossible. Si un a2

₌

_{0 et a}2 t - J impossible. 1 _' donc a2 ₁

+

a2 ₂

+

a2 ₃

Ainsi, pour tout i, a;

=

0, donc ai

=

O.

1, ce QUI est

36

Comme 3 divise a1,a2,a3, alors bi=~ E lN*. Ainsi, on a :

Donc ( a1 _{az !!:;!_) est un triplet de Markoff}

) 3 ) 3 ) 3 . 1 -(a2+a2+a2) 9 1 2 3 1

9

(al a2a3) 3(bl b2b3).

Supposons maintenant que 3 divise a1, a2 , a3 et que (ai, ~2, ~) est un triplet de Markoff.

Alors, on a:

===? a~

+

a~

+

a~

•

4.2 L'arbre de Markoff

On va construire l'arbre de Markoff en suivant la règle récursive suivante :

(x,z,y)

/

~

(x,3xz- y,z) (z, 3yz - x, y)

Figure 4.1 La règle pour construire l'arbre des triplets de Markoff

La racine de l'arbre est (1, 5, 2). Donc par la proposition 4.1.4, toutes les feuilles de l'arbre sont des triplets de Markoff, et la deuxième valeur de chaque triplet est le maximum. On

appelle (x,3xz -y,z) (respectivement (z,3yz- x, y)) le voisin gauche (respectivement

-37

droit) de (x, z, y).

Voici une illustration de l'arbre de Markoff :

(1,5,2)

~

---(1,13,5) (5,29,2)

/

~

/

~ (1, 34, 13) (13, 194, 5) (5, 433, 29) (29, 169, 2)

/

"

/

""'

/

""'

/

"

(1, 89, 34) (34, 1325, 13) (29, 14701, 169) (169, 985, 2)

1

\

1 \

Figure 4.2 L'arbre des triplets de Markoff

Théorème 4.2.1. Tous les triplets de Markoff propres apparaissent dans l'arbre de

Markoff sous la forme de triplets ordonnés qui les représentent.

Démonstration. Soit (x, z, y) un triplet de Markoff tel que x < y < z. On va raisonner

par récurrence sur z, le maximum du triplet.

Par la proposition 4.1.4, (x, y, 3xy - z) est un triplet de Markoff et 3xy - z < y. Si

x< 3xy - z, alors (x,z,y) est le voisin gauche de (x,y,3xy - z). En effet, (x,3xy

-(3xy- z), y) = (x, z, y). Si 3xy- z <x, alors (y, z, x) est le voisin droit de (3xy-z, y, x).

En effet, (y, 3yx- (3xy - z), x) = (y, z, x). Par récurrence, (x, y, 3xy - z) apparait dans

CHAPITRE V

L'ARBRE DES PAIRES DE CHRISTOFFEL

Dans la première section de ce chapitre, on construira l'arbre des paires de Christoffel et on prouvera que chaque paire de Christoffel est une base de F(a, b). Ensuite, on va démontrer que l'arbre des triplets de Markoff est une spécialisation de l'arbre de Christoffel. Ce n'est que dans la deuxième section qu'on justifiera la terminologie paires de Christoffel. On donnera également quelques propriétés des mots de Christoffel.

5.1 L'arbre des paires de Christoffel

La terminologie arbre des paires de Christoffel sera justifiée en 5.2. On construit l'arbre selon la règle récursive suivante (Berstel, 1990)

(u

,

uv)

(u

,

v)

/

~

(uv

,

v)

Figure 5.1 La règle de construction de l'arbre des paires de Christoffel

40

Voici un aperçu de l'arbre des paires de Christoffel (a, b)

~~

(a, ab) (ab, b)

/

~

/

~

(a, a2_{b) (a}2

b, ab) (ab, ab2) (ab2, b)

/ ~ / ~ / ~ / ~

(a, a3b) (a3b, a2b) (a2b, a2bab) (a2bab, a2b) (ab, abab2) (abab2, ab2) (ab2, ab3) (ab3, b)

1 \ 1 \

Figure 5.2 L'arbre des paires de Christoffel

Proposition 5.1.1. Toute paire de Christoffel ( u, v) dans l'arbre est une base de F(a, b).

Démonstration. On va le montrer par récurrence sur la longueur de la paire. Tout

d'abord, si l(u, v)l = 2, alors (u, v) = (a, b), qui est une base de F(a, b). Si l(u, v)l ~ 3, alors par la construction de l'arbre, (u,v) = (u,uv') ou (u,v) = (u'v,v) tels que (u',v) ou ( u, v') sont des paires de Christoffel de longueur plus petite. Alors, par récurrence,

elles forment une base de F(a, b). Il est connu que si (u', v) génère F(a, b), (u'v, v) aussi.

Il reste à montrer qu'il le génère librement. Posons z := u'v.

Soit w E {z,v,z-I,v-1_{}* un mot réduit et non-vide. On ne sait pas à priori si west}

réduit sur {u',v,u'-l,v-1_{}*. Alors, il suffit de montrer que si w}

=

_{1 comme mot sur} u', v, alors w = 1.

On va écarter le cas évident où w ne contient pas de z ou de z-1.

Supposons que w contient zou z-1_{. Puisque w}

=

_{1, on doit avoir un u' (contenu dans}

z) qui s'annule avec un u'-1 (contenu dans z-1). Soit w' de longueur minimale. Alors,

sans perte de généralité :

( - 1 /- 1) 1 ( 1 )

41

où w' ne contient que des v, v-1. Donc,

- 1

W= .. ·Z z ... ,

ce qui est impossible puisque w est réduit sur {z, v, z-1, v-1 }. Ainsi, w

=

1. Donc, si

(u',v) est une base de F(a,b), alors (u'v,v) aussi. L'autre cas est symétrique. Donc, on

a prouvé par récurrence que toute paire de Christoffel est une base de F( a, b). •

Soit J..L: {a, b}*---+ SL2(lN) l'homomorphisme de monoïdes tel que

Théorème 5.1.2. (Cohn, 1955; Cohn, 1972; Reutenauer, 2009; voir aussi Bombieri, 2007) L'arbre des triplets de Markoff est une spécialisation de l'arbre des paires de Chris-toffel par la fonction :

Remarque 5.1.3. Ce qu'on entend par spécialisation, c'est qu'on obtient l'arbre des

triplets de Markoff en remplaçant chaque paire ( u, v) dans l'arbre de Christoffel par

ifJ(u, v).

Démonstration. On va faire une preuve par récurrence sur la longueur de la paire de

christoffel. Rappelons d'abord la construction de l'arbre des paires de Christoffel et de

l'arbre des nombres de Markoff. (u, v)

/

~ (u,uv) (uv,v) (x,z,y)

/

~ (x,3xz- y,z) (z,3yz- x,y) Les racines sont respectivement (a, b) et (1, 5, 2).

42

Pour commencer, on a :

Par hypothèse de récurrence, on a ( ~ Tr p,( u), ~ Tr p,(uv), ~ Tr p.(v)) = (.x, z, y), un triplet de Markoff. Ainsi :

3xz- y 3

*

1 1 1

3

Tr p,(u);(II· p,(uv) -

3

Tr p,(v)

1

3

(Tr p,(u) TI:(p,(u)p,(v)) - Tr p,(v)) 1

3

Tr ((p,(u)) 2_{p,(v)) (par la proposition 1.2.1(i))} 1

3

Tr p,(uuv).

Par conséquent,(~ Tr p,(u), ~ Tr p,(uuv), ~ Tr p,(uv)) = (x, 3xz-y, z), qui est voisin gauche de (x, y, z). De plus: 3yz- x 3

*

1 1 1

3

Tr p,(v)

3

Tr p,(uv) -

3

Tr p,(u) 1

3

(Tr p,(v) TI·(p,(u)p,(v))-Tr {L(u)) 1

3

TI· (p,(u)(p,(v)f) (par la proposition 1.2.1(ii)) 1

=

3

TI· p,(uvv).

Ainsi, (~TI· p,( uv), ~ TI· p,( uvv), ~TI· p,(v)) = (z, 3yz-x, y), qui est voisin droit de (x, y, z) .

43 5.2 Les mots de Christoffel

Cette section ainsi que la suivante ne sont pas nécessaires à la preuve du théorème de

Perrine. On définira les mots de Christoffel à la manière géométrique de Berstel (Berstel,

1990, p.300-301).

Définition 5.2.1. Soit (i,j) un point entier sur le plan. On appelle les segments

[(i,j), (i

+

1,j)] et [(i,j), (i,j

+

1)] des pas élémentaires. Si la fin d'un segment coï

n-cide avec le début d'un autre, alors on dit qu'ils sont consécutifs. On appelle un chemin

discret une suite de pas élémentaires consécutifs.

Considérons le monoïde libre {a, b} * où a < b. On va coder un chemin discret en associant aux pas élémentaires [(i,j), (i+ 1,j)] et [(i,j), (i,j + 1)] 1es lettres a et b, respectivement.

On obtient donc un mot sur {a, b} *.

Soit p, q E 7l, tels que p et q soient premiers entre eux. On appelle discrétisation par

en-dessous du sement [(0, 0), (p, q)] l'unique chemin discret qui va de (0, 0) à (p, q) tel

que le chemin reste sous la diagonale [(0, 0), (p, q)] et tel que la région comprise entre le

chemin et la diagonale ne contienne aucun point entier.On le notera chqfp· Le mot qui

code ce chemin est appelé mot de Christoffel inférieuT de pente ~. Un mot de Chistoffel

injéTieur est propTe s'il est différent de ab.

On définit de manière analogue les mots de Christoffel supérieurs en considérant le

chemin discret au-dessus de la diagonale.

Exemple 5.2.2. Soit A

=

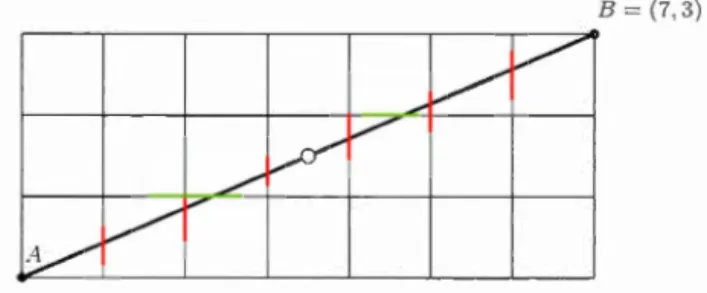
(0, 0) et B = (7, 3). Voici le chemin qui discrétise par en-dessous [A, B].

Donc, w ~

=

aaabaabaab est le mot de Christoffel inférieuT de pente ~. On peut remarquer 1

que

J

w

la

=

7 et

lwlb

=

3.

Définition 5.2.3. Soit p, q E 1N* tels que pet q sont premiers entre eux. L'intersection du segment ](0, 0), (p, q)[ avec les droites x= r, y= t, r, t E 1N*, constitue une suite de